Machine-Learning-Based Electric Power Forecasting
Abstract
1. Introduction
2. Literature Review
2.1. Power Forecasting Methods
2.2. Factors Influencing the Demand for Power
3. Research Framework and Forecasting Methods
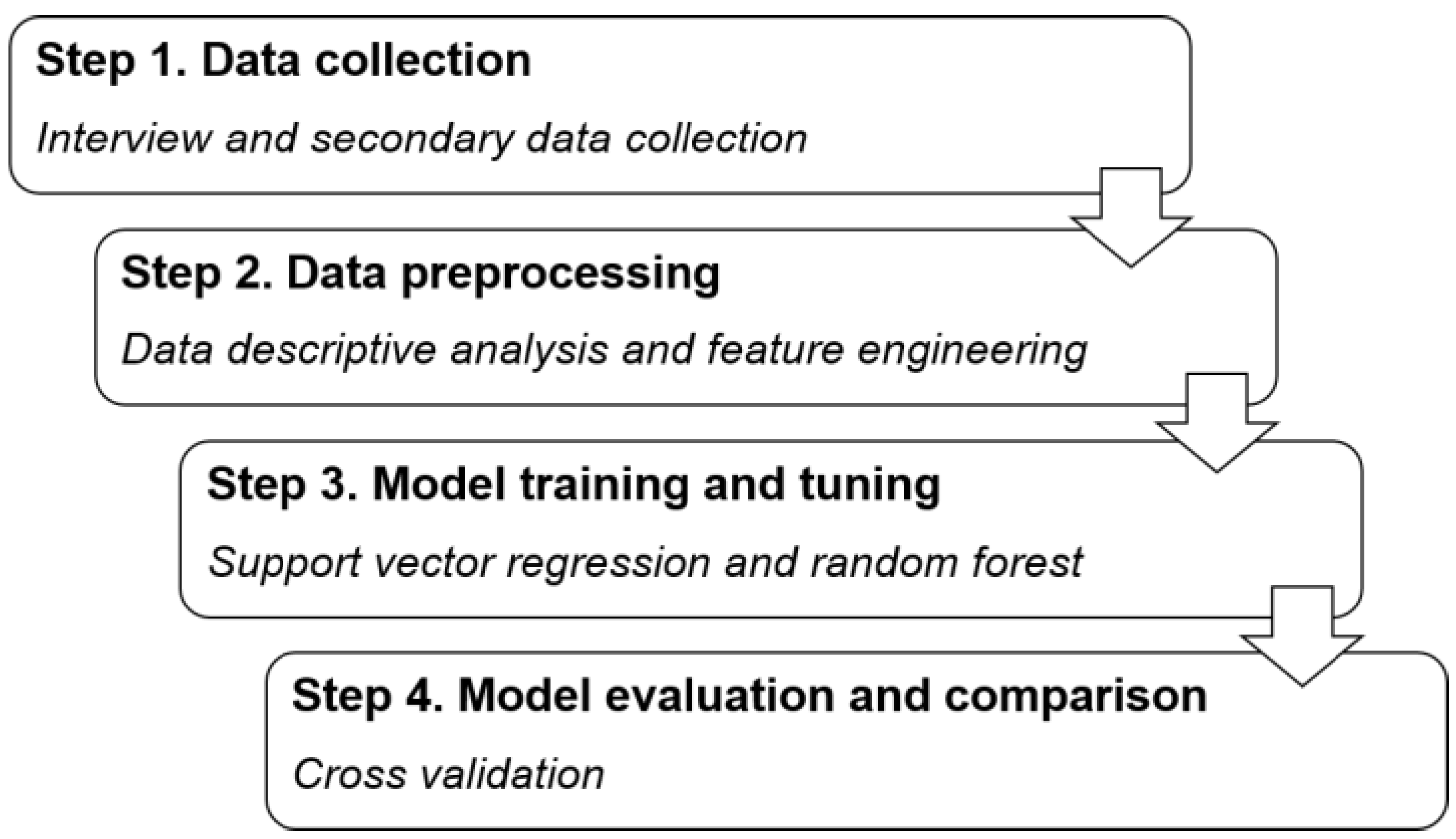
3.1. The Research Framework
3.2. The Support Vector Regression Model
3.3. The Random Forest Model
3.4. The Remarks
4. Case Analysis
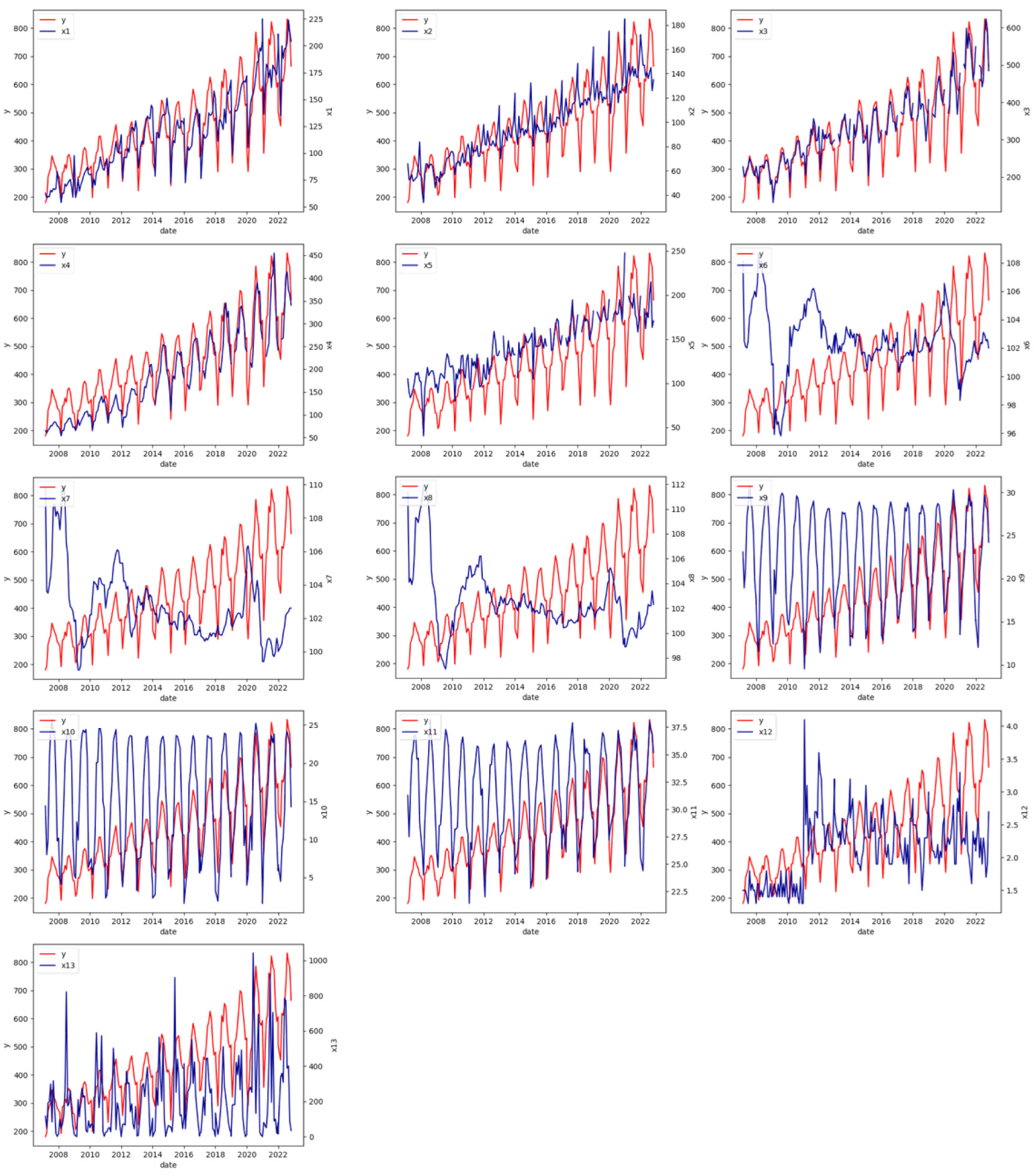
4.1. Dataset
4.2. Parameter Setting
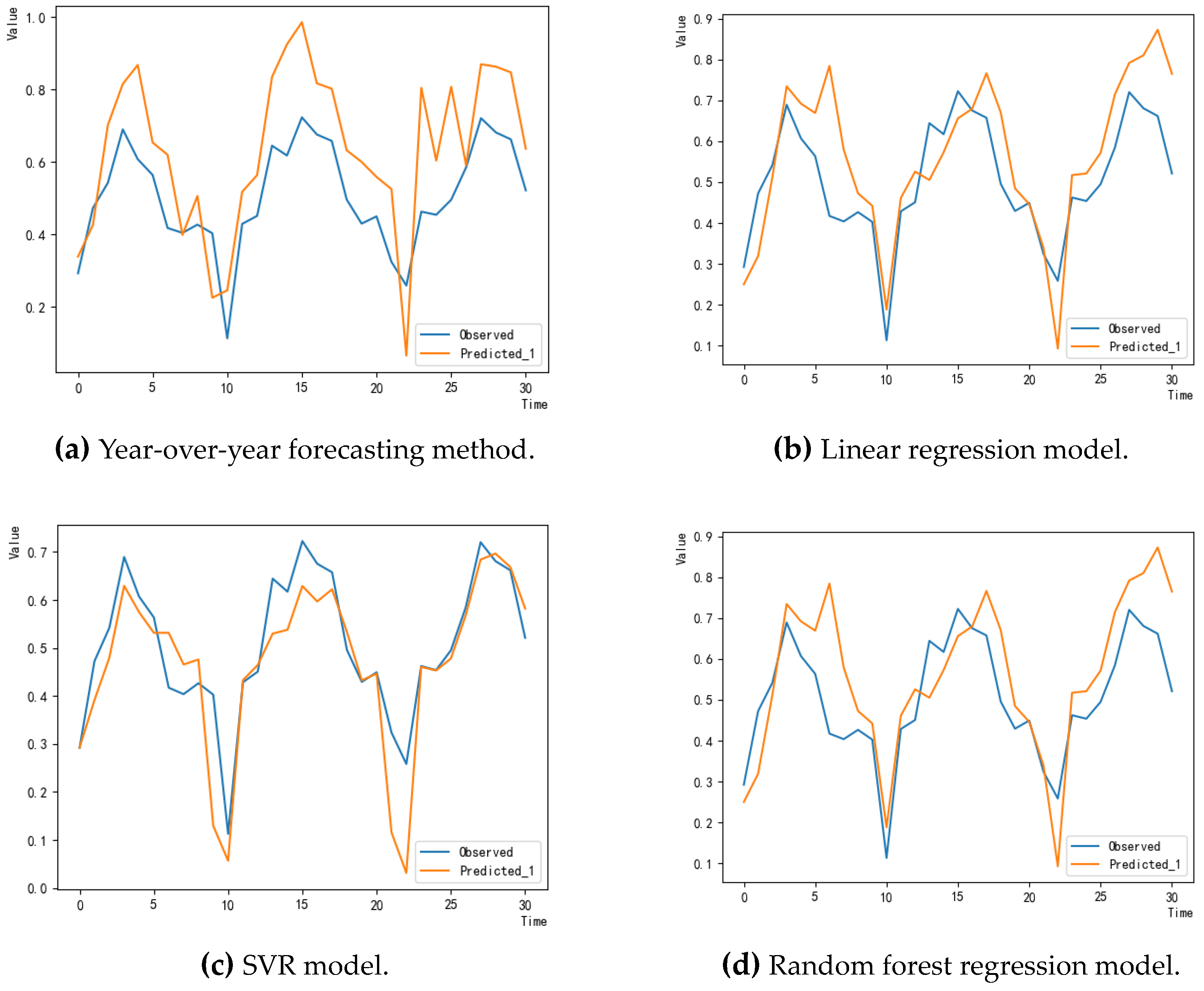
4.3. The Assessment of Forecasting Methods
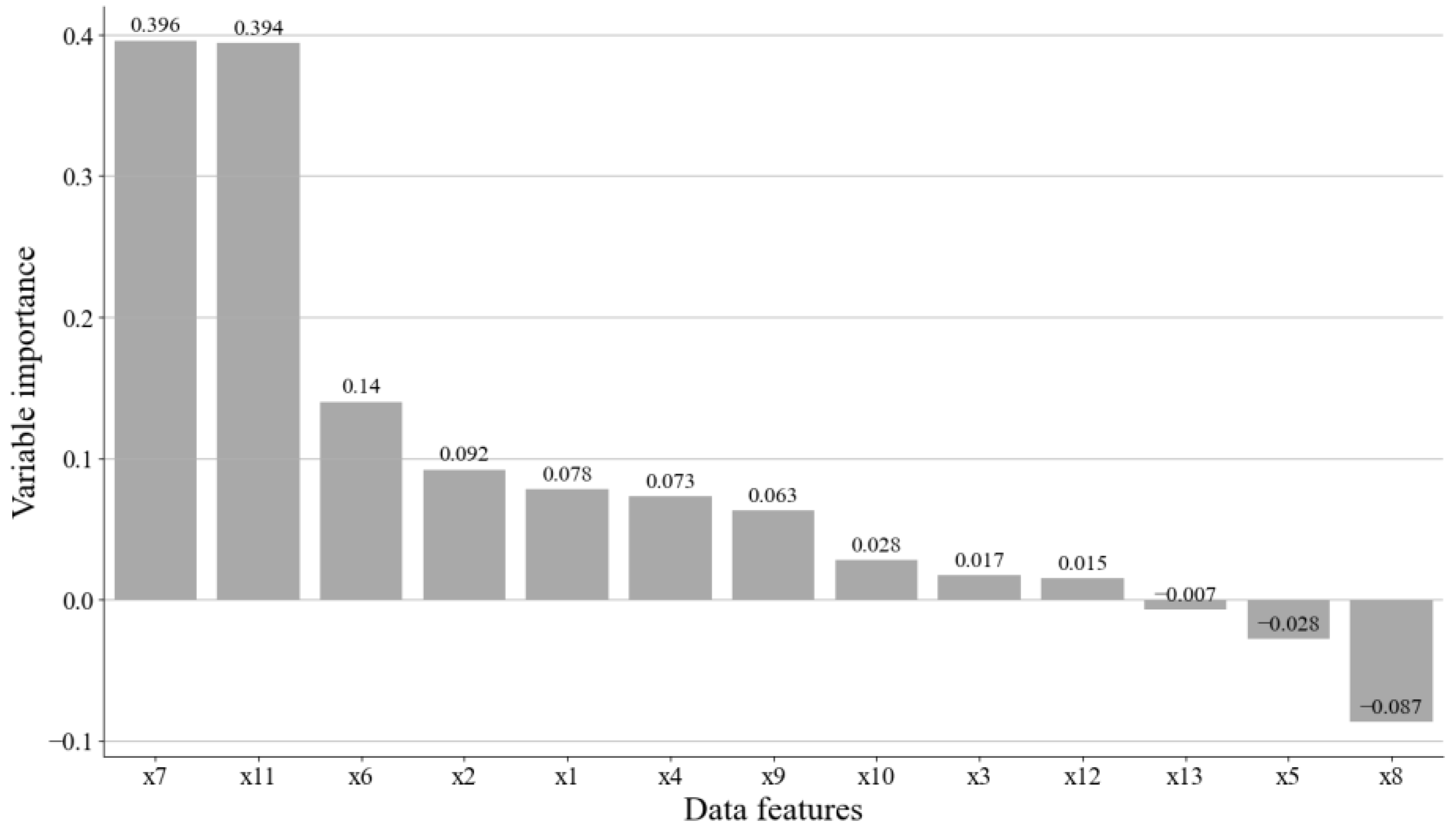
4.4. Forecasting Findings
4.5. Carbon Emissions and A Longer Horizon Forecast
5. Implications and Recommendations
5.1. Major Findings and Managerial Implications
5.2. Practical Recommendations
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dougherty, S.M. Investigation of Network Performance Prediction Literature Review (Technical Note 394); Institute for Transport Studies, University of Leeds: Leeds, UK, 1996. [Google Scholar]
- Bunn, D.; Farmer, E.D. Comparative Models for Electrical Load Forecasting; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Chen, J.F.; Wang, W.M.; Huang, C.M. Analysis of an adaptive time-series autoregressive moving-average (ARMA) model for short-term load forecasting. Electr. Power Syst. Res. 1995, 34, 187–196. [Google Scholar] [CrossRef]
- Hsu, C.C.; Chen, C.Y. Regional load forecasting in Taiwan—Applications of artificial neural networks. Energy Convers. Manag. 2003, 44, 1941–1949. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Granger, C.W.J. Combining forecasts-twenty years later. J. Forecast. 1989, 3, 167–173. [Google Scholar] [CrossRef]
- Uri, N.D. A note on energy demand estimation. Int. J. Energy Res. 1993, 3, 747–758. [Google Scholar] [CrossRef]
- Edwards, D.J.; Holt, G.D.; Harris, F.C. A comparative analysis between the multilayer perceptron “neural network” and multiple regression analysis for predicting construction plant maintenance costs. J. Qual. Maint. Eng. 2000, 6, 45–61. [Google Scholar] [CrossRef]
- Mohamed, Z.; Bodger, P. Forecasting electricity consumption in New Zealand using economic and demographic variables. Energy 2005, 30, 1833–1843. [Google Scholar] [CrossRef]
- Lord, D. Modeling motor vehicle crashes using Poisson-gamma models: Examining the effects of low sample mean values and small sample size on the estimation of the fixed dispersion parameter. Accid. Anal. Prev. 2006, 38, 751–766. [Google Scholar] [CrossRef]
- Aishwarya, S.; Balasubramanian, M. A comparative study on regression model and artificial neural network for the prediction of wall temperature in a building. J. Eng. Res. 2022, 10, 1–13. [Google Scholar]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity load forecasting: A systematic review. J. Electr. Syst. Inf. Technol. 2020, 7, 13. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, J.; Yang, L.; Li, X.; Pang, M. Decomposition-Based Dynamic Adaptive Combination Forecasting for Monthly Electricity Demand. Sustainability 2019, 11, 1272. [Google Scholar] [CrossRef]
- Ul Islam, B.; Ahmed, S.F. Short-Term Electrical Load Demand Forecasting Based on LSTM and RNN Deep Neural Networks. Math. Probl. Eng. 2022, 2022, 2316474. [Google Scholar] [CrossRef]
- Dimd, B.D.; Voller, S.; Cali, U.; Midtgard, O. A Review of Machine Learning-Based Photovoltaic Output Power Forecasting: Nordic Context. IEEE Access 2022, 10, 26404–26425. [Google Scholar] [CrossRef]
- Waheed, W.; Xu, Q. Optimal Short Term Power Load Forecasting Algorithm by Using Improved Artificial Intelligence Technique. In Proceedings of the 2020 2nd International Conference on Computer and Information Sciences (ICCIS) 2020, Sakaka, Saudi Arabia, 13–15 October 2020; pp. 1–4. [Google Scholar]
- Shi, J.; Li, C.; Yan, X. Artificial intelligence for load forecasting: A stacking learning approach based on ensemble diversity regularization. Energy 2023, 262, 125295. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adarnowski, J.F.; Li, Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inform. 2018, 35, 1–16. [Google Scholar] [CrossRef]
- AL-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Z.; Hong, W. A Hybrid Seasonal Mechanism with a Chaotic Cuckoo Search Algorithm with a Support Vector Regression Model for Electric Load Forecasting. Energies 2018, 11, 1009. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.; Li, J. Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model with Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Forecasting Short-term Electricity Demand in Residential Sector Based on Support Vector Regression and Fuzzy-rough Feature Selection with Particle Swarm Optimization. Procedia Eng. 2015, 118, 1162–1168. [Google Scholar]
- Lusis, P.; Khalilpour, K.R.; Andrew, L.; Liebman, A. Short-term residential load forecasting: Impact of calendar effects and forecast granularity. Appl. Energy 2017, 205, 654–669. [Google Scholar] [CrossRef]
- Tian, S.; Zhou, Q.; Cheng, H.; Liu, L.; Lu, L.; Jiang, L. Application of pigeon-inspired optimization algorithm based SVM in total power demand forecasting. Electr. Power Autom. Equip. 2020, 40, 173–179. [Google Scholar]
- Kenneth, B. Economic Development and End-Use Energy Demand. Energy J. 2001, 22, 2–5. [Google Scholar]
- Cheung, Y.K.; Thomson, E. Electricity Consumption and Economic Growth in China: A Cointegration Analysis. Pac. Asian J. Energy 2001, 2, 99–102. [Google Scholar]
- Costantini, V.; Martini, C. The causality between energy consumption and economic growth: A multi-sectoral analysis using non-stationary cointegrated panel data. Energy Econ. 2010, 32, 591–603. [Google Scholar] [CrossRef]
- Jovanovic, S.; Savic, S.; Bojic, M.; Djordjevic, Z.; Nikolic, D. The impact of the mean daily air temperature change on electricity consumption. Energy 2015, 88, 604–609. [Google Scholar] [CrossRef]
- Sheng, P.; He, Y.; Guo, X. The impact of urbanization on energy consumption and efficiency. Energy Environ. 2017, 28, 673–686. [Google Scholar] [CrossRef]
- Mir, A.A.; Alghassab, M.; Ullah, K.; Khan, Z.A.; Lu, Y.; Imran, M. A Review of Electricity Demand Forecasting in Low and Middle Income Countries: The Demand Determinants and Horizons. Sustainability 2020, 12, 5931. [Google Scholar] [CrossRef]
- Nkengfack, H.; Fotio, H.K. Energy Consumption, Economic Growth and Carbon Emissions: Evidence from the Top Three Emitters in Africa. Mod. Econ. 2019, 10, 52–71. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Alhmoud, L.; Zarour, E. Impact of the COVID-19 Pandemic on Electricity Demand and Load Forecasting. Sustainability 2021, 13, 1435. [Google Scholar] [CrossRef]
- Doveh, E.; Feigin, P.; Greig, D.; Hyams, L. Experience with FNN models for medium term power demand predictions. IEEE Trans. Power Syst 1999, 14, 538–546. [Google Scholar] [CrossRef]
- Kandil, M.S.; El-Debeiky, S.M.; Hasanien, N.E. Long-term load forecasting for fast developing utility using a knowledge-based expert system. IEEE Trans. Power Syst. 2002, 17, 491–496. [Google Scholar] [CrossRef]
- Daneshi, H.; Shahidehpour, M.; Choobbari, A.L. Long-term load forecasting in electricity market. In Proceedings of the 2008 IEEE International Conference on Electro/Information Technology, Ames, IA, USA, 18–20 May 2008; pp. 395–400. [Google Scholar]
- Zhang, Z.; Ye, S. Long term load forecasting and recommendations for china based on support vector regression. In Proceedings of the 2011 Fourth International Conference on Information Management, Innovation Management and Industrial Engineering (ICIII 2011), Shenzhen, China, 26–27 November 2011; pp. 597–602. [Google Scholar]
- Guan, C.; Luh, P.B.; Michel, L.D.; Wang, Y.; Friedland, P.B. Very Short-Term Load Forecasting: Wavelet Neural Networks with Data Pre-Filtering. IEEE Trans. Power Syst. 2013, 28, 30–41. [Google Scholar] [CrossRef]
- Mei, F.; Pan, Y.; Zhu, K.; Zheng, J. A Hybrid Online Forecasting Model for Ultrashort-Term Photovoltaic Power Generation. Sustainability 2018, 10, 820. [Google Scholar] [CrossRef]
- Bae, K.Y.; Jang, H.S.; Jung, B.C.; Sung, D.K. Effect of Prediction Error of Machine Learning Schemes on Photovoltaic Power Trading Based on Energy Storage Systems. Energies 2019, 12, 1249. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Leva, S.; Pavan, A.M.; Mellit, A.; Lughi, V.; Dolara, A. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies 2019, 12, 1621. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short-term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- VanDeventer, W.; Jamei, E.; Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Soon, T.K.; Horan, B.; Mekhilef, S.; Stojcevski, A. Short-term PV power forecasting using hybrid GASVM technique. Renew. Energy 2019, 140, 367–379. [Google Scholar] [CrossRef]
- Maitanova, N.; Telle, J.; Hanke, B.; Grottke, M.; Schmidt, T.; von Maydell, K.; Agert, C. A Machine Learning Approach to Low-Cost Photovoltaic Power Prediction Based on Publicly Available Weather Reports. Energies 2020, 13, 735. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A day-ahead PV power forecasting method based on LSTM-RNN model and time correlation modification under partial daily pattern prediction framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Eom, H.; Son, Y.; Choi, S. Feature-selective ensemble learning-based long-term regional PV generation forecasting. IEEE Access 2020, 8, 54620–54630. [Google Scholar] [CrossRef]
- Rana, M.; Rahman, A. Multiple steps ahead solar photovoltaic power forecasting based on univariate machine learning models and data re-sampling. Sustain. Energy Grids 2020, 21, 100286. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wei, Z.; Sun, G. Day-ahead photovoltaic power forecasting approach based on deep convolutional neural networks and meta learning. Int. J. Electr. Power 2020, 118, 105790. [Google Scholar] [CrossRef]
- Bendaoud, N.M.M.; Farah, N.; Ben Ahmed, S. Applying load profiles propagation to machine learning based electrical energy forecasting. Electr. Power Syst. Res. 2022, 203, 107635. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Pearson, K. Breakthroughs in Statistics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Baese, F.; Krause, P.; Bongartz, K.; Fluegel, W.A. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Awad, M.; Khanna, R. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python, Scikit-Learn, and TensorFlow; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Craven, M.W.; Shavlik, J.W. Extracting Thee-Structured Representations of Thained Networks. Adv. Neural Inf. Process. Syst. 1996, 8, 24–30. [Google Scholar]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Kang, J.; Reiner, D.M. What is the effect of weather on household electricity consumptions? Empirical evidence from Ireland. Energy Econ. 2022, 111, 106023. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Ghadimi, N. Electricity load forecasting by an improved forecast engine for building level consumers. Energy 2017, 135, 18–30. [Google Scholar] [CrossRef]

| Literature | Methods | Influencing Factors | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Power System | Economy | Weather | Society | ||||||||
| Total Load | Peak Load | GDP | Growth Rate | Industrial Structure | Others | Temperature | Others | Population | Others | ||
| Granger [6] | wavelet transform | √ | √ | ||||||||
| Uri [7] | terminal energy analysis | √ | √ | ||||||||
| Doveh et al. [33] | wavelet transform | √ | √ | √ | |||||||
| Cheung and Thomson [26] | statistical analysis | √ | √ | ||||||||
| Kenneth [25] | statistical analysis | √ | √ | √ | |||||||
| Kandil et al. [34] | expert system | √ | √ | √ | √ | ||||||
| Mohamed and Bodger [9] | statistical analysis | √ | √ | ||||||||
| Daneshi et al. [35] | statistical analysis | √ | √ | √ | √ | √ | |||||
| Costantini and Martini [27] | statistical analysis | √ | |||||||||
| Zhang and Ye [36] | artificial neural network | √ | |||||||||
| Guan et al. [37] | wavelet neural network | √ | √ | ||||||||
| Jovanovic [28] | statistical analysis | √ | √ | √ | √ | ||||||
| Mei et al. [38] | support vector machine and autoregressive integrated moving average | √ | √ | ||||||||
| Hu et al. [13] | ensemble learning | √ | √ | ||||||||
| Bae et al. [39] | artificial neural network and support vector machine | √ | √ | ||||||||
| Nespoli et al. [40] | artificial neural network | √ | √ | ||||||||
| Zhou et al. [41] | ensemble learning | √ | √ | ||||||||
| William et al. [42] | support vector machine and genetic algorithm | √ | √ | ||||||||
| Maitanova et al. [43] | long short-term memory | √ | √ | ||||||||
| Wang et al. [44] | long short-term memory and recurrent neural network | √ | √ | ||||||||
| Eom et al. [45] | ensemble learning | √ | √ | √ | |||||||
| Rana and Rahman [46] | univariate machine-learning models | √ | √ | ||||||||
| Zang et al. [47] | convolutional neural networks | √ | √ | ||||||||
| Waheed et al. [16] | support vector regression | √ | √ | √ | √ | √ | |||||
| Alasali et al. [32] | statistical analysis | √ | √ | √ | |||||||
| Ahmed et al. [14] | artificial neural network | √ | √ | √ | |||||||
| Bendaoud et al. [48] | load profiles and random forest | √ | √ | √ | √ | ||||||
| Shi et al. [17] | ensemble learning | √ | √ | √ | √ | ||||||
| This manuscript | support vector regression and random forest | √ | √ | √ | √ | √ | √ | √ | √ | ||
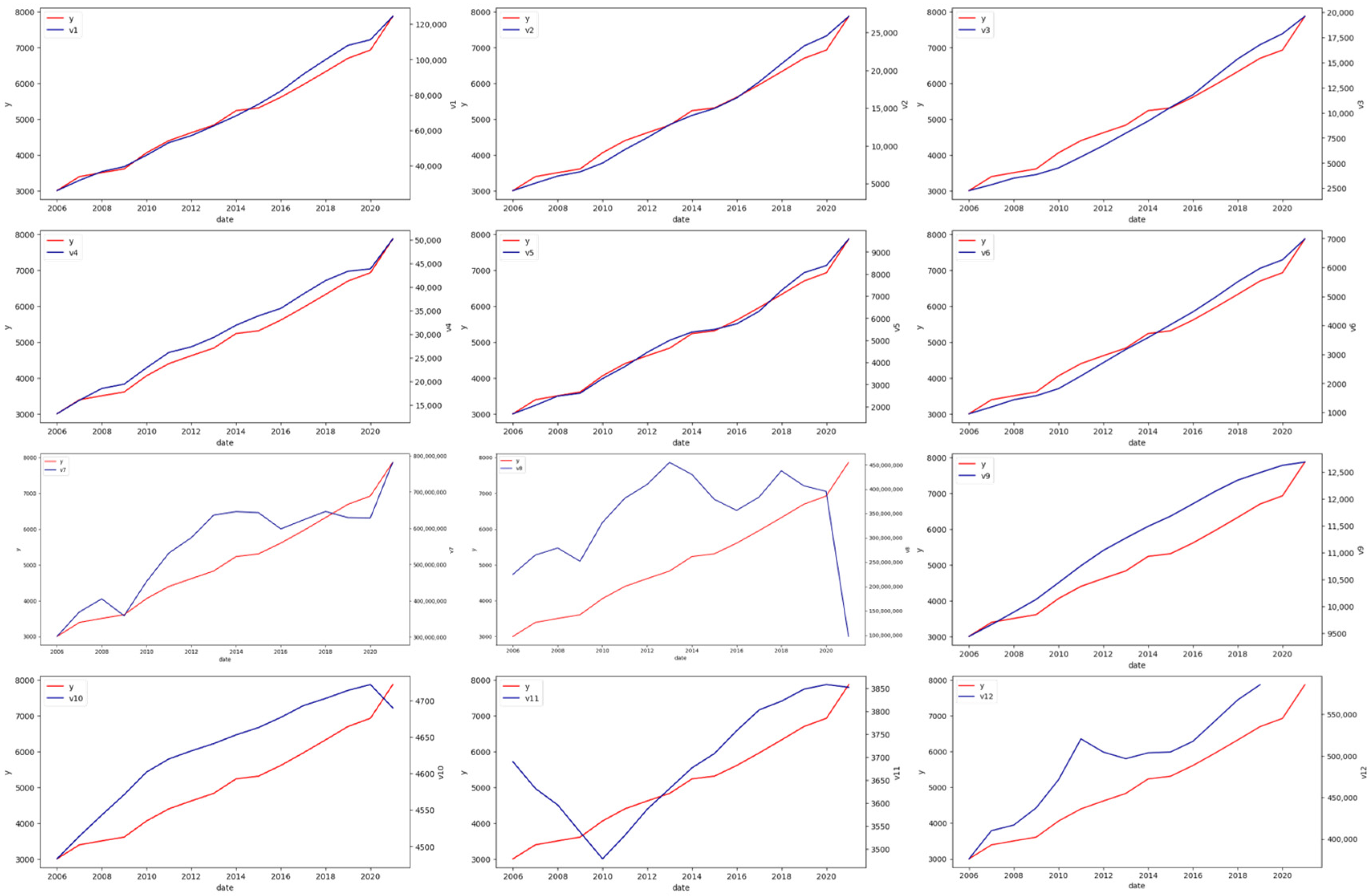
| Factors | Indicators | Explanations |
|---|---|---|
| Monthly power consumption amount in a region. | |
| ||
| Monthly power generation amount in a region. | |
| ||
| ||
| Monthly CPI in a region. | |
| ||
| ||
| Monthly measures of regional weather variations. | |
| ||
| ||
| ||
|
| Parameter | Explanation | The Set Value |
|---|---|---|
| kernel | The kernel function in SVR | “linear” |
| tol | The training threshold of the error term | 0.001 |
| C | The penalty factor for the error term | 1.0 |
| epsilon | for balancing model accuracy and complexity | 0.1 |
| max_iter | Maximum number of iterations; −1 means no limit | −1 |
| Parameter | Explanation | The Set Value |
|---|---|---|
| n_estimators | Number of decision trees in the forest | 43 |
| max_features | Number of features in a randomly selected tree model | 13 |
| max_depth | Maximum depth of the tree | None |
| min_samples_split | Minimum number of samples for node segmentation | 1.0 |
| bootstrap | Bootstrap mode | True |
| Model | MSE | MAE | ||
|---|---|---|---|---|
| Year-over-year forecasting | 0.031 | 0.155 | −0.490 | 0.843 |
| Linear regression | 0.016 | 0.098 | 0.244 | 0.909 |
| SVR | 0.008 | 0.061 | 0.608 | 0.944 |
| Random forest regression | 0.009 | 0.068 | 0.567 | 0.924 |
| Factors | Indicators | Explanations |
|---|---|---|
| Economic development D |
| Yearly indicators of regional economic development. Compared with the primary sector and the tertiary sector, the secondary sector contributes the most to the economy of Guangdong Province. |
| ||
| ||
| ||
| ||
| ||
| International trade T |
| Guangdong Province is China’s largest foreign trade province. |
| ||
| Social structure S |
| Yearly indicators of the regional population. |
| ||
| ||
| Green economy G |
| The amount of greenhouse gas emissions each year. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Hu, Q.; Wang, J.; Wang, X.; Zhu, Y. Machine-Learning-Based Electric Power Forecasting. Sustainability 2023, 15, 11299. https://doi.org/10.3390/su151411299
Chen G, Hu Q, Wang J, Wang X, Zhu Y. Machine-Learning-Based Electric Power Forecasting. Sustainability. 2023; 15(14):11299. https://doi.org/10.3390/su151411299
Chicago/Turabian StyleChen, Gang, Qingchang Hu, Jin Wang, Xu Wang, and Yuyu Zhu. 2023. "Machine-Learning-Based Electric Power Forecasting" Sustainability 15, no. 14: 11299. https://doi.org/10.3390/su151411299
APA StyleChen, G., Hu, Q., Wang, J., Wang, X., & Zhu, Y. (2023). Machine-Learning-Based Electric Power Forecasting. Sustainability, 15(14), 11299. https://doi.org/10.3390/su151411299







