A Hybrid-Strategy-Improved Dragonfly Algorithm for the Parameter Identification of an SDM
Abstract
:1. Introduction
- (i)
- A new improved algorithm (HIDA) is proposed. Tent chaotic mapping is used to generate the initial positions of dragonfly individuals traversing the search space to improve the algorithm’s search capability. Nonlinear inertial weight is used to enable the algorithm’s global search and local exploitation to be balanced. The influence of neighboring individuals is considered to improve the efficiency of communication between populations. The bubble-net strategy of the whale optimization algorithm is fused to improve the local exploitation capability of the DA. Finally, to enhance the algorithm’s ability to avoid local extremes, Cauchy perturbation is applied to the optimal positions.
- (ii)
- Experiments are conducted using benchmark functions as well as CEC functions. The results of the rank sum test, a comparison with the chosen comparison algorithms, and a comparison with the two improved dragonfly algorithms prove that HIDA performs well in finding the best solution and is a competitive algorithm.
- (iii)
- The results for the SDM with five unknown parameters, the engineering model with four parameters, the DDM with seven parameters, the TDM with nine parameters, and the STM-40/36 model with five parameters demonstrate the high accuracy of HIDA at different temperatures and irradiances. Seven classical engineering applications further demonstrate the good performance of HIDA.
2. Related Work
2.1. Mathematical Diode Modeling of PV Cell and Objective Function
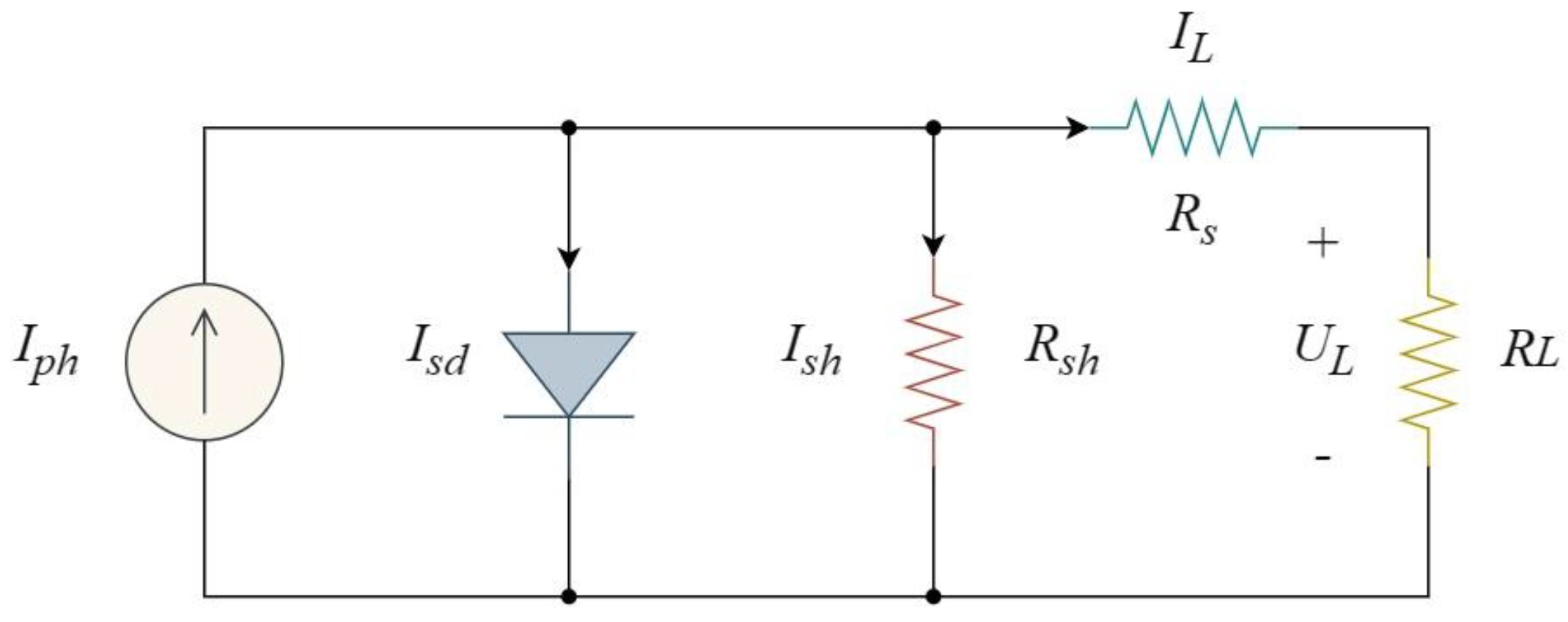
2.1.1. Modeling of Solar Photovoltaic System
2.1.2. Objective Function
2.2. Dragonfly Algorithm
3. Improved Dragonfly Algorithm
3.1. Tent Mapping Initialization
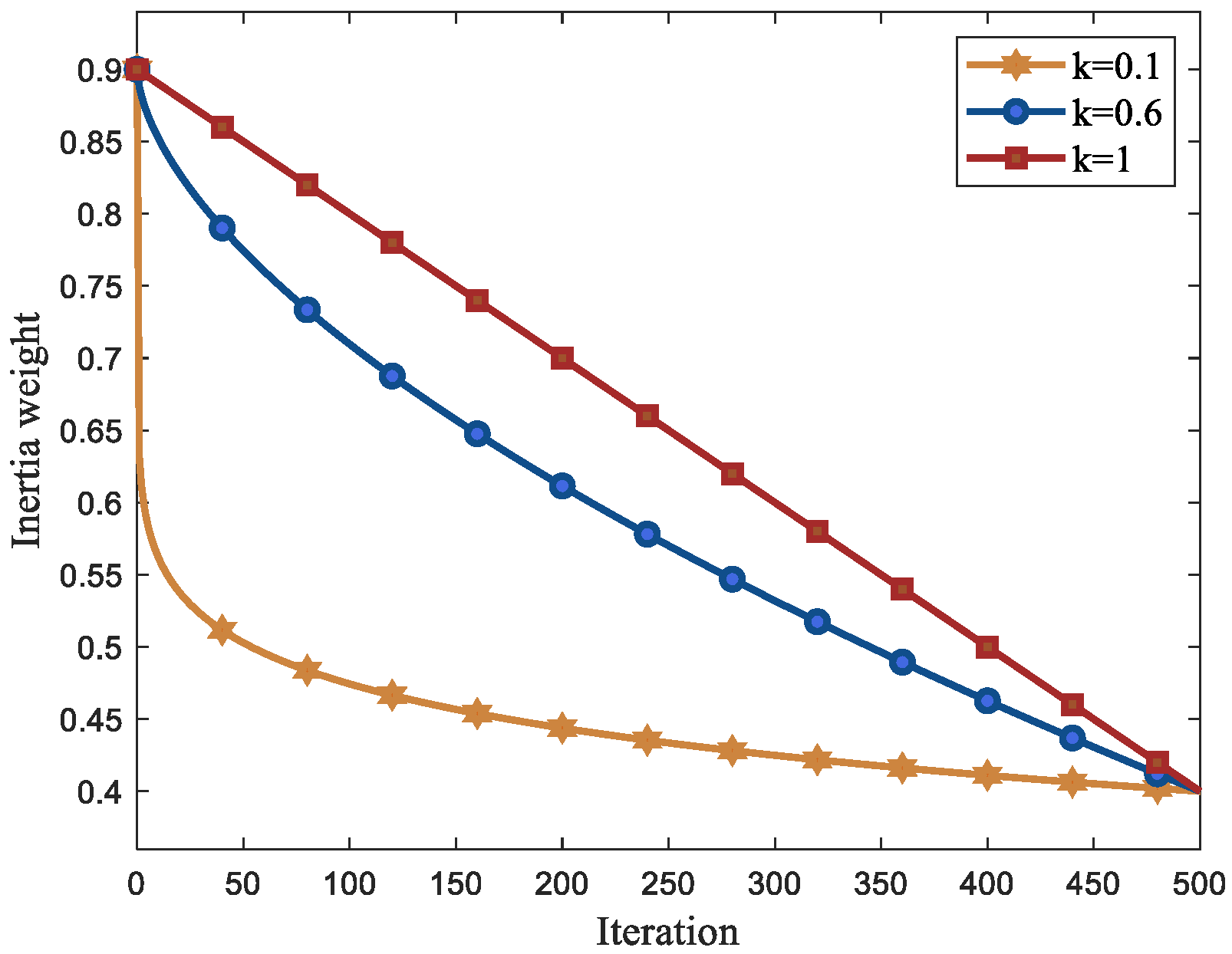
3.2. Nonlinear Inertial Weight
3.3. Hybrid Strategy
3.3.1. Adjacent Position Decision Strategy
3.3.2. Whale Optimization Algorithm Fusion Strategy
3.3.3. Optimal Position Perturbation Strategy
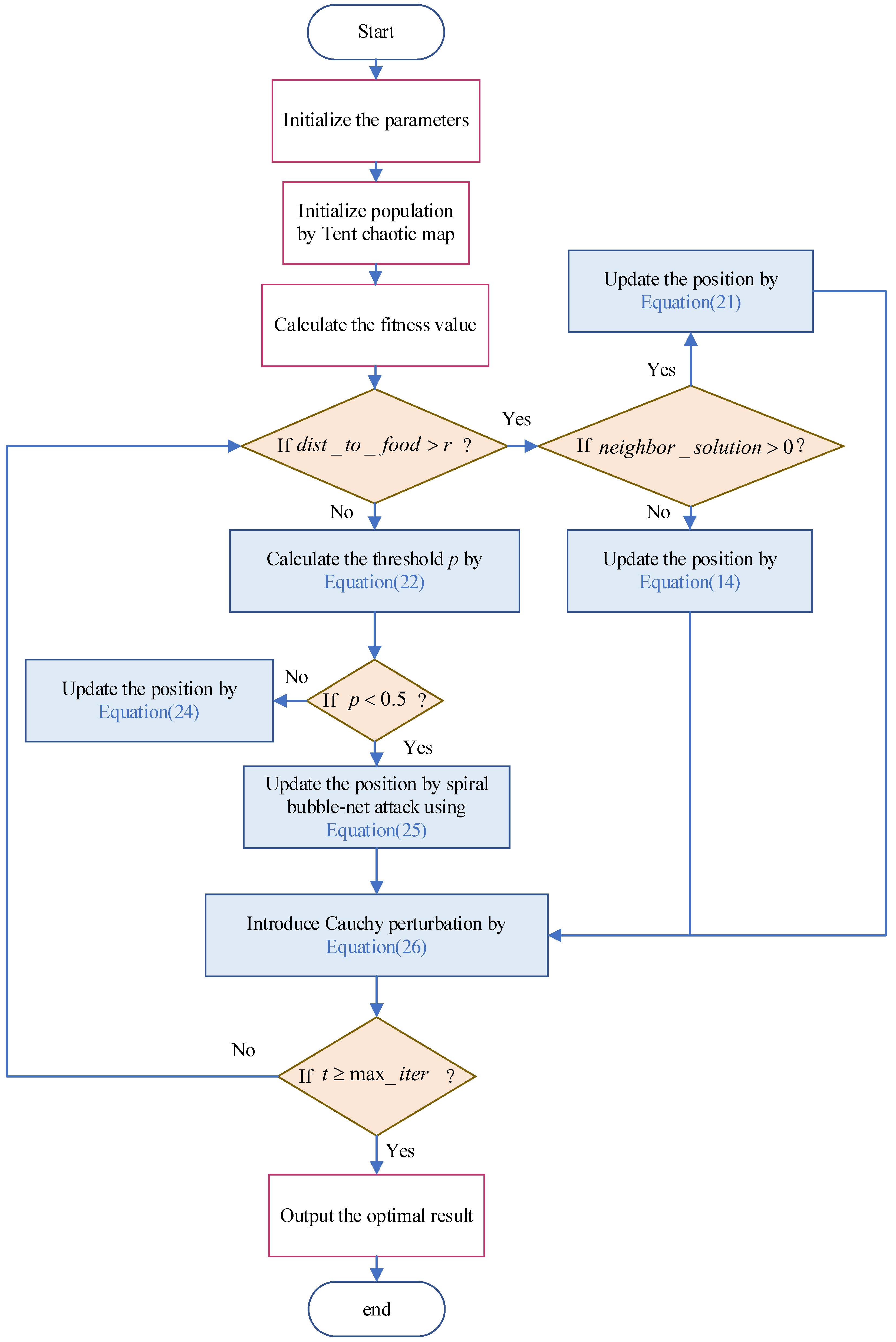
3.4. Main Steps and Process of Improved Dragonfly Algorithm
| Algorithm 1. HIDA |
| 1: Set the dragonfly population size to N, maximum number of iterations is ; |
| 2: Generate the initial location of the dragonfly individuals by tent chaotic map; |
| 3: Obtain the fitness value fit of each dragonfly; |
| 4: Set the position of optimal value as X+, the lowest as X−; |
| 5: Initialize effective radius and adaptive probability threshold ; |
| 6: while |
| 7: Update the weights using Equation (19); |
| 8: for |
| 9: Find the adjacent solution according to r; |
| 10: if |
| 11: if the adjacent exists |
| 12: Update the position using Equation (21); |
| 13: else |
| 14: Update the position by using Equation (14); |
| 15: end if |
| 16: else |
| 17: if |
| 18: Update the position using Equation (24); |
| 19: else |
| 20: Update the position by spiral bubble-net attack using Equation (25); |
| 21: end if |
| 22: end if |
| 23: Introduce the Cauchy perturbation to the optimal position according to Equation (26) and retain the solution with better fitness value to participate in the next iteration based on the greedy strategy. |
| 24: end while |
| 25: Return . |
4. Experimental Results
4.1. Function Test Experiment
4.1.1. Basic Benchmark Functions
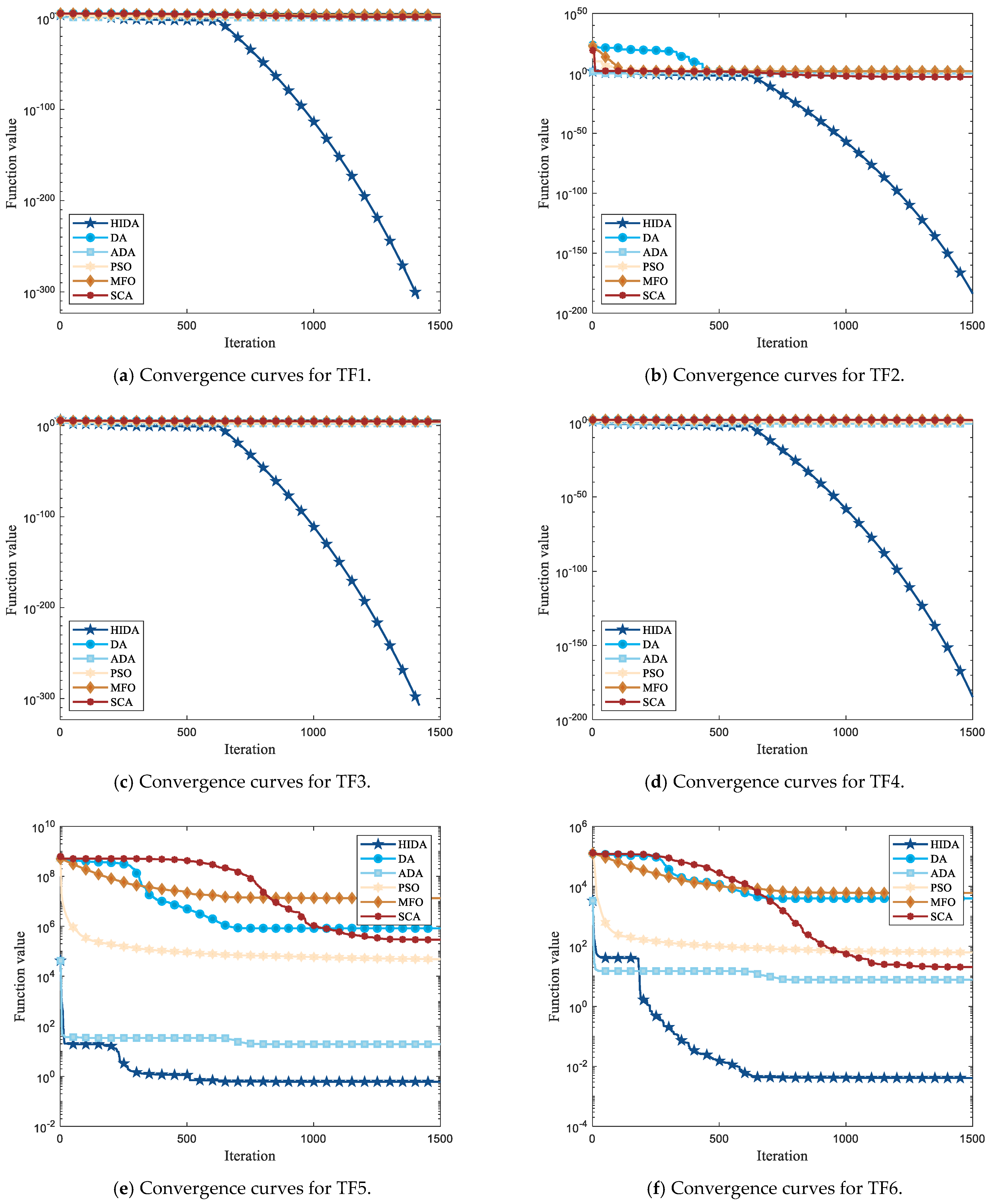
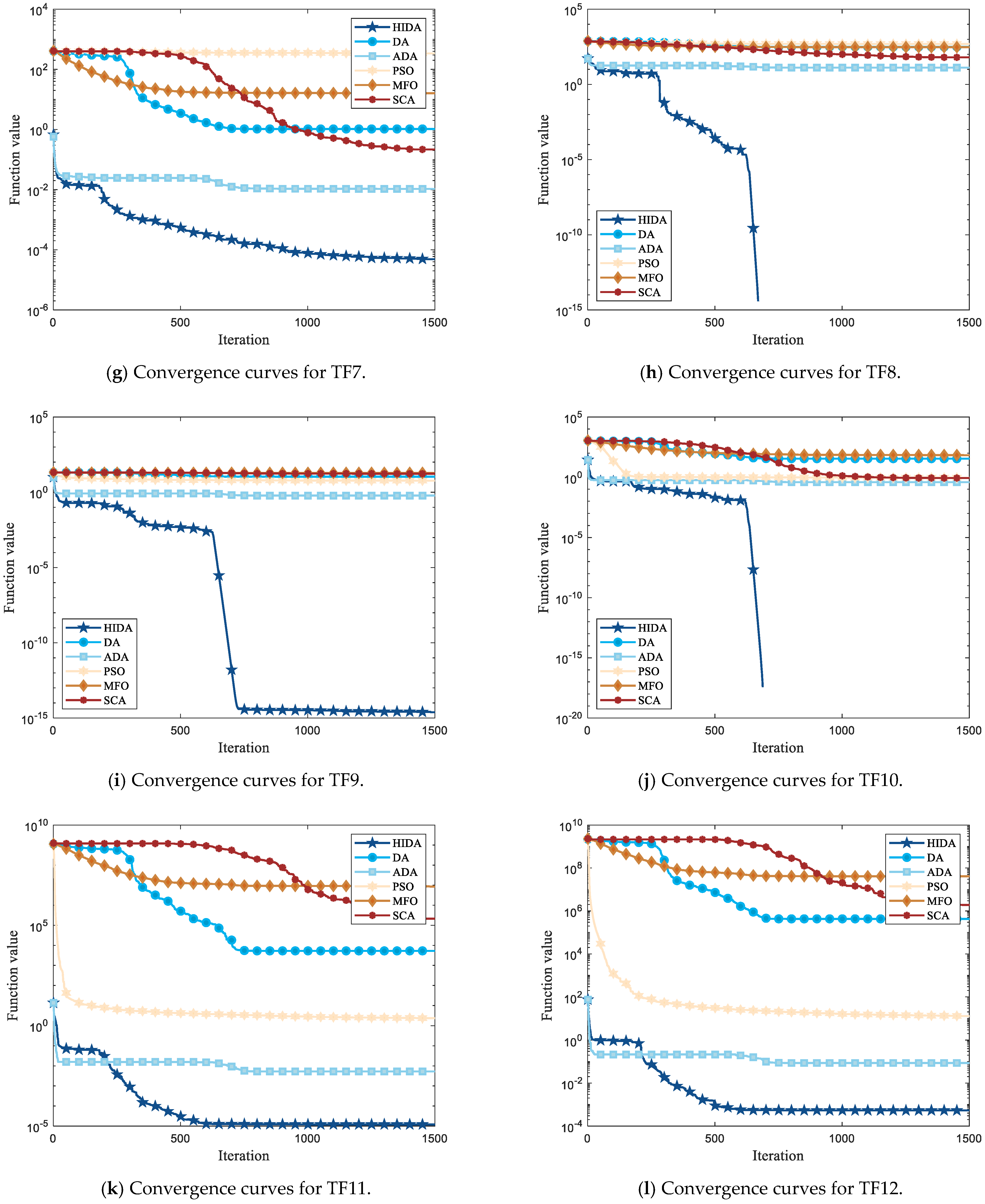
4.1.2. Algorithm Comparison and Analysis
4.1.3. Statistical Test
4.1.4. Comparison with Other Improved Dragonfly Algorithms
4.1.5. Benchmark Functions from CEC
4.1.6. Algorithm Complexity Analysis
4.2. Algorithm Application Experiment
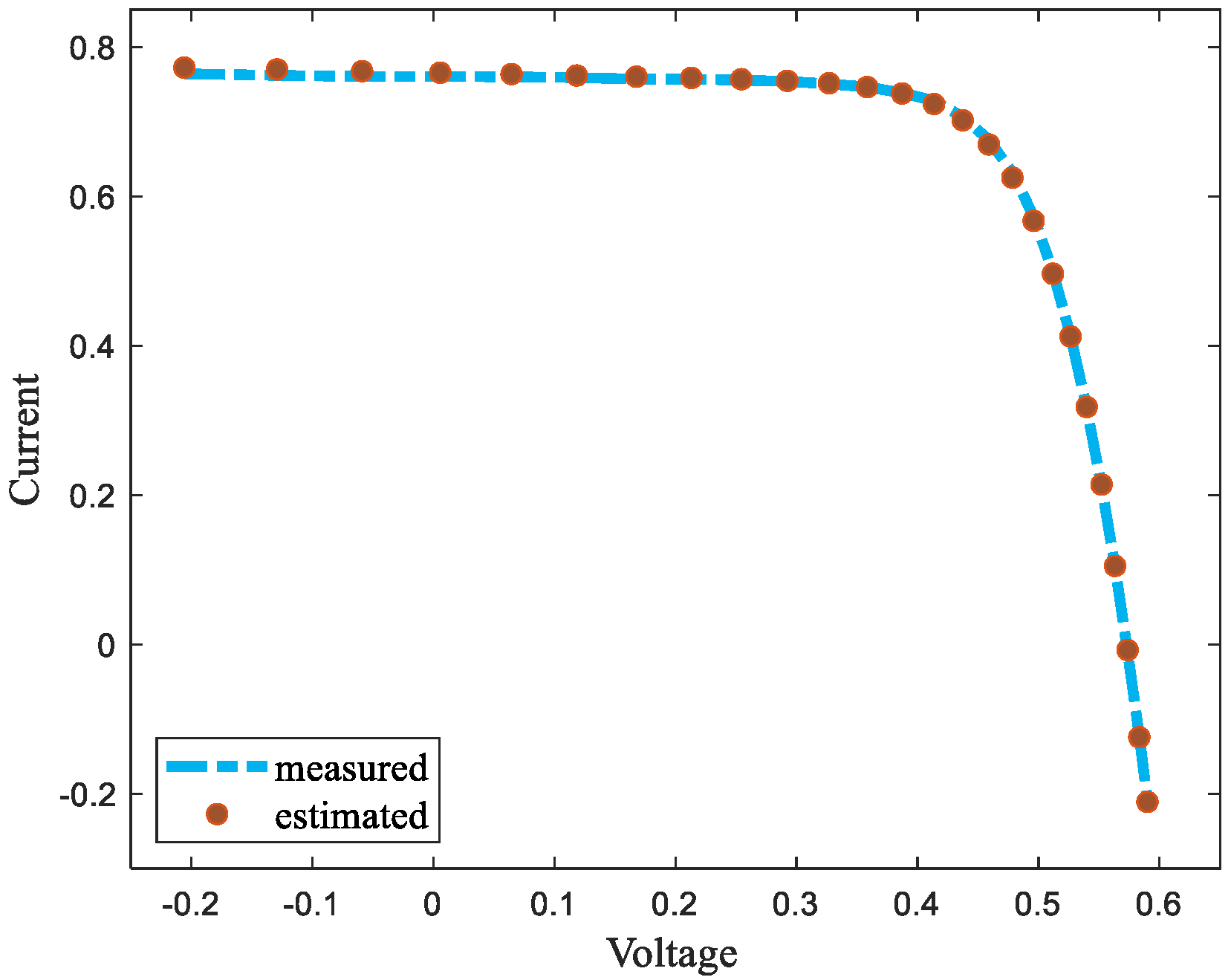
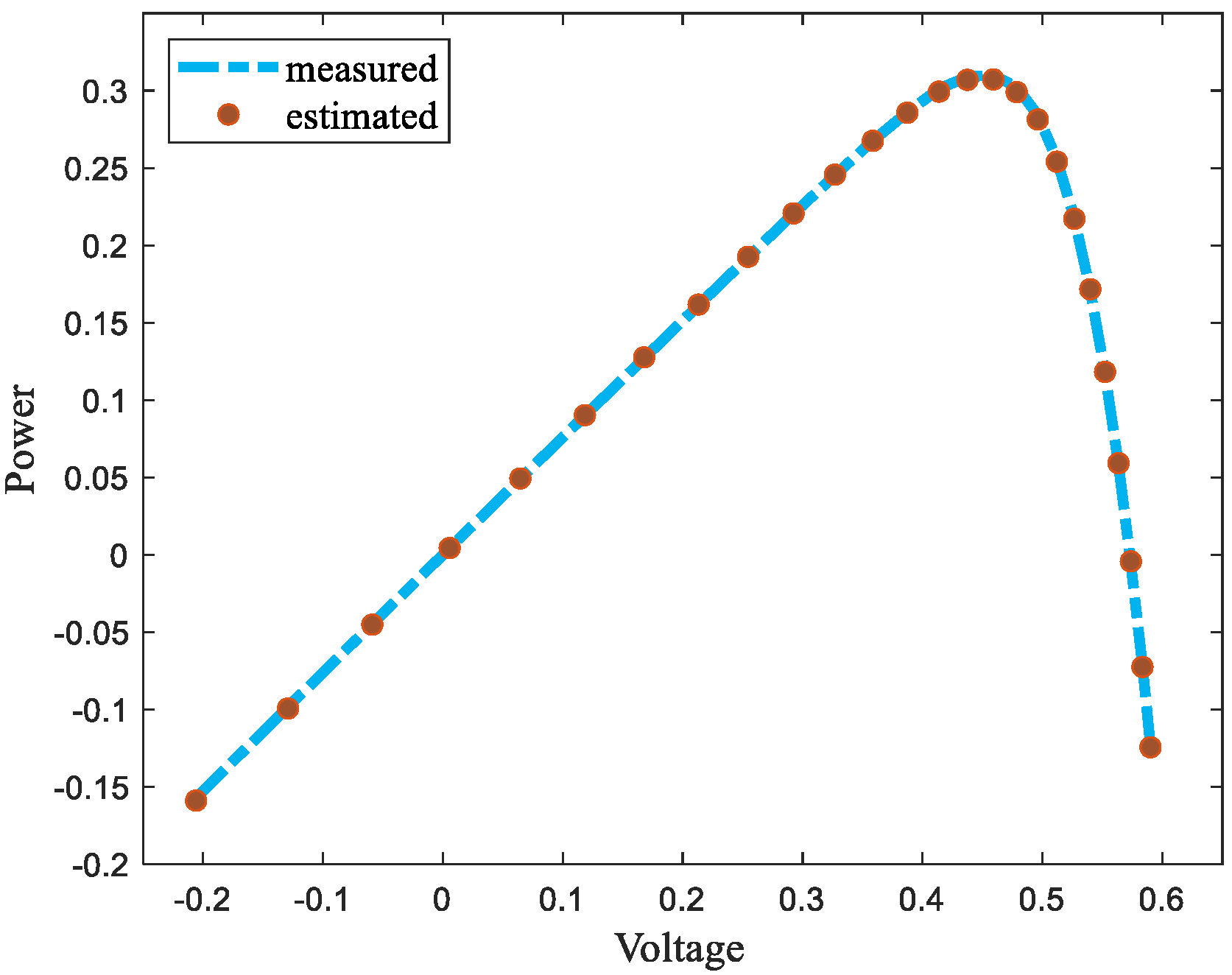
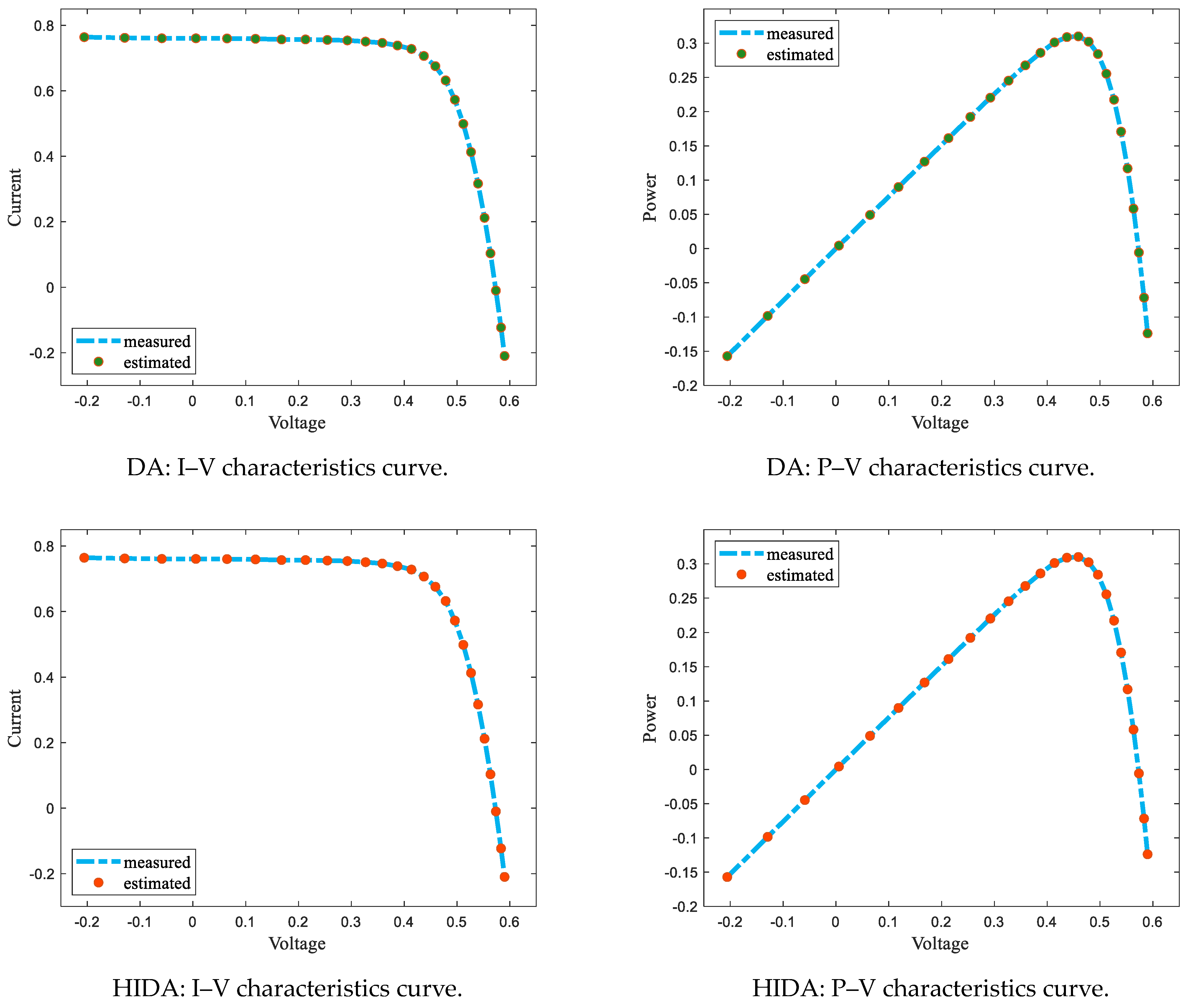
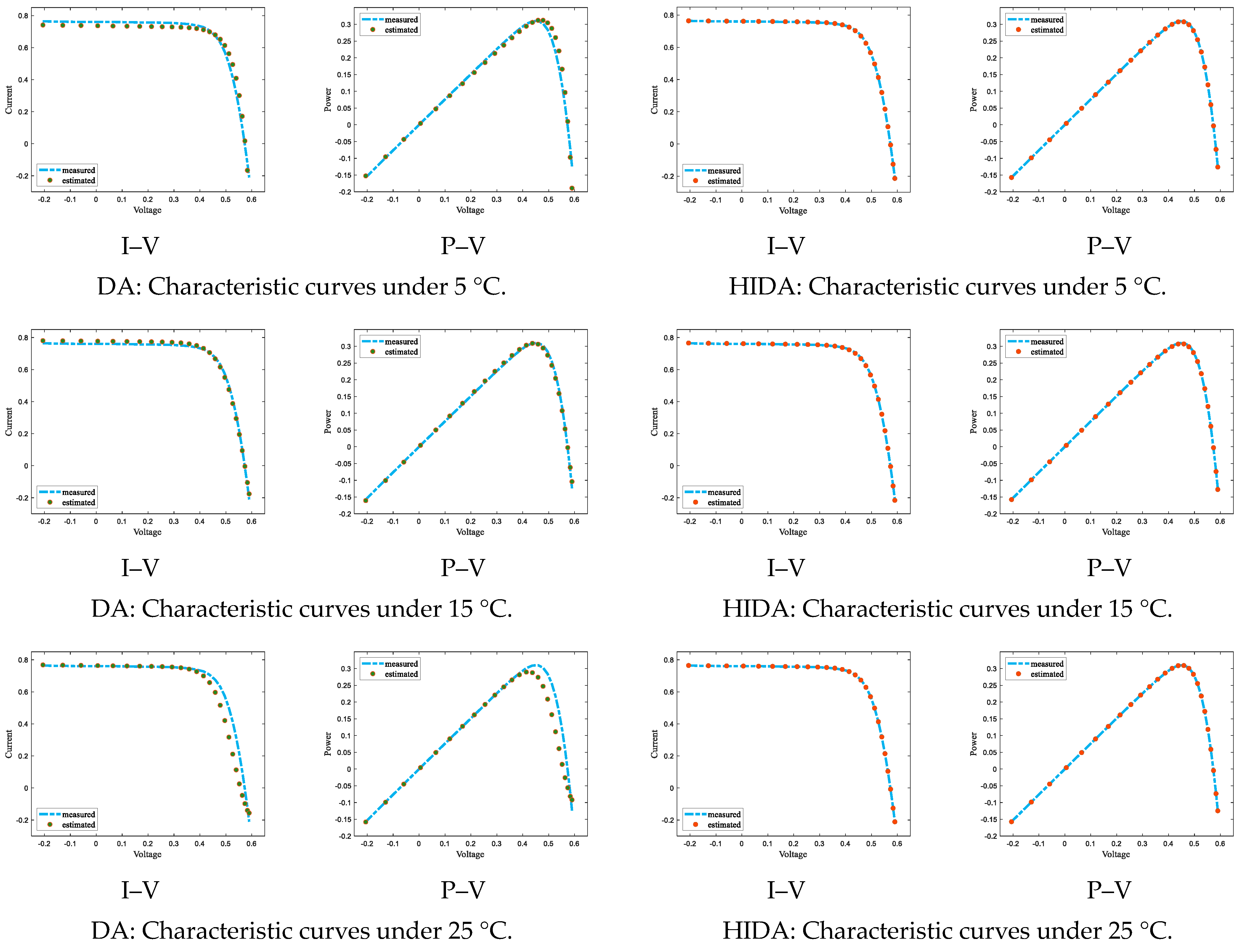
4.2.1. Parameter Estimation of Solar Photovoltaic Cell
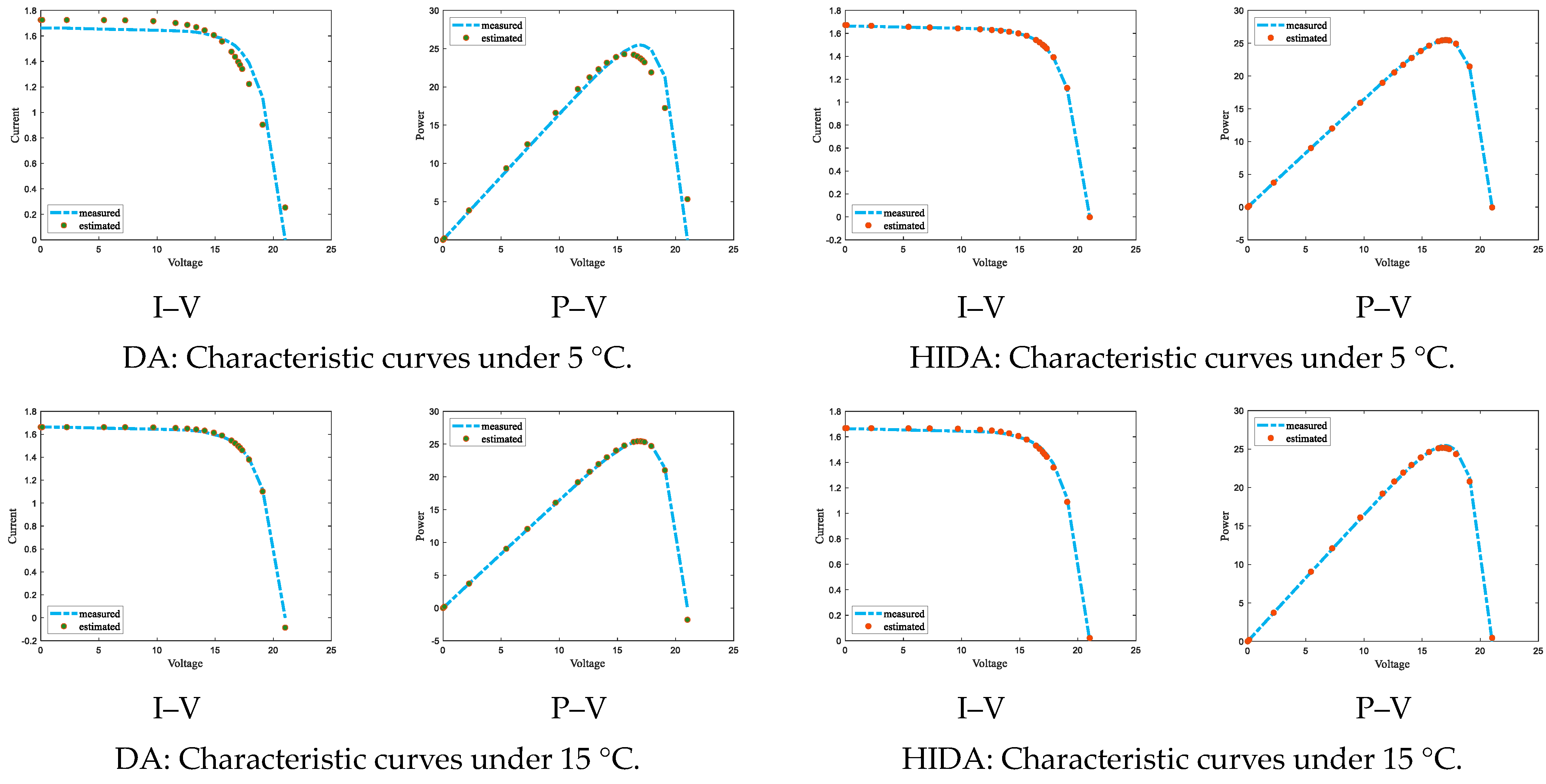
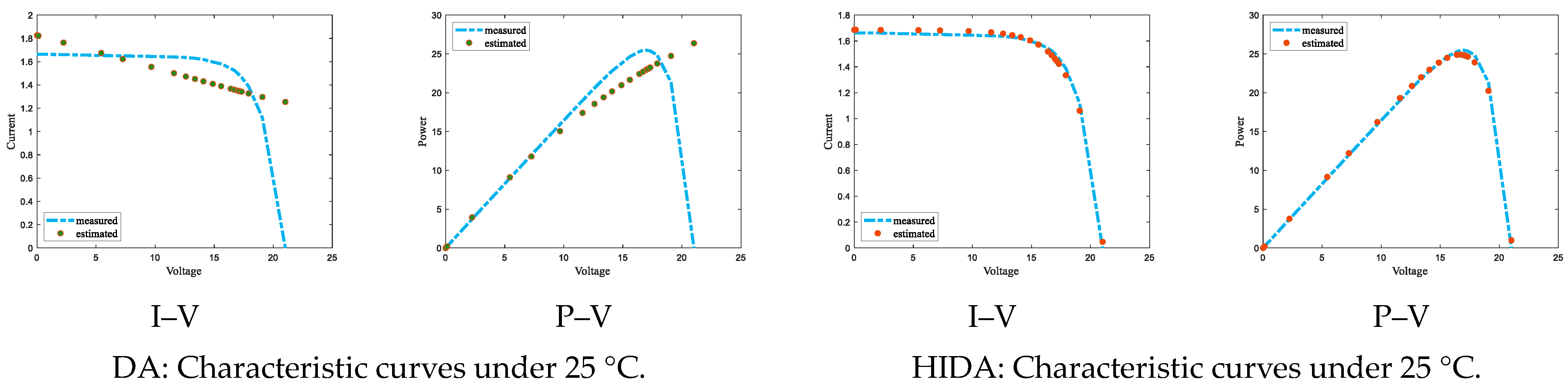
4.2.2. Parameter Estimation of Photovoltaic Array Engineering Model
- (1)
- Set the photo-generated current and the short-circuit current to equal, because the series resistance is much smaller than the diode’s forward resistance
- (2)
- is ignored due to the high value of the parallel resistance inside the PV cell, making much smaller than .
4.2.3. Experiments with Classical Circuit Models
4.2.4. Classical Engineering Application Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kazem, H.A. Prediction of grid-connected photovoltaic performance using artificial neural networks and experimental dataset considering environmental variation. Environ. Dev. Sustain. 2023, 25, 2857–2884. [Google Scholar] [CrossRef]
- Rahimi, N.; Park, S.; Choi, W.; Oh, B.; Kim, S.; Cho, Y.; Ahn, S.; Chong, C.; Kim, D.; Jin, C.; et al. A Comprehensive Review on Ensemble Solar Power Forecasting Algorithms. J. Electr. Eng. Technol. 2023, 18, 719–733. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P.; Cheshta, J.K. Game Theory-Based Framework of Solar–Wind Renewable Energy System. J. Inst. Eng. India Ser. B 2019, 100, 575–587. [Google Scholar] [CrossRef]
- Sun, C.; Zou, Y.; Qin, C.; Zhang, B.; Wu, X. Temperature effect of photovoltaic cells: A review. Adv. Compos. Hybrid Mater. 2022, 5, 2675–2699. [Google Scholar] [CrossRef]
- Wang, J.J.; Pazlai, M.M.; Kong, B.L. Research on MPPT of photovoltaic system based on improved salp swarm algorithm. Acta Energ. Sol. Sin. 2022, 43, 191–197. (In Chinese) [Google Scholar]
- Goswami, A.; Sadhu, P.K. Adoption of floating solar photovoltaics on waste water management system: A unique nexus of water-energy utilization, low-cost clean energy generation and water conservation. Clean Technol. Environ. Policy 2023, 25, 343–368. [Google Scholar] [CrossRef]
- Obiora, V.; Saha, C.; Bazi, A.A.; Koushik, G. Optimization of solar photovoltaic (PV) parameters using meta-heuristics. Microsyst. Technol. 2021, 27, 3161–3169. [Google Scholar] [CrossRef]
- Al-Subhi, A. Efficient mathematical models for parameters estimation of single-diode photovoltaic cells. Energy Syst. 2022, 1–22. [Google Scholar] [CrossRef]
- Samadhiya, A.; Namrata, K.; Gupta, D. Uncertainty quantification in deterministic parameterization of single diode model of a silicon solar cell. Optim. Eng. 2021, 22, 2429–2456. [Google Scholar] [CrossRef]
- Ayyarao, T.S.L.V. Parameter estimation of solar PV models with quantum-based avian navigation optimizer and Newton–Raphson method. J. Comput. Electron. 2022, 21, 1338–1356. [Google Scholar] [CrossRef]
- Gafar, M.; El-Sehiemy, R.A.; Hasanien, H.M.; Amlak, A. Optimal parameter estimation of three solar cell models using modified spotted hyena optimization. J. Ambient Intell. Humaniz. Comput. 2022, 1–12. [Google Scholar] [CrossRef]
- Zeng, Y.J.; Wang, L.; Huang, C. Parameter identification of solar cell model based on Jaya-DA algorithm. Acta Energ. Sol. Sin. 2022, 43, 198–202. [Google Scholar]
- Houssein, E.H.; Nageh, G.; Abd Elaziz, M.; Younis, E. An efficient Equilibrium Optimizer for parameters identification of photovoltaic modules. PeerJ Comput. Sci. 2021, 7, 708–738. [Google Scholar] [CrossRef] [PubMed]
- Rawa, M.; Calasan, M.; Abusorrah, A.; Alhussainy, A.A.; Al-Turki, Y.; Ali, Z.M.; Sindi, H.; Mekhilef, S.; Aleem, S.H.A.; Bassi, H. Single Diode Solar Cells-Improved Model and Exact Current-Voltage Analytical Solution Based on Lambert’s W Function. Sensors 2022, 22, 4173. [Google Scholar]
- Mengue, F.D.; Kammogne, A.S.T.; Siewe, M.S.; Yamapi, R.; Fotsin, H.B. A new hybrid method based on differential evolution to determine the temperature-dependent parameters of single-diode photovoltaic cells. J. Comput. Electron. 2021, 20, 2511–2521. [Google Scholar] [CrossRef]
- Singla, M.K.; Nijhawan, P.; Oberoi, A.S. Parameter estimation of three diode solar PV cell using chaotic dragonfly algorithm. Soft Comput. 2022, 26, 11567–11598. [Google Scholar] [CrossRef]
- Hang, P.P.; Fan, G.J.; Sun, W.Z.; Shi, B.; Zhang, X. Identification of LVRT characteristics of photovoltaic inverters based on data testing and PSO algorithm. Electr. Power Autom. Equip. 2020, 40, 49–54. (In Chinese) [Google Scholar]
- Elsheikh, A.H.; Abd Elaziz, M. Review on applications of particle swarm optimization in solar energy systems. Int. J. Environ. Sci. Technol. 2019, 16, 1159–1170. [Google Scholar] [CrossRef]
- Kang, T.; Yao, J.A.; Jin, M.; Zhu, X.; Wen, W. Parameter identification of photovoltaic module models using improved SOS algorithm. Appl. Res. Comput. 2020, 37, 1034–1042. (In Chinese) [Google Scholar]
- Wu, Z.Q.; Shen, D.D.; Shang, M.Y.; Qi, S.Q. Parameter identification of photovoltaic cell model based on improved grasshopper optimization algorithm. Acta Metrol. Sin. 2020, 41, 1536–1543. (In Chinese) [Google Scholar] [CrossRef]
- Mokeddem, D. Parameter Extraction of Solar Photovoltaic Models Using Enhanced Levy Flight Based Grasshopper Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 171–179. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Xie, Z.K.; Liu, C.Y.; Wang, G.Y. Lion Swarm Optimization Based on Chaotic Search Strategy and Application in Parameters Identification of Photovoltaic Cell Models. Acta Metrol. Sin. 2021, 42, 415–423. (In Chinese) [Google Scholar]
- Kang, P.P.; Zhu, S.Y.; Wang, H.; Fan, G.W.; Yang, G.X. Parameter identification of comprehensive load model with photovoltaic generation based on the IBOA algorithm. Renew. Energy Resour. 2021, 39, 1541–1547. (In Chinese) [Google Scholar]
- Zhang, Z.; Wang, X.Y.; Wang, L. Photovoltaic Array Parameter Identification Based on Sparrow Search Algorithm. Electr. Drive 2022, 52, 75–80. (In Chinese) [Google Scholar]
- Kumar, C.; Mary, D.M. Parameter estimation of three-diode solar photovoltaic model using an Improved-African Vultures optimization algorithm with Newton–Raphson method. J. Comput. Electron. 2021, 20, 2563–2593. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Korashy, A.; Almalaq, A.; Domínguez, G.J.L. An enhanced Harris Hawk optimization algorithm for parameter estimation of single, double and triple diode photovoltaic models. Soft Comput. 2022, 26, 7233–7257. [Google Scholar] [CrossRef]
- Sumathi, M.; Vijayaraj, N.; Raja, S.; Rajkamal, M. HHO-ACO hybridized load balancing technique in cloud computing. Int. J. Inf. Technol. 2023, 15, 1357–1365. [Google Scholar] [CrossRef]
- Gupta, J.; Nijhawan, P.; Ganguli, S. Parameter estimation of different solar cells using a novel swarm intelligence technique. Soft Comput. 2022, 26, 5833–5863. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Huang, Z. Spiral-based chaotic chicken swarm optimization algorithm for parameters identification of photovoltaic models. Soft Comput. 2021, 25, 12875–12898. [Google Scholar] [CrossRef]
- Tefek, M.F. Artificial bee colony algorithm based on a new local search approach for parameter estimation of photovoltaic systems. J. Comput. Electron. 2021, 20, 2530–2562. [Google Scholar] [CrossRef]
- Zheng, X.; Li, X.; Li, Y.; Liu, Y. An improved artificial bee Colony algorithm based on cat mapping and differential variation. J. Data Inf. Manag. 2022, 4, 119–135. [Google Scholar] [CrossRef]
- Bayoumi, A.S.A.; El-Sehiemy, R.A.; Abaza, A. Effective PV Parameter Estimation Algorithm Based on Marine Predators Optimizer Considering Normal and Low Radiation Operating Conditions. Arab. J. Sci. Eng. 2022, 47, 3089–3104. [Google Scholar] [CrossRef]
- Sattar, M.A.E.; Al Sumaiti, A.; Ali, H.; Ahmed, A.Z.D. Marine predators algorithm for parameters estimation of photovoltaic modules considering various weather conditions. Neural Comput. Appl. 2021, 33, 11799–11819. [Google Scholar] [CrossRef]
- Noroozi, M.; Mohammadi, H.; Efatinasab, E.; Lashgari, A.; Eslami, M.; Khan, B. Golden Search Optimization Algorithm. IEEE Access 2022, 10, 37515–37532. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Wu, H.; Peng, Q.; Shi, M.; Xing, L.; Cheng, S. Drunkard Adaptive Walking Chaos Wolf Pack Algorithm in Parameter Identification of Photovoltaic Module Model. Energies 2022, 15, 6340. [Google Scholar] [CrossRef]
- Hussein, M.R. Parameters extraction of single and double diodes photovoltaic models using Marine Predators Algorithm and Lambert W function. Sol. Energy 2020, 209, 674–693. [Google Scholar]
- Ibrahim, I.A.; Hossain, M.J.; Duck, B.C. A hybrid wind driven-based fruit fly optimization algorithm for identifying the parameters of a double-diode photovoltaic cell model considering degradation effects. Sustain. Energy Technol. Assess. 2022, 50, 101685. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Alshinwan, M.; Abualigah, L.; Shehab, M.; Abd, E.M.; Khasawneh, A.M.; Alabool, H.; Hamad, H.A. Dragonfly algorithm: A comprehensive survey of its results, variants, and applications. Multimed. Tools Appl. 2021, 80, 14979–15016. [Google Scholar] [CrossRef]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic dragonfly algorithm: An improved metaheuristic algorithm for feature selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Shirani, M.R.; Safi-Esfahani, F. Dynamic scheduling of tasks in cloud computing applying dragonfly algorithm, biogeography-based optimization algorithm and Mexican hat wavelet. J. Supercomput. 2021, 77, 1214–1272. [Google Scholar] [CrossRef]
- Yousefpoor, E.; Barati, H.; Barati, A. A hierarchical secure data aggregation method using the dragonfly algorithm in wireless sensor networks. Peer-to-Peer Netw. Appl. 2021, 14, 1917–1942. [Google Scholar] [CrossRef]
- Latchoumi, T.P.; Parthiban, L. Quasi Oppositional Dragonfly Algorithm for Load Balancing in Cloud Computing Environment. Wirel. Pers. Commun. 2022, 122, 2639–2656. [Google Scholar] [CrossRef]
- Debnath, S.; Baishya, S.; Sen, D.; Arif, W. A hybrid memory-based dragonfly algorithm with differential evolution for engineering application. Eng. Comput. 2021, 37, 2775–2802. [Google Scholar] [CrossRef]
- Xue, F.; Ma, X.; Tian, B.; Wu, H. Photovoltaic global maximum power tracking based on improved dragonfly algorithm. Electr. Power 2022, 55, 131–137. (In Chinese) [Google Scholar]
- Lin, T.; Feng, J.J.; Zhao, Y. Study on dragonfly algorithm based on elite strategy and sines and cosines mechanism. Microelectron. Comput. 2020, 37, 24–30. (In Chinese) [Google Scholar]
- Zhong, L.; Zhou, Y.; Luo, Q.; Zhong, K. Wind driven dragonfly algorithm for global optimization. Concurr. Comput. 2021, 33, 6054–6081. [Google Scholar] [CrossRef]
- Du, X.X.; Wang, H.; Cui, L.H.; Luo, J.Q.; Liu, Y.; Zhang, J.F.; Wang, Y.P. Dragonfly algorithm based on clustering and detection elite guidance. J. Zhejiang Univ. (Eng. Sci.) 2022, 56, 977–986. (In Chinese) [Google Scholar]
- Xiao, W.B.; Liu, W.Q.; Wu, H.M.; Zhang, H.M. Review of Parameter extraction methods for single-diode model of solar cell. Acta Phys. Sin. 2018, 67, 25–35. (In Chinese) [Google Scholar]
- Zhang, S.P.; Gao, D. Dragonfly Algorithm Based on Random Substitution and Hybrid Mutation. Sci. Technol. Eng. 2020, 20, 9108–9115. (In Chinese) [Google Scholar]
- Lan, Y.X. Grasshopper optimization algorithm based on chaos and Cauchy mutation and feature selection. Microelectron. Comput. 2021, 38, 21–30. (In Chinese) [Google Scholar]
- Chen, G.; Zeng, G.H.; Huang, B.; Liu, J. HHO algorithm combining mutualism and lens imaging learning. Comput. Eng. Appl. 2022, 58, 76–86. (In Chinese) [Google Scholar]
- Zhou, P.; Dong, C.Y.; Chen, X.Y.; Qi, Y.S.; Zhao, X.Y.; Wang, Q.L. A Salp Swarm Algorithm Based on Stepped Tent Chaos and Simulated Annealing. Acta Electron. Sin. 2021, 49, 1724–1735. (In Chinese) [Google Scholar]
- Xu, H.; Zhang, D.M.; Wang, Y.R.; Song, T.T.; Fan, Y. Spectrum allocation based on improved binary grey wolf optimizer. Comput. Eng. Des. 2021, 42, 1353–1359. (In Chinese) [Google Scholar]
- Zhang, Y.; Yuan, S.J.; Da, L.X.; Zhou, J. Adaptive opposition-based learning cuckoo algorithm based on local search enhancement strategy. Math. Pract. Theory 2020, 50, 191–200. (In Chinese) [Google Scholar]
- Liu, X.F.; Liu, P.Z.; Luo, Y.M.; Fan, Y.L. Improved artificial bee colony algorithm based on enhanced local search. CAAI Trans. Intell. Syst. 2017, 12, 684–693. (In Chinese) [Google Scholar]
- Li, A.L.; Quan, L.X.; Cui, G.M.; Xie, S.F. A sparrow search algorithm combining sine-cosine and Cauchy mutation. Comput. Eng. Appl. 2022, 58, 91–99. (In Chinese) [Google Scholar]
- Eslami, M.; Neshat, M.; Khalid, S.A. A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers. Sustainability 2022, 14, 541. [Google Scholar] [CrossRef]
- Julien, P.; Inés, C.; Kevin, L.; Olivier, S. Generalizing the Wilcoxon rank-sum test for interval data. Int. J. Approx. Reason. 2015, 56, 108–121. [Google Scholar]
- Chen, G.; Gao, M.; Zhang, Z.; Li, S.Y. Hybridization of Chaotic Grey Wolf Optimizer and Dragonfly Algorithm for Short-Term Hydrothermal Scheduling. IEEE Access 2020, 8, 142996–143020. [Google Scholar] [CrossRef]
- Aci, C.I.; Gulcan, H. A modified dragonfly optimization algorithm for single- and multi objective problems using Brownian motion. Comput. Intell. Neurosci. 2019, 2019, 6871298. [Google Scholar] [CrossRef] [Green Version]
- Ayyarao, T.L.V.; Kumar, P.P. Parameter estimation of solar PV models with a new proposed war strategy optimization algorithm. Int. J. Energy Res. 2022, 46, 7215–7238. [Google Scholar] [CrossRef]
- Saxena, A.; Sharma, A.; Shekhawat, S. Parameter extraction of solar cell using intelligent grey wolf optimizer. Evol. Intell. 2022, 15, 167–183. [Google Scholar] [CrossRef]
- Sun, H.; Xiao, H.W.; Li, X.H.; Li, X.; Du, H.J. Review in photovoltaic cell model. Chin. J. Power Sources 2016, 40, 743–745. (In Chinese) [Google Scholar]
- Wu, Z.Q.; Liu, C.Y. Parameter Identification of Photovoltaic Cell Engineering Model Based on IHHO Algorithm. Acta Metrol. Sin. 2021, 42, 221–227. (In Chinese) [Google Scholar]
- Abdelkader, A.; Rached, B.M.; Bilel, T.; Laith, A.; Ezzeddine, T. Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik 2022, 253, 168600. [Google Scholar]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M.B. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Reda, M.; Marwa, S.; Laila, A.F.; Mohamed, A.; Karam, S. A comparative study of optimization algorithms for parameter estimation of PV solar cells and modules: Analysis and case studies. Energy Rep. 2022, 8, 13047–13065. [Google Scholar]
- Gao, S.C.; Wang, K.Y.; Tao, S.C.; Jin, T.; Dai, H.W.; Cheng, J.J. A state-of-the-art differential evolution algorithm for parameter estimation of solar photovoltaic models. Energy Convers. Manag. 2021, 230, 113784. [Google Scholar] [CrossRef]
- Eslami, M.; Akbari, E.; Seyed, S.S.T.; Ibrahim, B.F. A novel hybrid algorithm based on rat swarm optimization and pattern search for parameter extraction of solar photovoltaic models. Energy Sci. Eng. 2022, 10, 2689–2713. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Eslami, M.; Noroozi, M.; Mohammadi, H.; Kamari, O.; Palani, S. Modified Salp Swarm Optimization for Parameter Estimation of Solar PV Models. IEEE Access 2022, 10, 110181–110194. [Google Scholar] [CrossRef]
- Krishna, A.B.; Saxena, S.; Kamboj, V.K. A novel statistical approach to numerical and multidisciplinary design optimization problems using pattern search inspired Harris hawks optimizer. Neural Comput. Appl. 2021, 33, 7031–7072. [Google Scholar] [CrossRef]
- Che, Y.; He, D. An enhanced seagull optimization algorithm for solving engineering optimization problems. Appl. Intell. 2022, 52, 13043–13081. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Diffused Memetic Optimizer for reactive berth allocation and scheduling at marine container terminals in response to disruptions. Swarm Evol. Comput. 2023, 80, 101334. [Google Scholar] [CrossRef]
- Emilio, S.; Nelishia, P. A study of ant-based pheromone spaces for generation constructive hyper-heuristics. Swarm Evol. Comput. 2022, 72, 101095. [Google Scholar]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Pasha, J.; Nwodu, A.L.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Wang, H.; Dulebenets, M.A. Exact and metaheuristic algorithms for the vehicle routing problem with a factory-in-a-box in multi-objective settings. Adv. Eng. Inform. 2022, 52, 101623. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Fazlollahtabar, H.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Preventive maintenance for the flexible flowshop scheduling under uncertainty: A waste-to-energy system. Environ. Sci. Pollut. Res. 2021, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Maiyue, C.; Ying, T. SF-FWA: A Self-Adaptive Fast Fireworks Algorithm for effective large-scale optimization. Swarm Evol. Comput. 2023, 80, 101314. [Google Scholar]



| Functions | Range | Optimum | Characteristics |
|---|---|---|---|
| [−100, 100] | 0 | Unimodal | |
| [−10, 10] | 0 | Unimodal | |
| [−100, 100] | 0 | Unimodal | |
| [−100, 100] | 0 | Unimodal | |
| [−30, 30] | 0 | Unimodal | |
| [−100, 100] | 0 | Unimodal | |
| [−1.28, 1.28] | 0 | Unimodal | |
| [−5.12, 5.12] | 0 | Multimodal | |
| [−32, 32] | 0 | Multimodal | |
| [−600, 600] | 0 | Multimodal | |
| [−50, 50] | 0 | Multimodal | |
| [−50, 50] | 0 | Multimodal |
| Functions | Metric | PSO | DA | MFO | ADA | SCA | HIDA |
|---|---|---|---|---|---|---|---|
| Mean | 6.52 × 101 | 3.27 × 103 | 6.00 × 103 | 3.29 | 1.68 × 101 | 0.00 | |
| Std | 1.37 × 101 | 1.32 × 103 | 9.32 × 104 | 5.50 | 4.08 × 101 | 0.00 | |
| Best | 4.65 × 101 | 6.11 × 102 | 6.04 × 10−3 | 7.71 × 10−10 | 1.30 × 10−2 | 0.00 | |
| Worst | 9.98 × 101 | 5.62 × 103 | 3.00 × 104 | 1.93 × 101 | 1.86 × 102 | 0.00 | |
| Mean | 4.15 × 101 | 2.83 × 101 | 6.67 × 101 | 6.58 × 10−1 | 1.05 × 10−3 | 2.0 × 10−184 | |
| Std | 4.81 | 9.42 | 3.72 × 101 | 1.06 | 2.59 × 10−3 | 0.00 | |
| Best | 3.37 × 101 | 1.18 × 101 | 1.00 × 101 | 4.17 × 10−5 | 2.69 × 10−7 | 6.8 × 10−197 | |
| Worst | 5.64 × 101 | 5.43 × 101 | 1.80 × 102 | 4.16 | 1.21 × 10−2 | 2.3 × 10−183 | |
| Mean | 1.18 × 103 | 3.93 × 104 | 4.20 × 104 | 2.30 × 102 | 2.96 × 104 | 0.00 | |
| Std | 2.42 × 102 | 2.22 × 104 | 2.20 × 104 | 3.85 × 102 | 1.46 × 104 | 0.00 | |
| Best | 6.67 × 102 | 1.09 × 104 | 9.38 × 103 | 1.52 × 10−7 | 8.73 × 103 | 0.00 | |
| Worst | 1.64 × 103 | 1.20 × 105 | 1.06 × 105 | 1.64 × 103 | 6.89 × 104 | 0.00 | |
| Mean | 4.06 | 3.32 × 101 | 8.28 × 101 | 1.88 × 10−1 | 5.30 × 101 | 2.2 × 10−185 | |
| Std | 3.81 × 10−1 | 8.83 | 5.49 | 2.93 × 10−1 | 1.12 × 101 | 0.00 | |
| Best | 3.46 | 1.88 × 101 | 7.46 × 101 | 4.43 × 10−4 | 2.89 × 101 | 1.5 × 10−191 | |
| Worst | 5.15 | 5.45 × 101 | 9.28 × 101 | 1.08 | 7.27 × 101 | 2.0 × 10−184 | |
| Mean | 4.78 × 104 | 8.29 × 105 | 1.33 × 107 | 1.95 × 101 | 2.89 × 105 | 6.06 × 10−1 | |
| Std | 1.38 × 104 | 5.44 × 105 | 3.69 × 107 | 2.73 × 101 | 5.47 × 105 | 2.89 | |
| Best | 2.69 × 104 | 5.57 × 104 | 1.30 × 102 | 6.59 × 10−3 | 1.62 × 102 | 3.05 × 10−5 | |
| Worst | 8.44 × 104 | 2.35 × 106 | 1.6 × 108 | 9.82 × 101 | 2.25 × 106 | 1.59 × 101 | |
| Mean | 6.23 × 101 | 3.93 × 103 | 6.00 × 103 | 7.62 | 2.03 × 101 | 4.07 × 10−3 | |
| Std | 1.23 × 101 | 1.71 × 103 | 7.71 × 103 | 1.62 × 101 | 2.97 × 101 | 7.09 × 10−3 | |
| Best | 3.24 × 101 | 1.70 × 103 | 8.08 × 10−3 | 5.50 × 10−3 | 8.50 × 101 | 5.14 × 10−8 | |
| Worst | 9.56 × 101 | 8.17 × 103 | 3.01 × 104 | 7.26 × 101 | 1.69 × 102 | 3.72 × 10−2 | |
| Mean | 3.38 × 102 | 1.04 | 1.60 × 101 | 1.06 × 10−2 | 2.17 × 10−1 | 4.88 × 10−5 | |
| Std | 6.89 × 101 | 5.17 × 10−1 | 1.85 × 101 | 1.17 × 10−2 | 1.91 × 10−1 | 5.81 × 10−5 | |
| Best | 2.12 × 102 | 1.85 × 10−1 | 3.51 × 10−1 | 1.06 × 10−4 | 3.42 × 10−2 | 1.93 × 10−6 | |
| Worst | 4.63 × 102 | 2.44 | 7.95 × 101 | 4.22 × 10−2 | 8.01 × 10−1 | 2.50 × 10−4 | |
| Mean | 4.91 × 102 | 3.13 × 102 | 3.00 × 102 | 1.31 × 101 | 6.29 × 101 | 0.00 | |
| Std | 4.49 × 101 | 6.11 × 101 | 5.21 × 101 | 1.76 × 101 | 4.89 × 101 | 0.00 | |
| Best | 3.77 × 102 | 1.21 × 102 | 1.82 × 102 | 3.41 × 10−8 | 1.18 | 0.00 | |
| Worst | 5.63 × 102 | 4.45 × 102 | 3.82 × 102 | 5.10 × 101 | 1.67 × 102 | 0.00 | |
| Mean | 5.82 | 1.06 × 101 | 1.93 × 101 | 5.92 × 10−1 | 1.69 × 101 | 2.43 × 10−15 | |
| Std | 3.72 × 10−1 | 1.83 | 1.08 | 8.34 × 10−1 | 7.43 | 1.79 × 10−15 | |
| Best | 5.27 | 6.28 | 1.49 × 101 | 1.96 × 10−6 | 4.33 × 10−2 | 8.88 × 10−16 | |
| Worst | 6.66 | 1.46 × 101 | 1.99 × 101 | 2.64 | 2.05 × 101 | 4.44 × 10−15 | |
| Mean | 8.93 × 10−1 | 3.45 × 101 | 6.65 × 101 | 3.82 × 10−1 | 8.48 × 10−1 | 0.00 | |
| Std | 5.53 × 10−2 | 1.26 × 101 | 7.81 × 101 | 4.24 × 10−1 | 3.43 × 10−1 | 0.00 | |
| Best | 7.88 × 10−1 | 1.80 × 101 | 5.45 × 10−3 | 3.91 × 10−11 | 9.73 × 10−2 | 0.00 | |
| Worst | 9.87 × 10−1 | 7.02 × 101 | 2.71 × 102 | 1.27 | 1.76 | 0.00 | |
| Mean | 2.34 | 5.30 × 103 | 8.53 × 106 | 5.31 × 10−3 | 2.13 × 105 | 1.21 × 10−5 | |
| Std | 1.10 | 1.56 × 104 | 4.67 × 107 | 8.91 × 10−3 | 4.50 × 105 | 3.90 × 10−5 | |
| Best | 1.05 | 8.05 | 6.03 × 10−1 | 9.69 × 10−8 | 3.44 | 2.65 × 10−10 | |
| Worst | 6.09 | 7.18 × 104 | 2.56 × 108 | 3.32 × 10−2 | 1.85 × 106 | 2.09 × 10−4 | |
| Mean | 1.28 × 101 | 4.30 × 105 | 4.10 × 107 | 8.63 × 10−2 | 1.91 × 106 | 5.34 × 10−4 | |
| Std | 2.56 | 4.88 × 105 | 1.25 × 108 | 1.57 × 10−1 | 4.16 × 106 | 1.50 × 10−3 | |
| Best | 6.89 | 2.14 × 101 | 1.69 | 2.37 × 10−4 | 9.10 | 3.04 × 10−8 | |
| Worst | 1.80 × 101 | 1.86 × 106 | 4.1 × 108 | 7.89 × 10−1 | 1.72 × 107 | 8.07 × 10−3 |
| Functions | Metric | PSO | DA | MFO | ADA | SCA | HIDA |
|---|---|---|---|---|---|---|---|
| Mean | 5.18 × 102 | 2.05 × 104 | 3.42 × 104 | 1.49 × 101 | 6.11 × 103 | 0.00 | |
| Std | 5.10 × 101 | 7.97 × 103 | 1.77 × 104 | 3.08 × 101 | 4.37 × 103 | 0.00 | |
| Best | 4.07 × 102 | 6.02 × 103 | 6.00 × 103 | 2.36 × 10−9 | 7.54 × 101 | 0.00 | |
| Worst | 6.35 × 102 | 3.65 × 104 | 7.93 × 104 | 1.23 × 102 | 1.99 × 104 | 0.00 | |
| Mean | 2.31 × 1010 | 1.04 × 102 | 2.01 × 102 | 1.58 | 2.03 | 1.1 × 10−183 | |
| Std | 1.26 × 1011 | 3.83 × 101 | 5.55 × 101 | 2.24 | 3.56 | 0.00 | |
| Best | 3.07 × 102 | 3.86 × 101 | 1.19 × 102 | 1.04 × 10−3 | 1.31 × 10−2 | 3.7 × 10−219 | |
| Worst | 6.88 × 1011 | 2.19 × 102 | 3.55 × 102 | 9.64 | 1.85 × 101 | 1.1 × 10−182 | |
| Mean | 2.33 × 104 | 2.62 × 105 | 2.27 × 105 | 2.99 × 103 | 2.50 × 105 | 0.00 | |
| Std | 4.86 × 103 | 8.96 × 104 | 8.04 × 104 | 6.04 × 103 | 6.57 × 104 | 0.00 | |
| Best | 1.41 × 104 | 1.14 × 105 | 1.18 × 105 | 5.75 × 10−9 | 1.32 × 105 | 0.00 | |
| Worst | 3.51 × 104 | 4.84 × 105 | 3.82 × 105 | 2.65 × 104 | 4.21 × 105 | 0.00 | |
| Mean | 1.29 × 101 | 4.92 × 101 | 9.49 × 101 | 3.84 × 10−1 | 8.72 × 101 | 8.3 × 10−185 | |
| Std | 1.43 | 7.11 | 1.69 | 5.34 × 10−1 | 3.60 | 0.00 | |
| Best | 9.33 | 3.82 × 101 | 9.16 × 101 | 1.20 × 10−3 | 7.85 × 101 | 8.0 × 10−196 | |
| Worst | 1.64 × 101 | 6.00 × 101 | 9.80 × 101 | 2.21 | 9.37 × 101 | 1.4 × 10−183 | |
| Mean | 9.29 × 105 | 1.25 × 107 | 8.76 × 107 | 2.76 × 101 | 7.18 × 107 | 9.56 × 10−1 | |
| Std | 1.83 × 105 | 7.23 × 106 | 7.53 × 107 | 7.61 × 101 | 4.48 × 107 | 3.14 | |
| Best | 5.60 × 105 | 2.67 × 106 | 3.08 × 106 | 1.58 × 10−6 | 7.16 × 106 | 2.28 × 10−5 | |
| Worst | 1.31 × 106 | 2.98 × 107 | 2.41 × 108 | 3.91 × 102 | 2.10 × 108 | 1.30 × 101 | |
| Mean | 5.28 × 102 | 1.88 × 104 | 3.90 × 104 | 1.35 × 101 | 6.04 × 103 | 1.02 × 10−2 | |
| Std | 5.82 × 101 | 9.95 × 103 | 1.44 × 104 | 3.60 × 101 | 4.38 × 103 | 1.56 × 10−2 | |
| Best | 4.38 × 102 | 2.98 × 103 | 9.04 × 103 | 1.20 × 10−4 | 1.06 × 103 | 4.85 × 10−6 | |
| Worst | 6.64 × 102 | 3.99 × 104 | 7.22 × 104 | 1.73 × 102 | 1.87 × 104 | 7.35 × 10−2 | |
| Mean | 2.83 × 103 | 1.70 × 101 | 2.33 × 102 | 1.06 × 10−2 | 9.90 × 101 | 4.08 × 10−5 | |
| Std | 2.39 × 102 | 1.07 × 101 | 1.29 × 102 | 1.72 × 10−2 | 5.30 × 101 | 3.63 × 10−5 | |
| Best | 2.34 × 103 | 6.68 × 10−1 | 2.24 × 101 | 1.63 × 10−4 | 2.18 × 101 | 5.29 × 10−6 | |
| Worst | 3.41 × 103 | 4.49 × 101 | 4.96 × 102 | 9.07 × 10−2 | 2.45 × 102 | 1.79 × 10−4 | |
| Mean | 1.60 × 103 | 9.29 × 102 | 9.08 × 102 | 1.52 × 101 | 2.61 × 102 | 0.00 | |
| Std | 7.03 × 101 | 1.59 × 102 | 7.48 × 101 | 3.23 × 101 | 1.43 × 102 | 0.00 | |
| Best | 1.48 × 103 | 6.32 × 102 | 7.52 × 102 | 4.87 × 10−8 | 6.45 × 101 | 0.00 | |
| Worst | 1.76 × 103 | 1.23 × 103 | 1.05 × 103 | 1.20 × 102 | 6.72 × 102 | 000 | |
| Mean | 8.69 | 1.26 × 101 | 1.98 × 101 | 5.09 × 10−1 | 1.84 × 101 | 1.84 × 10−15 | |
| Std | 3.10 × 10−1 | 2.86 | 2.55 × 10−1 | 7.84 × 10−1 | 5.11 | 1.60 × 10−15 | |
| Best | 8.03 | 3.04 | 1.93 × 101 | 5.52 × 10−5 | 4.08 | 8.88 × 10−16 | |
| Worst | 9.19 | 1.99 × 101 | 1.99 × 101 | 2.95 | 2.07 × 101 | 4.44 × 10−15 | |
| Mean | 1.13 | 1.80 × 102 | 3.24 × 102 | 3.65 × 10−1 | 6.37 × 101 | 0.00 | |
| Std | 1.19 × 10−2 | 7.02 × 101 | 1.22 × 102 | 4.90 × 10−1 | 5.05 × 101 | 0.00 | |
| Best | 1.11 | 6.23 × 101 | 1.57 × 102 | 3.17 × 10−7 | 1.71 | 0.00 | |
| Worst | 1.16 | 3.67 × 102 | 5.90 × 102 | 1.53 | 1.87 × 102 | 0.00 | |
| Mean | 2.65 × 101 | 2.74 × 106 | 1.69 × 108 | 2.58 × 10−3 | 1.81 × 108 | 3.84 × 10−6 | |
| Std | 2.23 × 101 | 3.60 × 106 | 1.64 × 108 | 4.81 × 10−3 | 9.86 × 107 | 9.88 × 10−6 | |
| Best | 9.07 | 7.22 × 101 | 6.03 × 106 | 1.20 × 10−6 | 2.78 × 107 | 3.83 × 10−9 | |
| Worst | 1.34 × 102 | 1.63 × 107 | 4.86 × 108 | 2.40 × 10−2 | 4.08 × 108 | 3.97 × 10−5 | |
| Mean | 5.40 × 103 | 2.15 × 107 | 2.78 × 108 | 5.53 × 10−1 | 3.61 × 108 | 1.38 × 10−3 | |
| Std | 4.36 × 103 | 1.81 × 107 | 2.88 × 108 | 1.05 | 1.89 × 108 | 4.23 × 10−3 | |
| Best | 7.92 × 102 | 2.39 × 106 | 1.00 × 107 | 1.47 × 10−4 | 7.99 × 107 | 4.57 × 10−10 | |
| Worst | 2.54 × 104 | 7.43 × 107 | 9.49 × 108 | 4.18 | 7.57 × 108 | 2.32 × 10−2 |
| Functions | Metric | PSO | DA | MFO | ADA | SCA | HIDA |
|---|---|---|---|---|---|---|---|
| Mean | 1.64 × 103 | 3.96 × 104 | 1.35 × 105 | 7.42 | 2.35 × 104 | 0.00 | |
| Std | 1.59 × 102 | 2.15 × 104 | 2.20 × 104 | 2.09 × 101 | 1.81 × 104 | 0.00 | |
| Best | 1.28 × 103 | 6.67 × 103 | 9.36 × 104 | 7.27 × 10−9 | 2.68 × 103 | 0.00 | |
| Worst | 1.95 × 103 | 9.35 × 104 | 1.77 × 105 | 1.03 × 102 | 9.69 × 104 | 0.00 | |
| Mean | 2.4 × 1038 | 1.67 × 102 | 4.46 × 102 | 2.73 | 1.25 × 101 | 4.5 × 10−184 | |
| Std | 9.17 × 1038 | 5.90 × 101 | 5.90 × 101 | 3.12 | 1.35 × 101 | 0.00 | |
| Best | 1.41 × 1016 | 5.33 × 101 | 3.36 × 102 | 7.96 × 10−4 | 8.81 × 10−1 | 2.9 × 10−193 | |
| Worst | 3.88 × 1039 | 2.94 × 102 | 5.51 × 102 | 1.08 × 101 | 5.65 × 101 | 4.4 × 10−183 | |
| Mean | 8.14 × 104 | 8.62 × 105 | 6.12 × 105 | 8.93 × 103 | 8.05 × 105 | 0.00 | |
| Std | 1.50 × 104 | 3.48 × 105 | 1.66 × 105 | 1.58 × 104 | 1.70 × 105 | 0.00 | |
| Best | 5.23 × 104 | 3.09 × 105 | 3.54 × 105 | 3.18 × 10−3 | 5.08 × 105 | 0.00 | |
| Worst | 1.11 × 105 | 1.58 × 106 | 9.25 × 105 | 6.17 × 104 | 1.10 × 106 | 0.00 | |
| Mean | 1.98 × 101 | 5.69 × 101 | 9.70 × 101 | 2.08 × 10−1 | 9.50 × 101 | 5.8 × 10−185 | |
| Std | 1.27 | 9.18 | 1.05 | 3.04 × 10−1 | 1.22 | 0.00 | |
| Best | 1.76 × 101 | 4.14 × 101 | 9.36 × 101 | 1.20 × 10−3 | 9.30 × 101 | 1.1 × 10−191 | |
| Worst | 2.31 × 101 | 7.97 × 101 | 9.84 × 101 | 1.48 | 9.73 × 101 | 8.8 × 10−184 | |
| Mean | 5.66 × 106 | 3.38 × 107 | 4.3 × 108 | 7.70 × 101 | 2.93 × 108 | 8.23 × 10−1 | |
| Std | 8.15 × 105 | 1.60 × 107 | 1.21 × 108 | 1.11 × 102 | 5.08 × 107 | 4.36 | |
| Best | 4.37 × 106 | 6.43 × 106 | 1.88 × 108 | 1.82 × 10−3 | 1.88 × 108 | 8.27 × 10−5 | |
| Worst | 7.03 × 106 | 7.58 × 107 | 7.64 × 108 | 4.84 × 102 | 3.90 × 108 | 2.39 × 101 | |
| Mean | 1.62 × 103 | 3.49 × 104 | 1.43 × 105 | 5.94 | 2.08 × 104 | 1.08 × 10−2 | |
| Std | 1.47 × 102 | 1.74 × 104 | 2.43 × 104 | 8.40 | 1.12 × 104 | 1.97 × 10−2 | |
| Best | 1.26 × 103 | 9.74 × 103 | 8.16 × 104 | 7.90 × 10−4 | 2.36 × 103 | 2.33 × 10−9 | |
| Worst | 1.91 × 103 | 7.84 × 104 | 1.97 × 105 | 3.34 × 101 | 4.23 × 104 | 9.11 × 10−2 | |
| Mean | 8.50 × 103 | 8.82 × 101 | 1.35 × 103 | 1.29 × 10−2 | 8.26 × 102 | 3.54 × 10−5 | |
| Std | 4.95 × 102 | 7.59 × 101 | 3.70 × 102 | 1.50 × 10−2 | 3.22 × 102 | 2.62 × 10−5 | |
| Best | 7.53 × 103 | 1.55 × 101 | 7.24 × 102 | 7.52 × 10−5 | 1.46 × 102 | 4.77 × 10−6 | |
| Worst | 9.15 × 103 | 3.06 × 102 | 2.15 × 103 | 5.21 × 10−2 | 1.39 × 103 | 1.14 × 10−4 | |
| Mean | 2.86 × 103 | 1.61 × 103 | 1.81 × 103 | 2.81 × 101 | 4.80 × 102 | 0.00 | |
| Std | 8.91 × 101 | 2.37 × 102 | 1.04 × 102 | 5.25 × 101 | 2.09 × 102 | 0.00 | |
| Best | 2.63 × 103 | 1.07 × 103 | 1.54 × 103 | 8.73 × 10−7 | 7.51 × 101 | 0.00 | |
| Worst | 3.05 × 103 | 1.99 × 103 | 2.07 × 103 | 2.03 × 102 | 9.35 × 102 | 0.00 | |
| Mean | 1.05 × 101 | 1.28 × 101 | 1.99 × 101 | 3.50 × 10−1 | 1.83 × 101 | 2.55 × 10−15 | |
| Std | 3.18 × 10−1 | 2.28 | 5.71 × 10−2 | 5.51 × 10−1 | 4.39 | 1.80 × 10−15 | |
| Best | 9.75 | 6.88 | 1.96 × 101 | 3.23 × 10−5 | 7.54 | 8.88 × 10−16 | |
| Worst | 1.12 × 101 | 1.64 × 101 | 1.99 × 101 | 1.92 | 2.07 × 101 | 4.44 × 10−15 | |
| Mean | 1.42 | 2.81 × 102 | 1.28 × 103 | 5.96 × 10−1 | 1.92 × 102 | 0.00 | |
| Std | 2.85 × 10−2 | 1.66 × 102 | 1.82 × 102 | 5.20 × 10−1 | 1.09 × 102 | 0.00 | |
| Best | 1.36 | 5.62 × 101 | 8.51 × 102 | 7.72 × 10−7 | 4.48 × 101 | 0.00 | |
| Worst | 1.47 | 6.28 × 102 | 1.64 × 103 | 1.54 | 4.79 × 102 | 0.00 | |
| Mean | 1.01 × 104 | 1.20 × 107 | 8.46 × 108 | 6.60 × 10−3 | 7.60 × 108 | 1.66 × 10−6 | |
| Std | 1.26 × 104 | 1.34 × 107 | 3.56 × 108 | 1.45 × 10−2 | 2.49 × 108 | 5.00 × 10−6 | |
| Best | 1.88 × 102 | 1.46 × 105 | 2.28 × 108 | 4.05 × 10−7 | 3.56 × 108 | 3.04 × 10−9 | |
| Worst | 4.48 × 104 | 5.54 × 107 | 1.65 × 109 | 6.07 × 10−2 | 1.42 × 109 | 2.74 × 10−5 | |
| Mean | 2.70 × 105 | 6.22 × 107 | 1.73 × 109 | 4.05 × 10-1 | 1.46 × 109 | 1.01 × 10−3 | |
| Std | 1.29 × 105 | 5.28 × 107 | 5.44 × 108 | 1.03 | 4.86 × 108 | 2.00 × 10−3 | |
| Best | 5.58 × 104 | 5.70 × 106 | 2.44 × 108 | 7.72 × 10−6 | 4.98 × 108 | 4.95 × 10−8 | |
| Worst | 5.46 × 105 | 1.99 × 108 | 2.67 × 109 | 5.19 | 2.65 × 109 | 8.82 × 10−3 |
| Metric | |||||||
|---|---|---|---|---|---|---|---|
| PSO | P | 1.21 × 10−12 | 3.02 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| DA | P | 1.21 × 10−12 | 3.02 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| MFO | P | 1.21 × 10−12 | 3.02 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| ADA | P | 1.21 × 10−12 | 3.02 × 10−11 | 1.21 × 10−12 | 2.92 × 10−11 | 8.48 × 10−9 | 8.98 × 10−10 |
| S | |||||||
| SCA | P | 1.21 × 10−12 | 3.02 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| PSO | P | 3.02 × 10−11 | 1.21 × 10−12 | 1.45 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| DA | P | 3.02 × 10−11 | 1.21 × 10−12 | 1.45 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| MFO | P | 3.02 × 10−11 | 1.21 × 10−12 | 1.45 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| ADA | P | 4.98 × 10−11 | 1.21 × 10−12 | 1.45 × 10−11 | 1.21 × 10−12 | 9.76 × 10−10 | 7.08 × 10−8 |
| S | |||||||
| SCA | P | 3.02 × 10−11 | 1.21 × 10−12 | 1.45 × 10−11 | 1.21 × 10−12 | 3.02 × 10−11 | 3.02 × 10−11 |
| S | |||||||
| Statistical result | |||||||
| Metric | |||||||
|---|---|---|---|---|---|---|---|
| HIDA | Mean | 2.8 × 10−122 | 5.40 × 10−62 | 8.1 × 10−121 | 1.48 × 10−62 | 4.30 × 10−1 | 2.42 × 10−2 |
| Std | 1.2 × 10−121 | 1.75 × 10−61 | 3.5 × 10−120 | 4.07 × 10−62 | 1.27 | 6.91 × 10−2 | |
| CGWO-DA | Mean | 2.86 × 10−46 | 6.69 × 10−28 | 5.34 × 10−9 | 6.99 × 10−12 | 2.71 × 101 | 5.10 × 10−1 |
| Std | 5.93 × 10−46 | 7.47 × 10−28 | 2.77 × 10−8 | 9.47 × 10−12 | 7.05 × 10−1 | 3.15 × 10−1 | |
| HIDA | Mean | 7.39 × 10−5 | 0.00 | 3.26 × 10−15 | 0.00 | 5.31 × 10−5 | 1.73 × 10−4 |
| Std | 4.52 × 10−5 | 0.00 | 1.70 × 10−15 | 0.00 | 8.38 × 10−5 | 3.01 × 10−4 | |
| CGWO-DA | Mean | 1.20 × 10−3 | 6.71 × 10−1 | 1.60 × 10−14 | 2.36 × 10−3 | 3.57 × 10−2 | 6.21 × 10−1 |
| Std | 6.00 × 10−4 | 2.41 | 3.30 × 10−15 | 6.49 × 10−3 | 1.90 × 10−2 | 2.23 × 10−1 |
| Metric | |||||||
|---|---|---|---|---|---|---|---|
| HIDA | Mean | 1.3 × 10−123 | 1.21 × 10−62 | 3.2 × 10−121 | 2.27 × 10−62 | 1.05 | 9.69 × 10−3 |
| Std | 3.5 × 10−123 | 3.61 × 10−62 | 1.0 × 10−120 | 3.92 × 10−62 | 2.29 | 1.31 × 10−2 | |
| The modified DA | Mean | 4.93 | 8.68 × 10−1 | 8.40 × 101 | 1.78 | 5.74 × 102 | 5.58 |
| Std | 7.16 × 10−18 | 3.76 × 10−5 | 2.10 × 10−6 | 2.78 × 10−3 | 6.79 | 1.32 × 10−15 | |
| HIDA | Mean | 7.78 × 10−5 | 0.00 | 2.78 × 10−15 | 0.00 | 1.98 × 10−4 | 2.14 × 10−3 |
| Std | 5.34 × 10−5 | 0.00 | 1.80 × 10−15 | 0.00 | 2.76 × 10−4 | 7.05 × 10−3 | |
| The modified DA | Mean | 2.22 × 10−2 | 2.47 × 101 | 2.32 | 4.34 × 10−1 | 1.29 | 6.71 × 10−1 |
| Std | 4.69 × 10−3 | 9.48 | 4.87 × 10−1 | 7.35 × 10−2 | 9.83 × 10−2 | 4.63 × 10−3 |
| Functions | Name | Characteristics | Range | Optimum | |
|---|---|---|---|---|---|
| CEC2013 | CEC04 | Rotated Discus Function | Unimodal | −1100 | |
| CEC16 | Rotated Katsuura Function | Multimodal | 200 | ||
| CEC17 | Lunacek Bi-Rastrigin Function | Multimodal | 300 | ||
| CEC20 | Expanded Scaffer’s F6 Function | Composition | 600 | ||
| CEC24 | Composition Function 4 (n = 3, Rotated) | Composition | 1000 | ||
| CEC2014 | CEC05 | Shifted and Rotated Ackley’s Function | Multimodal | 500 | |
| CEC12 | Shifted and Rotated Katsuura Function | Multimodal | 1200 | ||
| CEC23 | Composition Function 1 (n = 5) | Composition | 2300 | ||
| CEC24 | Composition Function 2 (n = 3) | Composition | 2400 | ||
| CEC25 | Composition Function 3 (n = 3) | Composition | 2500 | ||
| CEC26 | Composition Function 4 (n = 5) | Composition | 2600 | ||
| CEC28 | Composition Function 6 (n = 5) | Composition | 2800 |
| Metric | |||||||
|---|---|---|---|---|---|---|---|
| PSO | Mean | 4.88 × 104 | 2.03 × 102 | 9.73 × 102 | 6.15 × 102 | 1.39 × 103 | 5.21 × 102 |
| Std | 1.11 × 104 | 4.29 × 10−1 | 1.10 × 102 | 2.81 × 10−2 | 5.91 × 101 | 5.64 × 10−2 | |
| DA | Mean | 1.02 × 105 | 2.28 × 102 | 7.76 × 103 | 6.15 × 102 | 1.41 × 103 | 5.21 × 102 |
| Std | 2.57 × 104 | 6.03 × 10−1 | 1.02 × 102 | 1.63 × 10−1 | 5.37 × 101 | 9.11 × 10−2 | |
| MFO | Mean | 1.98 × 105 | 2.04 × 102 | 2.62 × 103 | 6.15 × 102 | 1.38 × 103 | 5.21 × 102 |
| Std | 6.16 × 104 | 1.59 | 2.60 × 102 | 3.63 × 10−1 | 5.74 × 101 | 1.10 × 10−1 | |
| SOA | Mean | 4.67 × 104 | 2.03 × 102 | 8.48 × 102 | 6.15 × 102 | 1.30 × 103 | 5.21 × 102 |
| Std | 7.79 × 103 | 4.71 × 10−1 | 6.21 × 101 | 6.40 × 10−1 | 1.01 × 101 | 5.78 × 10−2 | |
| WOA | Mean | 9.90 × 104 | 2.03 × 102 | 9.84 × 102 | 6.15 × 102 | 1.32 × 103 | 5.21 × 102 |
| Std | 3.50 × 104 | 5.69 × 10−1 | 1.14 × 102 | 1.70 × 10−1 | 9.72 | 1.19 × 10−1 | |
| GWO | Mean | 5.04 × 104 | 2.03 × 102 | 5.25 × 102 | 6.15 × 102 | 1.26 × 103 | 5.21 × 102 |
| Std | 5.97 × 103 | 4.19 × 10−1 | 4.33 × 101 | 1.31 | 1.02 × 101 | 5.51 × 10−2 | |
| HIDA | Mean | 3.87 × 104 | 2.03 × 102 | 1.24 × 103 | 6.15 × 102 | 1.33 × 103 | 5.21 × 102 |
| Std | 6.61 × 102 | 4.08 × 10−1 | 6.57 × 101 | 4.80 × 10−4 | 1.36 × 101 | 5.42 × 10−2 | |
| Metric | |||||||
| PSO | Mean | 1.20 × 103 | 2.61 × 103 | 2.63 × 103 | 2.72 × 103 | 2.79 × 103 | 7.77 × 103 |
| Std | 4.97 × 10−1 | 6.33 × 10−2 | 1.04 × 101 | 5.48 | 2.53 × 101 | 7.29 × 102 | |
| DA | Mean | 1.20 × 103 | 2.72 × 103 | 2.66 × 103 | 2.75 × 103 | 2.77 × 103 | 6.99 × 103 |
| Std | 7.19 × 10−1 | 4.51 × 101 | 1.23 × 101 | 2.18 × 101 | 5.08 × 101 | 1.31 × 103 | |
| MFO | Mean | 1.20 × 103 | 3.00 × 103 | 2.91 × 103 | 2.77 × 103 | 2.71 × 103 | 6.11 × 103 |
| Std | 1.15 × 101 | 7.27 × 101 | 3.10 × 101 | 3.69 × 101 | 4.11 | 7.87 × 102 | |
| SOA | Mean | 1.20 × 103 | 2.68 × 103 | 2.60 × 103 | 2.71 × 103 | 2.70 × 103 | 4.25 × 103 |
| Std | 5.34 × 10−1 | 3.38 × 101 | 1.23 × 10−2 | 1.05 × 101 | 7.78 × 10−1 | 2.95 × 102 | |
| WOA | Mean | 1.20 × 103 | 2.68 × 103 | 2.61 × 103 | 2.72 × 103 | 2.73 × 103 | 5.42 × 103 |
| Std | 7.56 × 10−1 | 1.59 × 101 | 6.87 | 2.00 × 101 | 6.51 × 101 | 6.69 × 102 | |
| GWO | Mean | 1.20 × 103 | 2.64 × 103 | 2.60 × 103 | 2.71 × 103 | 2.75 × 103 | 4.01 × 103 |
| Std | 1.34 × 101 | 6.50 × 101 | 8.34 × 10−3 | 5.58 | 6.02 × 101 | 2.58 × 102 | |
| HIDA | Mean | 1.20 × 103 | 2.50 × 103 | 2.60 × 103 | 2.70 × 103 | 2.73 × 103 | 6.01 × 103 |
| Std | 3.29 × 10−1 | 1.19 × 10−13 | 8.14 × 10−4 | 1.69 × 10−13 | 4.02 × 101 | 2.07 × 103 |
| Voltage/V | Current/A | Voltage/V | Current/A |
|---|---|---|---|
| 0.764 | −0.2057 | 0.728 | 0.4137 |
| 0.762 | −0.1291 | 0.7065 | 0.4373 |
| 0.7605 | −0.0588 | 0.6755 | 0.4590 |
| 0.7605 | 0.0057 | 0.632 | 0.4784 |
| 0.76 | 0.0646 | 0.573 | 0.496 |
| 0.759 | 0.1185 | 0.499 | 0.5119 |
| 0.757 | 0.1678 | 0.413 | 0.5265 |
| 0.757 | 0.2132 | 0.3165 | 0.5398 |
| 0.7555 | 0.2545 | 0.212 | 0.5521 |
| 0.754 | 0.2924 | 0.1035 | 0.5633 |
| 0.7505 | 0.3269 | −0.01 | 0.5736 |
| 0.7465 | 0.3585 | −0.123 | 0.5833 |
| 0.7385 | 0.3873 | −0.21 | 0.59 |
| PRM | UB | LB |
|---|---|---|
| 100 | 0 | |
| 1 | 0 | |
| 2 | 1 | |
| 1 | 0 | |
| 0.5 | 0 |
| TEMP | PRM | Method | |||||
|---|---|---|---|---|---|---|---|
| HIDA | DA | WOA | GWO | MFO | HHO | ||
| 0 °C | 0.7616 | 0.7861 | 0.7597 | 0.7590 | 0.7608 | 0.7531 | |
| 0.5278 | 0.6164 | 0.2648 | 0.1715 | 0.2597 | 0.0015 | ||
| 55.8763 | 91.0819 | 68.0952 | 64.9598 | 49.0832 | 74.7758 | ||
| 0.0343 | 0.0780 | 0.0374 | 0.0392 | 0.0373 | 0.0632 | ||
| 1.7177 | 1.7402 | 1.6376 | 1.5913 | 1.6358 | 1.2162 | ||
| 8 °C | 0.7598 | 0.7592 | 0.7606 | 0.7613 | 0.7598 | 0.7589 | |
| 0.3616 | 0.4298 | 0.6159 | 0.3675 | 0.5913 | 0.2205 | ||
| 71.4923 | 47.6686 | 74.5341 | 56.7082 | 63.6258 | 86.3956 | ||
| 0.0358 | 0.0341 | 0.0335 | 0.0363 | 0.0338 | 0.0386 | ||
| 1.6251 | 1.6456 | 1.6869 | 1.6271 | 1.6818 | 1.5714 | ||
| 14 °C | 0.7614 | 0.7616 | 0.7599 | 0.7612 | 0.7600 | 0.7593 | |
| 0.2515 | 0.7161 | 0.3361 | 0.2420 | 0.6739 | 0.3665 | ||
| 41.6191 | 51.4359 | 69.9134 | 43.8436 | 75.3860 | 86.3543 | ||
| 0.0373 | 0.0321 | 0.0364 | 0.0372 | 0.0331 | 0.0362 | ||
| 1.5530 | 1.6701 | 1.5832 | 1.5488 | 1.6621 | 1.5925 | ||
| 20 °C | 0.7606 | 0.7932 | 0.7601 | 0.7619 | 0.7597 | 0.7891 | |
| 0.5967 | 0.1751 | 0.4076 | 0.3919 | 0.5803 | 0.0258 | ||
| 88.1007 | 52.9407 | 71.8980 | 47.1064 | 76.4283 | 63.1466 | ||
| 0.0342 | 0.1085 | 0.0355 | 0.0359 | 0.0338 | 0.0441 | ||
| 1.6141 | 1.4983 | 1.5715 | 1.5676 | 1.6750 | 1.3252 | ||
| 26 °C | 0.7612 | 0.7606 | 0.7614 | 0.7602 | 0.7609 | 0.7616 | |
| 0.9563 | 0.6868 | 0.4235 | 0.3758 | 0.2962 | 0.3230 | ||
| 73.2298 | 54.5625 | 49.3822 | 63.3955 | 49.3590 | 43.1086 | ||
| 0.0311 | 0.0319 | 0.0348 | 0.0357 | 0.0366 | 0.0360 | ||
| 1.6369 | 1.5986 | 1.5445 | 1.5315 | 1.5069 | 1.5161 | ||
| 32 °C | 0.7604 | 0.7666 | 0.7594 | 0.7608 | 0.7604 | 0.7599 | |
| 0.6612 | 0.6197 | 0.3187 | 0.4553 | 0.9514 | 0.4231 | ||
| 84.9927 | 70.1958 | 77.8816 | 63.0971 | 58.9697 | 75.5183 | ||
| 0.0335 | 0.0362 | 0.0370 | 0.0352 | 0.0313 | 0.0352 | ||
| 1.5621 | 1.5508 | 1.4844 | 1.5215 | 1.6039 | 1.5136 | ||
| 38 °C | 0.7601 | 0.7664 | 0.7616 | 0.7612 | 0.7606 | 0.7612 | |
| 0.4384 | 0.8570 | 0.2876 | 0.2649 | 0.4398 | 0.9741 | ||
| 73.9126 | 85.6477 | 42.6690 | 44.4881 | 61.6287 | 77.4674 | ||
| 0.0351 | 0.0426 | 0.0367 | 0.0367 | 0.0349 | 0.0313 | ||
| 1.4881 | 1.5619 | 1.4461 | 1.4381 | 1.4886 | 1.5759 | ||
| TEMP | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 °C | 8 °C | 14 °C | 20 °C | 26 °C | 32 °C | 38 °C | ||
| RMSE | DA | 4.53 × 10−2 | 1.02 × 10−1 | 5.90 × 10−2 | 1.26 × 10−1 | 5.79 × 10−2 | 6.52 × 10−2 | 7.63 × 10−2 |
| MFO | 1.24 × 10−1 | 2.18 × 10−3 | 2.08 × 10−3 | 2.09 × 10−3 | 1.57 × 10−1 | 2.08 × 10−3 | 3.08 × 10−2 | |
| WOA | 5.64 × 10−3 | 2.93 × 10−2 | 3.18 × 10−3 | 4.88 × 10−2 | 1.99 × 10−2 | 1.26 × 10−3 | 4.26 × 10−3 | |
| HHO | 1.21 × 10−2 | 1.75 × 10−3 | 1.69 × 10−3 | 1.89 × 10−2 | 2.09 × 10−3 | 3.96 × 10−3 | 2.14 × 10−3 | |
| GWO | 3.59 × 10−3 | 1.04 × 10−2 | 3.49 × 10−3 | 7.76 × 10−3 | 2.77 × 10−3 | 3.52 × 10−3 | 5.49 × 10−3 | |
| HIDA | 1.31 × 10−3 | 1.01 × 10−3 | 1.46 × 10−3 | 1.45 × 10−3 | 2.10 × 10−3 | 1.51 × 10−3 | 3.11 × 10−3 | |
| Parameter | LB | UB |
|---|---|---|
| (V) | 30 | 40 |
| (V) | 25 | 35 |
| (A) | 2 | 10 |
| (A) | 2 | 8 |
| Number of Test Group | ||
|---|---|---|
| No.1 | 1000 | 10 |
| No.2 | 1000 | 15 |
| No.3 | 1000 | 20 |
| No.4 | 1000 | 25 |
| No.5 | 1000 | 30 |
| No.6 | 500 | 25 |
| No.7 | 650 | 25 |
| No.8 | 800 | 25 |
| No.9 | 950 | 25 |
| No.10 | 1100 | 25 |
| Number | Algorithm | RMSE | ||||
|---|---|---|---|---|---|---|
| No.1 | DA | 30 | 29.2941 | 7.63161 | 5.12377 | 0 |
| HIDA | 31.25 | 28.35 | 7.32 | 7.262 | 0 | |
| No.2 | DA | 37.4712 | 31.9661 | 2.03157 | 2.56828 | 3.14 × 10−4 |
| HIDA | 31.25 | 24.4562 | 7.2944 | 7.5290 | 1.24 × 10−9 | |
| No.3 | DA | 37.6318 | 25 | 7.35477 | 8 | 6.30 × 10−3 |
| HIDA | 31.3979 | 33.74 | 2 | 7.22 | 9.81 × 10−6 | |
| No.4 | DA | 30 | 29.2941 | 7.63161 | 5.12377 | 2.56 × 10−13 |
| HIDA | 30.01 | 30.0653 | 2.0525 | 4.2920 | 0 | |
| No.5 | DA | 33.8981 | 35 | 2.27678 | 6.5647 | 2.40 × 10−8 |
| HIDA | 31.25 | 28.8738 | 5.15286 | 5.58377 | 1.73 × 10−15 | |
| No.6 | DA | 38.8812 | 35 | 2 | 2.44428 | 2.84 × 10−7 |
| HIDA | 39.7002 | 34.7647 | 2.17224 | 2.12754 | 2.33 × 10−14 | |
| No.7 | DA | 39.0699 | 30.7876 | 2.6315 | 2.88846 | 2.22 × 10−6 |
| HIDA | 33.3171 | 32.2484 | 5.176 | 6.50024 | 1.16 × 10−14 | |
| No.8 | DA | 35.4175 | 31.5476 | 2 | 2.07339 | 3.12 × 10−4 |
| HIDA | 34.8152 | 27.7991 | 3.6506 | 4.18334 | 1.62 × 10−13 | |
| No.9 | DA | 36.8098 | 30.0237 | 2.05152 | 2.84683 | 0.012921 |
| HIDA | 36.4092 | 34.0105 | 3.38801 | 5.48152 | 0.019944 | |
| No.10 | DA | 38.9795 | 35 | 6.35218 | 5.13714 | 0.12586 |
| HIDA | 36.1361 | 25.7918 | 4.67209 | 6.26081 | 6.4310−7 |
| Parameter | LB | UB |
|---|---|---|
| () | 0 | 1 |
| () | 0 | 1 |
| () | 0 | 0.5 |
| () | 0 | 100 |
| 1 | 2 |
| Parameter | LB | UB |
|---|---|---|
| () | 0 | 2 |
| () | 0 | 50 |
| () | 0 | 0.36 |
| () | 0 | 1000 |
| 1 | 60 |
| Voltage/V | Current/A | Voltage/V | Current/A |
|---|---|---|---|
| 0.000 | 1.663 | 14.880 | 1.597 |
| 0.118 | 1.663 | 15.590 | 1.581 |
| 2.237 | 1.661 | 16.400 | 1.542 |
| 5.434 | 1.653 | 16.710 | 1.524 |
| 7.260 | 1.650 | 16.980 | 1.500 |
| 9.680 | 1.645 | 17.130 | 1.485 |
| 11.590 | 1.640 | 17.320 | 1.465 |
| 12.600 | 1.636 | 17.910 | 1.388 |
| 13.370 | 1.629 | 19.080 | 1.118 |
| 14.090 | 1.619 | 21.020 | 0.000 |
| Algorithm | T = 5 °C | |||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | ||||||||
| DA | 0.73651 | 3.92 × 10−7 | 0 | 43.884 | 1.7032 | 5.88 × 10−7 | 1.87176 | 0.046553 |
| HIDA | 0.762025 | 6.38 × 10−7 | 0.0301296 | 71.1489 | 2 | 8.43 × 10−7 | 1.76253 | 0.0031434 |
| T = 15 °C | ||||||||
| DA | 0.777943 | 7.53 × 10−7 | 0.0380212 | 63.4313 | 1.85498 | 1.00 × 10−6 | 1.7391 | 0.01737 |
| HIDA | 0.762496 | 7.85 × 10−7 | 0.0287002 | 54.9234 | 1.83636 | 7.33 × 10−7 | 1.71132 | 0.003856 |
| T = 25 °C | ||||||||
| DA | 0.79259 | 6.92 × 10−7 | 0.0639931 | 35.5565 | 1.59057 | 4.03 × 10−7 | 1.94292 | 0.088207 |
| HIDA | 0.761596 | 5.74 × 10−7 | 0.0336924 | 58.9493 | 1.58317 | 3.07 × 10−9 | 1.77333 | 0.0016405 |
| Algorithm | T = 5 °C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | ||||||||||
| DA | 0.73 | 8.79 × 10−7 | 0.025 | 68.18 | 1.93 | 3.42 × 10−7 | 1.72 | 1.11 × 10−7 | 1.72 | 0.023 |
| HIDA | 0.76 | 1.00 × 10−6 | 0.019 | 100 | 2 | 1.00 × 10−6 | 1.84 | 1.00 × 10−6 | 2 | 0.011 |
| T = 15 °C | ||||||||||
| DA | 0.82 | 2.08 × 10−7 | 0.053 | 37.71 | 1.54 | 2.29 × 10−9 | 1.35 | 2.69 × 10−7 | 1.73 | 0.062 |
| HIDA | 0.76 | 2.83 × 10−7 | 0.033 | 71.14 | 1.65 | 2.09 × 10−7 | 1.93 | 2.13 × 10−7 | 1.60 | 0.002 |
| T = 25 °C | ||||||||||
| DA | 0.46 | 5.03 × 10−7 | 0.001 | 45.81 | 1.96 | 5.19 × 10−7 | 1.66 | 5.38 × 10−7 | 1.94 | 0.246 |
| HIDA | 0.76 | 0 | 0.032 | 37.46 | 1.88 | 5.45 × 10−7 | 1.62 | 2.13 × 10−7 | 1.59 | 0.003 |
| Algorithm | T = 5 °C | |||||
|---|---|---|---|---|---|---|
| RMSE | ||||||
| DA | 1.725472 | 3.94 × 10−5 | 0.01927654 | 657.2033 | 2.31366 | 0.10595 |
| HIDA | 1.6737 | 8.91 × 10−7 | 0.005223 | 9.5262 | 1.6904 | 0.0046089 |
| T = 15 °C | ||||||
| DA | 1.662472 | 7.80 × 10−6 | 0 | 750.9523 | 1.908739 | 0.021485 |
| HIDA | 1.668033 | 1.93 × 10−5 | 0 | 260.4144 | 2.071242 | 0.016495 |
| T = 25 °C | ||||||
| DA | 1.84453 | 3.87 × 10−5 | 0.0108882 | 0.989867 | 15.3303 | 0.31465 |
| HIDA | 1.68633 | 4.37 × 10−5 | 0 | 61.0625 | 2.15905 | 0.03228 |
| Engineering Problem | Algorithm | Mean | Std |
|---|---|---|---|
| Pressure vessel design | DA | 1.0069 × 106 | 6.6822 × 105 |
| HIDA | 8.8013 × 105 | 1.6648 × 106 | |
| Gear train design | DA | 1.5273 × 10−3 | 3.7362 × 10−3 |
| HIDA | 2.7591 × 10−4 | 8.1504 × 10−4 | |
| Cantilever beam design | DA | 6.5916 | 1.6363 |
| HIDA | 1.5530 | 3.8314 × 10−2 | |
| Three bar truss design | DA | 2.7106 × 102 | 7.0500 |
| HIDA | 2.6976 × 102 | 2.9407 | |
| Gas transmission compressor design | DA | 7.1438 × 107 | 1.8868 × 108 |
| HIDA | 1.2387 × 106 | 1.6696 × 104 | |
| Car side design | DA | 2.6640 × 101 | 1.3003 |
| HIDA | 2.6629 × 101 | 1.0763 | |
| Piston rod optimization | DA | 1.3009 × 102 | 2.6634 × 102 |
| HIDA | 4.3767 × 101 | 2.4095 × 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhang, D.; He, Q.; Li, L. A Hybrid-Strategy-Improved Dragonfly Algorithm for the Parameter Identification of an SDM. Sustainability 2023, 15, 11791. https://doi.org/10.3390/su151511791
Zhao J, Zhang D, He Q, Li L. A Hybrid-Strategy-Improved Dragonfly Algorithm for the Parameter Identification of an SDM. Sustainability. 2023; 15(15):11791. https://doi.org/10.3390/su151511791
Chicago/Turabian StyleZhao, Jianping, Damin Zhang, Qing He, and Lun Li. 2023. "A Hybrid-Strategy-Improved Dragonfly Algorithm for the Parameter Identification of an SDM" Sustainability 15, no. 15: 11791. https://doi.org/10.3390/su151511791
APA StyleZhao, J., Zhang, D., He, Q., & Li, L. (2023). A Hybrid-Strategy-Improved Dragonfly Algorithm for the Parameter Identification of an SDM. Sustainability, 15(15), 11791. https://doi.org/10.3390/su151511791





