Three-Dimensional Numerical Modeling and Analysis for the Municipal Solid-Waste Incineration of the Grate Furnace for Particulate-Matter Generation
Abstract
:1. Introduction
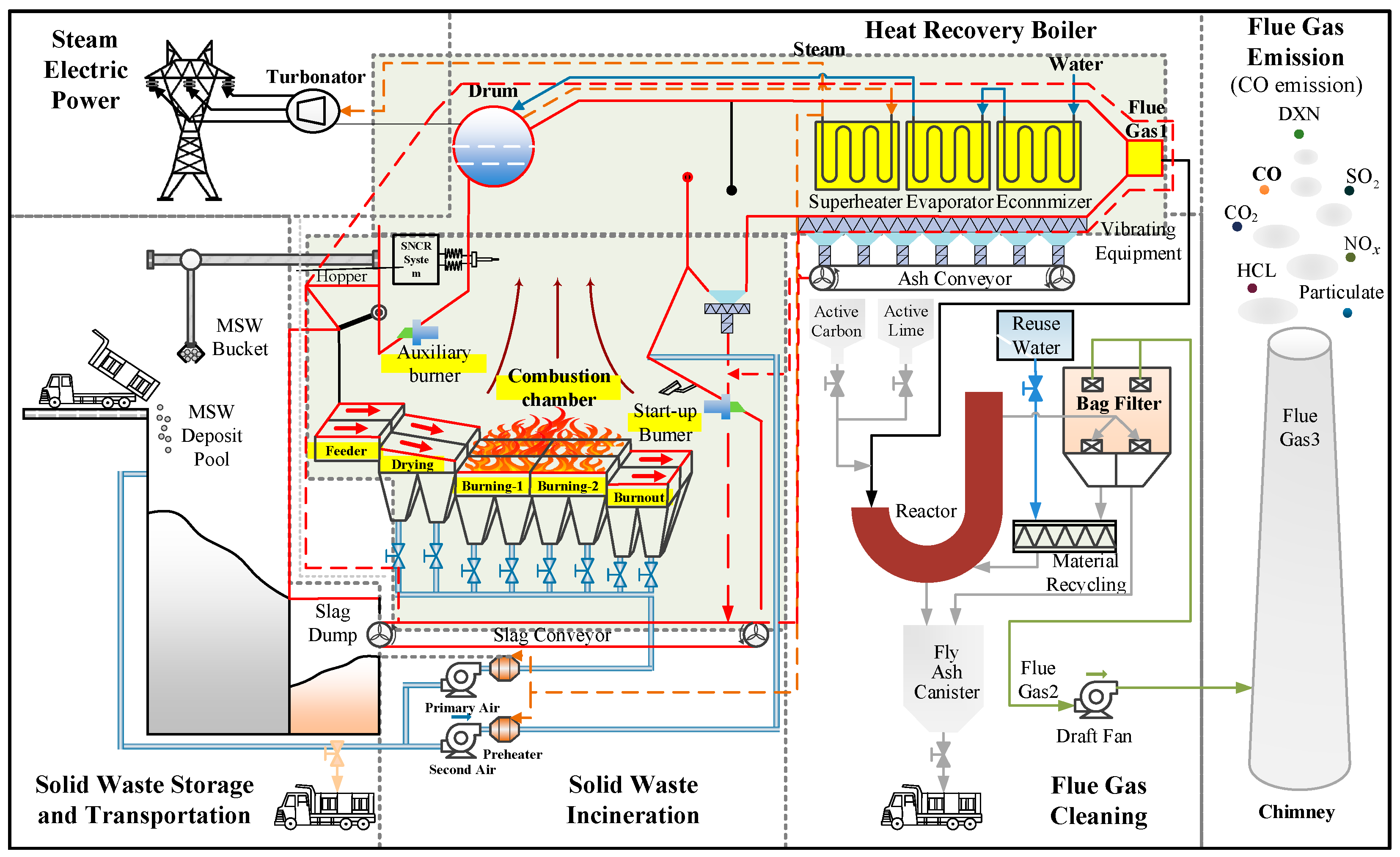
2. Description of Municipal Solid-Waste Incineration Process with Regard to PM Generation
2.1. Process Description
2.2. Analysis of Influencing Factors of Particle Concentration
3. Material and Methods
3.1. Material
3.2. Methods
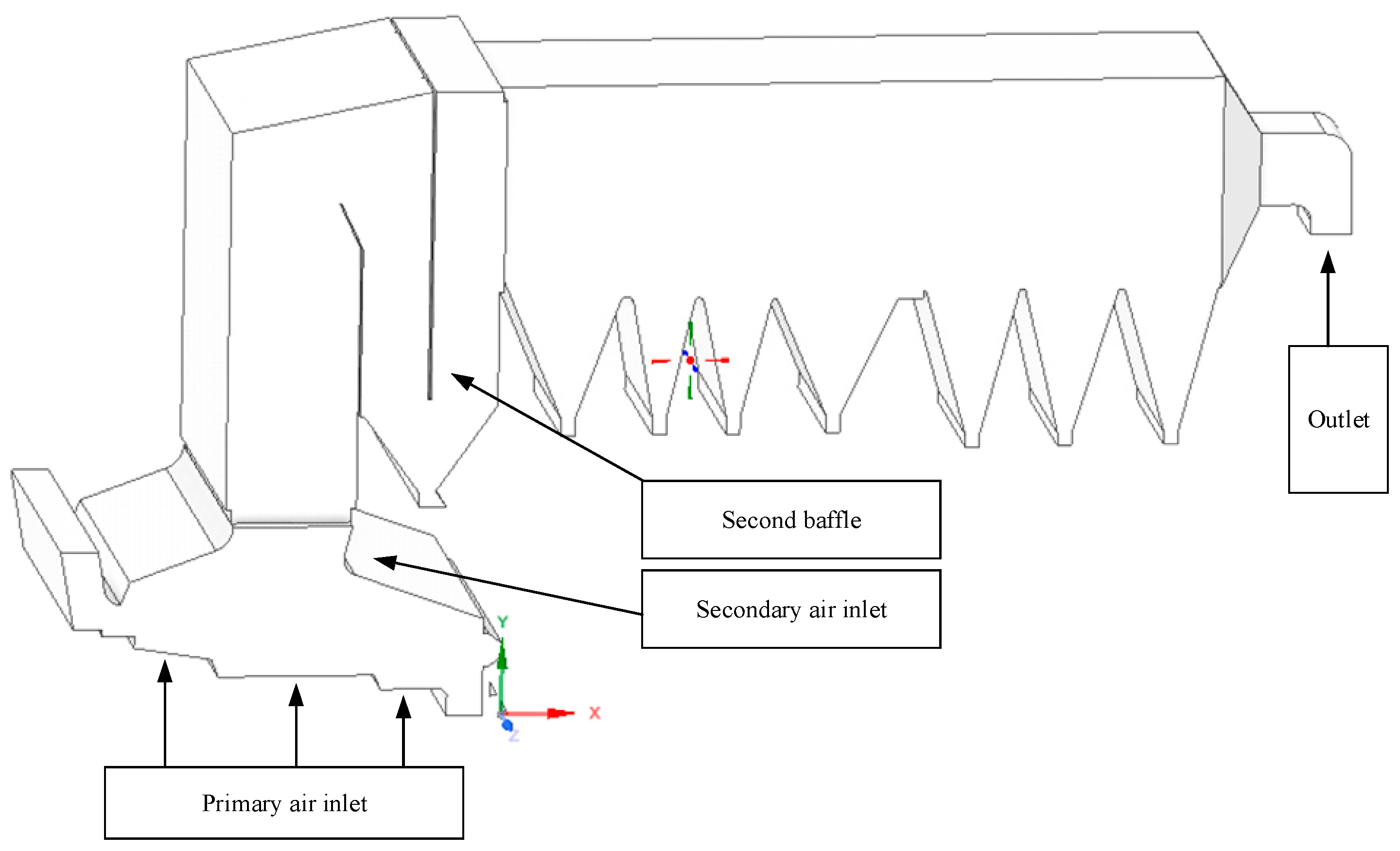
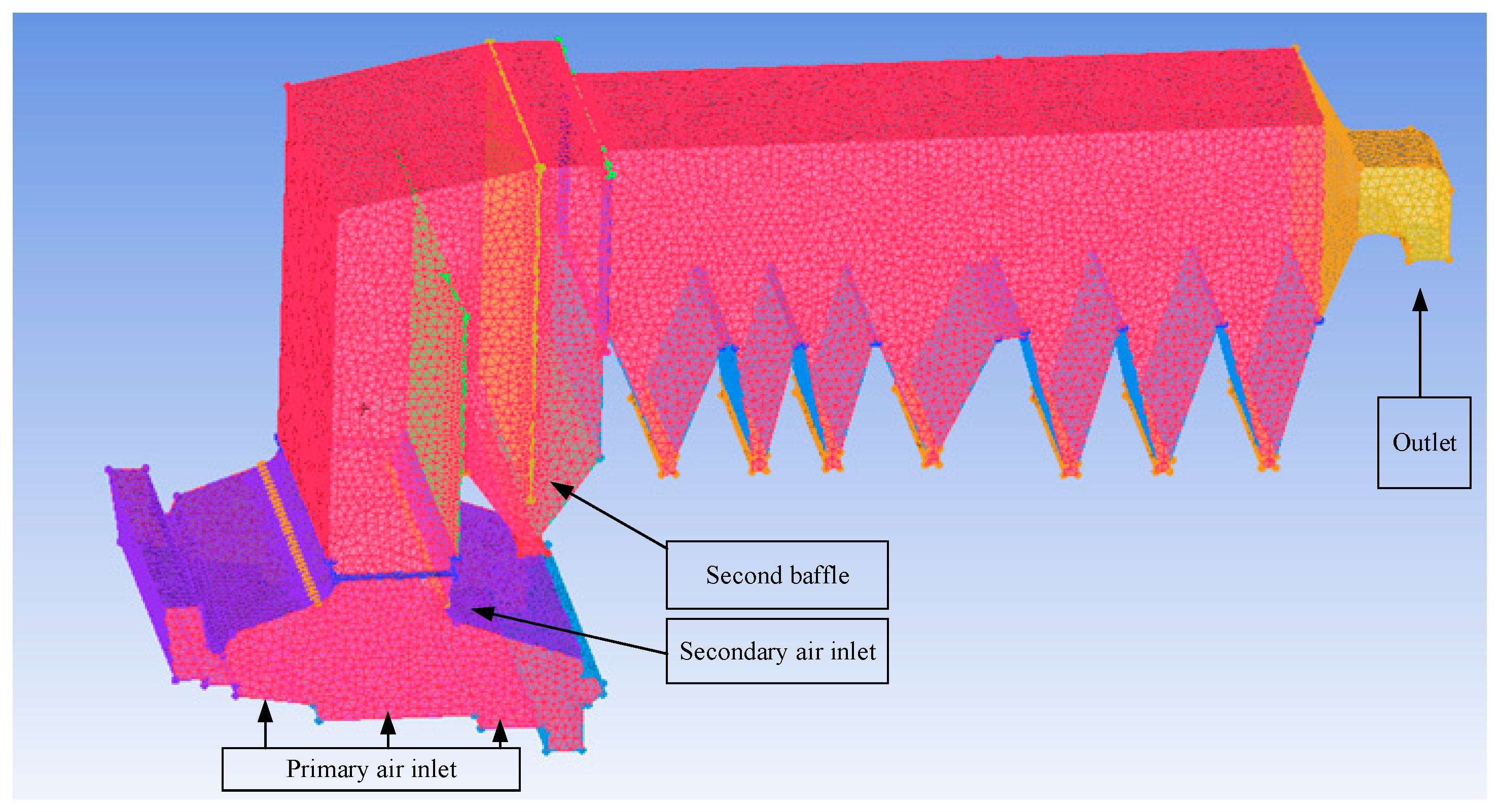
3.2.1. 3D Modeling Module for Incinerator and Waste Heat Boiler
3.2.2. Three-Dimensional Model Solver Module
3.2.3. Single-Factor Analysis Module
3.2.4. Orthogonal-Experiment Analysis Module
4. Experimental Results
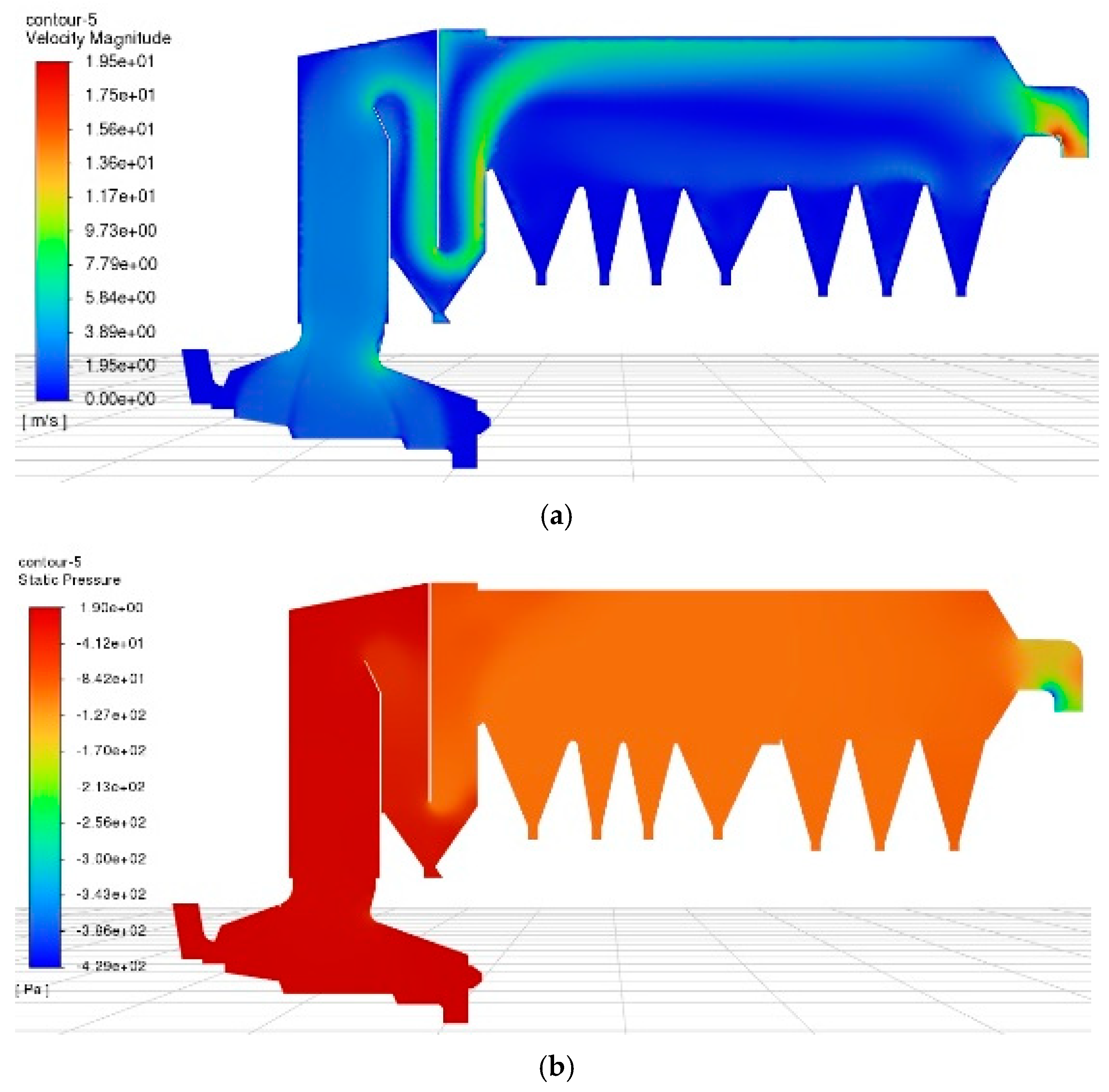
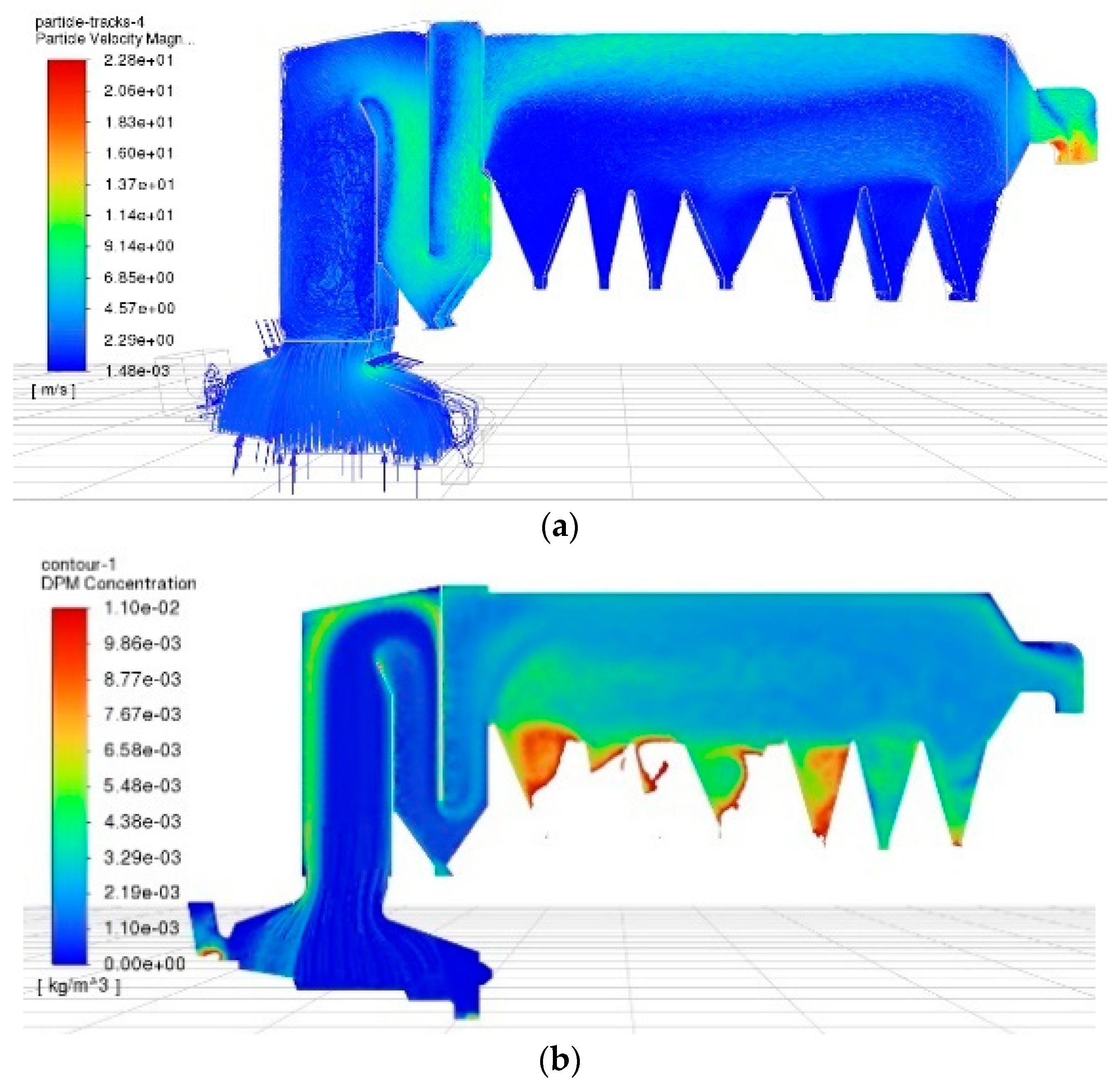
4.1. 3D Modeling Results under Benchmark Working Conditions of an Actual MSWI Plant
4.2. Results of the Single Factor Analysis and Discussion
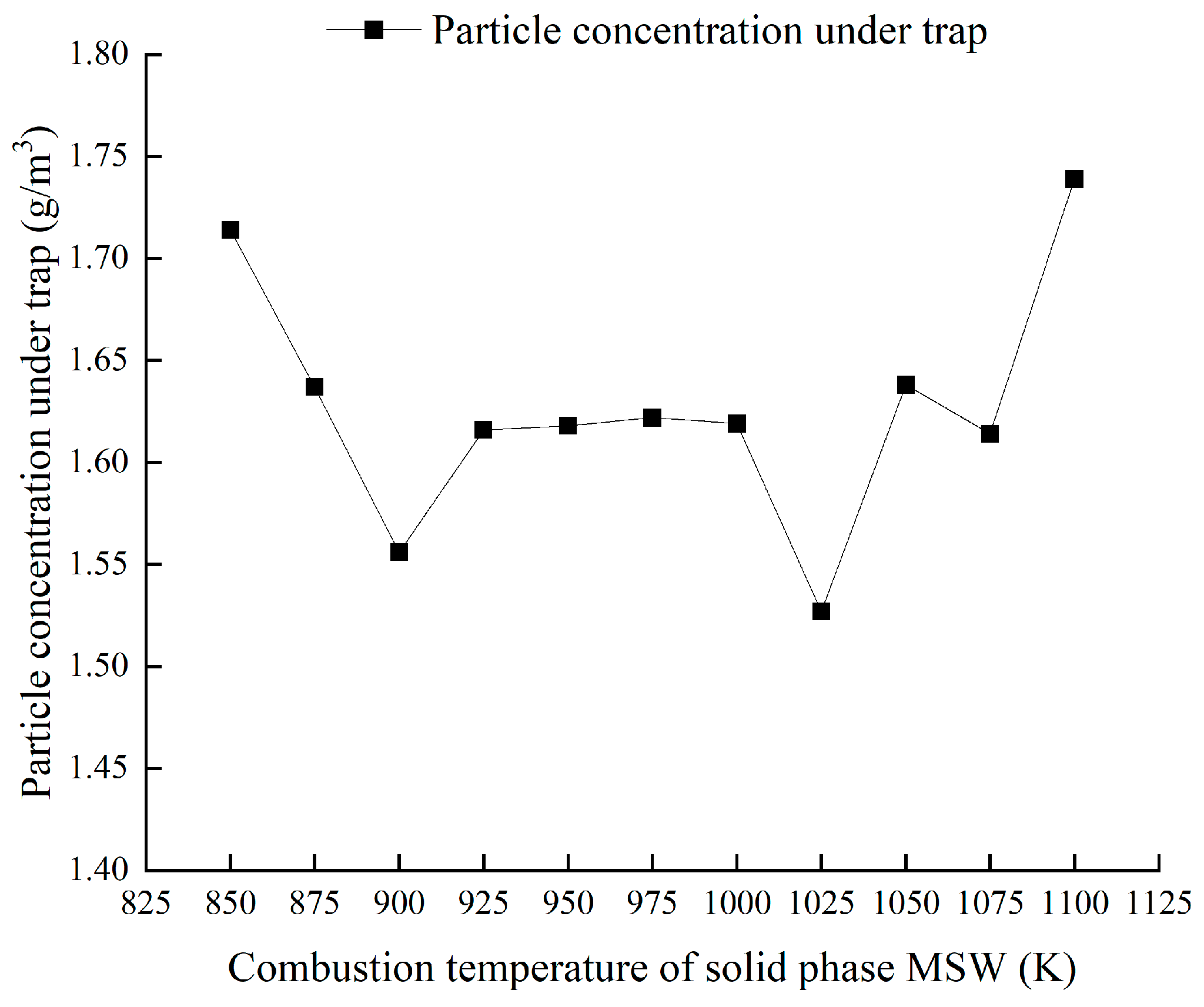
4.2.1. Analysis of the Effect of the Combustion Temperature of Solid-Phase MSW on PM Concentration at the Outlet
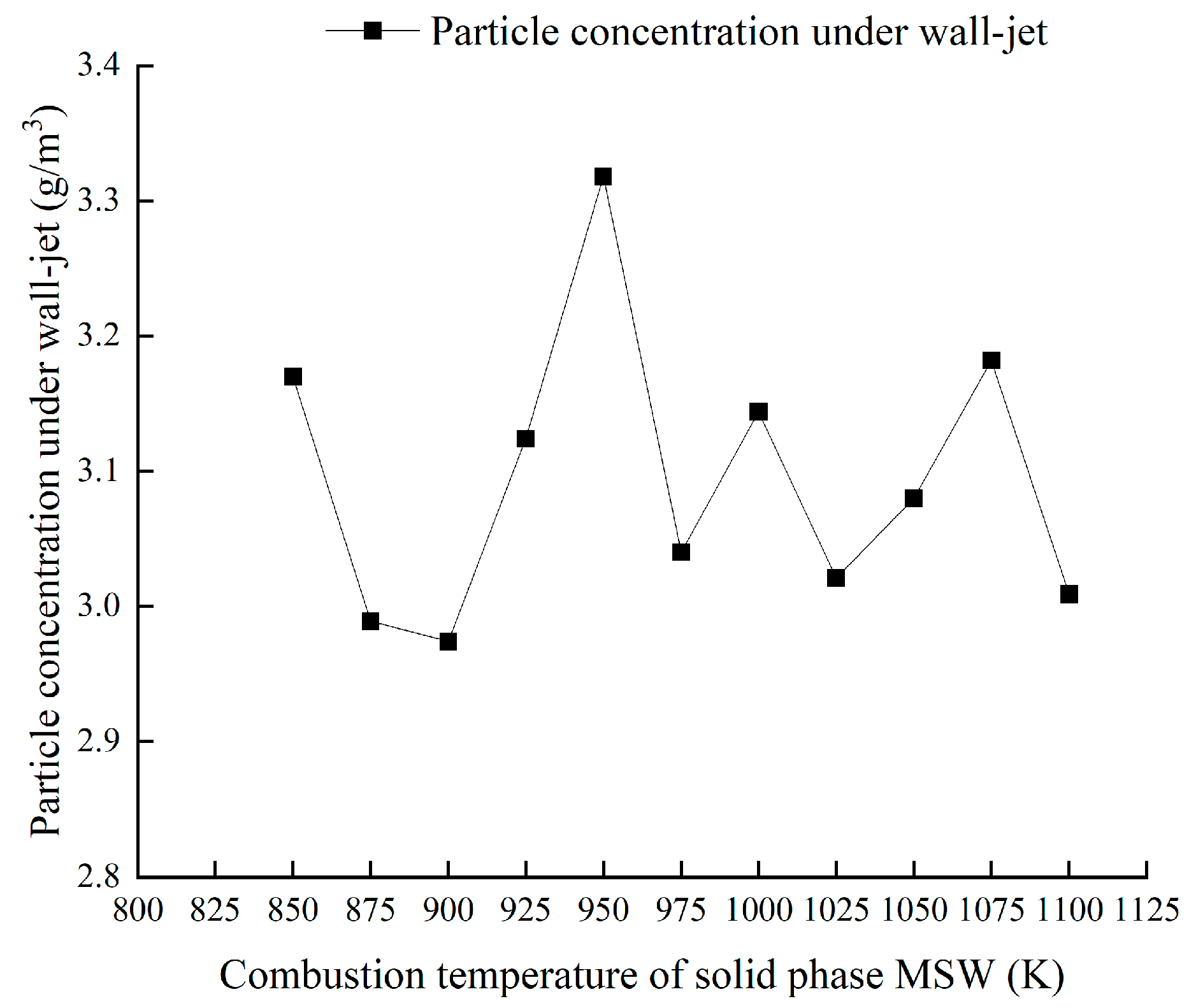
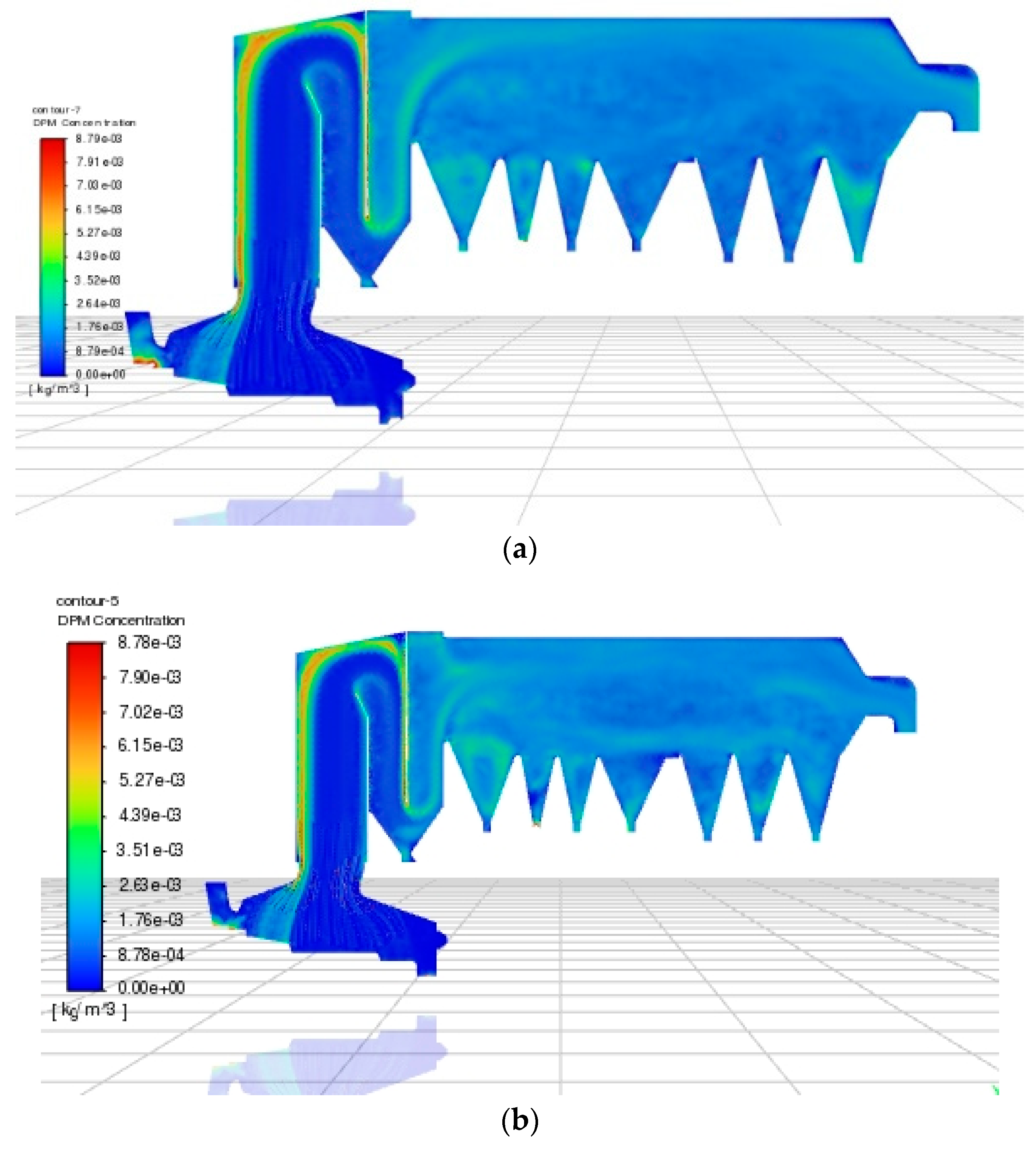
4.2.2. Analysis of the Effect of Different Wall’s PM Collision Methods on the PM Concentration Analysis at the Outlet
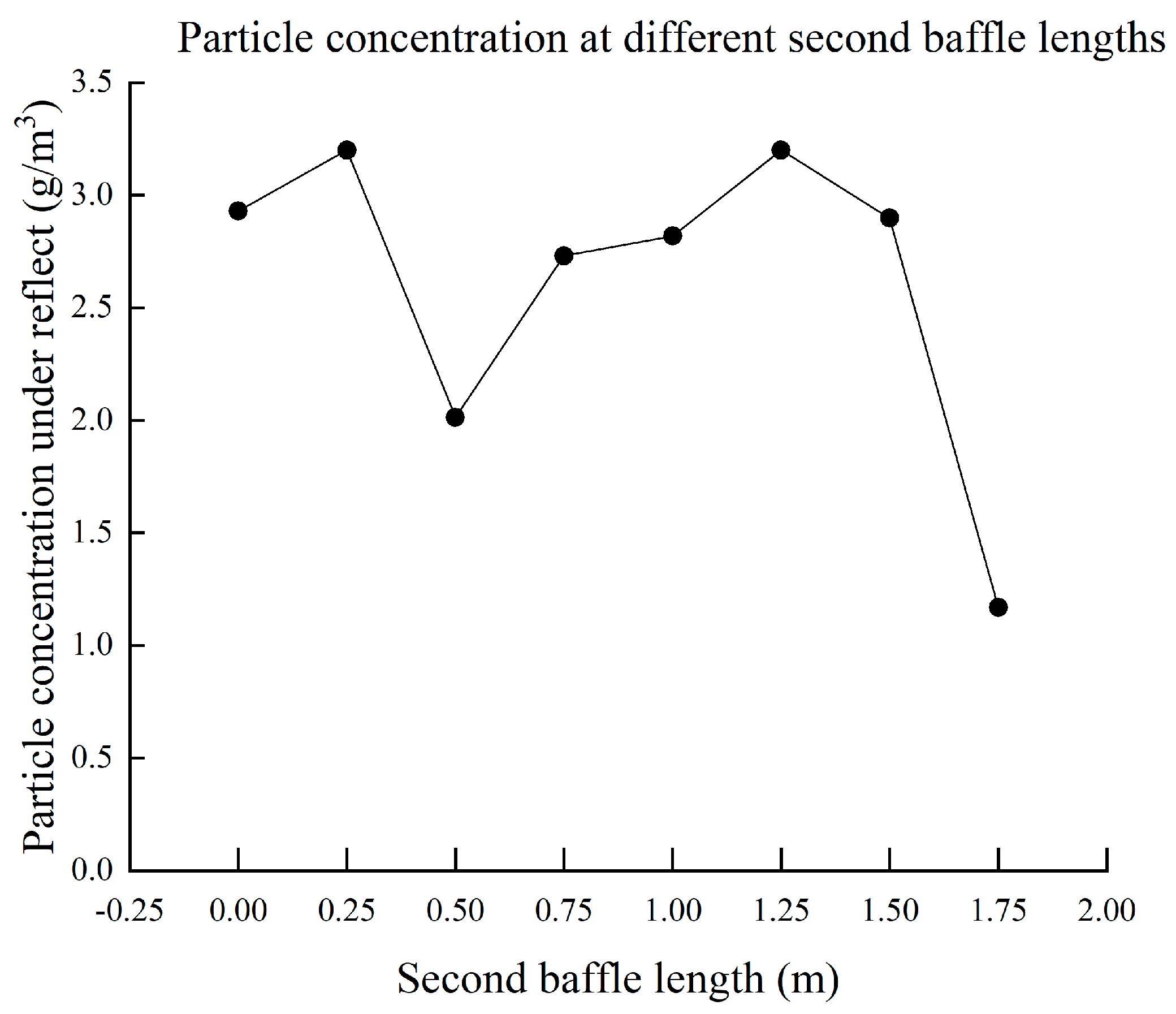
4.2.3. Effect of the Second Baffle Length on the Concentration of Exported PM
4.3. Results of Orthogonal Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Order | Symbols | Meaning |
| 1 | Gas density | |
| 2 | Velocity in the -direction | |
| 3 | Velocity in the -direction | |
| 4 | Rate of conversion of the MSW to the gas | |
| 5 | Gas pressure | |
| 6 | Resistance of the bed to gas flow | |
| 7 | Resistance of the bed to gas flow | |
| 8 | Gas enthalpy | |
| 9 | Thermal diffusion coefficient | |
| 10 | Heat gain in the gas phase due to combustion | |
| 11 | The th component of the velocity | |
| 12 | The th component of the velocity | |
| 13 | Cartesian coordinates | |
| 14 | Fluid density | |
| 15 | Viscosity | |
| 16 | Model coefficient | |
| 17 | Model coefficient | |
| 18 | Model coefficient | |
| 19 | Model coefficient | |
| 20 | Model coefficient | |
| 21 | Model coefficient | |
| 22 | Hybrid function | |
| 23 | Turbulent kinetic energy | |
| 24 | Specific turbulence dissipation rate | |
| 25 | Average speed | |
| 26 | Turbulence intensity | |
| 27 | Empirical constants of the K-Omega model | |
| 28 | Characteristic length of the obstacle | |
| 29 | Reynolds stress | |
| 30 | Kronecker function | |
| 31 | Power vortex viscosity | |
| 32 | Vortex viscosity | |
| 33 | Fluid phase velocity | |
| 34 | PM velocity | |
| 35 | Reynolds number | |
| 36 | Particulate matter | |
| 37 | Saffman lift and virtual mass force | |
| 38 | Particulate-matter density | |
| 39 | Particulate-matter size | |
| 40 | Viscosity coefficient | |
| 41 | Correction factor | |
| 42 | Parameter | |
| 43 | Parameter | |
| 44 | Geometric mean | |
| 45 | Standard deviation | |
| 46 | Particulate-matter concentration value | |
| 47 | Number of concentration values | |
| 48 | Percentile | |
| 49 | Number of deviations of percentile from the median | |
| 50 | Normal reflect coefficient | |
| 51 | Tangential reflect factor | |
| 52 | Inertia force | |
| 53 | Pressure gradient force | |
| 54 | False quality force | |
| 55 | Solid phase speed | |
| 56 | Magnus lift | |
| 57 | Angular velocity of the particulate-matter rotation | |
| 58 | Traction coefficient | |
| 59 | Constant | |
| 60 | Constant | |
| 61 | Constant | |
| 62 | Particulate-matter quality | |
| 63 | Gravitational acceleration | |
| 64 | Particulate-matter concentration at the incinerator outlet | |
| 65 | Combustion temperature of the solid-phase MSW | |
| 66 | Wall’s particulate-matter collision mode | |
| 67 | Length of the second baffle | |
| 68 | Orthogonal-experiment particulate-matter concentration value | |
| 69 | Design value of the orthogonal experiment | |
| 70 | Design value of the orthogonal experiment | |
| 71 | Design value of the orthogonal experiment | |
| 72 | Range | |
| 73 | Factor in orthogonal experiment | |
| 74 | Level of factor | |
| 75 | The average value of experimental data r at level of factor | |
| 76 | Number of times this level occurs in the experiment |
References
- Chhay, L.; Reyad, M.A.H.; Suy, R.; Islam, M.R.; Mian, M.M. Municipal solid waste generation in China: Influencing factor analysis and multi-model forecasting. J. Mater. Cycles Waste Manag. 2018, 20, 1761–1770. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.L.; Liu, Z.J.; Chen, L.Z.; Wang, Y.Z. Harmless treatment of municipal solid waste incinerator fly ash through shaft furnace. Waste Manag. 2021, 124, 110–117. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, Q.; Shen, X.; Chen, B.; Esfahani, S.S. The Mechanism of Household Waste Sorting Behaviour-A Study of Jiaxing, China. Int. J. Environ. Res. Public Health 2022, 19, 2447. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Anjum, R.; Raza, S.T.; Bazai, N.A.; Ihtisham, M. Technologies for municipal solid waste management: Current status, challenges, and future perspectives. Chemosphere 2022, 288, 132403. [Google Scholar] [CrossRef] [PubMed]
- Yan, M.; Tian, X.; Antoni; Yu, C.; Zhou, Z.; Hantoko, D.; Kanchanatip, E.; Khan, M.S. Influence of multi-temperature primary air on the characteristics of MSW combustion in a moving grate incinerator. J. Environ. Chem. Eng. 2021, 9, 106690. [Google Scholar] [CrossRef]
- Xia, H.; Tang, J.; Yu, W.; Qiao, J. Online Measurement of Dioxin Emission in Solid Waste Incineration Using Fuzzy Broad Learning. IEEE Trans. Ind. Inform. 2023, 1–11. [Google Scholar] [CrossRef]
- Zhuang, J.; Tang, J.; Aljerf, L. Comprehensive review on mechanism analysis and numerical simulation of municipal solid waste incineration process based on mechanical grate. Fuel 2022, 320, 123826. [Google Scholar] [CrossRef]
- Zhuang, J.; Tang, J.; Xia, H.; Qiao, J.; Ihtisham, M. MSWI Process Simulation Based on Coupling Combustion of Solid Phase on Grate and Gas Phase in Furnace. Proc. CSEE 2022, 42, 8961–8972. [Google Scholar]
- Tang, J.; Zhuang, J.; Qiao, J. Numerical Simulation and Analysis for Incineration Process Inside the Grate Furnace for Municipal Solid Waste. Control Eng. China 2022, 29, 1921–1927. [Google Scholar]
- Luo, Z.; Chen, W.; Wang, Y.; Cheng, Q.; Yuan, X.; Li, Z.; Yang, J. Numerical Simulation of Combustion and Characteristics of Fly Ash and Slag in a “V-type” Waste Incinerator. Energies 2021, 14, 7518. [Google Scholar] [CrossRef]
- Hu, Z.; Jiang, E.; Ma, X. Numerical simulation on operating parameters of SNCR process in a municipal solid waste incinerator. Fuel 2019, 245, 160–173. [Google Scholar] [CrossRef]
- Gu, T.; Ma, W.; Berning, T.; Guo, Z.; Andersson, R.; Yin, C. Advanced simulation of a 750 t/d municipal solid waste grate boiler to better accommodate feedstock changes due to waste classification. Energy 2022, 254, 124338. [Google Scholar] [CrossRef]
- Yan, M.; Antoni; Wang, J.; Hantoko, D.; Kanchanatip, E. Numerical investigation of MSW combustion influenced by air preheating in a full-scale moving grate incinerator. Fuel 2021, 285, 119193. [Google Scholar] [CrossRef]
- Yang, X.; Liao, Y.; Ma, X.; Zhou, J. Effects of air supply optimization on NOx reduction in a structurally modified municipal solid waste incinerator. Appl. Therm. Eng. 2022, 201, 117706. [Google Scholar] [CrossRef]
- Xia, Z.; Long, J.; Yan, S.; Bai, L.; Du, H.; Chen, C. Two-fluid simulation of moving grate waste incinerator: Comparison of 2D and 3D bed models. Energy 2021, 216, 119257. [Google Scholar] [CrossRef]
- Hu, Z.; Jiang, E.; Ma, X. Numerical simulation on NOX emissions in a municipal solid waste incinerator. J. Clean. Prod. 2019, 233, 650–664. [Google Scholar] [CrossRef]
- Ogawa, N.; Amano, T.; Nagai, Y.; Hagiwara, K.; Honda, T.; Koike, Y. Water repellents for the leaching control of heavy metals in municipal solid waste incineration fly ash. Waste Manag. 2021, 124, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Shunda, L.; Jiang, X.; Zhao, Y.; Yan, J. Disposal technology and new progress for dioxins and heavy metals in fly ash from municipal solid waste incineration: A critical review. Environ. Pollut. 2022, 311, 119878. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Wu, J.; Zhang, Y.; Zhang, J.; Feng, Y.; Li, P. Characteristics of Component Particle Size Distributions of Particulate Matter Emitted from a Waste Incineration Plant. Environ. Sci. 2019, 40, 2533–2539. [Google Scholar]
- Xia, H.; Tang, J.; Aljerf, L.; Wang, T.; Qiao, J.; Xu, Q.; Wang, Q.; Ukaogo, P. Investigation on dioxins emission characteristic during complete maintenance operating period of municipal solid waste incineration. Environ. Pollut. 2023, 318, 120949. [Google Scholar] [CrossRef]
- Xia, H.; Tang, J.; Aljerf, L.; Wang, T.; Gao, B.; Xu, Q.; Wang, Q.; Ukaogo, P. Assessment of PCDD/Fs formation and emission characteristics at a municipal solid waste incinerator for one year. Sci. Total Environ. 2023, 883, 163705. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.; Pham, Q.V.; Nguyen, T.P.M.; Vu, V.T.; Do, T.H.; Hoang, M.T.; Thu Thuy Thi, N.; Minh, T.B. Distribution characteristics and ecological risks of heavy metals in bottom ash, fly ash, and particulate matter released from municipal solid waste incinerators in northern Vietnam. Environ. Geochem. Health 2022, 45, 2579–2590. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yu, J.; Cui, Y.; He, J.; Xue, P.; Cao, W.; Ying, H.; Gao, W.; Yan, Y.; Hu, B.; et al. Characteristics of fine particulate matter and its sources in an industrialized coastal city, Ningbo, Yangtze River Delta, China. Atmos. Res. 2018, 203, 105–117. [Google Scholar] [CrossRef]
- Kitamura, H.; Dahlan, A.V.; Tian, Y.; Shimaoka, T.; Yamamoto, T.; Takahashi, F. Intra- and inter-particle heterogeneity of municipal solid waste incineration fly ash particles. J. Mater. Cycles Waste Manag. 2019, 21, 925–941. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, X.; Liu, X. Pollution and Risk Assessment of Heavy Metals in Fine Slag Particles from Waste Incineration. Environ. Impact Assess. 2022, 44, 60–65+70. [Google Scholar]
- Bernasconi, D.; Caviglia, C.; Destefanis, E.; Agostino, A.; Boero, R.; Marinoni, N.; Bonadiman, C.; Pavese, A. Influence of speciation distribution and particle size on heavy metal leaching from MSWI fly ash. Waste Manag. 2022, 138, 318–327. [Google Scholar] [CrossRef]
- Zhang, R.; Wei, X.; Hao, Q.; Si, R. Bioleaching of Heavy Metals from Municipal Solid Waste Incineration Fly Ash: Availability of Recoverable Sulfur Prills and Form Transformation of Heavy Metals. Metals 2020, 10, 815. [Google Scholar] [CrossRef]
- Zhao, H.; Tian, Y.; Wang, R.; Wang, R.; Zeng, X.; Yang, F.; Wang, Z.; Chen, M.; Shu, J. Seasonal Variation of the Mobility and Toxicity of Metals in Beijing’s Municipal Solid Waste Incineration Fly Ash. Sustainability 2021, 13, 6532. [Google Scholar] [CrossRef]
- Wei, X.; Shao, N.; Yan, F.; Wang, P.; Xie, F.; Zhang, Z. Safe disposal and recyclability of MSWI fly ash via mold-pressing and alkali-activation technology: Promotion of metakaolin and mechanism. J. Environ. Chem. Eng. 2022, 10, 107166. [Google Scholar] [CrossRef]
- Paithankar, J.G.; Saini, S.; Dwivedi, S.; Sharma, A.; Chowdhuri, D.K. Heavy metal associated health hazards: An interplay of oxidative stress and signal transduction. Chemosphere 2021, 262, 128350. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, X. Detoxification, solidification and recycling of municipal solid waste incineration fly ash: A review. Chem. Eng. J. 2021, 420, 130349. [Google Scholar] [CrossRef]
- Yang, W.; Pudasainee, D.; Gupta, R.; Li, W.; Wang, B.; Sun, L. Particulate matter emission during municipal solid waste combustion: Submicron particulates formation mechanism. Fuel 2022, 310, 122271. [Google Scholar] [CrossRef]
- Dahlan, A.V.; Kitamura, H.; Tian, Y.; Sakanakura, H.; Shimaoka, T.; Yamamoto, T.; Takahashi, F. Heterogeneities of fly ash particles generated from a fluidized bed combustor of municipal solid waste incineration. J. Mater. Cycles Waste Manag. 2020, 22, 836–850. [Google Scholar] [CrossRef]
- Yan, L.; Sun, F.; Zheng, P. Research on adhesion mechanism of ash particles and ammonium bisulfate on the metal wall in coal-fired boilers. Fuel 2020, 277, 118021. [Google Scholar] [CrossRef]
- Heinl, E.; Bohnet, M. Calculation of particle–wall adhesion in horizontal gas–solids flow using CFD. Powder Technol. 2005, 159, 95–104. [Google Scholar] [CrossRef]




| Industrial Analysis | Elementary Analysis | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Moisture (ar) | Fixed Carbon (d) | Volatile (d) | Ash (d) | C (d) | H (d) | N (d) | Cl (d) | S (d) | O (d) |
| 36.3 | 14.16 | 60.08 | 25.76 | 47.66 | 6.17 | 0.33 | 0.88 | 0.17 | 19.03 |
| Setting Parameters | Primary Air Inlet | Secondary Air Inlet | Outlet | Wall |
|---|---|---|---|---|
| Temperature (K) | 1080 | 1080 | 473 | Thermal insulation |
| Material | Air | Air | Air | Aluminium |
| Serial Number | Setting Parameters | Set Value |
|---|---|---|
| 1 | Injection source | Surface |
| 2 | Spraying surface | Primary air inlet |
| 3 | Materials | Ash-solid |
| 4 | Diameter Distribution | Rosin-Rammler |
| 5 | Jet Type | Face normal direction injection |
| Serial Number | Setting Parameters | Set Value |
|---|---|---|
| 1 | Temperature (K) | 300 |
| 2 | Speed size (m/s) | 0.7 |
| 3 | Total flow (kg/s) | 0.22 |
| 4 | Minimum diameter (μm) | 30 |
| 5 | Maximum diameter (μm) | 75 |
| 6 | Average diameter (μm) | 45 |
| 7 | Dispersion coefficient | 3.5 |
| 8 | Number of diameters | 10 |
| 9 | Drag force criterion | Grace |
| 10 | Rotating drag force criterion | Dennis-et-al |
| 11 | Magnus’ Law of Liftoff | Oesterle-Bui-Dinh |
| 12 | Rough wall model | Open |
| 13 | Discrete random trajectory model | Open |
| 14 | Number of attempts | 3 |
| 15 | Time scale constants | 0.15 |
| Level | A | B (K) | C (m) |
|---|---|---|---|
| 1 | Reflect | 875 | 11.70 |
| 2 | Wall-jet | 900 | 11.95 |
| 3 | Trap | 925 | 12.20 |
| 4 | - | 950 | 12.45 |
| 5 | - | 975 | 12.70 |
| 6 | - | 1000 | 12.95 |
| Cases | A | B | C | PM Concentration g/m3 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 2.372 |
| 2 | 2 | 1 | 2 | 2.744 |
| 3 | 3 | 1 | 3 | 0.276 |
| 34 | 3 | 6 | 2 | 0.252 |
| 35 | 1 | 6 | 3 | 3.249 |
| 36 | 2 | 6 | 4 | 2.960 |
| Indicators | A | B | C |
|---|---|---|---|
| Range | 2.3967 | 0.6569 | 1.7442 |
| Primary and secondary order | A > C > B | ||
| Optimal level |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Tang, J.; Xia, H.; Aljerf, L.; Gao, B.; Akele, M.L. Three-Dimensional Numerical Modeling and Analysis for the Municipal Solid-Waste Incineration of the Grate Furnace for Particulate-Matter Generation. Sustainability 2023, 15, 12337. https://doi.org/10.3390/su151612337
Liang Y, Tang J, Xia H, Aljerf L, Gao B, Akele ML. Three-Dimensional Numerical Modeling and Analysis for the Municipal Solid-Waste Incineration of the Grate Furnace for Particulate-Matter Generation. Sustainability. 2023; 15(16):12337. https://doi.org/10.3390/su151612337
Chicago/Turabian StyleLiang, Yongqi, Jian Tang, Heng Xia, Loai Aljerf, Bingyin Gao, and Mulugeta Legesse Akele. 2023. "Three-Dimensional Numerical Modeling and Analysis for the Municipal Solid-Waste Incineration of the Grate Furnace for Particulate-Matter Generation" Sustainability 15, no. 16: 12337. https://doi.org/10.3390/su151612337
APA StyleLiang, Y., Tang, J., Xia, H., Aljerf, L., Gao, B., & Akele, M. L. (2023). Three-Dimensional Numerical Modeling and Analysis for the Municipal Solid-Waste Incineration of the Grate Furnace for Particulate-Matter Generation. Sustainability, 15(16), 12337. https://doi.org/10.3390/su151612337








