Does the One-Child Policy Improve Chinese Human Capital? A Propensity Score Matching Analysis
Abstract
:1. Introduction
2. History of China’s Family Planning and Literature Review
2.1. The Evolution of China’s Population Policy
2.2. Literature Review
3. Empirical Structure and Data
3.1. Estimation Strategy
3.2. Data Source
3.3. Data Modification
3.4. Descriptive Statistics
3.5. Logit Model and the Test of the Assumptions
3.6. Test of Post-Matching Balance and Common Support Assumption (CSA)
4. Empirical Results
4.1. Overall Results
4.2. Sensitivity Analysis
5. Subsample Analysis
5.1. Descriptive Statistics Divided by Gender
5.2. Logit Model
5.3. Checking the CSA and Post-Matching Balance Test
5.4. Subsample Results
5.5. Sensitivity Analysis of the ATT
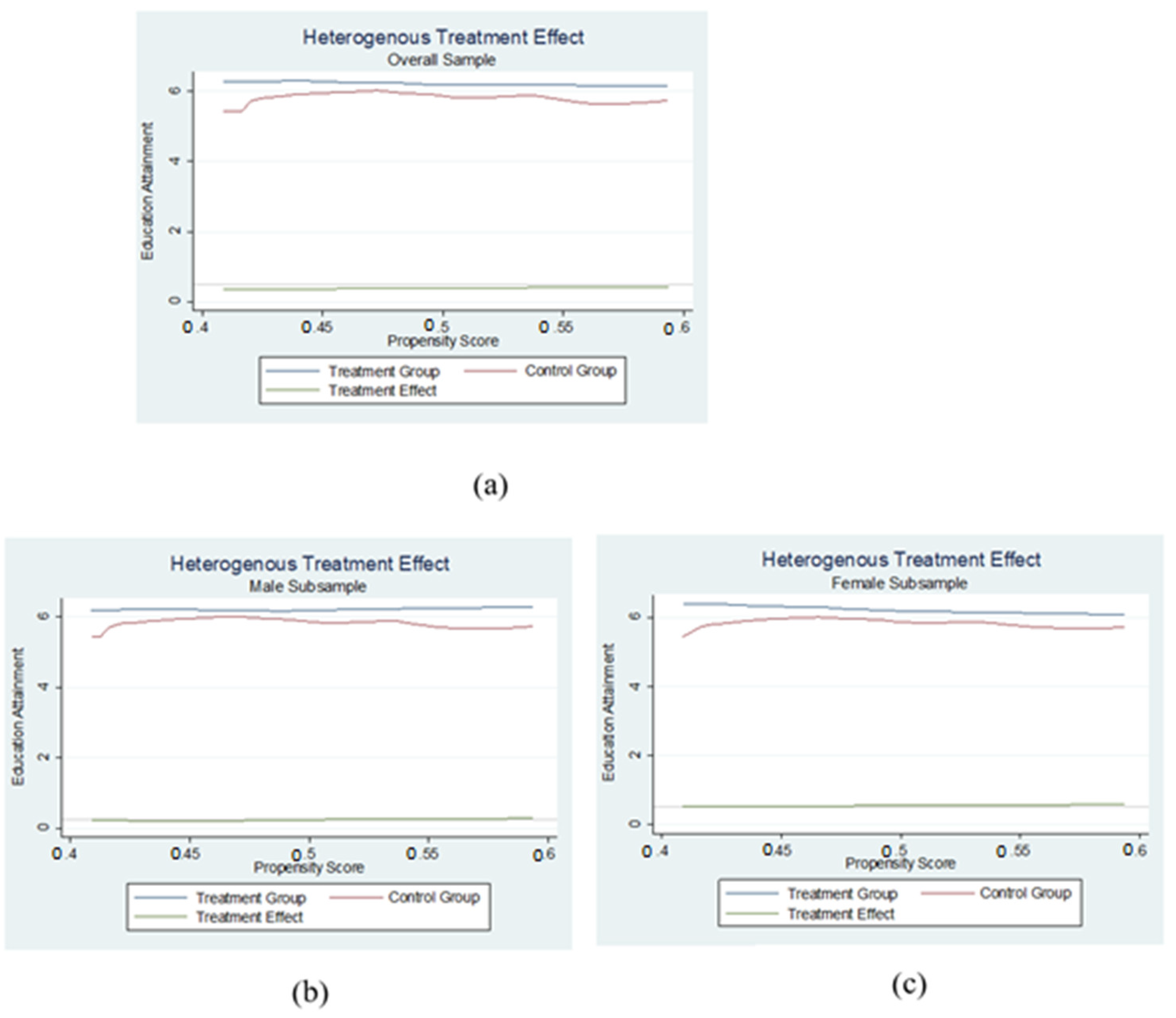
5.6. Non-Parametric Treatment Effect
6. The Effect of the OCP on Income Level
6.1. Marginal Effect of OCP on Individual Income
6.2. Sensitivity Analysis
6.3. Non-Parametric Treatment Effect
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Becker, G.S. An economic analysis of fertility. In Demographic and Economic Change in Developed Countries; Becker, G.S., Ed.; Princeton University Press: Princeton, NJ, USA, 1960; pp. 209–240. [Google Scholar]
- Becker, G.S.; Tomes, N. An equilibrium theory of the distribution of income and intergenerational mobility. J. Polit. Econ. 1979, 87, 1153–1189. [Google Scholar] [CrossRef]
- Zhang, J.S. The evolution of China’s one-child policy and its effects on family outcomes. J. Econ. Perspect. 2017, 31, 141–161. [Google Scholar] [CrossRef] [Green Version]
- Hatton, T.J.; Martin, R.M. Fertility decline and the heights of children in Britain, 1886-1938. Explor. Econ. Hist. 2010, 47, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Angrist, J.; Lavy, V.; Scholosser, A. Multiple experiments for the causal link between the quantity and quality of children. J. Labor Econ. 2010, 28, 773–824. [Google Scholar] [CrossRef]
- Galor, O. From physical to human capital accumulation: Inequality and the process of development. Rev. Econ. Stud. 2004, 71, 1001–1027. [Google Scholar] [CrossRef]
- De La Croix, D.; Doepke, M. Inequality and growth: Why differential fertility matters. Am. Econ. Rev. 2003, 93, 1091–1113. [Google Scholar] [CrossRef] [Green Version]
- Strulik, H.; Prettner, K.; Prskawetz, A. The past and future of knowledge-based growth. J. Econ. Growth 2013, 18, 411–438. [Google Scholar] [CrossRef]
- Zhang, C. The evolution of Chinese family planning. Mark. Demogr. Anal. 2000, 6, 47–54. [Google Scholar]
- Qian, Y.M.; Chen, J.M. The revolution of Mao’s thought about population and the reasons: An empirical analysis based on Mao’s statement of Chinese population. Mao Zedong Thought Study 2017, 34, 6–15. [Google Scholar]
- Mao, Z.D. The Selected Works of MaoZedong; People’s Publishing House: Beijing, China, 1991. [Google Scholar]
- Yang, K. The Overview of the Chinese Population and Family Planning; People’s Publishing House: Beijing, China, 2001. [Google Scholar]
- Chen, W. The discussion about the evolution of the Chinese population during the “Cultural Revolution”. J. Cent. South Univ. 2011, 17. [Google Scholar]
- Li, B.J.; Zhang, H.L. Does population control lead to better child quality? Evidence from China’s one-child policy enforcement. J. Comp. Econ. 2017, 45, 246–260. [Google Scholar] [CrossRef]
- Ma, L.; Fang, X.M.; Lei, Z.; Cai, X.C. Does only child’s gender affect the fertility desire of only-child parents to bear a second child? Study Chinese Gen. Soc. Sur. 2016, 6, 17–26. [Google Scholar]
- Ahn, N. Effects of the one-child family policy on second and third births in Hebei, Shaanxi and Shanghai. J. Popul. Econ. 1994, 7, 63–78. [Google Scholar] [CrossRef]
- Liao, P.J. The one-child policy: A macroeconomic analysis. J. Dev. Econ. 2013, 101, 49–63. [Google Scholar] [CrossRef]
- Li, J.L. China’s one-child policy: How and how well has it worked? A case study of Hebei Province, 1979-88. Popul. Dev. Rev. 1995, 21, 563–585. [Google Scholar] [CrossRef]
- Rosenzweig, M.R.; Zhang, J.S. Do population control policies induce more human capital investment? Twins, birthweight, and China’s ‘one child’ policy. Rev. Econ. Stud. 2009, 76, 1149–1174. [Google Scholar] [CrossRef] [Green Version]
- Liu, H. The quality-quantity trade-off: Evidence from the relaxation of China’s one-child policy. J. Popul. Econ. 2014, 27, 565–603. [Google Scholar] [CrossRef]
- Qin, X.Z.; Zhuang, C.C.; Yang, R.D. Does the one-child policy improve children’s human capital in urban China? A regression discontinuity design. J. Comp. Econ. 2017, 45, 287–303. [Google Scholar] [CrossRef]
- Almond, D.; Li, H.; Zhang, S. Land Reform and Sex Selection in China; Working Paper 19153; NBER: Cambridge, MA, USA, 2017. [Google Scholar]
- Austin, P.C. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar. Behav. Res. 2011, 46, 399–425. [Google Scholar] [CrossRef] [Green Version]
- Caliendo, M.; Kopeinig, S. Some practical guidance for the implementation of propensity score matching. J. Econ. Surv. 2008, 22, 31–73. [Google Scholar] [CrossRef] [Green Version]
- Li, H.B.; Zhang, J.S.; Zhu, Y. The quantity-Quality Trade-off of children In a developing country: Identification using Chinese twins. Demography 2008, 45, 223–243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erola, J.; Jalonen, S.; Lehti, H. Parental education, class and income over early life course and children’s achievement. Res. Soc. Strat. Mobil. 2016, 44, 33–43. [Google Scholar] [CrossRef] [Green Version]
- Aakvik, A. Bounding a matching estimator: The case of a Norwegian training program. Oxford B. Econ. Stat. 2001, 63, 115–144. [Google Scholar] [CrossRef]
- Abadie, A.; Imbens, G.W. Large sample properties of matching estimators for average treatment effects. Econometrica 2006, 74, 235–267. [Google Scholar] [CrossRef]
- Abadie, A. Bias-corrected matching estimators for average treatment effects. J. Bus. Econ. Stat. 2011, 29, 1–12. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Essama-Nssah, B. Propensity Score Matching and Policy Impact Analysis: A Demonstration in Eviews; World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Diprete, T.A.; Gangl, M. Assessing bias in the estimation of causal effects: Rosenbaum bounds on matching estimators and instrumental variables estimation with imperfect instruments. Sociol. Methodol. 2004, 34, 271–310. [Google Scholar] [CrossRef] [Green Version]
- Paudel, J.; de Araujo, P. Demographic responses to a political transformation: Evidence of women’s empowerment from Nepal. J. Comp. Econ. 2017, 45, 325–344. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Y.D. Sources of China’s economic growth 1952–1999: Incorporating human capital accumulation. China Econ. Rev. 2003, 14, 32–53. [Google Scholar] [CrossRef] [Green Version]
- Bosworth, B. Accounting for growth: Comparing China and India. J. Econ. Perspect. 2008, 22, 45–67. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Qiu, M.Y. The impact of education on income inequality and intergenerational mobility. China Econ. Rev. 2016, 37, 110–125. [Google Scholar] [CrossRef]
- McElroy, M.; Yang, D.T. Carrots and sticks: Fertility effects of China’s population policies. Am. Econ. Rev. 2000, 90, 389–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Definition | Treatment Group (OCP) | Control Group (Pre-OCP) | |
|---|---|---|---|
| Educational attainment | Time of schooling (years) | 6.212 (3.038) | 5.822 (3.053) |
| Pre-tax income | GDP per capita (CNY) | 28,687.64 (53,983.22) | 27,290.59 (66,826.96) |
| After-tax income | GDP per capita (CNY | 28,377.7 (52,770.18) | 26,871.29 (64,075.55) |
| Male | Male = 1, Female = 0 | 0.518 (0.500) | 0.513 (0.500) |
| Rural | Rural = 1, Urban = 0 | 0.414 (0.493) | 0.384 (0.486) |
| Father’s educational attainment | Father’s education level: time of schooling (years) | 2.572 (3.209) | 3.010 (3.266) |
| Mother’s educational attainment | Mother’s education level: time of schooling (years) | 1.596 (2.767) | 1.830 (2.807) |
| East | East = 1, others = 0 | 0.464 (0.499) | 0.428 (0.495) |
| West | West = 1, others = 0 | 0.227 (0.419) | 0.252 (0.434) |
| Observations | Sample size | 6190 | 5335 |
| Characteristics | Marginal Effect |
|---|---|
| Rural | 0.297 *** (0.079) |
| Male | 0.056 (0.076) |
| Father’s educational attainment | −0.037 *** (0.006) |
| Mother’s educational attainment | −0.011 (0.007) |
| East | 0.246 *** (0.072) |
| West | 0.052 (0.086) |
| Male * East | −0.027 (0.088) |
| Male * West | −0.054 (0.101) |
| Rural * East | −0.229 ** (0.091) |
| Rural * West | −0.248 (0.102) |
| Male * Rural | −0.063 (0.078) |
| Observations | 11,525 |
| Log likelihood | −7910.108 |
| LR chi2(11) | 93.34 |
| Pre-Matching | Post-Matching | |||||
|---|---|---|---|---|---|---|
| Covariable | Mean | p-Value | Mean | p-Value | ||
| Treated | Control | Treated | Control | |||
| Rural | 0.414 | 0.384 | 0.001 | 0.414 | 0.414 | 1.000 |
| Father’s educational attainment | 2.571 | 3.011 | 0.000 | 2.571 | 2.571 | 1.000 |
| East | 0.464 | 0.428 | 0.000 | 0.464 | 0.464 | 1.000 |
| Rural * East | 0.149 | 0.130 | 0.003 | 0.149 | 0.149 | 1.000 |
| Observations | 6190 | 5335 | 11,525 | 6190 | 5335 | 11,525 |
| Educational Attainment | ||
|---|---|---|
| Pre-Matching | Post Matching | |
| NNM | 0.390 *** (0.057) | 0.407 *** (0.058) |
| KM | 0.390 *** (0.057) | 0.398 *** (0.057) |
| Matching | No | Yes |
| Observations | 11,525 | 11,525 |
| Hidden Bias | Upper and Lower Bounds | p-Value | ||
|---|---|---|---|---|
| t-hat+ | t-hat− | Sig+ | Sig− | |
| 1 | 5.812 *** | 5.812 *** | 0 | 0 |
| 1.25 | 5.757 *** | 5.840 *** | 0 | 0 |
| 1.5 | 5.757 *** | 5.849 *** | 0 | 0 |
| 1.75 | 5.738 *** | 5.849 *** | 0 | 0 |
| 2 | 5.738 *** | 5.849 *** | 0 | 0 |
| 2.25 | 5.738 *** | 5.859 *** | 0 | 0 |
| 2.5 | 5.701 *** | 5.867 *** | 0 | 0 |
| 2.75 | 5.701 *** | 5.867 *** | 0 | 0 |
| 3 | 5.701 *** | 5.899 *** | 0 | 0 |
| Definition | Treatment Group | Control Group | |||||
|---|---|---|---|---|---|---|---|
| Overall | Male | Female | Overall | Male | Female | ||
| Educational attainment | Time of schooling (years) | 6.212 (3.038) | 6.253 (3.028) | 6.168 (3.047) | 5.822 (3.053) | 5.995 (3.008) | 5.639 (3.091) |
| Male | Male = 1, Female = 0 | 0.518 (0.500) | 1.000 (0.000) | 0.000 (0.000) | 0.513 (0.500) | 1.000 (0.000) | 0.000 (0.000) |
| Rural | Rural = 1, Urban = 0 | 0.414 (0.493) | 0.433 (0.496) | 0.394 (0.489) | 0.384 (0.486) | 0.410 (0.492) | 0.357 (0.479) |
| Father’s educational attainment | Father’s education level: time of schooling (years) | 2.572 (3.209) | 2.461 (3.153) | 2.691 (3.266) | 3.010 (3.266) | 2.886 (3.262) | 3.141 (3.266) |
| Mother’s educational attainment | Mother’s education level: time of schooling (years) | 1.596 (2.767) | 1.522 (2.717) | 1.677 (2.817) | 1.830 (2.807) | 1.724 (2.765) | 1.942 (2.847) |
| East | East = 1, others = 0 | 0.464 (0.499) | 0.467 (0.499) | 0.462 (0.499) | 0.428 (0.495) | 0.429 (0.495) | 0.426 (0.495) |
| West | West = 1, others = 0 | 0.227 (0.419) | 0.222 (0.416) | 0.231 (0.421) | 0.252 (0.434) | 0.252 (0.434) | 0.252 (0.434) |
| Observations | Sample size | 6190 | 3.209 | 2981 | 5335 | 2736 | 2599 |
| Characteristics | Marginal Effect | ||
|---|---|---|---|
| Overall | Male | Female | |
| Rural | 0.297 *** (0.079) | 0.214 ** (0.094) | 0.319 *** (0.098) |
| Male | 0.056 (0.076) | - | - |
| Father’s educational attainment | −0.037 *** (0.006) | −0.038 *** (0.009) | −0.036 *** (0.009) |
| Mother’s educational attainment | −0.011 (0.007) | −0.008 (0.011) | −0.013 (0.106) |
| East | 0.246 *** (0.072) | 0.081 *** (0.081) | 0.241 *** (0.080) |
| West | 0.052 (0.086) | −0.066 (0.100) | 0.112 (0.098) |
| Male *East | −0.027 (0.088) | - | - |
| Male * West | −0.054 (0.101) | - | - |
| Rural * East | −0.229 ** (0.091) | −0.255 ** (0.125)- | −0.198 (0.132) |
| Rural * West | −0.248 (0.102) | −0.118 (0.142) | −0.385 *** (0.147) |
| Male * Rural | −0.063 (0.078) | - | - |
| Observations | 11,525 | 5945 | 5580 |
| Log likelihood | −7910.108 | −4079.347 | −3833.781 |
| LR chi2(11) | 93.34 | 45.15 | 41.79 |
| Panel A. Male Subsample | ||||||
|---|---|---|---|---|---|---|
| Characteristics | Pre-Matching | Post-Matching | ||||
| Mean | p-Value | Mean | p-Value | |||
| Treated | Control | Treated | Control | |||
| Rural | 0.433 | 0.410 | 0.065 | 0.433 | 0.433 | 1.000 |
| Father’s educational attainment | 2.461 | 2.886 | 0.000 | 2.461 | 2.461 | 1.000 |
| East | 0.467 | 0.429 | 0.004 | 0.467 | 0.467 | 1.000 |
| Observations | 3209 | 2736 | 5945 | 3209 | 2736 | 5945 |
| Panel B. Female subsample | ||||||
| Characteristics | Pre-matching | Post-matching | ||||
| Mean | p-value | Mean | p-value | |||
| Treated | Control | Treated | Control | |||
| Rural | 0.394 | 0.357 | 0.005 | 0.394 | 0.394 | 1.000 |
| Father’s educational attainment | 2.691 | 3.141 | 0.000 | 2.691 | 2.691 | 0.000 |
| East | 0.462 | 0.426 | 0.006 | 0.462 | 0.462 | 1.000 |
| Observations | 2981 | 2599 | 5580 | 2981 | 2599 | 5580 |
| Educational Attainment | ||||||
|---|---|---|---|---|---|---|
| Overall | Male | Female | ||||
| Pre-Matching | Post Matching | Pre-Matching | Post Matching | Pre-Matching | Post Matching | |
| NNM | 0.390 *** (0.057) | 0.407 *** (0.058) | 0.257 *** (0.079) | 0.265 *** (0.079) | 0.529 *** (0.082) | 0.559 *** (0.083) |
| KM | 0.390 *** (0.057) | 0.398 *** (0.057) | 0.257 *** (0.079) | 0.265 *** (0.079) | 0.529 *** (0.082) | 0.539 *** (0.083) |
| Matching | No | Yes | No | Yes | No | Yes |
| Observations | 11,525 | 11,525 | 5945 | 5945 | 5580 | 5580 |
| Panel A. Male Subsample | ||||
|---|---|---|---|---|
| Hidden Bias | Upper and Lower Bounds | p-Value | ||
| t-hat+ | t-hat− | sig+ | sig− | |
| 1 | 5.949 *** | 5.949 *** | 0 | 0 |
| 1.25 | 5.939 *** | 5.978 *** | 0 | 0 |
| 1.5 | 5.898 *** | 6.029 *** | 0 | 0 |
| 1.75 | 5.870 *** | 6.057 *** | 0 | 0 |
| 2 | 5.864 *** | 6.060 *** | 0 | 0 |
| 2.25 | 5.864 *** | 6.065 *** | 0 | 0 |
| 2.5 | 5.864 *** | 6.075 *** | 0 | 0 |
| 2.75 | 5.855 *** | 6.080 *** | 0 | 0 |
| 3 | 5.835 *** | 6.094 *** | 0 | 0 |
| Panel B. Female subsample | ||||
| Hidden bias | Upper and Lower Bounds | p-value | ||
| t-hat+ | t-hat− | sig+ | sig− | |
| 1 | 5.664 *** | 5.664 *** | 0 | 0 |
| 1.25 | 5.617 *** | 5.680 *** | 0 | 0 |
| 1.5 | 5.561 *** | 5.696 *** | 0 | 0 |
| 1.75 | 5.548 *** | 5.711 *** | 0 | 0 |
| 2 | 5.501 *** | 5.746 *** | 0 | 0 |
| 2.25 | 5.479 *** | 5.760 *** | 0 | 0 |
| 2.5 | 5.442 *** | 5.780 *** | 0 | 0 |
| 2.75 | 5.442 *** | 5.807 *** | 0 | 0 |
| 3 | 5.430 | 5.822 | 0 | 0 |
| Panel A. Pre-Tax Income | ||||||
|---|---|---|---|---|---|---|
| Overall | Male | Female | ||||
| Pre-Matching | Post Matching | Pre-Matching | Post Matching | Pre-Matching | Post Matching | |
| NNM | 1397.050 (1125.516) | 1723.058 (1157.910) | 377.266 (1826.556) | 488.707 (1903.058) | 2314.761 * (1241,418) | 2914.655 ** (1245.638) |
| KM | 1397.050 (1125.516) | 1714.194 (1152.403) | 377.266 (1826.556) | 714.263 (1893.209) | 2314.761 * (1241,418) | 2631.699 ** (1238.963) |
| Matching | No | Yes | No | Yes | No | Yes |
| Observations | 11,525 | 11,525 | 5945 | 5945 | 5580 | 5580 |
| Panel B. After-tax income | ||||||
| Overall | Male | Female | ||||
| Pre-matching | Post matching | Pre-matching | Pre-matching | Post matching | Pre-matching | |
| NNM | 1540, 335 (1088.092) | 1862.929 * (1117.627) | 634.751 (1751.079) | 757.462 (1821.040) | 2338.767 * (1223.141) | 2931.299 ** (1227.647) |
| KM | 1540, 335 (1088.092) | 1848.584 * (1112.387) | 634.751 (1751.079) | 959.199 (1811.747) | 2338.767 * (1223.141) | 2643.662 ** (1221.045) |
| Matching | No | Yes | No | Yes | No | Yes |
| Observations | 11,525 | 11,525 | 5945 | 5945 | 5580 | 5580 |
| Overall Sample | Male Subsample | Female Subsample | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper and Lower Bounds | p-Value | Upper and Lower Bounds | p-Value | Upper and Lower Bounds | p-Value | |||||||
| t-hat+ | t-hat− | sig+ | sig− | t-hat+ | t-hat− | sig+ | sig− | t-hat+ | t-hat− | sig+ | sig− | |
| Panel A. The sensitivity analysis for pre-tax income | ||||||||||||
| 1 | 26848.3 *** | 26,848.3 *** | 0 | 0 | 33,772.5 *** | 33,772.5 *** | 0 | 0 | 18,793.4 *** | 18,793.4 *** | 0 | 0 |
| 1.25 | 26742.5 *** | 27,010.3 *** | 0 | 0 | 32,929 *** | 34,152.8 *** | 0 | 0 | 16,706.9 *** | 19,333.7 *** | 0 | 0 |
| 1.5 | 26715.2 *** | 27,138.8 *** | 0 | 0 | 31,022.1 *** | 35,863.7 *** | 0 | 0 | 16,706.9 *** | 16,555.7 *** | 0 | 0 |
| 1.75 | 26622.1 *** | 27,205.1 *** | 0 | 0 | 28,169 *** | 36,944 *** | 0 | 0 | 15,910.1 *** | 21,285 *** | 0 | 0 |
| 2 | 26609.4 *** | 27,743.3 *** | 0 | 0 | 27,219.3 *** | 37,753.9 *** | 0 | 0 | 15,308.8 *** | 21,741.4 *** | 0 | 0 |
| 2.25 | 26609.4 *** | 27,244.6 *** | 0 | 0 | 26,197.2 *** | 38,709.9 *** | 0 | 0 | 14,833.2 *** | 21,974.3 *** | 0 | 0 |
| 2.5 | 26543.1 *** | 27,310.9 *** | 0 | 0 | 26,190.3 *** | 38,716.8 *** | 0 | 0 | 14,541.1 *** | 21,974.3 *** | 0 | 0 |
| 2.75 | 26543.1 *** | 27,376.4 *** | 0 | 0 | 26,077.8 *** | 38,716.8 *** | 0 | 0 | 13,928.9 *** | 22,217 *** | 0 | 0 |
| 3 | 26516.3 *** | 27,376.4 *** | 0 | 0 | 26,077.8 *** | 38,716.8 *** | 0 | 0 | 13,744.3 *** | 23,221.2 *** | 0 | 0 |
| Panel B. The sensitivity analysis for after-tax income | ||||||||||||
| 1 | 26,530.6 *** | 26,530.6 *** | 0 | 0 | 33,727.7 *** | 33,272.7 *** | 0 | 0 | 18,608.4 *** | 18,608.4 *** | 0 | 0 |
| 1.25 | 26,428.8 *** | 26,687.1 *** | 0 | 0 | 32,743.2 *** | 33,758.2 *** | 0 | 0 | 16,671.4 *** | 19,219.5 *** | 0 | 0 |
| 1.5 | 26,402 *** | 26,810.8 *** | 0 | 0 | 30,954.1 *** | 35,371.8 *** | 0 | 0 | 16,588.8 *** | 19,716.1 *** | 0 | 0 |
| 1.75 | 26,311.9 *** | 26,874.7 *** | 0 | 0 | 28,128.3 *** | 36,519.5 *** | 0 | 0 | 15,796 *** | 21,552 *** | 0 | 0 |
| 2 | 26,300.2 *** | 26,910.9 *** | 0 | 0 | 27,177.6 *** | 37,534.8 *** | 0 | 0 | 15,237.1 *** | 21,556.4 *** | 0 | 0 |
| 2.25 | 26,300.2 *** | 26,912.7 *** | 0 | 0 | 26,162.6 *** | 38,147 *** | 0 | 0 | 14,761.6 *** | 21,788.6 *** | 0 | 0 |
| 2.5 | 26,236.3 *** | 26,976.5 *** | 0 | 0 | 26,111.8 *** | 38,197.7 *** | 0 | 0 | 14,516.2 *** | 21,788.6 *** | 0 | 0 |
| 2.75 | 26,236.3 *** | 27,039.5 *** | 0 | 0 | 26,019.1 *** | 38,197.7 *** | 0 | 0 | 13,723.5 *** | 22,031.9 *** | 0 | 0 |
| 3 | 26,210.1 *** | 27,039.5 *** | 0 | 0 | 26,029.1 *** | 38,197.7 *** | 0 | 0 | 13,655.5 *** | 22,837.8 *** | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Huang, Z.; Cai, J. Does the One-Child Policy Improve Chinese Human Capital? A Propensity Score Matching Analysis. Sustainability 2023, 15, 12373. https://doi.org/10.3390/su151612373
Wang Z, Huang Z, Cai J. Does the One-Child Policy Improve Chinese Human Capital? A Propensity Score Matching Analysis. Sustainability. 2023; 15(16):12373. https://doi.org/10.3390/su151612373
Chicago/Turabian StyleWang, Ziqi, Ziyao Huang, and Jingjing Cai. 2023. "Does the One-Child Policy Improve Chinese Human Capital? A Propensity Score Matching Analysis" Sustainability 15, no. 16: 12373. https://doi.org/10.3390/su151612373
APA StyleWang, Z., Huang, Z., & Cai, J. (2023). Does the One-Child Policy Improve Chinese Human Capital? A Propensity Score Matching Analysis. Sustainability, 15(16), 12373. https://doi.org/10.3390/su151612373






