Study of Centrality Measures in the Network of Green Spaces in the City of Krakow
Abstract
:1. Introduction
2. Literature Review
2.1. Benefits of Natural Space
2.2. Network Approach in Urban Studies
2.3. Centrality Concept and Its Application
2.4. Research Contribution
3. Materials and Methods
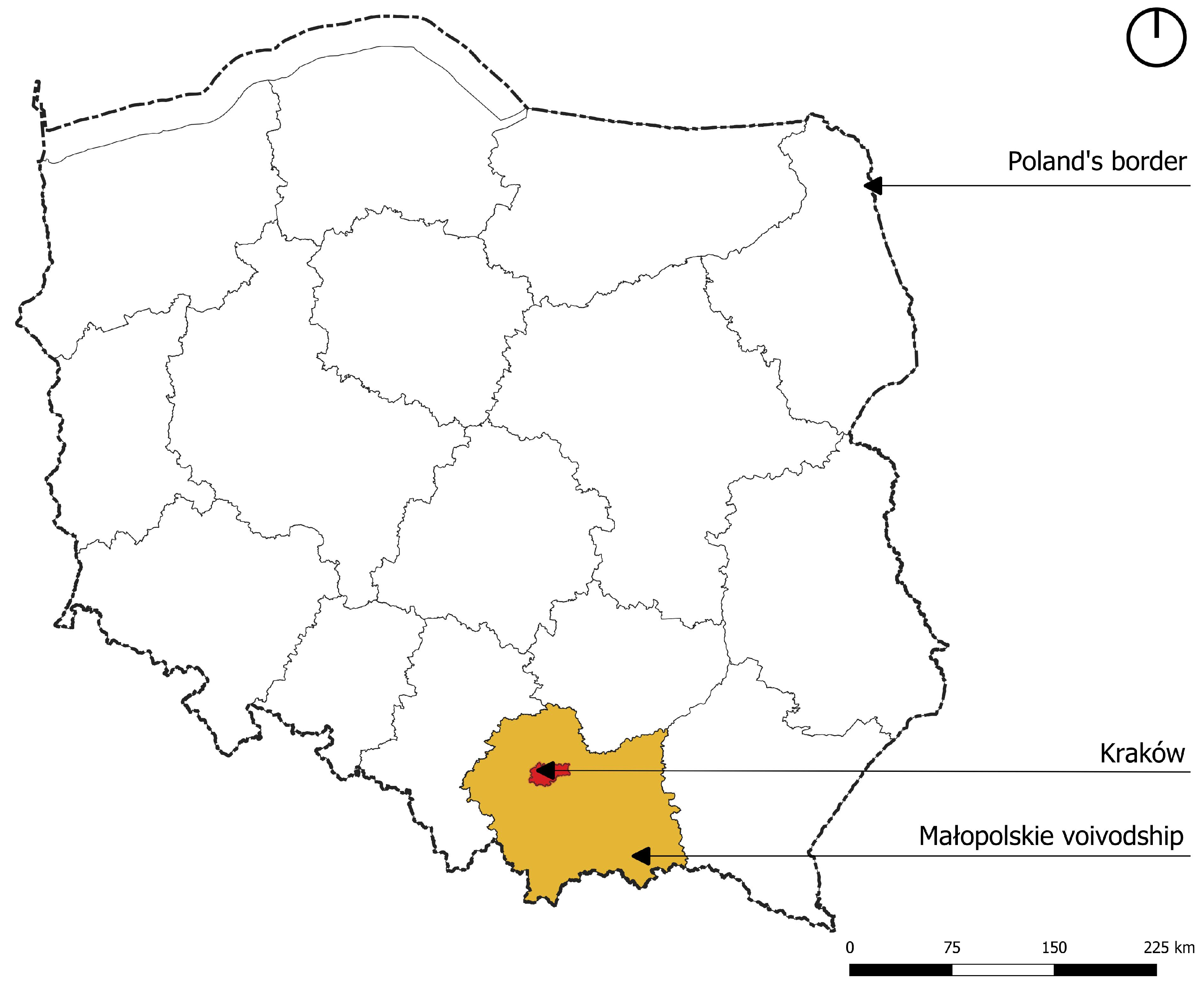
3.1. Krakow as a Research Area
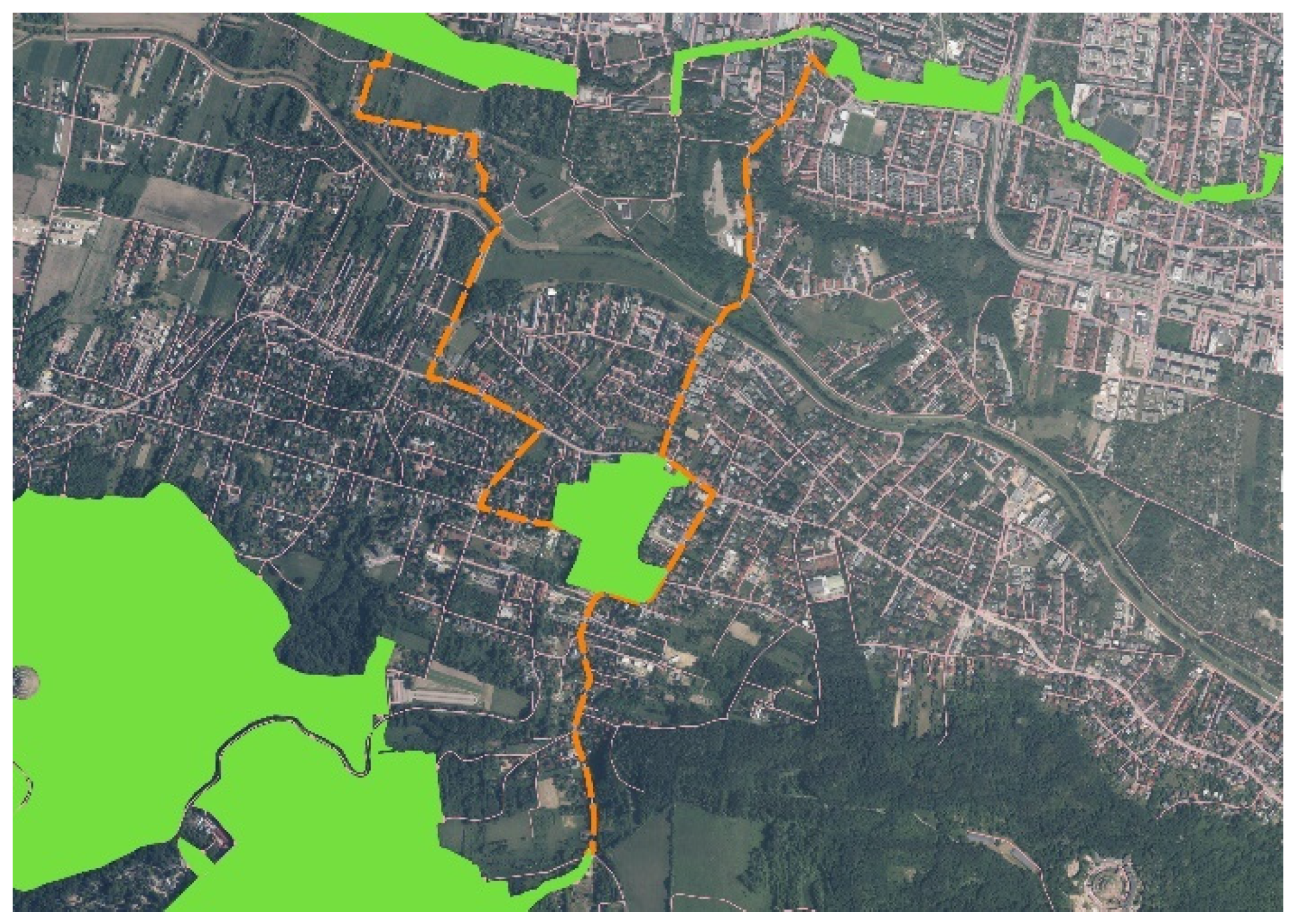
3.2. Selection of Parks and Green Areas
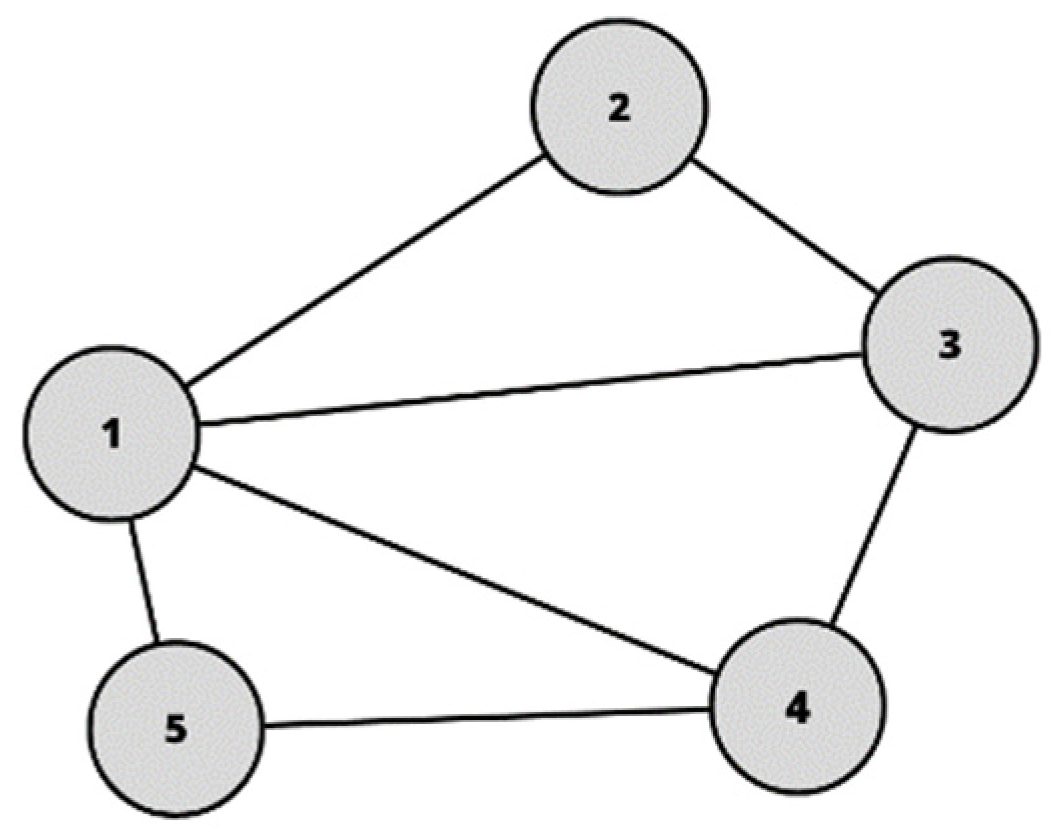
3.3. Network and Graph
3.4. Centrality Measures
3.5. Mapping Centralities
4. Results
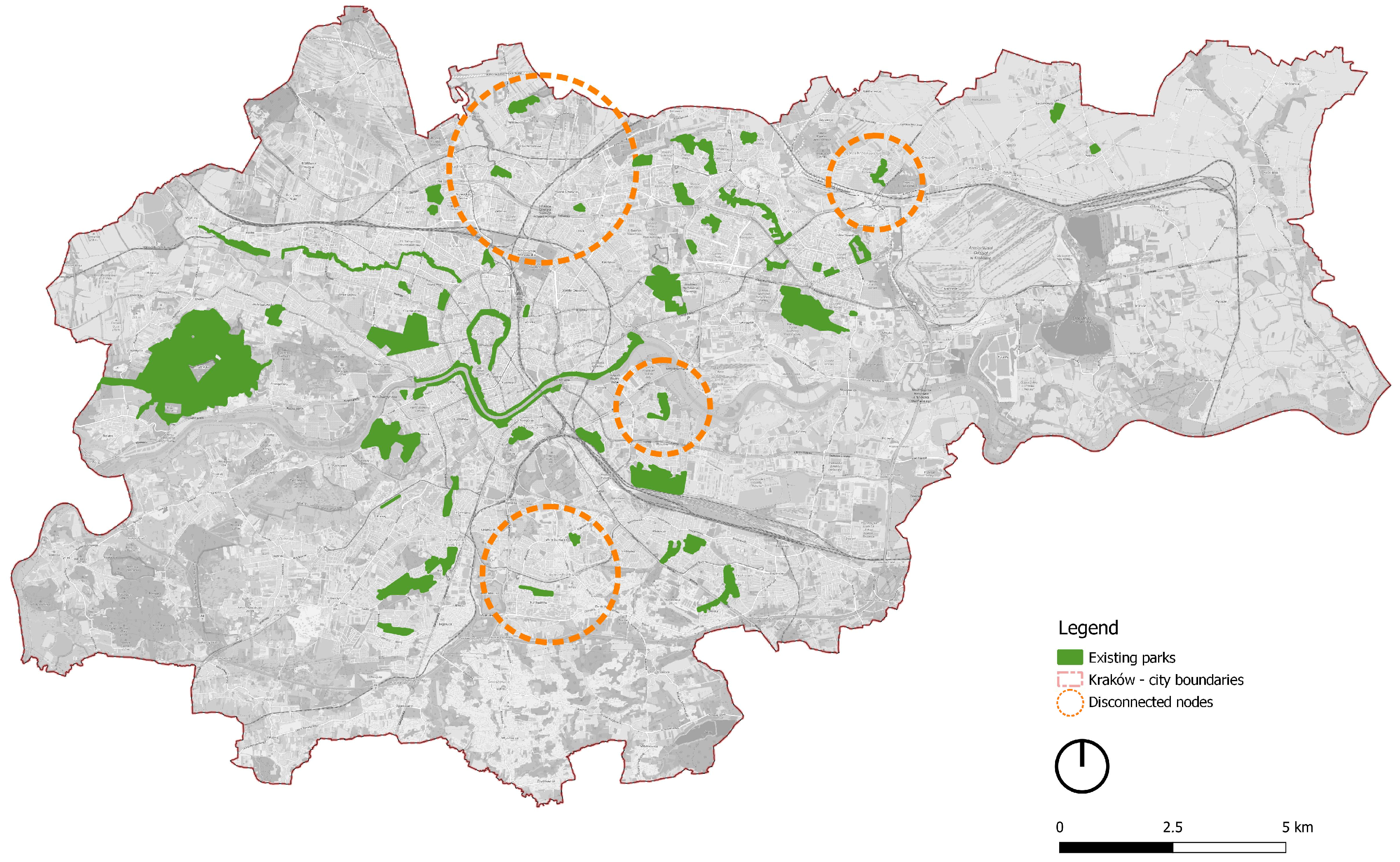
4.1. Network and Graph Results
4.2. Centrality Results
4.2.1. Single Centrality Measures
4.2.2. Compound Centrality Index
4.3. Centrality Distribution in Krakow
5. Conclusions and Discussion
6. Study Limitations and Further Research
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities “just green enough”. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef]
- Madureira, H.; Nunes, F.; Oliveira, J.V.; Cormier, L.; Madureira, T. Urban residents’ beliefs concerning green space benefits in four cities in France and Portugal. Urban For. Urban Green. 2015, 14, 56–64. [Google Scholar] [CrossRef]
- Ekkel, E.D.; de Vries, S. Nearby green space and human health: Evaluating accessibility metrics. Landsc. Urban Plan. 2017, 157, 214–220. [Google Scholar] [CrossRef]
- Garau, C.; Pavan, V.M. Evaluating Urban Quality: Indicators and Assessment Tools for Smart Sustainable Cities. Sustainability 2018, 10, 575. [Google Scholar] [CrossRef]
- Giedych, R.; Maksymiuk, G. Specific features of parks and their impact on regulation and cultural ecosystem services provision in Warsaw, Poland. Sustainability 2017, 9, 792. [Google Scholar] [CrossRef]
- Hwang, Y.H.; Nasution, I.K.; Amonkar, D.; Hahs, A. Urban green space distribution related to land values in fast-growing megacities, Mumbai and Jakarta-unexploited opportunities to increase access to greenery for the poor. Sustainability 2020, 12, 4982. [Google Scholar] [CrossRef]
- Ying, J.; Zhang, X.; Zhang, Y.; Bilan, S. Green infrastructure: Systematic literature review. Econ. Res. Istraz. 2022, 35, 343–366. [Google Scholar] [CrossRef]
- United Nations (Habitat III). New Urban Agenda; United Nations: Quito, Ecuador, 2017. [Google Scholar]
- World Health Organization. Urban Green Spaces: A Brief for Action; WHO: Geneva, Switzerland, 2017. [Google Scholar]
- Durkheim, E. Suicide. A Study in Sociology; Free Press: New York, NY, USA, 1951. [Google Scholar]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network analysis in the social sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Batty, M. New Science of Cities; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Liu, W.; Hou, Q.; Xie, Z.; Mai, X. Urban network and regions in China: An analysis of daily migration with complex networks model. Sustainability 2020, 12, 3208. [Google Scholar] [CrossRef]
- Sharma, S.; Ram, S. Investigation of Road Network Connectivity and Accessibility in Less Accessible Airport Regions: The Case of India. Sustainability 2023, 15, 5747. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Hansen, D.L.; Shneiderman, B.; Smith, M.A.; Himelboim, I. Calculating and Visualizing Network Metrics; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128177563. [Google Scholar]
- Gialampoukidis, I.; Kalpakis, G.; Tsikrika, T.; Papadopoulos, S.; Vrochidis, S.; Kompatsiaris, I. Detection of terrorism-related twitter communities using centrality scores. In Proceedings of the MFSec 2017—Proceedings of the 2nd International Workshop on Multimedia Forensics and Security, co-located with ICMR 2017, Bucharest, Romania, 6 June 2017; pp. 21–25. [Google Scholar] [CrossRef]
- Gu, J.; Abroms, L.C.; Broniatowski, D.A.; Evans, W.D. An Investigation of Influential Users in the Promotion and Marketing of Heated Tobacco Products on Instagram: A Social Network Analysis. Int. J. Environ. Res. Public Health 2022, 19, 1686. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Yin, H.; Nakagoshi, N.; Zong, Y. Urban green space network development for biodiversity conservation: Identification based on graph theory and gravity modeling. Landsc. Urban Plan. 2010, 95, 16–27. [Google Scholar] [CrossRef]
- Maes, J.; Zulian, G.; Günther, S.; Martijn, T.; Raynal, J. Enhancing Resilience of Urban Ecosyxstems throug Green Infrastructure (EnRoute); Office of the European Union: Luxembourg, 2019; ISBN 9789276002710. [Google Scholar]
- Mears, M.; Brindley, P.; Jorgensen, A.; Maheswaran, R. Population-level linkages between urban greenspace and health inequality: The case for using multiple indicators of neighbourhood greenspace. Health Place 2020, 62, 102284. [Google Scholar] [CrossRef] [PubMed]
- Hunter, M.C.R.; Gillespie, B.W.; Chen, S.Y.P. Urban nature experiences reduce stress in the context of daily life based on salivary biomarkers. Front. Psychol. 2019, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Li, Q. Effect of forest bathing trips on human immune function. Environ. Health Prev. Med. 2010, 15, 9–17. [Google Scholar] [CrossRef]
- Wang, R.; Helbich, M.; Yao, Y.; Zhang, J.; Liu, P.; Yuan, Y.; Liu, Y. Urban greenery and mental wellbeing in adults: Cross-sectional mediation analyses on multiple pathways across different greenery measures. Environ. Res. 2019, 176, 108535. [Google Scholar] [CrossRef] [PubMed]
- Maas, J.; Verheij, R.A.; Groenewegen, P.P.; De Vries, S.; Spreeuwenberg, P. Green space, urbanity, and health: How strong is the relation? J. Epidemiol. Community Health 2006, 60, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Korpilo, S.; Kajosaari, A.; Rinne, T.; Hasanzadeh, K.; Raymond, C.M.; Kyttä, M. Coping with Crisis: Green Space Use in Helsinki Before and During the COVID-19 Pandemic. Front. Sustain. Cities 2021, 3, 1–13. [Google Scholar] [CrossRef]
- Kim, D.; Jin, J. Does happiness data say urban parks are worth it? Landsc. Urban Plan. 2018, 178, 1–11. [Google Scholar] [CrossRef]
- van den Berg, A.E.; Maas, J.; Verheij, R.A.; Groenewegen, P.P. Green space as a buffer between stressful life events and health. Soc. Sci. Med. 2010, 70, 1203–1210. [Google Scholar] [CrossRef] [PubMed]
- European Environmental Agency. Urban Green Infrastructure—Interactive Map. Available online: https://eea.maps.arcgis.com/apps/MapSeries/index.html?appid=42bf8cc04ebd49908534efde04c4eec8 (accessed on 4 October 2020).
- Kothencz, G.; Kolcsár, R.; Cabrera-Barona, P.; Szilassi, P. Urban Green Space Perception and Its Contribution to Well-Being. Int. J. Environ. Res. Public Health 2017, 14, 766. [Google Scholar] [CrossRef] [PubMed]
- Kaczynski, A.T.; Potwarka, L.R.; Saelens P, B.E. Association of park size, distance, and features with physical activity in neighborhood parks. Am. J. Public Health 2008, 98, 1451–1456. [Google Scholar] [CrossRef] [PubMed]
- Pereira, G.; Foster, S.; Martin, K.; Christian, H.; Boruff, B.J.; Knuiman, M.; Giles-Corti, B. The association between neighborhood greenness and cardiovascular disease: An observational study. BMC Public Health 2012, 12, 466. [Google Scholar] [CrossRef] [PubMed]
- Markevych, I.; Schoierer, J.; Hartig, T.; Chudnovsky, A.; Hystad, P.; Dzhambov, A.M.; de Vries, S.; Triguero-Mas, M.; Brauer, M.; Nieuwenhuijsen, M.J.; et al. Exploring pathways linking greenspace to health: Theoretical and methodological guidance. Environ. Res. 2017, 158, 301–317. [Google Scholar] [CrossRef]
- Sturiale, L.; Scuderi, A. The role of green infrastructures in urban planning for climate change adaptation. Climate 2019, 7, 119. [Google Scholar] [CrossRef]
- Giannakis, E.; Bruggeman, A.; Poulou, D.; Zoumides, C.; Eliades, M. Linear Parks along Urban Rivers: Perceptions of Thermal Comfort and Climate Change Adaptation in Cyprus. Sustainability 2016, 8, 1023. [Google Scholar] [CrossRef]
- Jarvis, I.; Gergel, S.; Koehoorn, M.; van den Bosch, M. Greenspace access does not correspond to nature exposure: Measures of urban natural space with implications for health research. Landsc. Urban Plan. 2020, 194, 103686. [Google Scholar] [CrossRef]
- McCormick, R. Does Access to Green Space Impact the Mental Well-being of Children: A Systematic Review. J. Pediatr. Nurs. 2017, 37, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Onose, D.A.; Iojă, I.C.; Niță, M.R.; Vânău, G.O.; Popa, A.M. Too Old for Recreation? How Friendly Are Urban Parks for Elderly People? Sustainability 2020, 12, 790. [Google Scholar] [CrossRef]
- Reid, C.E.; Kubzansky, L.D.; Li, J.; Shmool, J.L.; Clougherty, J.E. It’s not easy assessing greenness: A comparison of NDVI datasets and neighborhood types and their associations with self-rated health in New York City. Health Place 2018, 54, 92–101. [Google Scholar] [CrossRef]
- Wysmułek, J.; Hełdak, M.; Kucher, A. The Analysis of Green Areas’ Accessibility in Comparison with Statistical Data in Poland. Int. J. Environ. Res. Public Health 2020, 17, 4492. [Google Scholar] [CrossRef]
- Pouya, S.; Aghlmand, M. Evaluation of urban green space per capita with new remote sensing and geographic information system techniques and the importance of urban green space during the COVID-19 pandemic. Environ. Monit. Assess. 2022, 194, 633. [Google Scholar] [CrossRef] [PubMed]
- Kabisch, N.; Haase, D. Green justice or just green? Provision of urban green spaces in Berlin, Germany. Landsc. Urban Plan. 2014, 122, 129–139. [Google Scholar] [CrossRef]
- Haaland, C.; Konijnendijk van den Bosch, C. Challenges and strategies for urban green-space planning in cities undergoing densification: A review. Urban For. Urban Green. 2015, 14, 760–771. [Google Scholar] [CrossRef]
- ALGG. Available online: https://www.london.gov.uk/programmes-and-strategies/environment-and-climate-change/environment-publications/all-london-green-grid (accessed on 2 June 2023).
- Nycgovparks. Available online: https://www.nycgovparks.org/facilities/bikeways (accessed on 2 June 2023).
- Zou, H.; Wang, X. Progress and gaps in research on urban green space morphology: A review. Sustainability 2021, 13, 1202. [Google Scholar] [CrossRef]
- Lin, Y.; Zhou, Y.; Lin, M.; Wu, S.; Li, B. Exploring the disparities in park accessibility through mobile phone data: Evidence from Fuzhou of China. J. Environ. Manag. 2021, 281, 111849. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zhao, J.; Meitner, M.J.; Hu, Y.; Xu, X. Characteristics of urban green spaces in relation to aesthetic preference and stress recovery. Urban For. Urban Green. 2019, 41, 6–13. [Google Scholar] [CrossRef]
- Sun, Y.; Tan, S.; He, Q.; Shen, J. Influence Mechanisms of Community Sports Parks to Enhance Social Interaction: A Bayesian Belief Network Analysis. Int. J. Environ. Res. Public Health 2022, 19, 1466. [Google Scholar] [CrossRef] [PubMed]
- Giles-Corti, B.; Broomhall, M.H.; Knuiman, M.; Collins, C.; Douglas, K.; Ng, K.; Lange, A.; Donovan, R.J. Increasing walking: How important is distance to, attractiveness, and size of public open space? Am. J. Prev. Med. 2005, 28, 169–176. [Google Scholar] [CrossRef]
- Bedi, P.; Sharma, C. Community detection in social networks. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2016, 6, 115–135. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space 1984; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Hillier, B. Space is the Machine—A Configurational Theory of Architecture; Space Syntax: London, UK, 2007; ISBN 978-0-9556224-0-3. [Google Scholar]
- Space Syntax. Available online: https://www.spacesyntax.org/ (accessed on 12 June 2023).
- Crucitti, P.; Latora, V.; Porta, S. Centrality in networks of urban streets. Chaos 2006, 16, 015113. [Google Scholar] [CrossRef]
- Louf, R.; Barthelemy, M. A typology of street patterns. J. R. Soc. Interface 2014, 11, 20140924. [Google Scholar] [CrossRef]
- Mehmood, M.S.; Li, G.; Jin, A.; Rehman, A.; Wijeratne, V.P.I.S.; Zafar, Z.; Khan, A.R.; Khan, F.A. The spatial coupling effect between urban street network’s centrality and collection & delivery points: A spatial design network analysis-based study. PLoS ONE 2021, 16, e0251093. [Google Scholar] [CrossRef]
- He, S.; Yu, S.; Wei, P.; Fang, C. A spatial design network analysis of street networks and the locations of leisure entertainment activities: A case study of Wuhan, China. Sustain. Cities Soc. 2019, 44, 880–887. [Google Scholar] [CrossRef]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2006, 45, 167–256. [Google Scholar] [CrossRef]
- Rodrigues, F.A. Network Centrality: An Introduction; Springer International Publishing: Cham, Switzerland, 2019; pp. 177–196. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks. Soc. Netw. 1979, 1, 215–239. [Google Scholar] [CrossRef]
- Bonacich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Jeong, W.; Yu, U. Critical phenomena and strategy ordering with hub centrality approach in the aspiration-based coordination game. Chaos 2021, 31, 093114. [Google Scholar] [CrossRef] [PubMed]
- Agryzkov, T.; Tortosa, L.; Vincent, J.F.; Wilson, R.; Vicent, J.F.; Wilson, R. A Centrality Measure for Urban Networks Based on the Eigenvector Centrality Concept. Environ. Plan. B Urban Anal. City Sci. 2017, 46, 668–689. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. Multiple centrality assessment in Parma: A network analysis of paths and open spaces. Urban Des. Int. 2008, 13, 41–50. [Google Scholar] [CrossRef]
- Chen, J.; Chang, Z. Rethinking urban green space accessibility: Evaluating and optimizing public transportation system through social network analysis in megacities. Landsc. Urban Plan. 2015, 143, 150–159. [Google Scholar] [CrossRef]
- Boeing, G. Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood. Urban Sci. 2019, 3, 28. [Google Scholar] [CrossRef]
- Pérez-Campaña, R.; Abarca-Álvarez, F.J.; Talavera-Garcia, R. Centralities in the city border: A method to identify strategic urban-rural interventions. Ri-Vista 2016, 14, 38–53. [Google Scholar] [CrossRef]
- GUS Biuletyn Statystyczny. 2022. Available online: https://stat.gov.pl/obszary-tematyczne/inne-opracowania/informacje-o-sytuacji-spoleczno-gospodarczej/biuletyn-statystyczny-nr-22022,4,123.html (accessed on 12 June 2023).
- UMK. Kierunki Rozwoju i Zarządzania Terenami Zieleni w Krakowie na lata 2019–2030; UMK: Kraków, Poland, 2019. (In Polish) [Google Scholar]
- Zachariasz, A. Zielony Kraków dla przyjemności i pożytku szanownej Publiczności; Wydawnictwo Politechniki Krakowskiej: Krakow, Poland, 2019. [Google Scholar]
- Hodor, K. Urban parks and their value: Cracow example. Tech. Trans. 2016, 2016, 253–274. [Google Scholar]
- Dudzic-Gyurkovich, K.; Suchoń, F.; Gyurkovich, J.; Stawiarski, G.; Boba-Dyga, B.; Olesiak, J. Conservation of 19th century defensive structure. The case of Fort Swoszowice in Cracow, Poland. Int. J. Conserv. Sci. 2022, 13, 417–430. [Google Scholar]
- Suchoń, F. Cracow—City—Fortress. In Kraków: Wybrane Problemy Ewolucji Struktury Miejskiej Cracow: Selected Problems of the Urban Structure Evolution; Gyurkovich, J., Matusik, A., Suchoń, F., Eds.; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2016; pp. 273–294. [Google Scholar]
- Kwartnik-Pruc, A.; Trembecka, A. Public green space policy implementation: A case study of Krakow, Poland. Sustainability 2021, 13, 538. [Google Scholar] [CrossRef]
- Feltynowski, M.; Kronenberg, J.; Bergier, T.; Kabisch, N.; Łaszkiewicz, E.; Strohbach, M.W. Challenges of urban green space management in the face of using inadequate data. Urban For. Urban Green. 2018, 31, 56–66. [Google Scholar] [CrossRef]
- Geoportal. Available online: https://www.geoportal.gov.pl/ (accessed on 12 June 2023).
- Lityński, P.; Hołuj, A. Urban sprawl risk delimitation: The concept for spatial planning policy in Poland. Sustainability 2020, 12, 2637. [Google Scholar] [CrossRef]
- Blečić, I.; Congiu, T.; Fancello, G.; Trunfio, G.A. Planning and design support tools for walkability: A guide for Urban analysts. Sustainability 2020, 12, 4405. [Google Scholar] [CrossRef]
- Rigolon, A. A complex landscape of inequity in access to urban parks: A literature review. Landsc. Urban Plan. 2016, 153, 160–169. [Google Scholar] [CrossRef]
- Schipperijn, J.; Ekholm, O.; Stigsdotter, U.K.; Toftager, M.; Bentsen, P.; Kamper-Jørgensen, F.; Randrup, T.B. Factors influencing the use of green space: Results from a Danish national representative survey. Landsc. Urban Plan. 2010, 95, 130–137. [Google Scholar] [CrossRef]
- Schindler, M.; Le Texier, M.; Caruso, G. How far do people travel to use urban green space? A comparison of three European cities. Appl. Geogr. 2022, 141, 102673. [Google Scholar] [CrossRef]
- Jacomy, M.; Venturini, T.; Heymann, S.; Bastian, M. ForceAtlas2, a continuous graph layout algorithm for handy network visualization designed for the Gephi software. PLoS ONE 2014, 9, e98679. [Google Scholar] [CrossRef]
- Sarvari, H.; Abozinadah, E.; Mbaziira, A.; McCoy, D. Constructing and analyzing criminal networks. In Proceedings of the 2014 IEEE Security and Privacy Workshops, San Jose, CA, USA, 17–18 May 2014; pp. 84–91. [Google Scholar] [CrossRef]
- Golbeck, J. Network Structure and Measures. Anal. Soc. Web 2013, 5, 25–44. [Google Scholar] [CrossRef]
- Singh, A.; Singh, R.R.; Iyengar, S.R.S. Node-weighted centrality: A new way of centrality hybridization. Comput. Soc. Netw. 2020, 7, 6. [Google Scholar] [CrossRef]
- Perez, C.; Germon, R. Graph Creation and Analysis for Linking Actors: Application to Social Data. In Automating Open Source Intelligence: Algorithms for OSINT; Elsevier B.V.: Amsterdam, The Netherlands, 2016; pp. 103–129. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Cardillo, A.; Belli, E.; Càrdenas, F.; Cormenzana, B.; et al. Street Centrality and the Location of Economic Activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Agryzkov, T.; Tortosa, L.; Vicent, J.F. A variant of the current flow betweenness centrality and its application in urban networks. Appl. Math. Comput. 2019, 347, 600–615. [Google Scholar] [CrossRef]
- Kazerani, A.; Winter, S. Can betweenness centrality explain traffic flow. In Proceedings of the 12th AGILE International Conference on Geographic Information Science, Hannover, Germany, 2–5 June 2009; pp. 1–9. Available online: https://people.eng.unimelb.edu.au/winter/pubs/kazerani09centrality.pdf (accessed on 12 June 2023).
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Węcławowicz, G. Urban Development in Poland, from the Socialist City to the Post-Socialist and Neoliberal City. In Artificial Towns in the 21st Century. Social Polarisation in the New Town Regions of East-Central Europe; Institute for Sociology Centre for Social Sciences Hungarian Academy of Sciences: Budapest, Hungary, 2016; pp. 65–82. Available online: https://rcin.org.pl/igipz/Content/62816/PDF/WA51_81767_151633-r2016_Urban-Development-in.pdf (accessed on 12 June 2023).
- Gyurkovich, M.; Sotoca, A.; Szarata, A.; Matusik, A.; Poklewski-Koziełł, D.; Szczerek, E.; Suchoń, F. Housing estates from the second half of the twentieth century as urban heritage structures: Example of housing estates in mistrzejowice, cracow. Wiad. Konserw. 2021, 2021, 54–65. [Google Scholar] [CrossRef]
- Romańczyk, K. Pitfalls of revitalisation. A case study of Kraków. Stud. Reg. Lokal. 2018, 74, 5–25. [Google Scholar] [CrossRef]
- Wu, C.; Smith, D.; Wang, M. Simulating the urban spatial structure with spatial interaction: A case study of urban polycentricity under different scenarios. Comput. Environ. Urban Syst. 2021, 89, 101677. [Google Scholar] [CrossRef]
- Butts, C.T. Revisiting the foundations of network analysis. Science 2009, 325, 414–416. [Google Scholar] [CrossRef]
- Gupta, K.; Roy, A.; Luthra, K.; Maithani, S.; Mahavir. GIS based analysis for assessing the accessibility at hierarchical levels of urban green spaces. Urban For. Urban Green. 2016, 18, 198–211. [Google Scholar] [CrossRef]
- Wolff, M. Taking one step further—Advancing the measurement of green and blue area accessibility using spatial network analysis. Ecol. Indic. 2021, 126, 107665. [Google Scholar] [CrossRef]
- Tu, X.; Huang, G.; Wu, J.; Guo, X. How do travel distance and park size influence urban park visits? Urban For. Urban Green. 2020, 52, 126689. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, P.Y.; Richards, D. Relative importance of quantitative and qualitative aspects of urban green spaces in promoting health. Landsc. Urban Plan. 2021, 213, 104131. [Google Scholar] [CrossRef]
- Dudzic-Gyurkovich, K. Public Space and Urban Barriers in Cracow. Analysis of Existing State. Tech. Trans/Czas. Tech. 2018, 2018, 19–34. [Google Scholar]
- Gil, J. Street network analysis “edge effects”: Examining the sensitivity of centrality measures to boundary conditions. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 819–836. [Google Scholar] [CrossRef]






| Name | Network ID | Area (ha) 1 | Type |
|---|---|---|---|
| Błonia Krakowskie | 22 | 41.18 | Public meadow |
| Bulwary Wisły | 53 | 45.01 | Linear river park |
| Fort Batowice | 5 | 9.02 | Greenery connected with former military building |
| Fort Mistrzejowice | 30 | 5.73 | Greenery connected with former military building |
| Las Wolski | 48 | 387.12 | Forest |
| Łąki Nowohuckie | 38 | 63.80 | Public meadow |
| Park Aleksandry | 45 | 14.79 | Park |
| Park Bednarskiego | 7 | 8.45 | Park |
| Park Borkowski | 54 | 30.25 | Forest |
| Park Czyżyny | 35 | 3.11 | Park |
| Park Decjusza | 12 | 10.29 | Park |
| Park Dębnicki A | 11 | 3.42 | Park |
| Park Dębnicki B | 3 | 1.32 | Park |
| Park Duchacki | 8 | 3.08 | Park |
| Park Jerzmanowskich | 1 | 5.93 | Park |
| Park Jordana | 15 | 20.80 | Park |
| Park Klasztorna | 23 | 0.88 | Park |
| Park Kleparski | 14 | 3.85 | Park |
| Park Kościuszki | 21 | 5.26 | Park |
| Park Krakowski | 6 | 5.27 | Park |
| Park Krowoderski | 43 | 8.95 | Park |
| Park Kurdwanów | 18 | 5.02 | Park |
| Park Lilli Wenedy | 10 | 11.01 | Park |
| Park Lotników Polskich | 55 | 41.65 | Park |
| Park Łuczanowice | 34 | 6.69 | Park |
| Park Maćka i Doroty | 4 | 8.16 | Park |
| Park Miejski Bagry Wielkie | 36 | 48.11 | Park connected with water reservoir |
| Park Młynówka Królewska | 44 | 28.37 | Linear park |
| Park Ogród Płaszów | 52 | 9.07 | Park |
| Park Ratuszowy | 13 | 2.22 | Park |
| Park Reduta | 33 | 6.86 | Park |
| Park Re-Kreacja | 46 | 0.97 | Linear park |
| Park Rzeczny Wilga | 47 | 8.79 | River park |
| Park Rżąka | 16 | 3.60 | Park |
| Park Skalskiego | 19 | 6.08 | Park |
| Park Skałki Twardowskiego | 39 | 53.09 | Park connected with water reservoir |
| Park Solvay | 49 | 13.11 | Park |
| Park Strzelecki | 9 | 1.54 | Park |
| Park Szwedzki | 27 | 2.29 | Park |
| Park Tysiąclecia | 32 | 10.15 | Park |
| Park Wadów | 25 | 2.37 | Park |
| Park Wincentego a’Paulo | 28 | 2.07 | Park |
| Park Wiśniowy Sad | 2 | 3.93 | Park |
| Park Witkowicki | 31 | 10.41 | Forest |
| Park Wyspiańskiego | 26 | 2.43 | Park |
| Park Zabłocie—Stacja Wisła | 17 | 1.45 | Park |
| Park Zaczarowanej Dorożki | 20 | 2.11 | Park |
| Park Zielony Jar Wandy | 41 | 6.17 | Park |
| Park Żeromskiego | 50 | 4.12 | Park |
| Planty Bieńczyckie | 40 | 17.26 | Park |
| Planty Floriana Nowackiego | 24 | 2.58 | Park |
| Planty Krakowskie | 42 | 19.80 | Park |
| Planty Mistrzejowickie | 29 | 11.15 | Park |
| Staw Płaszowski | 37 | 12.63 | Park connected with water reservoir |
| Zalew Nowohucki | 51 | 7.68 | Park connected with water reservoir |
| Rank | DC | CC | BC | EC | ||||
|---|---|---|---|---|---|---|---|---|
| Node | Value | Node | Value | Node | Value | Node | Value | |
| 1. | 53 | 248 | 12 | 1 | 53 | 517.867 | 53 | 1 |
| 2. | 38 | 148 | 48 | 1 | 55 | 360 | 22 | 0.959 |
| 3. | 13 | 120 | 25 | 1 | 35 | 350 | 42 | 0.831 |
| 4. | 42 | 116 | 34 | 1 | 40 | 224.333 | 15 | 0.774 |
| 5. | 40 | 116 | 54 | 0.75 | 32 | 188.333 | 40 | 0.701 |
| 6. | 27 | 112 | 49 | 0.75 | 37 | 170.5 | 6 | 0.688 |
| 7. | 15 | 108 | 4 | 0.5 | 42 | 168.567 | 38 | 0.636 |
| 8. | 22 | 104 | 47 | 0.5 | 36 | 140 | 13 | 0.621 |
| 9. | 29 | 104 | 53 | 0.319 | 19 | 130 | 3 | 0.573 |
| 10. | 6 | 100 | 55 | 0.3 | 10 | 110 | 11 | 0.573 |
| Centrality Measure | Mean | Standard Deviation | Standard Error | Gini Coefficient |
|---|---|---|---|---|
| Weighted Degree (DC) | 55.85455 | 47.75843 | 6.38093 | 0.45313 |
| Closeness (CC) | 0.275676 | 0.25104 | 0.03385 | 0.41383 |
| Betweenness (BC) | 54.52727 | 104.3927 | 14.07631 | 0.78227 |
| Eigenvector (EC) | 0.27188 | 0.28395 | 0.03829 | 0.56452 |
| Rank | Node | Name | DBE Value |
|---|---|---|---|
| 1. | 53 | Bulwary Wisły | 255.622 |
| 2. | 35 | Park Czyżyny | 134.077 |
| 3. | 55 | Park Lotników Polskich | 129.414 |
| 4. | 40 | Planty Bieńczyckie | 113.678 |
| 5. | 42 | Planty Krakowskie | 95.132 |
| 6. | 32 | Park Tysiąclecia | 92.270 |
| 7. | 38 | Łąki Nowohuckie | 70.101 |
| 8. | 19 | Park Skalskiego | 68.794 |
| 9. | 37 | Staw Płaszowski | 63.539 |
| 10. | 13 | Park Ratuszowy | 60.985 |
| 11. | 7 | Park Bednarskiego | 58.425 |
| 12. | 44 | Park Młynówka Królewska | 56.157 |
| Centrality Measure | Mean | Standard Deviation | Standard Error | Gini Coefficient |
|---|---|---|---|---|
| Compound centrality index (DBE) | 36.88457 | 44.54499 | 6.00644 | 0.55790 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudzic-Gyurkovich, K. Study of Centrality Measures in the Network of Green Spaces in the City of Krakow. Sustainability 2023, 15, 13458. https://doi.org/10.3390/su151813458
Dudzic-Gyurkovich K. Study of Centrality Measures in the Network of Green Spaces in the City of Krakow. Sustainability. 2023; 15(18):13458. https://doi.org/10.3390/su151813458
Chicago/Turabian StyleDudzic-Gyurkovich, Karolina. 2023. "Study of Centrality Measures in the Network of Green Spaces in the City of Krakow" Sustainability 15, no. 18: 13458. https://doi.org/10.3390/su151813458
APA StyleDudzic-Gyurkovich, K. (2023). Study of Centrality Measures in the Network of Green Spaces in the City of Krakow. Sustainability, 15(18), 13458. https://doi.org/10.3390/su151813458






