Energy and Exergy Analysis of a Combined Cooling Heating and Power System with Regeneration

Abstract

Solar assisted trigeneration system has proved to be a potential method in generating power with net zero carbon emissions. The present work aims to address the potential ways to improve the efficiency of the solar energy-integrated carbon dioxide trigeneration system. A regeneration integrated combined cooling, heating, and power system is proposed. With a comprehensive thermodynamic model, the proposed system is simulated for various operating conditions. A component-level exergy analysis is also conducted to estimate the total irreversibility of the system. As the gas cooler exit temperature increases, the overall system irreversibility also increases. When the bleed mass is 20% of the total mass, the system has the lowest energy destruction rate. The potential component that contributes most to system irreversibility is the gas cooler, followed by the regenerator and expansion valve. The proposed system with regeneration yields 29% more COP than the conventional system when operating at lower compressor discharge pressure and a gas cooler exit temperature of 34 °C. It is inferred from the obtained results that to reduce the total irreversibility of the system, it is advised to operate the system at a lower compressor discharge pressure and gas cooler exit temperature.

1. Introduction

The major energy demand for humankind is fulfilled by thermal power plants. This type of energy generation accounts 57.4% of total power generated in India [1] and 80% globally [2]. The energy demand for other applications, such as transport, steel and cement production, and other manufacturing industry processes, contributes 89% of global CO₂ emissions [3]. The United Nations has set a target, as part of the the Paris Agreement, to reach net zero carbon emissions by 2050 and reduce them by 45% by 2030. India is one of the countries contributing the most CO₂ emissions in the world. Hence it is important to work on all possible ways to reduce the country’s CO₂ emissions by finding alternative means to produce power and reduce the emission of greenhouse gases. There are many alternative working fluids available for power plants; however, CO₂ is a good alternative because it is non-flammable, non-toxic, and environmentally secure. The Global Warming Potential of CO₂ is 1. Due to its favorable thermodynamic properties, such as its low critical temperature pressure (31.1 °C, 7.38 MPa), CO₂ attracts many researchers to consider it as a good alternative to address the global warming issue. If CO₂ operates beyond critical temperature and pressure, it is called supercritical CO₂ (sCO₂). At supercritical condition, sCO₂′s specific enthalpy and density behavior dramatically favors the exchange of heat. As a result, researchers have shown increasing interest over the last decade in effectively using sCO₂ for waste heat recovery, power production, HVAC applications etc. Considering cost, plant size, water conservation, better efficiency, and low emissions, it is important to integrate renewable energy sources with sCO₂ while targeting net zero emissions. Solar energy is naturally available and abundant. Technologies such as solar towers, solar concentrators, flat plate collectors, and evacuated pipes already share the renewable energy market. Researchers are now able to attempt to integrate these technologies with sCO₂ applications. However, the efficiency of these thermal systems must be improved.

To promote renewable energy sources for electricity production, solar energy-based power cycles are receiving attention from many researchers [4,5,6,7,8,9,10]. Considering the thermal and economic advantages of CO₂, it has become a better alternative working fluid in place of the steam-powered Rankine cycle. CO₂ occupies relatively less space and consumes less water in order to produce the same amount of power. The feasibility of CO₂ in a solar energy-powered Rankine cycle was reported by Xin-Rong et al. [11]. Evacuated solar collectors were used to absorb heat from solar radiation. The plant could work in a moderate temperature range between 30 °C and 200 °C. The plant could achieve a maximum temperature of 194 °C during peak hours and an average of 185 °C. However, the study did not use a real turbine for producing power but reported that a moderately suitable temperature can be achieved using sCO₂ to produce power. Linares et al. [12] employed shell and tube exchangers and used molten salts to store solar thermal energy, which was supplied to sCO₂ before entering the high-pressure turbine. The novel recompression cycle creates high inlet turbine pressure by following a split expansion cycle. Intercooling and reheating allowed them to reach 52.6% efficiency. The thermodynamic, environmental, and economic advantages of using sCO₂ power plants were reported by White et al. [7]. They focused on the technical challenges of operating at high temperatures (300 °C to 800 °C) such as turbines, heat exchangers, materials selection, and control system design, etc. They discussed the combination of reheat and recuperation cycles. The reheat cycles assist in increasing the average temperature for heat addition whereas the recompression cycle enhances thermal efficiency by employing low and high-temperature recuperators.

Combined cooling and power production was attempted by Shi et al. [13] by recovering waste heat from engine combustion exhaust gases, which are in the range of 200 °C to 500 °C. They conducted thermodynamic analysis to investigate the conversion of waste heat energy into a useful form. They reported that their system could achieve 2.9% fuel savings and a 4.8% power increase. An internal heat exchanger was introduced to explore the performance of the sCO₂ Rankine cycle under four different heat sources, including solar energy, waste heat recovery from a coal-fired plant, exhaust gas from a fluidized bed combustor, and from a cement plant [14]. Thermodynamic modeling was simulated using Aspen Plus 11.1 software. For each of the cases, the thermal efficiency significantly increased for the same pressure when the internal heat exchanger was used. Recently, Wang et al. [15] reported the suitability of sCO₂ and transcritical CO₂ (tCO₂) as a working fluid in power cycles for low and medium-range heat sources. They concluded that the recompression layout is more suitable for high-temperature sources with high-specific heat systems. They stated that in order to commercialize sCO₂ plants, the industry should develop suitable equipment for smooth operations.

Sarkar et al. [16] developed a thermodynamic model to simulate simultaneous heating and cooling using sCO₂ as the working fluid. Various parameters were discussed for optimum conditions. A correlation for maximum COP was presented by them. However, the model has limitations in that the evaporator temperatures should be within the range of ±10 °C and cooler temperatures should be within 30 °C to 50 °C. Because of its thermal properties, CO₂ is considered for use in natural circulation loop (NCL) in either its supercritical or transcritical conditions. With many research works devoted to NCL [17,18,19,20,21], a model was developed to simulate the steady-state analysis using sCO₂ as a secondary fluid by Kiran Kumar and Ram Gopal [22]. Their model can predict the optimum length and diameter of the heat exchanger in a rectangular loop. Further, they experimentally verified their model [17] for single- and two-phase fluid in NCL. Ajay Kumar Yadav et al. [18,19] reported a new correlation for friction factor and heat transfer in NCL using CO₂ and water as working fluids in CFD simulations. They found that near the critical point, the sCO₂ produces higher heat transfer. To reduce the heat transfer loss and pressure drop within the cooling and heating systems, nanofluid refrigerants were introduced [23].

Siva Reddy et al. [24] presented a detailed review of solar thermal power plants. Based on the temperature of heat sources, they classified the power plants as either low-, medium, or high-temperature technologies. In the early days, to generate power directly from solar energy at low temperatures, solar ponds and flat plate collectors were used; however, the plant efficiency was very low. When parabolic concentrators were introduced, the fluid could reach 400 °C, so plant efficiency was improved. Techno-economic analysis is presented for 50 MWe for parabolic trough collector and parabolic dish concentrator-based solar power plants. They reported that the unit cost may vary from Rs 7 to Rs 22 based on the location and lifespan of the power plant. Pradeep Garg et al. [25] successfully employed thermodynamic analysis for sCO₂ considering complete CO₂ in the vapor phase with transcritical and sub-critical CO₂ in the Brayton power cycle. They found that the sCO₂ cycle produced the highest efficiency (32%) when compared to the remaining cycles at 600 °C inlet temperature and 85 bar at the exhaust of turbine. In addition, they concluded that the sCO₂ cycle reduces the necessary size of the plant components. Thermodynamic analysis of the transcritical Rankine cycle was tested by Pradeep Garg et al. [26] for a 100 kW power plant using tCO₂. The results were compared with steam and both were given identical efficiencies; however, tCO₂ requires less space, as it works on single loop, when compared to steam powerplant. The lower volumetric flow was another advantage of using tCO₂. Ravindra and Ramgopal [27] analyzed solar-supported combined cooling, heating, and power systems (CCHP) using sCO₂. The turbine exhaust was allowed to flow through a gas cooler. After the gas cooler, the fluid was allowed to expand, in case 1, through the throttling valve and, in case 2, through the low-pressure turbine. It is noticed that irrespective of gas cooler exit temperature, the COP of the system increases if the fluid expands through the turbine rather than through the throttle valve. An innovative method was reported by Sagar Khivsara et al. [28] to measure solar radiation from sCO₂ at both high pressure and temperature. From the available literature, it is evident that sCO₂ is gaining more attention for use as a working fluid for power production and heat transfer. However, there are very few studies on the use of solar energy-integrated combined heating, cooling, and power systems in India. Particularly, there is a lack of experiments to find the COP in connection with important parameters of the CCHP system. Harahap et al. [29] attempted to simulate a micro CCHP system with a biomass heat source using Engineering Equation Solver (EES) software and quantified the exergy destruction rate of potential components. Energy, exergy, and economic analysis of cogeneration and poly-generation systems is gaining momentum in recent studies [30,31,32,33,34] because it predicts the potential components that contribute more to the overall irreversibility of the system and also justify the feasibility and economic viability of any additional component integration into the system.

Combined cooling, heating, and power cycles are receiving increasing interest due to their advantage of engaging the system for multiple applications. Jiangfeng Wang [35] performed a parametric analysis for a CCHP system with transcritical CO₂ driven by solar energy. To reduce the work of the compressor, a novel ejector was introduced after the gas cooler. Solar energy was collected using a concentric parabolic collector and stored in a thermal storage device, which consisted of thermal oil. CO₂ absorbs this heat energy from this storage and gains additional heat from an auxiliary heater (AH) before entering the turbine. They concluded that a rise in turbine inlet temperature and back pressure leads to an increase in thermal efficiency. A similar study was carried out by Ravindra and Ramgopal [27] with minor modifications in the solar heater and following a single loop CO₂ cycle. They made use of sCO₂ for power production and tCO₂ for cooling. The model tested for two cases. In the first, they determined that if the fluid entered in to the evaporator, it would be expanded either in a low-pressure turbine so additional work would be drawn; in the second case, the fluid conventionally expanded through the throttling valve. Results showed that using an additional turbine would increase overall performance in CCHP system by more than 50%.

The above study clearly shows that CCHP systems are gaining momentum in commercial applications, but, despite this, a comprehensive analysis on the system performance of the CCHP system with a regenerator is limited. In addition, component level exergy analysis and its effect on overall system irreversibility is less explored. Thus, the present work supplements a systematic energy analysis of a CCHP system with a regenerator for various operating conditions at gas cooler outlet and compressor discharge. Furthermore, an extensive component wise exergy analysis has been carried out to justify the addition of regenerator and to identify the other improvisation factors. The novelty of the present work is not limited to just quantifying the system energy and exergy values, but also to identifying the operating range in which the system could operate with a maximum COP and minimum exergy destruction rate.

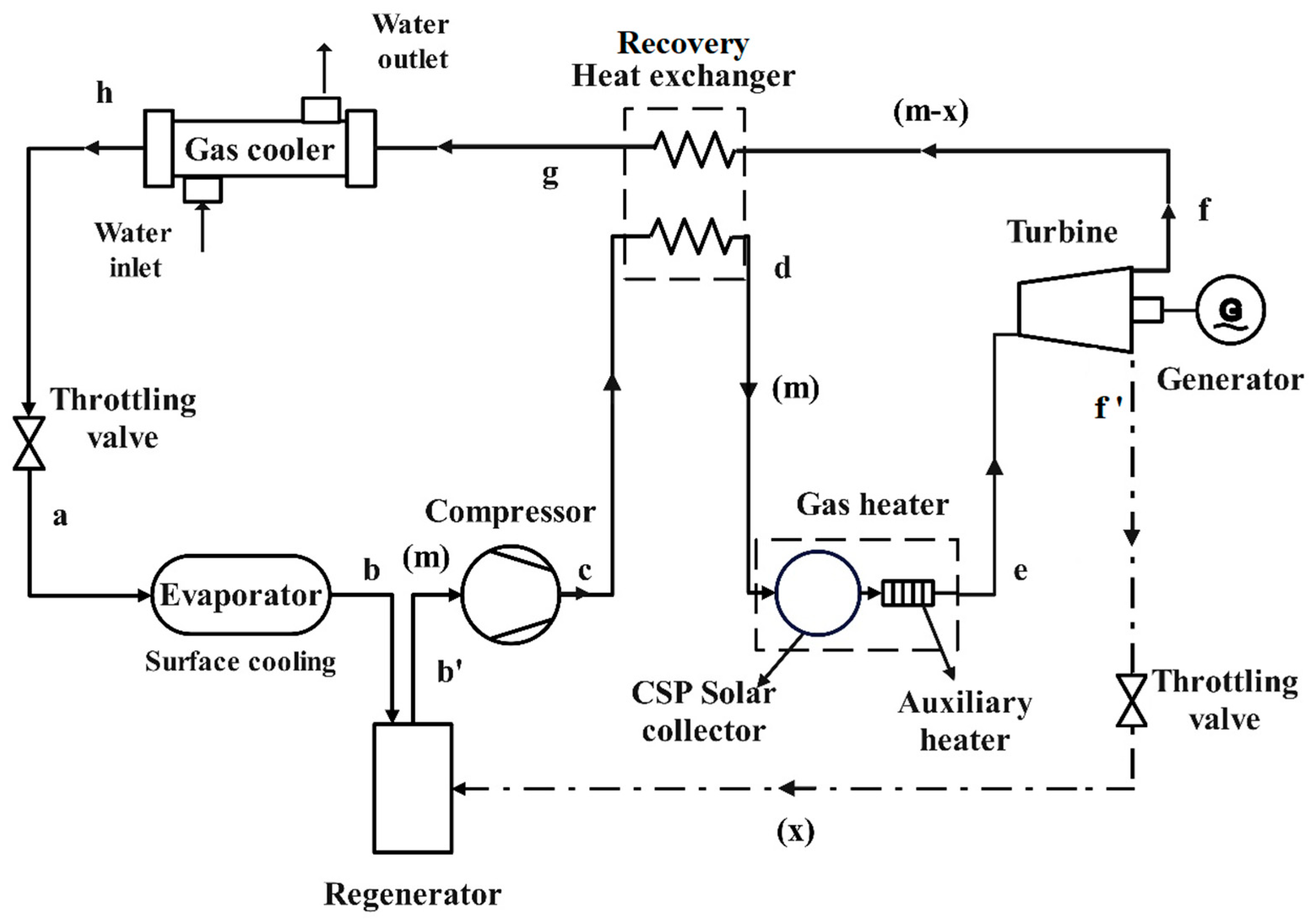
2. Methodology

The proposed CCHP with a regenerator involves combined heating, cooling, and power production using CO₂ as the working fluid. As shown in Figure 1, high pressure sCO₂ from the compressor discharge is preheated in the heat exchanger before entering the gas heater. The gas heater consists of a concentrating solar-thermal power (CSP) and AH as a heat source. The AH is complimentary and only functions when required. Solar energy is the prime source of energy, but the electric heater provide additional support to the system during fluctuations in solar energy.

At state point e, the sCO₂ attains the maximum system temperature and enters the turbine. The high pressure, high temperature sCO₂ produces power in the turbine. Fraction of mass ($x$) is withdrawn from the turbine exit and fed to the regenerator while the remaining mass ($\dot{m}-x$) enters the gas cooler after passing through the heat exchanger. The heat output from the gas cooler is used for heating. Gas cooler exit is defined by state point h and, from there, the sCO₂ undergoes an isenthalpic expansion through the throttling valve. As the working fluid enters the evaporator at state point a, it will be saturated liquid. The fluid absorbs heat from the cooling space as it exits the evaporator at state point b. The bleed mass ($x$) from the turbine mixes with the remaining mass in both the regenerator and the exit as total mass ($\dot{m}$). At the compressor suction (state point b’), the fluid will be completely vapor. The proposed CCHP system is also represented on a T-s diagram, as shown in Figure 2.

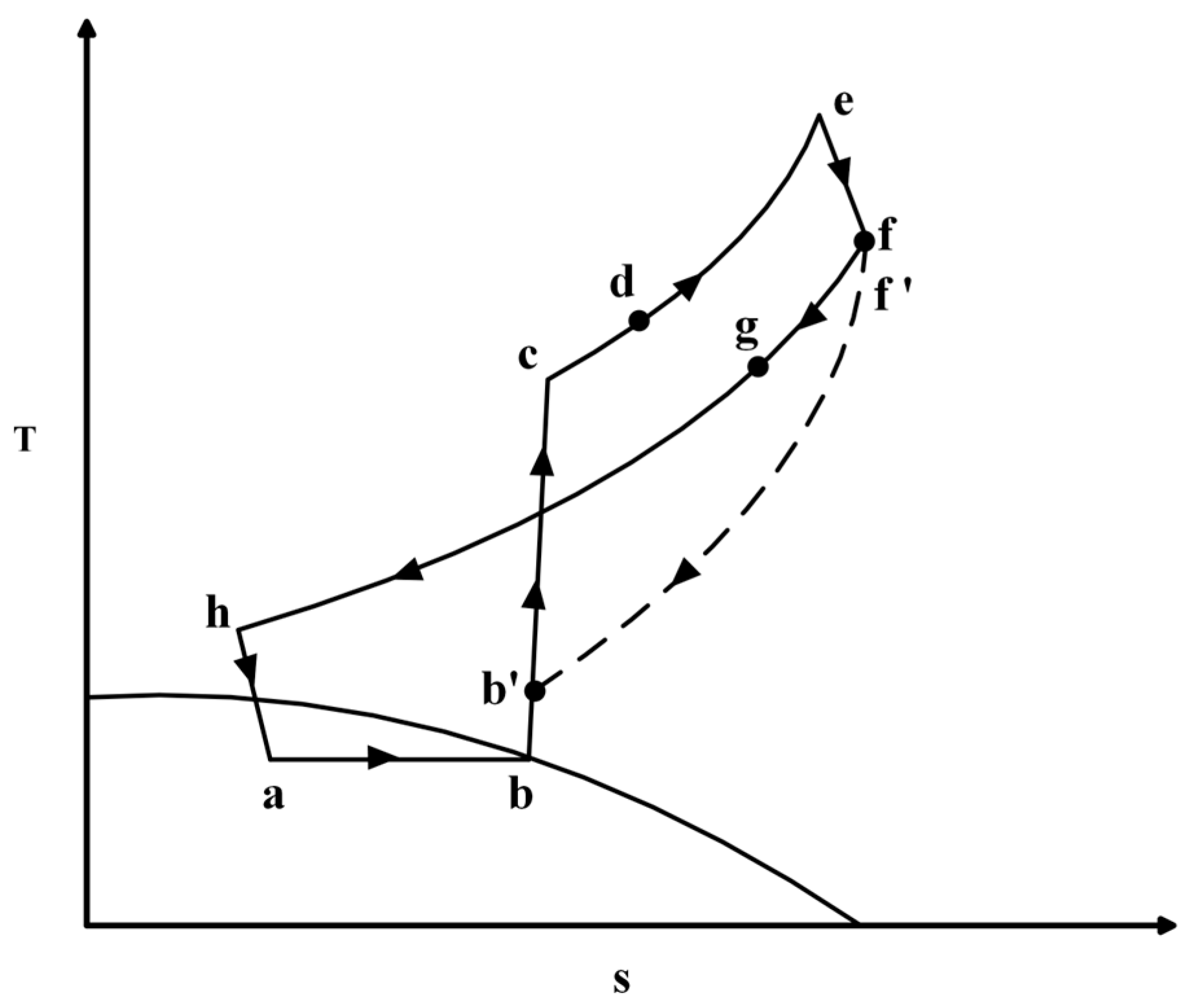
2.1. Thermodynamic Analysis

The following assumptions have been made to simplify the thermodynamic model of the proposed CCHP system with regeneration:

• Pressure drops in the connecting tubes, the gas cooler, and the evaporator are neglected.
• No heat losses to the environment from the system, except for the gas cooler.
• Across the components, the change in potential and kinetic energy are negligible.
• The expansion valve or throttle valves have isenthalpic flow.
• Total mass flow rate within the system is assumed to be 1 kg/s [27].
• Recovery heat exchanger has a known effectiveness.
• Isentropic efficiency of the turbine is fixed.
• At the inlet and exit of the evaporator, the working fluid is in saturated liquid and vapor state, respectively.

Each component in the CCHP system is analyzed using conservation of mass and energy equations. All the assumed default values and range of operating conditions considered for the system simulation are given in

Table 1. Parameters considered for system simulation.

Parameters	Fixed Values/Ranges
Isentropic efficiency of the turbine	0.85
Inlet temperature of turbine	450 °C
Turbine exit pressure (Pmed)	75 bar
Suction pressure of compressor (Plow)	40 bar at 5.3 °C
Compressor discharge pressure (Phigh)	250 bar/170–250 bar
Evaporator temperature	5.3 °C
Gas cooler exit temperature	34 °C/34–42 °C
Effectiveness of recovery heat exchanger	0.9
Bleed mass (x)	0.2 kg/s/0.2–0.5 kg/s

[27].

2.1.1. Turbine

The power output from the turbine is obtained by solving Equations (1)–(6).

$$s_e=f(P_c,T_e)$$

(1)

$$h_e=f(P_c,T_e)$$

(2)

$$s_{f,isen}=s_e$$

(3)

$$h_{f,isen}=f(s_{f,isen},P_f)$$

(4)

The actual enthalpy at the turbine exit is derived from the isentropic efficiency as:

$${\eta }_{turb}=\frac{h_e-h_f}{h_e-h_{f,isen}}$$

(5)

Then, the turbine power output can be derived as:

$$W_{turb}=\dot{m}(h_e-h_f)$$

(6)

Additionally,

$$T_f=f(P_f,h_f)$$

(7)

$$s_f=f(P_f,h_f)$$

(8)

2.1.2. Regenerator

$\left(x\right)$ amount of working fluid is extracted from the exit of the turbine and fed to the regenerator. As a result, the mass flow rate at the inlet of the gas cooler will be $(\dot{m}-x)$. The associated state point properties can be obtained from Equations (9)–(14).

$$h_{f^{\prime }}=f(P_f,T_f)$$

(9)

$$s_{f^{\prime }}=f(P_f,h_{f^{\prime }})$$

(10)

For the regenerator, from the energy balance equation

$$(\dot{m}-x)h_b+x{h}_{f^{\prime }}=\dot{m}\left(h_{b^{\prime }}\right)$$

(11)

$$h_b=f(P_b,x=1)$$

(12)

$$s_b=f(P_b,x=1)$$

(13)

$$s_{b^{\prime }}=f(P_b,h_{b^{\prime }})$$

(14)

2.1.3. Compressor

The empirical correlation developed by Robinson and Groll [36] is used to calculate the isentropic efficiency of the compressor, as shown in Equation (15).

$${\eta }_{comp}=0.815+0.022\left(\frac{P_c}{P_b}\right)-0.0041{\left(\frac{P_c}{P_b}\right)}^2+0.0001{\left(\frac{P_c}{P_b}\right)}^3$$

(15)

At the compressor discharge side,

$$h_{c,isen}=f(P_c,s_{b^{\prime }})$$

(16)

By using Equations (15) and (16), the actual enthalpy at the compressor exit can be obtained:

$${\eta }_{comp}=\frac{h_{c,isen}-h_{b^{\prime }}}{h_c-h_{b^{\prime }}}$$

(17)

Also,

$$T_c=f(P_c,h_c)$$

(18)

$$s_c=f(P_c,h_c)$$

(19)

Then, the compressor work can be expressed as:

$$W_{comp}=\dot{m}(h_c-h_{b^{\prime }})$$

(20)

By using Equations (6) and (20), the total net work of the system can be calculated as:

$$W_{net}=(W_{turb}-W_{comp})$$

(21)

2.1.4. Expansion Valve

Properties at gas cooler exit can be obtained from:

$$h_h=f(P_f,T_h)$$

(22)

$$s_h=f(P_f,T_h)$$

(23)

Assuming isenthalpic throttling,

$$h_a=h_h$$

(24)

Also,

$$s_a=f(P_b,h_a)$$

(25)

2.1.5. Evaporator

The evaporator capacity can be calculated by using Equation (26).

$$Q_{eva}=(\dot{m}-x)(h_b-h_a)$$

(26)

2.1.6. Recovery Heat Exchanger

Assuming counter flow and applying energy balance equation, the heat transfer rate between the compressor discharge fluid and turbine exhaust fluid can be quantified as shown in Equation (27).

$$\left(\dot{m}-x\right)\left(h_f-h_g\right)=\dot{m}\left(h_d-h_c\right)$$

(27)

Additionally,

$$Q_{Hex}=\mathsf{\epsilon } C_{min}(T_f-T_c)$$

(28)

Now, the properties of fluid entering the solar heater and gas cooler is estimated by using Equations (29)–(32).

$$h_g=f(P_f,T_g)$$

(29)

$$s_g=f(P_f,h_g)$$

(30)

$$h_d=f(P_c,T_d)$$

(31)

$$s_g=f(P_c,h_d)$$

(32)

2.1.7. Solar Assisted Heater

The effect of AH is not considered in the present thermodynamic procedure since the primary focus is on the solar assisted heater. Further, when fully functioning, the solar heater alone can generate the required temperature difference across the gas heater. So, in the solar assisted heater, the heat transfer rate is given by:

$$Q_{solar}=\dot{m}(h_e-h_d)$$

(33)

2.1.8. Gas Cooler

Similarly, using Equation (34), the heating output to the user in the gas cooler can be calculated as:

$$Q_{gc}=(\dot{m}-x)(h_g-h_h)$$

(34)

Finally, the COP of the CCHP system with regenerator is defined as [27]:

$${COP}_{regen}=\frac{W_{net}+Q_{eva}+Q_{gc}}{Q_{solar}}$$

(35)

2.1.9. CCHP System without Regeneration

For a CCHP system without regeneration, the mass flow rate throughout the loop remains constant and the compressor work is expressed as:

$$W_{comp}=\dot{m}(h_c-h_b)$$

(36)

In addition, heating output becomes,

$$Q_{gc}=\dot{m}(h_g-h_h)$$

(37)

The above equations are solved in MATLAB to determine the system performance, cooling effect, heating output, and net work done. By integrating the REFPROP database with MATLAB, the thermodynamic properties at each state point are calculated. Equation (1) to Equation (34) provide a clear understanding of how to solve a CCHP system thermodynamically. All the processes involved in the system are solved separately so that future studies in this direction can be easily accelerated by modifying the equations depending on the system modifications.

2.2. Exergy Analysis

A systematic component level exergy analysis is carried out for the CCHP system with a regenerator and the conventional CCHP system without a regenerator in order to identify the contribution of each component to the total irreversibility of the system, especially the regenerator. For one lower and one higher gas cooler exit temperatures (34 °C and 40 °C, respectively), the system is simulated for various gas cooler exit pressures. Since the proposed CCHP system is suitable for cooling applications, the cooling room temperature ($T_w$) for the evaporator is assumed to be 20 °C, while the reference temperature ($T_0$) is 35 °C. This reference temperature is the ambient temperature; since the proposed system is simulated for higher ambient conditions, it is considered as 35 °C.

2.2.1. Exergy Analysis of the CCHP System with Regenerator

Exergy destruction rate in the compressor is expressed as:

$$I_{comp}=\dot{m}{T}_0(s_c-s_{b^{\prime }})$$

(38)

Exergy destruction rate in the turbine is derived as:

$$I_{turb}=\dot{m}{T}_0(s_f-s_e)$$

(39)

In the gas cooler, the irreversibility is expressed as:

$$I_{gc}=(\dot{m}{-x)T}_0[\left(\frac{h_g-h_h}{T_0}\right)-\left(s_g-s_h\right)]$$

(40)

Irreversibility in the expansion valve is given as:

$$I_{exp}=\left(\dot{m}{-x)T}_0\right(s_a-s_h)$$

(41)

Exergy destruction rate in the regenerator is given by:

$$I_{regen}=\dot{m}\left(h_{b^{\prime }}-T_0{s}_{b^{\prime }}\right)-\left[\right(\dot{m}-x)\left(h_b-T_0{s}_b\right)+x\left(h_{f^{\prime }}-T_0{s}_{f^{\prime }}\right)]$$

(42)

In the solar heater, the irreversibility is expressed as:

$$I_{solar}={\dot{m}T}_0(\left(\frac{h_e-h_d}{T_e}\right)-\left(s_e-s_d\right))$$

(43)

In evaporator, the irreversibility is defined as:

$$I_{eva}=(\dot{m}{-x)T}_0[\left(s_b-s_a\right)-\left(\frac{h_b-h_a}{T_w}\right)]$$

(44)

Exergy destruction rate in the recovery heat exchanger is given by:

$$I_{RHex}=\left(\dot{m}-x\right)\left[\left(h_f-h_g\right)-T_0\left(s_{\mathrm{f}}-s_{\mathrm{g}}\right)\right]+\dot{m}\left[\left(h_c-h_d\right)-T_0\left(s_{\mathrm{c}}-s_{\mathrm{d}}\right)\right]$$

(45)

Equation (39) gives the total exergy destruction rate of the CCHP system with regeneration.

$$I_{total}=I_{comp}+I_{turb}+I_{gc}+I_{exp}+I_{regen}+I_{solar}+I_{eva}+I_{RHex}$$

(46)

2.2.2. Exergy Analysis of Conventional CCHP System without Regeneration

In compressor, the irreversibility is expressed as:

$$I_{comp}^c=\dot{m}{T}_0(s_{\mathrm{c}}-s_{\mathrm{b}})$$

(47)

And the total irreversibility of the system is expressed as:

$$I_{total}^c=I_{comp}+I_{turb}+I_{gc}+I_{exp}+I_{solar}+I_{eva}+I_{RHex}$$

(48)

3. Results and Discussion

The behavior of the CCHP systems with and without regeneration were investigated thermodynamically for various operating conditions; the relative performance variables are discussed below. Additionally, the performance deficiencies of individual system components are identified and quantified with a systematic exergy analysis. Finally, the proposed CCHP system is compared with a conventional CCHP system working under the same operating conditions.

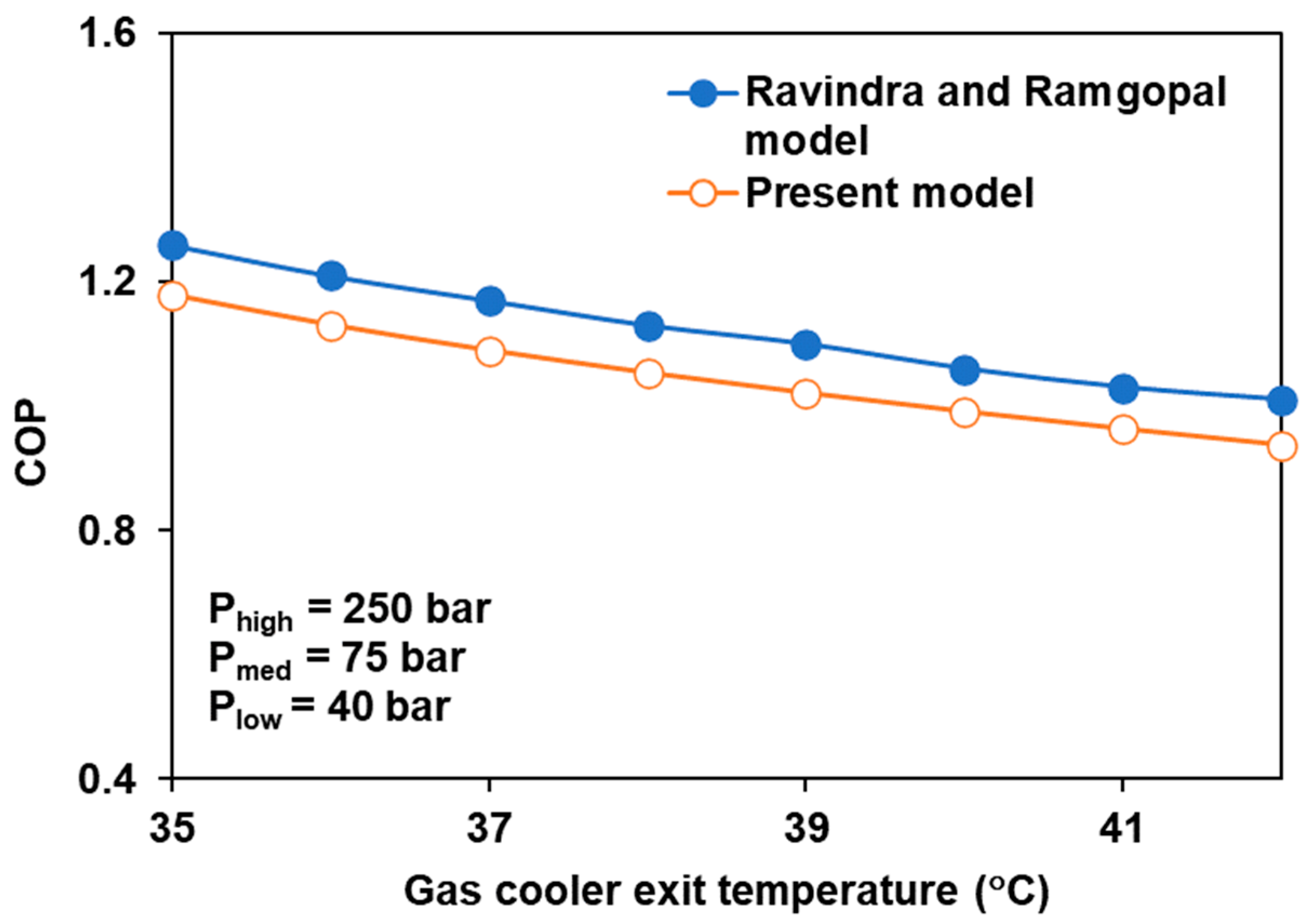
3.1. Validation of the Thermodynamic Model

Ravindra and Ramgopal [27] reported a similar thermodynamic study without regeneration and it is used to validate the thermodynamic simulation procedure adopted for the present study. The corresponding COP value thus obtained are shown in Figure 3. The predicted values of the present thermodynamic model are in good agreement with the results of Ravindra and Ramgopal [27]. At any given gas cooler exit temperature, the present model predicted the COP values with 94% accuracy.

The adopted thermodynamic model [27] is then modified with a regenerator. For both the cases (without and with regeneration), the results obtained are discussed in following sections.

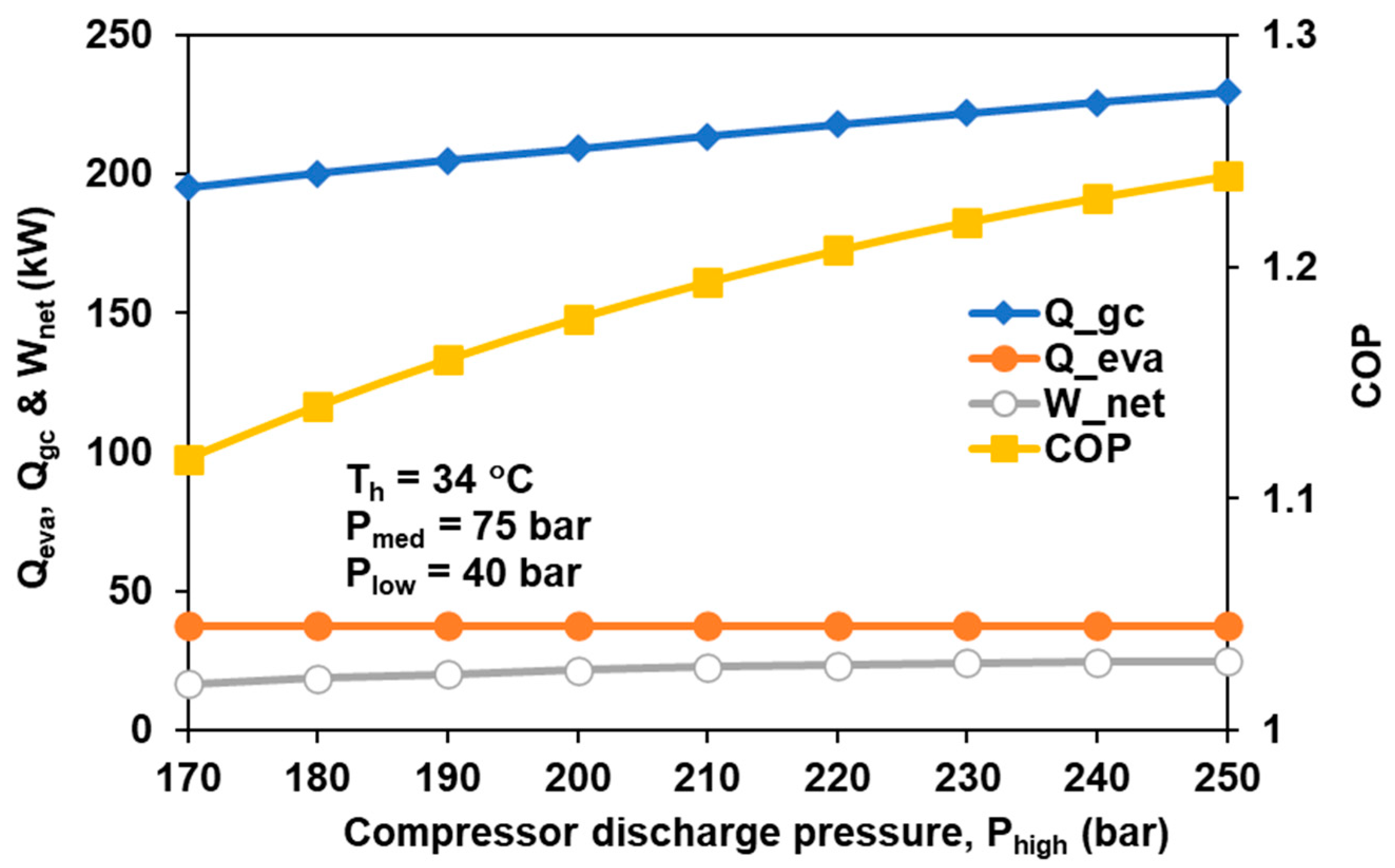
3.2. Conventional CCHP System Simulation for Various System Maximum Pressure

As the system maximum pressure (P_high) is increased, the COP also increases, as shown in Figure 4. However, the cooling effect remains unchanged and, thus, it is independent of P_high. With an increase in P_high, the pressure ratio across the compressor also increases, which directly increases the compressor work rate. It will also increase the enthalpy difference across the solar collector and, thus, the solar heat input also increases. Simultaneously, the turbine power output increases and the net work of the system collectively increases with the increase in P_high. Further, the heat transfer between the turbine exit fluid and the compressor discharge fluid is decreased in the recovery heat exchanger, which, in turn, increases the heating output. The combined effect of these processes directly compliments the system COP.

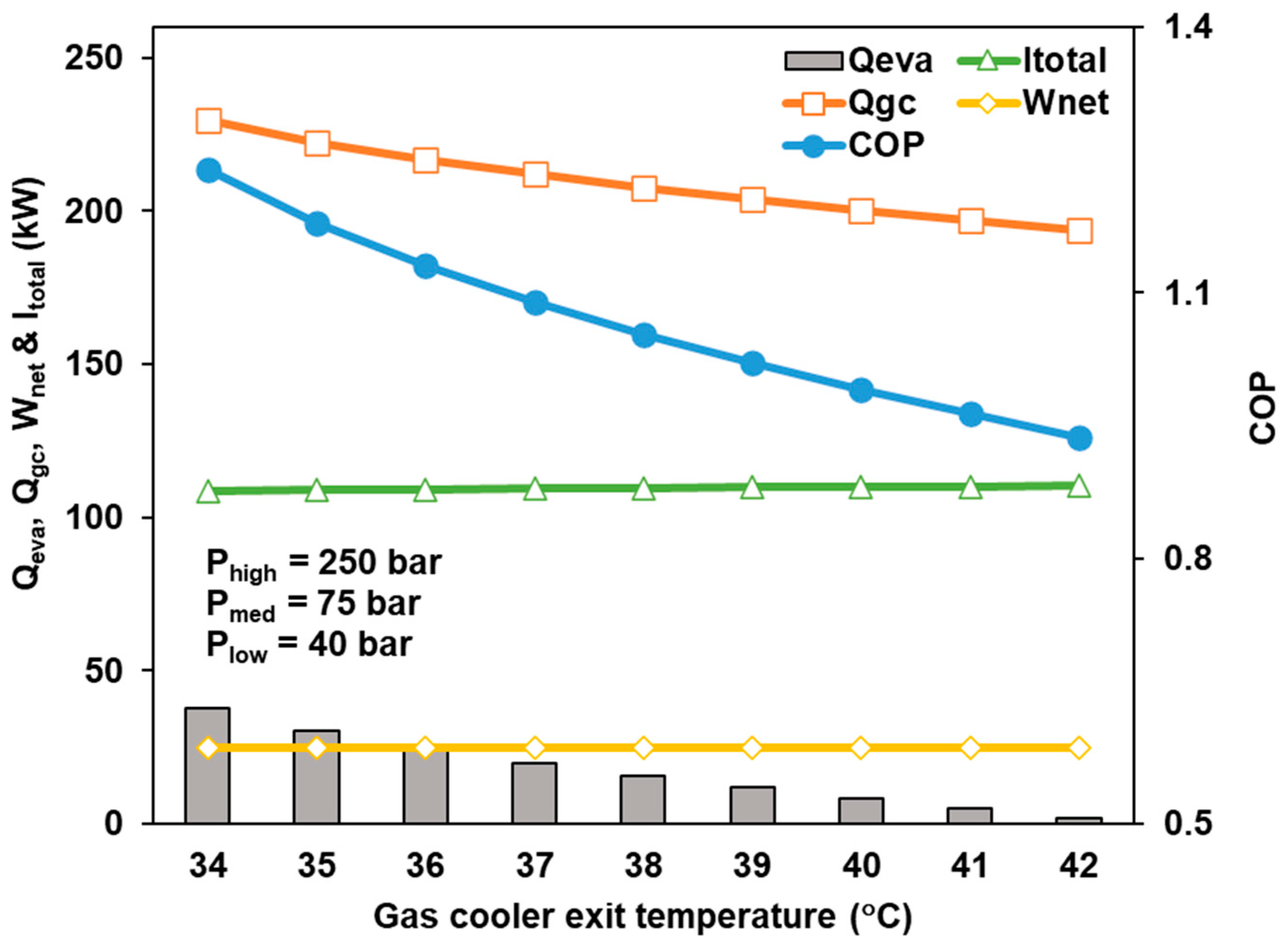
3.3. Effect of Gas Cooler Exit Temperature on Conventional CCHP System Performance

For a system maximum pressure of 250 bar, the system is simulated at different gas cooler outlet temperatures in order to obtain the various system performance parameters, as shown in Figure 5. It also depicts the effect of gas cooler exit temperature on total system irreversibility. As the gas cooler exit temperature increases, the vapor fraction of CO₂ leaving the expansion valve also increases, and thus the cooling effect reduces drastically as more vapor CO₂ enters the evaporator inlet. Across the gas cooler, the enthalpy difference reduces, and hence the heating output reduces with an increase in the gas cooler exit temperature. The turbine work and compressor work remain unaffected, as is reflected in the net work performed, shown in Figure 5. It is also evident that the overall system irreversibility increases with an increase in gas cooler exit temperature. Though the increase is marginal, careful attention is required to select the operating conditions of the system in order to reduce the overall energy destruction rate of the system.

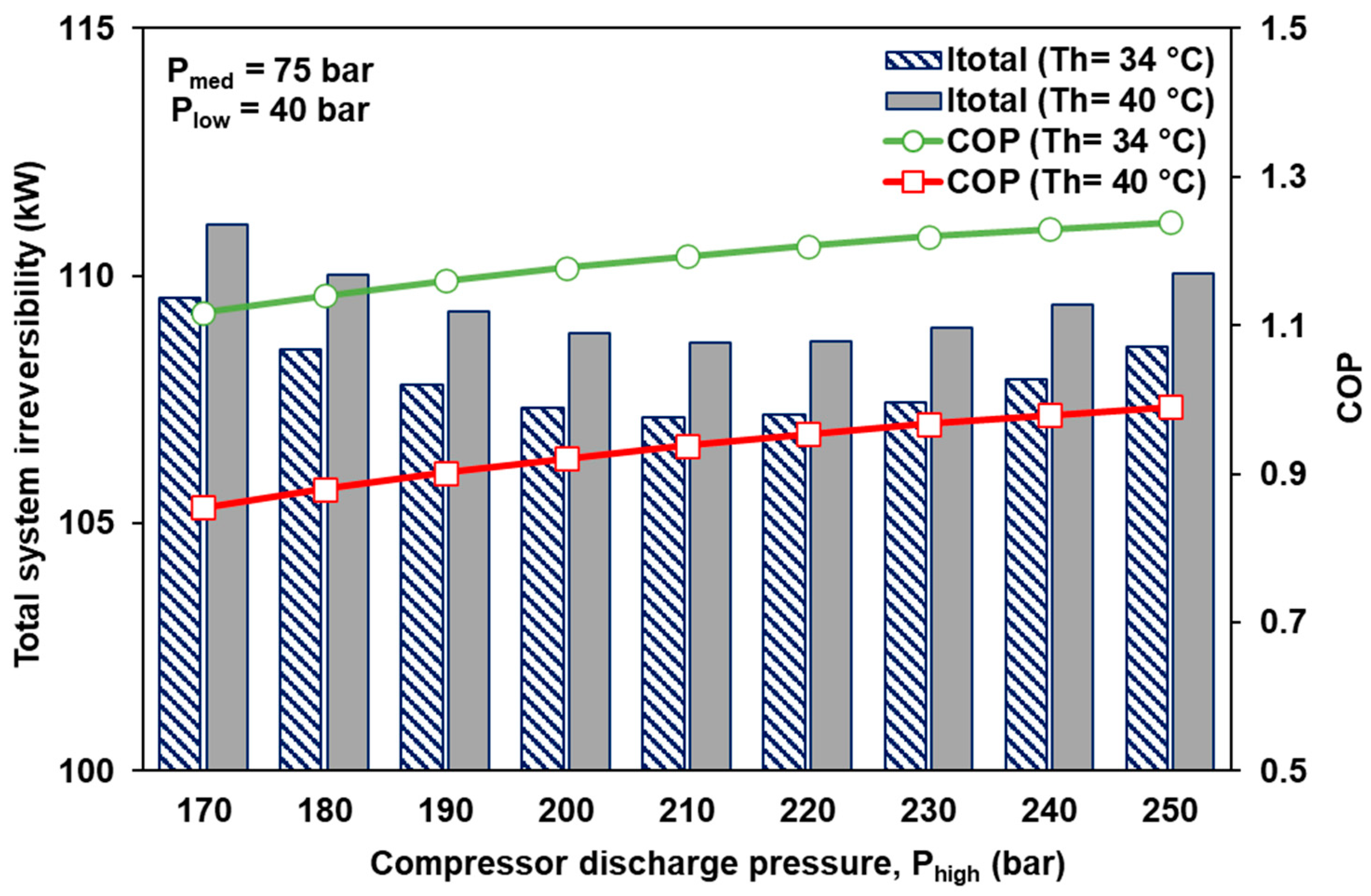
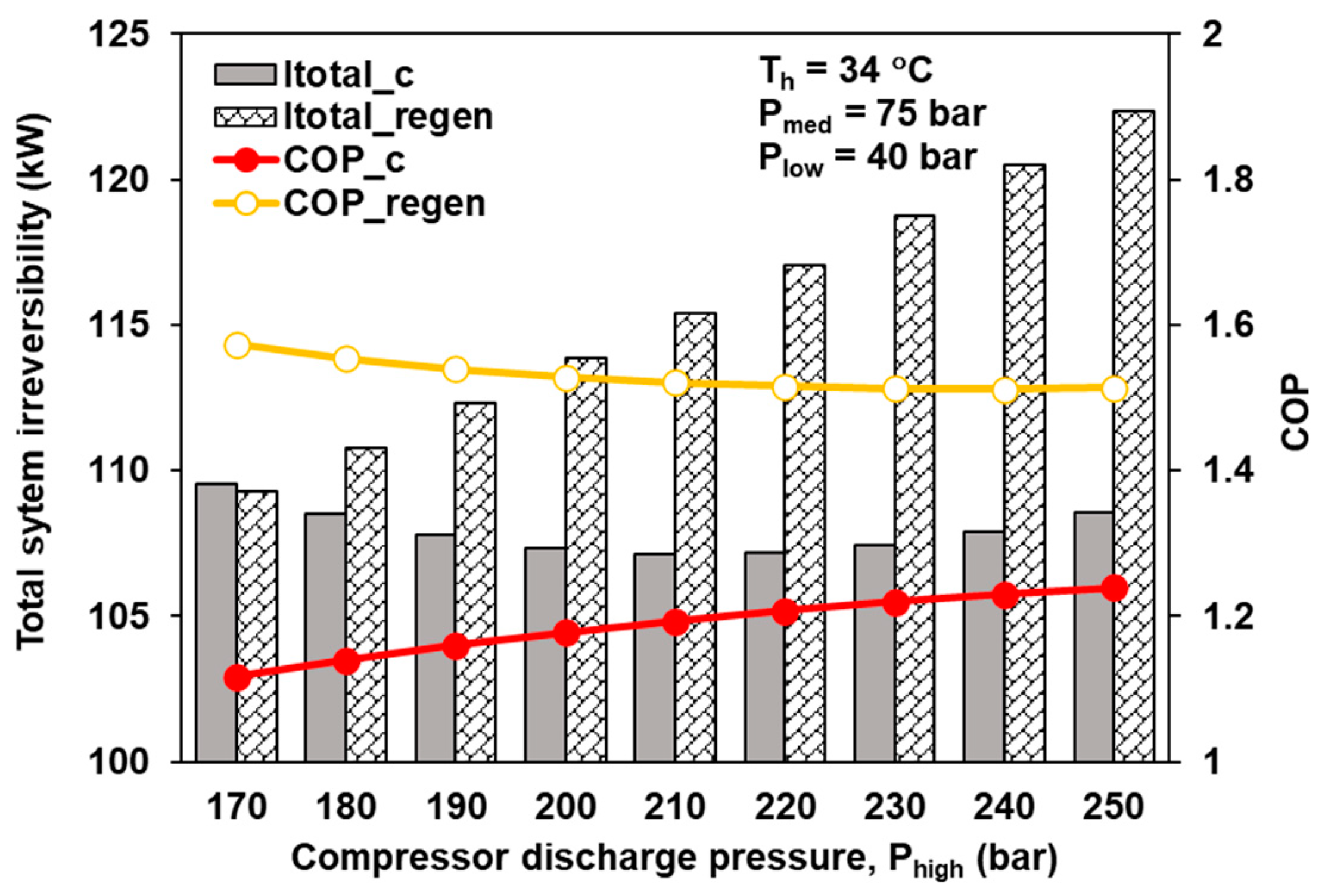
3.4. Effect of System Maximum Pressure on Total System Irreversibility

In order to understand the total exergy destruction rate of the conventional CCHP system without a regenerator, gas cooler exit temperature is fixed at two values (34 °C and 40 °C) and the system maximum pressure is varied from 170 bar to 250 bar. The obtained results are presented in Figure 6. The operating values are selected carefully in order to study the system performance at higher ambient conditions. It is found that at higher system maximum pressure, the system COP reduced by 20% when the gas cooler exit temperature is increased to 40 °C from 34 °C, while the reduction in COP is 23% towards lower system maximum pressure. However, the maximum deviation in total system irreversibility is only 1.87%. This is because more vapor accumulates at the evaporator inlet as the gas cooler exit temperature increases, which reduces the cooling effect. In addition, the compressor needs to perform more work to compress this additional vapor. The combined effect of these two phenomena results in a drastic reduction in COP, while the exergy destruction in the compressor and evaporator has no significant effect on the total irreversibility of the system.

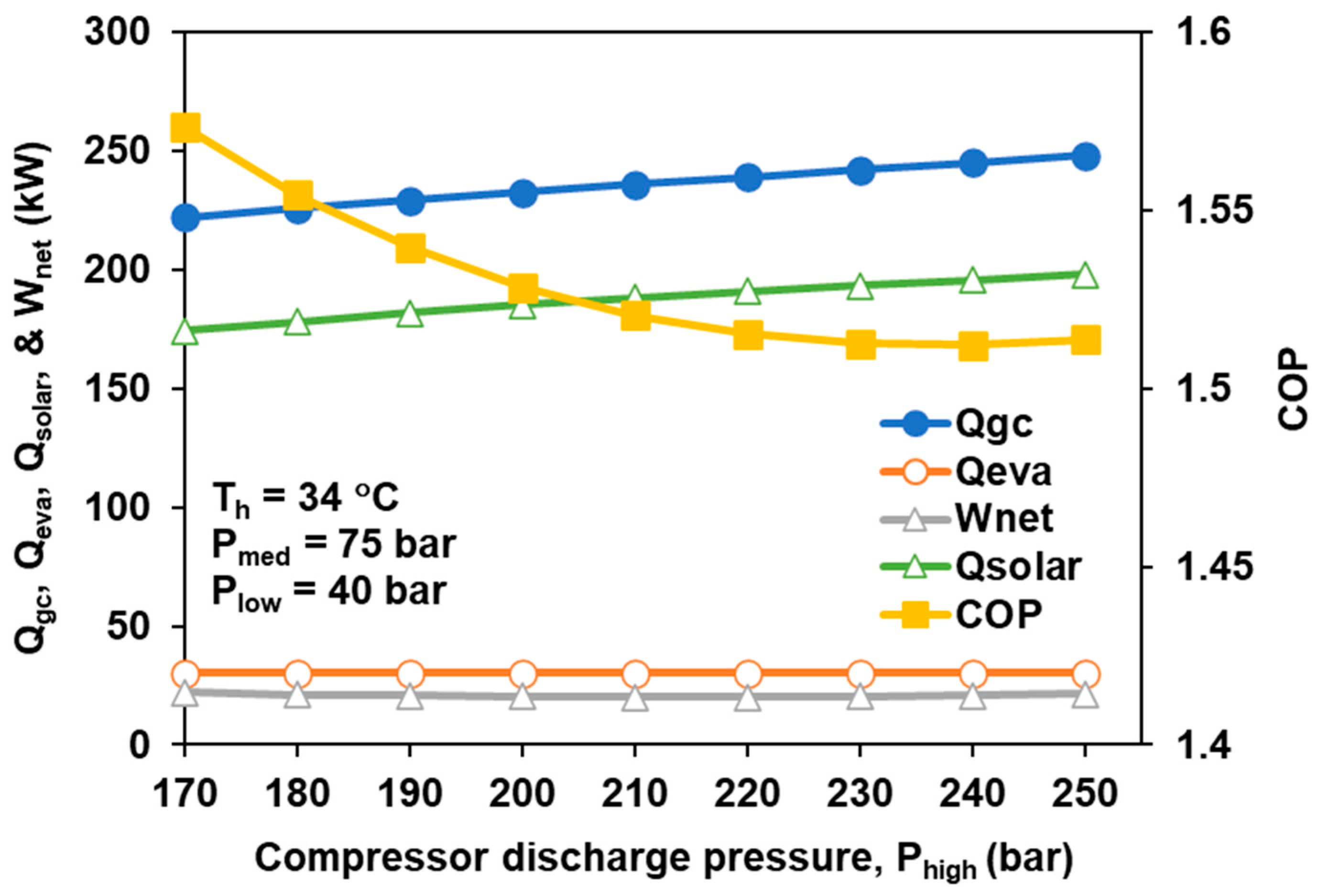
3.5. Effect of System Maximum Pressure on CCHP System Perfromance with Regeneration

We noted that when the system is operated at higher maximum system pressure, the COP is reduced by 3%, as shown in Figure 7. We observed that the refrigerating effect is unaffected by the variation in system maximum pressure. Further, the CO₂ entering the compressor is more superheated and this will cause the compressor to do additional work. Across the solar heater, the difference in enthalpy is high, which is reflected in the solar heat input to the system. Even though the heating output is favorable, the combined effect of the factors discussed above results in lower COP value. However, with regeneration added to the system, the overall COP of the system is improved when compared to the CCHP system without a regenerator.

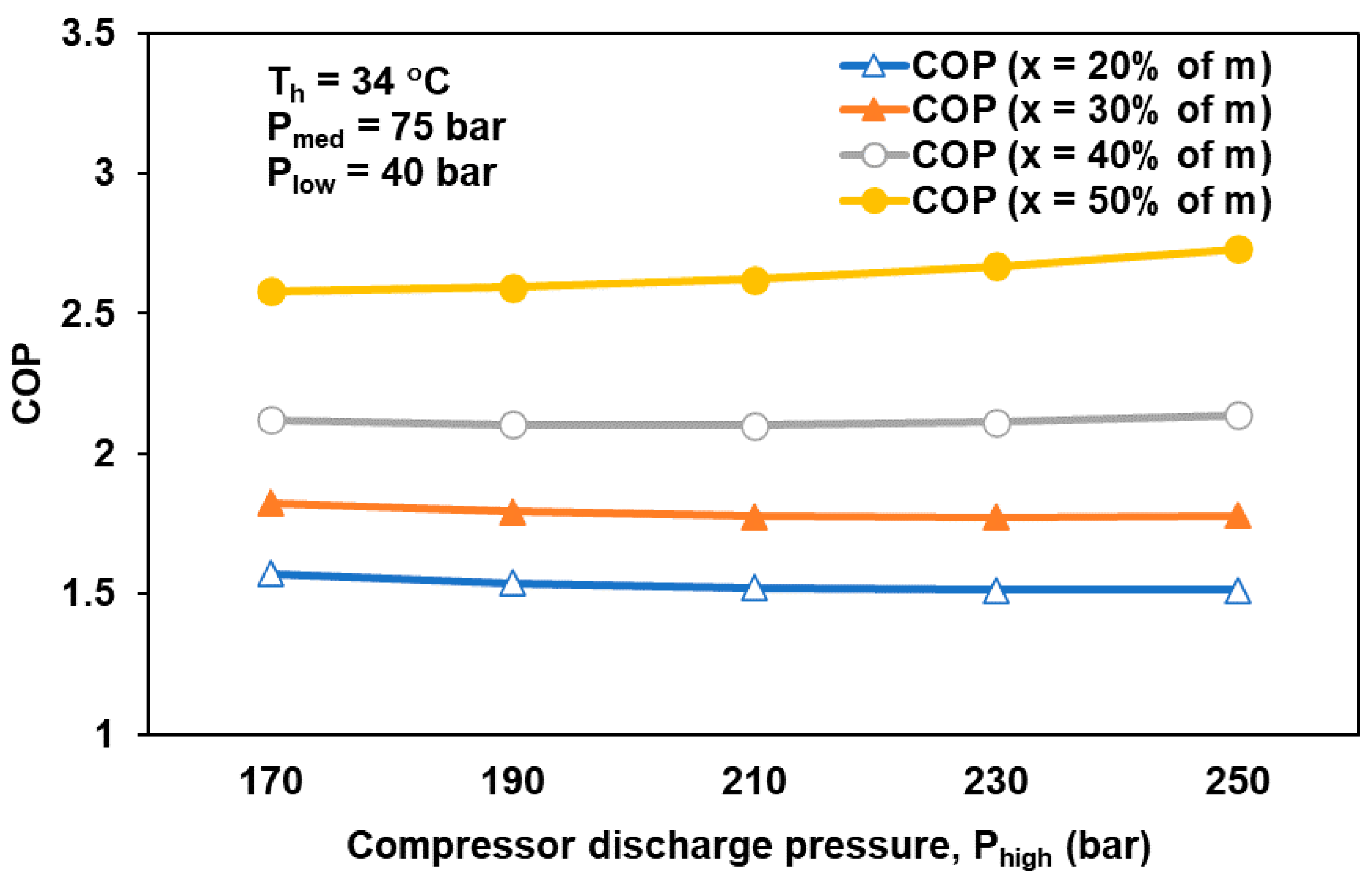
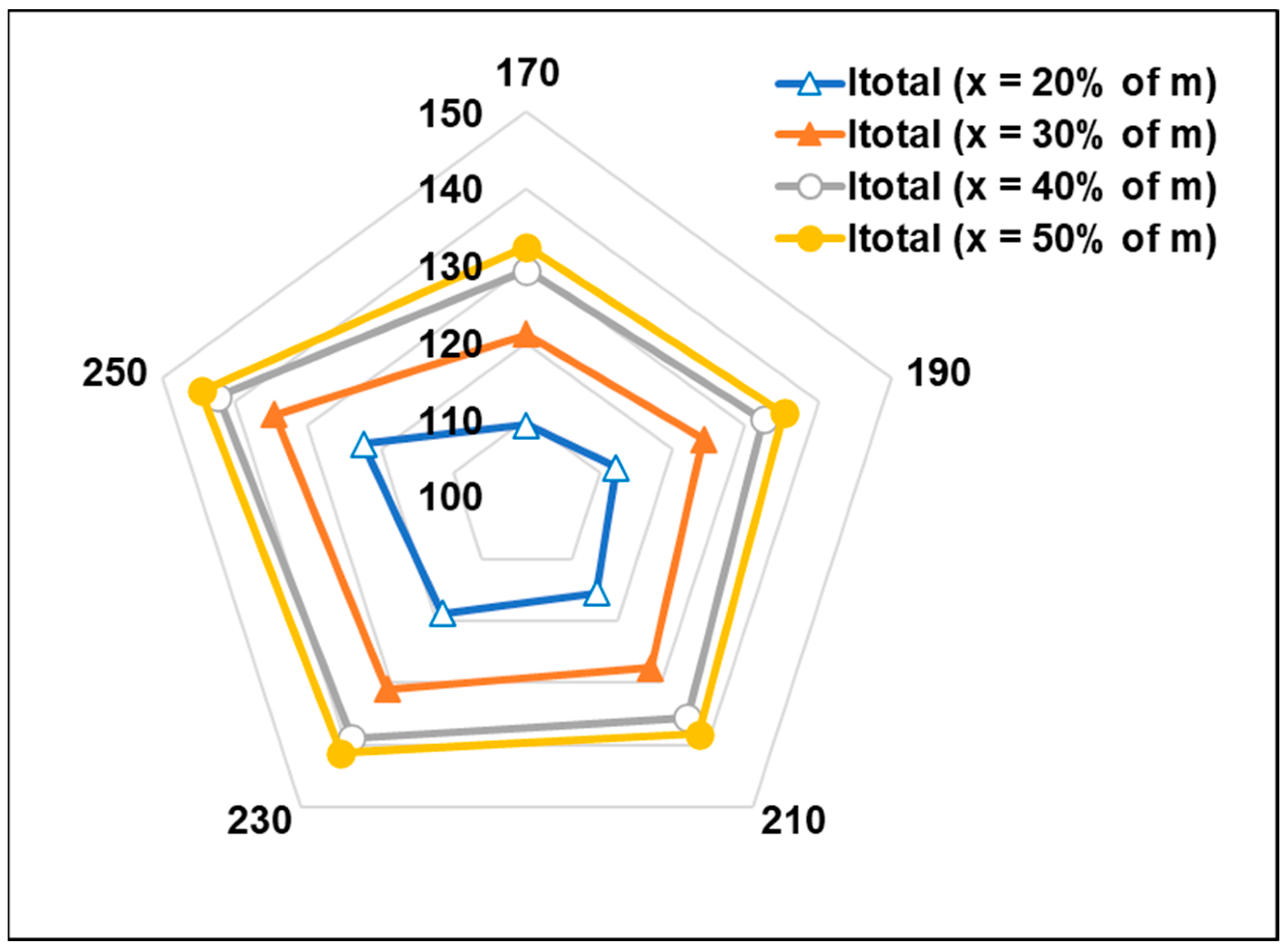
3.6. Effect of Bleed Mass on System Performance and Total Irreversibility

The system performance is simulated for bleed mass from 0.2 kg/s to 0.5 kg/s; the results are presented in Figure 8. With an increase in bleed mass, the system COP also increases, and marked the highest value of 2.7 at 250 bar of system maximum pressure. Considering the energy analysis alone, the bleed mass cannot be fixed for a particular operating condition. The COP of the system may increase theoretically, however its effect on the total system irreversibility must be analyzed before fixing a bleed mass when it comes to practical applications.

In Figure 9, the system maximum pressure is plotted on a pentagonal radar graph, with each vertices representing respective pressure values in bar. The vertical axis represents the total irreversibility in kW. Operating at 170 bar, when the bleed mass increases from 0.2 kg/s to 0.5 kg/s, the total system irreversibility is increased by almost 21%; at 250 bar, it is 18%.

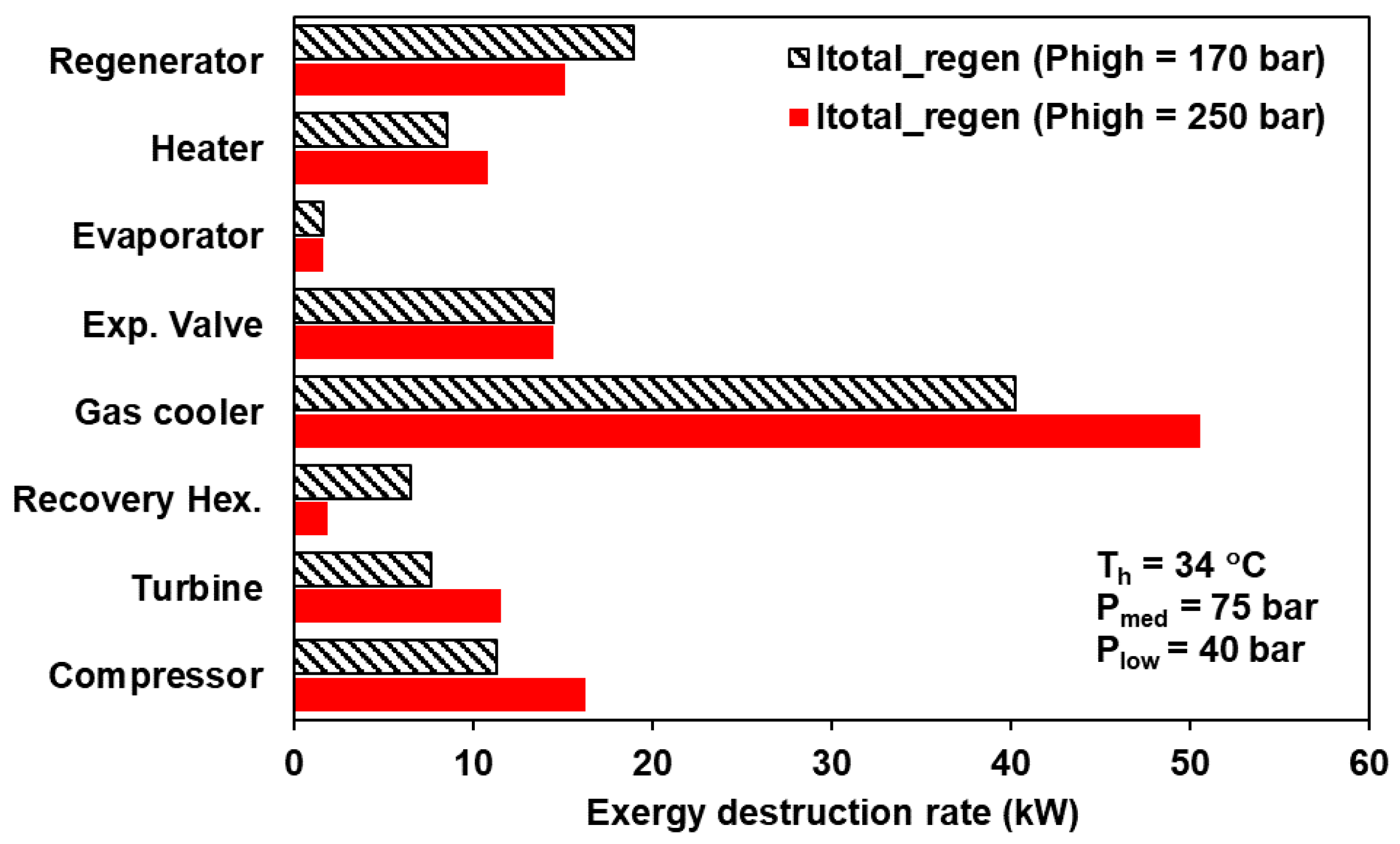
3.7. Component Level Exergy Destruction Rates

Studying the irreversibility of individual components in any system gives an insight into the contribution of each component to overall system irreversibility. This will help in identifying the potential components that have to be modified or replaced in order to improve the system performance. Figure 10 represents the component level irreversibility of the system operating at a gas cooler exit temperature of 34 °C and two system maximum pressures (170 bar and 250 bar, respectively). Working at high pressure yields higher system irreversibility; however, by adding a regenerator, the heat transfer between the working fluid across the recovery heat exchanger is enhanced and its exergy destruction rate drops by 71%. The percentage wise contribution of individual components to total system irreversibility is depicted in Figure S1. The gas cooler contributes most to the total system irreversibility, followed by the regenerator and the expansion valve. However, adding a regenerator improves the overall COP of the system. Further, the exergy destruction rate of the regenerator falls by 20% when operating at a higher system maximum pressure. Before implementing the proposed system for any practical application, suitable system modifications have to be adopted in order to reduce the overall irreversibility of the system. One potential modification is the replacement of the expansion valve by an ejector. This could reduce the exergy destruction rate of expansion process by almost 50%, as reported by Ahammed et. al. [37].

3.8. Comparison of Proposed System with Conventional CCHP System

To justify the addition of a regenerator in a CCHP system, a comparative study has been carried out with a conventional system. The results are presented in Figure 11. At any given system maximum pressure, the CCHP system with a regenerator outperforms the conventional system in terms of COP. At lower system maximum pressures, the improvement in COP is 29%, while at higher system maximum pressures it is 18%. However, the total irreversibility of the system exhibits a different trend. With a regenerator, and operating at a 170 bar system maximum pressure, the total irreversibility is reduced by 0.6%; for any other system maximum pressure, the irreversibility of the CCHP system with a regenerator increases by maximum of 10%.

4. Conclusions

The current study employed thermodynamic and exergy analysis on a CCHP system with and without a regenerator in order to investigate the system performance, cooling effect, heating output, and component level exergy destruction rate. By adding a regenerator, the COP of the CCHP system is improved by almost 37%, with 0.3 kg/s of bleed mass and with the gas cooler operating between 35 °C and 42 °C. For a conventional system without a regenerator, operating at higher system maximum pressure provides a constant cooling effect and higher heating output with a lower power consumption. On the other hand, with a regenerator, the system must operate at a lower compressor discharge pressure in order to deliver maximum performance with lesser irreversibility. The cooling effect of the CCHP system with a regenerator is very sensitive to gas cooler exit temperature and, when increased from 34 °C to 40 °C with a 0.2 kg/s bleed mass, the cooling effect drops by almost 78%. The conclusions from the present work are as follows:

• The total irreversibility of the CCHP system with a regenerator is lower towards lower gas cooler exit temperature.
• The gas cooler contributes 37% to overall system irreversibility, followed by the regenerator (about 17%).
• The bleed mass should be kept as low as possible, thereby directly complimenting the total irreversibility of the system.
• With an increase in bleed mass (maximum 0.5 kg/s), the overall COP of the system marks the highest value (about 2.73 at 250 bar system maximum pressure and 34 °C gas cooler exit temperature).
• Thus, there should be a tradeoff between the system COP and total irreversibility in order to fix the bleed mass.
• For any given application, a CCHP system with and without a regenerator is advised to operate at a lower gas cooler exit temperature in order to produce the maximum refrigerating effect and heating output with marginal system net work.
• However, the suitable operating range of the CCHP system with a regenerator is not limited to lower gas cooler exit temperatures and compressor discharge pressures. The system can even work at a higher operating condition by compromising the COP.

The future perspective of this study is not limited to an experimental validation, but also to carefully modify/replace the existing system components in order to improve the overall performance of the system with minimum system irreversibility. It is suggested to replace the expansion valve with an ejector. This may reduce the compression ratio, reduce the compressor work, and improve the refrigerating effect.