Analysis of Vertical Temperature Gradients and Their Effects on Hybrid Girder Cable-Stayed Bridges

Abstract

The real temperature distribution within 24 h of the main beam in a single-tower hybrid beam cable-stayed bridge is analysed according to its actual section and material parameters, as well as other factors of local atmospheric temperature, geographical environment, and solar intensity. The results show that the internal temperature distribution in the steel–concrete composite beam is uneven, and the temperature of the steel is higher than that at the surface of the concrete slab. Then, a finite element model of the whole bridge is established using the thermal–mechanical sequential coupling function in ABAQUS to acquire the structural response under the action of a 24-h temperature field. The results show that the vertical temperature gradients have a great influence on the longitudinal stress in the lower flange of the steel I-beam, with a maximum compressive stress of 11.9 MPa in the daytime and a maximum tensile stress of 13.36 MPa at midnight. The temperature rise leads to a downward deflection of the main span, and the maximum deflection occurs at the 1/4 main span. There was an obvious temperature gradient in the concrete slab, with a difference between the maximum and minimum value of 14 °C. Similarly, the longitudinal compressive stress of the concrete slab increases with increasing temperature in the daytime, but the peak time is obviously inconsistent with that of the steel beam.

1. Introduction

Steel–concrete composite beams [1,2,3] (SCCBs) have been extensively used in bridges recently, especially in medium- and long-span cable-stayed bridges, due to the combined advantages of steel and concrete. The concrete is mainly compressed, and the steel beam is tensioned, giving full play to the material characteristics with high bearing capacity. The flange plate of a composite beam is usually wide. Single-tower double-span cable-stayed bridges generally adopt an asymmetric span layout, with the main beam adopting the hybrid composite beam. In other words, the main span is composed of a lightweight SCCB, while the side span is composed of a concrete main beam to balance the cable force on both sides of the tower.

Bridges are easily affected by changes in environmental and climate temperature conditions, such as solar radiation [3,4,5,6,7,8,9]. However, the thermal conductivities of steel and concrete are very different. Steel has good thermal conductivity and fast heat transfer [10,11,12], which is approximately 50 times higher than that of concrete. As a consequence, when the air temperature changes suddenly, the temperature change rate of steel is much higher than concrete, thus causing a large temperature difference between the steel girder and concrete slab.

Many previous studies have investigated the temperature discrepancy between steel and concrete in SCCB bridges. Zuk et al. [13] measured the temperature of a simply supported SCCB bridge and found that the largest temperature difference of 22 °C inside the concrete occurred in summer. In contrast, the vertical temperature difference in the steel girder was small. Su [14], Chen [15], and Wu [16] studied the temperature fields and daily variation curves of various SCCBs. According to their research, there is a large temperature difference near the junction of the concrete slab and steel girder.

Liu et al. [17] considered solar radiation and shadow shielding in an SCCB bridge and obtained the temperature decomposition index of the temperature field. The temperature field was decomposed using the finite element software ABAQUS, and the influence of bridge section parameters and seasons on the above index was studied. Moreover, Zhu et al. [18] proposed two vertical temperature gradient patterns for a steel box concrete-composite girder bridge by applying the three-dimensional occlusion algorithm.

Under solar radiation, due to the poor thermal conductivity of the concrete slab, the temperature is distributed nonlinearly along the vertical direction of the SCCB, which results in a large temperature stress in the concrete slab and steel girder and generates a large shear force at the interface. Many studies have shown that the effect of temperature in some parts of the SCCB even exceeds the dynamic load [19]. In particular, the statically indeterminate structures, such as SCCB cable-stayed bridges, further intensify the secondary internal forces from temperature. In addition, there are obvious vertical temperature gradients between the steel girder and concrete slab due to different thermal conductivities. The temperature differences and transverse temperature gradients at the beam–tower and beam–cable boundaries lead to obvious temperature effects in SCCB or hybrid beam cable-stayed bridge systems.

In terms of a hybrid beam cable-stayed bridge, Ling et al. [20] found that the longitudinal displacement of the side span varied linearly with temperature. Based on the field-measured data, Xu et al. [21] considered the response changes of four temperature loads on a cable-stayed bridge. The midspan deflection reached its maximum value due to the vertical temperature gradient of the main beam. Zhou et al. [22] monitored the temperature of a steel box girder cable-stayed bridge and discussed the effects of seasonal temperature and daily temperature changes on the midspan deflection, horizontal projection length, and other properties.

Su et al. [14] analysed a three-span steel–concrete double-sided composite box girder under the action of sunshine from 6 a.m. to 6 p.m. by using the software ANSYS and the indirect thermal–mechanical coupling method. They found that the peak stress of the concrete lagged behind that of the steel girder, and the tension of the concrete bottom slab inhibited the deformation of the steel–concrete composite beam, which was beneficial to the overall structure. Zhou et al. [23] measured the temperature in a section of an SCCB (box girder) onsite and deduced the temperature difference–shear stress curve. It was found that the material characteristics and temperature gradient mode were important factors affecting the bending deformation of the composite beam. Wang et al. [24] studied the temperature effect on an SCCB cable-stayed bridge and simulated the temperature fields of the main beam, bridge tower, and stay cable. Based on the thermal–mechanical coupling model, they analysed the average temperature, temperature difference, and the temperature distribution law of each component.

H.A. Abdel-Gawwad et al. [25] studied the effects of curing conditions on the physical–mechanical properties and fire resistance of cement mortar (CM) containing active magnesium oxide (MgO). They found that the physical and mechanical properties and the high-temperature resistance of ordinary cementitious composites without MgO curing in tap water (TW) are superior to samples curing using normal carbonation (NC) and accelerated carbonation (AC). MgO adversely affects the performance of TW-cured CM due to the formation of magnesium silicate hydrate with lower binding capacity compared to calcium silicate hydrate. The best curing conditions and MgO types they obtained are AC and MgO 1250, which have the highest engineering and high-temperature resistance.

To the best of the authors’ knowledge, these studies focused on the temperature distribution over time and the effect of temperature gradients on the internal stress and deflection of a hybrid girder cable-stayed bridge. In this paper, the field test and finite element simulation were combined to analyse the temperature gradient of the steel girder and concrete slab of the hybrid girder cable-stayed bridge. The variation rules of stress and deflection of the bridge beam were also compared. It is beneficial to improve the understanding of daily temperature variation on the secondary stress in the structure system of the hybrid girder cable-stayed bridge. This paper analyses the different deflections of the temperature change caused by sunlight on the steel–concrete and concrete deflection of cable-stayed bridges. A large number of field tests and simulative data are provided in this study for the development of the stability of cable-stayed bridges in the future.

2. Temperature Field Theory

2.1. Heat Transfer of Bridges

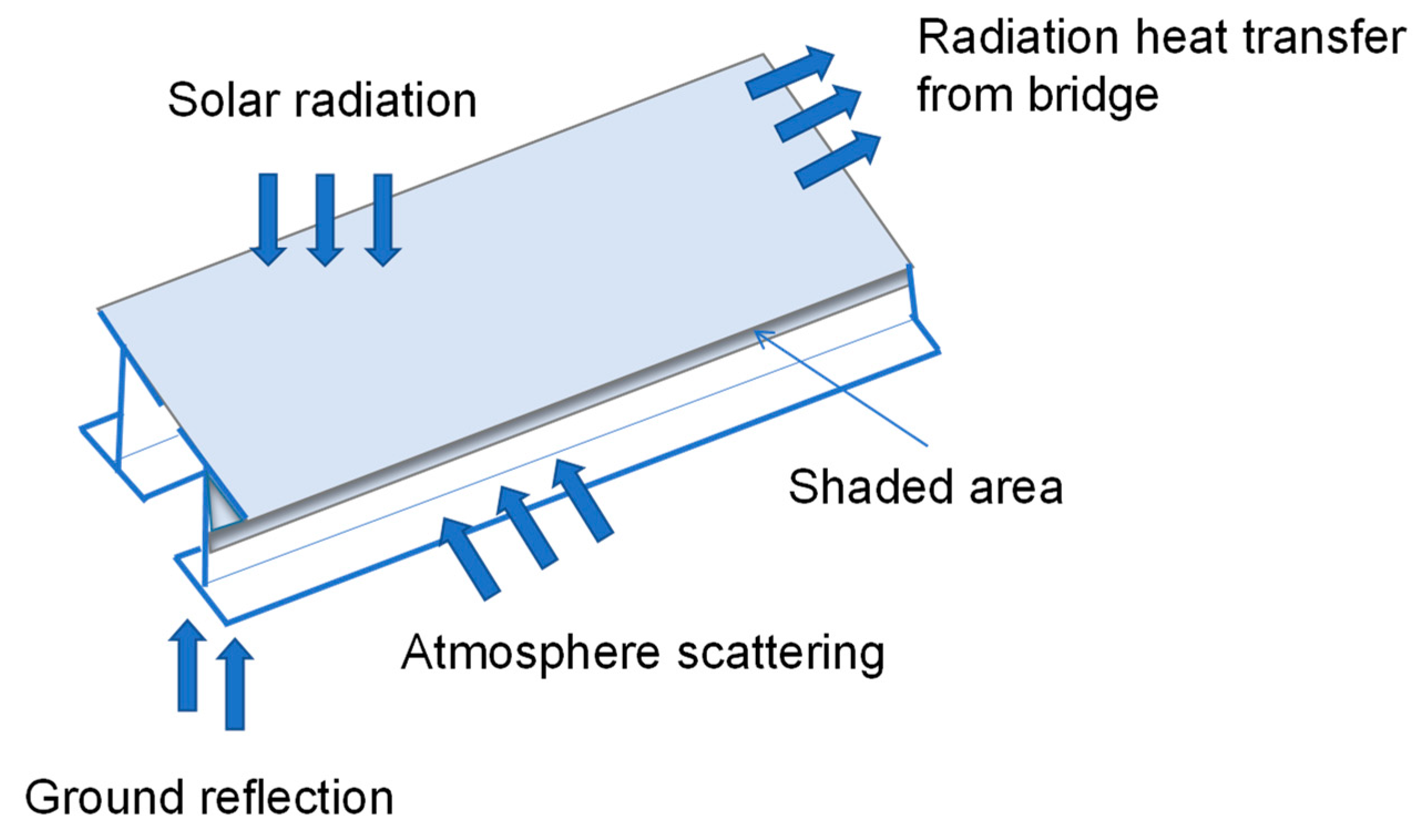
Solar radiation is prone to affect the temperature fields of bridges, which is the critical factor to determine the daily temperature cycles of bridge components. Consequently, solar radiation is the main kind of heat transfer in bridges (as shown in Figure 1); the other two kinds are convective heat transfer and radiative heat transfer.

In three-dimensional space, the differential equation of transient heat conduction is as follows:

$$\rho \mathrm{c}\frac{\partial T}{\partial t}=\frac{\partial }{\partial t}({\lambda }_x\frac{\partial T}{\partial x})+\frac{\partial }{\partial t}({\lambda }_y\frac{\partial T}{\partial y})+\frac{\partial }{\partial t}({\lambda }_z\frac{\partial T}{\partial z})+q_{\mathrm{\Omega }}$$

(1)

In the above formula, ρ is the material density $\mathrm{kg}/{\mathrm{m}}^3$; c is the specific heat capacity of the material, $\mathrm{J}/(\mathrm{k}\mathrm{g}\cdot \mathrm{K})$; T is the time, s; ${\lambda }_x$, ${\lambda }_y$,${\lambda }_z$ are the thermal conductivities of the material along x, y, and z directions, respectively; and q_Ω is the intensity of the internal heat source, $\mathrm{W}/{\mathrm{m}}^3$.

For any plane, the general analysis process of its received solar radiation at any time is as follows: the relative position of the sun to the plane is firstly analysed, followed by the refraction and scattering of solar radiation by the Earth’s atmosphere.

Convective heat transfer, including both natural convection and forced convection, is often caused by relative displacements between various parts of fluids. The convection in the boxes of bridge girders and in the tower cavity under no wind conditions is natural convection. The connection between air and the surfaces of beams under wind conditions is a kind of forced convection.

Thermal radiation is an electromagnetic wave excited by the thermal motion of microparticles in an object. It is emitted by the radiating object and propagates in a straight line. Objects with a temperature above absolute zero continuously convert thermal energy into radiant energy and emit thermal radiation to the surrounding environment. At the same time, they constantly absorb the thermal radiation projected on their surfaces by other objects and convert this absorbed radiant energy into thermal energy again.

2.2. Finite Element Method for Solving the Temperature Field

To obtain the temperature field distribution under specific boundary conditions, the differential equation of transient heat conduction in three-dimensional space is deduced based on the Fourier heat conduction law. After that, the finite element method (FEM) combined with the variational principle is used to analyse the temperature field.

3. Example Analysis of Numerical Method

3.1. Bridge Example

Bridge A is a single-tower hybrid composite-beam cable-stayed bridge with a span arrangement of 385 m (230 m + 115 m + 40 m). The main span is composed of a steel–concrete composite beam (SCCB), while the side span is composed of a concrete beam (CB). The main tower is 136 m in height, consolidated with the main beam. The structural diagram of the bridge is shown in Figure 2a–c.

3.2. Material Parameters

The heat transfer coefficients vary with the position and direction of the main beam. In this paper, the heat transfer coefficient values from the study [12] are adopted. The specific thermal performance parameters and convective heat transfer coefficients of each component are presented in

Table 1. Thermal performance parameters of the materials.

Material Property	Steel	Concrete
Density/(kg/m3)	7850	2500
Specific heat/(J/kg·°C)	480	840
Heat conduction/(W/m·°C)	58.15	1.28
Coefficient of thermal expansion (1/°C)	10 × 10−6	10 × 10−6
Emissivity	0.7	0.5
Elasticity modulus/(N/m2)	2.1 × 1011	3.45 × 1011

and

Table 2. Convective heat transfer coefficients at the boundaries.

Boundary Location	Convective Heat Transfer Coefficient (W/m2·°C)
Concrete top slab	25.1
Side of concrete slab and external surface of I-beam	17.5
I-beam inner surface	12.8
I-beam bottom	9.8

, respectively.

4. Temperature Field of the SCCB in the Main Span

4.1. Three-Dimensional Finite Element Mode

One segment of the SCCB is intercepted, and the temperature field of the FEM three-dimensional model is established using ABAQUS. The steel girder and concrete slab are simulated using an eight-node hexahedral linear heat transfer element (DC3D8) with a binding tie setting in the joint surface to ensure the effective transmission of temperature.

The solar radiation, thermal convection, and thermal radiation are simulated by inputting the radiation intensity value, convection coefficient, and emissivity, respectively. The initial temperature is set to 21 °C, and 24 × 7 analysis steps are conducted with each step lasting 3600 s.

4.2. Solar Radiation Calculation

According to the Duffie model [26], the radiation from any dayside is equal to the sum of the direct radiation, scattered radiation, and ground-reflected radiation. The amount of radiation on the shadow surface is equal to the sum of the scattered radiation and ground-reflected radiation. Considering the local latitude and bridge orientation (north–south), the total solar radiation values of the upper flange, web, and lower flange in the four seasons are calculated, as shown in Figure 3 below.

As shown in Figure 3, the solar radiation values of the upper flange and lower flange are both symmetrically distributed over time and reach a maximum value at 12:00 noon. The solar radiation of the top plate is mainly related to the solar radiation intensity, while the radiation intensity of the bottom plate is affected by the reflection from the ground because it is not directly irradiated by the sun.

The web temperature field is affected by direct radiation, atmospheric scattering, and ground reflection. However, due to the orientation and the shielding effect, the radiation intensity of the calculation surface changed at 12:00, when the surface changed from the dayside to the shadow surface. Therefore, considering the shielding relationship, the radiation of the east and west webs shows different trends, and the values are semi-symmetrical to each other.

The radiation intensity is the highest in summer because the sunshine time is the longest. By contrast, the radiation intensity is the shortest in winter. The radiation intensity difference between the web and upper flange is the largest in summer and the smallest in winter. Overall, it can be concluded that solar radiation varies significantly with the seasons.

The solar radiation intensities of the web and flange in the SCCB and CB are calculated and presented in

Table 3. Solar radiation intensity in the SCCB (Unit: W·m⁻²).

Time	Upper Flange	East Web		West Web		Lower Flange
		Dayside	Shadow Surface	Dayside	Shadow Surface
7:00	306.79	653.76	61.52	61.52		61.36
8:00	522.53	746.16	86.82	86.82		104.51
9:00	720.11	714.31	107.96	107.96		144.02
10:00	878.49	592.21	124.34	124.34		175.70
11:00	983.45	135.20		135.20		196.69
12:00	1026.93	186.36		139.90		205.39
13:00	1008.42	137.85		187.5		201.68
14:00	927.49	129.38		524.34	129.38	185.50
15:00	789.09	115.13		674.70	115.13	157.82
16:00	605.11	95.80		746.18	95.80	121.02
17:00	393.52	72.12		708.41	72.12	78.70
18:00	181.84	44.29		517.81	44.29	36.37

and

Table 4. Solar radiation intensity in the CB (Unit: W·m⁻²).

Time	Top Plate	East Web	West Web	Bottom Plate
7:00	306.79	653.76	61.52	61.36
8:00	522.53	746.16	86.82	104.51
9:00	720.11	714.31	107.96	144.02
10:00	878.49	592.21	124.34	175.70
11:00	983.45	407.45	135.20	196.69
12:00	1026.93	186.36	93.43	205.39
13:00	1008.42	137.85	321.91	201.68
14:00	927.49	129.38	524.34	185.50
15:00	789.09	115.13	674.70	157.82
16:00	605.11	95.80	746.18	121.02
17:00	393.52	72.12	708.41	78.70
18:00	181.84	44.29	517.81	36.37
19:00	22.20	10.12	126.96	4.44

, respectively.

It can be seen from Table 3 and Table 4 that when the bridge axis is located in the north–south direction, the maximum solar radiation intensity of the east/west web appears at sunrise/sunset, which is higher than that of the upper flange (or top plate). This is owing to the small solar altitude angle and the low solar radiation angle at sunrise/sunset, so the webs are not easily shaded by the steel flange (or top plate). As the solar altitude angle increases, the amount of solar radiation received by the upper flange increases, then gradually exceeds the solar radiation received by the webs, reaching the highest point at 12 o’clock, and then gradually decreases to lower than the amount of solar radiation received by the west web at sunset.

4.3. Validation

In order to verify whether the above solar radiation model is accurate, reference [17] was selected to compare the field-measured data of solar radiation on the level of sunny days in autumn. The results show that the radiation model in this paper is slightly higher than the measured value because the measured structure surface in reference [17] is sheltered by trees, so the radiation is basically consistent.

4.4. Temperature Distribution of a Section in the SCCB

The temperature gradient curves of the SCCB along the vertical distribution over 24 h are shown in Figure 4. It can be seen that the temperature distribution is uneven in the concrete slab, and the vertical gradient distribution is nonlinear, presenting a ‘C’ distribution mode. In the process of warming up, the lowest temperature point of the concrete slab occurs on the central axis of the concrete slab. The maximum internal temperature difference occurs at 14:00 with a value of approximately 14 °C. During the cooling process, the largest temperature difference at night also occurs on the central axis. The temperature difference was about 3.63 °C at 2:00 a.m., showing an inverse ‘C’ distribution mode. This is due to the poor thermal conductivity of concrete, resulting in the slowly altered temperature of the concrete slab.

On sunny days, due to the shadow shielding effect and the deviation of the sun, the highest temperature point of the steel girder always shifts downwards. After the direct sunlight period, the temperature differences of the web are small because the steel beam has good thermal conductivity and fast temperature transmission to both sides. Moreover, because of the shadow shielding effect, the lower flange only receives radiation that is reflected by the ground and scattered by the air; hence, the temperature is higher in the middle of the web during the warming process, and the temperature is slightly lower at both web ends. The opposite trend is observed during the cooling process, and the maximum temperature difference between the concrete slab and steel girder is 13.35 °C.

4.5. Temperature Field of the CB in the Side Span

The temperature gradient curves along the vertical distribution of the CB of the side span over 24 h are shown in Figure 5. The internal vertical gradient temperature distribution of the CB across the side span is generally C-shaped. In the daytime, when the sun shines on the surface, the concrete surface temperature reaches its highest at 15:00 p.m. and its lowest at 5:00 a.m. Within 0.5 m from the surface, the internal concrete temperature difference is small. The radiation is scattered and reflected by the bottom, and the temperature is always higher than that inside the concrete. Therefore, the temperature in the middle of the concrete is the lowest.

5. Temperature Effect Analysis of Bridge A

The indirect thermal mechanical coupling method is used to obtain the stress field of Bridge A. First, the full bridge finite element model (FEM) is established using ABAQUS (as shown in Figure 6). Then, combined with the results of the segmental temperature field calculated above, the structural temperature field is obtained. The parameter is imported into the whole bridge FEM, and the stress field of the structure is generated from the temperature. In the above temperature effect calculation, only the temperature degree of freedom was designed for the element, and the grid type was set to heat transfer elements. In the calculation of the stress field, these elements are converted to three-dimensional stress elements.

The tower and stayed cables are simulated using beam and link elements, respectively. The main beam, deck slab, and cross beam are simulated using solid elements. The slip between the steel girder and the concrete slab can be ignored. Connections between the deck–main beam and the main beam–cross beam are simulated using binding. Consolidation connections are set among the tower, beam, and pier. The tower bottom is restrained under consolidation, and the other supports are vertically restrained. The stayed cables are prestressed using the cooling method according to the completed cable force in the design.

To determine the influence of the temperature vertical gradient on Bridge A, the effect S_g under the action of structural self-weight was calculated and the effect under the combined load of the self-weight and temperature gradient S_c was analysed. Afterwards, by subtracting the structural response effect of the self-weight, the effect of only the temperature gradient was obtained as S_t = S_c − S_g. The results for the main sections (concrete slab, I-steel upper flange, I-steel web, and I-steel lower flange) are presented later.

5.1. Deflection Analysis

The steel girder arched upward, as shown in Figure 7a, because of the action of the temperature gradient, with a maximum value of 0.066 m at the 3/4 span of the SCCB part from the tower. The deflection reaches the maximum value at 18:00, and it falls to the minimum value at 6:00. The deformation amplitude of the CB affected by the temperature gradient is significantly lower than that of the SCCB. Under the action of the temperature gradient, the concrete decks also show upward deflection (see Figure 7b). At 6:00, the deflection value is the smallest, which is basically concentrated near 0.003 m. At 14:00, the deflection value reaches 0.012 m. Due to the constraints at the bridge tower, the deflection at the bridge tower is 0.

5.2. Temperature Effect Analysis

The stress distribution of the east web changes obviously with time under the action of sunshine (as shown in Figure 8). The east web is first exposed to sunshine in the morning. Then, the sun gradually moves westward over time. The longitudinal stress reaches its greatest at night, with a sudden change at the joint of the SCCB and CB. At 10 a.m., the longitudinal stress of the SCCB is about 4 MPa, which is significantly lower than at other times. Therefore, it can be inferred that under the action of the temperature vertical gradient, the longitudinal tensile stress of the steel girder decreases and the compressive stress increases.

Additionally, Figure 8b shows that the longitudinal stress of the lower flange of the east web attains the maximum value at 1/4 of the span, with a maximum compressive stress of 11.9 MPa at 14:00. At approximately 2/3 of the main span, the longitudinal tensile stress reaches the maximum value of 13.36 MPa at 2 a.m. At night, the compressive stress reaches the minimum value of 4.78 MPa. The peak value of the tensile stress at 10:00 is smaller than those at other time points.

Furthermore, when the temperature is high, the compressive stress of the steel girder at 1/4 of the main span approaches its maximum value. The tensile stress at 2/3 of the main span gradually approaches its maximum value at a low temperature. It is concluded that sunshine affects the longitudinal stress of the upper/lower flange of the steel girder at different positions.

The concrete slab is directly exposed to solar radiation, in contrast to the web. At 14:00, the received solar radiation is the strongest (as shown in Figure 9). Therefore, the longitudinal stress of the bridge deck at 14:00 is higher than that at other times. The longitudinal stress of CB generated in the side span of the bridge deck is compressive stress, which is obviously larger than that of the SCCB in the main span. At 14:00, the largest stress of approximately 4 MPa appears in the middle area between the main tower and the subsidiary pier.

6. Conclusions

This paper focuses on the temperature field distribution and the structural responses to a temperature vertical gradient in a hybrid beam (combined with an SCCB and CB) cable-stayed bridge. Based on the results of the field test and numerical simulation analysis, the following conclusions can be drawn:

(1) Based on the basic theory of heat transfer and the temperature field, the solar radiation of the main span and side span sections was calculated, and the temperature gradient of the main beam was obtained using ABAQUS. The results showed that there was an obvious temperature gradient in the concrete slab with a difference between the maximum and minimum value of 14 °C. When the steel web was in direct sunlight, there was an obvious nonlinear temperature gradient, and the maximum temperature difference reached 13.35 °C. The concrete showed obvious hysteresis, reaching its temperature peak later than the steel girder.

(2) Based on the temperature field distribution, a 3D FEM of the whole bridge was established. Due to the temperature gradient, the maximum deflection value of the steel beam is 0.066 m at the 3/4 span of the SCCB part. The deflection reaches the maximum value at 18:00 and drops to the minimum value at 6:00. The deformation amplitude of the CB affected by the temperature gradient was significantly lower than that of the SCCB. Under the action of a temperature gradient, the concrete bridge deck also shows an upward deflection. At 6:00, the deflection value is minimal, basically concentrated at 0 003 m. At 14:00, the deflection value reaches 0.012 m. Due to constraints at the pylon, the deflection at the pylons is 0. Then, the structural responses to the temperature vertical gradient were investigated based on the indirect thermal mechanical coupling principle using ABAQUS. The results show that the temperature rise leads to downward deflection of the main span, and the maximum deflection occurs at the 1/4 span. In addition, the longitudinal stress of the upper/lower flanges of the steel girder decreases with increasing temperature. The stress of the concrete slab increases obviously with increasing temperature. The longitudinal stress at the end of the main span is affected by the temperature change significantly, and the occurrence of the maximum stress of the concrete obviously lags behind that of the steel girder.

(3) The longitudinal stress in the upper flange is compressive and the longitudinal stress in the lower part is tensile stress during the daytime, but it was tensile stress everywhere at night. The CB at the end of the side span shows an obvious anti ‘C’ stress distribution. The middle is tensioned, and the top and bottom plates are compressed. The internal stress gradient increases with the temperature difference. In the future, experiments will be carried out, and the preliminary theoretical analysis and finite element analysis will be specific to the experiment to explore the influence of temperature on the material, such as adding new materials to improve the temperature strength, etc., which are all aspects worth exploring.