Undrained Shear Properties of Shallow Clayey-Silty Sediments in the Shenhu Area of South China Sea
Abstract
:1. Introduction
2. Materials and Methods
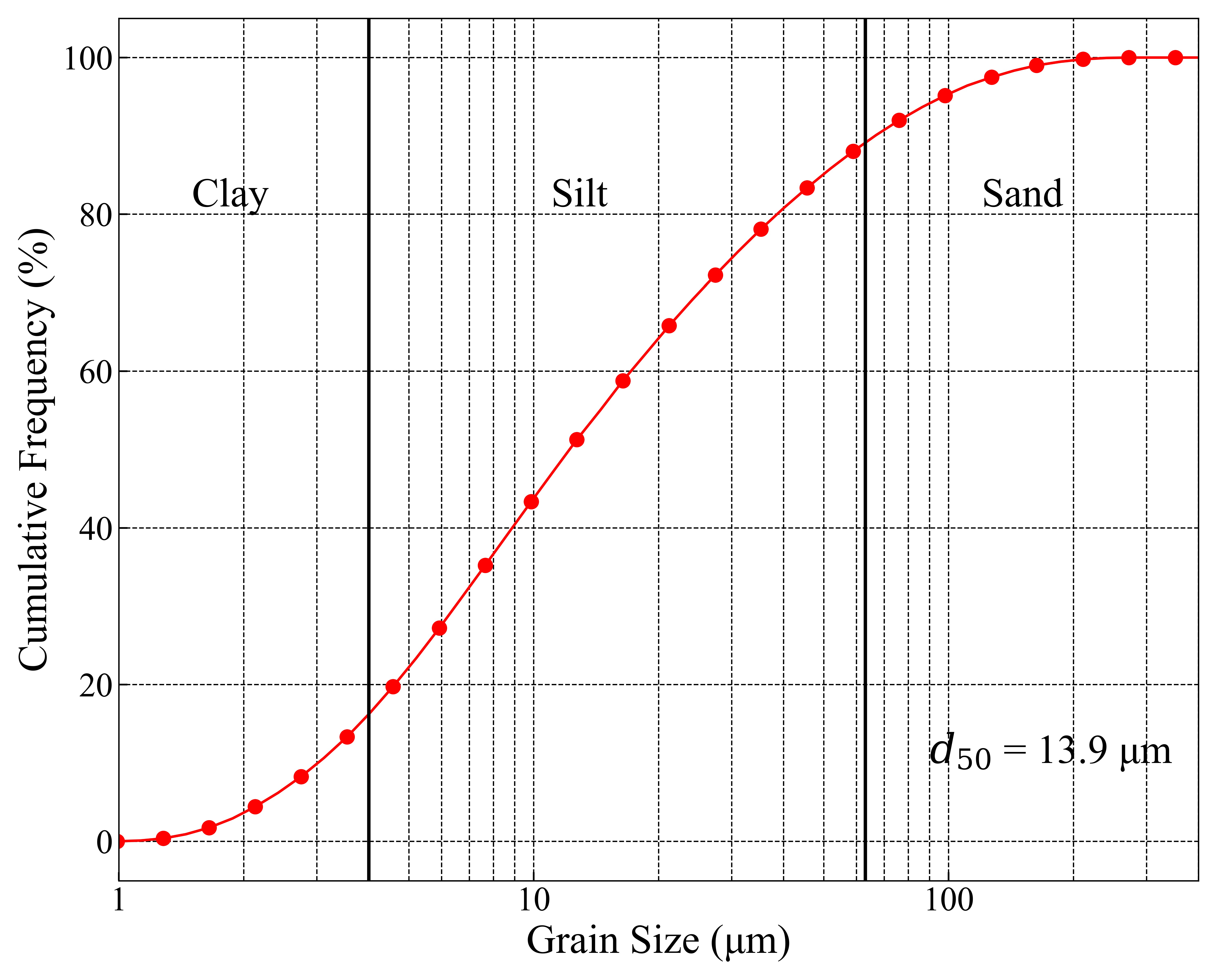
2.1. Test Materials
2.2. Test Procedure and Method
2.2.1. Test Specimen Preparation
2.2.2. Consolidation and Undrained Shear
2.2.3. Method to Predict the Pore Pressure Coefficient at Failure
3. Results
3.1. Isotropic Loading and Unloading Characteristics
3.2. Normalized Undrained Shear Strength and Mohr-Coulomb Strength Parameters for NC Specimens
3.3. Effects of OCR on
3.4. Pore Water Pressure Responses
4. Discussion
5. Conclusions
- The isotropic compression index and isotropic swelling index are 0.175 and 0.029, respectively. There is a linear relationship between and for NC specimens with an average of 0.42, while values of of OC specimens nonlinearly increase with increasing OCR.
- Only positive responses in the excess pore pressure are observed in CU tests for NC specimens, which increase with increasing . However, the increasing OCR leads to a reduction in excess pore pressure responses where there is a critical value of OCR = 3 dictating whether the remolded clayey-silty specimens develop negative pore pressure.
- Although values of of NC clayey-silty sediments differ between areas ranging from 0.25 to 0.43, it could be reasonably assumed as where the values mostly vary from 0.65 to 0.95. Moreover, values of of OC specimens can be well described by an exponential function related to the OCR and parameter .
- A model is proposed based on the relation between OCR and to predict the of remolded clayey-silty sediments of SCS. The prediction is in agreement with the experimental data in this study, as well as previous test results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| pore pressure coefficient | |
| pore pressure coefficient at failure | |
| predicted | |
| pore pressure coefficient | |
| effective cohesion | |
| curvature coefficient | |
| nonuniformity coefficients | |
| CS | critical state |
| CSL | critical state line |
| CU | consolidated undrained |
| void ratio | |
| FL | failure line |
| specific gravity | |
| GHSZ | gas hydrate stability zone |
| NC | normally consolidated |
| NCL | normally consolidated line |
| NGH | natural gas hydrate |
| OC | overconsolidated |
| OCR | overconsolidation ratio, equal to |
| present effective stress/ confining pressure | |
| preconsolidation pressure | |
| mean effective stress, equal to | |
| deviatoric stress, equal to | |
| deviatoric stress at failure | |
| SCS | South China Sea |
| undrained shear strength, equal to | |
| normalized undrained shear strength | |
| of OC sediments | |
| excess pore water pressure | |
| excess pore water pressure at failure | |
| water content | |
| axial strain | |
| parameter , equal to | |
| isotropic compression index | |
| isotropic compression index at critical state | |
| isotropic swelling index | |
| normal effective stresses | |
| , | initial major and minor principal stresses |
| , | major total and effective principal stresses |
| , | minor total and effective principal stresses |
| tensile strength of the hydrate mass | |
| shear stress |
References
- Sloan, E.D. Fundamental principles and applications of natural gas hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Boswell, R. Is Gas Hydrate Energy Within Reach? Science 2009, 325, 957–958. [Google Scholar] [CrossRef] [PubMed]
- Shaibu, R.; Sambo, C.; Guo, B.; Dudun, A. An assessment of methane gas production from natural gas hydrates: Challenges, technology and market outlook. Adv. Geo-Energy Res. 2021, 5, 318–332. [Google Scholar] [CrossRef]
- Cui, Y.; Lu, C.; Wu, M.; Peng, Y.; Yao, Y.; Luo, W. Review of exploration and production technology of natural gas hydrate. Adv. Geo-Energy Res. 2018, 2, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. The second natural gas hydrate production test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Li, J.; Ye, J.; Qin, X.; Qiu, H.; Wu, N.; Lu, H.; Xie, W.; Lu, J.; Peng, F.; Xu, Z.; et al. The first offshore natural gas hydrate production test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Li, B.; Kou, B.; Li, B.; Li, J.; Zeng, J.; Niu, Q.; Shao, Y.; Zhang, K.; Yu, H.; Wang, Y. Application of wellhead suction anchor technology in the second trial production of natural gas hydrates in the South China Sea. China Geol. 2022, 5, 293–299. [Google Scholar] [CrossRef]
- Yang, S.; Ren, Y.; Andersen, K.H. Effects of thixotropy and reconsolidation on the undrained shear characteristics of remoulded marine clays. Ocean Eng. 2021, 239, 109888. [Google Scholar] [CrossRef]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics; Cambridge University Press: Cambridge, UK, 1991; ISBN 9780521332491. [Google Scholar]
- Liu, F.; Sun, H.; Jung, J.; Zhang, X.; Ju, X. Experimental study of pullout capacity of plate anchors shallowly embedded in hydrate bearing sediments. Ocean Eng. 2019, 173, 548–555. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y.; Kim, G.-Y.; Kang, N.K.; Yi, B.-Y.; Jung, J.W.; Im, J.-H.; Son, B.-K.; Bahk, J.-J.; Chun, J.-H.; Ryu, B.-J.; et al. Physical properties of sediments from the Ulleung Basin, East Sea: Results from Second Ulleung Basin Gas Hydrate Drilling Expedition, East Sea (Korea). Mar. Pet. Geol. 2013, 47, 43–55. [Google Scholar] [CrossRef]
- Zhao, Y.; Kong, L.; Xu, R.; Liu, J.; Sang, S. Mechanical properties of remolded hydrate-bearing clayey-silty sediments. J. Nat. Gas Sci. Eng. 2022, 100, 104473. [Google Scholar] [CrossRef]
- Wu, P.; Li, Y.; Wang, L.; Wang, L.; Sun, X.; Liu, W.; Song, Y. Triaxial tests on the overconsolidated methane hydrate-bearing clayey-silty sediments. J. Pet. Sci. Eng. 2021, 206, 109035. [Google Scholar] [CrossRef]
- Luo, T.; Zou, D.; Zhao, X.; Zhang, C.; Han, T.; Song, Y. Strength behaviours of methane hydrate-bearing marine sediments in the South China Sea. J. Nat. Gas Sci. Eng. 2022, 100, 104476. [Google Scholar] [CrossRef]
- Dong, L.; Liao, H.; Li, Y.; Meng, Q.; Hu, G.; Wang, J.; Wu, N. Analysis of the Mechanical Properties of the Reconstituted Hydrate-Bearing Clayey-Silt Samples from the South China Sea. J. Mar. Sci. Eng. 2022, 10, 831. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Liu, L.; Sun, J.; Liu, H.; Meng, Q. Experimental study on evolution behaviors of triaxial-shearing parameters for hydrate-bearing intermediate fine sediment. Adv. Geo-Energy Res. 2018, 2, 43–52. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, L.; Jin, Y.; Wu, N. Characterization and development of marine natural gas hydrate reservoirs in clayey-silt sediments: A review and discussion. Adv. Geo-Energy Res. 2021, 5, 75–86. [Google Scholar] [CrossRef]
- Liu, L.; Lu, X.; Zhang, X.; Liu, C.; Du, B. Numerical simulations for analyzing deformation characteristics of hydrate-bearing sediments during depressurization. Adv. Geo-Energy Res. 2017, 1, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Bartetzko, A.; Kopf, A.J. The relationship of undrained shear strength and porosity with depth in shallow (<50 m) marine sediments. Sediment. Geol. 2007, 196, 235–249. [Google Scholar] [CrossRef]
- Hanzawa, H.; Adachi, K. Overconsolidation of Alluvial Clays. Soils Found. 1983, 23, 106–118. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Hao, B.; Gu, C.; Wang, J.; Pan, L. Effect of anisotropic consolidation stress paths on the undrained shear behavior of reconstituted Wenzhou clay. Eng. Geol. 2018, 242, 23–33. [Google Scholar] [CrossRef]
- Mayne, P.W.; Stewart, H.E. Pore Pressure Behavior of Ko-Consolidated Clays. J. Geotech. Eng. 1988, 114, 1340–1346. [Google Scholar] [CrossRef]
- Mayne, P.W. Determining OCR in Clays from Laboratory Strength. J. Geotech. Eng. 1988, 114, 76–92. [Google Scholar] [CrossRef]
- Skempton, A.W. The Pore-Pressure Coefficients A and B. Géotechnique 1954, 4, 143–147. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, K.; Geng, W.; Gaamom, A.; Xiao, J. Effect of initial water content on undrained shear strength of K0 consolidated clay. Soils Found. 2021, 61, 1453–1463. [Google Scholar] [CrossRef]
- Khera, R.P.; Krizek, R.J. Effect of Principal Consolidation Stress Difference on Undrained Shear Strength. Soils Found. 1968, 8, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, X.; Shen, J.; Zhu, C. Particle size and confining-pressure effects of shear characteristics of coral sand: An experimental study. Bull. Eng. Geol. Environ. 2022, 81, 97. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Lu, Y.; Cui, J.; Wang, X.; Zhu, C. Strength and dilatancy of coral sand in the South China Sea. Bull. Eng. Geol. Environ. 2021, 80, 8279–8299. [Google Scholar] [CrossRef]
- GB/T50123-2019; CSBTS (China State Bureau of Quality and Technical Supervision) Chinese Standard for Soil Test Method, 2019. CSBTS: Beijing, China, 2019.
- ASTM D4767-11R20; Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils, 2020. ASTM: West Conshohocken, PA, USA, 2020.
- Kuang, Y.; Yang, L.; Li, Q.; Lv, X.; Li, Y.; Yu, B.; Leng, S.; Song, Y.; Zhao, J. Physical characteristic analysis of unconsolidated sediments containing gas hydrate recovered from the Shenhu Area of the South China sea. J. Pet. Sci. Eng. 2019, 181, 106173. [Google Scholar] [CrossRef]
- Wang, X.; Hutchinson, D.R.; Wu, S.; Yang, S.; Guo, Y. Elevated gas hydrate saturation within silt and silty clay sediments in the Shenhu area, South China Sea. J. Geophys. Res. 2011, 116, B05102. [Google Scholar] [CrossRef] [Green Version]
- ASTM D2216-19; ASTM Standard Test Method for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass, 2019. ASTM: West Conshohocken, PA, USA, 2019.
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1943; ISBN 9780470172766. [Google Scholar]
- Graham, J.; Li, E.C.C. Comparison of Natural and Remolded Plastic Clay. J. Geotech. Eng. 1985, 111, 865–881. [Google Scholar] [CrossRef]
- Ladd, C.C.; Foott, R. New Design Procedure for Stability of Soft Clays. J. Geotech. Eng. Div. 1974, 100, 763–786. [Google Scholar] [CrossRef]
- Henkel, D.J. The Relationships Between the Strength, Pore-Water Pressure, and Volume-Change Characteristics of Saturated Clays. Géotechnique 1959, 9, 119–135. [Google Scholar] [CrossRef]
- Wang, L.; Sun, X.; Shen, S.; Wu, P.; Liu, T.; Liu, W.; Zhao, J.; Li, Y. Undrained triaxial tests on water-saturated methane hydrate–bearing clayey-silty sediments of the South China Sea. Can. Geotech. J. 2021, 58, 351–366. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Kida, M.; Katagiri, J.; Nagao, J.; Tenma, N. Pressure-core-based reservoir characterization for geomechanics: Insights from gas hydrate drilling during 2012–2013 at the eastern Nankai Trough. Mar. Pet. Geol. 2017, 86, 1–16. [Google Scholar] [CrossRef]
- Priest, J.A.; Hayley, J.L.; Smith, W.E.; Schultheiss, P.; Roberts, J. PCATS triaxial testing: Geomechanical properties of sediments from pressure cores recovered from the Bay of Bengal during expedition NGHP-02. Mar. Pet. Geol. 2019, 108, 424–438. [Google Scholar] [CrossRef]
- Yoneda, J.; Oshima, M.; Kida, M.; Kato, A.; Konno, Y.; Jin, Y.; Jang, J.; Waite, W.F.; Kumar, P.; Tenma, N. Pressure core based onshore laboratory analysis on mechanical properties of hydrate-bearing sediments recovered during India’s National Gas Hydrate Program Expedition (NGHP) 02. Mar. Pet. Geol. 2019, 108, 482–501. [Google Scholar] [CrossRef]
- Priest, J.A.; Druce, M.; Roberts, J.; Schultheiss, P.; Nakatsuka, Y.; Suzuki, K. PCATS Triaxial: A new geotechnical apparatus for characterizing pressure cores from the Nankai Trough, Japan. Mar. Pet. Geol. 2015, 66, 460–470. [Google Scholar] [CrossRef]
- Winters, W.J.; Wilcox-Cline, R.W.; Long, P.; Dewri, S.K.; Kumar, P.; Stern, L.; Kerr, L. Comparison of the physical and geotechnical properties of gas-hydrate-bearing sediments from offshore India and other gas-hydrate-reservoir systems. Mar. Pet. Geol. 2014, 58, 139–167. [Google Scholar] [CrossRef] [Green Version]
- Wei, R.; Jia, C.; Liu, L.; Wu, N. Analysis of the Characteristics of Pore Pressure Coefficient for Two Different Hydrate-Bearing Sediments under Triaxial Shear. J. Mar. Sci. Eng. 2022, 10, 509. [Google Scholar] [CrossRef]
- Tang, B.; Liu, T.; Zhou, B. Duncan–Chang E-υ Model Considering the Thixotropy of Clay in the Zhanjiang Formation. Sustainability 2022, 14, 12258. [Google Scholar] [CrossRef]
- David, W.; Mark, C. Offshore Geotechnical Engineering; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781315272474. [Google Scholar]
- Song, B.; Cheng, Y.; Yan, C.; Han, Z.; Ding, J.; Li, Y.; Wei, J. Influences of hydrate decomposition on submarine landslide. Landslides 2019, 16, 2127–2150. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Ansari, U.; Han, Y.; Liu, X.; Yan, C. Experimental investigation on hydrate dissociation in near-wellbore region caused by invasion of drilling fluid: Ultrasonic measurement and analysis. Environ. Sci. Pollut. Res. 2022, 29, 36920–36937. [Google Scholar] [CrossRef] [PubMed]
- Randolph, M.F. Offshore Geotechnics—The Challenges of Deepwater Soft Sediments. In Geotechnical Engineering State of the Art and Practice; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 241–271. [Google Scholar]
- Bishop, A.W. The Use of Pore-Pressure Coefficients in Practice. Géotechnique 1954, 4, 148–152. [Google Scholar] [CrossRef]

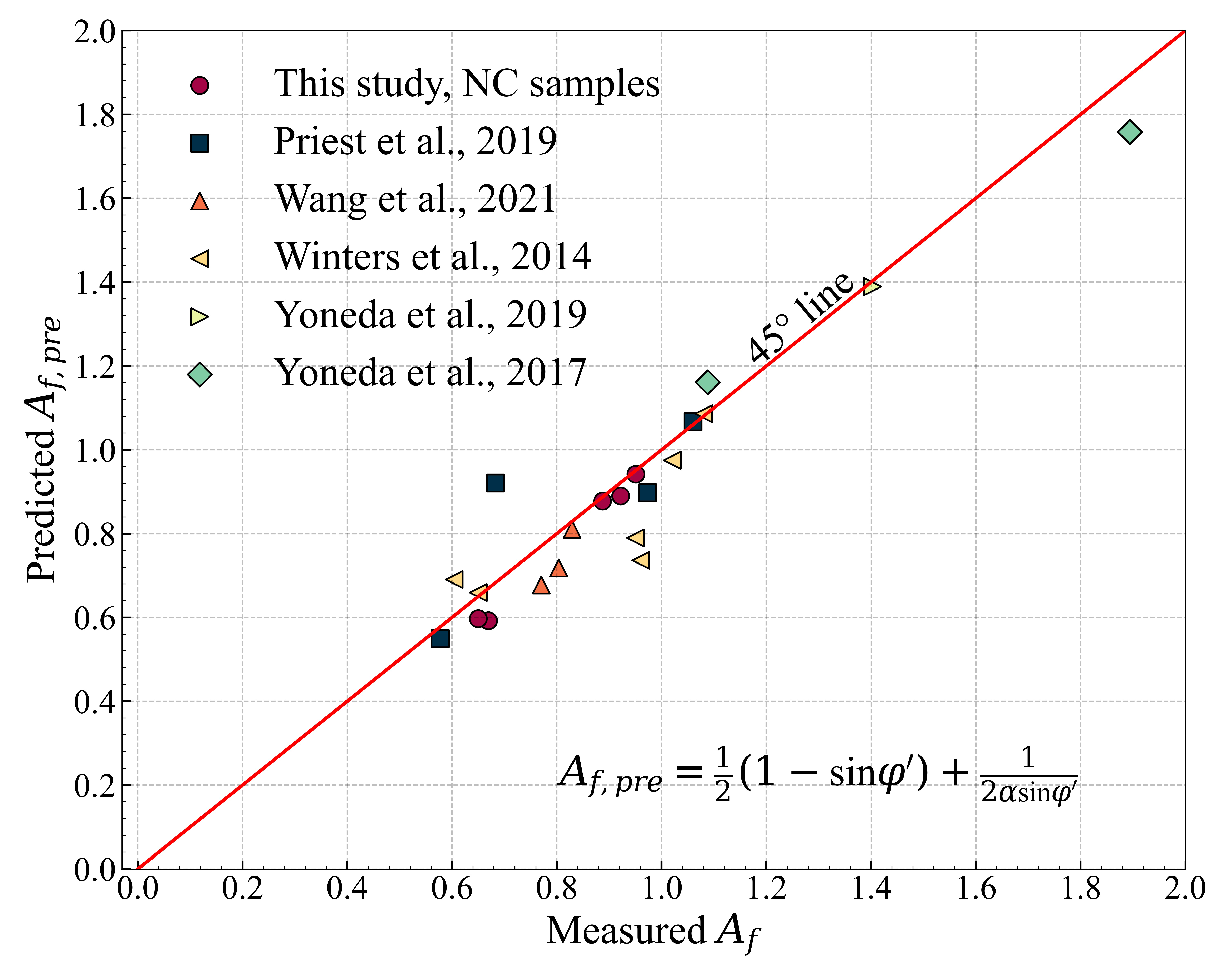



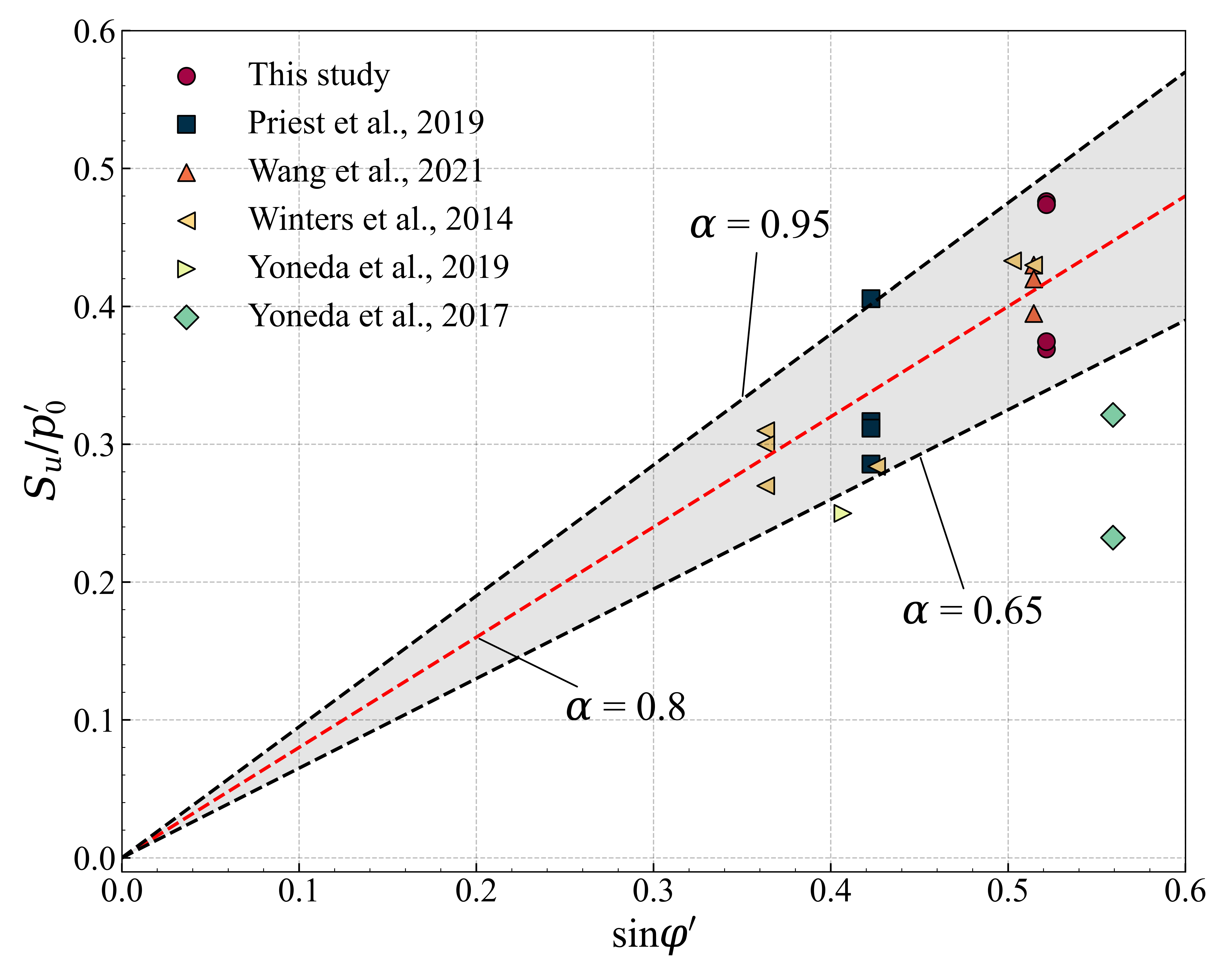


| Location | Test Condition | Reference | |||
|---|---|---|---|---|---|
| Krishna-Godavari Basin, India | CU tests | 0.31–0.4 | 25° | 0.67–0.95 | Priest et al. (2019) [40] |
| Krishna-Godavari Basin, India | CU tests | 0.25 | 24° | 0.61 | Yoneda et al. (2019) [41] |
| Krishna-Godavari Basin, India | CU tests | 0.27–0.43 | 21°–31° | 0.65–0.86 | Winters et al. (2014) [43] |
| Nankai Trough, Japan | CU tests | 0.42 | Not available | / | Priest et al. (2015) [42] |
| Nankai Trough, Japan | CU tests | 0.29 | 34° | 0.52 | Yoneda et al. (2017) [39] |
| Shenhu Area, China | CU tests | 0.39–0.43 | 31° | 0.76–0.84 | Wang et al. (2021) [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, R.; Liu, L.; Jia, C.; Zhao, H.; Dong, X.; Bu, Q.; Liu, C.; Wu, N. Undrained Shear Properties of Shallow Clayey-Silty Sediments in the Shenhu Area of South China Sea. Sustainability 2023, 15, 1175. https://doi.org/10.3390/su15021175
Wei R, Liu L, Jia C, Zhao H, Dong X, Bu Q, Liu C, Wu N. Undrained Shear Properties of Shallow Clayey-Silty Sediments in the Shenhu Area of South China Sea. Sustainability. 2023; 15(2):1175. https://doi.org/10.3390/su15021175
Chicago/Turabian StyleWei, Ruchun, Lele Liu, Chao Jia, Hualin Zhao, Xiao Dong, Qingtao Bu, Changling Liu, and Nengyou Wu. 2023. "Undrained Shear Properties of Shallow Clayey-Silty Sediments in the Shenhu Area of South China Sea" Sustainability 15, no. 2: 1175. https://doi.org/10.3390/su15021175





