Recovery Strategies for Urban Rail Transit Network Based on Comprehensive Resilience
Abstract
:1. Introduction
2. Network Construction and Integrated Resilience
2.1. Network Construction and Problem Statement
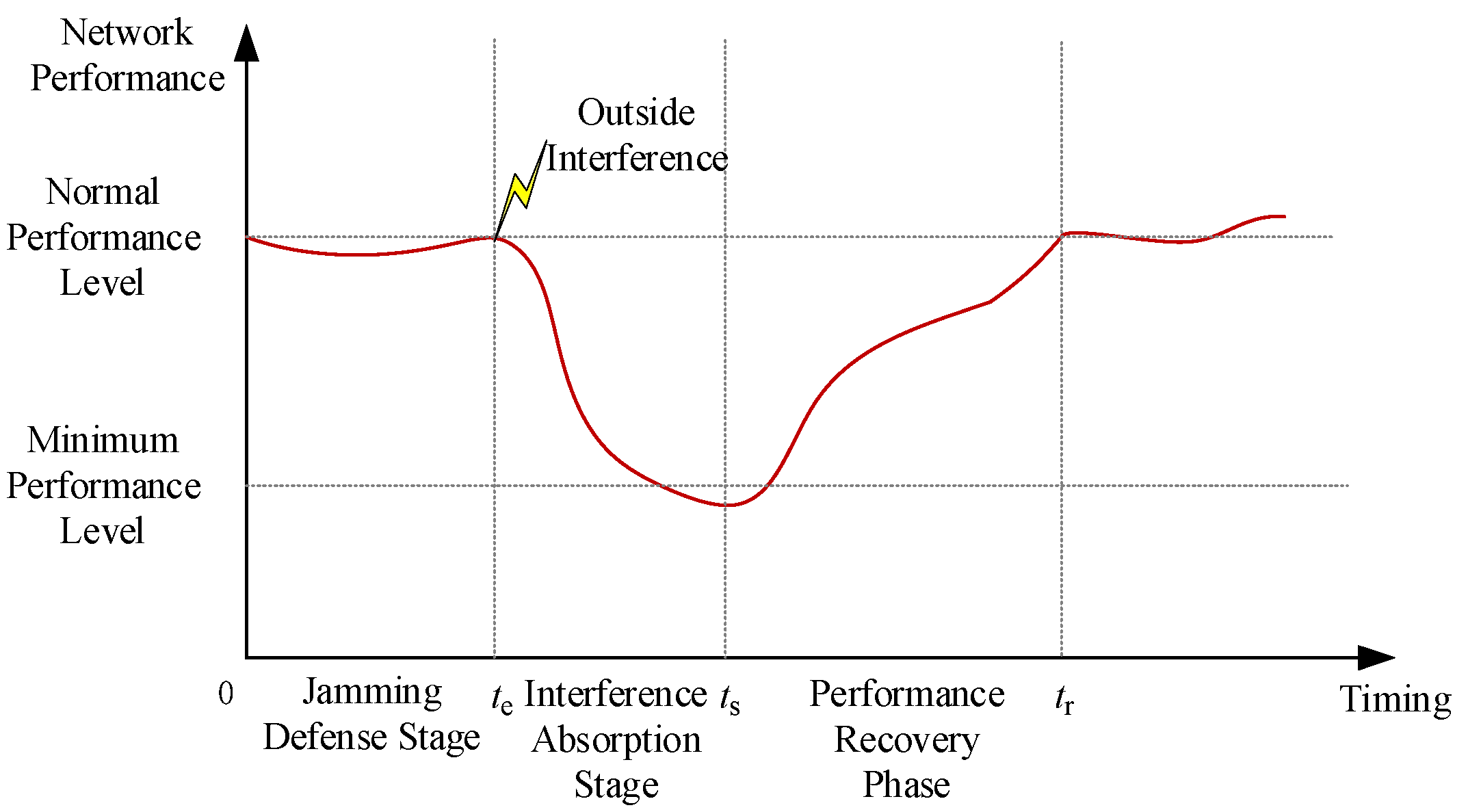
2.2. Integrated Resilience of Rail Transit Networks
3. Rail Transit Network Recovery Model
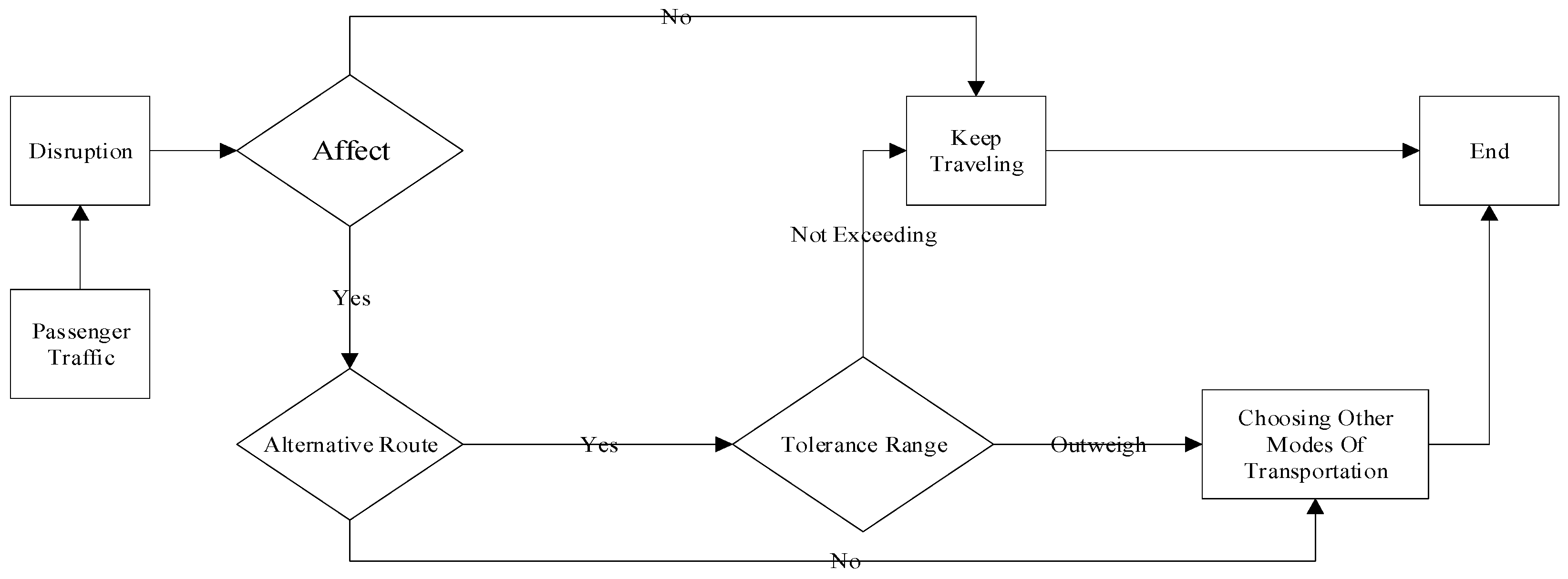
3.1. Basic Assumptions
3.2. Upper-Level Model
3.3. Lower-Level Model
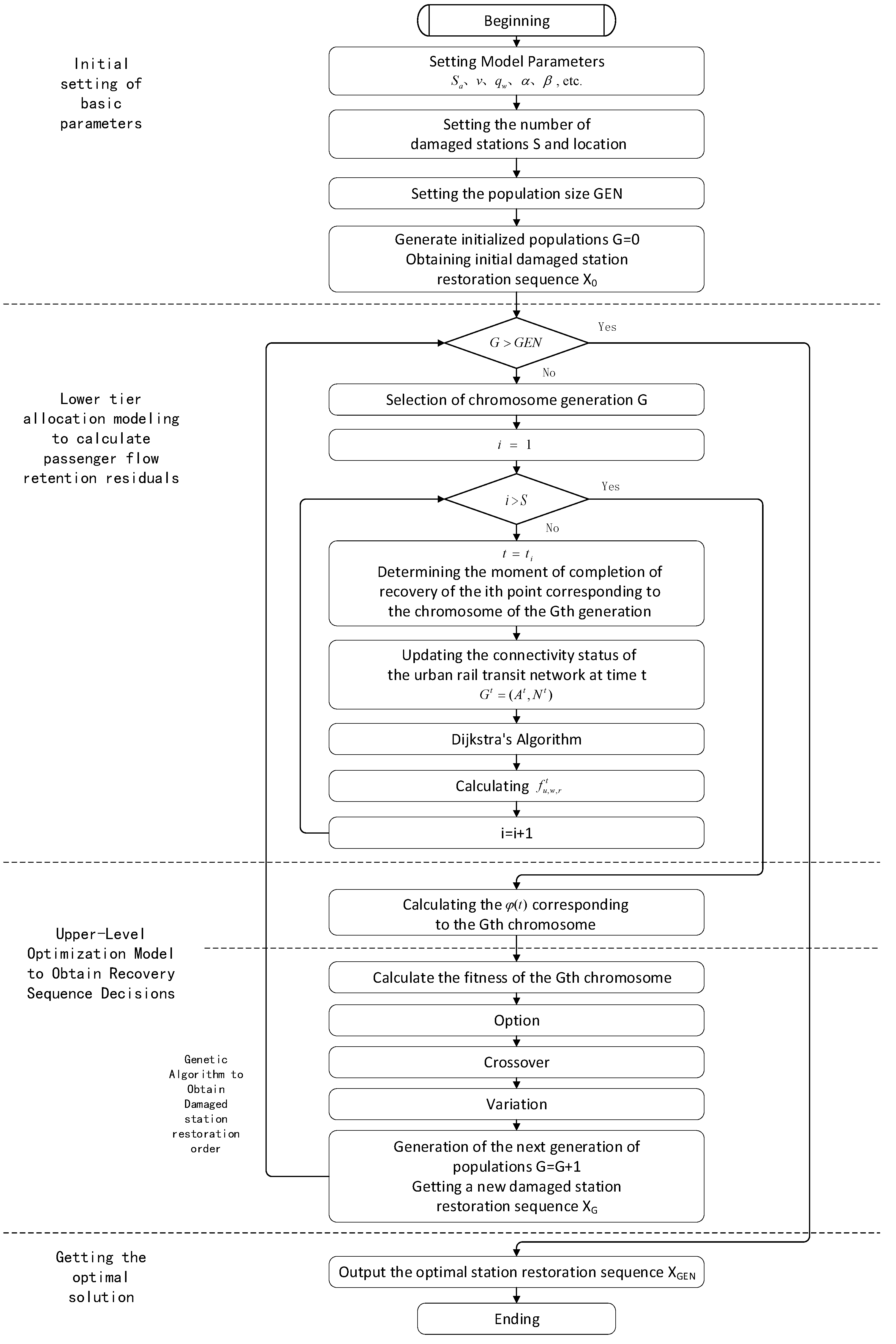
3.4. Algorithm Design
4. Case Study
4.1. Analysis of Urban Rail Transit Network Structure
4.2. Interference Scenario Design
4.3. Model Solution
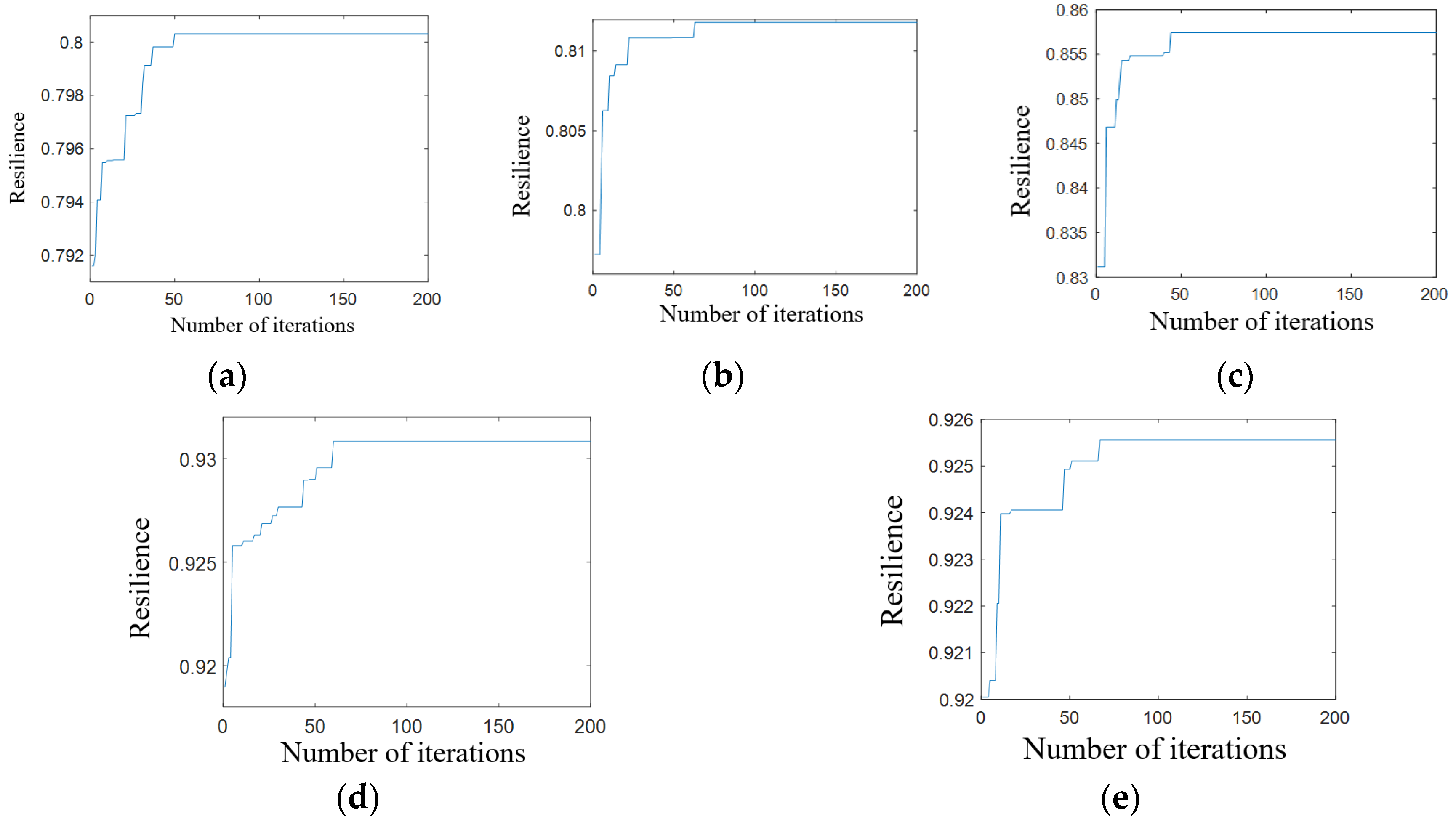
4.4. Analysis of Results
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Q.; Yang, D.; Li, P.; Liang, S.; Zhang, Z. Resilient city: A Bibliometric analysis and visualization. Discret. Dyn. Nat. Soc. 2021, 2021, 5558497. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Jin, F. Robustness of China’s air transport network from 1975 to 2017. Phys. A Stat. Mech. Its Appl. 2020, 539, 122876. [Google Scholar] [CrossRef]
- Wang, S.; Chen, C.; Zhang, J.; Gu, X.; Huang, X. Vulnerability assessment of urban road traffic systems based on traffic flow. Int. J. Crit. Infrastruct. Prot. 2022, 38, 100536. [Google Scholar] [CrossRef]
- Hong, J.; Tamakloe, R.; Lee, S.; Park, D. Exploring the topological characteristics of complex public transportation networks: Focus on Variations in both single and integrated systems in the Seoul metropolitan area. Sustainability 2019, 11, 5404. [Google Scholar] [CrossRef]
- Gao, P.; Hu, J.; Wei, G. Robustness Analysis of Urban Transit Network Based on Complex Network with Varied Weight. Comput. Simul. 2013, 30, 153–156. [Google Scholar] [CrossRef]
- Yin, Y.; Huang, W.; Xie, A.; Li, H.; Gong, W.; Zhang, Y. Syncretic K-shell algorithm for node importance identification and invulnerability evaluation of urban rail transit network. Appl. Math. Model. 2023, 120, 400–419. [Google Scholar] [CrossRef]
- Yoon, Y.J. Planning of Optimal Rehabilitation Strategies for Infrastructure Using Time Float and Multiyear Prioritization Approach. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Zheng, W.; Hu, J.; Wen, C.; Tang, R. Research on urban rail failure recovery considering network resilience. China Saf. Sci. J. 2023, 33, 179. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, G.; Song, J. Resilience-based restoration sequence optimization for metro networks: A case study in China. J. Adv. Transp. 2022, 2022, 8595356. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, G.; Ma, J.; Gao, J.; Zhu, X. Decision-making method of repair sequence for metro network based on resilience evaluation. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 14. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, H.; Lu, Q.-C.; Lin, S.; Song, J. Vulnerability Analysis of Bus Network Based on Land-Use Type of Bus Stops: The Case of Xi’an, China. Sustainability 2023, 15, 12566. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, X.; Wu, J.; Chen, A.; Wei, Y.; Gao, Z. Measuring the resilience of an urban rail transit network: A multi-dimensional evaluation model. Transp. Policy 2022, 129, 38–50. [Google Scholar] [CrossRef]
- Hosseini, Y.; Mohammadi, R.K.; Yang, T.Y. Resource-based seismic resilience optimization of the blocked urban road network in emergency response phase considering uncertainties. Int. J. Disaster Risk Reduct. 2023, 85, 103496. [Google Scholar] [CrossRef]
- Sarhadi, H.; Tulett, D.M.; Verma, M. An analytical approach to the protection planning of a rail intermodal terminal network. Eur. J. Oper. Res. 2017, 257, 511–525. [Google Scholar] [CrossRef]
- Starita, S.; Scaparra, M.P. Optimizing dynamic investment decisions for railway systems protection. Eur. J. Oper. Res. 2016, 248, 543–557. [Google Scholar] [CrossRef]
- Starita, S.; Scaparra, M.P. Passenger railway network protection: A model with variable post-disruption demand service. J. Oper. Res. Soc. 2018, 69, 603–618. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, Y. Transportation infrastructure restoration optimization considering mobility and accessibility in resilience measures. Transp. Res. Part C Emerg. Technol. 2020, 117, 102700. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, P.; Xu, B.; Cui, X. Resilience-based protection decision optimization for metro network under operational incidents. J. Transp. Eng. 2023, 23, 209–220. [Google Scholar] [CrossRef]
- von Ferber, C.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Public transport networks: Empirical analysis and modeling. Eur. Phys. J. B 2009, 68, 261–275. [Google Scholar] [CrossRef]
- Berche, B.; von Ferber, C.; Holovatch, T.; Holovatch, Y. Public transport networks under random failure and directed attack. Physics 2010, 2, 42–54. [Google Scholar] [CrossRef]
- Saadat, Y.; Ayyub, B.M.; Zhang, Y.; Zhang, D.; Huang, H. Resilience of metrorail networks: Quantification with Washington, DC as a case study. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2019, 5, 041011. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Renschler, C.; Arendt, L.; Bruneau, M.; Reinhorn, A.M. Community resilience index for road network systems. In Proceedings of the 8th International Conference on Structural Dynamics, Leuven, Belgium, 4–6 July 2011; pp. 370–376. [Google Scholar]
- Ma, C.Q.; Zhang, S.; Chen, Q.; Rui, C. Characteristics and Vulnerability of Rail Transit Network based on Perspective of Passenger Flow Characteristics. J. Traffic Transp. Eng. 2020, 20, 208–216. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Nan, C.; Sansavini, G. A quantitative method for assessing resilience of interdependent infrastructures. Reliab. Eng. Syst. Saf. 2017, 157, 35–53. [Google Scholar] [CrossRef]
- Ouyang, M.; Dueñas-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Saf. 2012, 36/37, 23–31. [Google Scholar] [CrossRef]
- Wardrop, J.G. Some theoretical aspects of road traffic research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Du, F.; Huang, H.; Zhang, F.; Ayyub, B.M.; Beer, M. Resiliency assessment of urban rail transit networks: Shanghai metro as an example. Saf. Sci. 2018, 106, 230–243. [Google Scholar] [CrossRef]
- Chen, J.Q.; Zuo, T.; Zhu, M.; Peng, Q.; Yin, Y. Repair strategies for a damaged urban rail transit network. J. Saf. Environ. 2022, 22, 316–323. [Google Scholar] [CrossRef]
- Dui, H.; Zheng, X.; Wu, S. Resilience analysis of maritime transportation systems based on importance measures. Reliab. Eng. Syst. Saf. 2021, 209, 107461. [Google Scholar] [CrossRef]
- Baroud, H.; Barker, K.; Ramirez-Marquez, J.E. Importance measures for inland waterway network resilience. Transp. Res. Part E Logist. Transp. Rev. 2014, 62, 55–67. [Google Scholar] [CrossRef]
- Chen, G.F.; Wei, H. Tunnel gas risk assessment based on EW-AHP and unascertained measurement theory. Nonferrous Met. Sci. Eng. 2021, 12, 89–95. [Google Scholar] [CrossRef]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
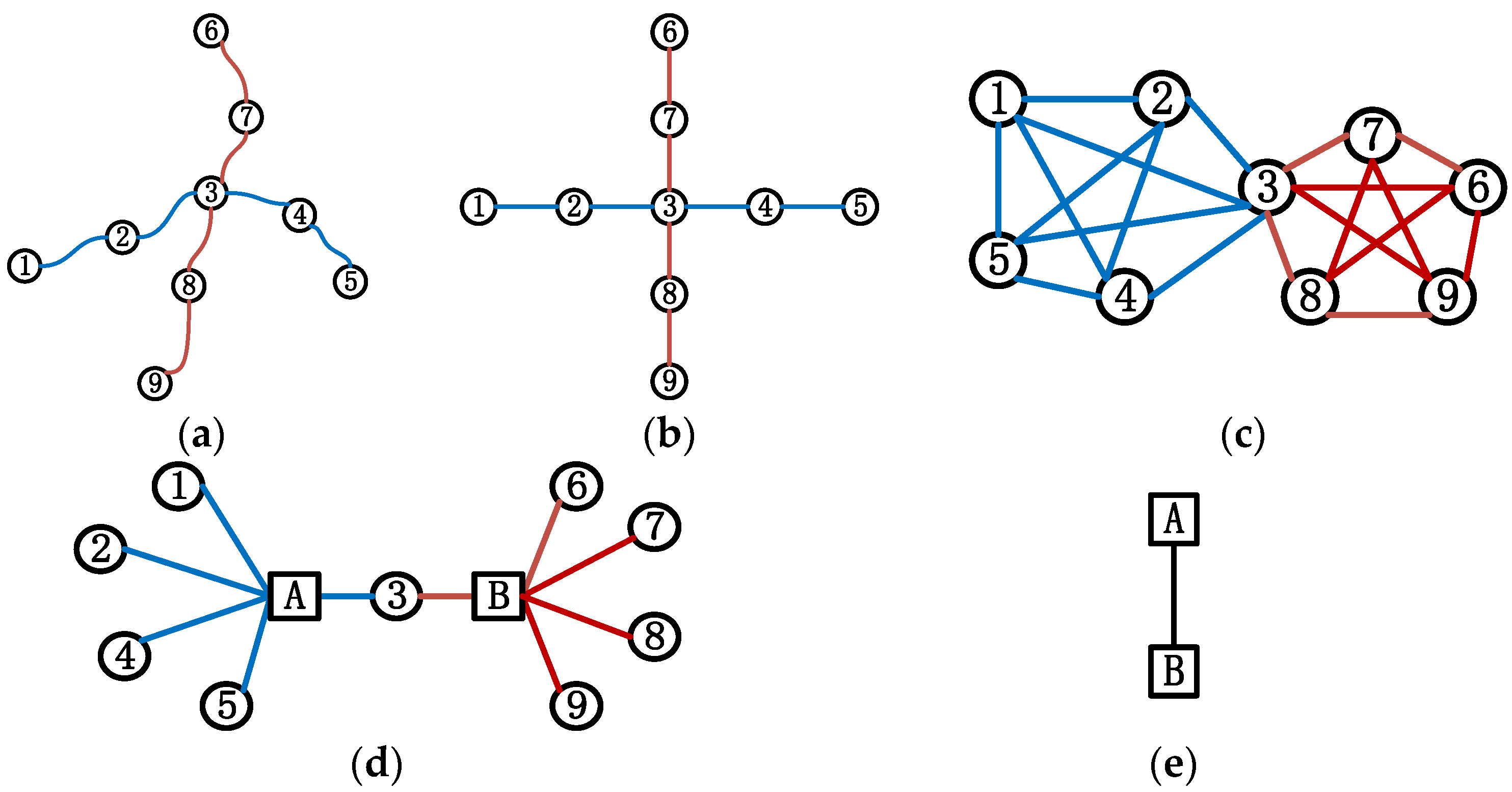
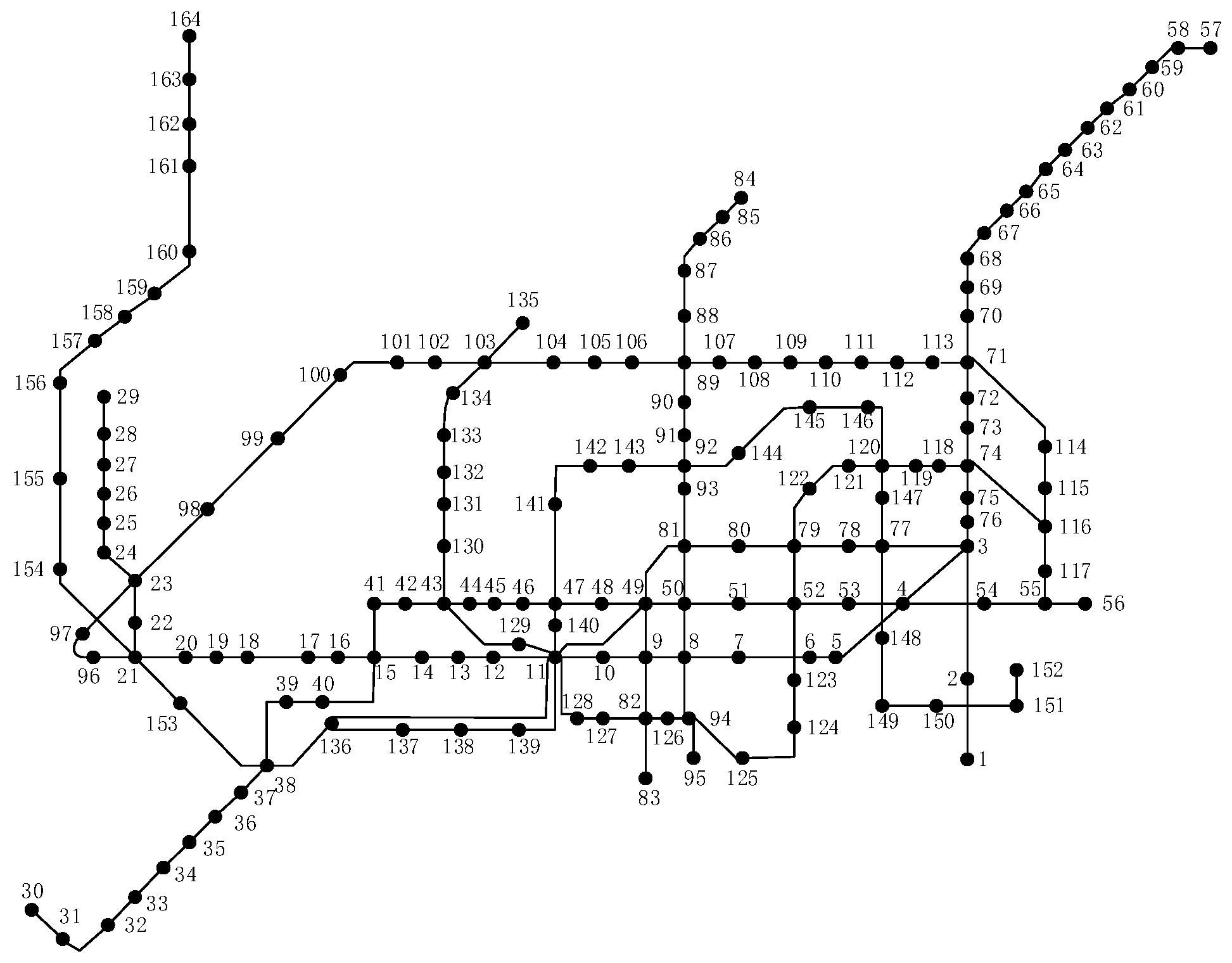
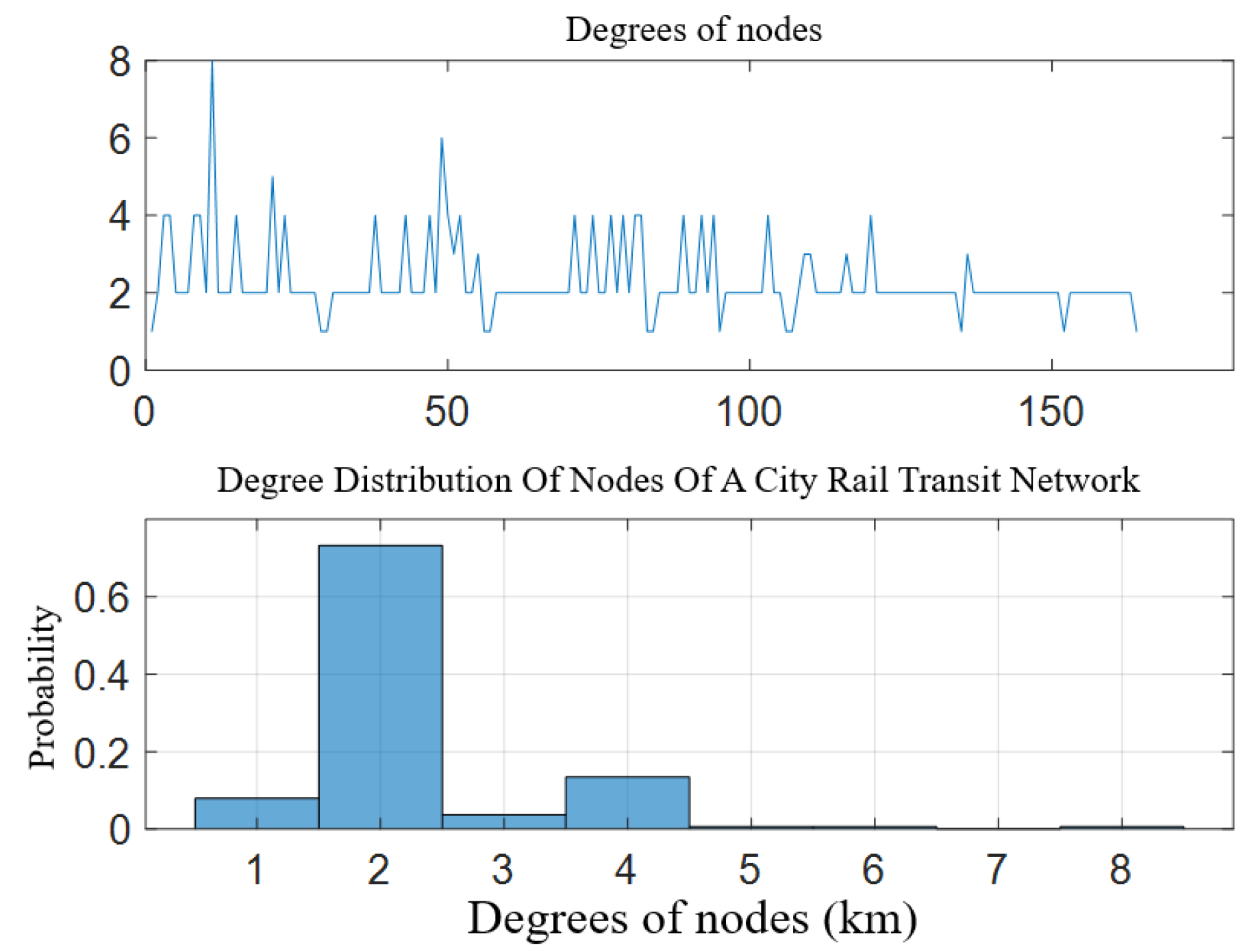
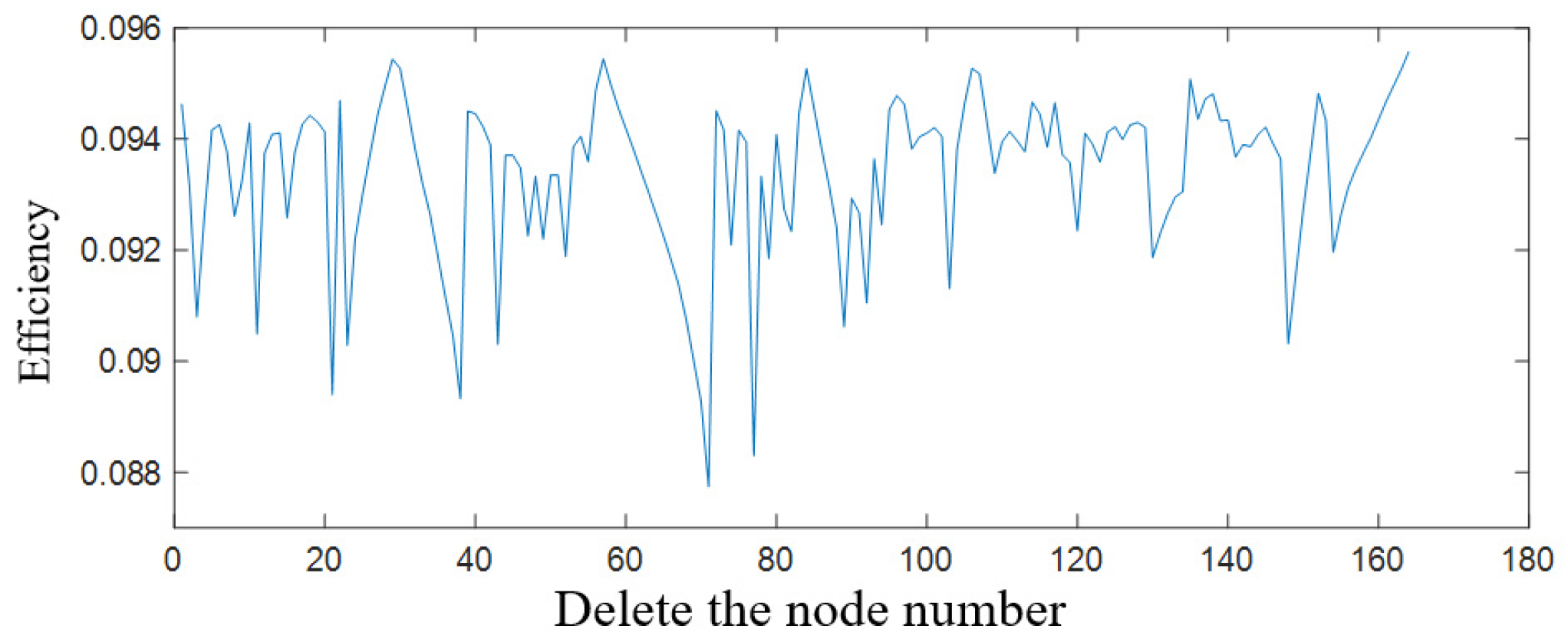


| Ordered List | Network Efficiency Ranking | Passenger Retention Ranking | |||
|---|---|---|---|---|---|
| Nodes | Degree | Nodes | Network Efficiency | Nodes | Patronage Retention Rate |
| 11 | 8 | 71 | 0.0877 | 71 | 0.8582 |
| 49 | 5 | 77 | 0.0883 | 70 | 0.8826 |
| 21 | 5 | 70 | 0.0893 | 69 | 0.8905 |
| 120 | 4 | 38 | 0.0893 | 68 | 0.9024 |
| 103 | 4 | 21 | 0.0894 | 109 | 0.9161 |
| 94 | 4 | 69 | 0.0900 | 89 | 0.9184 |
| 92 | 4 | 23 | 0.0903 | 67 | 0.9231 |
| 89 | 4 | 43 | 0.0903 | 66 | 0.9293 |
| 82 | 4 | 148 | 0.0903 | 88 | 0.9294 |
| 81 | 4 | 37 | 0.0905 | 3 | 0.9307 |
| Type of Interference | Interference Method | Node Number |
|---|---|---|
| Target Interference | Degree | 11 49 21 120 103 94 92 89 82 81 |
| Network Efficiency | 71 77 70 38 21 69 23 43 148 37 | |
| Patronage Retention Rate | 71 70 69 68 109 89 67 66 88 3 | |
| Range Interference | Waterlogged | 4 53 70 71 72 113 148 162 163 164 |
| Random Interference | Randomized function | 5 6 47 64 74 78 126 128 131 164 |
| Scenario | Recovery Strategy | Station Restoration Sequence | Network Resilience | ||
|---|---|---|---|---|---|
| Target Interference | Interference based on Degree | Integrated Resilient Optimal Recovery | 11 103 89 92 21 94 82 81 49 120 | 0.800318428 | |
| Randomized Recovery | 103 81 11 120 89 94 92 49 21 82 | 0.74546206 | |||
| Criticality-Based Prioritized Recovery Strategy | Based On Degree | 11 49 21 120 103 94 92 89 82 81 | 0.773513976 | ||
| Based On Network Efficiency | 21 11 89 92 103 49 82 120 94 81 | 0.794944533 | |||
| Based On The Degree Of Traffic Loss | 89 103 21 82 94 49 92 11 120 81 | 0.712920272 | |||
| Interference based on Network Efficiency | Integrated Resilient Optimal Recovery | 21 23 71 77 69 70 148 43 37 38 | 0.811797298 | ||
| Randomized Recovery | 69 71 23 38 148 21 43 70 37 77 | 0.726484518 | |||
| Criticality-Based Prioritized Recovery Strategy | Based On Degree | 21 23 38 43 71 77 37 69 70 148 | 0.802326971 | ||
| Based On Network Efficiency | 71 77 70 38 21 69 23 43 148 37 | 0.739769381 | |||
| Based On The Degree Of Traffic Loss | 71 70 69 23 38 21 37 77 148 43 | 0.772879502 | |||
| Interference based on Patronage Retention | Integrated Resilient Optimal Recovery | 71 3 88 89 109 70 69 67 66 68 | 0.857429135 | ||
| Randomized Recovery | 88 71 66 68 69 70 67 89 109 3 | 0.790675767 | |||
| Criticality-Based Prioritized Recovery Strategy | Based On Degree | 71 89 3 66 67 68 69 70 88 109 | 0.818073808 | ||
| Based On Network Efficiency | 71 70 69 89 68 3 103 67 66 88 | 0.816691631 | |||
| Based On The Degree Of Traffic Loss | 71 70 69 68 109 89 67 66 88 3 | 0.815236679 | |||
| Range Interference | Waterlogged | Integrated Resilient Optimal Recovery | 71 70 148 4 113 53 72 162 163 164 | 0.930825361 | |
| Randomized Recovery | 4 148 71 53 70 113 164 163 72 162 | 0.911348662 | |||
| Criticality-Based Prioritized Recovery Strategy | Based On Degree | 4 71 70 113 53 163 162 72 148 164 | 0.911008611 | ||
| Based On Network Efficiency | 71 70 148 4 113 53 163 162 72 164 | 0.928465347 | |||
| Based On The Degree Of Traffic Loss | 71 70 4 148 72 162 113 53 163 164 | 0.926634499 | |||
| Random Interference | Randomized Function | Integrated Resilient Optimal Recovery | 64 74 78 47 131 5 6 128 164 126 | 0.925559653 | |
| Randomized Recovery | 131 6 78 74 5 47 128 164 64 126 | 0.900800084 | |||
| Criticality-Based Prioritized Recovery Strategy | Based On Degree | 74 47 78 64 131 5 6 128 126 164 | 0.921360873 | ||
| Based On Network Efficiency | 74 47 131 64 78 126 5 6 128 164 | 0.921035007 | |||
| Based On The Degree Of Traffic Loss | 64 6 47 128 74 5 78 131 126 164 | 0.921597407 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Zuo, H.; Zhou, Z.; Bai, Y. Recovery Strategies for Urban Rail Transit Network Based on Comprehensive Resilience. Sustainability 2023, 15, 15018. https://doi.org/10.3390/su152015018
Zheng M, Zuo H, Zhou Z, Bai Y. Recovery Strategies for Urban Rail Transit Network Based on Comprehensive Resilience. Sustainability. 2023; 15(20):15018. https://doi.org/10.3390/su152015018
Chicago/Turabian StyleZheng, Mingming, Hanzhang Zuo, Zitong Zhou, and Yuhan Bai. 2023. "Recovery Strategies for Urban Rail Transit Network Based on Comprehensive Resilience" Sustainability 15, no. 20: 15018. https://doi.org/10.3390/su152015018
APA StyleZheng, M., Zuo, H., Zhou, Z., & Bai, Y. (2023). Recovery Strategies for Urban Rail Transit Network Based on Comprehensive Resilience. Sustainability, 15(20), 15018. https://doi.org/10.3390/su152015018






