Analysis and Comparison of Wind Potential by Estimating the Weibull Distribution Function: Application to Wind Farm in the Northern of Morocco
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site Location
2.2. Estimating Energy Density/Production
2.3. Weibull Probability Distribution Function
2.4. Parameters Estimations
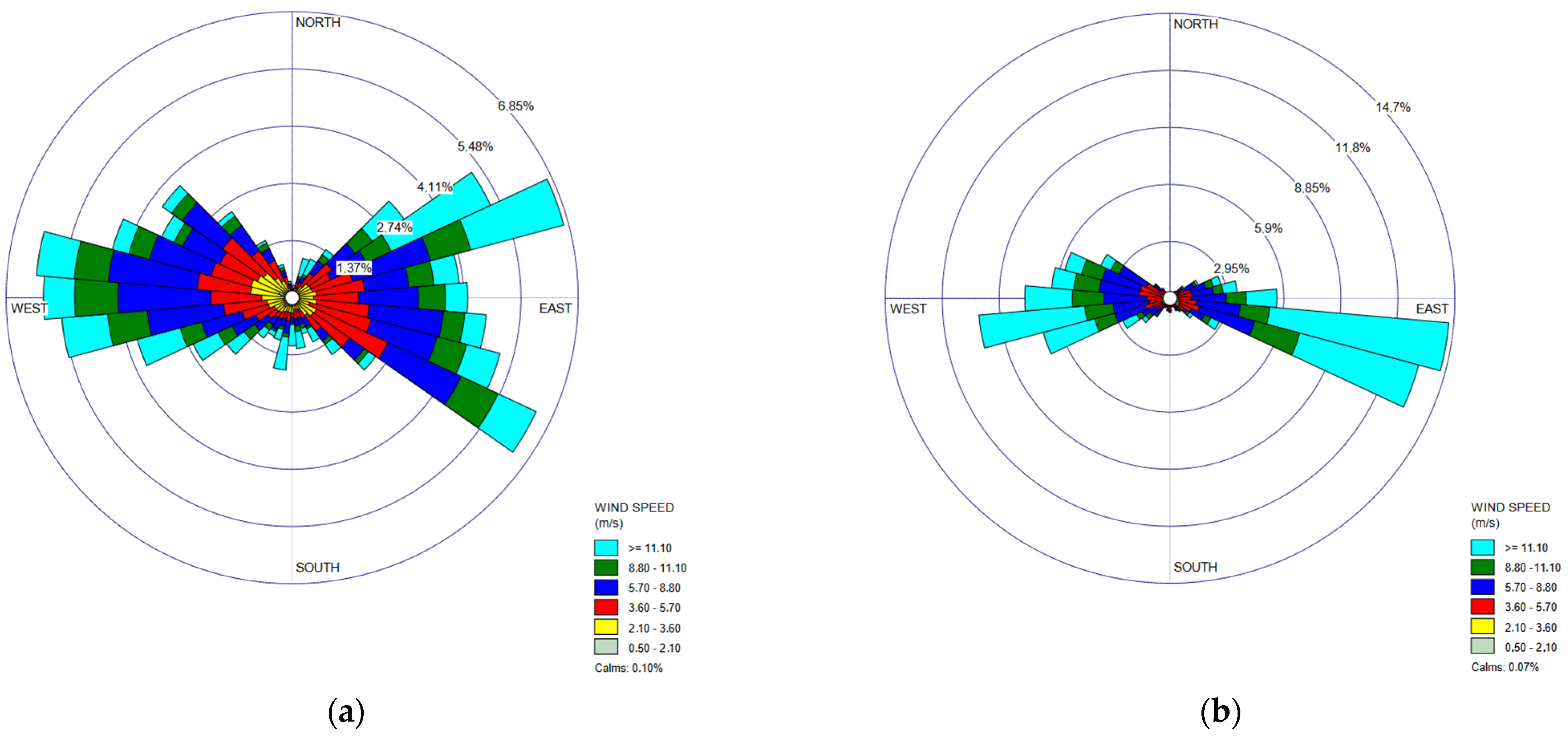
2.5. Wind Rose
2.6. Data Sample
2.7. Statistical Study
3. Results and Discussion
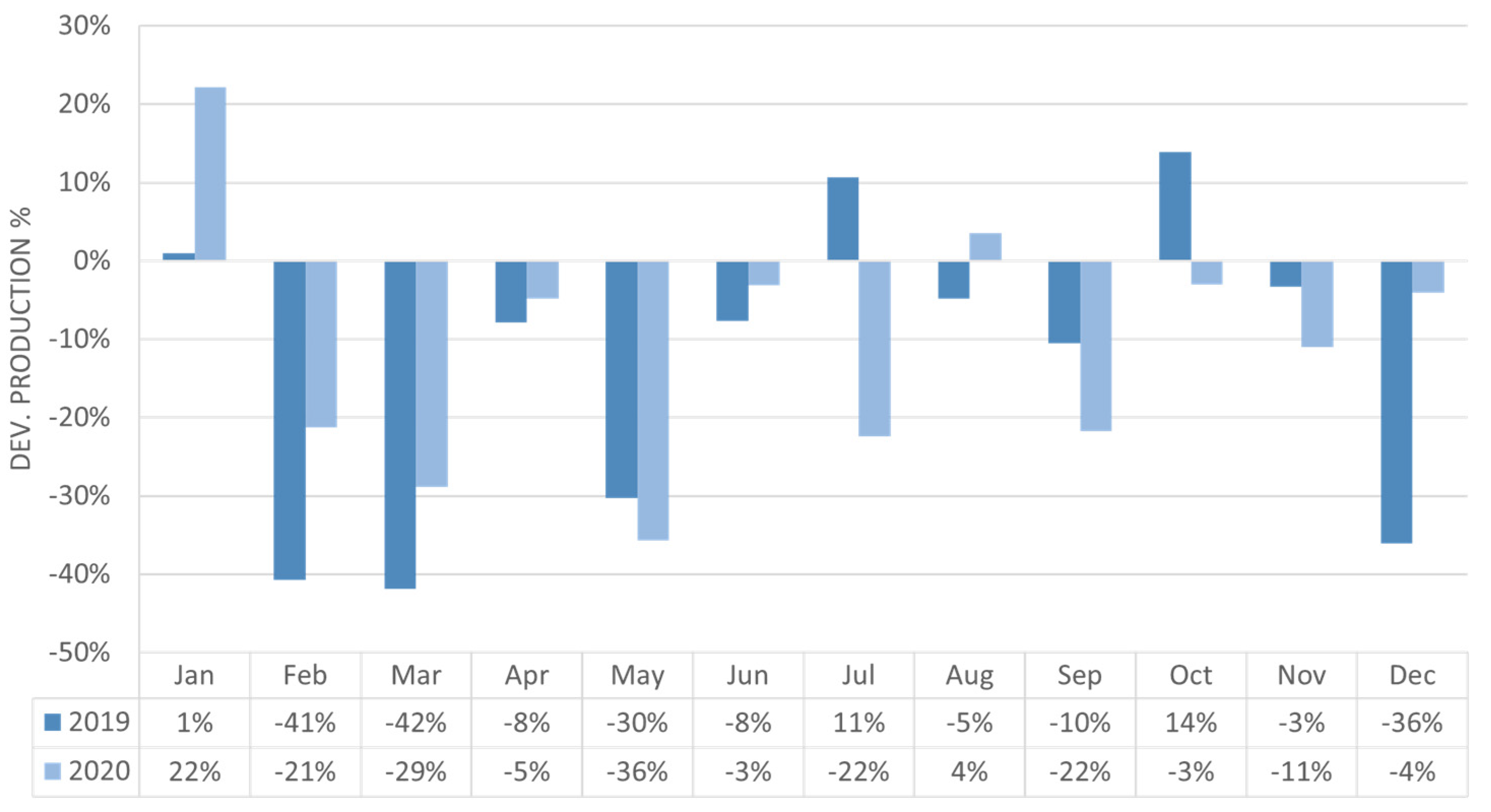
3.1. Deviation from the Theoretical Forecasted Production
- Calculation of the Weibull distribution factors (c, k).
- Determination of the energy density.
- Computation of the expected energy production.
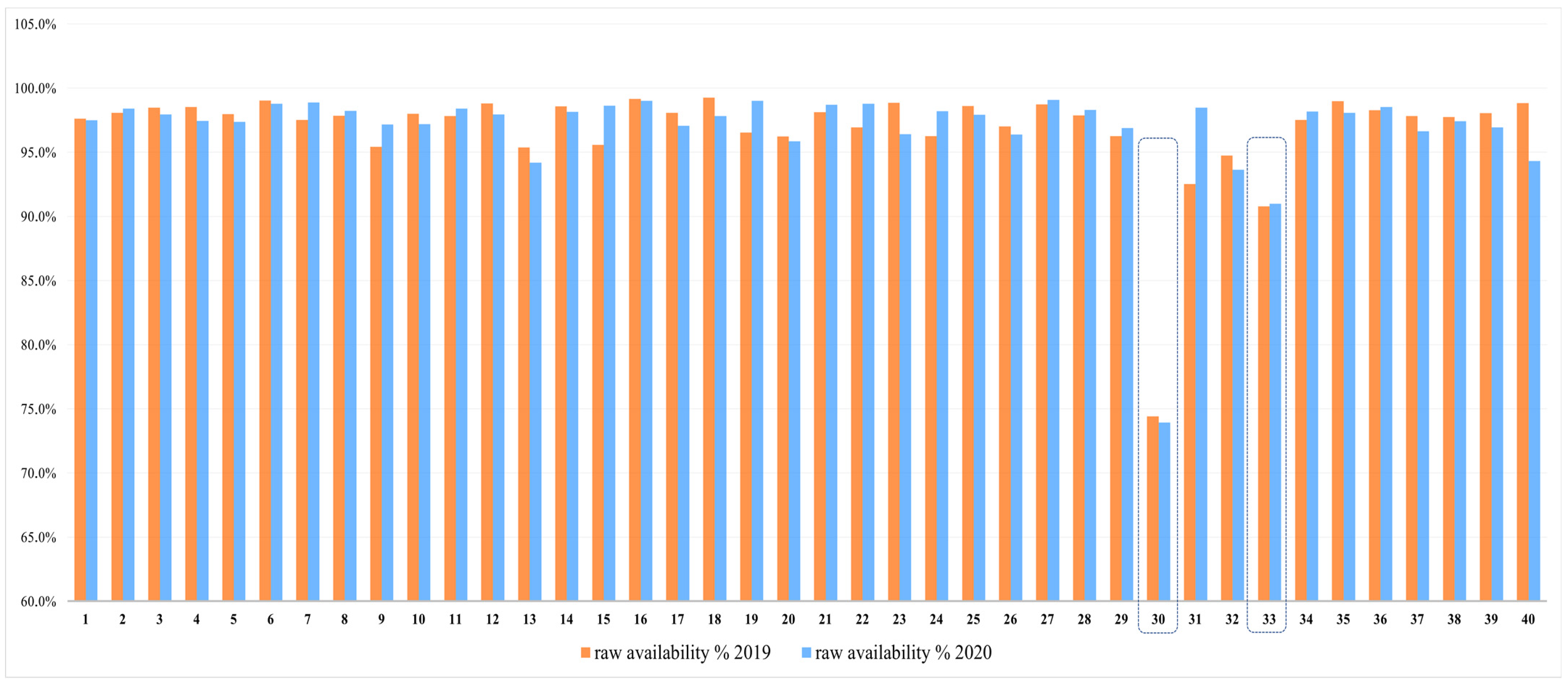
3.2. Availability Calculation Contribution
- ➢
- Wind speed sensor (anemometer);
- ➢
- Temperature sensor PT100;
- ➢
- Vibration sensor;
- ➢
- Yaw rotations counter (twist sensor).
4. Conclusions
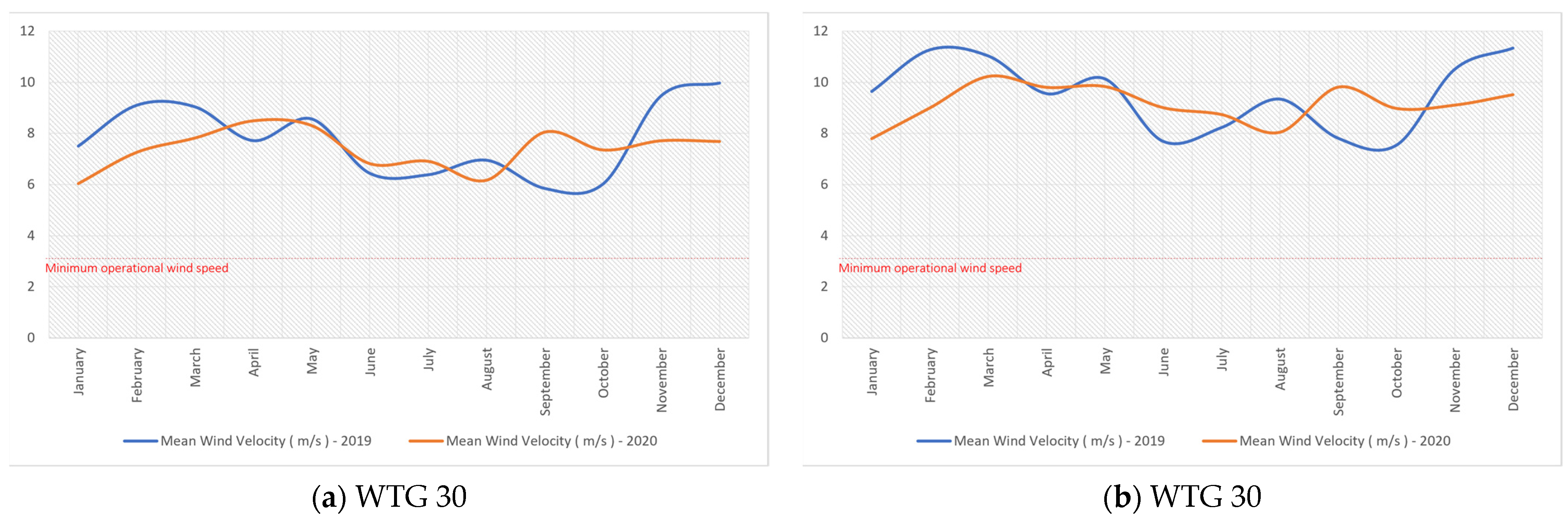
- The monthly average wind speed over a two-year period ranged from 2.1 m/s to 9.1 m/s, which is conducive to efficient wind energy production.
- Specifically, the period from October to April revealed relatively higher average wind speeds, which is of considerable importance for energy production.
- This analysis demonstrated a remarkable alignment between the Weibull distribution curves and the measured data at the production site during the 2019–2020 period, with minor divergences.
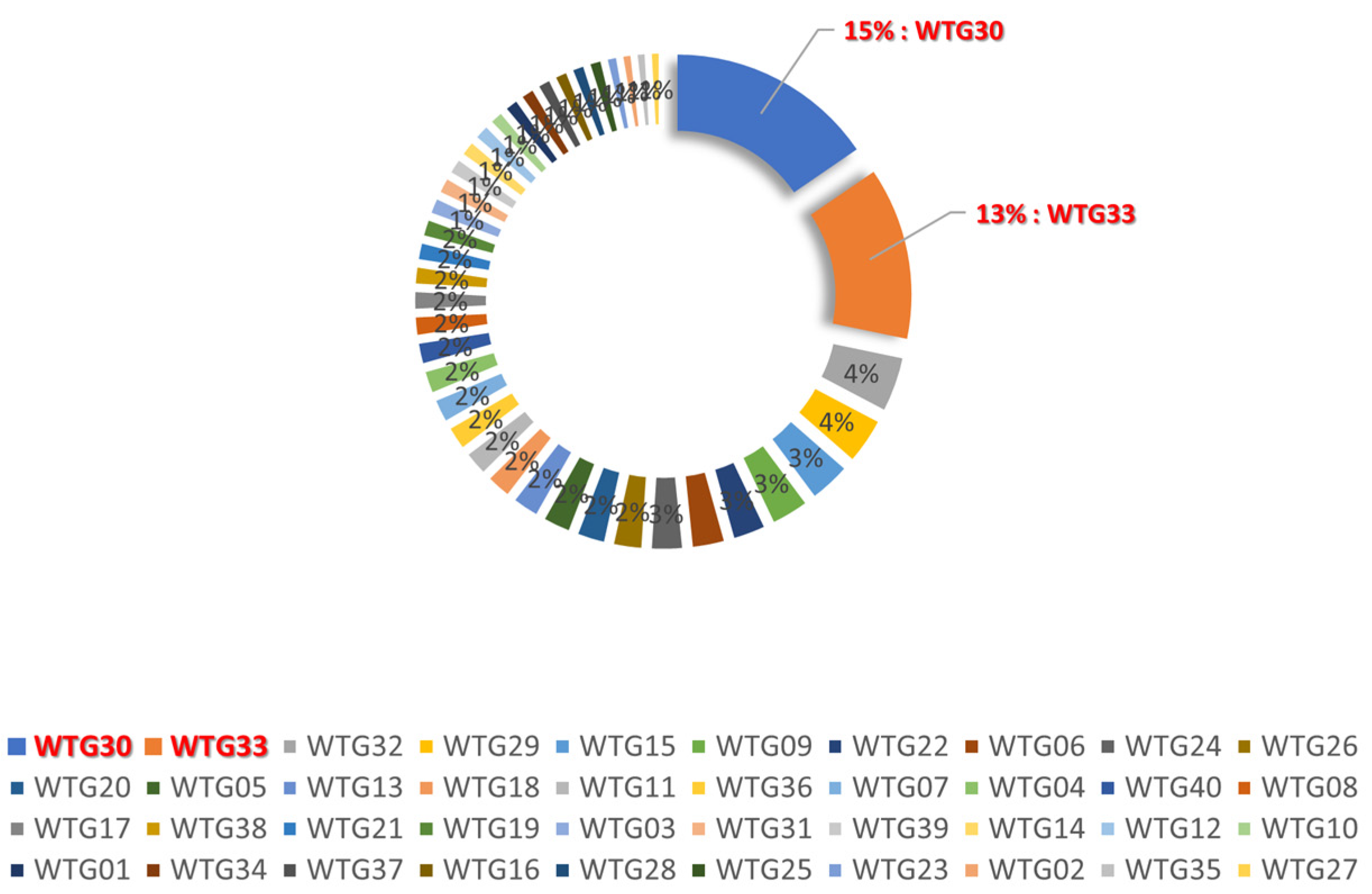
- Among the 40 wind turbines installed in the park, turbines WGT30 and WGT33 exhibited insufficient electrical energy production. This issue can be primarily attributed to orientation problems in the “Yaw system”.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Probability density function. | |
| Weibull shape factor. | |
| Weibull scale factor in m/s. | |
| Cumulative distribution function. | |
| Wind speed in m/s. | |
| Mean wind speed in m/s. | |
| Gamma function. | |
| Most probable wind speed in m/s. | |
| Wind power density in W. | |
| Air density kg/m3. | |
| Actual wind power density in w. | |
| Standard deviation. |
References
- El Mourabit, Y.; Derouich, A.; Allouhi, A.; El Ghzizal, A.; El Ouanjli, N.; Zamzoumyes, O. Sustainable production of wind energy in the main Morocco’s sites using permanent magnet synchronous generators. Int. Trans. Electr. Energy Syst. 2020, 30, e12390. [Google Scholar] [CrossRef]
- Dogan, E.; Seker, F. The influence of real output, renewable and non-renewable energy, trade and financial development on carbon emissions in the top renewable energy countries. Renew. Sustain. Energy Rev. 2016, 60, 1074–1085. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Youness, E.M.; Aziz, D.; Abdelaziz, E.G.; Jamal, B.; Najib, E.O.; Othmane, Z.; Khalid, M.; Bossoufi, B. Implementation and validation of backstepping control for PMSG wind turbine using dSPACE controller board. Energy Rep. 2019, 5, 807–821. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Ahmed, A.; Uddin, G.S.; Sohag, K. Biomass energy, technological progress and the environmental kuznets curve: Evidence from selected european countries. Biomass Bioenergy 2016, 90, 202–208. [Google Scholar] [CrossRef]
- Islam, M.; Mekhilef, S.; Saidur, R. Progress and recent trends of wind energy technology. Renew. Sustain. Energy Rev. 2013, 21, 456–468. [Google Scholar] [CrossRef]
- El Mourabit, Y.; Derouich, A.; El Ghzizal, A.; El Ouanjli, N.; Zamzoum, O. Nonlinear backstepping control for pmsg wind turbine used on the real wind profile of the dakhla-morocco city. Int. Trans. Electr. Energy Syst. 2020, 30, e12297. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Xia, J.; Dai, Y.; Sheng, Y.; Yue, J. Performance evaluation and accuracy enhancement of a day-ahead wind power forecasting system in china. Renew. Energy 2012, 43, 234–241. [Google Scholar] [CrossRef]
- Zamzoum, O.; El, Y.; Errouha, M.; Derouich, A.; El, A. Active and reactive power control of wind turbine based on doubly fed induction generator using adaptive sliding mode approach. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 397–406. [Google Scholar] [CrossRef]
- Dabbaghiyan, A.; Fazelpour, F.; Abnavi, M.D.; Rosen, M.A. Evaluation of wind energy potential in province of Bushehr, Iran. Renew. Sustain. Energy Rev. 2016, 55, 455–466. [Google Scholar] [CrossRef]
- Chandel, S.S.; Murthy, K.S.R.; Ramasamy, P. Wind resource assessment for decentralised power generation: Case study of a complex hilly terrain in western himalayan region. Sustain. Energy Technol. Assess. 2014, 8, 18–33. [Google Scholar] [CrossRef]
- Ayodele, T.; Ogunjuyigbe, A. Wind energy potential of vesleskarvet and the feasibility of meeting the south african’s sanae iv energy demand. Renew. Sustain. Energy Rev. 2016, 56, 226–234. [Google Scholar] [CrossRef]
- Allouhi, A.; Zamzoum, O.; Islam, M.; Saidur, R.; Kousksou, T.; Jamil, A.; Derouich, A. Evaluation of wind energy potential in morocco’s coastal regions. Renew. Sustain. Energy Rev. 2017, 72, 311–324. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Wu, J.; Geng, W. Comparison of numerical methods and metaheuristic optimization algorithms for estimating parameters for wind energy potential assessment in low wind regions. Renew. Sustain. Energy Rev. 2017, 69, 1199–1217. [Google Scholar] [CrossRef]
- Loi n° 13-09 relative aux énergies renouvelables, promulguée par Dahir n° 1-10-16 du 26 Safar 1431 (11 février 2010) publiée au Bulletin officiel n° 5822 du 1er rabii II 1431 (18 mars 2010). Available online: https://www.amee.ma/ (accessed on 22 June 2023).
- Bousla, M.; Haddi, A.; El Mourabit, Y.; Sadki, A.; Mouradi, A.; El Kharrim, A. Detection and Prevention of Repetitive Major Faults of a WTG by Analysis of Alarms Through SCADA. In Digital Technologies and Applications. ICDTA 2023. Lecture Notes in Networks and Systems; Motahhir, S., Bossoufi, B., Eds.; Springer: Cham, Switzerland, 2023; Volume 668. [Google Scholar] [CrossRef]
- Kang, S.; Khanjari, A.; You, S.; Lee, J.-H. Comparison of different statistical methods used to estimate weibull parameters for wind speed contribution in nearby an offshore site, Republic of Korea. Energy Rep. 2021, 7, 7358–7373. [Google Scholar] [CrossRef]
- Mahmood, F.H.; Resen, A.K.; Khamees, A.B. Wind characteristic analysis based on weibull distribution of al-salman site, Iraq. Energy Rep. 2020, 6, 79–87. [Google Scholar] [CrossRef]
- Justus, C.G.; Hargraves, W.R.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. (1962–1982) 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Lun, I.Y.; Lam, J.C. A study of weibull parameters using long-term wind observations. Renew. Energy 2000, 20, 145–153. [Google Scholar] [CrossRef]
- Werapun, W.; Tirawanichakul, Y.; Waewsak, A. Comparative study of five methods to estimate weibull parameters for wind speed on Phangan Island, Thailand. Energy Procedia 2015, 79, 976–981. [Google Scholar] [CrossRef]
- Chang, T.P. Estimation of wind energy potential using different probability density functions. Appl. Energy 2011, 88, 1848–1856. [Google Scholar] [CrossRef]
- Mathew, S. Wind Energy: Fundamentals, Resource Analysis and Economics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 45–88. [Google Scholar] [CrossRef]
- Garcia, A.; Torres, J.; Prieto, E.; de Francisco, A. Fitting wind speed distributions: A case study. Sol. Energy 1998, 62, 139–144. [Google Scholar] [CrossRef]
- Jaramillo, O.A.; Borja, M.A. Wind speed analysis in La Ventosa, Mexico: A bimodal probability distribution case, Renew. Energy 2004, 29, 1613–1630. [Google Scholar] [CrossRef]
- Shata, A.S.A.; Hanitsch, R. Evaluation of wind energy potential and electricity generation on the coast of Mediterranean Sea in Egypt, Renew. Energy 2006, 31, 1183–1202. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Akpinar, S. An assessment on seasonal analysis of wind energy characteristics and wind turbine characteristics. Energy Convers. Manag. 2005, 46, 1848–1867. [Google Scholar] [CrossRef]
- Al Buhari, M.H. A statistical analysis of wind speed data and an assessment of wind energy potential in Taiz-Yemen. Assiut Univ. Bull. Environ. Res. 2006, 9, 21–32. [Google Scholar]
- Egbert, B.; Rienk, V.G. Environmental Physics, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar]
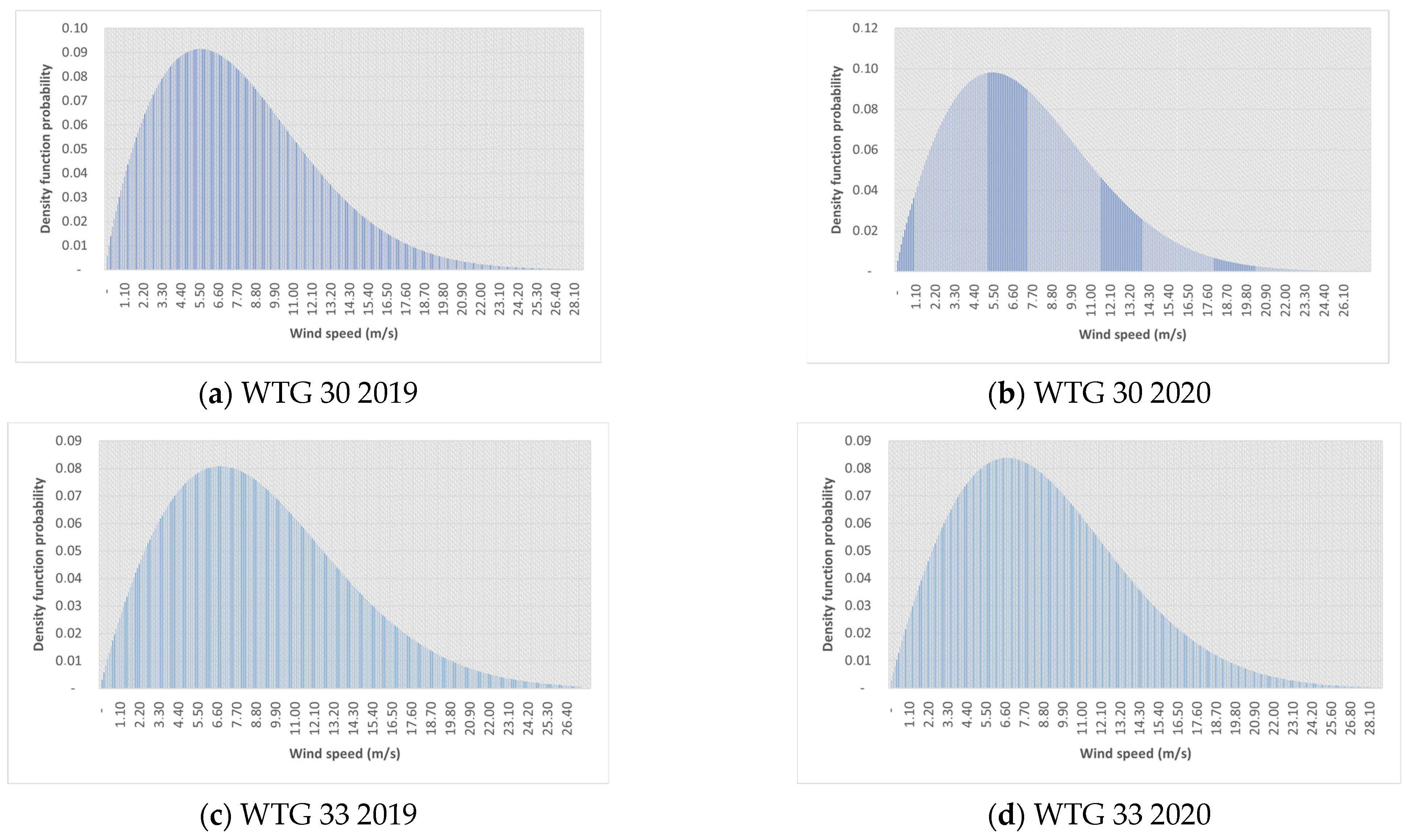
| Production | 2019 | 2020 |
|---|---|---|
| Real [Gwh] | 417.2 | 400.7 |
| Theoretical [Gwh] | 429.9 | 429.9 |
| Difference [%] | 2.97 | 6.81 |
| 2019 | 2020 | |||
|---|---|---|---|---|
| Shape Factor | Scale Factor | Shape Factor | Scale Factor | |
| January | 1.93 ± 0.024 | 8.73 ± 0.072 | 1.82 ± 0.021 | 6.86 ± 0.059 |
| February | 1.44 ± 0.019 | 10.52 ± 0.121 | 1.32 ± 0.017 | 7.51 ± 0.096 |
| March | 1.78 ± 0.022 | 11.28 ± 0.100 | 1.77 ± 0.021 | 9.39 ± 0.083 |
| April | 1.79 ± 0.022 | 9.54 ± 0.085 | 1.93 ± 0.024 | 10.60 ± 0.088 |
| May | 1.64 ± 0.019 | 10.86 ± 0.105 | 1.45 ± 0.018 | 9.89 ± 0.108 |
| June | 1.61 ± 0.019 | 7.47 ± 0.074 | 1.64 ± 0.019 | 8.12 ± 0.080 |
| July | 1.86 ± 0.021 | 7.53 ± 0.065 | 1.31 ± 0.016 | 8.80 ± 0.106 |
| August | 1.55 ± 0.018 | 8.45 ± 0.086 | 1.58 ± 0.018 | 7.61 ± 0.076 |
| September | 1.32 ± 0.016 | 6.47 ± 0.080 | 1.78 ± 0.023 | 10.89 ± 0.101 |
| October | 1.63 ± 0.019 | 6.96 ± 0.069 | 1.78 ± 0.001 | 9.00 ± 0.003 |
| November | 2.77 ± 0.032 | 10.79 ± 0.063 | 1.67 ± 0.022 | 9.30 ± 0.089 |
| December | 1.94 ± 0.023 | 11.72 ± 0.095 | 1.88 ± 0.023 | 8.83 ± 0.074 |
| Time | Shape Factor k | Scale Factor c | Mean Velocity | Velocity Frequency [m/s] | Energetic Velocity [m/s] | Capacity [W/m2] | Power [W] | Energy [GWh] | Variance |
|---|---|---|---|---|---|---|---|---|---|
| January 2019 | 1.93 | 8.73 | 7.74 | 5.99 | 12.60 | 233.25 | 1,483,137.90 | 1.10 | 17.40 |
| February 2019 | 1.44 | 10.52 | 9.55 | 4.65 | 19.22 | 637.99 | 4,056,637.29 | 2.73 | 45.13 |
| March 2019 | 1.78 | 11.28 | 10.04 | 7.11 | 17.20 | 556.29 | 3,537,138.36 | 2.63 | 33.88 |
| April 2019 | 1.79 | 9.54 | 8.48 | 6.06 | 14.48 | 333.36 | 2,119,669.27 | 1.53 | 23.92 |
| May 2019 | 1.64 | 10.86 | 9.71 | 6.14 | 17.62 | 557.49 | 3,544,802.003 | 2.64 | 36.76 |
| June 2019 | 1.61 | 7.47 | 6.69 | 4.11 | 12.30 | 186.39 | 1,185,160.04 | 0.85 | 18.01 |
| July 2019 | 1.85 | 7.53 | 6.68 | 4.956 | 11.17 | 157.09 | 998,830.28 | 0.74 | 13.99 |
| August 2019 | 1.55 | 8.45 | 7.60 | 4.32 | 14.44 | 289.65 | 1,841,709.87 | 1.37 | 25.12 |
| September 2019 | 1.32 | 6.47 | 5.97 | 2.19 | 13.07 | 181.51 | 1,154,106.11 | 0.83 | 20.95 |
| October 2019 | 1.63 | 6.96 | 6.24 | 3.87 | 11.41 | 149.65 | 951,531.06 | 0.71 | 15.46 |
| November 2019 | 2.77 | 10.79 | 9.60 | 9.18 | 13.13 | 331.64 | 2,108,722.01 | 1.52 | 14.08 |
| December 2019 | 1.94 | 11.72 | 10.39 | 8.07 | 16.88 | 561.80 | 3,572,235.05 | 2.66 | 31.12 |
| January 2020 | 1.82 | 6.86 | 6.10 | 4.42 | 10.32 | 121.89 | 775,024.75 | 0.58 | 12.06 |
| February 2020 | 1.32 | 7.51 | 6.91 | 2.59 | 15.06 | 279.23 | 1,775,492.66 | 1.24 | 27.80 |
| March 2020 | 1.77 | 9.39 | 8.35 | 5.88 | 14.37 | 322.93 | 2,053,351.85 | 1.53 | 23.72 |
| April 2020 | 1.93 | 10.60 | 9.40 | 7.27 | 15.30 | 417.05 | 2,651,825.60 | 1.91 | 25.63 |
| May 2020 | 1.45 | 9.89 | 8.97 | 4.40 | 18.01 | 526.56 | 3,348,108.20 | 2.49 | 39.60 |
| June 2020 | 1.64 | 8.12 | 7.26 | 4.56 | 13.22 | 234.19 | 1,489,104.60 | 1.07 | 20.71 |
| July 2020 | 1.31 | 8.80 | 8.11 | 2.97 | 17.78 | 456.09 | 2,900,043.38 | 2.16 | 38.73 |
| August 2020 | 1.58 | 7.61 | 6.84 | 4.04 | 12.77 | 204.74 | 1,301,849.87 | 0.97 | 19.56 |
| September 2020 | 1.78 | 10.89 | 9.69 | 6.84 | 16.65 | 502.73 | 3,196,609.82 | 2.30 | 31.77 |
| October 2020 | 1.78 | 9.00 | 8.01 | 5.68 | 13.72 | 282.06 | 1,793,498.07 | 1.33 | 21.53 |
| November 2020 | 1.67 | 9.30 | 8.31 | 5.39 | 14.90 | 342.11 | 2,175,310.18 | 1.57 | 26.14 |
| December 2020 | 1.88 | 8.83 | 7.84 | 5.91 | 12.97 | 249.04 | 1,583,504.52 | 1.18 | 18.70 |
| Production | 2019 | 2020 |
|---|---|---|
| Real [Gwh] | 417.2 | 400.7 |
| Theoretical [Gwh] | 487.7 | 417.7 |
| Difference [%] | 14.47 | 4.06 |
| 2019 | 2020 | |||||
|---|---|---|---|---|---|---|
| WTG | Wind Conditions OK [4–25 m/s] Hours Number | True Prod > 0 | Raw Availability % | Wind Conditions OK [4–25 m/s] Hours Number | True Prod > 0 | Raw Availability % |
| T1 | 39,937 | 38,987 | 97.62% | 38,334 | 37,375 | 97.50% |
| T2 | 38,325 | 37,582 | 98.06% | 37,000 | 36,413 | 98.41% |
| T3 | 39,591 | 38,991 | 98.48% | 38,876 | 38,077 | 97.94% |
| T4 | 40,239 | 39,642 | 98.52% | 39,549 | 38,537 | 97.44% |
| T5 | 40,837 | 40,009 | 97.97% | 40,114 | 39,055 | 97.36% |
| T6 | 42,058 | 41,654 | 99.04% | 41,797 | 41,290 | 98.79% |
| T7 | 43,025 | 41,958 | 97.52% | 42,334 | 41,859 | 98.88% |
| T8 | 42,898 | 41,973 | 97.84% | 41,156 | 40,422 | 98.22% |
| T9 | 43,463 | 41,477 | 95.43% | 42,421 | 41,216 | 97.16% |
| T10 | 44,398 | 43,507 | 97.99% | 43,392 | 42,178 | 97.20% |
| T11 | 43,179 | 42,242 | 97.83% | 41,600 | 40,938 | 98.39% |
| T12 | 38,333 | 37,875 | 98.81% | 38,772 | 37,978 | 97.95% |
| T13 | 42,293 | 40,336 | 95.37% | 41,853 | 39,418 | 94.18% |
| T14 | 40,455 | 39,876 | 98.57% | 40,816 | 40,060 | 98.15% |
| T15 | 45,087 | 43,090 | 95.57% | 44,785 | 44,174 | 98.64% |
| T16 | 40,146 | 39,811 | 99.17% | 40,439 | 40,037 | 99.01% |
| T17 | 40,062 | 39,288 | 98.07% | 40,296 | 39,111 | 97.06% |
| T18 | 40,248 | 39,945 | 99.25% | 40,531 | 39,649 | 97.82% |
| T19 | 39,924 | 38,545 | 96.55% | 39,843 | 39,443 | 99.00% |
| T20 | 40,569 | 39,038 | 96.23% | 40,513 | 38,837 | 95.86% |
| T21 | 45,205 | 44,358 | 98.13% | 44,006 | 43,434 | 98.70% |
| T22 | 44,713 | 43,349 | 96.95% | 43,461 | 42,933 | 98.79% |
| T23 | 44,554 | 44,041 | 98.85% | 43,155 | 41,606 | 96.41% |
| T24 | 43,194 | 41,574 | 96.25% | 43,083 | 42,305 | 98.19% |
| T25 | 45,375 | 44,737 | 98.59% | 45,022 | 44,083 | 97.91% |
| T26 | 44,855 | 43,514 | 97.01% | 44,477 | 42,873 | 96.39% |
| T27 | 42,002 | 41,463 | 98.72% | 41,322 | 40,941 | 99.08% |
| T28 | 44,118 | 43,180 | 97.87% | 43,463 | 42,724 | 98.30% |
| T29 | 44,652 | 42,978 | 96.25% | 42,950 | 41,609 | 96.88% |
| T30 | 40,879 | 30,422 | 74.42% | 41,259 | 30,505 | 73.94% |
| T31 | 45,370 | 41,977 | 92.52% | 44,906 | 44,220 | 98.47% |
| T32 | 45,715 | 43,312 | 94.74% | 44,868 | 42,008 | 93.63% |
| T33 | 44,503 | 40,399 | 90.78% | 44,326 | 40,332 | 90.99% |
| T34 | 44,577 | 43,474 | 97.53% | 45,487 | 44,662 | 98.19% |
| T35 | 44,604 | 44,148 | 98.98% | 45,103 | 44,239 | 98.08% |
| T36 | 45,498 | 44,713 | 98.27% | 44,441 | 43,787 | 98.53% |
| T37 | 45,138 | 44,153 | 97.82% | 44,428 | 42,933 | 96.64% |
| T38 | 43,706 | 42,720 | 97.74% | 42,926 | 41,814 | 97.41% |
| T39 | 44,157 | 43,298 | 98.05% | 42,821 | 41,506 | 96.93% |
| T40 | 44,420 | 43,905 | 98.84% | 24,751 | 23,342 | 94.31% |
| Availability % | 96.8% |
| Unavailability % | 3.2% |
| Production | 2019 | 2020 |
|---|---|---|
| Real [Gwh] | 417.2 | 400.7 |
| Theoretical [Gwh] | 487.7 | 417.7 |
| Initial difference [%] | 14.5% | 4.1% |
| Unavailability % | 3.20% | |
| Corrected difference [%] | 11.26% | 4.07% |
| 2019 | 2020 | |
|---|---|---|
| R2 | 0.92 | 0.94 |
| χ2 | 0.91 | 0.99 |
| RMSE | 0.032 | 0.019 |
| Sub-Component | Issue | Recommendations |
|---|---|---|
| Anemometer |
|
|
| Temperature sensor PT 100 |
|
|
| Vibrations sensors |
|
|
| Yaw rotations counter |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bousla, M.; Haddi, A.; El Mourabit, Y.; Sadki, A.; Mouradi, A.; El Kharrim, A.; Mobayen, S.; Zhilenkov, A.; Bossoufi, B. Analysis and Comparison of Wind Potential by Estimating the Weibull Distribution Function: Application to Wind Farm in the Northern of Morocco. Sustainability 2023, 15, 15087. https://doi.org/10.3390/su152015087
Bousla M, Haddi A, El Mourabit Y, Sadki A, Mouradi A, El Kharrim A, Mobayen S, Zhilenkov A, Bossoufi B. Analysis and Comparison of Wind Potential by Estimating the Weibull Distribution Function: Application to Wind Farm in the Northern of Morocco. Sustainability. 2023; 15(20):15087. https://doi.org/10.3390/su152015087
Chicago/Turabian StyleBousla, Mohamed, Ali Haddi, Youness El Mourabit, Ahmed Sadki, Abderrahman Mouradi, Abderrahman El Kharrim, Saleh Mobayen, Anton Zhilenkov, and Badre Bossoufi. 2023. "Analysis and Comparison of Wind Potential by Estimating the Weibull Distribution Function: Application to Wind Farm in the Northern of Morocco" Sustainability 15, no. 20: 15087. https://doi.org/10.3390/su152015087
APA StyleBousla, M., Haddi, A., El Mourabit, Y., Sadki, A., Mouradi, A., El Kharrim, A., Mobayen, S., Zhilenkov, A., & Bossoufi, B. (2023). Analysis and Comparison of Wind Potential by Estimating the Weibull Distribution Function: Application to Wind Farm in the Northern of Morocco. Sustainability, 15(20), 15087. https://doi.org/10.3390/su152015087












