Forecasting the Tourist Arrival Volumes and Tourism Income with Combined ANN Architecture in the Post COVID-19 Period: The Case of Turkey

Abstract

Accurate forecasting of tourism demand and income holds paramount importance for both the tourism industry and the national economy. This study aims to address several objectives: (1) specify the best forecasting model in the prediction of tourist arrival volumes and tourism income for Turkey; (2) assess the degree of impact exerted by various determinants on the tourism forecasts; (3) generate forecasts for tourist arrival volumes and tourism income using the most suitable models; and (4) examine potential scenarios illustrating the ramifications of the Russia-Ukraine war on tourist arrival volumes and tourism income. The forecasting models employed in this study encompass a comprehensive set of statistical methods, including ETS, ARIMA, TRAMO-SEATS, X13, X11, STL, Grey, and their combinations with ANN. In the ANN models, exogenous variables such as the global financial crisis, the Turkey-Russia warplane crash crisis, the COVID-19 pandemic, and USD/TRY exchange rates are incorporated. The results unveil the identification of five superior models: ETS, Grey, hybrid ETS-ANN, hybrid Grey-ANN, and hybrid ARIMA-ANN models, which exhibit the lowest MAPE and sMAPE values. Forecasts for the forthcoming quarters are examined under two scenarios: assuming the continuity or cessation of the Russia-Ukraine war. Comparative analysis of the relative effects of exogenous variables indicates that COVID-19 has the most substantial impact on tourist arrival volumes, and tourism income is primarily influenced by the USD/TRY exchange rate.

1. Introduction

The tourism industry, characterized by its rapid and sustained growth, has progressively gained significance within global economies. The influx of international visitors has witnessed a remarkable escalation, transitioning from a mere 25.2 million in 1950 to 439 million in 1990, ultimately surging to an astonishing 1.4 billion in 2019 [1]. This exponential rise in foreign tourist arrivals bears substantial implications for economic landscapes, elevating the prominence of tourism as a pivotal contributor to national and international prosperity. Meeting the needs of these tourists requires not only expanding infrastructure, such as airports, transportation systems, and communication networks, but also establishing new businesses in tourism regions, including shopping centers, pharmacies, and car rental services. The consequential impact of these developments extends across various sectors, triggering a multiplier effect on economies and employment rates [2]. The World Travel and Tourism Council’s report highlights that prior to the COVID-19 pandemic, the tourism sector accounted for a substantial 10.4% of global GDP and constituted 10.6% of total employment [3]. However, the pandemic inflicted severe setbacks on the sector, resulting in an estimated loss of USD 4.5 trillion and a staggering 62 million job losses [4]. It is worth noting that incidents such as wars, policy issues, financial crises, and natural disasters exert significant influences on the tourism sector.

Against this backdrop, accurate and comprehensive forecasting of tourism demand assumes paramount importance in guiding countries’ strategic planning and decision-making processes [5,6]. Accurate forecasts facilitate decision-making for tourism and hospitality businesses, resource management, marketing and pricing strategies, and infrastructure development, among other critical areas [7,8,9,10]. For businesses, precise forecasting helps to mitigate unnecessary costs, such as unsold event tickets and unconsumed food, while aiding in resource allocation by analyzing priorities and potential risks [11,12]. Governments, on the other hand, can leverage forecasts to inform policies and precautions aimed at enhancing the tourism sector and optimizing income. Disregarding the significance of forecasting may lead to redundant investments, resource waste, and ineffective policy management.

While these statements are globally applicable, in the context of our study and our focus on Turkey, forecasts related to the tourism sector hold a particular significance, depending on its position in world tourism. Despite Turkey being one of the nations with sizable international shares, according to data from the World Trade Organization, there is little study in the literature explicitly focused on projecting tourist demand studies for Turkey [13]. It has been evaluated that increasing forecasting analysis is crucial for reducing resource wastage and adopting more effective policies in Turkey.

Nonetheless, forecasting tourism data accurately and reliably poses considerable challenges due to the intricate interplay of multiple factors that influence tourism demand and income. These factors encompass a wide range of economic factors such as conflicts and wars between nations [14,15,16], and global factors exemplified by the profound impact of the COVID-19 pandemic [17,18,19].

1.1. Tourism Demand Forecasting in the World

Accurate tourism demand and income forecasts are critical for both the industry and the national economy. Since tourism forecasts are affected by several factors, especially the uncertainty of market conditions, the methods are diversified among studies. Hence, there is no unique forecasting method because of differences among countries, locations, and time intervals.

In the literature, while some studies use univariate time-series models [20,21,22] and econometric approaches [22,23,24], others use artificial intelligence-based models [25,26,27] and other methods.

Among the studies employing time-series methods, Chen et al. [28] analyze the forecasting of inbound tourism demand in Hong Kong using a multi-series structural time-series model and highlight its superior accuracy compared to ARIMA and exponential smoothing (ES) methods. Apergis et al. [29] examine the performance of four alternative univariate seasonal time-series forecasting models using data from 20 Croatian countries and conclude that the SARIMA model with Fourier transformation yields better results than the SARIMA, AR, and fractionally integrated ARMA models. Chu [20] assesses the reliability of forecasting by considering nine tourist destinations in the Asia-Pacific region, finding that the performance of the ARMA-based models utilized in the study is satisfactory.

Unlike univariate time-series models, econometric methods offer the advantage of comprehending the causal relationship between the dependent variable and explanatory variables [7]. Huang and Hao [30] present a novel two-step procedure involving a double-boosting algorithm and a support vector regression-based deep belief network (DBN) approach for tourism demand forecasting. The study demonstrates that this method significantly outperforms other models. Grey prediction models are used in some studies to characterize unknown systems with limited samples. Li et al. [31] examine international tourism demand using a linear almost ideal demand system (LAIDS) and conclude that the dynamic error correction LAIDS model provides better results than its static counterpart. De Mello and Fortuna [24] focus on the dynamic almost ideal demand system (DAIDS) for modeling tourism demand and highlight the advantageous and robust results of the dynamic model compared to static AIDS and other restricted models in terms of reconciling data and theory.

In recent years, the advancement of information technology has led to an increased use of artificial = intelligence-based models in tourism forecasting studies. Claveria et al. [32] compare the performance of a multi-layer perceptron, a radial basis function, and an Elman network as artificial neural network techniques for tourist demand forecasting and find that the multi-layer perceptron and radial basis function models yield better results than the Elman network. Artificial-intelligence-based models receive more attention due to their ability to explain non-linear relationships and patterns among time series [33]. Nguyen et al. [34] examine the tourism demand forecasting of Vietnam using an artificial neural network (ANN) and suggest that policymakers can implement this method for its accurate forecasting. Pai and Hong [25] assert that an improved neural network model for forecasting arrivals outperforms the ARIMA approaches.

Furthermore, some studies incorporate neural networks with adaptive neuro-fuzzy inference systems to overcome a large number of input variables for multivariate forecasting [35], while others prefer using ensemble deep-learning approaches to address challenges such as the curse of dimensionality and high model complexity [36]. He et al. [37] propose a new multiscale mode learning-based model for forecasting tourist arrivals by introducing mode decomposition models and the convolutional neural network model. Salamanis et al. [38] analyze tourism demand forecasting using the long short-term memory network, which allows for the incorporation of data from exogenous variables. As partly similar to our study, the forecasting tourism demand study of Lin et al. [39] uses ARIMA, ANN, and multivariate adaptive regression splines (MARS) modelling approaches. The findings obtained indicate the outperformance of ARIMA. Zhang et al. [40] focus the issue by using seasonal and trend decomposition using a loess and duo attention deep learning model (STL-DADLM). They assert that the results of the proposed method are effective in terms of increasing accuracy for forecasting. Hassani et al. [41] analyze the results of singular spectrum analysis (SSA), ARIMA, exponential smoothing (ETS), and neural networks (NN), and the performance comparison shows the higher performance of SSA among other models. With the aim of obtaining a better performance, Cuhadar [42] compares exponential smoothing, Box–Jenkins, and an ANN model for Turkey’s tourism revenues forecasting and concludes that the ANN model outperforms the other models.

Apart from these methods, the grey model, particularly GM(1,1), is one of the most commonly used approaches for tourism demand forecasting. However, GM(1,1) faces stability issues in certain cases, despite its advantage of handling uncertain systems with limited samples and poor information. To address this, various optimization methods have been proposed, such as background value optimization [43,44,45], parameter optimization [46,47], accumulated generating operator optimization [48,49], and initial condition optimization [50,51,52]. Some studies adopt hybrid approaches that combine multiple methods to achieve more accurate results [53]. Ma [54] analyzes tourism demand forecasting using the grey model and BP neural network theory, while Hu [55] combines neural network-based interval grey prediction models and asserts their superiority over other interval models. Another study by Hu [56] employs fractional grey prediction models with Fourier series for tourism demand forecasting, highlighting their enhanced performance compared to other models.

1.2. Tourism Demand Forecasting in Turkey

Limited research exists in the literature focusing on tourism demand forecasting studies specifically for Turkey, despite Turkey being one of the countries with significant international shares, as per data from the World Trade Organization [13]. Among the notable studies conducted for Turkey, Soysal and Omurgonulsen [57] aimed to identify the most suitable model for tourism demand forecasting in Turkey based on the 2000–2007 period. Their comparative analysis revealed that Winter’s method outperformed moving average and exponential smoothing methods, providing better forecasting results. Onder and Hasgul [58] utilized Box–Jenkins models and artificial neural network models to forecast the number of foreign visitors between 2008 and 2010. The study suggested that while the artificial neural network model had a higher error value, it could serve as an alternative for forecasting. However, Winter’s method demonstrated a lower error value.

In another study, Cuhadar [59] focused on modeling and forecasting inbound tourism demand using data from the 1987–2012 period. The analysis employed feed-forward-back-propagation (MLP), radial basis function (RBF), and the time delay artificial neural network model (TDNN). The findings indicated that MLP yielded the most accurate results for demand forecasting. Karahan [60] evaluated the performance of artificial neural network methods by considering six independent variables and the 2010–2013 period. The results supported the higher predictability of using this method in the tourism sector.

Overall, it is evident that the number of tourism demand forecasting studies specific to Turkey is limited in the literature, despite Turkey’s significant international presence in the tourism market. The existing studies highlight the effectiveness of various methods, including Winter’s method and artificial neural network models, in forecasting tourism demand for Turkey. However, there is a need for further research and exploration in this area to enhance the understanding and accuracy of tourism demand forecasting in Turkey.

1.3. Originality of this Study

This paper focuses on the tourism demand forecasting of Turkey, which is the fourth country in the world in terms of international tourist arrivals [61]. When looking at the existing literature, this paper is distinguished from other studies focused on Turkey in terms of the period examined, the determinants considered, and the methods used. This paper, covering the years between 2010 and 2021, tries to make a forecast for tourism demand under the unexpected COVID-19 pandemic effect. In addition to this, the impact of the exchange rate, the global financial crisis (GFC), the Turkey-Russia warplane crash crisis, and the Russia-Ukraine war are also analyzed for tourism demand forecasting.

The methodologies employed also set this study significantly apart from others. The present study uses parametric (including TRAMO-SEATS, exponential smoothing-based models (ETS), and ARIMA), semi-parametric (including X-13 ARIMA-SEATS), and non-parametric statistical methods (including X11, STL decomposition), and the grey model, a relatively new statistical approach in forecasting. With the aim of improving the accuracy of the above-mentioned methods, non-linear artificial neural networks (ANN) based on multilayer perceptrons (MLP) are applied to tourism data as well.

The methods chosen are TRAMO-SEATS [62,63,64], ETS [28,65,66], ARIMA [67,68,69], X-13 ARIMA SEATS [70], X11, STL decomposition, the grey model [54,55,71], ANN [42,72], and MLP [73,74], which are widely used forecasting methods in the literature. Each of the aforementioned techniques is initially applied simply to the study of tourist data, and then it is integrated with the ANN technique to incorporate the exogenous factors listed below: the global financial crisis, Turkey-Russia warplane crash crisis, the COVID-19 pandemic, and USD/TRY exchange rates.

The objectives of this study are to: (1) specify the best forecasting model for the prediction of tourist arrival volumes and tourism income in Turkey; (2) investigate the degree of the impacts of several determinants on the tourism forecasts; (3) forecast the arrival volumes of tourists and tourism income by using the most appropriate models; and (4) discuss alternative scenarios of the potential impacts of the Russia-Ukraine war on the tourist arrival volumes and tourism income.

Accordingly, the applied forecasting approach is expected to contribute to the existing tourism demand forecasting literature by including unexpected variables (i.e., crises) that may negatively affect the forecast values.

The remainder of this paper is organized as follows: Section 2 presents the methods used for analysis. Section 3 interprets the research workflow of this study and the model construction. The results of analyses of tourist arrival volume and tourism income data are discussed in Section 4. Finally, conclusions and future recommendations are summarized in the last section.

2. Methodology

This study compares alternative statistical models and their combinations with the ANN approach for tourism demand forecasting under the effects of several country-specific and global determinants, with the aim of reaching the best forecasting model. The forecasting models constructed in this study are based on the following statistical models: ETS, ARIMA, TRAMO-SEATS, X13 (ARIMA SEATS), X11, STL, and the grey model.

A common denominator among these statistical forecasting methods is the use of past data in the analyses. After analyzing tourist arrival volumes and tourism income data with these methods, non-linear ANN is implemented to integrate the statistical methods with the preselected determinants, aiming to capture the variances in the data due to exogenous variables and hence improve the accuracy of the forecasts.

2.1. Exponential Smoothing Model (ETS)

The parametric exponential time series, or exponential smoothing model, developed by Brown in 1956 [75], contains a group of methods in which forecasts are expressed by weighted combinations of past observations. The basic model can be formulated by generalizing an exponentially weighted moving average as follows:

S_t+1 = αY_t + (1 − α) S_t−1,

(1)

where S_t+1 represents the smoothed level of the series at time t + 1, Y_t is the actual value of the time series at time t, and α is smoothing constant. Then, the method was improved by Holt in 1957 [76] and Winters [77], by adding trend and seasonality components.

2.2. Autoregressive Integrated Moving Averages Model (ARIMA)

The ARIMA model, which was developed by Box and Jenkins [78], helps to analyze a given time series by using its own past values; hence, it can be used to estimate future values. This parametric model is a combination of AR and MA and can be formulated as follows:

Φ_p(B)(1 − B)^dY_t = θ_q(B)ε_t

(2)

where Φ_p is the autoregressive parameter to be estimated, d is the order of differencing, B is the Box–Jenkins backshift operator, Y_t is a time series, θ_q is the moving average parameter, and ε_t is a series of unknown random errors that are assumed to follow a normal distribution.

2.3. TRAMO-SEATS

The TRAMO-SEATS (time-series regression with ARIMA noise missing observations and outliers–signal extraction in ARIMA time series) model, which was developed by Gomez and Maravall [79], is used to estimate and forecast regression models that have non-stationary ARIMA errors and any sequence of missing values. It fits a seasonal ARIMA model (p,d,q)(P,D,Q)s to Y_t which is a monthly or quarterly series. This parametric model, in which s represents the integer of the series, can be formulated as follows:

Φ(B)δ(B)Y_t = θ(B) ε_t

(3)

δ(B) = (1 − B)^d(1 − B^s)^D

(4)

Φ(B) = (1 + Φ₁B + … + Φ_PB^p)(1 + ф₁B^s + … + ф_pB^Ps)

(5)

θ(B) = (1 + θ₁B + … + θ_qB^q)(1 + Θ₁B^s + … + Θ_QB^Qs)

(6)

2.4. X-13 ARIMA-SEATS

The X-13 ARIMA SEATS model combines seasonal adjustment functions with TRAMO-SEATS. It enables modeling extensive time series and selecting the model for linear regression models with ARIMA errors using regARIMA models. It provides an advantage by detecting outliers automatically and analyzing regression after defining the outlining regression variables. By using the notation X13 ARIMA–SEATS model, an ARIMA model for seasonal time series can be formulated as follows:

Φ(B) ф(B^s) (1 − B)^d(1 − B^s)^D Y_t = θ(B) Θ(B^s) ε_t

(7)

2.5. X11

The nonparametric X11 model, proposed by Shiskin et al. [80], is used for a seasonally adjusted series. This model has an advantage in terms of making comparisons among consecutive months or quarters by eliminating the seasonal component from an economic series and deleting working-day effects. This seasonally adjusted series provides more information about trends than the unadjusted series.

2.6. Seasonal and Trend (STL) Decomposition Using Loess

The STL decomposition model, which was introduced by Cleveland et al. [81], is a deterministic nonparametric model that allows decomposing time series. This model analyzes the behavior of the trend by using locally weighted linear regression (LOESS) and finds the seasonal component by choosing one model among many models. While updating the trend and seasonal components, this model detrends, smooths the subseries of data, filters the smoothed seasonality, detrends the smoothed cycle-subseries, deseasonalizes, and smooths the deseasonalized series, respectively [82]. Differently from the SEATS and X11 models, this model is able to control any type of seasonality without being restricted to monthly or quarterly data. It has advantages in terms of controlling the smoothness of the trend cycle and the rate of change.

2.7. Grey Model

The grey model, introduced by Deng [83], enables the generation of individual point forecasts for combinations of forecasts without the data conforming to any statistical assumption. Limited numbers are sufficient to handle the behavior of uncertain systems. To understand the regularities concealed in the data sequences, this model uses one-order accumulation and treats each sample with equal weight. GM (1,1) is the most commonly used grey model to analyze the variable to be forecast. When considering an original sequence, $x^{\left(0\right)}=\left(x_1^{\left(0\right)},x_2^{\left(0\right)},\dots , x_n^{\left(0\right)}\right)$ which is composed of n data samples, a one-order sequence can be further generated from this sequence as follows:

$$x_k^{\left(1\right)}={{\displaystyle \sum }}_{j=1}^k{x}_j^{\left(0\right)} k=1, 2, \dots , n$$

(8)

Then, the model can be approximated by:

$$\frac{d{x}^{\left(1\right)}}{dt}+a{x}^{\left(1\right)}=b$$

(9)

where a represents the developing coefficient and b represents the control variable. The solution of the differential equation can be expressed as follows:

$${\widehat{x}}_k^{\left(1\right)}=\left(x_1^{\left(0\right)}-\frac{b}{a}\right)e^{-a\left(k-1\right)}+\frac{b}{a}$$

(10)

Here, a and b can be estimated by using ordinary least squares (OLS). Noting that ${\widehat{x}}_1^{\left(1\right)}={\widehat{x}}_1^{\left(0\right)}$,

$${\widehat{x}}_k^{\left(0\right)}=\left(1-e^0\right)\left(x_1^{\left(0\right)}-\frac{b}{a}\right)e^{-a\left(k-1\right)}$$

(11)

To implement the grey method, an optimized GM (1,1) is constructed after collecting data sequences. When predicted values and residuals are computed, the Fourier series is used to generate new residuals, and the functional link net (FLN) is applied. After these procedures, revised residuals are generated to create new predicted values, and performance is evaluated.

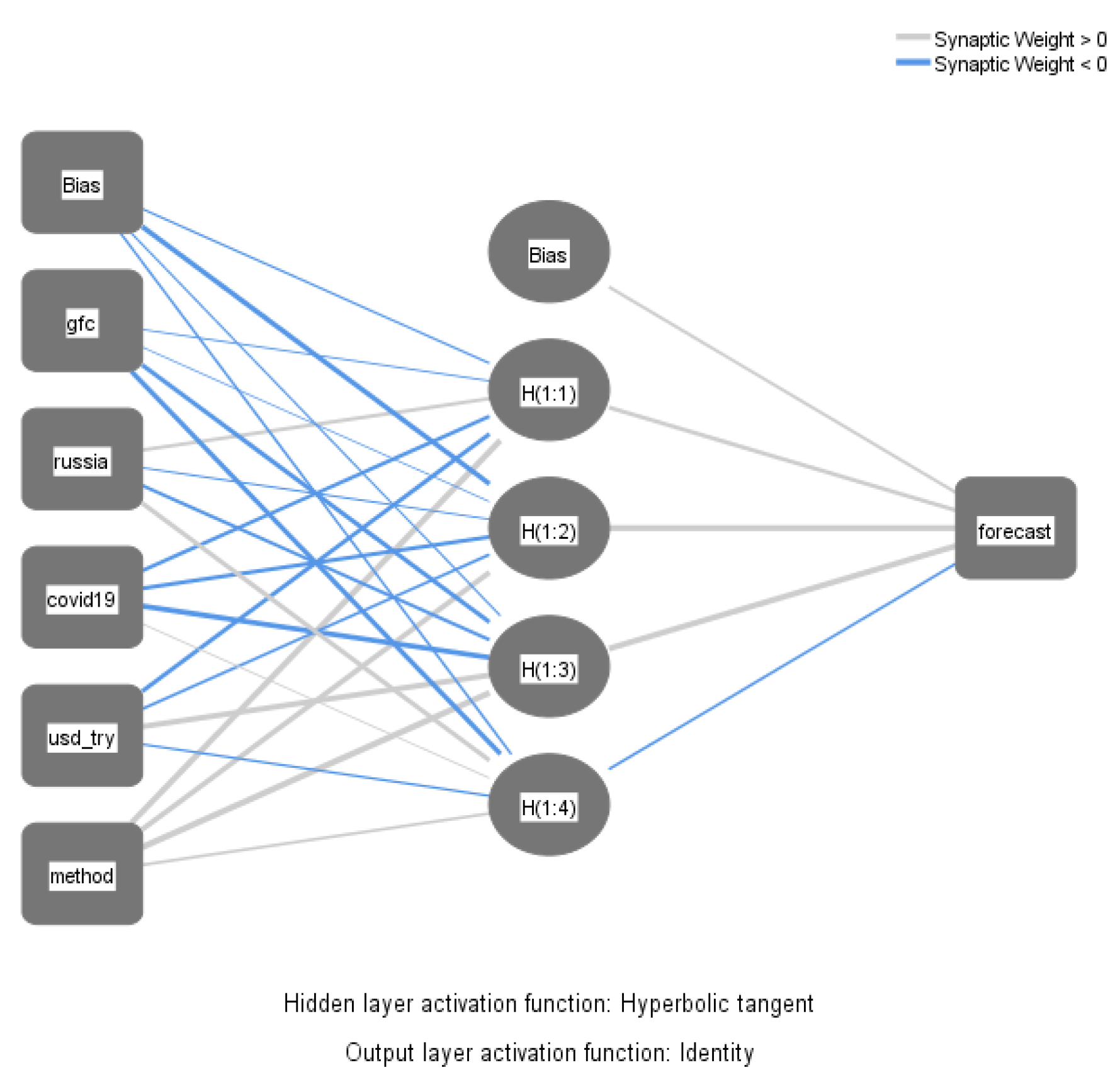
2.8. Artificial Neural Networks (ANN)

Artificial neural networks (ANN) use an interconnected group of artificial neurons. This group provides process information by benefiting from a connectionist approach. The model is useful for solving more complex problems than more traditional machine-learning techniques.

An ANN model consists of the following components: an input layer that represents the independent variables; one or more hidden layer(s) in which the data are processed; interconnections between adjacent layers; and an output layer representing the dependent variable [84]. A multi-layer perceptron (MLP) can be defined as a supplement to a feed-forward neural network. In terms of learning non-linear models and models in real-time, the MLP provides benefits. The ANN architecture is given in Figure 1.

In Figure 1, the inputs represent the independent variables, which are processed through several hidden layers. The ANN model yields future forecasts in the form of system output.

2.9. Measuring Forecast Error

MAPE is known as quite a common technique for measuring forecast errors, with the advantage of displaying errors as percentages. MAPE and sMAPE is one of the most common measurements for forecasting accuracy and hence several studies use this technique [6,9,12,27,56,74].

MAPE values are calculated as follows:

$$MAPE=\frac{{{\displaystyle \sum }}_{t=1}^n\frac{\left|A_t-F_t\right|}{A_t}\ast 100}{n}$$

(12)

where A_t and F_t represent the real and forecast values for period t, respectively [85].

sMAPE, on the other hand, eliminates MAPE’s problem of large or infinite error values and limits them to a range between 0% and 100% [86]. For the selected top-performing models, the symmetric MAPE (sMAPE) is also calculated for the robustness assessment. The formula for sMAPE is given as:

$$sMAPE=\frac{1}{n}{{\displaystyle \sum }}_{t=1}^n\frac{\left|A_t-F_t\right|}{\left(\left|A_t\right|+\left|F_t\right|\right)/2}$$

(13)

where A_t and F_t represent real and forecast values for period t, respectively [87].

3. Empirical Study

3.1. Research Workflow

The research workflow of this study for tourism demand forecasting is summarized in Figure 2.

The explanation of each step is given as follows:

• The steps begin with acquiring the quarterly inbound tourist arrival volumes and tourism income data between 2010 and 2021 and constructing alternate forecasting models for both data by using seven statistical forecasting methods, including ETS ARIMA, TRAMO-SEATS, X13 (ARIMA SEATS), X11, STL, and the grey model.
• The next step is to identify the factors that have been considered potential exogenous tourism demand forecasting determinants. These factors include (1) the global financial crisis (GFC), (2) the Russia warplane crash crisis, (3) the COVID-19 pandemic, and (4) the USD/TRY exchange rate.
• In the third step, constructing non-linear ANN models combines the effect of exogenous variables with the outcomes of each statistical model, where the forecasts for the previous quarters are derived using statistical methods and the determinants are treated as independent variables.
• The fourth step is evaluating and comparing the performance of each forecasting model based on mean absolute percentage error (MAPE) calculations. The best models offering more accurate results with lower MAPEs are determined. The symmetric MAPE (sMAPE) is also calculated for the robustness assessment of the selected top-performing models. The sensitivity analyses providing the average importance degrees of independent variables in ANN models are also carried out in the same step.
• The last step is to make tourist arrival volumes and tourism income forecasts for the future with the best alternative methods under two possible scenarios: in the case of the continuum of the war between Russia and Ukraine or in the case of no war between these two countries.

3.2. Data Collection

This study employs a quarterly time series of tourist arrivals and income generated from tourism in Turkey, which is the first country in terms of best-performing destinations in terms of receipts [88]. Data are retrieved from the Turkish Statistical Institute [89] and are publicly available (Appendix A). Tourist arrival volumes contain the departing visitors who are not using Republic passports on departure. Tourism income includes the total individual and package tour expenditures made in Turkey by foreigners and citizen visitors resident abroad without real estate expenditures, repair-maintenance expenses for residences, durables, transfers, etc.

Figure 3 and Figure 4 show the quarterly tourist arrival volumes and the quarterly tourism income in Turkey, respectively, between the years 2010 and 2021.

A decrease in 2016 due to the Russia warplane crash crisis and a sharp decline in 2020 due to the COVID-19 break can easily be recognized both in quarterly tourist arrival volumes (Figure 3) and tourism income data (Figure 4).

Correspondingly, the factors included in the models in this study are (1) the global financial crisis (GFC), (2) the Russia warplane crash crisis, (3) the COVID-19 pandemic, and (4) the USD/TRY exchange rate. Since Russia accounts for a high percentage of Turkey’s tourist arrival volumes, the political conflicts related to Russia directly affect the tourism demand in Turkey. According to the data of the Turkish Ministry of Culture and Tourism [90], the percentage of departing foreigners from Russia in 2021 was 18.9%. The effect of the GFC in 2008 is included in the model for the year 2010 from Q1 to Q4. The crisis with Russia emanating from the warplane crash has impacted tourism from 2015/Q4 to 2016/Q2. While the factor of the USD/TRY exchange rate has a continuous effect on tourism demand, the COVID-19 pandemic impact is taken from 2020/Q1 to 2021/Q4.

The effects of the global financial crisis (GFC), the Russia warplane crash crisis, the COVID-19 pandemic, and the Russia-Ukraine war are included in the ANN models as dummy variables. On the other hand, the USD/TRY exchange rate for the past years is taken directly from the Central Bank of the Republic of Turkey [91], and expectations for future quarters are obtained from the Central Bank of the Republic of Turkey [92].

3.3. Analyses Based on Statistical Methods

The first-step analyses based on traditional statistical methods are performed with the help of the EViews 12 software program, while grey model forecasts with seasonal adjustments are completed using the Microsoft Excel program.

Table 1. MAPE values of forecasts with statistical methods.

Tourist Arrival Volumes
	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
MAPE (%)	38.27	10.60	23.61	50.24	42.64	41.64	42.53
Tourism Income
	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
MAPE (%)	35.56	13.89	25.22	36.80	32.23	31.53	33.21

shows the resulting errors in forecasts with these seven methods. The MAPE measure is used as a performance indicator to assess the accuracy of the forecasts.

The method resulting in the lowest MAPE value is considered the most accurate forecasting method. According to Table 1, ETS is the best method for predicting tourist arrival volumes, with the lowest MAPE of 10.60%, followed by the grey model (23.61%) and ARIMA (38.27%). The best two methods are the same for tourism income, with the following errors: 13.89% for ETS and 25.22% for the grey model. The third-best model is found as X11 with a 31.53% error.

3.4. Analyses Based on ANN Architecture

A non-linear ANN forecasting model is composed of inputs, or independent variables, and outputs, or dependent variables. While the outputs in each ANN model are the forecasts for tourist arrival volume or tourism income, the inputs include the exogenous variables as well as the backward forecasts for the previous quarters provided by each statistical method. The architecture of ANN for tourism forecasting is summarized in Figure 5.

In Figure 5, the inputs of the ANN model can be seen on the left-hand side of the graph as the exogenous variables and the initial forecasts with the single methods. Here, the data are processed through four hidden layers and yield future forecasts as an output.

ANN analyses are performed, and the results are visualized by the non-linear ANN (MLP) module of IBM SPSS 25 software. The model is trained on 70% of the available data and tested on the remaining 30%. Training descriptors for tourist arrival volume and tourism income data are given in

Table 2. Training descriptors.

Tourist Arrival Volumes
Descriptives	Real Data	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
Mean	8,111,749	7,921,572	8,004,952	8,150,912	8,071,696	8,135,298	8,105,853	8,144,688
Maximum	14,863,339	11,116,433	14,904,902	13,533,463	10,519,820	9,663,073	9,556,936	9,603,545
Minimum	3,439,745	3,043,528	3,178,758	3,956,245	3,234,423	5,645,297	5,938,079	6,005,351
Std. Dev.	3,592,095	2,514,645	3,671,428	3,439,157	1,275,583	1,013,784	942,158	930,061
Skewness	0.5037	−0.7541	0.3299	0.3687	−1.4385	−0.7164	−0.5605	−0.5262
Kurtosis	−0.9963	−0.6472	−1.1610	−1.2191	6.1505	0.2491	−0.1668	−0.4273
Tourism Income
Descriptives	Real Data	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
Mean	5,617,131,932	5,486,351,279	5,642,751,056	5,652,588,737	5,616,023,536	5,628,893,978	5,609,851,138	5,606,373,623
Maximum	10,438,970,617	7,562,957,796	10,418,373,684	9,289,135,905	7,410,325,339	7,511,246,600	7,222,489,736	7,070,713,580
Minimum	2,404,603,191	2,712,704,756	2,487,840,636	2,876,410,689	2,647,972,488	3,617,653,600	3,773,731,883	3,722,743,337
Std. Dev.	2,293,071,000	1,425,397,283	2,408,799,994	2,108,819,185	1,038,033,689	980,644,223	963,126,662	953,328,132
Skewness	0.5275	−0.6428	0.4780	0.4246	−0.7631	−0.3551	−0.3100	−0.2920
Kurtosis	−0.7296	−0.6242	−1.0101	−0.8788	1.0102	−0.2376	−0.7003	−0.7474

.

Each ANN model makes unique non-linear connections by changing the number of hidden layers between inputs and outputs based on the “Feed-Forward-Back-Propagation (FFBP)” algorithm. For this reason, ANN analyses are repeated ten times (a ten-fold cross-validation technique; [93]) for each model.

4. Results and Discussion

The resulting MAPE scores on the average of forecasts with ANN models are interpreted in

Table 3. MAPE values of forecasts with ANN models including exogenous variables.

Tourist Arrival Volumes
ANN	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
ANN (1)	18.37	11.93	15.63	48.12	39.19	39.44	42.08
ANN (2)	19.82	12.11	15.85	49.32	44.62	42.30	45.37
ANN (3)	17.92	14.39	16.70	41.02	41.47	42.20	44.00
ANN (4)	18.94	16.45	15.47	47.79	42.27	39.40	44.50
ANN (5)	17.56	11.40	13.49	44.02	43.70	40.06	41.03
ANN (6)	20.45	10.46	18.05	42.46	44.08	42.12	43.83
ANN (7)	24.07	14.21	14.79	45.67	41.66	41.97	41.61
ANN (8)	16.52	11.35	13.63	45.34	49.37	48.13	43.95
ANN (9)	18.43	12.70	14.40	45.11	48.35	49.16	42.11
ANN (10)	26.01	15.75	17.87	51.68	44.16	42.58	41.95
Average MAPE (%)	19.81	13.07	15.59	46.05	43.89	42.74	43.04
Tourism Income
ANN	ARIMA	ETS	Grey	STL	TRAMO	X11	X13
ANN (1)	25.27	16.97	16.93	38.56	33.31	30.71	32.81
ANN (2)	23.99	16.40	19.97	32.69	31.56	32.25	38.17
ANN (3)	27.72	12.44	18.28	33.68	30.55	29.32	39.52
ANN (4)	30.09	16.12	19.00	37.14	28.58	33.77	34.19
ANN (5)	29.81	13.75	18.99	34.32	28.80	31.01	32.89
ANN (6)	25.71	11.77	18.11	38.43	31.66	33.68	33.35
ANN (7)	37.21	16.88	19.80	35.87	31.71	33.32	32.29
ANN (8)	29.24	15.16	20.48	33.46	30.29	31.77	32.72
ANN (9)	30.58	12.38	18.37	35.23	28.70	31.17	33.89
ANN (10)	39.31	13.62	22.13	37.96	32.02	38.22	39.68
Average MAPE (%)	29.89	14.55	19.21	35.73	30.72	32.52	34.95

Note: Initial learning rate: 0.4, lower boundary of learning rate: 0.001, learning rate reduction in epochs: 10, momentum: 0.9, interval center: 0 interval offset: +/−0.5.

.

As can be seen in Table 3, ANN models result in significant improvements for both tourist arrival volumes and tourism income forecasts based on the following methods: ARIMA, the grey model, and STL. On the other hand, the error values of ETS, X11, and X13 have slightly increased with ANN models. Compared to the single TRAMO method, the hybrid TRAMO-ANN approach yielded mixed results, with increased accuracy for tourist arrival volumes and decreased accuracy for tourism income.

Even then, ETS-based ANN models yield the most accurate results for both datasets, followed by grey and ARIMA-based ANN models. With the aim of clarifying the impacts of the exogenous variables, a sensitivity analysis is carried out for each dataset.

Table 4. Sensitivity analyses.

Tourist Arrival Volumes
Statistical Method	GFC	Russia	COVID-19	USD/TRY	Method
ARIMA	0.057	0.060	0.181	0.085	0.616
ETS	0.027	0.050	0.079	0.108	0.736
Grey	0.044	0.046	0.244	0.167	0.498
STL	0.074	0.091	0.102	0.131	0.602
TRAMO	0.055	0.112	0.086	0.081	0.666
x11	0.075	0.078	0.117	0.108	0.622
x13	0.069	0.112	0.098	0.098	0.623
Average Effect	0.057	0.078	0.130	0.111	0.623
Tourism Income
Statistical Method	GFC	Russia	COVID-19	USD/TRY	Method
ARIMA	0.063	0.094	0.115	0.148	0.580
ETS	0.052	0.048	0.113	0.127	0.659
Grey	0.071	0.049	0.194	0.146	0.539
STL	0.082	0.117	0.101	0.123	0.577
TRAMO	0.071	0.080	0.049	0.085	0.715
x11	0.057	0.093	0.067	0.108	0.675
x13	0.089	0.065	0.072	0.109	0.665
Average Effect	0.069	0.078	0.102	0.121	0.630

Note: GFC: Global financial crisis; Russia: Turkey-Russia warplane crash crisis; USD/TRY: Exchange rate.

interprets the results of sensitivity analyses.

The sensitivity analyses in Table 4 show the average importance of exogenous variables and forecasts with statistical methods (all independent variables) in the ANN models. According to the results, we can say that the past forecasts with the statistical methods are the most significant variables for both datasets, with the percentages changing from 53.9% to 73.6%.

The GFC and Russia warplane crisis have the lowest percentages in all models due to the short period of time they affect. Between these two variables, the Russia warplane crisis has a relatively higher impact compared to the GFC, with a rate of 7.8% for both datasets.

The effect of the COVID-19 determinant is the highest in grey-based models, with 24.4% for tourist arrival volumes and 19.4% for tourism income. While the average importance degree of COVID-19 is 13% for tourist arrival volumes, it is slightly lower (10.2%) for tourism income.

As is expected, the USD/TRY exchange rate is, on average, the most important exogenous determinant (12.1%) for tourism income and the second (11.1%) for tourist arrival volumes after COVID-19.

The gap between the percentages of methods of the two most accurate tourist arrival volume models, ETS and grey, is remarkable, such that the ETS-based model has 73.6% and the grey-based model has 49.8%, which are the highest and lowest rates, respectively, in between all models. However, this gap is not obvious for tourism income, where the highest gap occurs between the TRAMO (71.5%) and ARIMA (58%) methods.

In the previous sections, for each dataset, a total of 14 models were constructed, 7 of which were based solely on statistical methods, and the other 7 were non-linear ANN models combining these statistical methods with exogenous variables. Among these 14 models, the 5 most accurate were selected with the help of MAPE calculations.

Table 5. The five best forecasting models.

Tourist Arrival Volumes				Tourism Income
Order	Model	MAPE (%)	sMAPE (%)	Order	Model	MAPE (%)	sMAPE (%)
1	ETS	10.60	10.29	1	ETS	13.89	13.08
2	Hybrid ETS-ANN	13.07	11.79	2	Hybrid ETS-ANN	14.55	14.22
3	Hybrid Grey-ANN	15.59	14.53	3	Hybrid Grey-ANN	19.21	17.18
4	Hybrid ARIMA-ANN	19.81	18.12	4	Grey	25.22	21.47
5	Grey	23.61	19.73	5	Hybrid ARIMA-ANN	29.89	26.21

indicates the MAPE and sMAPE values of the five best models.

According to Table 5, the most accurate model with the lowest MAPE and sMAPE levels is the ETS model for both datasets. Although the sMAPE values of each model are somewhat lower than the MAPE values, they are parallel and provide the same outcomes. sMAPE values are better for large errors, as in the case of the grey model, which drops from 23.61% to 19.73% for tourist arrival volumes and from 25.22% to 21.47% for tourism income. When combined with other variables, the accuracy of ETS-based ANN models slightly increases, which can be attributed to the disruptive effect of the non-homogeneity of the COVID-19 variable over the last two years.

However, there is no similar effect on the other models, and it can be concluded that ANN models perform better in general. Although these five best models are common for tourist arrival volumes and tourism income, there are minor differences among them. First, the MAPE values are smaller for tourist arrival volumes compared to tourism income, and second, the hybrid ARIMA-ANN and grey models are ranked fourth and fifth alternately between the two categories.

The top five models listed in Table 5 are used to forecast tourist arrival volumes and tourism income for the next four quarters, from 2022/Q1 to 2022/Q4. For single models of ETS and grey, the forecasts are performed only based on the past historical data of tourist arrivals and tourism income. On the other hand, hybrid models of ARIMA-ANN, ETS-ANN, and grey ANN combine a variety of inputs. The most basic of these inputs consists of future forecasts made with the available statistical methodology. For instance, the main input of the hybrid ARIMA-ANN model is the future forecasts made with the single ARIMA method. The one other numerical input is based on future forecasts of the USD/TRY exchange rate. The remainder of the inputs include dummy variables containing the binary status of whether or not a given status is present. These variables are the occurrence of the global financial crisis, the Turkey-Russia warplane crash crisis, and the COVID-19 pandemic. After combining and processing all of the inputs through several hidden layers, the output of each model provides the forecasts for the next quarters. These non-linear hybrid-ANN models are run under two scenarios: (1) war and (2) no war between Russia and Ukraine. The resulting forecast values are summarized in

Table 6. Forecasts for the next quarters.

Tourist Arrival Volumes a
Quarter	ETS	Grey	ARIMA-ANN No War	ARIMA-ANN War	ETS-ANN No War	ETS-ANN War	Grey-ANN No War	Grey-ANN War
2022-1	3.996	3.836	8.048	8.156	7.840	7.100	7.961	7.813
2022-2	7.759	8.406	7.994	8.120	7.698	7.147	7.887	7.798
2022-3	15.313	12.340	7.957	8.090	7.593	7.181	7.829	7.792
2022-4	6.792	5.982	7.933	8.069	7.521	7.202	7.787	7.789
2022	33.860	30.564	31.932	32.435	30.651	28.630	31.464	31.192
Tourism Income a
Quarter	ETS	Grey	ARIMA-ANN No War	ARIMA-ANN War	ETS-ANN No War	ETS-ANN War	Grey-ANN No War	Grey-ANN War
2022-1	3061.391	2709.035	5716.705	5710.603	5679.672	5506.653	5229.354	5086.742
2022-2	4762.321	4821.020	5785.448	5808.871	5581.146	5462.529	5217.826	4918.407
2022-3	11,219.267	7760.082	5833.152	5884.278	5509.701	5425.885	5209.862	4802.213
2022-4	6027.208	4644.254	5863.359	5936.245	5462.872	5398.807	5204.656	4727.546
2022	25,070.187	19,934.390	23,198.665	23,339.998	22,233.392	21,793.874	20,861.699	19,534.909

Note: ^a: million.

.

Table 6 indicates the forecasts for the year 2022. It can be concluded that 2022 forecasts with the single ETS method yield the highest forecast values both for tourist arrival volumes (33.860 million) and tourism income (USD 25,070.187 million). Compared to the war scenario, the no-war scenario results in higher volumes and income in the hybrid ETS-ANN and hybrid grey-ANN models, as expected. However, the hybrid ARIMA-ANN model yields lower volumes and income under a no-war scenario.

Although the differences between the alternate models of tourism income forecasts are slightly higher than those of tourist arrival volume forecasts, all five of these models provide consistent results despite the disruptive impacts of exogenous variables.

The graphs indicating the real tourist arrival volumes and tourism income versus forecasts under two scenarios can be seen in Figure 6. These graphs successfully demonstrate how accurate the forecasts are. This means that the more the actual and forecast graphs overlap from 2010 to 2021, the more accurate the forecasts are.

Graphs show that forecasts with ETS models fit the real tourist arrival volumes and tourism income very well, and grey models are second and ARIMA models are third in fitting the real data for both datasets. Since ANN models smooth the data, the differences between these models are less obvious in graphs. We can say that all these models successfully reflect the variations in data up to the year 2020, in which COVID-19 breakdowns cause a sharp decrease in each tourism data point.

5. Conclusions

The tourism industry holds significant importance for economies, contributing over 10% to global GDP prior to the COVID-19 pandemic [3]. Accurate forecasting of tourism demand and income plays a crucial role in resource allocation, risk analysis, and decision-making for both businesses and policymakers, aiding in areas such as marketing strategies, infrastructure development, and optimal resource utilization [7,8,9,10]. Failure to consider forecasting can result in redundant investments, resource waste, and policy mismanagement. Thus, precise and comprehensive demand and income forecasts are critical for stakeholders in the tourism industry, including service providers and policymakers.

However, forecasting tourism data accurately poses challenges due to numerous exogenous variables influencing demand and income. Selecting appropriate determinants and methods that align with available tourism data leads to lower error rates and more successful estimates. This study focuses on forecasting tourist arrivals and tourism income in Turkey, the fourth-largest country in terms of international tourist arrivals. The uniqueness of this research lies in the examined period, included determinants, and utilized methods.

The study examines tourism data from 2010 to 2021, considering the effects of various factors such as the COVID-19 pandemic, USD/TRY exchange rates, the global financial crisis, the Turkey-Russia warplane crash crisis, and the Russia-Ukraine war. While the global financial crisis, exchange rates, and COVID-19 pandemic are considered as worldwide factors [17,18,19], the Turkey-Russia warplane crash crisis and Russia-Ukraine war are considered as country-specific factors affecting tourism in Turkey [14,15,16].

Fourteen alternative models based on seven statistical methods are employed, with a non-linear artificial neural network (ANN) approach that incorporates the aforementioned exogenous variables. The results reveal that the top five models for tourism forecasts are ETS, the grey model, hybrid ETS-ANN, hybrid grey-ANN, and hybrid ARIMA-ANN models, with varying MAPE values between 10.60% and 23.61% and sMAPE values between 10.29% and 19.73% for tourist arrivals, and 13.89% and 29.89% for tourism income.

The COVID-19 pandemic has had a significant disruptive impact on both tourist arrivals and tourism income, affecting all models. Comparing the relative effects of exogenous variables, COVID-19 emerges as the factor with the highest impact on tourist arrivals, while the USD/TRY exchange rate exerts the most influence on tourism income. These findings suggest that while complete prevention of the impact of pandemics like COVID-19 on the tourism sector may be challenging, the sector can mitigate the effects by providing a hygienic environment, implementing safe transportation measures, and establishing pre-prepared crisis measures. Such proactive measures can limit losses in the tourism sector and subsequently benefit the economy.

Forecasts for the upcoming quarters are made under two alternative scenarios regarding the Russia-Ukraine war: (1) war and (2) no war. The results indicate that in the absence of war, both tourist arrivals and tourism income exhibit higher values according to the two most accurate ANN models (hybrid ETS-ANN and hybrid grey-ANN).

In summary, the non-linear ANN approach utilizing the feed-forward-back-propagation algorithm proves to be a valuable tool for tourism data forecasting, enabling simultaneous processing of multiple variables and generating accurate results despite the data’s high fluctuations. The practical implication of this study is expected to assist policymakers and business managers in their resource allocation and planning activities. This approach can also be effectively adapted for forecasting in other sectors. It is important to note that this study is limited to the included data and variables, and future research on tourism forecasting may incorporate additional determinants such as diverse tourism data derived from search engines. It is believed that future studies will provide more accurate results, since the training data in the ANN models catch the recovery after the COVID-19 break by the extension of the COVID-19 free period. Additionally, employing deep-learning approaches such as long short-term memory analysis can further enhance accuracy in future studies.

6. Discussion

In our analysis, except for hybrid models among the top five models, the forecasting power of ETS and the grey model is found to have overperformance compared to other models. Comparing to the literature, although the performance of the ETS model for forecasting is seen as lower than the alternative models [41,42], our findings support the opposite. On the other hand, the grey model is generally addressed in the literature by optimizing it or with another model to prevent the disadvantages of this model [55,56,94]. In these studies, their high performances are clearly demonstrated.

For the rest of the three models among the top models, our results lend color to the overperformance of hybrid models on forecasting models as supported by many studies in the literature [53,54,55,56]. Of them, hybrid ETS-ANN, hybrid grey-ANN, and hybrid ARIMA-ANN show overperformance compared to Tramo-Seats, X13, X11, and STL. Although the analyses in the literature on more accurate forecasting models for tourism demand forecasting show different results, our comprehensive study which compares many models used in the studies is thought to be more valid. The low rate of MAPE and sMAPE supports this thought robustly.

As factors, the impact of COVID-19 is expectedly negative and compatible with the literature [17,18,19]; moreover, its impact is not only on the tourism sector but other sectors as well. For the impact of the exchange rate, its importance on forecasting is supported by other studies [94,95,96,97]. Considering all the results mentioned above, this study is expected to fill the gap in the literature and contribute to future studies.