Advancing Shear Capacity Estimation in Rectangular RC Beams: A Cutting-Edge Artificial Intelligence Approach for Assessing the Contribution of FRP
Abstract
:1. Introduction
2. Materials and Methods
2.1. Extreme Gradient Boosting
- High Predictive Accuracy: XGBoost often outperforms other ML algorithms in terms of predictive accuracy. It effectively reduces bias and variance, leading to models that generalize well to new, unseen data.
- Efficiency and Scalability: XGBoost is engineered for efficiency and speed. It employs a number of optimization techniques, including parallelization and approximation algorithms, which make it highly scalable and capable of handling large datasets.
- Feature Importance: XGBoost provides a feature importance score, allowing users to understand which features have the most impact on the model’s predictions. This information is crucial for feature selection and understanding the underlying relationships in the data.
- Robustness to Overfitting: The algorithm includes regularization terms, such as L1 (Lasso) and L2 (Ridge) penalties, which help prevent overfitting. This ensures that the model does not become overly complex and remains capable of generalizing to unseen data.
- Handling Missing Values: XGBoost has a built-in mechanism to handle missing values during the training process, reducing the need for extensive data preprocessing.
- Black-Box Nature: Like many ensemble methods, the interpretability of XGBoost models can be a challenge. Understanding the exact decision-making process within the model can be complex, especially when dealing with a large number of features and trees.
- Resource Intensive: Although XGBoost is efficient, it can be computationally demanding, especially when training very large models on limited hardware. This may limit its practicality in resource-constrained environments.
- Sensitivity to Hyperparameters: The proper tuning of hyperparameters is crucial for achieving optimal performance with XGBoost. This process can be time-consuming and may require some expertise.
- Limited Support for Unstructured Data: XGBoost is designed primarily for structured data. It may not perform as effectively when applied to unstructured data types, such as text, images, or audio, without appropriate feature engineering.
- Potential for Overfitting: While XGBoost is designed to mitigate overfitting, it is not immune to it. Improper hyperparameter tuning or the use of very complex models can still lead to overfitting issues. Regularization techniques must be applied judiciously.
2.2. Random Forest
- High Predictive Accuracy: RF is renowned for its remarkable predictive accuracy. Combining the predictions of multiple decision trees effectively reduces overfitting, providing more reliable and accurate results compared to single decision trees.
- Robustness to Outliers: RF is robust against outliers and noisy data, as individual decision trees can be sensitive to extreme values. The ensemble nature of RF mitigates the impact of such anomalies on the overall model.
- Feature Importance: RF can evaluate the importance of features in the dataset. It assigns a relevance score to each feature, aiding in feature selection and providing insights into which attributes contribute most to the model’s predictions.
- Handling Missing Data: It can handle missing data without extensive data preprocessing. Using surrogate splits, RF can make predictions based on available information, making it more resilient to incomplete datasets.
- Reduction in Overfitting: RF reduces the risk of overfitting, a common problem in decision trees, by introducing randomness through feature subsampling and bootstrapping. This helps the model to generalize better to unseen data.
- Parallelization: RF can efficiently utilize parallel processing, as individual trees can be constructed independently. This makes it suitable for large datasets and computationally intensive tasks.
- Interpretability: While not as interpretable as a single decision tree, RF can provide insights into feature importance and how the model makes predictions, aiding in model understanding and feature engineering.
- Complexity: The ensemble of multiple decision trees can make the RF model complex, potentially requiring more memory and computational resources compared to single-decision trees.
- Computational Cost: Training an RF model can be computationally expensive, especially for large datasets or a high number of trees in the forest.
- Black-Box Nature: RFs are less interpretable compared to individual decision trees, making it challenging to understand the inner workings of the model, especially when dealing with a large number of trees.
- Not Suitable for Linear Relationships: RF may not perform as well as linear models when the underlying relationship between features and the target variable is linear, as it is inherently a non-linear model.
- Overhead in Hyperparameter Tuning: Tuning the hyperparameters of an RF, such as the number of trees and the depth of the tree, can be time-consuming and require careful experimentation to achieve optimal performance.
2.3. AdaBoost
- High Accuracy: AdaBoost often yields high predictive accuracy compared to individual weak learners. This is because it focuses on misclassified samples and iteratively improves the model’s performance.
- Versatility: AdaBoost can be applied to various types of weak learners, not just decision trees. This makes it adaptable to different types of data and problem domains.
- Reduced Overfitting: AdaBoost tends to reduce overfitting compared to training a single complex model. It does this by combining multiple weak models, each focusing on different aspects of the data.
- Handles Noisy Data Well: AdaBoost can handle noisy data and outliers to some extent. Since it gives more weight to misclassified samples, it tends to focus on difficult-to-classify data points.
- Feature Selection: AdaBoost implicitly performs feature selection by assigning more importance to features that are more informative in the context of the problem.
- Sensitivity to Noisy Data: While AdaBoost can handle some level of noise, it can still be sensitive to outliers or extremely noisy data. In extreme cases, it may overfit to the noise.
- Computationally Intensive: Training an AdaBoost model can be computationally intensive, especially when using a large number of weak learners or complex base models.
- Less Interpretable: The final ensemble model produced by AdaBoost may be less interpretable compared to individual weak models. It may not provide clear insights into the relationships between features and the target variable.
- Less Effective on Complex Relationships: AdaBoost may struggle with datasets where the underlying relationships are highly complex or not well-captured by simple weak models.
- Requires Sufficient Data: AdaBoost may not perform well on very small datasets or datasets with insufficient diversity. It relies on a variety of weak models to be effective.
2.4. ElasticNet
- Variable Selection: ElasticNet can perform variable selection by encouraging some of the coefficients to be exactly zero, effectively removing irrelevant features from the model. This is especially beneficial when dealing with high-dimensional datasets, where feature selection is critical.
- Balancing L1 and L2 Regularization: The α parameter allows for fine-tuning the balance between L1 and L2 regularization. This flexibility enables ElasticNet to capture the advantages of both Lasso (sparsity) and Ridge (stability).
- Robust to Multicollinearity: ElasticNet can handle multicollinearity, a situation where independent variables are highly correlated, by shrinking and selecting groups of correlated variables simultaneously. This aids in stability and interpretability.
- Generalization: ElasticNet often yields models that generalize well to new, unseen data. It can prevent overfitting by adding a regularization penalty to the loss function, which is crucial for dealing with noisy or limited data.
- Complexity in Choosing Hyperparameters: Selecting appropriate values for hyperparameters can be challenging. The optimal combination depends on the specific problem, and choosing the wrong values may lead to suboptimal results.
- Computational Cost: Its objective function involves both the L1 and L2 regularization terms, which makes it computationally more expensive than simple linear regression. This cost can be significant for large datasets.
- Less Interpretability: Although ElasticNet provides a balance between L1 and L2 regularization, the resulting models may be less interpretable than simple linear regression models. This is because some coefficients may be shrunken towards zero or other coefficients, making their individual interpretation less straightforward.
2.5. K-Nearest Neighbors
- Simplicity and Intuitiveness: KNN is relatively easy to understand and implement. It does not involve complex mathematical computations or assumptions about the underlying data distribution.
- No Training Phase: Unlike many other ML algorithms, K-NN does not require a training phase. This means that the model is readily available for prediction once the data is available.
- Flexibility to Data Distribution: KNN can be applied to both linear and non-linear relationships between features and the target variable. It is not sensitive to the underlying data distribution.
- Adaptability to New Data: As new data points become available, the KNN model can be easily updated to incorporate this new information.
- Computational Complexity: The main computational cost of KNN arises from the need to compute distances between all pairs of data points. As the dataset grows, this can become computationally expensive.
- Sensitivity to Feature Scaling: The performance of KNN can be influenced by the scale of the features. Therefore, it is essential to normalize or standardize the features before applying this algorithm.
- Memory Consumption: KNN requires storing the entire training dataset in memory, which can be impractical for very large datasets.
- Optimal K Selection: Choosing the appropriate value of K (the number of nearest neighbors to consider) can be challenging. A suboptimal choice of K may lead to poor model performance.
- Imbalanced Data: In classification tasks with imbalanced classes, KNN may be biased towards the majority class since it gives equal weight to all neighbors.
- Lack of Interpretability: KNN does not provide explicit information on the underlying relationships between features and the target variable. It does not offer coefficients or feature importance scores.
- Vulnerability to Noisy Data: Outliers and noisy data points can significantly impact the performance of KNN, potentially leading to incorrect predictions.
2.6. Gradient Boosting
- High Predictive Accuracy: GB often yields highly accurate predictions. GB incrementally improves its performance by iteratively addressing the shortcomings of the model, ultimately achieving superior performance compared to individual weak learners.
- Handles Heterogeneous Data: It is robust to different types of data (categorical or numerical) and can handle a mix of predictor variables effectively.
- Feature Importance: GB provides a measure of feature importance, indicating which variables are most influential in making accurate predictions.
- Handles Missing Data: It can handle missing data in a dataset without the need for imputation techniques. It does this by using the information from available predictors.
- Robust to Outliers: It is less sensitive to outliers in the data compared to other algorithms.
- Computationally Expensive: Training a gradient boosting model can be computationally expensive, especially when dealing with large datasets and complex weak learners.
- Prone to Overfitting: Without proper hyperparameter tuning, gradient boosting models can overfit the training data, leading to poor generalization performance on unseen data.
- Requires Careful Hyperparameter Tuning: Selecting the right hyperparameters is crucial for achieving optimal performance. This process can be time-consuming and may require domain knowledge.
- Less Interpretable: Unlike simpler models like linear regression, the inner workings of a gradient boosting model are more complex and less interpretable, making it challenging to explain the predictions to non-technical stakeholders.
- Less Efficient for High-Dimensional Data: GB may not perform as well in situations with a very large number of features, as it may struggle to effectively capture the interactions among them.
3. Experimental Database
4. AI-Based Analysis
5. Sensitivity Analysis by ANN
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| No | b | d | fc | fy | Asv | Sv | a/d | FRP Type | Scheme | Ef | εfrp | ffrp | n*tf | wf | sf | hf | beta | Vexp |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 250 | 420 | 13.3 | 500 | 0.096 | 400 | 3.33 | CFRP | U | 390 | 0.008 | 3000 | 0.22 | 150 | 225 | 450 | 45 | 66.5 |
| 2 | 250 | 420 | 13.3 | 500 | 0.096 | 400 | 3.33 | CFRP | U | 390 | 0.008 | 3000 | 0.22 | 1 | 1 | 450 | 90 | 27 |
| 3 | 250 | 420 | 13.3 | 500 | 0.096 | 400 | 3.33 | CFRP | U | 390 | 0.008 | 3000 | 0.22 | 150 | 300 | 450 | 60 | 13 |
| 4 | 250 | 420 | 13.3 | 500 | 0.096 | 400 | 3.33 | CFRP | U | 390 | 0.01 | 3000 | 0.22 | 150 | 300 | 450 | 45 | 28 |
| 5 | 250 | 420 | 13.3 | 500 | 0.096 | 400 | 3.33 | CFRP | U | 390 | 0.008 | 3000 | 0.22 | 50 | 100 | 450 | 45 | 35.5 |
| 6 | 200 | 380 | 35.1 | 500 | 0.074 | 400 | 3.29 | CFRP | U | 240 | 0.013 | 3500 | 0.11 | 100 | 400 | 450 | 90 | 41.2 |
| 7 | 200 | 395 | 36.8 | 500 | 0.072 | 400 | 3.29 | CFRP | U | 240 | 0.013 | 3500 | 0.11 | 50 | 400 | 450 | 90 | 33.4 |
| 8 | 200 | 395 | 35.8 | 500 | 0.072 | 400 | 3.29 | CFRP | U | 240 | 0.013 | 3500 | 0.11 | 50 | 600 | 450 | 90 | 30 |
| 9 | 150 | 255 | 19.3 | 350 | 0.41 | 125 | 2.98 | CFRP | SB | 228 | 0.017 | 3790 | 0.33 | 1 | 1 | 305 | 90 | 50.5 |
| 10 | 150 | 255 | 19.3 | 350 | 0.41 | 125 | 4 | CFRP | SB | 228 | 0.017 | 3790 | 0.33 | 50 | 125 | 305 | 90 | 80.5 |
| 11 | 150 | 255 | 27.5 | 460 | 0 | 0 | 2.98 | CFRP | U | 228 | 0.017 | 3790 | 0.165 | 1 | 1 | 305 | 90 | 54 |
| 12 | 150 | 255 | 27.5 | 460 | 0 | 0 | 2.98 | CFRP | U | 228 | 0.017 | 3790 | 0.33 | 1 | 1 | 305 | 90 | 92.5 |
| 13 | 150 | 255 | 27.5 | 460 | 0 | 0 | 2.98 | CFRP | U | 228 | 0.017 | 3790 | 0.165 | 50 | 125 | 305 | 90 | 67.5 |
| 14 | 150 | 255 | 27.5 | 460 | 0 | 0 | 4 | CFRP | U | 228 | 0.017 | 3790 | 0.165 | 1 | 1 | 305 | 90 | 62.5 |
| 15 | 150 | 255 | 27.5 | 460 | 0 | 0 | 4 | CFRP | U | 233.6 | 0.016 | 4490 | 0.165 | 1 | 1 | 305 | 90 | 90.5 |
| 16 | 150 | 250 | 22.82 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.165 | 1 | 1 | 300 | 90 | 45.3 |
| 17 | 150 | 250 | 22.82 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.495 | 1 | 1 | 300 | 90 | 38.1 |
| 18 | 150 | 250 | 22.82 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.495 | 1 | 1 | 300 | 90 | 65.5 |
| 19 | 150 | 250 | 26.06 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.33 | 1 | 1 | 300 | 90 | 31.5 |
| 20 | 150 | 250 | 26.06 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.495 | 1 | 1 | 300 | 90 | 51.8 |
| 21 | 150 | 250 | 26.06 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.495 | 1 | 1 | 300 | 90 | 86 |
| 22 | 150 | 250 | 26.06 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.33 | 1 | 1 | 300 | 90 | 47.3 |
| 23 | 150 | 250 | 26.06 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 4490 | 0.33 | 1 | 1 | 300 | 90 | 50.5 |
| 24 | 300 | 245 | 37.2 | 395 | 0 | 0 | 4.08 | CFRP | U | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 300 | 90 | 53 |
| 25 | 300 | 245 | 41 | 395 | 0 | 0 | 4.08 | CFRP | U | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 300 | 90 | 116.5 |
| 26 | 300 | 245 | 41.1 | 395 | 0 | 0 | 4.08 | CFRP | U | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 300 | 90 | 125.5 |
| 27 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | F | 105 | 0.013 | 1400 | 0.43 | 40 | 200 | 450 | 90 | 135 |
| 28 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | F | 105 | 0.013 | 1400 | 0.43 | 40 | 250 | 450 | 90 | 90 |
| 29 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | F | 105 | 0.013 | 1400 | 0.43 | 40 | 300 | 450 | 45 | 71 |
| 30 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | F | 105 | 0.013 | 1400 | 0.43 | 40 | 350 | 450 | 45 | 44 |
| 31 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | U | 105 | 0.013 | 1400 | 0.43 | 40 | 200 | 450 | 90 | 65 |
| 32 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | U | 105 | 0.013 | 1400 | 0.43 | 40 | 250 | 450 | 90 | 40 |
| 33 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | U | 105 | 0.013 | 1400 | 0.43 | 40 | 300 | 450 | 45 | 89 |
| 34 | 130 | 425 | 38 | 240 | 0.102 | 300 | 2.12 | CFRP | U | 105 | 0.013 | 1400 | 0.43 | 40 | 350 | 450 | 45 | 80 |
| 35 | 150 | 170 | 35.4 | 582 | 0 | 0 | 3 | CFRP | SB | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 200 | 90 | 11.3 |
| 36 | 150 | 170 | 33.5 | 582 | 0 | 0 | 3 | CFRP | SB | 230 | 0.015 | 3400 | 0.334 | 1 | 1 | 200 | 90 | 24.4 |
| 37 | 150 | 170 | 31.5 | 582 | 0 | 0 | 3 | CFRP | SB | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 200 | 90 | 19.4 |
| 38 | 150 | 170 | 31 | 582 | 0 | 0 | 3 | CFRP | SB | 230 | 0.015 | 3400 | 0.334 | 1 | 1 | 200 | 90 | 21.1 |
| 39 | 150 | 170 | 33.7 | 582 | 0 | 0 | 3 | CFRP | SB | 230 | 0.015 | 3400 | 0.334 | 1 | 1 | 200 | 90 | 41.6 |
| 40 | 150 | 170 | 34.4 | 582 | 0 | 0 | 3 | CFRP | U | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 200 | 90 | 29.3 |
| 41 | 150 | 170 | 35.4 | 582 | 0 | 0 | 3 | CFRP | U | 230 | 0.015 | 3400 | 0.167 | 1 | 1 | 200 | 90 | 46.6 |
| 42 | 150 | 296 | 41.03 | 494.5 | 0.127 | 160 | 3.04 | GFRP | F | 75.9 | 0.047 | 3600 | 0.12 | 1 | 1 | 350 | 90 | 56 |
| 43 | 150 | 296 | 41.03 | 494.5 | 0.127 | 160 | 3.04 | GFRP | F | 75.9 | 0.047 | 3600 | 0.24 | 1 | 1 | 350 | 90 | 84 |
| 44 | 150 | 296 | 41.03 | 494.5 | 0.127 | 160 | 3.04 | GFRP | F | 75.9 | 0.047 | 3600 | 0.36 | 1 | 1 | 350 | 90 | 93 |
| 45 | 150 | 222.5 | 30.5 | 303 | 0.169 | 200 | 2.7 | CFRP | F | 249 | 0.015 | 3635 | 0.167 | 30 | 100 | 250 | 90 | 44 |
| 46 | 150 | 222.5 | 30.5 | 303 | 0.169 | 200 | 2.7 | CFRP | F | 249 | 0.015 | 3635 | 0.167 | 30 | 150 | 250 | 90 | 46 |
| 47 | 150 | 222.5 | 30.5 | 303 | 0.169 | 200 | 1.8 | CFRP | F | 249 | 0.015 | 3635 | 0.167 | 30 | 100 | 250 | 90 | 44 |
| 48 | 150 | 222.5 | 30.5 | 303 | 0.169 | 200 | 1.8 | CFRP | F | 249 | 0.015 | 3635 | 0.167 | 30 | 50 | 250 | 90 | 34 |
| 49 | 150 | 222.5 | 30 | 361 | 0 | 0 | 2.47 | GFRP | F | 20.5 | 0.013 | 260 | 1.27 | 20 | 40 | 250 | 90 | 70 |
| 50 | 150 | 222.5 | 30 | 361 | 0 | 0 | 2.47 | GFRP | F | 20.5 | 0.013 | 260 | 1.27 | 20 | 80 | 250 | 90 | 55 |
| 51 | 150 | 222.5 | 30 | 361 | 0 | 0 | 1.35 | GFRP | F | 20.5 | 0.013 | 260 | 1.27 | 20 | 40 | 250 | 90 | 28 |
| 52 | 150 | 222.5 | 30 | 361 | 0 | 0 | 1.35 | GFRP | F | 20.5 | 0.013 | 260 | 1.27 | 20 | 80 | 250 | 90 | 11 |
| 53 | 150 | 222.5 | 17.8 | 361 | 0 | 0 | 2.92 | GFRP | F | 5.3 | 0.021 | 112 | 1.2 | 25 | 50 | 250 | 90 | 40 |
| 54 | 150 | 222.5 | 17.8 | 361 | 0 | 0 | 2.92 | GFRP | F | 5.3 | 0.021 | 112 | 1.2 | 25 | 100 | 250 | 90 | 35 |
| 55 | 150 | 222.5 | 17.8 | 361 | 0 | 0 | 1.8 | GFRP | F | 5.3 | 0.021 | 112 | 1.2 | 25 | 50 | 250 | 90 | 47 |
| 56 | 150 | 222.5 | 17.8 | 361 | 0 | 0 | 1.8 | GFRP | F | 5.3 | 0.021 | 112 | 1.2 | 25 | 100 | 250 | 90 | 35 |
| 57 | 180 | 426 | 67 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.072 | 1 | 1 | 500 | 45 | 122 |
| 58 | 180 | 426 | 59 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 29 |
| 59 | 180 | 426 | 71 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 132 |
| 60 | 180 | 426 | 53 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 180 |
| 61 | 180 | 426 | 67 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 181 |
| 62 | 180 | 426 | 47 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 126 |
| 63 | 180 | 426 | 53 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.11 | 1 | 1 | 500 | 45 | 166 |
| 64 | 180 | 426 | 71 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.165 | 1 | 1 | 500 | 45 | 209 |
| 65 | 180 | 426 | 54 | 500 | 0 | 0 | 2.93 | CFRP | SB | 234 | 0.019 | 4500 | 0.165 | 1 | 1 | 500 | 45 | 219 |
| 66 | 180 | 335 | 46 | 500 | 0.094 | 200 | 2.99 | CFRP | SB | 234 | 0.019 | 4500 | 0.165 | 1 | 1 | 400 | 90 | 62 |
| 67 | 180 | 335 | 46 | 500 | 0.094 | 200 | 2.99 | CFRP | SB | 234 | 0.019 | 4500 | 0.165 | 1 | 1 | 400 | 90 | 62 |
| 68 | 152.4 | 189.1 | 43.8 | 400 | 0 | 0 | 2.82 | CFRP | SB | 165 | 0.017 | 2800 | 1.5 | 40 | 127 | 228.6 | 90 | 27.6 |
| 69 | 152.4 | 189.1 | 43.8 | 400 | 0 | 0 | 2.82 | CFRP | SB | 165 | 0.017 | 2800 | 1.5 | 6 | 127 | 228.6 | 45 | 36.7 |
| 70 | 152.4 | 189.1 | 43.8 | 400 | 0 | 0 | 2.5 | CFRP | SB | 165 | 0.017 | 2800 | 1 | 1 | 1 | 228.6 | 90 | 7.5 |
| 71 | 152.4 | 189.1 | 43.8 | 400 | 0 | 0 | 2.5 | CFRP | SB | 165 | 0.017 | 2800 | 1.5 | 40 | 127 | 228.6 | 90 | 21 |
| 72 | 152.4 | 189.1 | 43.8 | 400 | 0 | 0 | 2.5 | CFRP | SB | 390 | 0.017 | 2800 | 1 | 1 | 1 | 228.6 | 90 | 8.3 |
| 73 | 150 | 280 | 37.6 | 540 | 0 | 0 | 2.5 | CFRP | U | 390 | 0.008 | 3000 | 0.334 | 25 | 190 | 300 | 90 | 10.8 |
| 74 | 150 | 280 | 37.6 | 540 | 0 | 0 | 3 | CFRP | U | 390 | 0.008 | 3000 | 0.334 | 25 | 95 | 300 | 90 | 31.5 |
| 75 | 150 | 120 | 49.5 | 540 | 0 | 0 | 3 | CFRP | U | 390 | 0.008 | 3000 | 0.334 | 25 | 80 | 150 | 90 | 18.6 |
| 76 | 150 | 120 | 49.5 | 540 | 0 | 0 | 3 | CFRP | U | 390 | 0.008 | 3000 | 0.334 | 25 | 40 | 150 | 90 | 33.7 |
| 77 | 150 | 250 | 41.43 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 52.9 |
| 78 | 150 | 250 | 41.43 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 231 | 0.015 | 3465 | 0.33 | 1 | 1 | 300 | 90 | 57.8 |
| 79 | 150 | 250 | 41.43 | 534 | 0.268 | 200 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 55.8 |
| 80 | 150 | 250 | 41.43 | 534 | 0.268 | 200 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.33 | 1 | 1 | 300 | 90 | 60.5 |
| 81 | 150 | 250 | 41.43 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 49.1 |
| 82 | 150 | 250 | 41.43 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.33 | 1 | 1 | 300 | 90 | 20.8 |
| 83 | 150 | 250 | 41.43 | 534 | 0.268 | 200 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 31.7 |
| 84 | 150 | 250 | 41.43 | 534 | 0.268 | 200 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.33 | 1 | 1 | 300 | 90 | 4 |
| 85 | 150 | 250 | 46.21 | 534 | 0.268 | 140 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 24.4 |
| 86 | 150 | 250 | 46.21 | 534 | 0.268 | 140 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.33 | 1 | 1 | 300 | 90 | 36.3 |
| 87 | 150 | 250 | 46.21 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.165 | 1 | 1 | 300 | 90 | 11.7 |
| 88 | 150 | 250 | 46.21 | 534 | 0.268 | 170 | 3.1 | CFRP | U | 230 | 0.015 | 3450 | 0.33 | 1 | 1 | 300 | 90 | 16.1 |
| 89 | 150 | 250 | 27.5 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 0.165 | 1 | 1 | 300 | 90 | 45.3 |
| 90 | 150 | 250 | 27.5 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 1.485 | 1 | 1 | 300 | 90 | 38.1 |
| 91 | 150 | 250 | 27.5 | 548 | 0 | 0 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 1.485 | 1 | 1 | 300 | 90 | 65.5 |
| 92 | 150 | 250 | 31.4 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 0.66 | 1 | 1 | 300 | 90 | 31.5 |
| 93 | 150 | 250 | 31.4 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 1.485 | 1 | 1 | 300 | 90 | 51.8 |
| 94 | 150 | 250 | 31.4 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 1.485 | 1 | 1 | 300 | 90 | 86 |
| 95 | 150 | 250 | 31.4 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 0.66 | 1 | 1 | 300 | 90 | 47.3 |
| 96 | 150 | 250 | 31.4 | 548 | 0.268 | 200 | 3 | CFRP | SB | 233.6 | 0.019 | 3350 | 0.66 | 1 | 1 | 300 | 90 | 50.5 |
| 97 | 75 | 155 | 27.4 | 500 | 0.216 | 120 | 2.9 | CFRP | U | 23.5 | 0.016 | 4200 | 0.11 | 20 | 60 | 180 | 90 | 24.3 |
| 98 | 75 | 155 | 27.4 | 500 | 0.216 | 120 | 2.9 | CFRP | U | 23.5 | 0.016 | 4200 | 0.11 | 20 | 60 | 180 | 90 | 5.1 |
| 99 | 75 | 155 | 27.4 | 500 | 0.216 | 120 | 2.9 | CFRP | F | 23.5 | 0.016 | 4200 | 0.11 | 20 | 60 | 180 | 90 | 25.4 |
| 100 | 75 | 155 | 27.4 | 500 | 0.216 | 120 | 2.9 | CFRP | F | 23.5 | 0.016 | 4200 | 0.11 | 20 | 60 | 180 | 90 | 25.9 |
| 101 | 150 | 305 | 27.4 | 500 | 0.123 | 135 | 2.95 | CFRP | U | 23.5 | 0.016 | 4200 | 0.22 | 40 | 120 | 360 | 90 | 4.8 |
| 102 | 150 | 305 | 27.4 | 500 | 0.123 | 135 | 2.95 | CFRP | U | 23.5 | 0.016 | 4200 | 0.22 | 40 | 120 | 360 | 90 | 9.9 |
| 103 | 150 | 305 | 27.4 | 500 | 0.123 | 135 | 2.95 | CFRP | F | 23.5 | 0.016 | 4200 | 0.22 | 40 | 120 | 360 | 90 | 86.5 |
| 104 | 150 | 305 | 27.4 | 500 | 0.123 | 135 | 2.95 | CFRP | F | 23.5 | 0.016 | 4200 | 0.22 | 40 | 120 | 360 | 90 | 100.5 |
| 105 | 300 | 660 | 27.4 | 500 | 0.051 | 240 | 2.7 | CFRP | U | 23.5 | 0.016 | 4200 | 0.44 | 80 | 240 | 720 | 90 | 25.4 |
| 106 | 300 | 660 | 27.4 | 500 | 0.051 | 240 | 2.7 | CFRP | U | 23.5 | 0.016 | 4200 | 0.44 | 80 | 240 | 720 | 90 | 21.8 |
| 107 | 300 | 660 | 27.4 | 500 | 0.051 | 240 | 2.7 | CFRP | F | 23.5 | 0.016 | 4200 | 0.44 | 80 | 240 | 720 | 90 | 333.6 |
| 108 | 300 | 660 | 27.4 | 500 | 0.051 | 240 | 2.7 | CFRP | F | 23.5 | 0.016 | 4200 | 0.44 | 80 | 240 | 720 | 90 | 343.2 |
| 109 | 250 | 220 | 34.7 | 551 | 0 | 0 | 2.2 | CFRP | SB | 235 | 0.015 | 3550 | 0.2 | 1 | 1 | 250 | 90 | 91.5 |
| 110 | 250 | 220 | 34.7 | 552 | 0 | 0 | 2.2 | CFRP | SB | 235 | 0.015 | 3550 | 0.2 | 50 | 100 | 250 | 90 | 32 |
| 111 | 250 | 220 | 34.7 | 554 | 0 | 0 | 2.2 | CFRP | SB | 158 | 0.02 | 3160 | 0.2 | 1 | 1 | 250 | 90 | 45.5 |
| 112 | 250 | 220 | 34.7 | 555 | 0 | 0 | 2.2 | CFRP | SB | 230 | 0.02 | 3160 | 0.2 | 1 | 1 | 250 | 45 | 47.5 |
| 113 | 250 | 420 | 21 | 476 | 0.096 | 400 | 3 | CFRP | F | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 130 |
| 114 | 250 | 420 | 21 | 476 | 0.096 | 300 | 3 | CFRP | F | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 170 |
| 115 | 250 | 420 | 21 | 476 | 0.096 | 200 | 3 | CFRP | F | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 85 |
| 116 | 250 | 420 | 21 | 476 | 0.096 | 400 | 3 | CFRP | U | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 100 |
| 117 | 250 | 420 | 21 | 476 | 0.096 | 300 | 3 | CFRP | U | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 110 |
| 118 | 250 | 420 | 21 | 476 | 0.096 | 200 | 3 | CFRP | U | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 65 |
| 119 | 250 | 420 | 21 | 476 | 0.096 | 400 | 3 | CFRP | SB | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 55 |
| 120 | 250 | 420 | 21 | 476 | 0.096 | 300 | 3 | CFRP | SB | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 45 |
| 121 | 250 | 420 | 21 | 476 | 0.096 | 200 | 3 | CFRP | SB | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 25 |
| 122 | 250 | 420 | 21 | 476 | 0.096 | 400 | 4 | CFRP | F | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 80 |
| 123 | 250 | 420 | 21 | 476 | 0.096 | 400 | 4 | CFRP | U | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 60 |
| 124 | 250 | 420 | 21 | 476 | 0.096 | 400 | 4 | CFRP | SB | 392 | 0.007 | 2600 | 0.191 | 1 | 1 | 450 | 90 | 45 |
| 125 | 250 | 240 | 25.3 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.14 | 1 | 1 | 270 | 90 | 13.8 |
| 126 | 250 | 240 | 25.3 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.21 | 1 | 1 | 270 | 90 | 27.6 |
| 127 | 250 | 240 | 25.3 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.28 | 1 | 1 | 270 | 90 | 26.4 |
| 128 | 250 | 240 | 25.3 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.42 | 1 | 1 | 270 | 90 | 37.2 |
| 129 | 250 | 240 | 25.3 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.56 | 1 | 1 | 270 | 90 | 60 |
| 130 | 250 | 450 | 32.6 | 350 | 0.056 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.42 | 1 | 1 | 500 | 90 | 103.8 |
| 131 | 250 | 240 | 32.6 | 350 | 0.106 | 150 | 3.13 | PET | F | 10 | 0.074 | 740 | 0.21 | 1 | 1 | 270 | 90 | 77.4 |
| 132 | 250 | 240 | 32.6 | 350 | 0.106 | 150 | 2.5 | PET | F | 10 | 0.074 | 740 | 0.42 | 1 | 1 | 270 | 90 | 103.2 |
| 133 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.005 | 3103 | 0.167 | 36 | 120 | 327 | 90 | 38.5 |
| 134 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.008 | 3103 | 0.167 | 36 | 120 | 327 | 90 | 30.2 |
| 135 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.01 | 3103 | 0.167 | 36 | 120 | 327 | 90 | 33.4 |
| 136 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.007 | 3103 | 0.167 | 36 | 120 | 327 | 90 | 45.7 |
| 137 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.005 | 3103 | 0.668 | 36 | 120 | 327 | 90 | 37.5 |
| 138 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.006 | 3103 | 0.668 | 36 | 120 | 327 | 90 | 61.3 |
| 139 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.007 | 3103 | 0.668 | 36 | 120 | 327 | 90 | 88 |
| 140 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.012 | 3103 | 0.668 | 36 | 120 | 327 | 90 | 100.5 |
| 141 | 200 | 297 | 27.3 | 398 | 0.28 | 120 | 2 | CFRP | U | 270.5 | 0.007 | 3103 | 0.668 | 36 | 120 | 327 | 90 | 112.8 |
| 142 | 180 | 303 | 47 | 310 | 0.122 | 160 | 1 | CFRP | U | 235 | 0.004 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 10 |
| 143 | 180 | 303 | 47 | 310 | 0.122 | 160 | 1.5 | CFRP | U | 235 | 0.008 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 37 |
| 144 | 180 | 303 | 47 | 310 | 0.122 | 160 | 2 | CFRP | U | 235 | 0.008 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 68 |
| 145 | 180 | 303 | 47 | 310 | 0.122 | 160 | 2.5 | CFRP | U | 235 | 0.008 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 62 |
| 146 | 180 | 303 | 55 | 310 | 0.122 | 160 | 3 | CFRP | U | 235 | 0.007 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 41 |
| 147 | 180 | 303 | 55 | 310 | 0.122 | 160 | 3.5 | CFRP | U | 235 | 0.007 | 4200 | 0.11 | 60 | 150 | 350 | 90 | 53 |
| 148 | 150 | 250 | 23.3 | 527 | 0.22 | 300 | 3 | CFRP | U | 390 | 0.008 | 3000 | 0.165 | 1 | 1 | 300 | 90 | 53.9 |
| 149 | 150 | 250 | 23.3 | 527 | 0.33 | 200 | 3 | CFRP | U | 390 | 0.008 | 3000 | 0.165 | 1 | 1 | 300 | 90 | 39.6 |
| 150 | 200 | 400 | 33.8 | 500 | 0.07 | 200 | 3.2 | CFRP | U | 230 | 0.015 | 3500 | 0.11 | 50 | 400 | 450 | 90 | 41.2 |
| 151 | 200 | 400 | 36 | 500 | 0.07 | 400 | 3.2 | CFRP | U | 230 | 0.015 | 3500 | 0.11 | 50 | 400 | 450 | 90 | 33.4 |
| 152 | 200 | 400 | 35.8 | 500 | 0.07 | 400 | 3.2 | CFRP | U | 230 | 0.015 | 3500 | 0.11 | 50 | 400 | 450 | 90 | 30.1 |
| 153 | 200 | 400 | 34.7 | 500 | 0.07 | 400 | 3.2 | CFRP | F | 230 | 0.015 | 3500 | 0.11 | 50 | 200 | 450 | 90 | 98.9 |
| 154 | 120 | 150 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | SB | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 260 | 90 | 20 |
| 155 | 120 | 150 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | SB | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 260 | 90 | 16.3 |
| 156 | 120 | 150 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | SB | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 260 | 90 | 13.8 |
| 157 | 120 | 175 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | F | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 200 | 90 | 25 |
| 158 | 120 | 175 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | F | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 200 | 90 | 23.8 |
| 159 | 120 | 175 | 40 | 280 | 0.39 | 120 | 2.57 | CFRP | F | 230 | 0.015 | 3500 | 0.26 | 50 | 100 | 200 | 90 | 22.5 |
| 160 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | U | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 90 | 25.2 |
| 161 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | U | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 90 | 30.7 |
| 162 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | U | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 45 | 35.8 |
| 163 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | F | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 90 | 39.4 |
| 164 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | U | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 45 | 42.5 |
| 165 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | SB | 89 | 0.035 | 3115 | 0.14 | 1 | 1 | 260 | 90 | 42.9 |
| 166 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | F | 89 | 0.035 | 3115 | 0.14 | 75 | 50 | 260 | 45 | 52.2 |
| 167 | 150 | 210 | 16.9 | 498.2 | 0.16 | 200 | 2.4 | BFRP | F | 89 | 0.035 | 3115 | 0.14 | 1 | 1 | 260 | 90 | 58.9 |
| 168 | 152 | 267 | 60 | 494 | 0.14 | 130 | 2.85 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 304.8 | 761 | 304.8 | 90 | 40.4 |
| 169 | 152 | 267 | 60 | 494 | 0.14 | 130 | 2.85 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 1 | 1 | 304.8 | 90 | 52 |
| 170 | 152 | 267 | 60 | 494 | 0.14 | 130 | 2.85 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 1 | 1 | 152.5 | 90 | 40.4 |
| 171 | 152 | 267 | 60 | 494 | 0.14 | 130 | 2.85 | CFRP | F | 234.5 | 0.02 | 3450 | 0.34 | 1 | 1 | 305 | 90 | 60.6 |
| 172 | 152 | 267 | 60 | 494 | 0.14 | 130 | 2.85 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 304.8 | 1195 | 304.8 | 45 | 69.3 |
| 173 | 152 | 267 | 44 | 494 | 0.14 | 130 | 2.85 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 304.8 | 1195 | 304.8 | 45 | 70.9 |
| 174 | 150 | 300 | 49.1 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 1 | 1 | 150 | 90 | 32.7 |
| 175 | 150 | 300 | 48.28 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 300 | 600 | 300 | 90 | 32.7 |
| 176 | 150 | 300 | 49.1 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 300 | 600 | 150 | 90 | 13.55 |
| 177 | 150 | 300 | 48.62 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 1 | 1 | 300 | 90 | 66.45 |
| 178 | 150 | 300 | 49.79 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 150 | 600 | 300 | 90 | 13.55 |
| 179 | 150 | 300 | 48.97 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 300 | 900 | 150 | 90 | 18.35 |
| 180 | 150 | 300 | 47.93 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 150 | 900 | 300 | 90 | 18.35 |
| 181 | 150 | 300 | 50.35 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 300 | 900 | 300 | 90 | 47.15 |
| 182 | 150 | 300 | 51.38 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 150 | 600 | 150 | 90 | 8.75 |
| 183 | 150 | 300 | 49.38 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 75 | 900 | 300 | 90 | 3.9 |
| 184 | 150 | 300 | 48.41 | 494 | 0 | 0 | 2 | CFRP | SB | 234.5 | 0.02 | 3450 | 0.34 | 150 | 900 | 150 | 90 | 8.75 |
| 185 | 250 | 360 | 36.95 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 300 | 200 | 150 | 90 | 138.3 |
| 186 | 250 | 360 | 36.95 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 300 | 200 | 150 | 90 | 91.5 |
| 187 | 250 | 360 | 24.47 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 1 | 1 | 150 | 90 | 96.26 |
| 188 | 250 | 360 | 24.47 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 1 | 1 | 150 | 90 | 55.37 |
| 189 | 250 | 360 | 22.64 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 1 | 1 | 150 | 90 | 133.6 |
| 190 | 250 | 360 | 22.64 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 1 | 1 | 150 | 90 | 136.6 |
| 191 | 250 | 360 | 20.5 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 300 | 200 | 150 | 90 | 123 |
| 192 | 250 | 360 | 20.5 | 500 | 0.11 | 380 | 3.5 | CFRP | U | 63 | 0.011 | 700 | 1 | 300 | 200 | 150 | 90 | 142.9 |
| 193 | 200 | 173 | 29.3 | 665.3 | 0.163 | 160 | 3 | CFRP | U | 230 | 0.015 | 3430 | 0.165 | 1 | 1 | 210 | 90 | 19.3 |
| 194 | 203 | 305 | 25.2 | 420 | 0 | 0 | 3 | CFRP | U | 228 | 0.015 | 3450 | 0.165 | 76 | 229 | 368 | 90 | 46.7 |
| 195 | 305 | 457 | 32 | 420 | 0 | 0 | 3 | CFRP | U | 228 | 0.015 | 3450 | 0.165 | 152 | 305 | 546 | 90 | 87.2 |
| 196 | 406 | 610 | 32 | 420 | 0 | 0 | 3 | CFRP | U | 228 | 0.015 | 3450 | 0.165 | 252 | 381 | 698.5 | 90 | 126.8 |
References
- Çiftçioğlu, A.Ö.; Naser, M.Z. Hiding in plain sight: What can interpretable unsupervised machine learning and clustering analysis tell us about the fire behavior of reinforced concrete columns? Structures 2022, 40, 920–935. [Google Scholar] [CrossRef]
- Shafaei, H.; Naderpour, H. Seismic fragility evaluation of FRP-retrofitted RC frames subjected to mainshock-aftershock records. Structures 2020, 27, 950–961. [Google Scholar] [CrossRef]
- Hemmatian, A.; Jalali, M.; Naderpour, H.; Nehdi, M.L. Machine learning prediction of fiber pull-out and bond-slip in fiber-reinforced cementitious composites. J. Build. Eng. 2023, 63, 105474. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. The damage effect on the dynamic characteristics of FRP-strengthened reinforced concrete structures. Compos. Struct. 2023, 309, 116731. [Google Scholar] [CrossRef]
- Nwankwo, C.O.; Mahachi, J.; Olukanni, D.O.; Musonda, I. Natural fibres and biopolymers in FRP composites for strengthening concrete structures: A mixed review. Constr. Build. Mater. 2023, 363, 129661. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Qian, S.-Y.; Wang, N.-W.; Xiong, W.; Wu, W.-Q. A review on stochastic multiscale analysis for FRP composite structures. Compos. Struct. 2022, 284, 115132. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, L.; Wu, Y.-F.; Liu, J. Flexural design of reinforced concrete structures strengthened with hybrid bonded FRP. Compos. Struct. 2021, 269, 113996. [Google Scholar] [CrossRef]
- Pohoryles, D.A.; Melo, J.; Rossetto, T.; Varum, H.; D’Ayala, D. Effect of slab and transverse beam on the FRP retrofit effectiveness for existing reinforced concrete structures under seismic loading. Eng. Struct. 2021, 234, 111991. [Google Scholar] [CrossRef]
- Wei, X.; Russell, J.; Živanović, S.; Mottram, J.T. Measured dynamic properties for FRP footbridges and their critical comparison against structures made of conventional construction materials. Compos. Struct. 2019, 223, 110956. [Google Scholar] [CrossRef]
- Ferracuti, B.; Savoia, M.; Zucconi, M. RC frame structures retrofitted by FRP-wrapping: A model for columns under axial loading and cyclic bending. Eng. Struct. 2020, 207, 110243. [Google Scholar] [CrossRef]
- Markou, G.; Garcia, R.; Mourlas, C.; Guadagnini, M.; Pilakoutas, K.; Papadrakakis, M. A new damage factor for seismic assessment of deficient bare and FRP-retrofitted RC structures. Eng. Struct. 2021, 248, 113152. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Wang, X.; Yu, T.; Xia, Y. Vibration-based FRP debonding detection using a Q-learning evolutionary algorithm. Eng. Struct. 2023, 275, 115254. [Google Scholar] [CrossRef]
- Zeng, J.J.; Chen, S.P.; Feng, P.; Zhuge, Y.; Peng, K.D.; Dai, J.G.; Fan, T.H. FRP bar-reinforced ultra-high-performance concrete plates with a grouting sleeve connection: Development and flexural behavior. Eng. Struct. 2023, 287, 116164. [Google Scholar] [CrossRef]
- Wu, R.; Xu, R.; Wang, G. Modeling and prediction of short/long term mechanical behavior of FRP-strengthened slabs using innovative composite finite elements. Eng. Struct. 2023, 281, 115727. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Doulabi, H.H. A flexible robust model for blood supply chain network design problem. Ann. Oper. Res. 2022, 328, 701–726. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Teimoori, S.; Mirzazadeh, A.; Pasandideh, S.H.R.; Tehrani, N.G. Robust Fuzzy chance constraint programming for multi-item EOQ model with random disruption and partial backordering under uncertainty. J. Ind. Prod. Eng. 2019, 36, 276–285. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Weber, G.-W. Fuzzy Mathematical Programming and Self-Adaptive Artificial Fish Swarm Algorithm for Just-in-Time Energy-Aware Flow Shop Scheduling Problem With Outsourcing Option. IEEE Trans. Fuzzy Syst. 2020, 28, 2772–2783. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the 13th International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996. [Google Scholar]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 Algorithms in Data Mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties. Int. Stat. Rev./Rev. Int. Stat. 1989, 57, 238–247. [Google Scholar] [CrossRef]
- Zhang, Y.; Haghani, A. A Gradient Boosting Method to Improve Travel Time Prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Naser, M.Z. Observational Analysis of Fire-Induced Spalling of Concrete through Ensemble Machine Learning and Surrogate Modeling. J. Mater. Civ. Eng. 2021, 33, 04020428. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and design equations for FRP-strengthening in shear. Constr. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Rehabilitation of rectangular simply supported RC beams with shear deficiencies using CFRP composites. Constr. Build. Mater. 2002, 16, 135–146. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. An experimentally based analytical model for the shear capacity of FRP-strengthened reinforced concrete beams. Mech. Compos. Mater. 2008, 44, 231–244. [Google Scholar] [CrossRef]
- Adhikary, B.; Mutsuyoshi, H. Behavior of Concrete Beams Strengthened in Shear with Carbon-Fiber Sheets. J. Compos. Constr. J Compos. Constr. 2004, 8, 258–264. [Google Scholar] [CrossRef]
- Diagana, C.; Li, A.; Gedalia, B.; Delmas, Y. Shear strengthening effectiveness with CFF strips. Eng. Struct. 2003, 25, 507–516. [Google Scholar] [CrossRef]
- Ianniruberto, U.; Imbimbo, M. Role of fiber reinforced plastic sheets in shear response of reinforced concrete beams: Experimental and analytical results. J. Compos. Constr. 2004, 8, 415–424. [Google Scholar] [CrossRef]
- Cao, S.Y.; Chen, J.F.; Teng, J.G.; Hao, Z.; Chen, J. Debonding in RC beams shear strengthened with complete FRP wraps. J. Compos. Constr. 2005, 9, 417–428. [Google Scholar] [CrossRef]
- Carolin, A.; Täljsten, B. Theoretical study of strengthening for increased shear bearing capacity. J. Compos. Constr. 2005, 9, 497–506. [Google Scholar] [CrossRef]
- Zhang, Z.; Hsu, C.-T.T. Shear strengthening of reinforced concrete beams using carbon-fiber- reinforced polymer laminates. J. Compos. Constr. 2005, 9, 158–169. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Dias, S.J.E. Near surface mounted CFRP laminates for shear strengthening of concrete beams. Cem. Concr. Compos. 2006, 28, 276–292. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber-reinforced polymer shear strengthening of reinforced concrete beams: Experimental study and analytical modeling. ACI Struct. J. 2006, 103, 720–728. [Google Scholar]
- Pellegrino, C.; Modena, C. Fiber reinforced polymer shear strengthening of reinforced concrete beams with transverse steel reinforcement. J. Compos. Constr. 2002, 6, 104–111. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Chen, Z.; Lee, S.; Ng, M.; Xu, M.; Tang, J. Effect of size on the failure of geometrically similar concrete beams strengthened in shear with FRP strips. J. Compos. Constr. 2007, 11, 487–496. [Google Scholar] [CrossRef]
- Kim, G.; Sim, J.; Oh, H. Shear strength of strengthened RC beams with FRPs in shear. Constr. Build. Mater. 2008, 22, 1261–1270. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M.; Rasulo, A. Experimental Response of RC Beams Strengthened in Shear by FRP Sheets. Open Civ. Eng. J. 2015, 7, 127–135. [Google Scholar] [CrossRef]
- Tidarut, J.; Jian-Guo, D.; Dawei, Z.; Mineo, S.; Tamon, U. Experimental Study on Shear Behavior of Reinforced-Concrete Members Fully Wrapped with Large Rupture-Strain FRP Composites. J. Compos. Constr. 2014, 18, A4013009. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, X.; Guo, M.; Huang, X.; Hu, B. Enhancing the Performance of CFRP Shear-Strengthened RC Beams Using ‘Ductile’ Anchoring Devices. Front. Mater. 2020, 7, 292. [Google Scholar] [CrossRef]
- Li, W.; Leung, C.K.Y. Effect of shear span-depth ratio on mechanical performance of RC beams strengthened in shear with U-wrapping FRP strips. Compos. Struct. 2017, 177, 141–157. [Google Scholar] [CrossRef]
- Gonzalez-Libreros, J.H.; Sneed, L.H.; D’Antino, T.; Pellegrino, C. Behavior of RC beams strengthened in shear with FRP and FRCM composites. Eng. Struct. 2017, 150, 830–842. [Google Scholar] [CrossRef]
- Matthys, S. Structural Behaviour and Design of Concrete Members Strengthened with Externally Bonded FRP Reinforcement; Ghent University: Ghent, Belgium, 2000. [Google Scholar]
- Tan, Z.; Ye, L.P. Experimental research on shear capacity of RC beam strengthened with externally bonded FRP sheets. China Civ. Eng. J. 2003, 36, 12–18. [Google Scholar]
- Allam, S.; Ebeido, T. Retrofitting of RC beams predamaged in shear using CFRP sheets. Alex. Eng. J. 2003, 42, 87–101. [Google Scholar]
- Saribiyik, A.; Abodan, B.; Balci, M.T. Experimental study on shear strengthening of RC beams with basalt FRP strips using different wrapping methods. Eng. Sci. Technol. Int. J. 2021, 24, 192–204. [Google Scholar] [CrossRef]
- Bukhari, I.A.; Vollum, R.L.; Ahmad, S.; Sagaseta, J. Shear strengthening of reinforced concrete beams with CFRP. Mag. Concr. Res. 2010, 62, 65–77. [Google Scholar] [CrossRef]
- Bukhari, I.A.; Vollum, R.; Ahmad, S.; Sagaseta, J. Shear Strengthening of Short Span Reinforced Concrete Beams with CFRP Sheets. Arab. J. Sci. Eng. 2013, 38, 523–536. [Google Scholar] [CrossRef]
- Alzate, A.; Arteaga, Á.; de Diego, A.; Perera, R. Shear strengthening of reinforced concrete beams using fibre reinforced polymers (frp). Eur. J. Environ. Civ. Eng. 2009, 13, 1051–1060. [Google Scholar] [CrossRef]
- Rizzo, A.; De Lorenzis, L. Behavior and capacity of RC beams strengthened in shear with NSM FRP reinforcement. Constr. Build. Mater. 2009, 23, 1555–1567. [Google Scholar] [CrossRef]
- Bae, S.; Tann, B.; Belarbi, A. Size effect of reinforced concrete beams strengthened in shear with externally bonded CFRP sheets. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering (CICE 2012), Rome, Italy, 13–15 June 2012. [Google Scholar]
- Zaitseva, E.; Rabcan, J.; Levashenko, V.; Kvassay, M. Importance analysis of decision making factors based on fuzzy decision trees. Appl. Soft Comput. 2023, 134, 109988. [Google Scholar] [CrossRef]
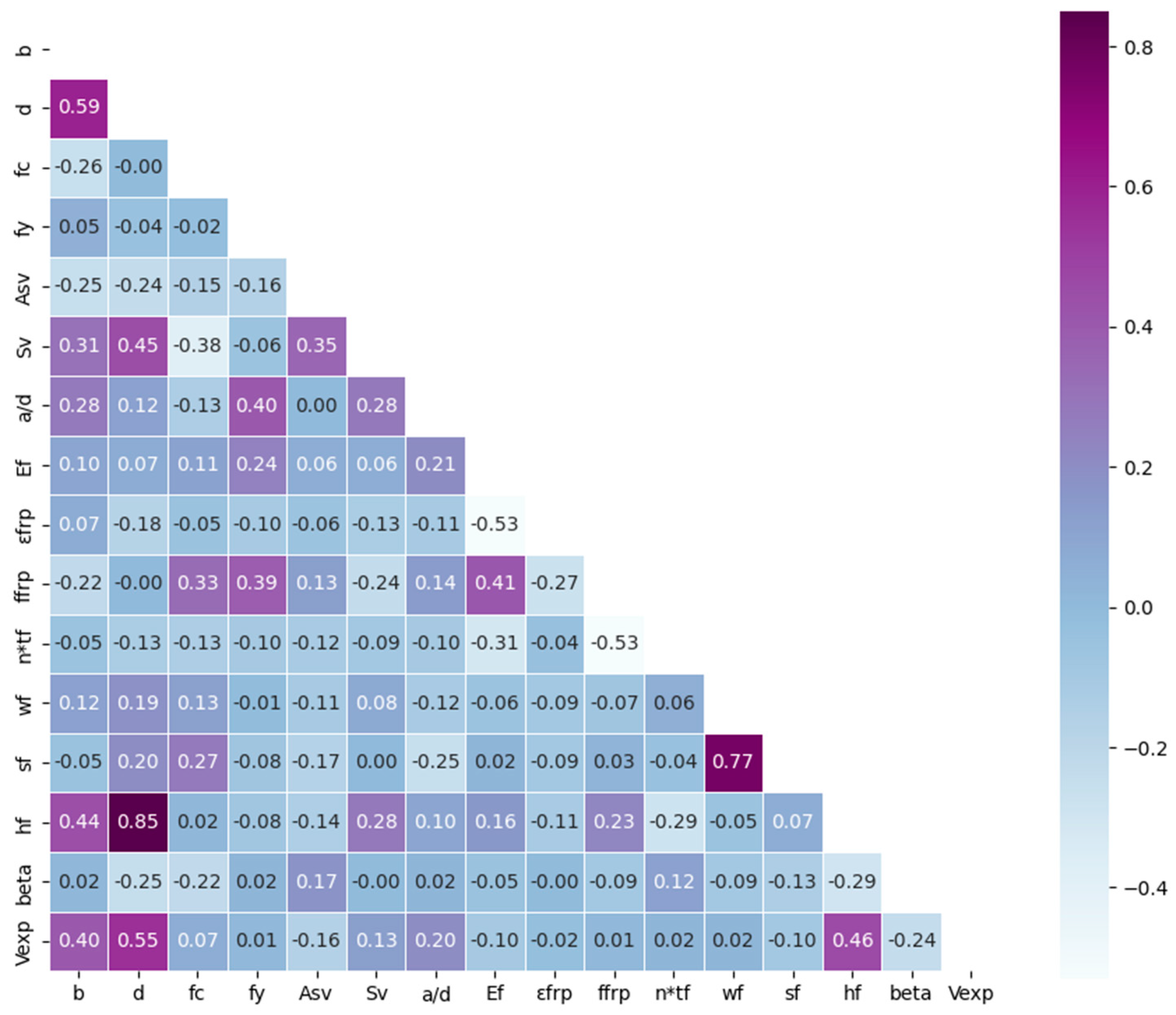






| Variables | Notation | Unit | Min | Mean | Std. | Max |
|---|---|---|---|---|---|---|
| Beam Width | b | mm | 75.00 | 180.40 | 52.02 | 406.00 |
| Beam Effective Depth | d | mm | 120.00 | 297.40 | 101.82 | 660.00 |
| Concrete Compressive Strength | fc | MPa | 13.30 | 34.13 | 12.20 | 71.00 |
| Yield Strength of Steel Reinforcement | fy | MPa | 240.00 | 458.20 | 90.47 | 665.30 |
| Transverse Steel Ratio | Asv | % | 0.00 | 0.12 | 0.11 | 0.41 |
| Spacing of Transverse Reinforcement | Sv | mm | 0.00 | 147.70 | 131.21 | 400.00 |
| Shear Span to Effective Depth Ratio | a/d | --- | 1.00 | 2.78 | 0.55 | 4.08 |
| Elastic Modulus of FRP | Ef | GPa | 5.30 | 200.95 | 109.80 | 392.00 |
| Ultimate Strain of FRP | εFRP | --- | 0.00 | 0.02 | 0.01 | 0.07 |
| Tensile Strength of FRP | fFRP | MPa | 112.00 | 3073.52 | 1151.52 | 4500.00 |
| Total Thickness of FRP | n × tf | mm | 0.07 | 0.38 | 0.35 | 1.50 |
| Width of FRP Strips | wf | mm | 1.00 | 42.94 | 74.07 | 304.80 |
| Spacing of FRP Strips | Sf | mm | 1.00 | 124.61 | 218.08 | 1195.00 |
| Height of FRP Strips | hf | mm | 150.00 | 323.52 | 115.90 | 720.00 |
| Angle of Inclination of FRP Strips | βeta | ° | 45.00 | 84.57 | 14.62 | 90.00 |
| Shear Capacity Contribution by FRP | Vexp | kN | 3.90 | 58.86 | 48.97 | 343.20 |
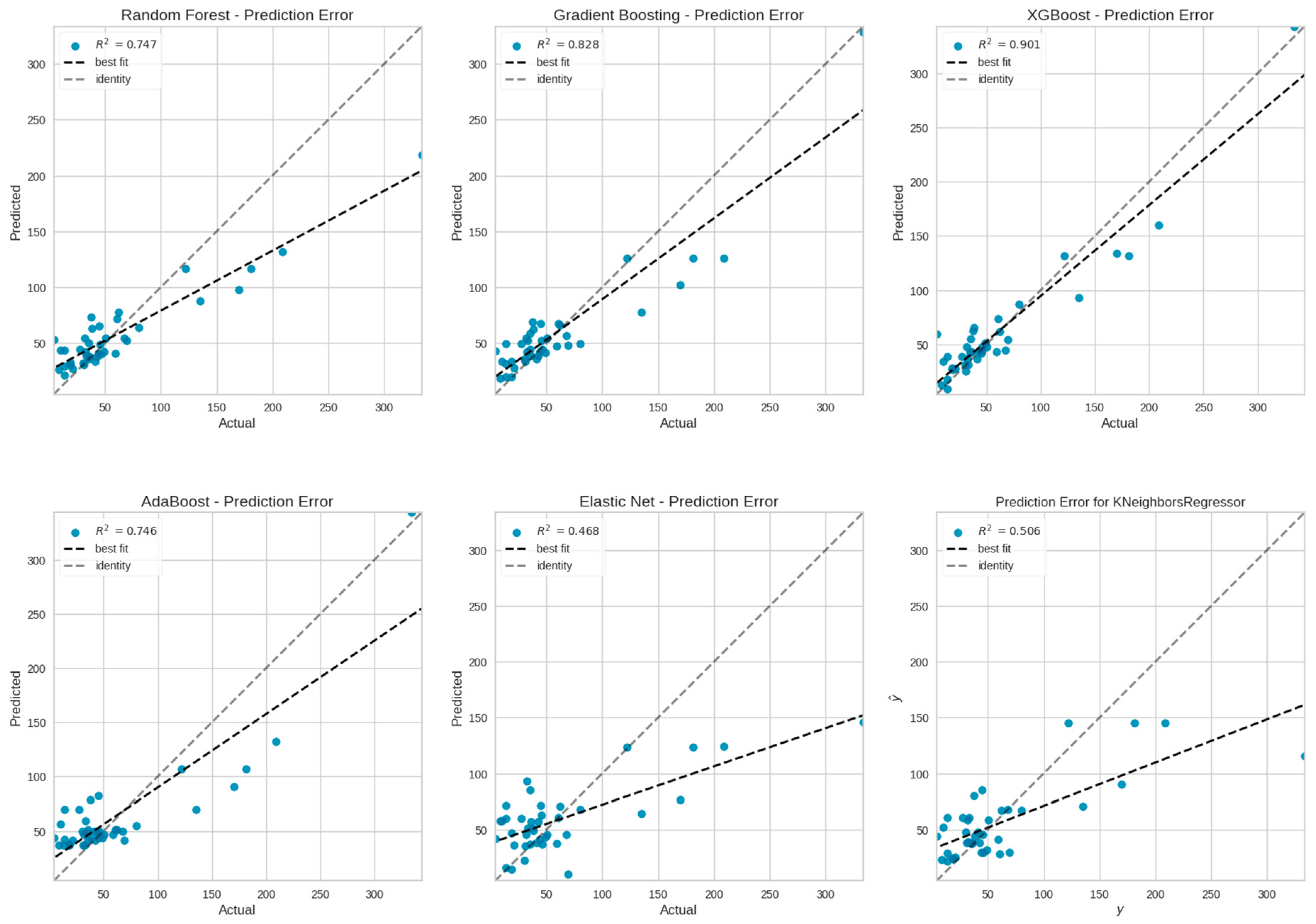
| Model | RMSE | MSE | MAE | R2 |
|---|---|---|---|---|
| XGBoost | 20.065 | 402.608 | 13.856 | 0.901 |
| GB | 26.454 | 699.823 | 18.427 | 0.828 |
| RF | 32.148 | 1033.504 | 21.275 | 0.747 |
| AdaBoost | 32.163 | 1034.457 | 24.163 | 0.746 |
| KNN | 44.888 | 2014.893 | 26.398 | 0.506 |
| Elastic Net | 46.566 | 2168.379 | 30.654 | 0.468 |
| 0.488 | 0.610 | −0.507 | 0.773 | 0.200 | −0.900 | −0.398 | 0.161 | 0.628 | 0.339 |
|---|---|---|---|---|---|---|---|---|---|
| −0.568 | 0.373 | 0.565 | −0.035 | 0.186 | −0.649 | −0.325 | 1.181 | 0.249 | 0.394 |
| 0.280 | −0.685 | 0.454 | 0.470 | 0.172 | 0.384 | 0.297 | −0.417 | 0.138 | −0.516 |
| 0.203 | −0.620 | 0.107 | −0.345 | −0.699 | 0.334 | 0.495 | 0.134 | 0.658 | −0.210 |
| −0.026 | −0.399 | 0.359 | 0.285 | −0.452 | 0.166 | 0.012 | 0.367 | 0.324 | 0.278 |
| −0.328 | −0.270 | 0.029 | −0.206 | −0.502 | −0.023 | 1.001 | −0.399 | −0.083 | −0.329 |
| 0.301 | −0.854 | 0.384 | 0.747 | 0.323 | 0.568 | 0.032 | −0.214 | −0.589 | −0.294 |
| 0.606 | −0.382 | 0.399 | −0.248 | 0.587 | −0.321 | −0.320 | −0.694 | 0.107 | −0.094 |
| −0.277 | 0.500 | 0.175 | 0.380 | 0.457 | −0.169 | 0.382 | 0.251 | −0.106 | 0.000 |
| −0.626 | −0.364 | −0.095 | 0.269 | 0.481 | −0.408 | 0.317 | −0.250 | −0.707 | 0.030 |
| −0.680 | 0.071 | −0.006 | −0.016 | −0.595 | 0.332 | −0.663 | 0.349 | −0.033 | 0.424 |
| −0.020 | −0.388 | −0.475 | 0.121 | −0.295 | 0.208 | 0.311 | 0.428 | −0.651 | 0.137 |
| −0.661 | 0.647 | −0.695 | 0.681 | 0.509 | 0.346 | −0.461 | −0.331 | −0.514 | 0.731 |
| −0.069 | 0.541 | −0.792 | −0.381 | −0.564 | −0.356 | 0.725 | 0.354 | 0.047 | −0.382 |
| 0.701 | 0.078 | −0.238 | 0.048 | −0.338 | −0.410 | −0.177 | −0.569 | −0.456 | −0.417 |
| −0.148 | −0.499 | 0.239 | 0.768 | −0.200 | −0.336 | −0.309 | 0.683 | −0.248 | −0.545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezami, N.; Özyüksel Çiftçioğlu, A.; Mirrashid, M.; Naderpour, H. Advancing Shear Capacity Estimation in Rectangular RC Beams: A Cutting-Edge Artificial Intelligence Approach for Assessing the Contribution of FRP. Sustainability 2023, 15, 16126. https://doi.org/10.3390/su152216126
Ezami N, Özyüksel Çiftçioğlu A, Mirrashid M, Naderpour H. Advancing Shear Capacity Estimation in Rectangular RC Beams: A Cutting-Edge Artificial Intelligence Approach for Assessing the Contribution of FRP. Sustainability. 2023; 15(22):16126. https://doi.org/10.3390/su152216126
Chicago/Turabian StyleEzami, Nima, Aybike Özyüksel Çiftçioğlu, Masoomeh Mirrashid, and Hosein Naderpour. 2023. "Advancing Shear Capacity Estimation in Rectangular RC Beams: A Cutting-Edge Artificial Intelligence Approach for Assessing the Contribution of FRP" Sustainability 15, no. 22: 16126. https://doi.org/10.3390/su152216126
APA StyleEzami, N., Özyüksel Çiftçioğlu, A., Mirrashid, M., & Naderpour, H. (2023). Advancing Shear Capacity Estimation in Rectangular RC Beams: A Cutting-Edge Artificial Intelligence Approach for Assessing the Contribution of FRP. Sustainability, 15(22), 16126. https://doi.org/10.3390/su152216126







