An Artificial Physarum polycephalum Colony for the Electric Location-Routing Problem
Abstract
:1. Introduction
2. Literature Review
3. Mathematical Formulation
3.1. Symbol Definitions
3.2. Building a Multi-Objective Function of the ELRP
4. Algorithm Design of APPC
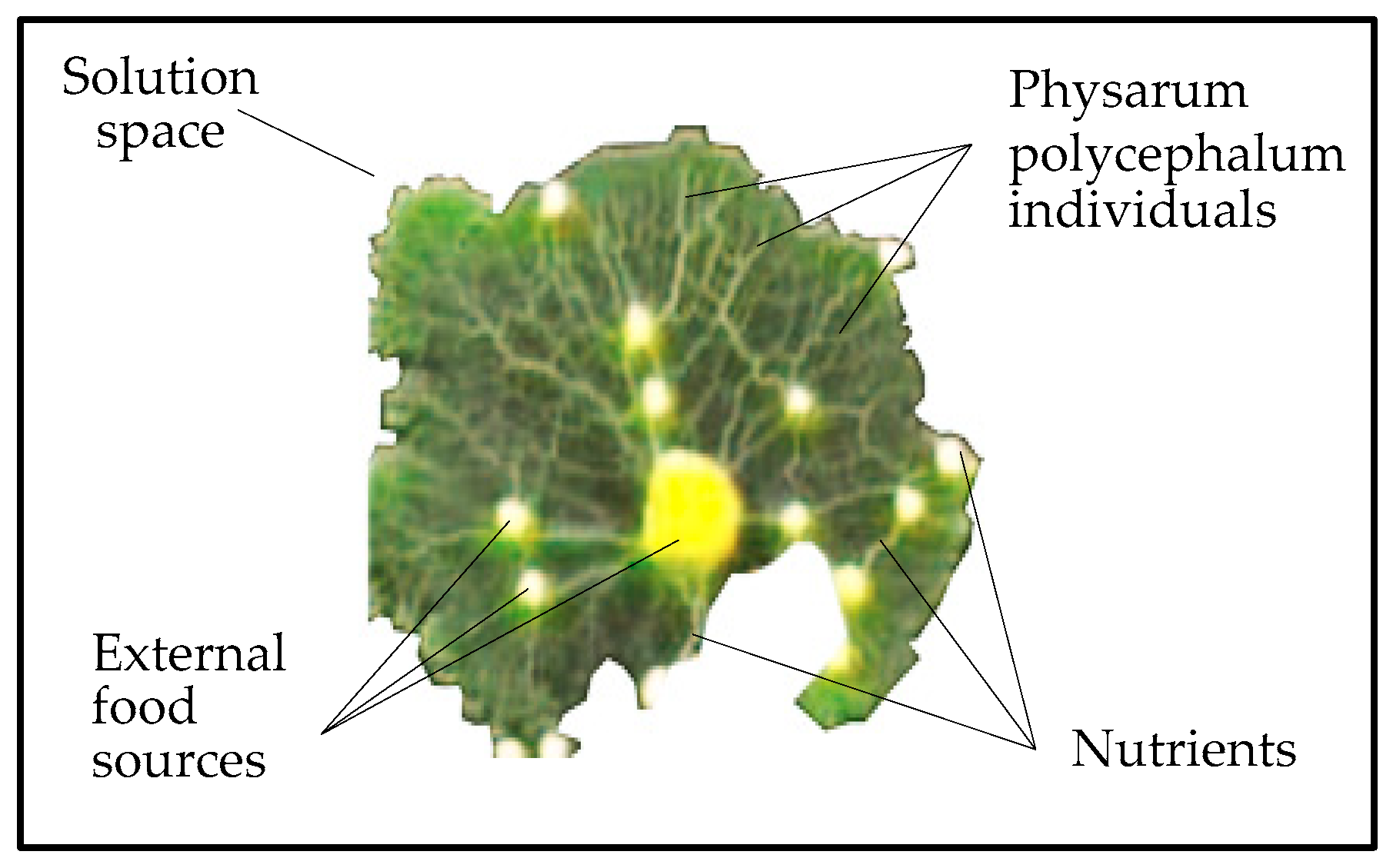
4.1. Artificial P. polycephalum Colony
4.2. Step 1: Initialization
4.3. Step 2: Expansion
| Algorithm 1: Expansion operation |
| 1: Input: the ELRP networks, [(xi,yi)]n, D= [Dij]n×n |
| 2: Input: electric vehicle parameters, Ui, cvk, vk, Qvk, pvk, Srkij, Sckj, cc, ch, co. |
| 3: Input: APPC parameters, M, ps, pf. |
| 4: Generate: random individuals {x} |
| 5: Define: the fitness function in Equations (9)–(18) |
| 6: Initialization: Ite_max, eth |
| 7: For iteration counter Ite = 1: Ite_max |
| 8: For APPC individual m= 1:M |
| 9: For node number i = 1:n |
| 10: To randomly select electric vehicle vk |
| 11: Social-learning by ps |
| 12: Free-learning by pf |
| 13: End for |
| 14: End for |
| 15: To update the APPC colony |
| 16: To calculate the fitness according to Equations (9)–(18) |
| 17: // Contraction operation |
| 18: End for |
4.4. Step 3: Contraction
| Algorithm 2: Contraction operation |
| 1: For iteration counter Ite = 1: Ite_max |
| 2: MergeSort(x, 1, M) |
| 3: To store the temporary optimal solution Temp_x = x(1) |
| 4: To store the temporary optimal fitness Temp_fitness = fitness(1) |
| 5: To calculate the iterative error e = |fitness (1)(Ite) − fitness(1)(Ite-1)| |
| 6: if e > eth |
| 7: select the best M of individuals |
| 8: return to the expansion algorithm |
| 9: else |
| 10: Exit |
| 11: End for // Ite_max |
| 12: output the optimal solution Temp_x |
| 13: output the optimal fitness Temp_fitness |
4.5. Step 4: End Judgment
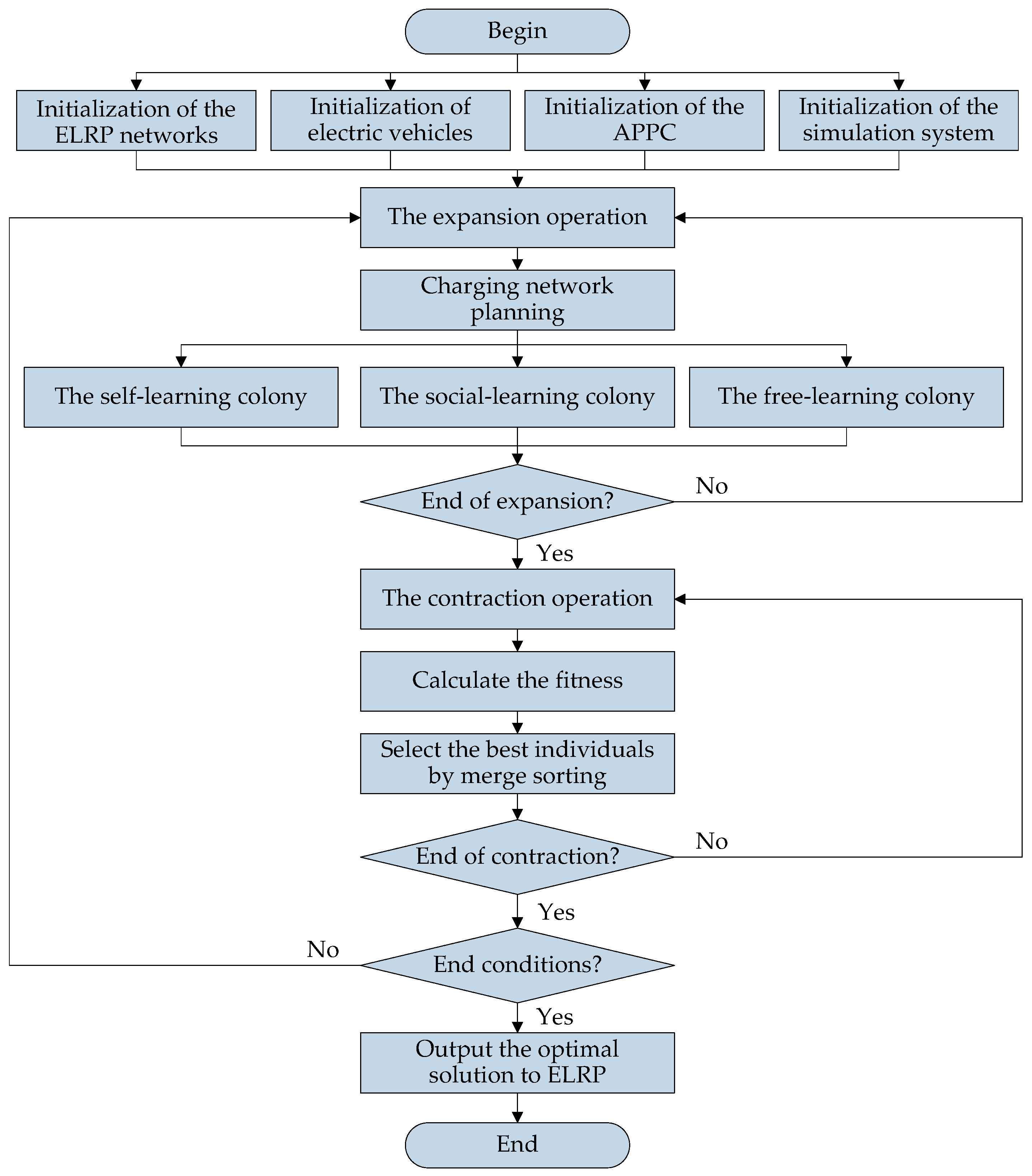
4.6. Algorithm Flow of APPC
4.7. Parameter Adjustment and Algorithm Improvement
5. Computational Results
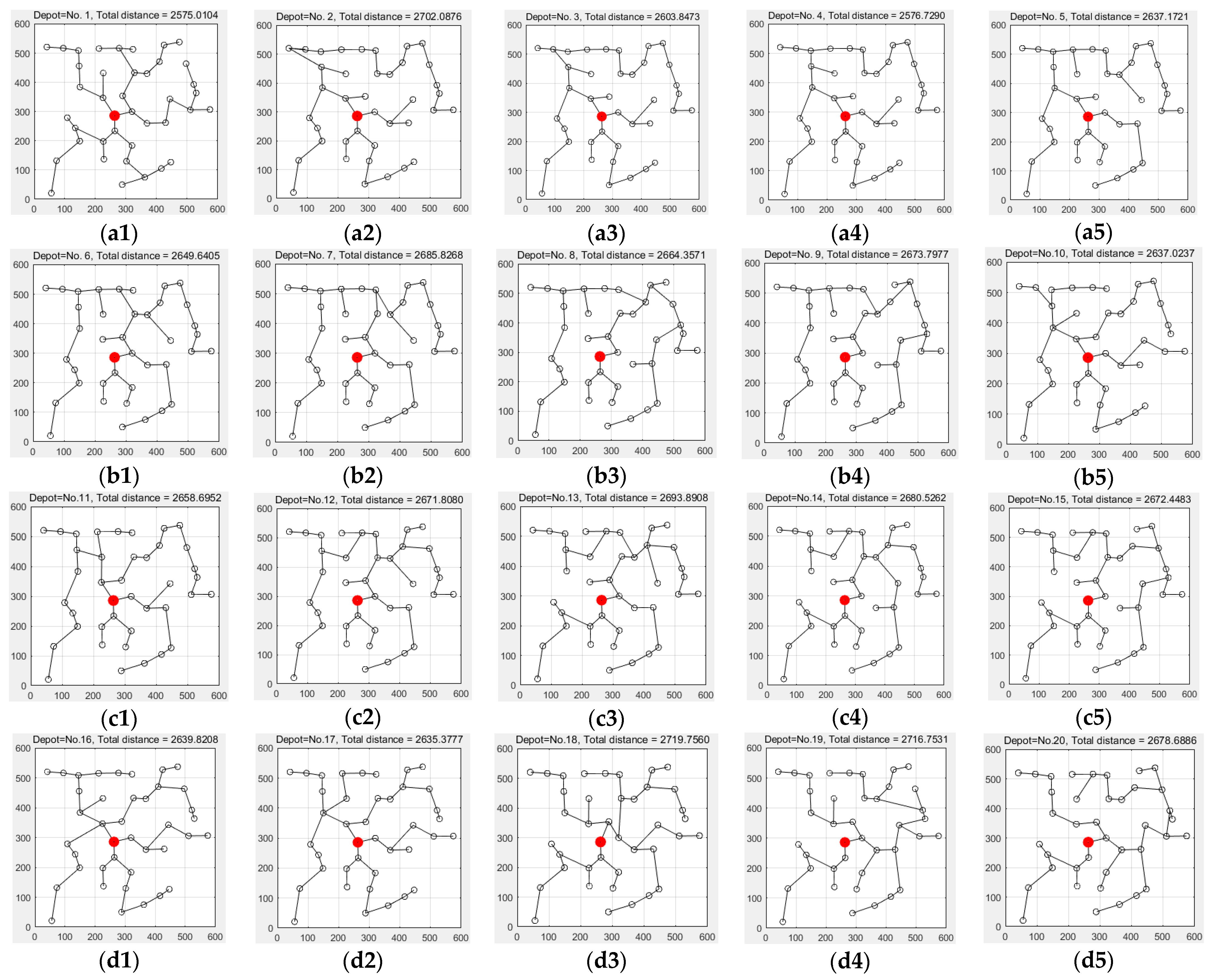
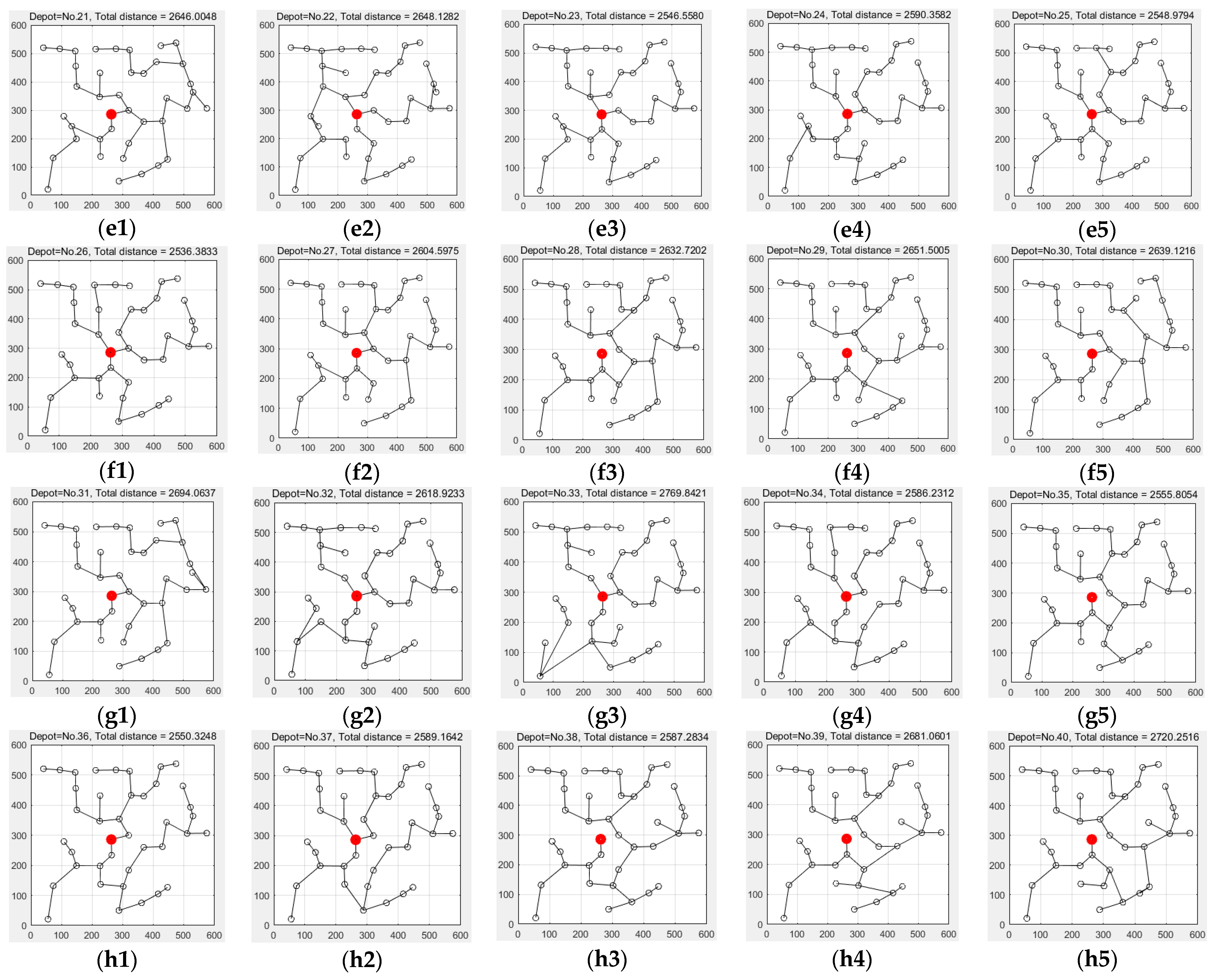
5.1. Design of Benchmark Test
5.2. Test Results
5.3. Sensitivity Analysis
5.4. Comparison of State-of-the-Art Algorithms
5.5. Insight for Engineering Applications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Liu, R.; Su, Y.; Zhang, X. Accelerating two-phase multiobjective evolutionary algorithm for electric location-routing problems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9121–9136. [Google Scholar] [CrossRef]
- Hung, Y.-C.; Michailidis, G. A novel data-driven approach for solving the electric vehicle charging station location-routing problem. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23858–23868. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, S.; Ngo, H. Dynamic wireless charging facility location problem for battery electric vehicles under electricity constraint. Netw. Spat. Econ. 2023, 23, 679–713. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Sun, Y.; Fan, J.; Wang, Z.; Wang, H. Collaborative multidepot electric vehicle routing problem with time windows and shared charging stations. Expert Syst. Appl. 2023, 219, 119654. [Google Scholar] [CrossRef]
- Londoño, A.A.; Gil Gonzalez, W.; Giraldo, O.D.M.; Escobar, J.W. A new matheheuristic approach based on Chu-Beasley genetic approach for the multi-depot electric vehicle routing problem. Int. J. Ind. Eng. Comput. 2023, 14, 555–570. [Google Scholar] [CrossRef]
- Ghorbani, E.; Fluechter, T.; Calvet, L.; Ammouriova, M.; Panadero, J.; Juan, A.A. Optimizing energy consumption in smart cities’ mobility: Electric vehicles, algorithms, and collaborative economy. Energies 2023, 16, 1268. [Google Scholar] [CrossRef]
- Amiri, A.; Amin, S.H.; Zolfagharinia, H. A bi-objective green vehicle routing problem with a mixed fleet of conventional and electric trucks: Considering charging power and density of stations. Expert Syst. Appl. 2023, 213, 119228. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, X.; Zhang, L.; Hua, W.; Li, K. A Pareto artificial fish swarm algorithm for solving a multi-objective electric transit network design problem. Transp. A Transp. Sci. 2020, 16, 1648–1670. [Google Scholar] [CrossRef]
- Ghobadi, A.; Fallah, M.; Tavakkoli-Moghaddam, R.; Kazemipoor, H. A fuzzy two-echelon model to optimize energy consumption in an urban logistics network with electric vehicles. Sustainability 2022, 14, 14075. [Google Scholar] [CrossRef]
- Li, J.; Xie, C.; Bao, Z. Optimal en-route charging station locations for electric vehicles: A new modeling perspective and a comparative evaluation of network-based and metanetwork-based approaches. Transp. Res. Part C Emerg. Technol. 2022, 142, 103781. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Sun, Y.; Wang, X.; Zhe, J.; Wang, H. Electric vehicle charging station location-routing problem with time windows and resource sharing. Sustainability 2022, 14, 11681. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, Z.; Chen, M. The home health care location-routing problem with a mixed fleet and battery swapping stations using a competitive simulated annealing algorithm. Expert Syst. Appl. 2023, 228, 120374. [Google Scholar] [CrossRef]
- Cai, Z.; Yang, Y.; Zhang, X.; Zhou, Y. Design a robust logistics network with an artificial Physarum swarm algorithm. Sustainability 2022, 14, 14930. [Google Scholar] [CrossRef]
- Moazzeni, S.; Tavana, M.; Darmian, S.M. A dynamic location-arc routing optimization model for electric waste collection vehicles. J. Clean. Prod. 2022, 364, 132571. [Google Scholar] [CrossRef]
- Kinene, A.; Birolini, S.; Cattaneo, M.; Granberg, T.A. Electric aircraft charging network design for regional routes: A novel mathematical formulation and kernel search heuristic. Eur. J. Oper. Res. 2023, 309, 1300–1315. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Zhang, X.; Zhou, Y.; Chen, J.; Ma, X. Optimal location planning of electric bus charging stations with integrated photovoltaic and energy storage system. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 1424–1446. [Google Scholar] [CrossRef]
- Schoenberg, S.; Dressler, F. Reducing waiting times at charging stations with adaptive electric vehicle route planning. IEEE Trans. Intell. Veh. 2023, 8, 95–107. [Google Scholar] [CrossRef]
- Emambocus, B.A.S.; Jasser, M.B.; Hamzah, M.; Mustapha, A.; Amphawan, A. An enhanced swap sequence-based particle swarm optimization algorithm to solve TSP. IEEE Access 2021, 9, 164820–164836. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Zhou, M.; Wang, J. Solving dynamic traveling salesman problems with deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2119–2132. [Google Scholar] [CrossRef]
- Alqahtani, M.; Hu, M. Dynamic energy scheduling and routing of multiple electric vehicles using deep reinforcement learning. Energy 2022, 244, 122626. [Google Scholar] [CrossRef]
- Manogaran, G.; Shakeel, P.M.; Priyan R, V.; Chilamkurti, N.; Srivastava, A. Ant colony optimization-induced route optimization for enhancing driving range of electric vehicles. Int. J. Commun. Syst. 2022, 35, e3964. [Google Scholar] [CrossRef]
- Nikzad, E.; Bashiri, M. A two-stage stochastic programming model for collaborative asset protection routing problem enhanced with machine learning: A learning-based matheuristic algorithm. Int. J. Prod. Res. 2022, 61, 81–113. [Google Scholar] [CrossRef]
- Zou, W.-Q.; Pan, Q.-K.; Meng, T.; Gao, L.; Wang, Y.-L. An effective discrete artificial bee colony algorithm for multi-AGVs dispatching problem in a matrix manufacturing workshop. Expert Syst. Appl. 2020, 161, 113675. [Google Scholar] [CrossRef]
- Heidari, A.; Imani, D.M.; Khalilzadeh, M.; Sarbazvatan, M. Green two-echelon closed and open location-routing problem: Application of NSGA-II and MOGWO metaheuristic approaches. Environ. Dev. Sustain. 2022, 25, 9163–9199. [Google Scholar] [CrossRef]
- Tero, A.; Takagi, S.; Saigusa, T.; Ito, K.; Bebber, D.P.; Fricker, M.D.; Yumiki, K.; Kobayashi, R.; Nakagaki, T. Rules for biologically inspired adaptive network design. Science 2010, 327, 439–442. [Google Scholar] [CrossRef]
- de Veluz, M.R.D.; Redi, A.A.N.P.; Maaliw, R.R., III; Persada, S.F.; Prasetyo, Y.T.; Young, M.N. Scenario-based multi-objective location-routing model for pre-disaster planning: A philippine case study. Sustainability 2023, 15, 4882. [Google Scholar] [CrossRef]
- Meidute-Kavaliauskiene, I.; Sütütemiz, N.; Yıldırım, F.; Ghorbani, S.; Činčikaitė, R. Optimizing multi cross-docking systems with a multi-objective green location routing problem considering carbon emission and energy consumption. Energies 2022, 15, 1530. [Google Scholar] [CrossRef]
- Tadaros, M.; Migdalas, A. Bi- and multi-objective location routing problems: Classification and literature review. Oper. Res. 2022, 22, 4641–4683. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Ran, L.; Liu, P.; Guo, Y. Robust location and sizing of electric vehicle battery swapping stations considering users’ choice behaviors. J. Energy Storage 2022, 55, 105561. [Google Scholar] [CrossRef]
- Matijević, L. General variable neighborhood search for electric vehicle routing problem with time-dependent speeds and soft time windows. Int. J. Ind. Eng. Comput. 2023, 14, 275–292. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Velimirovic, L.Z.; Janjic, A.; Vranic, P.; Velimirovic, J.D.; Petkovski, I. Determining the optimal route of electric vehicle using a hybrid algorithm based on fuzzy dynamic programming. IEEE Trans. Fuzzy Syst. 2023, 31, 609–618. [Google Scholar] [CrossRef]
- Liu, L.; Lee, L.S.; Seow, H.-V.; Chen, C.Y. Logistics center location-inventory-routing problem optimization: A systematic review using PRISMA method. Sustainability 2022, 14, 15853. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Kalayci, C.B. Variable neighborhood search algorithms to solve the electric vehicle routing problem with simultaneous pickup and delivery. Mathematics 2022, 10, 3108. [Google Scholar] [CrossRef]
- Cai, Z.; Zhang, Y.; Wu, M.; Cai, D. An entropy-robust optimization of mobile commerce system based on multi-agent system. Arab. J. Sci. Eng. 2016, 41, 3703–3715. [Google Scholar] [CrossRef]
- Yin, Y.; Zhao, X.; Lv, W. Emergency shelter allocation planning technology for large-scale evacuation based on quantum genetic algorithm. Front. Public Health 2023, 10, 1098675. [Google Scholar] [CrossRef]
- Liu, H.; Huang, J.; Yan, J. Solving the problem of green ll-ro using improved particle swarm optimization from a low-carbon perspective. Fresenius Environ. Bull. 2022, 31, 3955–3966. [Google Scholar]
- Haliem, M.; Mani, G.; Aggarwal, V.; Bhargava, B. A distributed model-free ride-sharing approach for joint matching, pricing, and dispatching using deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7931–7942. [Google Scholar] [CrossRef]
- Leite, M.R.C.O.; Bernardino, H.S.; Gonçalves, L.B. A variable neighborhood descent with ant colony optimization to solve a bilevel problem with station location and vehicle routing. Appl. Intell. 2022, 52, 7070–7090. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Yu, X.; Sun, W. Heuristic sequencing Hopfield neural network for pick-and-place location routing in multi-functional placers. Neurocomputing 2022, 472, 35–44. [Google Scholar] [CrossRef]
- Katiyar, S.; Khan, R.; Kumar, S. Artificial bee colony algorithm for fresh food distribution without quality loss by delivery route optimization. J. Food Qual. 2021, 2021, 4881289. [Google Scholar] [CrossRef]
- Cai, Z.; Jiang, S.; Dong, J.; Tang, S. An artificial plant community algorithm for the accurate range-free positioning of wireless sensor networks. Sensors 2023, 23, 2804. [Google Scholar] [CrossRef]
- Yu, N.K.; Jiang, W.; Hu, R.; Qian, B.; Wang, L. Learning whale optimization algorithm for open vehicle routing problem with loading constraints. Discret. Dyn. Nat. Soc. 2021, 2021, 8016356. [Google Scholar] [CrossRef]
- Cai, Z.; Xiong, Z.; Wan, K.; Xu, Y.; Xu, F. A node selecting approach for traffic network based on artificial slime mold. IEEE Access 2020, 8, 8436–8448. [Google Scholar] [CrossRef]
- Cai, Z.; Feng, Y.; Yang, S.; Yang, J. A state transition diagram and an artificial Physarum polycephalum colony algorithm for the flexible job shop scheduling problem with transportation constraints. Processes 2023, 11, 2646. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Amiri, A.; Zolfagharinia, H.; Amin, S.H. Routing a mixed fleet of conventional and electric vehicles for urban delivery problems: Considering different charging technologies and battery swapping. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2191804. [Google Scholar] [CrossRef]




| Reference Number | Authors | Year | Objective | Benchmark Test |
|---|---|---|---|---|
| [1] | Wang C, et al. | 2023 | The total driving distance, the number of charging facilities, and the number of vehicles. | Modified classic TS-MOEA to solve the ELRP. |
| [2] | Hung YC, et al. | 2022 | To minimize the demand’s mean response time. | Designed an ELRP test extracted from Seattle in Washington state. |
| [8] | Liu Y, et al. | 2020 | Minimizing the costs for passengers and operators. | The transit network in an urban region of Beijing. |
| [9] | Ghobadi A, et al. | 2022 | The fixed cost of using EVs, the transportation cost, the penalty cost of time windows, and the cost of energy consumption. | Revised the Solomon benchmark to ELRP. |
| [11] | Wang Y, et al. | 2022 | The operating cost and the number of EVs. | Adjusted the EVCS-LRPTWRS in Chongqing City. |
| [13] | Cai Z, et al. | 2022 | The relative robustness, the betweenness robustness, the edge robustness, and the closeness robustness. | Modified the road network of Mexico City. |
| [15] | Kinene A, et al. | 2023 | To maximize regional connectivity and minimize the total investment costs for charging stations at airports. | The under-utilized regional airports in Sweden. |
| [16] | Liu XH, et al. | 2023 | To minimize the infrastructure investment, vehicle operating, battery electric bus purchase, recharging, and carbon emission costs. | The network of battery electric buses in Beijing. |
| [17] | Schoenberg S, et al. | 2023 | The driving, waiting, and charging time. | Extracted the road network of German Bundesnetzagentur from OpenStreetMap. |
| [21] | Manogaran G, et al. | 2022 | The first phase is to control delay and prevent EV failures, the second phase is to optimize the inputs of power and travel time. | A numerical example. |
| [25] | Tero A, et al. | 2010 | Network planning. | Tokyo railway system. |
| [29] | Zhang NW, et al. | 2022 | The EV users’ choice behavior, service levels, charging rate, and battery swapping service rate. | Real-world data from NYCTTLC are used to generate instances. |
| [30] | Matijevic L | 2023 | To minimize the total distance traveled by all vehicles and minimize the penalty for missing time windows for customers. | Modified a benchmark dataset presented in [31]. |
| [32] | Velimirovic LZ, et al. | 2023 | The distance between the starting point, chargers, and final point, the amount of time spent at the charging station, and the attractiveness of the site. | A numerical example from the City of Niš. |
| [34] | Yilmaz Y, et al. | 2022 | To minimize the total distance traveled. | A numerical example. |
| [46] | Yang J, et al. | 2015 | To minimize total cost, including the construction cost of battery swap stations and EVs shipping cost. | Modified the classic VRP data sets to ELRP. |
| [47] | Amiri A, et al. | 2023 | To minimize the recharging cost, the initial recharging of the EVs, the acquisition cost, the labor cost, and the travel cost along the route. | Randomly generated several samples from Scarborough, Ontario. |
| Symbol | Definition |
|---|---|
| N | A network node set |
| E | A network edge set |
| V | An electric vehicle set |
| n | A parameter for the total number of all nodes |
| pvk | A parameter for the power consumption coefficient of electric vehicle vk |
| Srkij | A parameter for the traveling speed of electric vehicle vk on edge Eij |
| Sckj | A parameter for the charging speed of electric vehicle vk on node Nj |
| Qvk | A parameter for the maximum transportation volume of electric vehicle vk |
| cc | A parameter for the unit construction cost |
| ch | A parameter for the unit holding cost |
| co | A parameter for the unit operating cost |
| Ite_max | A parameter for the maximum iterations |
| M | A parameter for the population size of APPC |
| ps | A parameter for the social-learning probability |
| pf | A parameter for the free-learning probability |
| eth | A parameter for the error threshold |
| Ni | A node |
| Ui | The user demand on node Ni |
| i | The node number |
| (xi, yi) | The coordinates of node Ni |
| Eij | The edge between nodes Ni and Nj |
| Dij | The distance between nodes Ni and Nj |
| D∑ | The total distance of ELRP |
| di | The degree of node Ni |
| davg | The average degree of ELRP network |
| vk | An electric vehicle |
| V∑ | The total number of electric vehicles |
| cvk | The electric capacity of electric vehicle vk |
| Qvki | The transportation volume of electric vehicle vk on node Ni |
| Pvk | The power consumption of electric vehicle vk |
| Trkij | The traveling time of electric vehicle vk between nodes Ni and Nj |
| Tckj | The charging time of electric vehicle vk on node Nj |
| T∑ | The total time of the ELRP |
| Cc | The construction cost |
| Ch | The holding cost |
| Co | The operating cost |
| C∑ | The total cost |
| O∑ | The order fill rate |
| Ite | An iteration counter |
| m | The number of APPC individual |
| x | The variable of an artificial APPC individual |
| e | The solution error |
| Number of Branches | 1st Optimal Solution | 2nd Optimal Solution | 3rd Optimal Solution | 4th Optimal Solution | 5th Optimal Solution | 6th Optimal Solution |
|---|---|---|---|---|---|---|
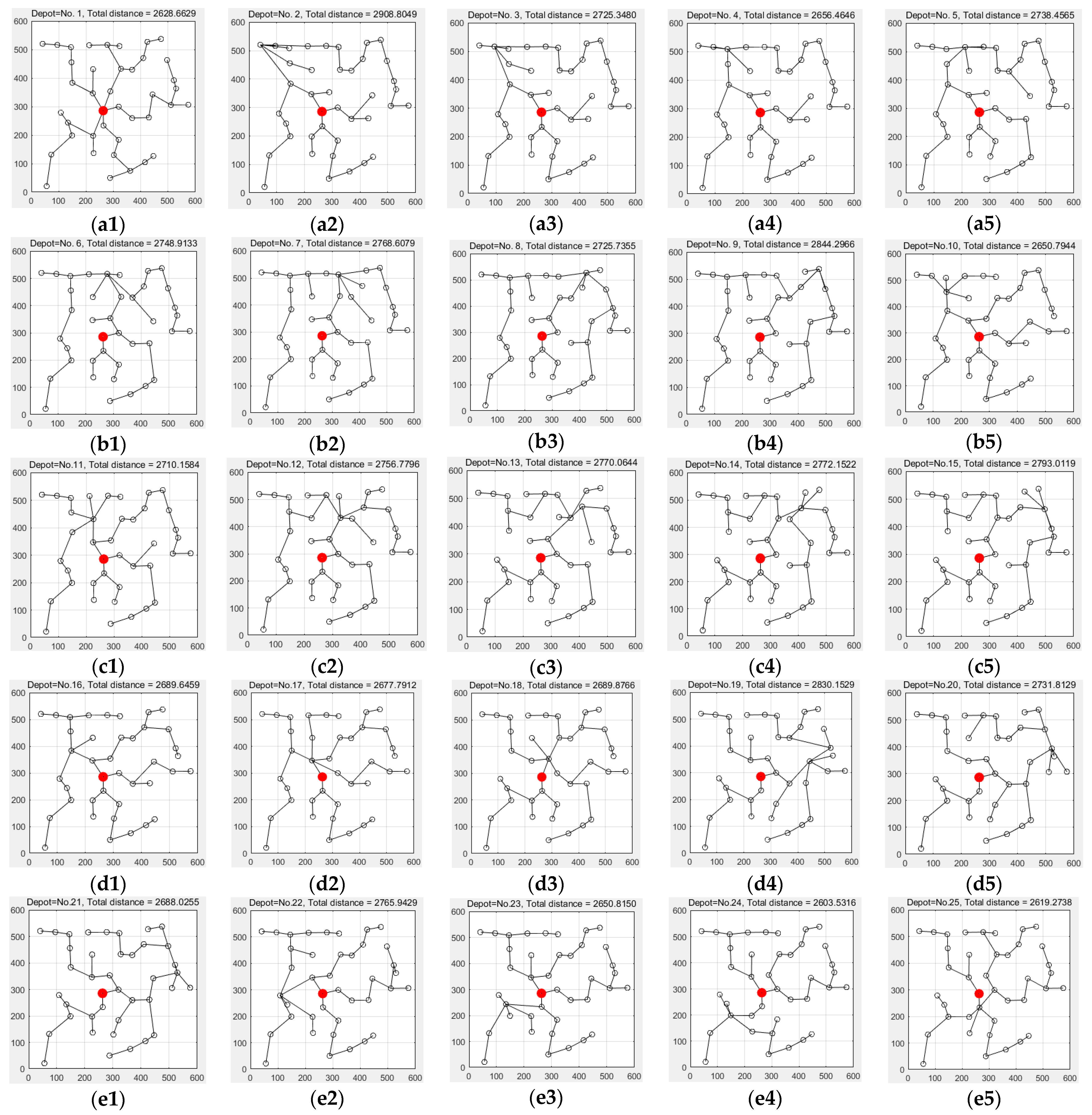
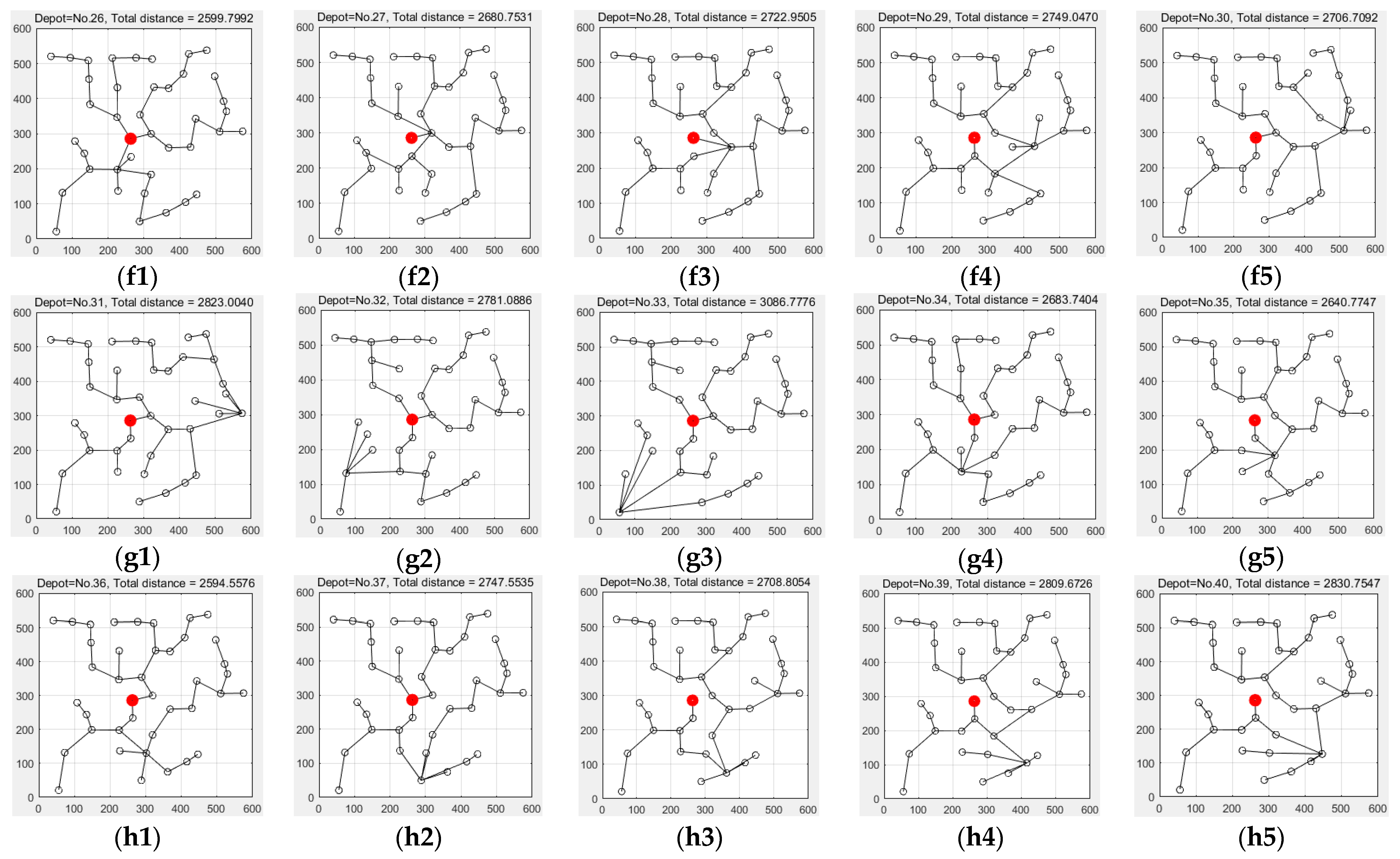
| 3 | No.26 (2536.3833) | No.23 (2546.5580) | No.25 (2548.9794) | No.36 (2550.3248) | No.35 (2555.8054) | No.1 (2575.0104) |
| 4 | No.36 (2553.6100) | No.26 (2556.3468) | No.23 (2572.7760) | No.25 (2576.8416) | No.1 (2585.5459)) | No.35 (2598.4972) |
| 5 | No.36 (2594.5576) | No.26 (2599.7992) | No.24 (2603.5316) | No.25 (2619.2738) | No.1 (2628.6629) | No.35 (2640.7747) |
| Traffic Jam | Total Distance D∑ | Total Time T∑ | Total Cost C∑ | Total EVs V∑ | Order Fill Rate O∑ |
|---|---|---|---|---|---|
| 0% | 2536.3833 | 58.3077 | 3855.3026 | 3.0000 | 0.9428 |
| 10% | 2607.4020 | 67.3486 | 4113.8546 | 3.0000 | 0.9107 |
| 20% | 2716.9129 | 79.7469 | 4458.1020 | 3.0000 | 0.8689 |
| 30% | 2863.6262 | 96.6129 | 4900.8896 | 3.0000 | 0.8185 |
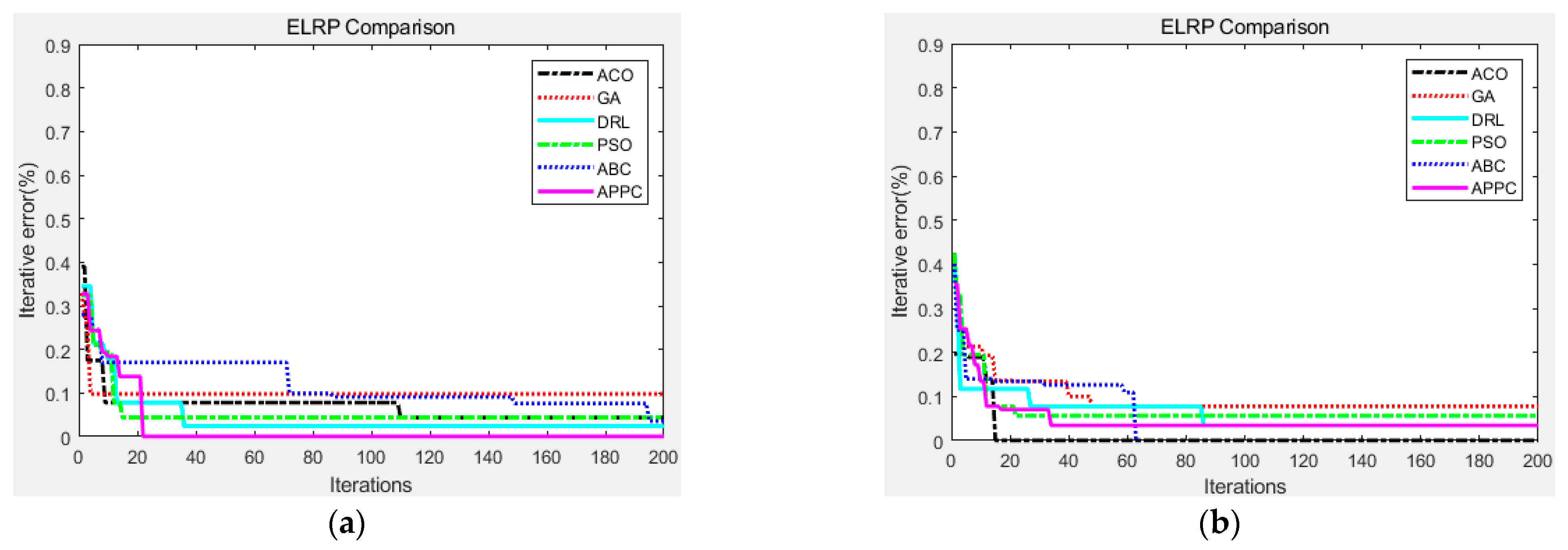
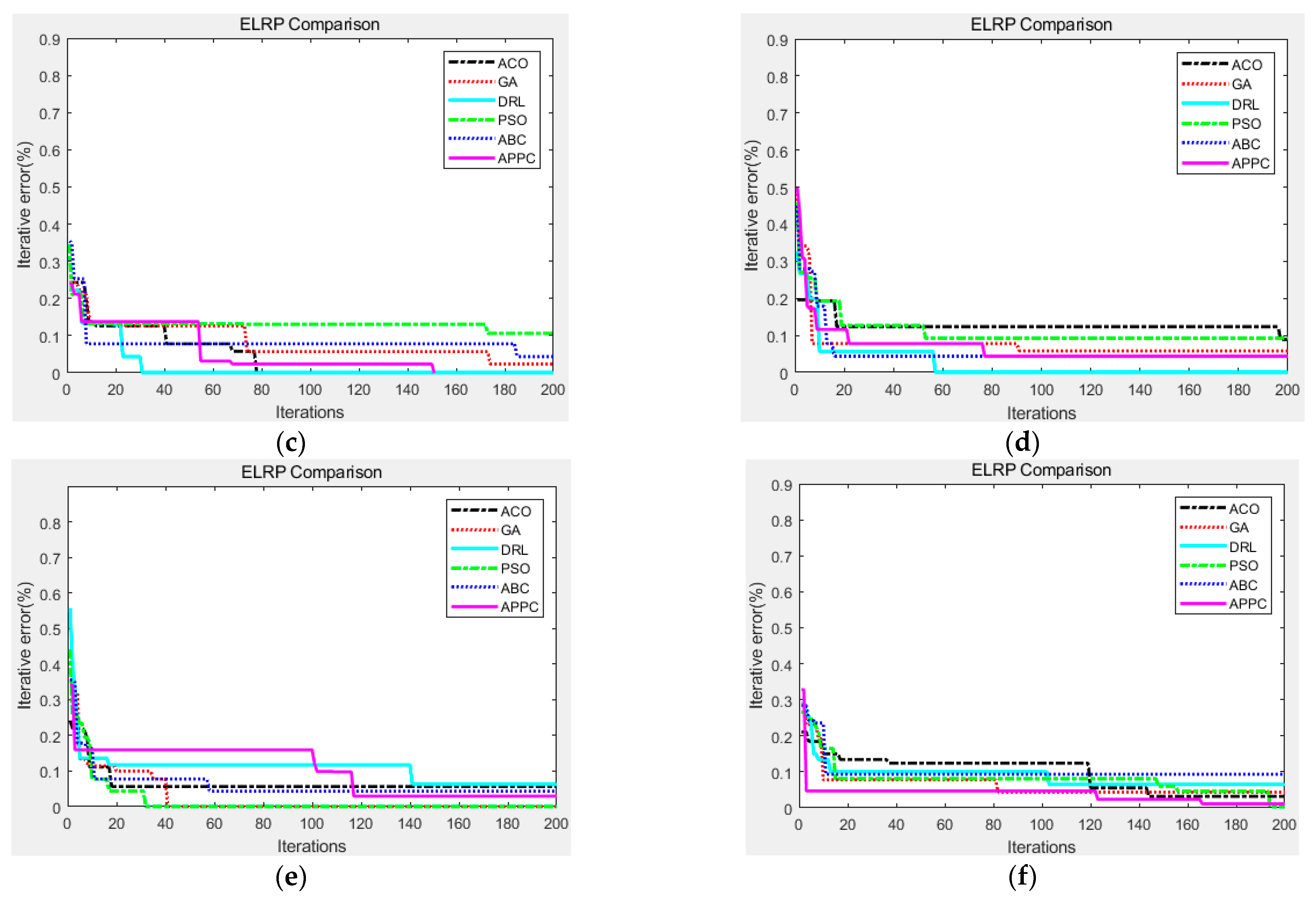
| Multi-Objective | GA [5,36] | PSO [18,37] | DRL [19,20,38] | ACO [21,39] | ABC [23,41] | Proposed APPC |
|---|---|---|---|---|---|---|
| Total distance D∑ | 7.215 × 10−4 | 5.571 × 10−4 | 4.962 × 10−4 | 6.519 × 10−4 | 7.066 × 10−4 | 5.804 × 10−4 |
| Total time T∑ | 5.732 × 10−4 | 7.194 × 10−4 | 5.607 × 10−4 | 6.144 × 10−4 | 5.417 × 10−4 | 6.081 × 10−4 |
| Total cost C∑ | 6.846 × 10−4 | 6.905 × 10−4 | 6.051 × 10−4 | 7.320 × 10−4 | 5.935 × 10−4 | 4.752 × 10−4 |
| Total EVs V∑ | 7.573 × 10−4 | 7.609 × 10−4 | 7.180 × 10−4 | 5.382 × 10−4 | 6.490 × 10−4 | 5.029 × 10−4 |
| Order fill rate O∑ | 5.967 × 10−4 | 5.728 × 10−4 | 6.236 × 10−4 | 7.038 × 10−4 | 7.473 × 10−4 | 4.694 × 10−4 |
| Computing time (ms) | 548 | 733 | 1557 | 562 | 619 | 571 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Wang, X.; Li, R.; Gao, Q. An Artificial Physarum polycephalum Colony for the Electric Location-Routing Problem. Sustainability 2023, 15, 16196. https://doi.org/10.3390/su152316196
Cai Z, Wang X, Li R, Gao Q. An Artificial Physarum polycephalum Colony for the Electric Location-Routing Problem. Sustainability. 2023; 15(23):16196. https://doi.org/10.3390/su152316196
Chicago/Turabian StyleCai, Zhengying, Xiaolu Wang, Rui Li, and Qi Gao. 2023. "An Artificial Physarum polycephalum Colony for the Electric Location-Routing Problem" Sustainability 15, no. 23: 16196. https://doi.org/10.3390/su152316196






