A Novel Three-Dimensional Composite Isolation Bearing and Its Application to the Mitigation of Earthquakes and Traffic-Induced Vibrations
Abstract
:1. Background
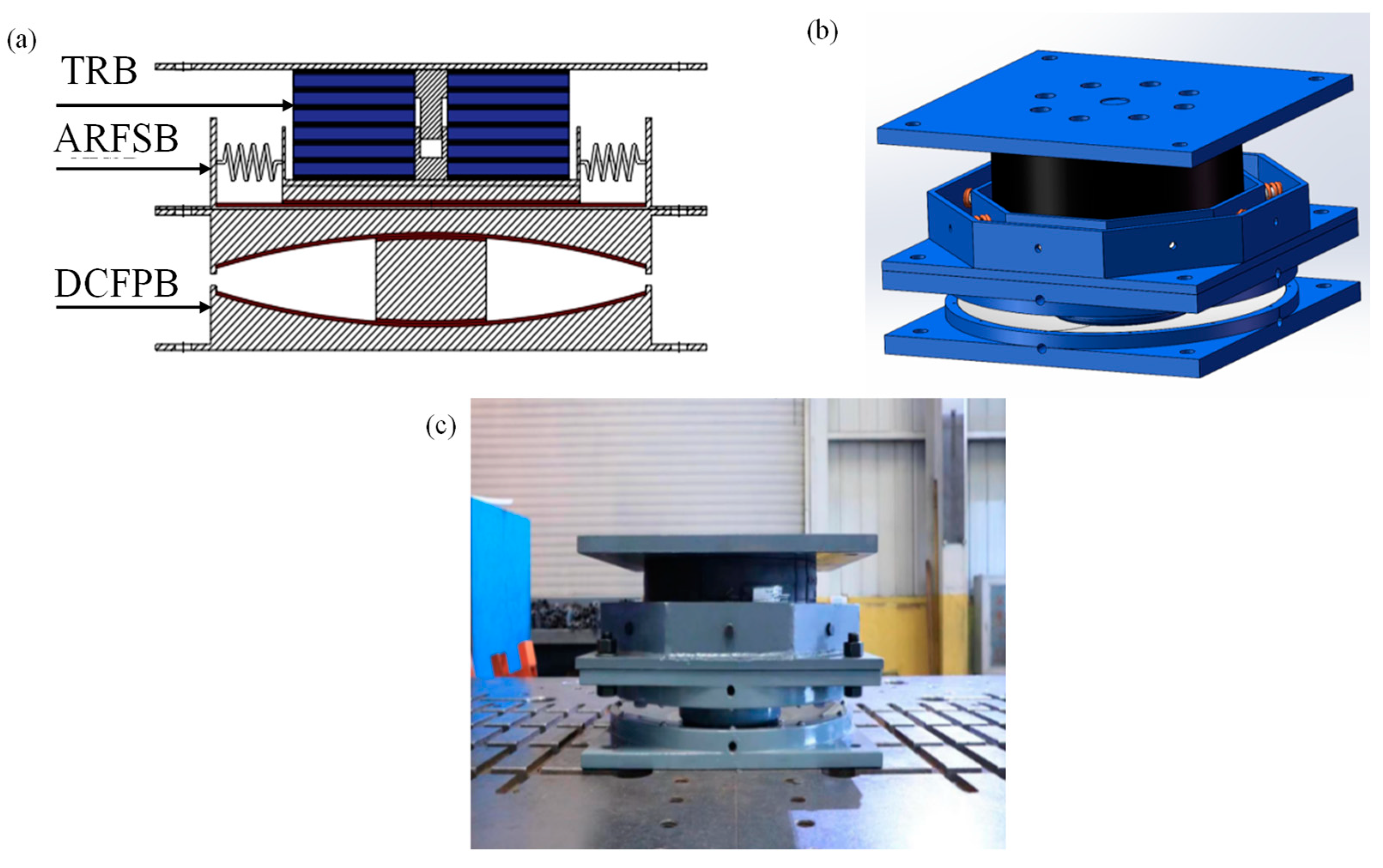
2. Design and Mechanism
3. Mechanical Property Analysis
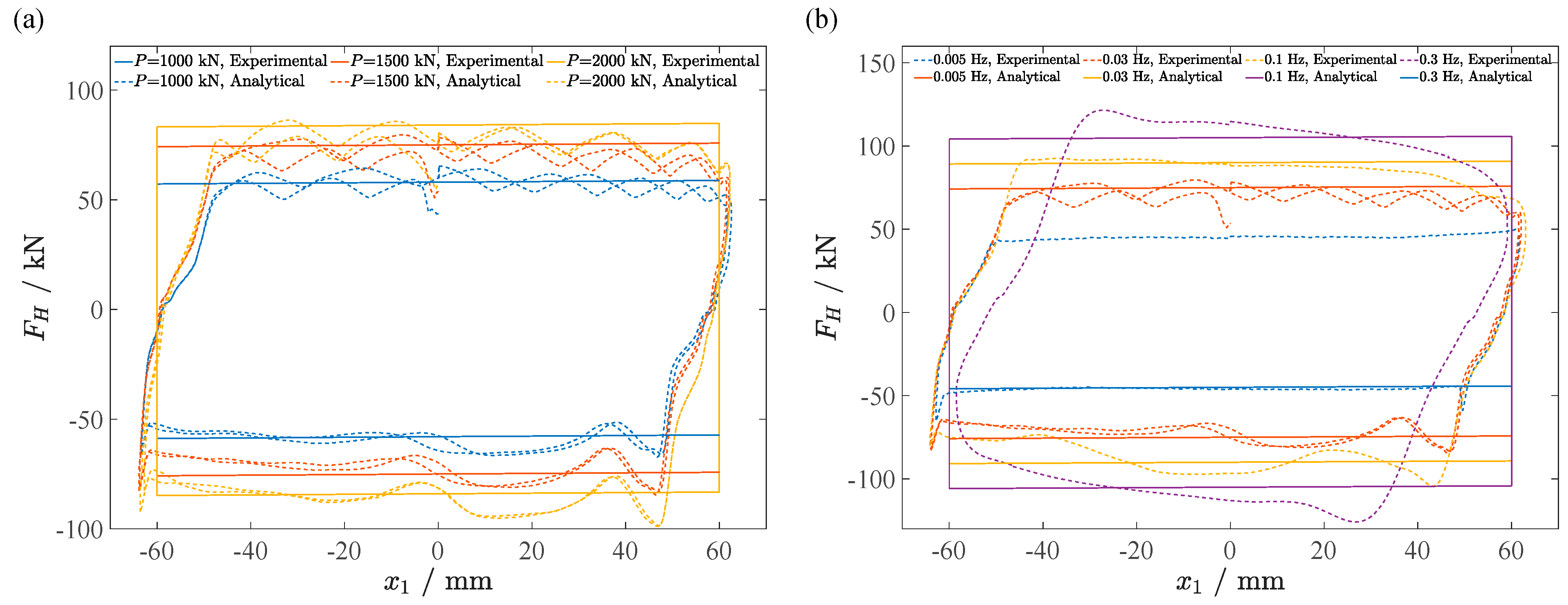
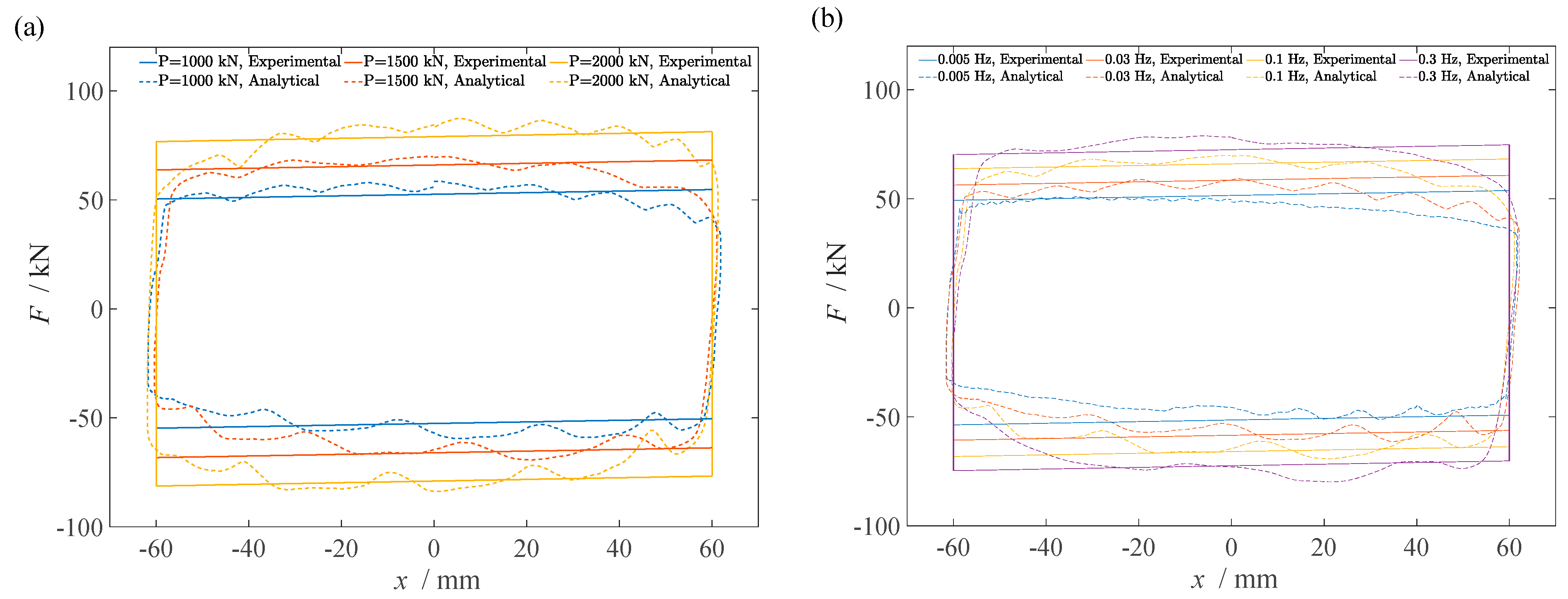
3.1. Analytical Hysteretic Model for the Horizontal Direction
3.2. Experimental Validation of the Proposed Hysteretic Model
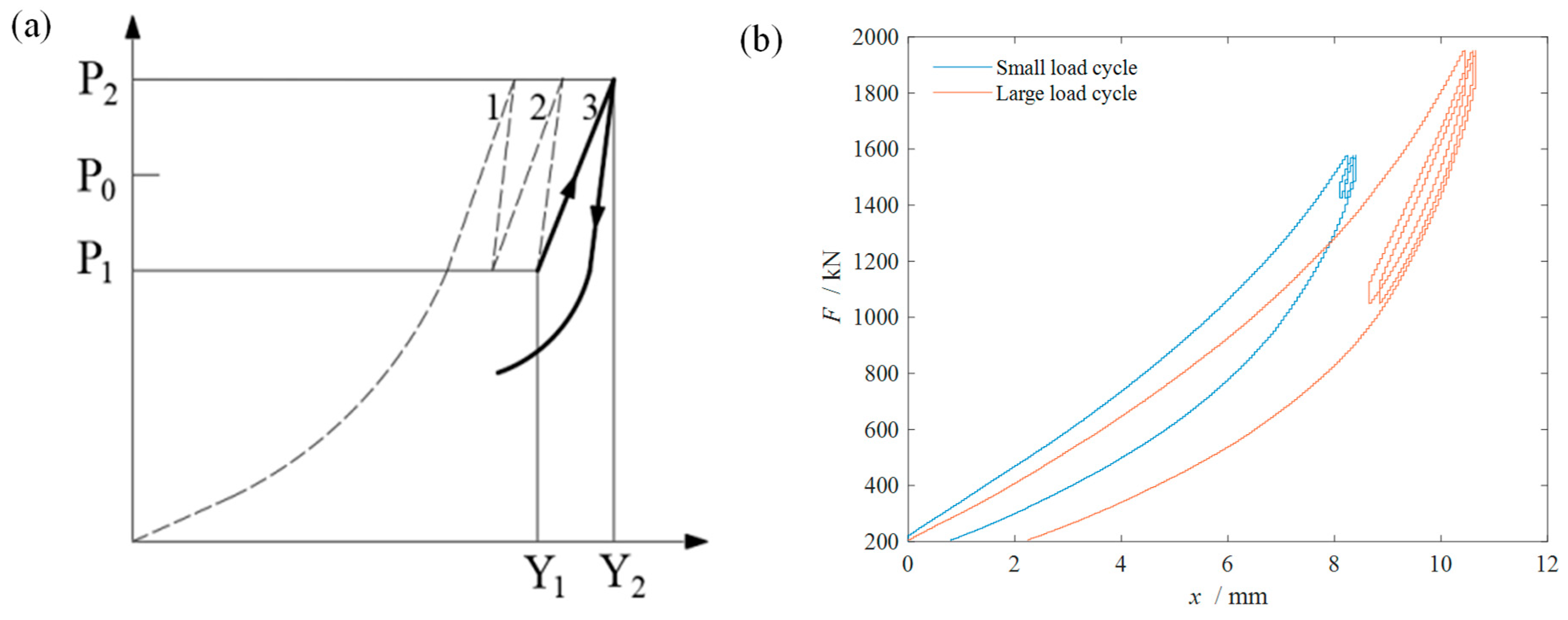
3.3. Fatigue Performance under Horizontal Loads
3.4. Vertical Compression Properties
4. Attenuation Effects of Traffic-Induced Vibrations
4.1. Setup of the Field Test
4.2. Analysis of the Attenuation Effects
5. Conclusions
- (1)
- The analytical hysteresis model proposed in this paper can accurately describe the horizontal hysteresis behaviors of the proposed isolation bearing;
- (2)
- A multi-cycle reciprocating loading test proves that the bearing proposed in this paper has satisfactory fatigue performance;
- (3)
- The vertical compression performance test shows that the proposed isolation bearing has a large axial compression sensitivity; and
- (4)
- The proposed isolation bearing can efficiently mitigate traffic-induced vibrations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARFSB | auto-reset flat slider bearing |
| CSSB | curved surface sliding bearing |
| DCFPB | double concave friction pendulum bearing |
| EB | elastomeric bearing |
| FPB | friction pendulum bearing |
| FREB | fiber-reinforced elastomeric bearing |
| FSSB | flat surface sliding bearing |
| HDRB | high-damping rubber bearing |
| LDRB | low-damping rubber bearing |
| LRB | lead-rubber bearing |
| SB | sliding bearing |
| SREB | steel-reinforced elastomeric bearing |
| TRB | thick rubber bearings |
| TSB | textured sliding bearing |
References
- Bertero, V.V. Performance-based seismic engineering: A critical review of proposed guidelines. In Seismic Design Methodologies for the Next Generation of Codes; Routledge: London, UK, 2019; pp. 1–31. [Google Scholar]
- Grigorian, M.; Moghadam, A.S.; Sedighi, S. Sustainable seismic design and health monitoring. Struct. Control Health Monit. 2022, 29, e3058. [Google Scholar] [CrossRef]
- Forcellini, D. The Role of Redundancy of Infrastructures on the Seismic Resilience (SR) of Sustainable Communities. Sustainability 2023, 15, 11849. [Google Scholar] [CrossRef]
- Xia, H.; Cao, Y.; De Guido, R.; Geert, D. Environmental problems of vibrations induced by railway traffic. Front. Archit. Civ. Eng. China 2007, 1, 142–152. [Google Scholar] [CrossRef]
- Bariker, P.; Kolathayar, S. A study on trenching techniques for vibration isolation: An overview. In Seismic Hazards and Risk: Select Proceedings of 7th ICRAGEE 2020; Springer: Singapore, 2021; pp. 283–293. [Google Scholar]
- Belbachir, A.; Benanane, A.; Ouazir, A.; Harrat, Z.R.; Hadzima-Nyarko, M.; Radu, D.; Işık, E.; Louhibi, Z.S.; Amziane, S. Enhancing the Seismic Response of Residential RC Buildings with an Innovative Base Isolation Technique. Sustainability 2023, 15, 11624. [Google Scholar] [CrossRef]
- De Luca, A.; Guidi, L.G. State of art in the worldwide evolution of base isolation design. Soil Dyn. Earthq. Eng. 2019, 125, 105722. [Google Scholar] [CrossRef]
- Chen, B.; Dai, J.; Song, T.; Guan, Q. Research and development of high-performance high-damping rubber Materials for high-damping rubber isolation bearings: A review. Polymers 2022, 14, 2427. [Google Scholar] [CrossRef]
- Avinash, A.; Krishnamoorthy, A.; Kamath, K.; Chaithra, M. Sliding Isolation Systems: Historical Review, Modeling Techniques, and the Contemporary Trends. Buildings 2022, 12, 1997. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Paradiso, M.; Rosati, L. Accurate and efficient modeling of the hysteretic behavior of sliding bearings. In Proceedings of the 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019. [Google Scholar]
- Calvi, P.M.; Calvi, G.M. Historical development of friction-based seismic isolation systems. Soil Dyn. Earthq. Eng. 2018, 106, 14–30. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Behaviour of the double concave friction pendulum bearing. Earthq. Eng. Struct. Dyn. 2006, 35, 1403–1424. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Yun, C.-B. Seismic response characteristics of bridges using double concave friction pendulum bearings with tri-linear behavior. Eng. Struct. 2007, 29, 3082–3093. [Google Scholar] [CrossRef]
- Song, F.; Yang, X.; Dong, W.; Zhu, Y.; Wang, Z.; Wu, M. Research and prospect of textured sliding bearing. Int. J. Adv. Manuf. Technol. 2022, 121, 1–25. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings. Compos. Struct. 2019, 211, 196–212. [Google Scholar] [CrossRef]
- Orfeo, A.; Tubaldi, E.; Muhr, A.H.; Losanno, D. Mechanical behaviour of rubber bearings with low shape factor. Eng. Struct. 2022, 266, 114532. [Google Scholar] [CrossRef]
- Weisman, J.; Warn, G.P. Stability of elastomeric and lead-rubber seismic isolation bearings. J. Struct. Eng. 2012, 138, 215–223. [Google Scholar] [CrossRef]
- De Domenico, D.; Losanno, D.; Vaiana, N. Experimental tests and numerical modeling of full-scale unbonded fiber reinforced elastomeric isolators (UFREIs) under bidirectional excitation. Eng. Struct. 2023, 274, 115118. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Z. Experimental and analytical investigations on compressive behavior of thick rubber bearings for mitigating subway-induced vibration. Eng. Struct. 2022, 270, 114879. [Google Scholar] [CrossRef]
- Pan, P.; Shen, S.; Shen, Z.; Gong, R. Experimental investigation on the effectiveness of laminated rubber bearings to isolate metro generated vibration. Measurement 2018, 122, 554–562. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Zhang, X.; Fan, J.; Xu, G. Semi-analytical simulation for ground-borne vibration caused by rail traffic on viaducts: Vibration-isolating effects of multi-layered elastic supports. J. Sound Vib. 2022, 516, 116540. [Google Scholar] [CrossRef]
- Sheng, T.; Shi, W.x.; Shan, J.z.; Hong, F.y.; Bian, X.c.; Liu, G.b.; Chen, Y. Base isolation of buildings for subway-induced environmental vibration: Field experiments and a semi-analytical prediction model. Struct. Des. Tall Spec. Build. 2020, 29, e1798. [Google Scholar] [CrossRef]
- Kikuchi, M.; Aiken, I.D. An analytical hysteresis model for elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 1997, 26, 215–231. [Google Scholar] [CrossRef]
- Murillo, C.; Thorel, L.; Caicedo, B. Ground vibration isolation with geofoam barriers: Centrifuge modeling. Geotext. Geomembr. 2009, 27, 423–434. [Google Scholar] [CrossRef]
- Massarsch, K.R. Vibration isolation using gas-filled cushions. In Soil Dynamics Symposium in Honor of Professor Richard D. Woods, Proceedings of the Geo-Frontiers 2005, Austin, TX, USA, 24–26 January 2005; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–20. [Google Scholar]
- Zou, C.; Wang, Y.; Zhang, X.; Tao, Z. Vibration isolation of over-track buildings in a metro depot by using trackside wave barriers. J. Build. Eng. 2020, 30, 101270. [Google Scholar] [CrossRef]
- Makris, N. Seismic isolation: Early history. Earthq. Eng. Struct. Dyn. 2019, 48, 269–283. [Google Scholar] [CrossRef]








| 0.005 Hz (1.2 mm/s) | 0.03 Hz (7.2 mm/s) | 0.1 Hz (24.0 mm/s) | 0.3 Hz (72.0 mm/s) | |
|---|---|---|---|---|
| 1000 kN | − | 0.040 | − | − |
| 1500 kN | 0.040 | 0.045 | 0.050 | 0.055 |
| 2000 kN | − | 0.055 | − | − |
| 0 Hz (0.0 mm/s) | 0.03 Hz (12.0 mm/s) | |
|---|---|---|
| 1000 kN | 0.025 | 0.035 |
| 1500 kN | 0.020 | 0.030 |
| 2000 kN | − | 0.025 |
| 0.005 Hz | 0.03 Hz | 0.1 Hz | 0.3 Hz | |
|---|---|---|---|---|
| 1000 kN | − | − | = 21.6, = 2.4 | − |
| 1500 kN | = 1.12, = 0.08 | = 6.72, = 0.48 | = 22.4, = 1.6 | = 67.0, = 5.0 |
| 2000 kN | − | − | = 22.8, = 1.2 | − |
| 0.005 Hz | 0.03 Hz | 0.1 Hz | 0.3 Hz | |
|---|---|---|---|---|
| 1000 kN | − | − | = 0.049, = 0.026 | − |
| 1500 kN | = 0.038, = 0.020 | = 0.044, = 0.021 | = 0.050, = 0.022 | = 0.56, = 0.0023 |
| 2000 kN | − | − | = 0.050, = 0.018 | − |
| Working Condition | Initial Stiffness | P = 1000 kN | P = 1500 kN | P = 2000 kN |
|---|---|---|---|---|
| Large load cycle Kvm/(kN·mm−1) | 248.13 | 311.87 | 508.47 | 772.25 |
| Small load cycle Kvc/(kN·mm−1) | 248.13 | 392.71 | 532.53 | 782.60 |
| Condition | Vibration Source |
|---|---|
| Condition 1 | Railway trains |
| Condition 2 | Automobiles |
| Condition 3 | Coming light rail transits |
| Condition 4 | Leaving light rail transits |
| Condition | Vibration Source | Before Isolation (m/s2) | After isolation (m/s2) | Attenuation Rate |
|---|---|---|---|---|
| Condition 1 | Railway trains | 0.029 | 0.013 | 52.9% |
| Condition 2 | Automobiles | 0.012 | 0.005 | 58.7% |
| Condition 3 | Coming metro trains | 0.021 | 0.006 | 69.0% |
| Condition 4 | Leaving metro trains | 0.013 | 0.004 | 67.4% |
| Condition | Vibration Source | Before Isolation (dB) | After Isolation (dB) | Decrease Rate |
|---|---|---|---|---|
| Condition 1 | Railway trains | 78.72 | 59.55 | 80.83% |
| Condition 2 | Automobiles | 53.56 | 32.67 | 79.11% |
| Condition 3 | Coming metro trains | 73.80 | 57.17 | 83.37% |
| Condition 4 | Leaving metro trains | 70.42 | 50.35 | 79.74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Xu, H.; Xu, Z.; Chen, X. A Novel Three-Dimensional Composite Isolation Bearing and Its Application to the Mitigation of Earthquakes and Traffic-Induced Vibrations. Sustainability 2023, 15, 16374. https://doi.org/10.3390/su152316374
Wu Q, Xu H, Xu Z, Chen X. A Novel Three-Dimensional Composite Isolation Bearing and Its Application to the Mitigation of Earthquakes and Traffic-Induced Vibrations. Sustainability. 2023; 15(23):16374. https://doi.org/10.3390/su152316374
Chicago/Turabian StyleWu, Qiaoyun, Hang Xu, Zhifeng Xu, and Xuyong Chen. 2023. "A Novel Three-Dimensional Composite Isolation Bearing and Its Application to the Mitigation of Earthquakes and Traffic-Induced Vibrations" Sustainability 15, no. 23: 16374. https://doi.org/10.3390/su152316374
APA StyleWu, Q., Xu, H., Xu, Z., & Chen, X. (2023). A Novel Three-Dimensional Composite Isolation Bearing and Its Application to the Mitigation of Earthquakes and Traffic-Induced Vibrations. Sustainability, 15(23), 16374. https://doi.org/10.3390/su152316374









