Strategic Decision-Making for Multi-Period Fleet Transition Towards Zero-Emission: Preliminary Study
Abstract
:1. Introduction
1.1. Fleet Transition in Solid Waste Management
2. Materials and Methods
2.1. MARKAL—An Overview
2.2. Fleet Transition Problem
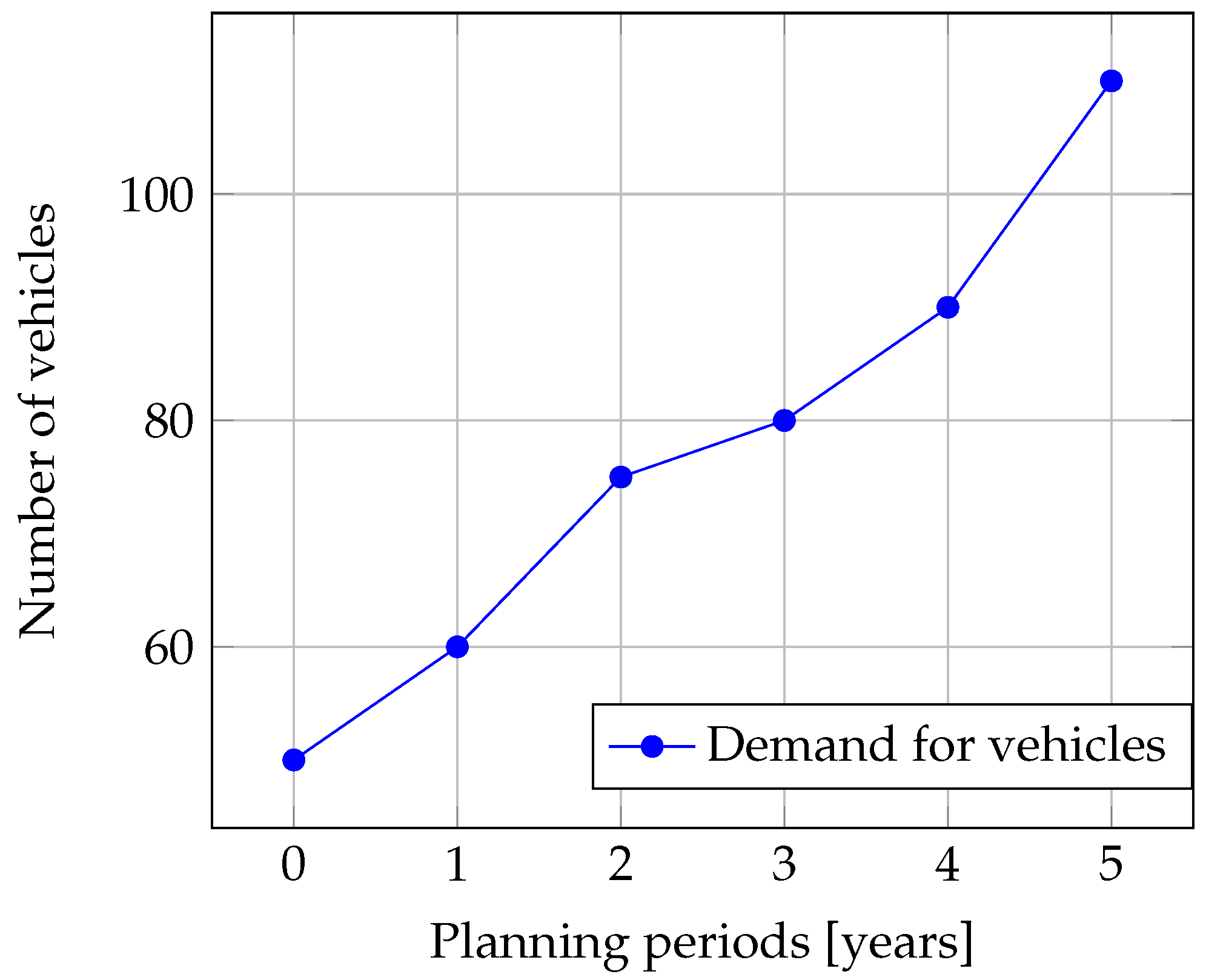
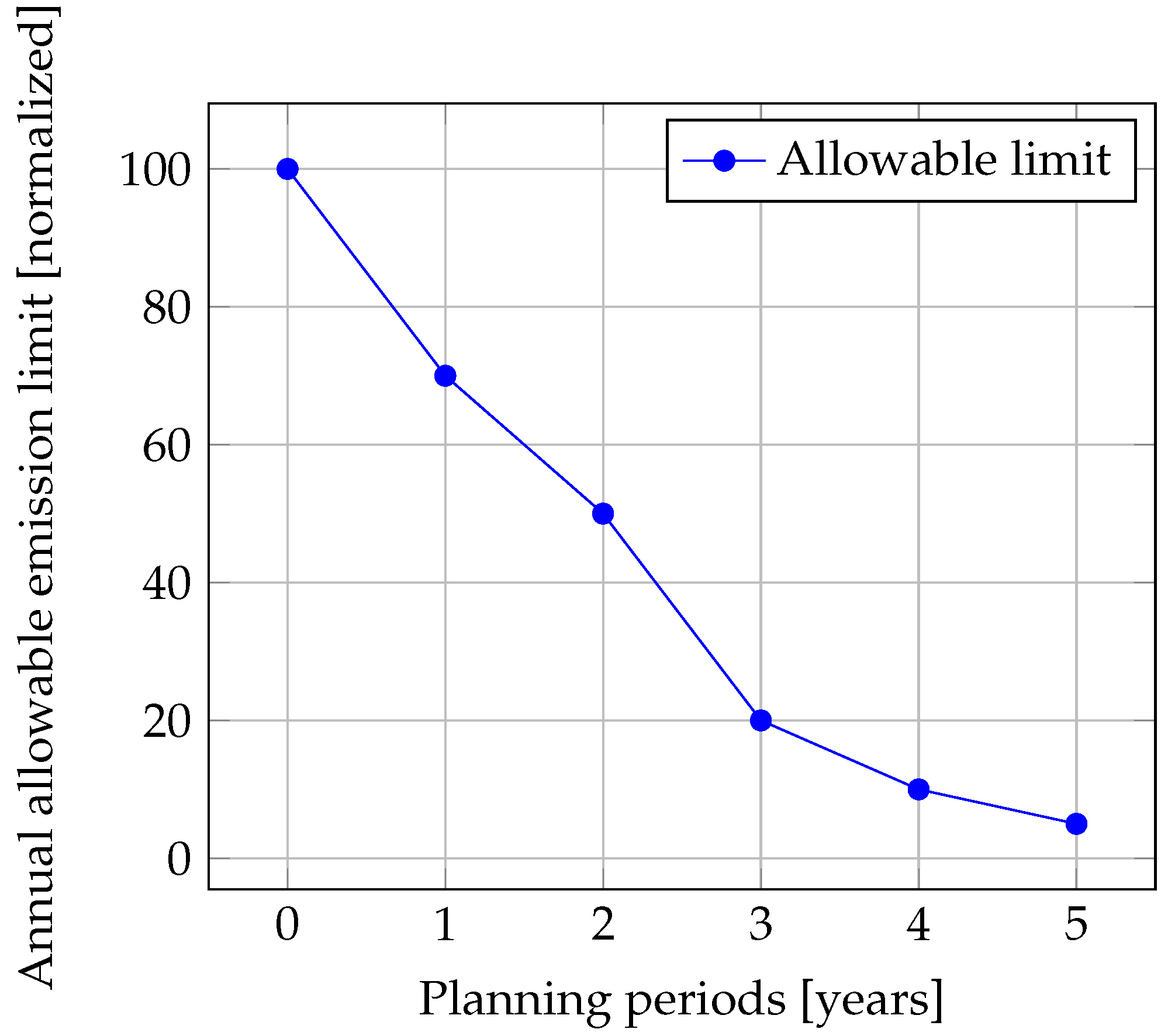
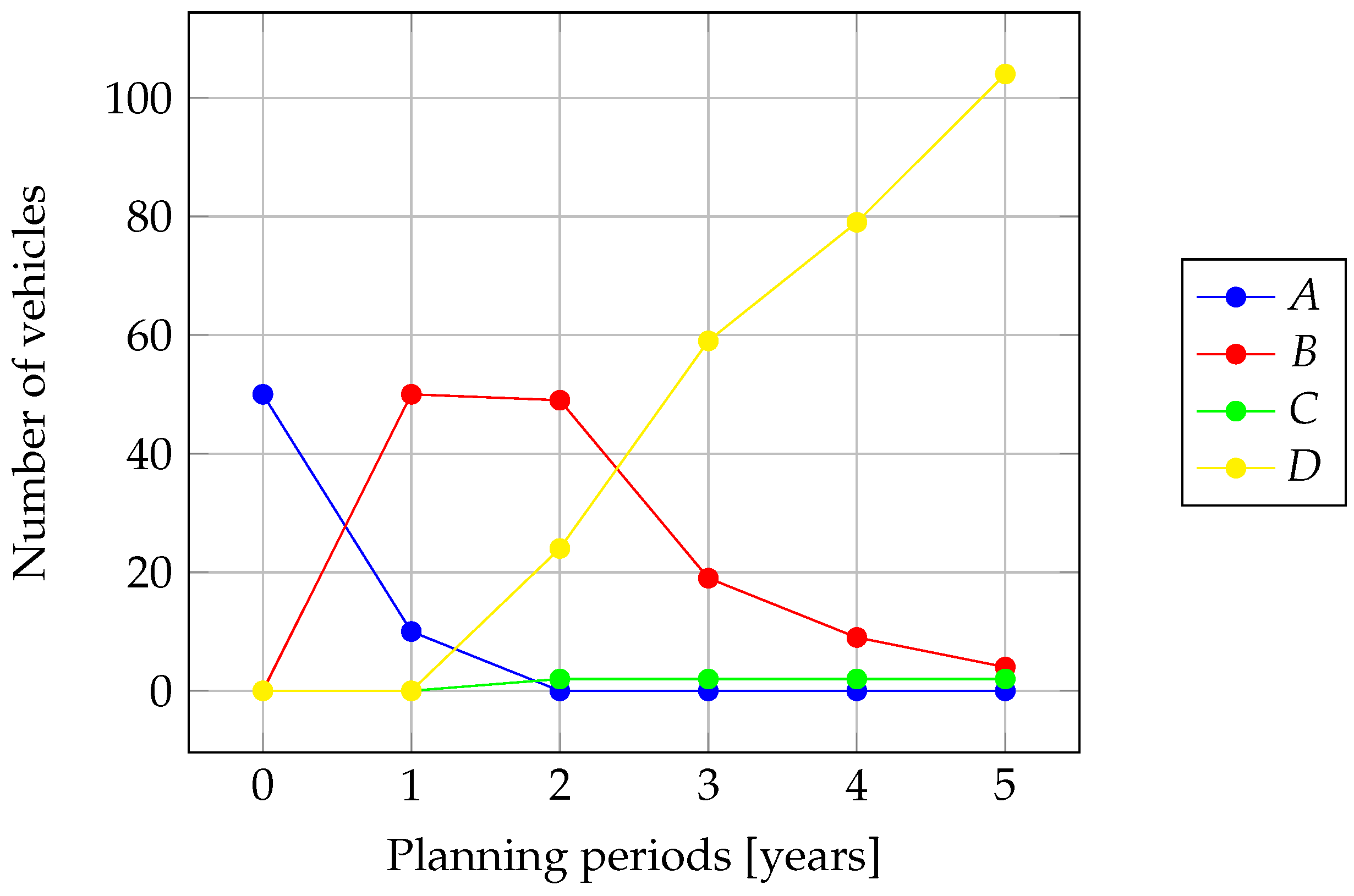
3. Computational Experiments—Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FTP | Fleet Transition Problem |
| MILP | Mixed–Integer Linear Programming |
| MSWM | Municipal Solid Waste Management |
| OR | Operations Research |
| SWM | Solid Waste Management |
| ZEV | Zero–Emission Vehicle |
References
- Iqbal, A.; Yasar, A.; Nizami, A.S.; Haider, R.; Sharif, F.; Sultan, I.A.; Tabinda, A.B.; Kedwaii, A.A.; Chaudhary, M.M. Municipal Solid Waste Collection and Haulage Modeling Design for Lahore, Pakistan: Transition toward Sustainability and Circular Economy. Sustainability 2022, 14, 6234. [Google Scholar] [CrossRef]
- Schmidt-Polończyk, N. Subjective individuals’ perception during evacuation in road tunnels: Post-experiment survey results. PLoS ONE 2023, 18, e0283461. [Google Scholar] [CrossRef]
- Matraku, D.; Çafuli, P. The Impact of Waste Management in the Macroeconomic Performance. Eur. J. Econ. Bus. Stud. 2015, 1, 2. [Google Scholar] [CrossRef]
- Kuzior, A.; Arefiev, S.; Poberezhna, Z. Informatization of innovative technologies for ensuring macroeconomic trends in the conditions of a circular economy. J. Open Innov. Technol. Mark. Complex. 2023, 9, 100001. [Google Scholar] [CrossRef]
- Korcyl, A.; Ksia̧żek, R.; Gdowska, K. A MILP model for the municipal solid waste selective collection routing problem. Decis. Mak. Manuf. Serv. 2019, 13, 17–35. [Google Scholar]
- Korcyl, A.; Ksia̧żek, R.; Gdowska, K. Modele optymalizacyjne dla problemu planowania tras odbioru odpadów. In Selected Big Data-Based Tools for Supporting Decision Making and Risk Management, 1st ed.; Iwaszczuk, N., Ed.; Wydawnictwa AGH: Kraków, Poland, 2020; pp. 215–230. [Google Scholar]
- Lozano, Á.; Caridad, J.; De Paz, J.F.; González, G.V.; Bajo, J. Smart waste collection system with low consumption LoRaWAN nodes and route optimization. Sensors 2018, 18, 1465. [Google Scholar] [CrossRef] [PubMed]
- Saukenova, I.; Oliskevych, M.; Taran, I.; Toktamyssova, A.; Aliakbarkyzy, D.; Pelo, R. Optimization of Schedules for Early Garbage Collection and Disposal in the Megapolis. East.-Eur. J. Enterp. Technol. 2022, 1, 13–23. [Google Scholar] [CrossRef]
- Oliskevych, M.; Danchuk, V. An Algorithm for Garbage Truck Routing in Cities with a Fixation on Container Filling Level. Transp. Probl. 2023, 18, 75–87. [Google Scholar] [CrossRef]
- Ksia̧żek, R.; Gdowska, K.; Korcyl, A. Recyclables collection route balancing problem with heterogeneous fleet. Energies 2021, 14, 7406. [Google Scholar] [CrossRef]
- Korcyl, A.; Gdowska, K.; Ksia̧żek, R. Optymalizacja tras odbioru odpadów komunalnych z wykorzystaniem różnych typów pojazdów i ograniczeniami czasowymi w obsłudze klienta. Logistyka 2015, 4, 9202–9211. [Google Scholar]
- Gdowska, K.; Ksia̧żek, R.; Korcyl, A. Fleet Optimization for a Selective Solid Waste Collection System. In Challanges and Modern Solution in Transportation; Maciej Stajniak, M., Kopeć, A., Toboła, M.S., Eds.; Instytut Naukowo-Wydawniczy Spatium: Radom, Poland, 2019; pp. 121–134. [Google Scholar]
- Fishbone, L.G.; Abilock, H. Markal, a linear-programming model for energy systems analysis: Technical description of the bnl version. Int. J. Energy Res. 1981, 5, 353–375. [Google Scholar] [CrossRef]
- Loulou, R.; Goldstein, G.; Noble, K. Documentation for the MARKAL Family of Models; Energy Technology Systems Analysis Programme: Paris, France, 2004; pp. 65–73. [Google Scholar]
- European Commission. A Clean Planet for All, a European Strategic Long Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy by 2050; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Koiwanit, J.; Hamontree, C. Greenhouse gas emissions comparison of solid waste transportation system: A case study in Thailand. IOP Conf. Ser. Earth Environ. Sci. 2020, 424, 012011. [Google Scholar] [CrossRef]
- Schmid, F.; Taube, L.; Rieck, J.; Behrendt, F. Electrification of Waste Collection Vehicles: Technoeconomic Analysis Based on an Energy Demand Simulation Using Real-Life Operational Data. IEEE Trans. Transp. Electrif. 2021, 7, 604–615. [Google Scholar] [CrossRef]
- Skowrońska-Szmer, A.; Kowalska-Pyzalska, A. Key Factors of Development of Electromobility AMONG Microentrepreneurs: A Case Study from Poland. Energies 2021, 14, 764. [Google Scholar] [CrossRef]
- Polish Parliament. Ustawa z Dnia 11 Stycznia 2018 r. o Elektromobilności i Paliwach Alternatywnych. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20180000317 (accessed on 5 November 2023).
- Danilecki, K.; Smurawski, P.; Urbanowicz, K. Optimization of Car Use Time for Different Maintenance and Repair Scenarios Based on Life Cycle Assessment. Appl. Sci. 2023, 13, 9843. [Google Scholar] [CrossRef]
- Elangovan, R.; Kanwhen, O.; Dong, Z.; Mohamed, A.; Rojas-Cessa, R. Comparative Analysis of Energy Use and Greenhouse Gas Emission of Diesel and Electric Trucks for Food Distribution in Gowanus District of New York City. Front. Big Data 2021, 4, 3820. [Google Scholar] [CrossRef] [PubMed]
- California Air Resources Board. Battery Electric Truck and Bus Energy Efficiency Compared to Conventional Diesel Vehicles. Available online: https://ww2.arb.ca.gov/sites/default/files/2018-11/180124hdbevefficiency.pdf (accessed on 5 November 2023).
- Endresen, J. Preparing for the Future of Electric Garbage Trucks. Master’s Thesis, SC Johnson College of Business, New York, NY, USA, 2021. [Google Scholar]
- Rogge, M.; van der Hurk, E.; Larsen, A.; Sauer, D.U. Electric bus fleet size and mix problem with optimization of charging infrastructure. Appl. Energy 2018, 211, 282–295. [Google Scholar] [CrossRef]
- Plachinda, P.; Morgan, J.; Coelho, M. Towards Net Zero: Modeling Approach to the Right-Sized Facilities. Sustainability 2023, 15, 163. [Google Scholar] [CrossRef]
- Prina, M.G.; Zubaryeva, A.; Rotondo, G.; Grotto, A.; Sparber, W. Optimal Fleet Transition Modeling for Sustainable Inland Waterways Transport. Appl. Sci. 2023, 13, 9524. [Google Scholar] [CrossRef]
- Ahani, P.; Arantes, A.; Garmanjani, R.; Melo, S. Optimizing Vehicle Replacement in Sustainable Urban Freight Transportation Subject to Presence of Regulatory Measures. Sustainability 2023, 15, 2266. [Google Scholar] [CrossRef]
- Berger, C.; Dubois, R.; Haurie, A.; Lessard, E.; Loulou, R.; Waaub, J.P. Canadian Markal: An Advanced Linear Programming System For Energy And Environmental Modelling. INFOR Inf. Syst. Oper. Res. 1992, 30, 222–239. [Google Scholar] [CrossRef]
- Kanudia, A.; Loulou, R. Robust responses to climate change via stochastic MARKAL: The case of Québec. Eur. J. Oper. Res. 1998, 106, 15–30. [Google Scholar] [CrossRef]
- Fragniere, E.; Haurie, A. MARKAL-Geneva: A model to assess energy-environment choices for a Swiss canton. In Operations Research and Environmental Management; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar] [CrossRef]
- Zonooz, M.R.F.; Nopiah, Z.M.; Yusof, A.M.; Sopian, K. A Review of MARKAL Energy Modeling. 2009. Available online: https://www.academia.edu/2593300/A_review_of_MARKAL_energy_modeling (accessed on 5 November 2023).
- Gryzunova, N.; Vedenyev, K.; Manuylenko, V.; Keri, I.; Bilczak, M. Distributed Energy as a Megatrend of Audit of Investment Processes of the Energy Complex. Energies 2022, 15, 9225. [Google Scholar] [CrossRef]
- McDowall, W.; Anandarajah, G.; Dodds, P.E.; Tomei, J. Implications of sustainability constraints on UK bioenergy development: Assessing optimistic and precautionary approaches with UK MARKAL. Energy Policy 2012, 47, 424–436. [Google Scholar] [CrossRef]
- Strachan, N.; Kannan, R.; Pye, S. Scenarios and Sensitivities on Long-Term UK Carbon Reductions Using the UK MARKAL and MARKAL-Macro Energy System Models; UK Energy Research Centre: London, UK, 2008. [Google Scholar]
- Taylor, P.G.; Upham, P.; McDowall, W.; Christopherson, D. Energy model, boundary object and societal lens: 35 years of the MARKAL model in the UK. Energy Res. Soc. Sci. 2014, 4, 32–41. [Google Scholar] [CrossRef]
- Yuan, X.; Zhu, M.; Liang, Y.; Shahrestani, M.; Kosonen, R. Comparison of Short and Long-Term Energy Performance and Decarbonization Potentials between Cogeneration and GSHP Systems under MARKAL Scenarios. Sustainability 2023, 15, 1604. [Google Scholar] [CrossRef]
- Sarica, K.; Tyner, W.E. Analysis of US renewable fuels policies using a modified MARKAL model. Renew. Energy 2013, 50, 701–709. [Google Scholar] [CrossRef]
- Victor, N.; Nichols, C.; Zelek, C. The U.S. power sector decarbonization: Investigating technology options with MARKAL nine-region model. Energy Econ. 2018, 73, 410–425. [Google Scholar] [CrossRef]
- Perissi, I.; Martelloni, G.; Bardi, U.; Natalini, D.; Jones, A.; Nikolaev, A.; Eggler, L.; Baumann, M.; Samsó, R.; Solé, J. Cross-validation of the MEDEAS energy-economy- environment model with the integrated MARKAL-EFOM system (TIMES) and the long-range energy alternatives planning system (LEAP). Sustainability 2021, 13, 1967. [Google Scholar] [CrossRef]
- Ma, X.; Chai, M.; Luo, L.; Luo, Y.; He, W.; Li, G. An assessment on Shanghai’s energy and environment impacts of using MARKAL model. J. Renew. Sustain. Energy 2015, 7, 013105. [Google Scholar] [CrossRef]
- Li, S.; Qiao, J.; Cui, H.; Wang, S. Realizing the environmental benefits of proactive environmental strategy: The roles of green supply chain integration and relational capability. Sustainability 2020, 12, 2907. [Google Scholar] [CrossRef]
- Chen, W.; Wu, Z.; He, J.; Gao, P.; Xu, S. Carbon emission control strategies for China: A comparative study with partial and general equilibrium versions of the China MARKAL model. Energy 2007, 32, 59–72. [Google Scholar] [CrossRef]
- Chen, W. The costs of mitigating carbon emissions in China: Findings from China MARKAL-MACRO modelling. Energy Policy 2005, 33, 885–896. [Google Scholar] [CrossRef]
- Amorim, F.; Pina, A.; Gerbelová, H.; Pereira da Silva, P.; Vasconcelos, J.; Martins, V. Electricity decarbonisation pathways for 2050 in Portugal: A TIMES (The Integrated MARKAL-EFOM System) based approach in closed versus open systems modelling. Energy 2014, 69, 104–112. [Google Scholar] [CrossRef]
- Monjardino, J.; Dias, L.; Fortes, P.; Tente, H.; Ferreira, F.; Seixas, J. Carbon neutrality pathways effects on air pollutant emissions: The Portuguese case. Atmosphere 2021, 12, 324. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Genikomsakis, K.N. Integration of seawater pumped-storage in the energy system of the Island of São Miguel (Azores). Sustainability 2018, 10, 3438. [Google Scholar] [CrossRef]
- Contaldi, M.; Gracceva, F.; Tosato, G. Evaluation of green-certificates policies using the MARKAL-MACRO-Italy model. Energy Policy 2007, 35, 797–808. [Google Scholar] [CrossRef]
- Behzadi Forough, A.; Norouzi, N.; Fani, M. More Secure Iranian Energy System: A Markal Based Energy Security Model for Iranian Energy Demand-side. Iran. J. Energy Environ. 2021, 12, 100–108. [Google Scholar] [CrossRef]
- Sulukan, E.; Sağlam, M.; Uyar, T.S.; Kirlidoğ, M. Determining Optimum Energy Strategies for Turkey by MARKAL Model. J. Nav. Sci. Eng. 2010, 6, 27–38. [Google Scholar]
- Zhakiyev, N.; Khamzina, A.; Zhakiyeva, S.; De Miglio, R.; Bakdolotov, A.; Cosmi, C. Optimization Modelling of the Decarbonization Scenario of the Total Energy System of Kazakhstan until 2060. Energies 2023, 16, 5142. [Google Scholar] [CrossRef]
- Madden, S.M.; Ryan, A.; Walsh, P. Exploratory Study on Modelling Agricultural Carbon Emissions in Ireland. Agriculture 2022, 12, 34. [Google Scholar] [CrossRef]
- Jaskólski, M.; Bućko, P. Modelling long-term transition from coal-reliant to low-emission power grid and district heating systems in Poland. Energies 2021, 14, 8389. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Gerbelova, H.; Bagheri, A.; Koutra, S.; Koukouzas, N. Strategic planning for carbon capture and storage implementation in the electricity sector of greece: A times based analysis. Processes 2021, 9, 1913. [Google Scholar] [CrossRef]
- Salvia, M.; Cosmi, C.; Macchiato, M.; Mangiamele, L. Waste management system optimisation for Southern Italy with MARKAL model. Resour. Conserv. Recycl. 2002, 34, 91–106. [Google Scholar] [CrossRef]
- Cosmi, C.; Cuomo, V.; Macchiato, M.; Mangiamele, L.; Masi, S.; Salvia, M. Waste management modeling by MARKAL model: A case study for Basilicata Region. Environ. Model. Assess. 2000, 5, 19–27. [Google Scholar] [CrossRef]
- Salvia, M.; Pietrapertosa, F.; Cosmi, C.; Cuomo, V.; Macchiato, M. Approaching the Kyoto targets: A case study for Basilicata region (Italy). Renew. Sustain. Energy Rev. 2004, 8, 73–90. [Google Scholar] [CrossRef]
- Gurobi Optimizer—Official Website. Available online: https://www.gurobi.com/solutions/gurobi-optimizer/ (accessed on 5 November 2023).

| Sets | |
|---|---|
| T | – planning horizon, i.e., the set of planning periods |
| R | – the set of the types of fueling available for the solid waste collection vehicles |
| Parameters | |
| – the number of solid waste collection vehicles needed in period t to perform solid waste collection service | |
| – the cost of shifting a vehicle from fuel r to fuel l | |
| – the cost of purchasing a vehicle fuelled with fuel r | |
| – maximum allowable emission in period t | |
| – emission produced by a vehicle operating on fuel r per its capacity unit | |
| q | – discount rate |
| – the initial number of vehicles operating on fuel r possessed by the company | |
| Decision variables | |
| – the number of vehicles operating on fuel r shifted to fuel l in the planning period t | |
| – the number of vehicles operating on fuel r possessed by the company in the planning period t | |
| – the number of vehicles operating on fuel r purchased by the company in the planning period t | |
| Fuel | The Number of Vehicles Possessed | The Cost of Purchasing a New Vehicle [Normalized] | Annual Emission [Normalized] |
|---|---|---|---|
| A | 50 | 30 | 2.0 |
| B | 0 | 35 | 1.0 |
| C | 0 | 45 | 0.5 |
| D | 0 | 50 | 0.0 |
| A | B | C | D | |
|---|---|---|---|---|
| A | – | 3 | 10 | 15 |
| B | – | – | 10 | 15 |
| C | – | – | – | 20 |
| D | – | – | 15 | – |
| Planning Periods [Years] | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| A | – | – | – | – | – | – |
| B | – | 10 | 2 | – | – | – |
| C | – | – | 1 | – | – | – |
| D | – | – | 12 | 5 | 10 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieda, B.; Książek, R.; Gdowska, K.; Korcyl, A. Strategic Decision-Making for Multi-Period Fleet Transition Towards Zero-Emission: Preliminary Study. Sustainability 2023, 15, 16690. https://doi.org/10.3390/su152416690
Bieda B, Książek R, Gdowska K, Korcyl A. Strategic Decision-Making for Multi-Period Fleet Transition Towards Zero-Emission: Preliminary Study. Sustainability. 2023; 15(24):16690. https://doi.org/10.3390/su152416690
Chicago/Turabian StyleBieda, Bogusław, Roger Książek, Katarzyna Gdowska, and Antoni Korcyl. 2023. "Strategic Decision-Making for Multi-Period Fleet Transition Towards Zero-Emission: Preliminary Study" Sustainability 15, no. 24: 16690. https://doi.org/10.3390/su152416690







