What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method
Abstract
1. Introduction
2. Construction of Restrictive Factor Indicator System
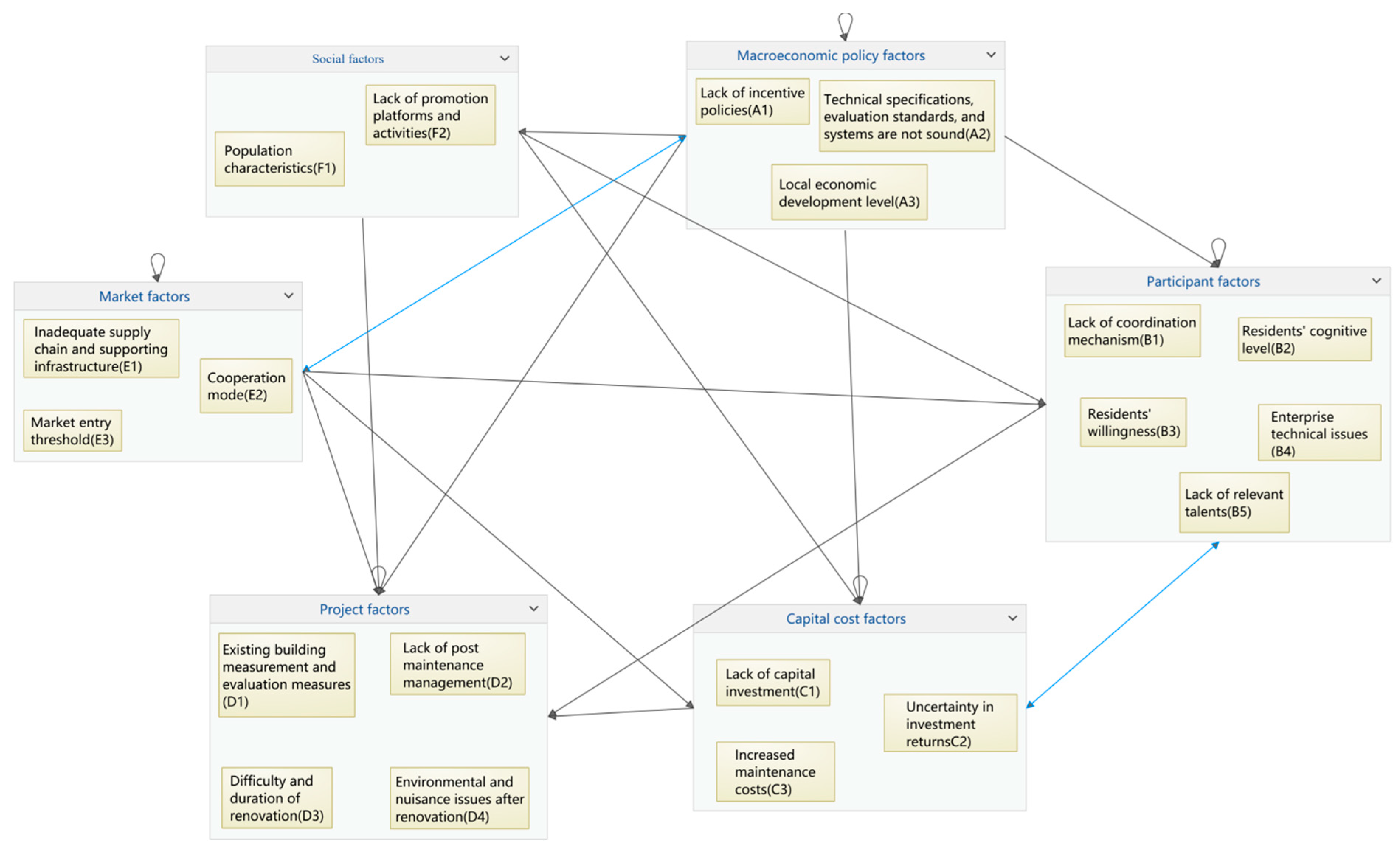
2.1. Macroeconomic Policy Factors
2.2. Participant Factors
2.3. Capital Cost Issues
2.4. Project Factors
2.5. Market Factors
2.6. Social Factors
3. Methodology
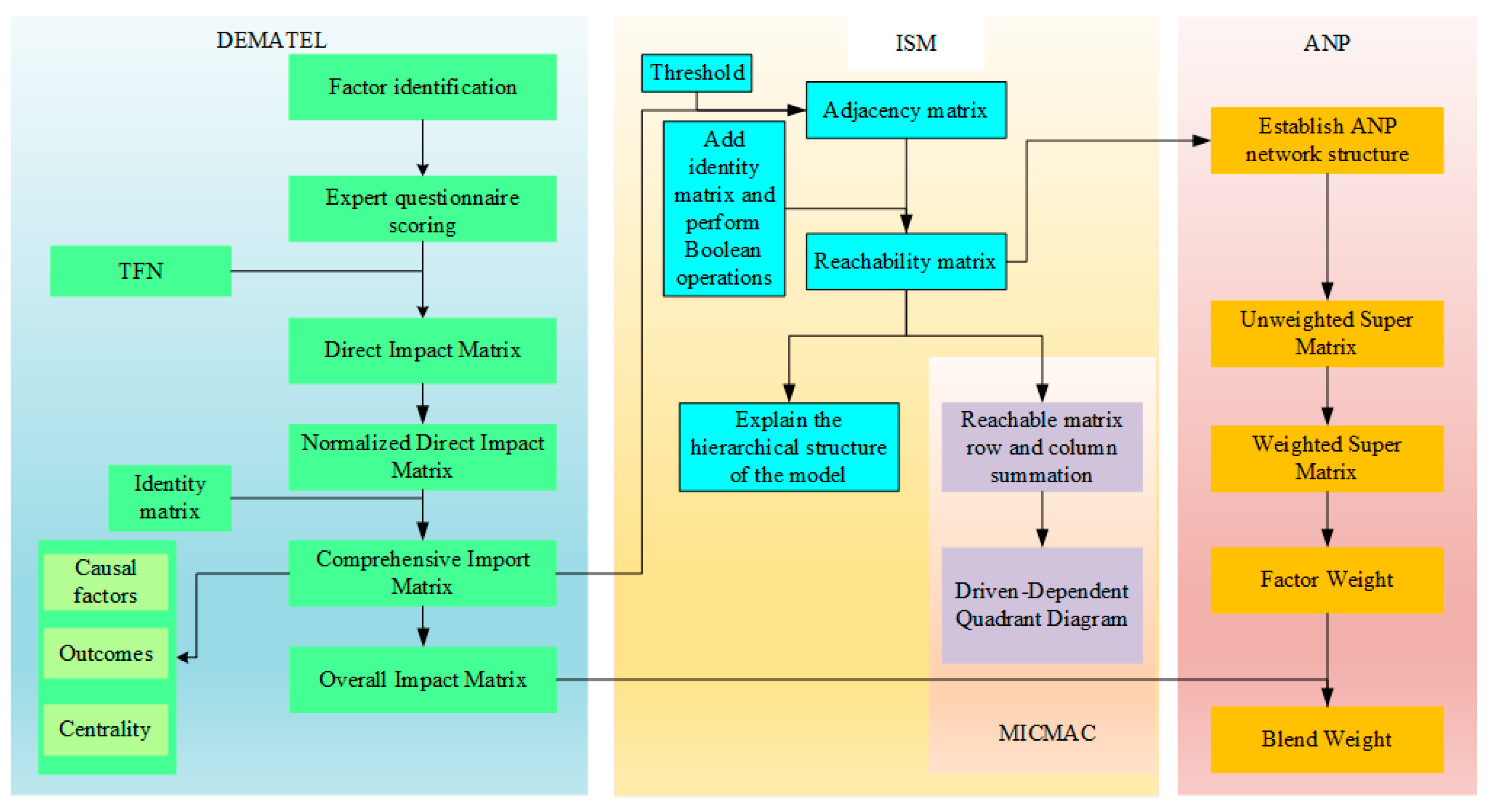
3.1. Research Framework
3.2. Research Methods
3.2.1. Triangular Fuzzy Number
3.2.2. Fuzzy DEMATEL-ISM-ANP Process
4. Results and Analysis
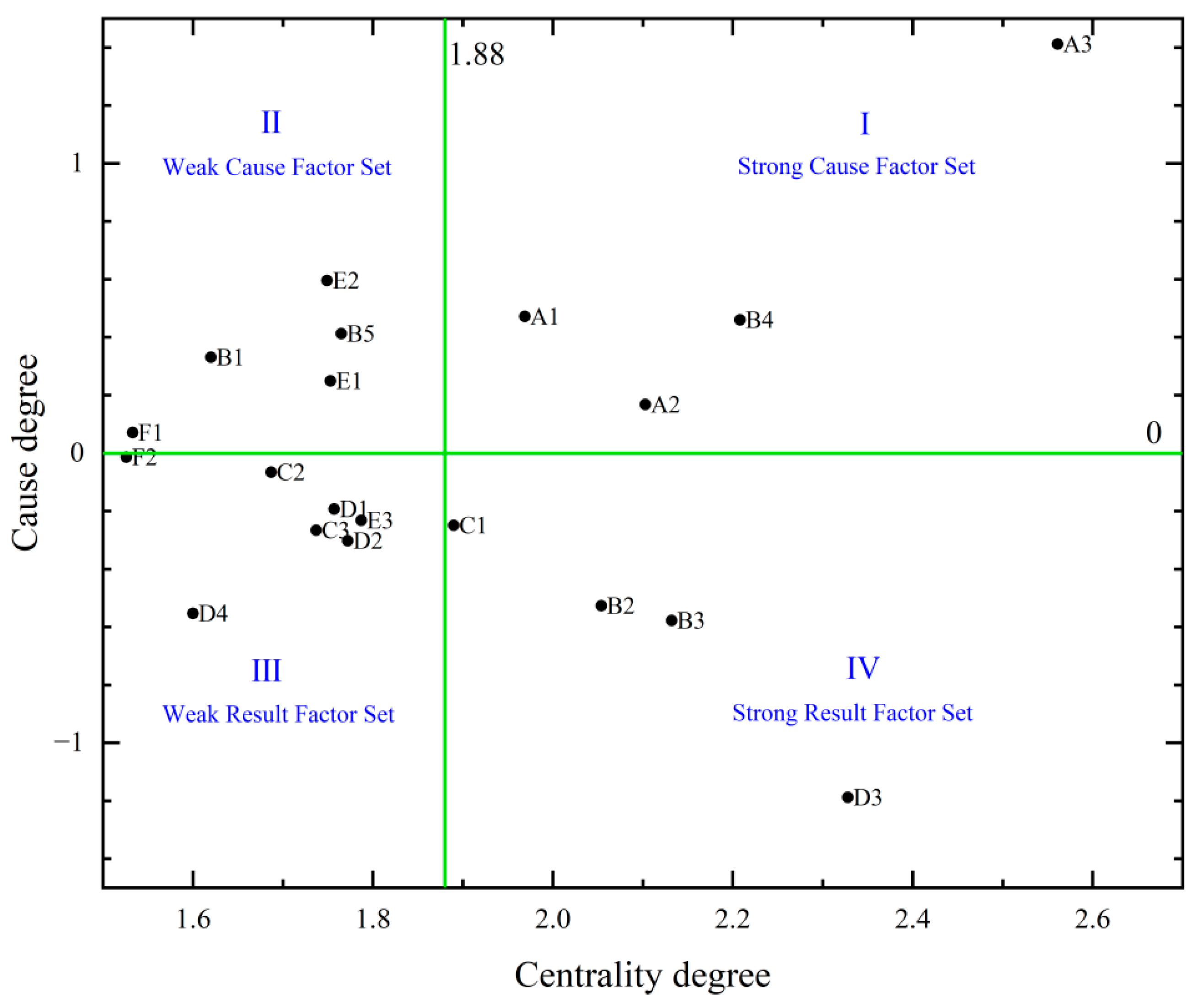
4.1. Analysis of Fuzzy DEMATEL Results
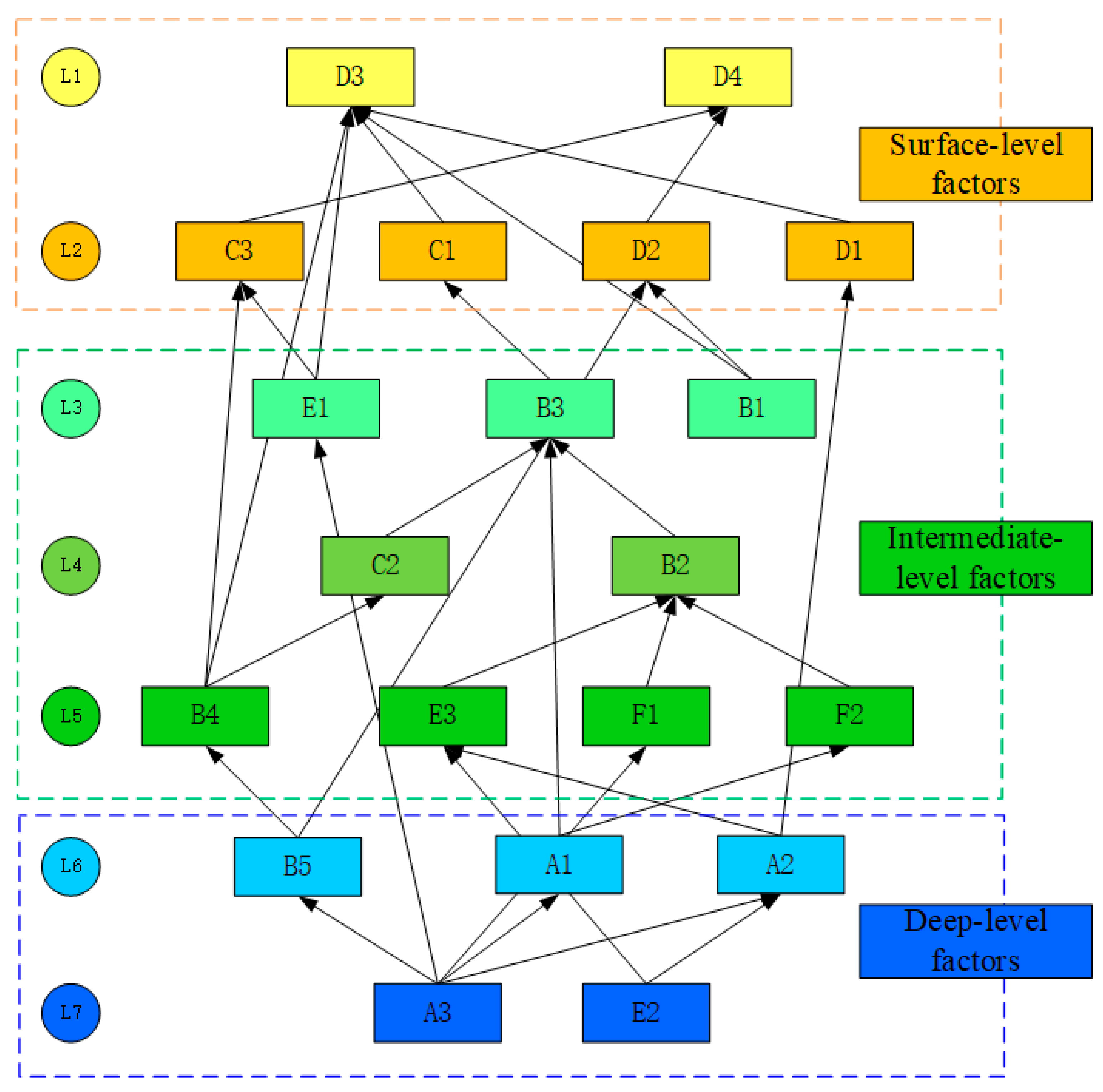
4.2. Analysis of ISM Results
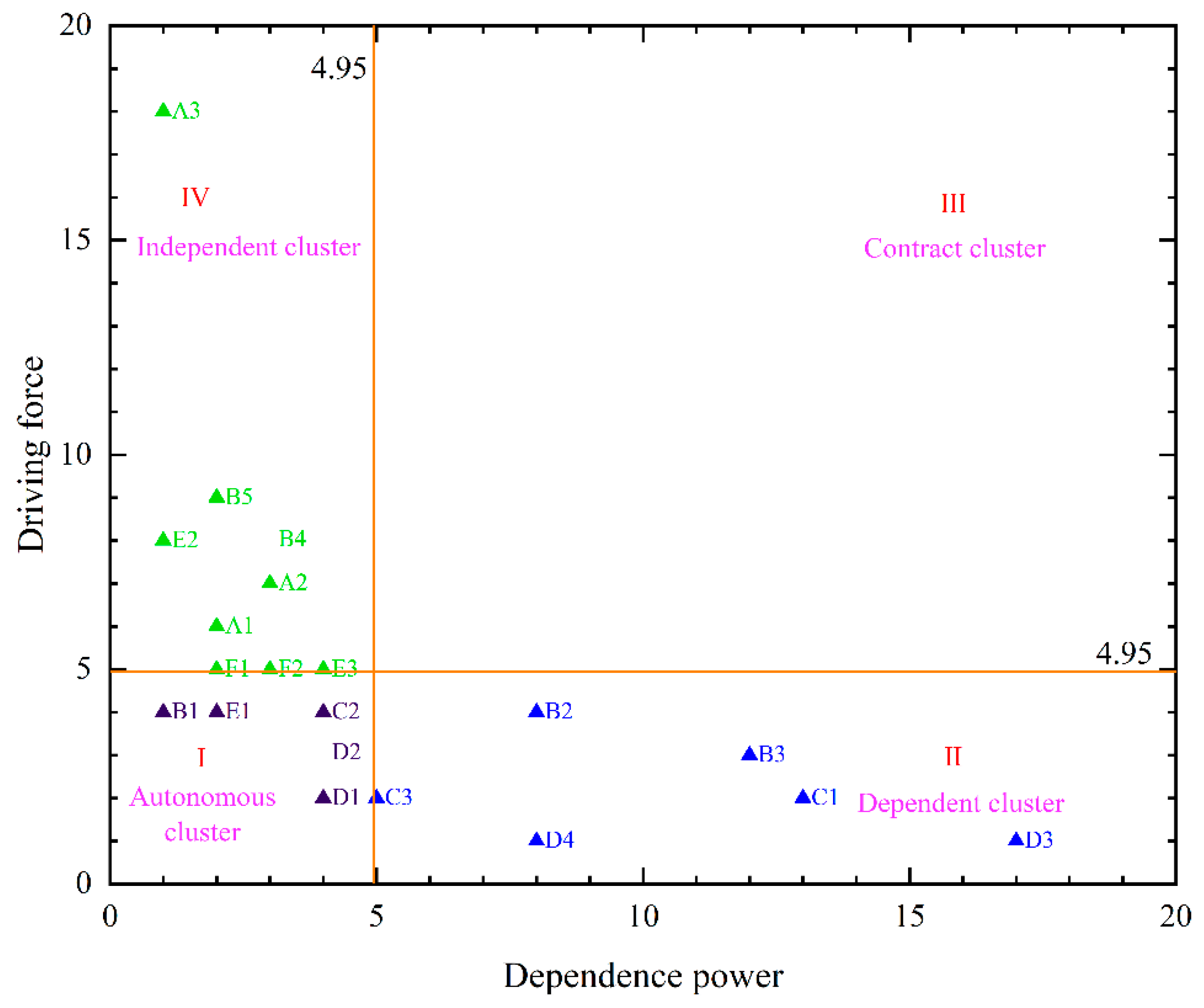
4.3. Micmac Result Analysis
4.4. ANP Result Analysis
5. Discussion
6. Conclusions and Prospects
- Through the investigation of constraints on the promotion of photovoltaic green roof renovation for existing buildings, the effectiveness of the fuzzy DEMATEL-ISM-ANP method in studying coupling relationships, the degree of influence factors, and the method of determining weights were verified.
- A literature review and expert suggestions were considered to summarize the factors influencing the promotion of PV green roof retrofits for existing buildings. Twenty indicators were finally identified and categorized into six groups: macroeconomic policy, participant organization, capital cost, project, market, and social factors.
- In determining the adjacency matrix of the ISM, the node degree method was introduced to determine the threshold value, which is more objective than the previously used expert determination method.
- Lack of incentive policies (A1), imperfect technical specifications and evaluation standard systems (A2), local economic development level (A3), enterprise technical problems (B4), lack of relevant talents (B5), and cooperation mode (E2) are key factors with strong driving force and low dependency, which influence other factors and affect the overall promotion. However, the dependent factors, namely, residents’ awareness (B2) and willingness (B3), are also key factors that need attention due to their strong influence on the results and high weights. Adjustments are needed not only in macroeconomic policies but also in stakeholder involvement to promote photovoltaic green roofs.
- Direct influencing factors, namely, C1, C3, D1, D2, D3, and D4, are most prominent in the system. They are mainly related to costs and project-specific factors. The weight of direct influencing factors is generally higher. However, due to the difficulty of changing them, improvements from fundamental to direct factors are necessary to achieve a positive cycle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, M.; Ma, X.; Cai, W.; Cai, W. Low carbon roadmap of residential building sector in China: Historical mitigation and prospective peak. Appl. Energy 2020, 273, 115247. [Google Scholar] [CrossRef]
- Salvalai, G.; Marrone, G.; Sesana, M.M.; Imperadori, M. Lightweight extensive green roof for building renovation: Summer performance analysis and application in a living laboratory. Energy Build. 2023, 298, 113589. [Google Scholar] [CrossRef]
- Lin, Y.; Cui, C.; Liu, X.; Mao, G.; Xiong, J.; Zhang, Y. Green Renovation and Retrofitting of Old Buildings: A Case Study of a Concrete Brick Apartment in Chengdu. Sustainability 2023, 15, 12409. [Google Scholar] [CrossRef]
- Tian, D.; Zhang, J.; Gao, Z. The advancement of research in cool roof: Super cool roof, temperature-adaptive roof and crucial issues of application in cities. Energy Build. 2023, 291, 113131. [Google Scholar] [CrossRef]
- Lamnatou, C.; Chemisana, D. A critical analysis of factors affecting photovoltaic-green roof performance. Renew. Sustain. Energy Rev. 2015, 43, 264–280. [Google Scholar] [CrossRef]
- Fleck, R.; Gill, R.; Pettit, T.J.; Torpy, F.R.; Irga, P.J. Bio-solar green roofs increase solar energy output: The sunny side of integrating sustainable technologies. Build. Environ. 2022, 226, 109703. [Google Scholar] [CrossRef]
- Zheng, Y.; Weng, Q. Modeling the Effect of Green Roof Systems and Photovoltaic Panels for Building Energy Savings to Mitigate Climate Change. Remote Sens. 2020, 12, 2402. [Google Scholar] [CrossRef]
- Jahanfar, A.; Drake, J.; Sleep, B.; Margolis, L. Evaluating the shading effect of photovoltaic panels on green roof discharge reduction and plant growth. J. Hydrol. 2019, 568, 919–928. [Google Scholar] [CrossRef]
- Schindler, B.Y.; Blank, L.; Levy, S.; Kadas, G.; Pearlmutter, D.; Blaustein, L. Integration of photovoltaic panels and green roofs: Review and predictions of effects on electricity production and plant communities. Isr. J. Ecol. Evol. 2016, 62, 68–73. [Google Scholar] [CrossRef]
- Nash, C.; Clough, J.; Gedge, D.; Lindsay, R.; Newport, D.; Ciupala, M.A.; Connop, S. Initial insights on the biodiversity potential of biosolar roofs: A London Olympic Park green roof case study. Isr. J. Ecol. Evol. 2016, 62, 74–87. [Google Scholar] [CrossRef]
- Ogaili, H.; Sailor, D.J. Measuring the Effect of Vegetated Roofs on the Performance of Photovoltaic Panels in a Combined System. J. Sol. Energy Eng. 2016, 138, 061009. [Google Scholar] [CrossRef]
- Kaewpraek, C. The Effect of Plants on the Energy Output of Green Roof Photovoltaic Systems in Tropical Climates. Sustainability 2021, 13, 4505. [Google Scholar] [CrossRef]
- Van der Roest, E.; Voeten, J.G.; Cirkel, D.G. Increasing solar panel output with blue-green roofs in water-circular and nature inclusive urban development. Build. Environ. 2023, 244, 110704. [Google Scholar] [CrossRef]
- Shafique, M.; Luo, X.; Zuo, J. Photovoltaic-green roofs: A review of benefits, limitations, and trends. Sol. Energy 2020, 202, 485–497. [Google Scholar] [CrossRef]
- Talwar, P.; Verma, N.; Khatri, H.; Ahire, P.D.; Chaudhary, G.; Lindenberger, C.; Vivekanand, V. A systematic review of photovoltaic-green roof systems in different climatic conditions focusing on sustainable cities and societies. Sustain. Cities Soc. 2023, 98, 104813. [Google Scholar] [CrossRef]
- Alonso-Marroquin, F.; Qadir, G. Synergy between Photovoltaic Panels and Green Roofs. Energies 2023, 16, 5184. [Google Scholar] [CrossRef]
- Jayasooriya, V.; Fernando, S.; Silva, C.; Muthukumaran, S. Comparative analysis on the effectiveness of green roofs and photovoltaic panels as sustainable rooftop technologies. Environ. Sci. Pollut. Res. Int. 2023, 30, 98977–98992. [Google Scholar] [CrossRef]
- Jahanfar, A.; Sleep, B.; Drake, J. Energy and carbon-emission analysis of integrated green-roof photovoltaic systems: Probabilistic approach. J. Infrastruct. Syst. 2018, 24, 04017044. [Google Scholar] [CrossRef]
- Torres, F.C.; Almenar, J.B.; Rugani, B. Photovoltaic-green roof energy communities can uphold the European Green Deal: Probabilistic cost-benefit analyses help discern economically convenient scenarios. J. Clean. Prod. 2023, 414, 137428. [Google Scholar] [CrossRef]
- Catalbas, M.C.; Kocak, B.; Yenipınar, B. Analysis of photovoltaic-green roofs in OSTIM industrial zone. Int. J. Hydrogen Energy 2021, 46, 14844–14856. [Google Scholar] [CrossRef]
- Todeschi, V.; Mutani, G.; Baima, L.; Nigra, M.; Robiglio, M. Smart Solutions for Sustainable Cities—The Re-Coding Experience for Harnessing the Potential of Urban Rooftops. Appl. Sci. 2020, 10, 7112. [Google Scholar] [CrossRef]
- Liu, G.; Tan, Y.; Li, X. China’s policies of building green retrofit: A state-of-the-art overview. Build. Environ. 2020, 169, 106554. [Google Scholar] [CrossRef]
- Zhang, X.L.; Shen, L.Y.; Tam, V.W.Y.; Lee, W.W.Y. Barriers to implement extensive green roof systems: A Hong Kong study. Renew. Sustain. Energy Rev. 2012, 16, 314–319. [Google Scholar] [CrossRef]
- Chen, S.; Gou, Z. An Investigation of Green Roof Spatial Distribution and Incentive Policies Using Green Buildings as a Benchmark. Land 2022, 11, 2067. [Google Scholar] [CrossRef]
- Kılıç, U.; Kekezoğlu, B. A review of solar photovoltaic incentives and Policy: Selected countries and Turkey. Ain Shams Eng. J. 2022, 13, 101669. [Google Scholar] [CrossRef]
- Liberalesso, T.; Oliveira Cruz, C.; Matos Silva, C.; Manso, M. Green infrastructure and public policies: An international review of green roofs and green walls incentives. Land Use Policy 2020, 96, 104693. [Google Scholar] [CrossRef]
- Chandel, R.; Chandel, S.S.; Malik, P. Perspective of new distributed grid connected roof top solar photovoltaic power generation policy interventions in India. Energy Policy 2022, 168, 113122. [Google Scholar] [CrossRef]
- Bo, L.; Cheng, S.; Li, D.; Isaeva, E.; Rocha, Á. Establishment and application of fuzzy comprehensive evaluation of green building design based on data mining. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2020, 38, 6815–6823. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, J.; Jin, H. A Review of Green Building Development in China from the Perspective of Energy Saving. Energies 2018, 11, 334. [Google Scholar] [CrossRef]
- Kelly, C.; Sen, B.; Tatari, O. A system dynamics analysis of the alternative roofing market and its potential impacts on urban environmental problems: A case study in Orlando, Florida. Resour. Conserv. Recycl. 2020, 153, 104556. [Google Scholar] [CrossRef]
- Golubchikov, O.; Deda, P. Governance, technology, and equity: An integrated policy framework for energy efficient housing. Energy Policy 2012, 41, 733–741. [Google Scholar] [CrossRef]
- Tsantopoulos, G.; Varras, G.; Chiotelli, E.; Fotia, K.; Batou, M. Public perceptions and attitudes toward green infrastructure on buildings: The case of the metropolitan area of Athens, Greece. Urban For. Urban Green. 2018, 34, 181–195. [Google Scholar] [CrossRef]
- Darko, A.; Chan, A.P.C.; Ameyaw, E.E.; He, B.J.; Olanipekun, A.O. Examining issues influencing green building technologies adoption: The United States green building experts’ perspectives. Energy Build. 2017, 144, 320–332. [Google Scholar] [CrossRef]
- Jim, C.Y.; Hui, L.C.; Rupprecht, C.D.D. Rupprecht.Public Perceptions of Green Roofs and Green Walls in Tokyo, Japan: A Call to Heighten Awareness. Environ. Manag. 2022, 70, 35–53. [Google Scholar] [CrossRef] [PubMed]
- Dutt, D.; Ranjan, A. Towards a just energy transition in Delhi: Addressing the bias in the rooftop solar market. Energy Policy 2022, 160, 112667. [Google Scholar] [CrossRef]
- Shen, W.X.; Tang, W.Z.; Siripanan, A.; Lei, Z.; Duffield, C.F.; Hui, F.K.P. Understanding the green technical capabilities and barriers to green buildings in developing countries: A case study of Thailand. Sustainability 2018, 10, 3585. [Google Scholar] [CrossRef]
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- He, Q.; Zhao, H.; Shen, L.; Dong, L.; Cheng, Y.; Xu, K. Factors Influencing Residents’ Intention toward Green Retrofitting of Existing Residential Buildings. Sustainability 2019, 11, 4246. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, Y.; Zheng, L.; Dai, Q.; Zhang, Z. What is the path of photovoltaic building (BIPV or BAPV) promotion?—The perspective of evolutionary games. Appl. Energy 2023, 340, 121033. [Google Scholar] [CrossRef]
- Getter, K.L.; Rowe, D.B. The role of extensive green roofs in sustainable development. HortScience 2006, 41, 1276–1285. [Google Scholar] [CrossRef]
- De Feijter, F.J.; van Vliet, B.J.M.; Chen, Y. Household inclusion in the governance of housing retrofitting: Analysing Chinese and Dutch systems of energy retrofit provision. Energy Res. Soc. Sci. 2019, 53, 10–22. [Google Scholar] [CrossRef]
- Hrovatin, N.; Zorić, J. Determinants of energy-efficient home retrofits in Slovenia: The role of information sources. Energy Build. 2018, 180, 42–50. [Google Scholar] [CrossRef]
- Chan, A.P.C.; Darko, A.; Olanipekun, A.O.; Ameyaw, E.E. Critical barriers to green building technologies adoption in developing countries: The case of Ghana. J. Clean. Prod. 2018, 172, 1067–1079. [Google Scholar] [CrossRef]
- Liu, G.; Li, X.; Tan, Y.; Zhang, G. Building green retrofit in China: Policies, barriers and recommendations. Energy Policy 2020, 139, 111356. [Google Scholar] [CrossRef]
- Yao, L.; Chini, A.; Zeng, R. Integrating cost-benefits analysis and life cycle assessment of green roofs: A case study in Florida. Hum. Ecol. Risk Assess. 2020, 26, 443–458. [Google Scholar] [CrossRef]
- Tabatabaee, S.; Mahdiyar, A.; Mohandes, S.R.; Ismail, S. Towards the Development of a Comprehensive Lifecycle Risk Assessment Model for Green Roof Implementation. Sustain. Cities Soc. 2022, 76, 103404. [Google Scholar] [CrossRef]
- Wong, G.K.L.; Jim, C.Y. Urban-microclimate effect on vector mosquito abundance of tropical green roofs. Build. Environ. 2017, 112, 63–76. [Google Scholar] [CrossRef]
- Hui, L.C.; Jim, C.; Tian, Y. Public views on green roofs and green walls in two major Asian cities and implications for promotion policy. Urban For. Urban Green. 2022, 70, 127546. [Google Scholar] [CrossRef]
- Lo, A.Y.H.; Jim, C.Y. Citizen attitude and expectation towards greenspace provision in compact urban milieu. Land Use Policy 2012, 29, 577–586. [Google Scholar] [CrossRef]
- Jungels, J.; Rakow, D.A.; Allred, S.B.; Skelly, S.M. Attitudes and aesthetic reactions toward green roofs in the Northeastern United States. Landsc. Urban Plan. 2013, 117, 13–21. [Google Scholar] [CrossRef]
- Brigglio, M.; Formosa, G. When households go solar: Determinants of uptake of a Photovoltaic Scheme and policy insights. Energy Policy 2017, 108, 154–162. [Google Scholar] [CrossRef]
- Li, H.; Shuying, F.; Skitmore, M.; Talebian, N. Willingness-to-pay for energy-saving retrofits of residential buildings and its influencing factors: The case of the Pearl River Delta, China. Technol. Econ. Dev. Econ. 2022, 28, 1684–1710. [Google Scholar]
- Liang, Y.; Wang, H.; Zhao, X. Analysis of factors affecting economic operation of electric vehicle charging station based on DEMATEL-ISM. Comput. Ind. Eng. 2022, 163, 107818. [Google Scholar] [CrossRef]
- Wu, W.W.; Lee, Y.T. Developing global managers’ competencies using the fuzzy DEMATEL method. Expert Syst. Appl. 2007, 32, 499–507. [Google Scholar] [CrossRef]
- Akyuz, E.; Celik, E. A fuzzy DEMATEL method to evaluate critical operational hazards during gas freeing process in crude oil tankers. J. Loss Prev. Process Ind. 2015, 38, 243–253. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Yadav, S.; Luthra, S.; Garg, D. Internet of things (IoT) based coordination system in Agri-food supply chain: Development of an efficient framework using DEMATEL-ISM. Oper. Manag. Res. 2020, 15, 1–27. [Google Scholar] [CrossRef]
- Warfield, J. Developing Interconnection Matrices in Structural Modeling. IEEE Trans. Syst. Man Cybern. 1974, SMC-4, 81–87. [Google Scholar] [CrossRef]
- Valmohammadi, C.; Dashti, S. Using interpretive structural modeling and fuzzy analytical process to identify and prioritize the interactive barriers of e-commerce implementation. Inf. Manag. 2016, 53, 157–168. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Y.; Huang, Z.; Cui, R. Understanding the resilience of coal industry ecosystem to economic shocks: Influencing factors, dynamic evolution and policy suggestions. Resour. Policy 2020, 67, 101682. [Google Scholar] [CrossRef]
- Feng, X.; Li, E.; Li, J.; Wei, C. Critical Influencing Factors of Employees’ Green Behavior: Three-Stage Hybrid Fuzzy DEMATEL–ISM–MICMAC Approach. Environ. Dev. Sustain. 2023, 25, 1–29. [Google Scholar] [CrossRef]
- Panahifar, F.; Byrne, P.J.; Heavey, C. ISM analysis of CPFR implementation barriers. Int. J. Prod. Res. 2014, 52, 5255–5272. [Google Scholar] [CrossRef][Green Version]
- Feng, Y.X.; Hong, Z.X.; Zhang, Z.F.; Zhang, Z.X.; Tan, J.R. Interval Analysis and DEMATEL-Based Reliability Apportionment for Energy Consumption Optimization with Energy Internet. IEEE Access 2017, 5, 4769–4778. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise Solution by MCDM Methods: A Comparative Analysis of VIKOR and TOPSIS. Eur. J. Opera. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Chai, Q.; Li, H.; Tian, W.; Zhang, Y. Critical Success Factors for Safety Program Implementation of Regeneration of Abandoned Industrial Building Projects in China: A Fuzzy DEMATEL Approach. Sustainability 2022, 14, 1550. [Google Scholar] [CrossRef]
- Kuzu, A.C. Risk analysis of break-in-two accident of ships using fuzzy DEMATEL method. Ocean Eng. 2021, 235, 109410. [Google Scholar] [CrossRef]
- Wu, W.W. Choosing knowledge management strategies by using a combined ANP and DEMATEL approach. Expert Syst. Appl. 2008, 35, 828–835. [Google Scholar] [CrossRef]
- Marlin, D.; Lamont, B.T.; Hoffman, J.J. Choice situation, strategy, and performance: A reexamination. Strateg. Manag. J. 1994, 15, 229–239. [Google Scholar] [CrossRef]
- Azevedo, S.; Carvalho, H.; Cruz-Machado, V. Using interpretive structural modelling to identify and rank performance measures. Balt. J. Manag. 2013, 8, 208–230. [Google Scholar] [CrossRef]


| Dimension | Number | Factors |
|---|---|---|
| Macroeconomic policy factors | A1 | Lack of incentive policies |
| A2 | Technical specifications, evaluation standards, and systems are not sound | |
| A3 | Local economic development level | |
| Participant factors | B1 | Lack of coordination mechanism |
| B2 | Residents’ cognitive level | |
| B3 | Residents’ willingness | |
| B4 | Enterprise technical issues | |
| B5 | Lack of relevant talents | |
| Capital cost factors | C1 | Lack of capital investment |
| C2 | Uncertainty in investment returns | |
| C3 | Increased maintenance costs | |
| Project factors | D1 | Existing building measurement and evaluation measures |
| D2 | Lack of post-maintenance management | |
| D3 | Difficulty and duration of the renovation | |
| D4 | Environmental and nuisance issues after renovation | |
| Market factors | E1 | Inadequate supply chain and supporting infrastructure |
| E2 | Cooperation mode | |
| E3 | Market entry threshold | |
| Social factors | F1 | Demographic characteristics |
| F2 | Lack of promotion platforms and activities |
| Language Operator | Triangular Fuzzy Number (TFN) |
|---|---|
| No impact (0) | (0, 0, 0.25) |
| Low impact (1) | (0, 0.25, 0.25) |
| Has a certain impact (2) | (0.25, 0.5, 0.75) |
| Has a high impact (3) | (0.5, 0.75,1) |
| Has a very significant impact (4) | (0.75, 1, 1) |
| A1 | A2 | A3 | B1 | B2 | B3 | B4 | B5 | C1 | C2 | C3 | D1 | D2 | D3 | D4 | E1 | E2 | E3 | F1 | F2 | |
| A1 | 0 | 0.1458125 | 0.0833 | 0.124975 | 0.1458125 | 0.87495 | 0.1979 | 0.1458125 | 0.1979 | 0.0833 | 0.0833 | 0.1979 | 0.1458125 | 0.0833 | 0.0833 | 0.156225 | 0.0833 | 0.0833 | 0.0833 | 0.87495 |
| A2 | 0.1041375 | 0 | 0.0833 | 0.1979 | 0.0833 | 0.0833 | 0.2708 | 0.0833 | 0.1041375 | 0.1041375 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.9166 | 0.0833 | 0.0833 |
| A3 | 0.9166 | 0.895775 | 0 | 0.1979 | 0.124975 | 0.1874875 | 0.1458125 | 0.572875 | 0.1979 | 0.124975 | 0.0833 | 0.16665 | 0.0833 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.87495 | 0.1458125 |
| B1 | 0.0833 | 0.0833 | 0.1041375 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.87495 | 0.87495 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| B2 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.854125 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| B3 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 |
| B4 | 0.0833 | 0.0833 | 0.22915 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.1041375 | 0.1041375 | 0.895775 | 0.8333 | 0.2499875 | 0.124975 | 0.854125 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| B5 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.9166 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.16665 | 0.8333 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| C1 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0 | 0.0833 | 0.0833 | 0.239575 | 0.1874875 | 0.895775 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| C2 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.2187375 | 0 | 0.0833 | 0.0833 | 0.124975 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| C3 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.895775 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| D1 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.124975 | 0.0833 | 0.0833 | 0 | 0.0833 | 0.895775 | 0.0833 | 0.0833 | 0.1770625 | 0.0833 | 0.0833 | 0.0833 |
| D2 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.0833 | 0.9166 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| D3 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1979 | 0.124975 | 0.0833 | 0.0833 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| D4 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| E1 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.1979 | 0.1041375 | 0.854125 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0 | 0.0833 | 0.0833 | 0.0833 | 0.0833 |
| E2 | 0.0833 | 0.895775 | 0.0833 | 0.2187375 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.270825 | 0.1458125 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.895775 | 0.0833 | 0.0833 |
| E3 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.0833 | 0.1041375 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.124975 | 0 | 0.0833 | 0.0833 |
| F1 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.9166 | 0.1979 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 | 0.0833 |
| F2 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.87495 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0.0833 | 0 |
| A1 | A2 | A3 | B1 | B2 | B3 | B4 | B5 | C1 | C2 | C3 | D1 | D2 | D3 | D4 | E1 | E2 | E3 | F1 | F2 | |
| A1 | 0.022 | 0.05 | 0.032 | 0.04 | 0.074 | 0.181 | 0.059 | 0.044 | 0.079 | 0.041 | 0.045 | 0.062 | 0.055 | 0.069 | 0.044 | 0.047 | 0.033 | 0.042 | 0.035 | 0.166 |
| A2 | 0.038 | 0.025 | 0.031 | 0.051 | 0.063 | 0.05 | 0.067 | 0.033 | 0.046 | 0.045 | 0.043 | 0.169 | 0.043 | 0.079 | 0.041 | 0.034 | 0.034 | 0.176 | 0.034 | 0.035 |
| A3 | 0.185 | 0.188 | 0.03 | 0.068 | 0.095 | 0.107 | 0.079 | 0.127 | 0.087 | 0.063 | 0.075 | 0.091 | 0.071 | 0.108 | 0.061 | 0.179 | 0.044 | 0.073 | 0.177 | 0.076 |
| B1 | 0.032 | 0.036 | 0.032 | 0.016 | 0.041 | 0.043 | 0.034 | 0.03 | 0.041 | 0.036 | 0.037 | 0.036 | 0.167 | 0.18 | 0.055 | 0.032 | 0.028 | 0.036 | 0.032 | 0.032 |
| B2 | 0.028 | 0.032 | 0.025 | 0.026 | 0.023 | 0.164 | 0.03 | 0.027 | 0.053 | 0.03 | 0.032 | 0.033 | 0.036 | 0.047 | 0.034 | 0.028 | 0.026 | 0.032 | 0.028 | 0.028 |
| B3 | 0.028 | 0.032 | 0.025 | 0.027 | 0.037 | 0.024 | 0.031 | 0.027 | 0.164 | 0.031 | 0.033 | 0.039 | 0.035 | 0.063 | 0.034 | 0.028 | 0.029 | 0.033 | 0.028 | 0.029 |
| B4 | 0.04 | 0.045 | 0.057 | 0.035 | 0.049 | 0.069 | 0.027 | 0.041 | 0.054 | 0.176 | 0.167 | 0.071 | 0.052 | 0.191 | 0.062 | 0.04 | 0.034 | 0.043 | 0.04 | 0.038 |
| B5 | 0.034 | 0.038 | 0.033 | 0.031 | 0.044 | 0.047 | 0.173 | 0.019 | 0.041 | 0.055 | 0.055 | 0.055 | 0.163 | 0.073 | 0.059 | 0.034 | 0.03 | 0.038 | 0.033 | 0.034 |
| C1 | 0.029 | 0.033 | 0.026 | 0.027 | 0.038 | 0.039 | 0.034 | 0.028 | 0.021 | 0.034 | 0.035 | 0.058 | 0.051 | 0.183 | 0.037 | 0.029 | 0.027 | 0.033 | 0.029 | 0.029 |
| C2 | 0.029 | 0.032 | 0.026 | 0.027 | 0.038 | 0.169 | 0.031 | 0.028 | 0.073 | 0.017 | 0.033 | 0.034 | 0.041 | 0.051 | 0.035 | 0.029 | 0.026 | 0.033 | 0.029 | 0.029 |
| C3 | 0.028 | 0.031 | 0.025 | 0.026 | 0.036 | 0.038 | 0.03 | 0.026 | 0.033 | 0.033 | 0.018 | 0.031 | 0.032 | 0.044 | 0.166 | 0.028 | 0.025 | 0.032 | 0.027 | 0.028 |
| D1 | 0.028 | 0.034 | 0.026 | 0.027 | 0.037 | 0.039 | 0.03 | 0.027 | 0.041 | 0.033 | 0.033 | 0.019 | 0.033 | 0.179 | 0.034 | 0.028 | 0.041 | 0.035 | 0.028 | 0.029 |
| D2 | 0.028 | 0.031 | 0.025 | 0.026 | 0.036 | 0.037 | 0.03 | 0.026 | 0.033 | 0.03 | 0.032 | 0.031 | 0.018 | 0.044 | 0.17 | 0.028 | 0.025 | 0.032 | 0.027 | 0.028 |
| D3 | 0.025 | 0.028 | 0.022 | 0.023 | 0.033 | 0.036 | 0.027 | 0.024 | 0.03 | 0.046 | 0.035 | 0.028 | 0.029 | 0.026 | 0.031 | 0.025 | 0.023 | 0.029 | 0.025 | 0.025 |
| D4 | 0.024 | 0.027 | 0.022 | 0.023 | 0.032 | 0.033 | 0.026 | 0.023 | 0.029 | 0.026 | 0.028 | 0.027 | 0.028 | 0.038 | 0.015 | 0.024 | 0.022 | 0.028 | 0.024 | 0.025 |
| E1 | 0.032 | 0.036 | 0.029 | 0.033 | 0.042 | 0.044 | 0.034 | 0.031 | 0.057 | 0.041 | 0.164 | 0.036 | 0.038 | 0.183 | 0.055 | 0.018 | 0.029 | 0.037 | 0.032 | 0.032 |
| E2 | 0.035 | 0.172 | 0.031 | 0.057 | 0.065 | 0.051 | 0.041 | 0.033 | 0.074 | 0.049 | 0.04 | 0.058 | 0.044 | 0.065 | 0.042 | 0.035 | 0.019 | 0.192 | 0.034 | 0.035 |
| E3 | 0.028 | 0.033 | 0.025 | 0.027 | 0.167 | 0.055 | 0.03 | 0.027 | 0.04 | 0.03 | 0.032 | 0.032 | 0.034 | 0.046 | 0.034 | 0.028 | 0.032 | 0.02 | 0.028 | 0.029 |
| F1 | 0.029 | 0.032 | 0.026 | 0.027 | 0.174 | 0.075 | 0.031 | 0.027 | 0.039 | 0.031 | 0.033 | 0.033 | 0.034 | 0.046 | 0.034 | 0.029 | 0.026 | 0.033 | 0.015 | 0.029 |
| F2 | 0.028 | 0.031 | 0.025 | 0.026 | 0.166 | 0.054 | 0.03 | 0.027 | 0.036 | 0.03 | 0.032 | 0.032 | 0.033 | 0.044 | 0.033 | 0.028 | 0.025 | 0.032 | 0.028 | 0.014 |
| Factor | Impact Degree D Value | Affected Degree C Value | Centricity D + C Value | Cause Degree D − C Value |
|---|---|---|---|---|
| A1 | 1.22 | 0.749 | 1.969 | 0.472 |
| A2 | 1.135 | 0.968 | 2.103 | 0.168 |
| A3 | 1.986 | 0.575 | 2.561 | 1.412 |
| B1 | 0.975 | 0.645 | 1.62 | 0.331 |
| B2 | 0.764 | 1.29 | 2.054 | −0.527 |
| B3 | 0.777 | 1.355 | 2.132 | −0.578 |
| B4 | 1.334 | 0.874 | 2.208 | 0.46 |
| B5 | 1.088 | 0.676 | 1.765 | 0.412 |
| C1 | 0.82 | 1.07 | 1.89 | −0.249 |
| C2 | 0.811 | 0.877 | 1.687 | −0.066 |
| C3 | 0.736 | 1.001 | 1.737 | −0.266 |
| D1 | 0.782 | 0.975 | 1.757 | −0.193 |
| D2 | 0.735 | 1.037 | 1.772 | −0.303 |
| D3 | 0.57 | 1.758 | 2.328 | −1.188 |
| D4 | 0.523 | 1.076 | 1.6 | −0.553 |
| E1 | 1.001 | 0.752 | 1.753 | 0.249 |
| E2 | 1.173 | 0.576 | 1.749 | 0.596 |
| E3 | 0.777 | 1.009 | 1.787 | −0.232 |
| F1 | 0.802 | 0.731 | 1.533 | 0.071 |
| F2 | 0.756 | 0.77 | 1.526 | −0.014 |
| A1 | A2 | A3 | B1 | B2 | B3 | B4 | B5 | C1 | C2 | C3 | D1 | D2 | D3 | D4 | E1 | E2 | E3 | F1 | F2 | |
| A1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| A2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| A3 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| B1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| B2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| B3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| B4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| B5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| C1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| C2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| C3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| D1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| D2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| D3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| D4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| E1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| E2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| E3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| F1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| F2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Factors | Reachable Set (R) | Antecedent Set (Q) | Intersection (A = R∩Q) |
|---|---|---|---|
| A1 | A1, B2, B3, C1, D3, F2 | A1, A3 | A1 |
| A2 | A2, B2, B3, C1, D1, D3, E3 | A2, A3, E2 | A2 |
| A3 | A1, A2, A3, B2, B3, B4, B5, C1, C2, C3, D1, D2, D3, D4, E1, E3, F1, F2 | A3 | A3 |
| B1 | B1, D2, D3, D4 | B1 | B1 |
| B2 | B2, B3, C1, D3 | A1, A2, A3, B2, E2, E3, F1, F2 | B2 |
| B3 | B3, C1, D3 | A1, A2, A3, B2, B3, B4, B5, C2, E2, E3, F1, F2 | B3 |
| B4 | B3, B4, C1, C2, C3, D3, D4 | A3, B4, B5 | B4 |
| B5 | B3, B4, B5, C1, C2, C3D2, D3, D4 | A3, B5 | B5 |
| C1 | C1, D3 | A1, A2, A3, B2, B3, B4, B5, C1, C2, E2, E3, F1, F2 | C1 |
| C2 | B3, C1, C2, D3 | A3, B4, B5, C1 | C2 |
| C3 | C3, D4 | A3, B4, B5, C3, E1 | C3 |
| D1 | D1, D3 | A2, A3, D1, E2 | D1 |
| D2 | D2, D4 | A3, B1, B5, D2 | D2 |
| D3 | D3 | A1, A2, A3, B1, B2, B3, B4, B5, C1, C2, D1, D3, E1, E2, E2, F1, F2 | D3 |
| D4 | D4 | A3, B1, B4, B5, C3, D2, D4, E1 | D4 |
| E1 | C3, D3, D4, E1 | A3, E1 | E1 |
| E2 | A2, B2, B3, C1, D1, D3, E2, E3 | E2 | E2 |
| E3 | B2, B3, C1, D3, E3 | A2, A3, E2, E3 | E3 |
| F1 | B2, B3, C1, D3, F1 | A3, F1 | F1 |
| F2 | B2, B3, C1, D3, F2 | A1, A3, F2 | F2 |
| Factors | Dependence | Driving Force | Factors | Dependence | Driving Force |
|---|---|---|---|---|---|
| A1 | 2 | 6 | C3 | 5 | 2 |
| A2 | 3 | 7 | D1 | 4 | 2 |
| A3 | 1 | 18 | D2 | 4 | 2 |
| B1 | 1 | 4 | D3 | 17 | 1 |
| B2 | 8 | 4 | D4 | 8 | 1 |
| B3 | 12 | 3 | E1 | 2 | 4 |
| B4 | 3 | 7 | E2 | 1 | 8 |
| B5 | 2 | 9 | E3 | 4 | 5 |
| C1 | 13 | 2 | F1 | 2 | 5 |
| C2 | 4 | 4 | F2 | 3 | 5 |
| Factors | Weight | Sort | Factors | Weight | Sort |
|---|---|---|---|---|---|
| A1 | 0.041 | 9 | C3 | 0.019 | 17 |
| A2 | 0.051 | 6 | D1 | 0.038 | 11 |
| A3 | 0.030 | 14 | D2 | 0.059 | 5 |
| B1 | 0.031 | 13 | D3 | 0.237 | 1 |
| B2 | 0.045 | 8 | D4 | 0.079 | 3 |
| B3 | 0.060 | 4 | E1 | 0.033 | 12 |
| B4 | 0.038 | 10 | E2 | 0.046 | 7 |
| B5 | 0.026 | 15 | E3 | 0.014 | 20 |
| C1 | 0.099 | 2 | F1 | 0.018 | 18 |
| C2 | 0.019 | 16 | F2 | 0.017 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xiang, Y.; Xia, Y.; Yang, W.; Tang, X.; Lin, T. What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method. Sustainability 2023, 15, 16862. https://doi.org/10.3390/su152416862
Li H, Xiang Y, Xia Y, Yang W, Tang X, Lin T. What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method. Sustainability. 2023; 15(24):16862. https://doi.org/10.3390/su152416862
Chicago/Turabian StyleLi, Hongbing, Yuran Xiang, Yaohui Xia, Wanjun Yang, Xiaoting Tang, and Tao Lin. 2023. "What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method" Sustainability 15, no. 24: 16862. https://doi.org/10.3390/su152416862
APA StyleLi, H., Xiang, Y., Xia, Y., Yang, W., Tang, X., & Lin, T. (2023). What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method. Sustainability, 15(24), 16862. https://doi.org/10.3390/su152416862






