Performance Analysis and Multi-Objective Optimization of a Cooling-Power-Desalination Combined Cycle for Shipboard Diesel Exhaust Heat Recovery
Abstract
:1. Introduction
2. Materials and Methods
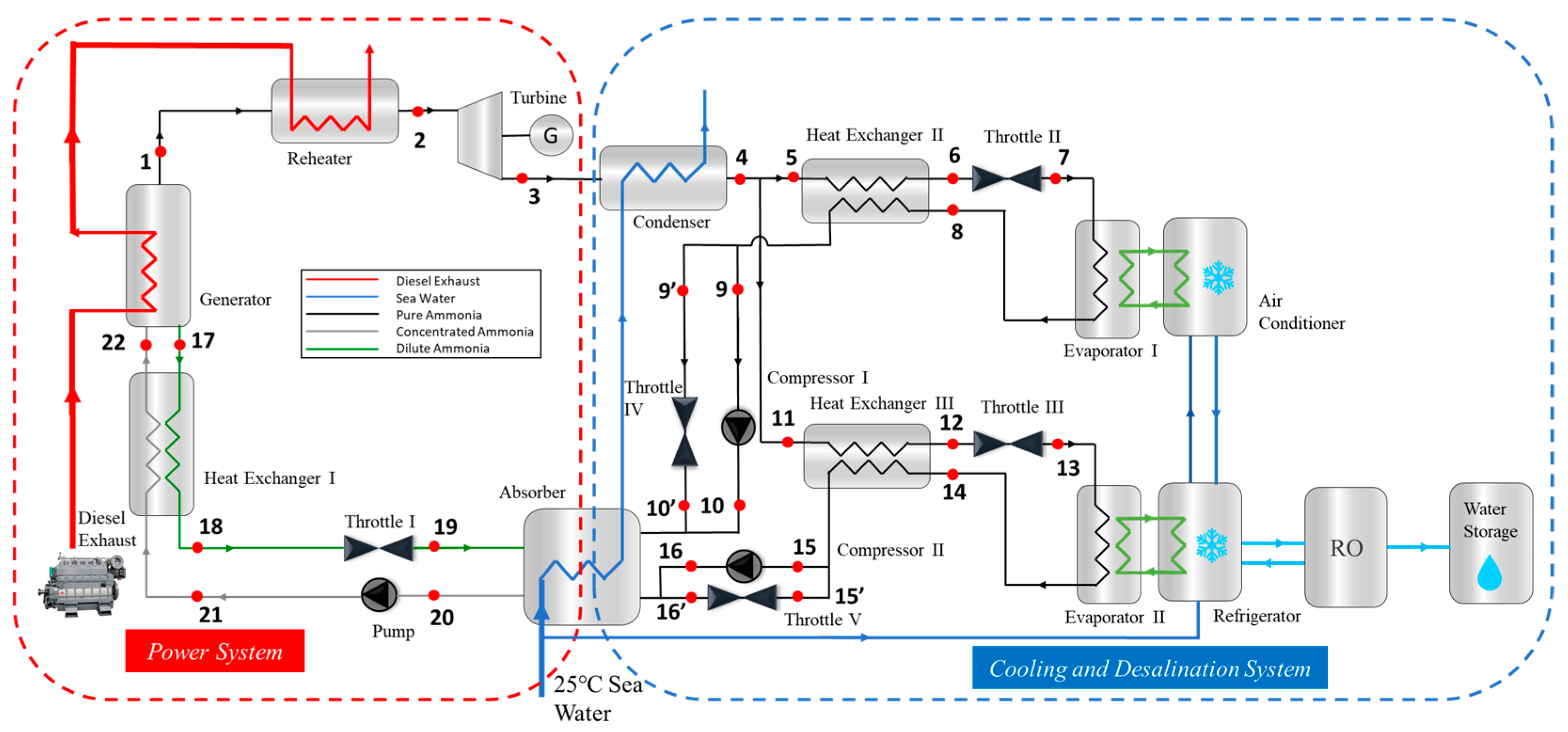
2.1. Cycle Operating Principle
2.2. Mathematical Model
2.2.1. Mathematical Model Analysis
2.2.2. Cycle Performance Evaluation
2.2.3. Heat Exchanger Model
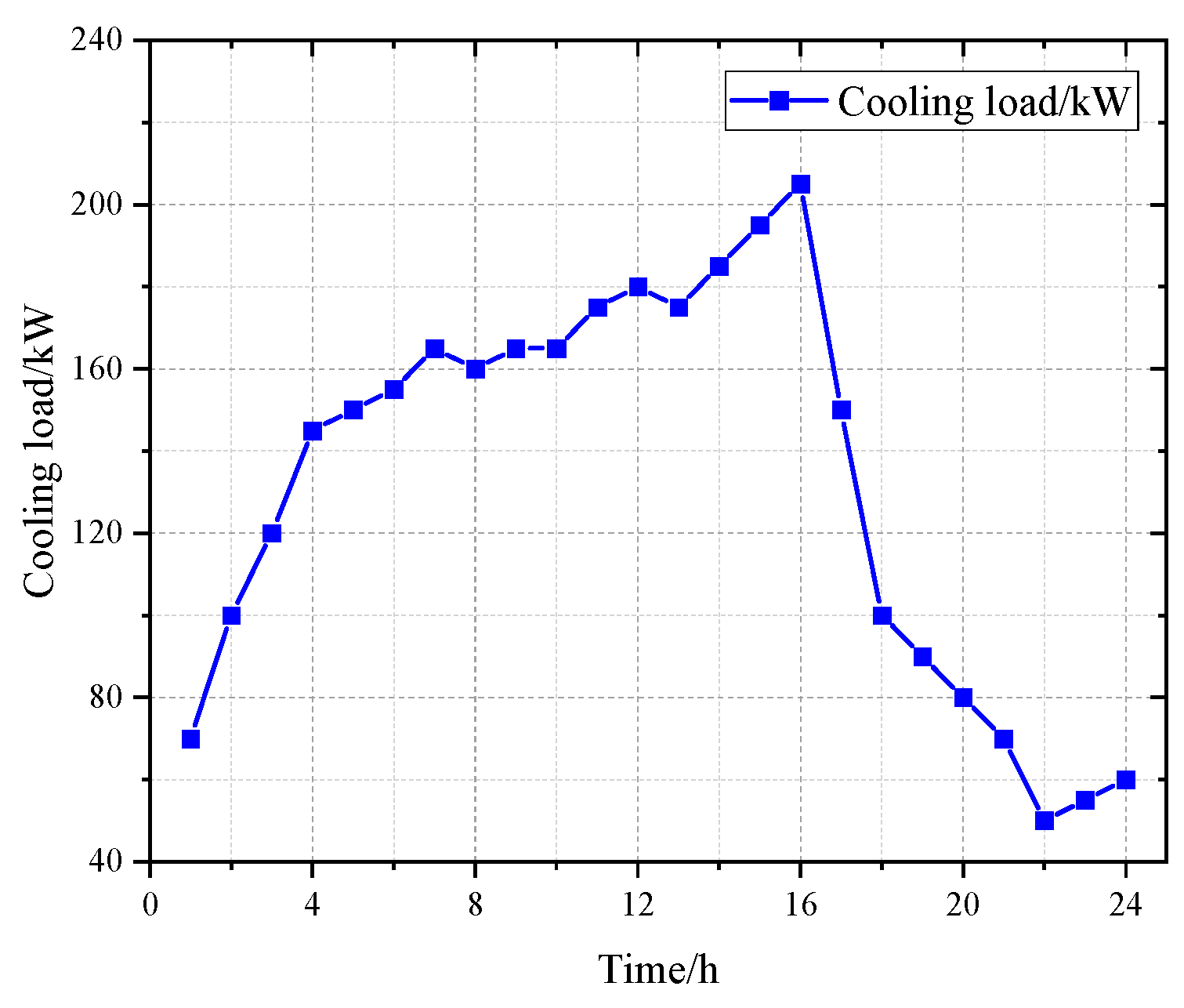
2.2.4. Cooling-Load Model
2.3. Multi-Objective Optimization
2.3.1. Methods of Optimization and Decision-Making
2.3.2. Objective Functions and Decision Variables
2.3.3. Model Based Assumptions
- (1)
- Pressure loss and energy loss in the pipes and all heat exchangers are negligible.
- (2)
- Chemical reactions that may occur during the cycle of working fluids are ignored.
- (3)
- The heat source (diesel engine exhaust), the cold source (surface seawater), and the cycle working fluid are assumed to be in a stable and uniform flow state.
- (4)
- The heat exchanger is assumed to have a certain heat exchange temperature difference.
- (5)
- The outlets of the evaporator, condenser, and absorber are all assumed to be saturated.
2.3.4. Model Validation
2.4. Economic Analysis of Desalination
3. Results and Discussions
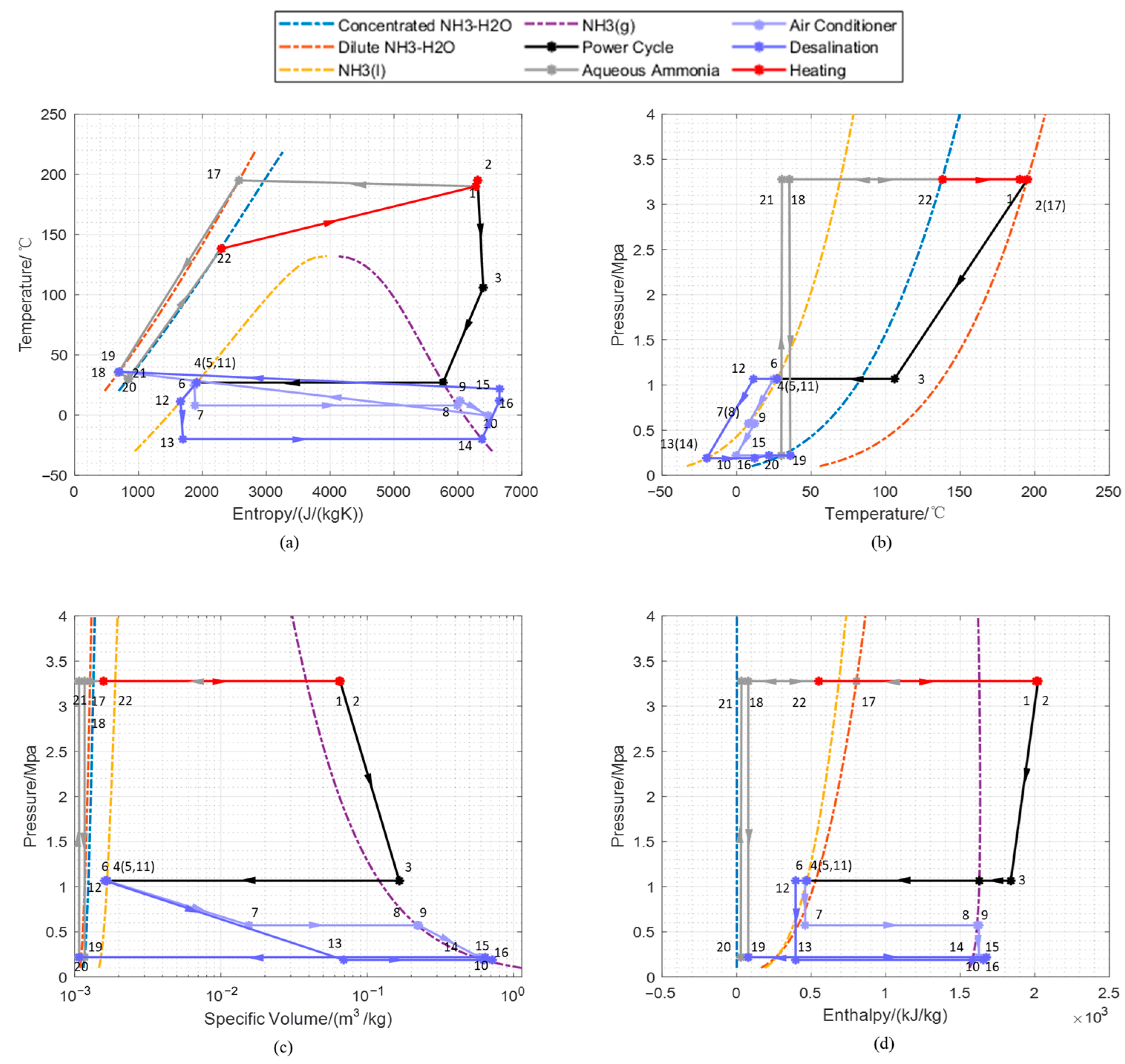
3.1. Cycle Performance under Initial Working Conditions
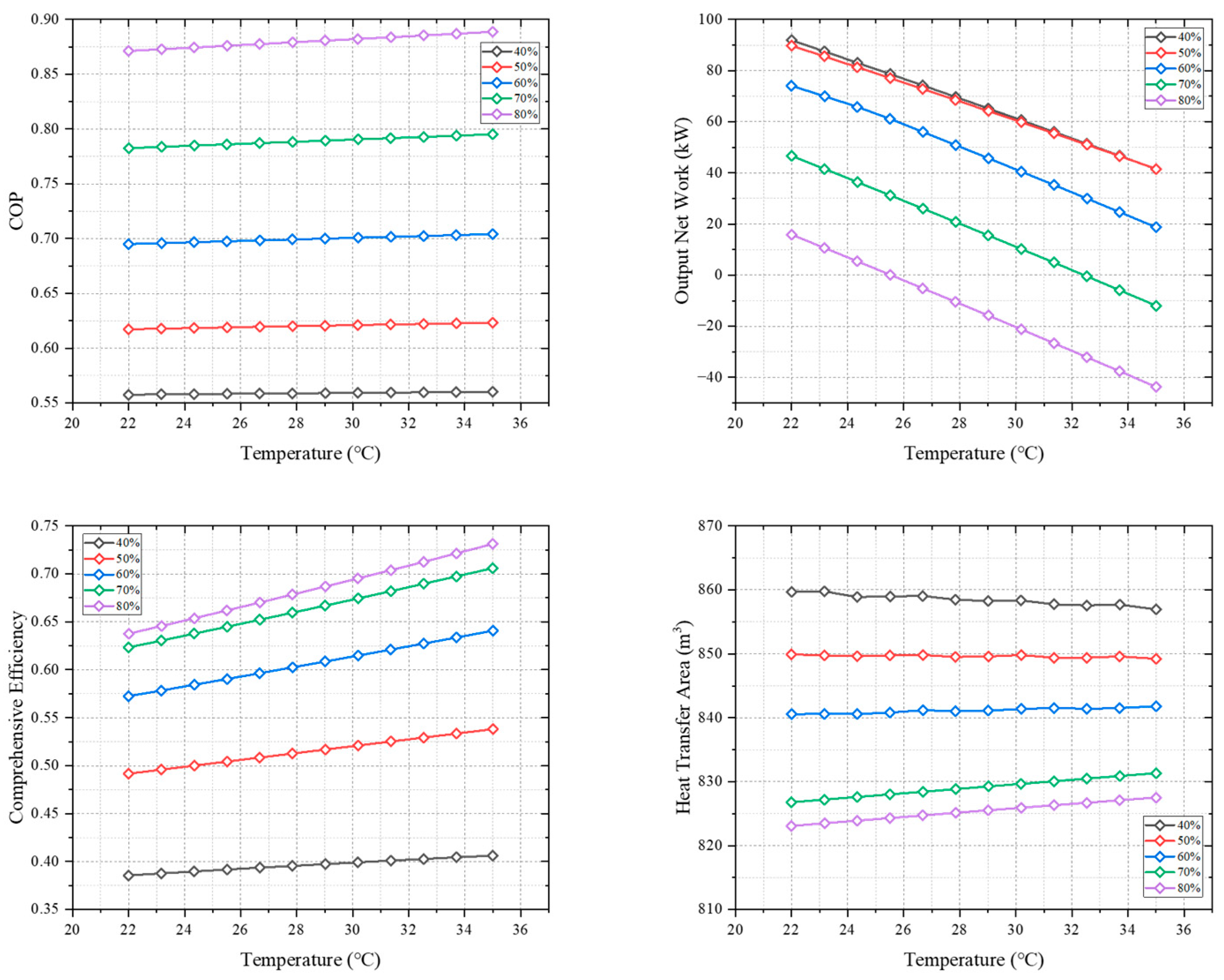
3.2. Cycle Performance under Variable Working Conditions
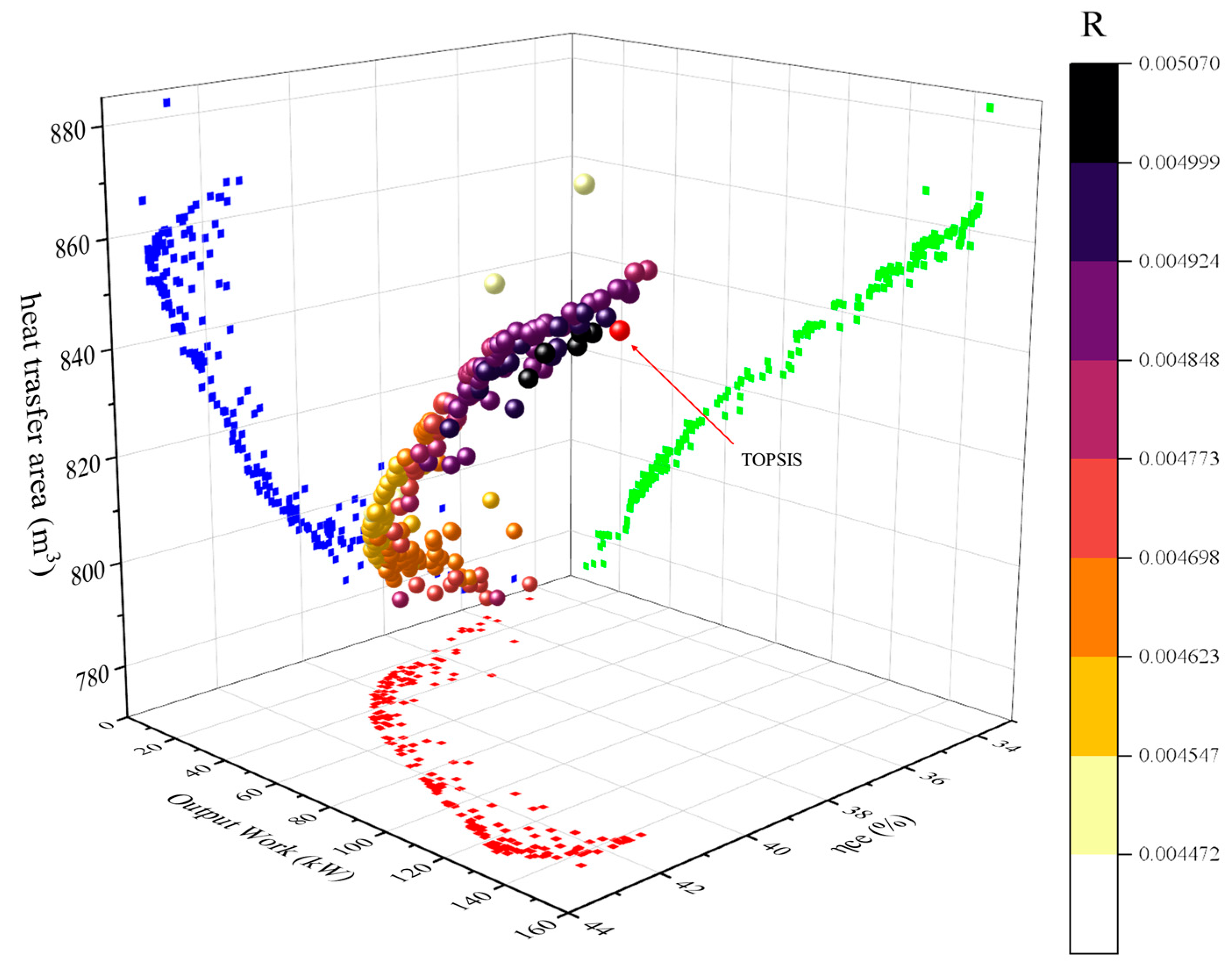
3.3. Multi-Objective Optimization Results and Analysis
3.4. Exergy Analysis
3.5. Performance Comparison between the CPDCC and other Cycles
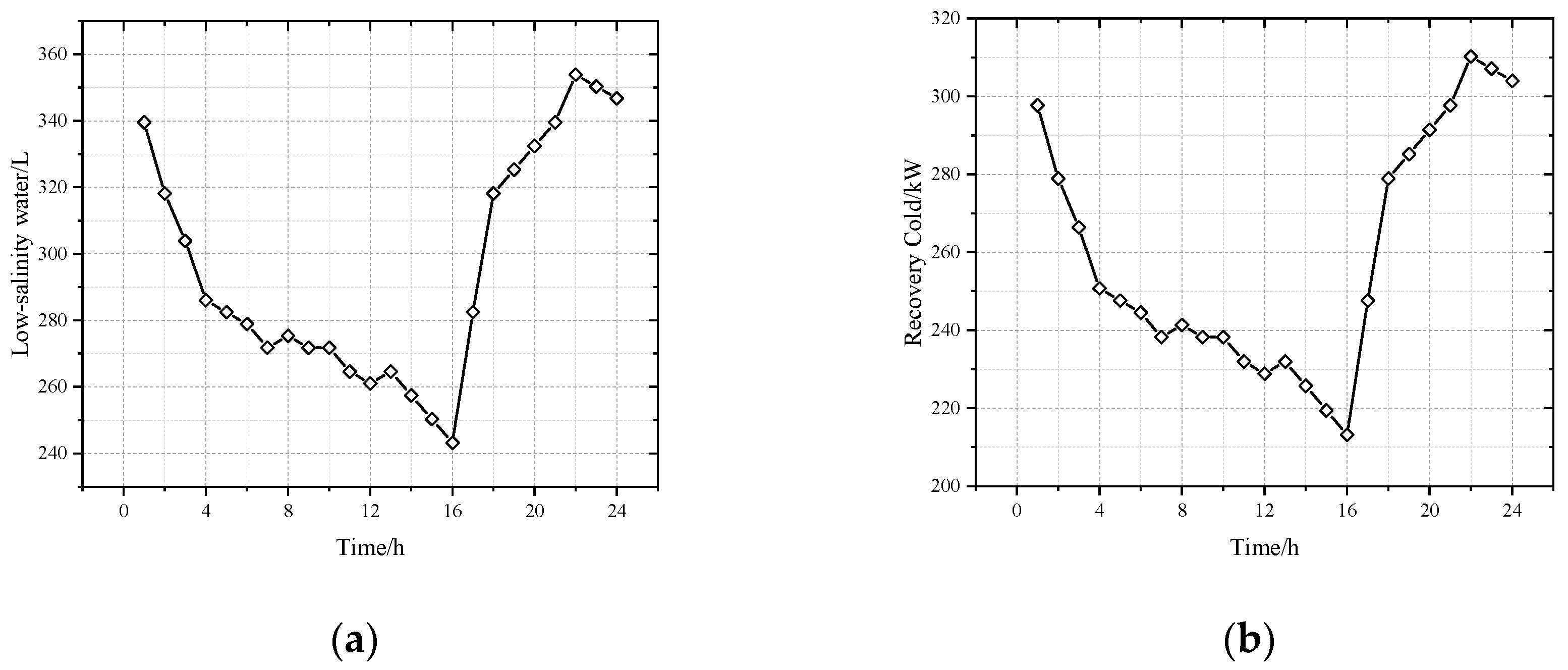
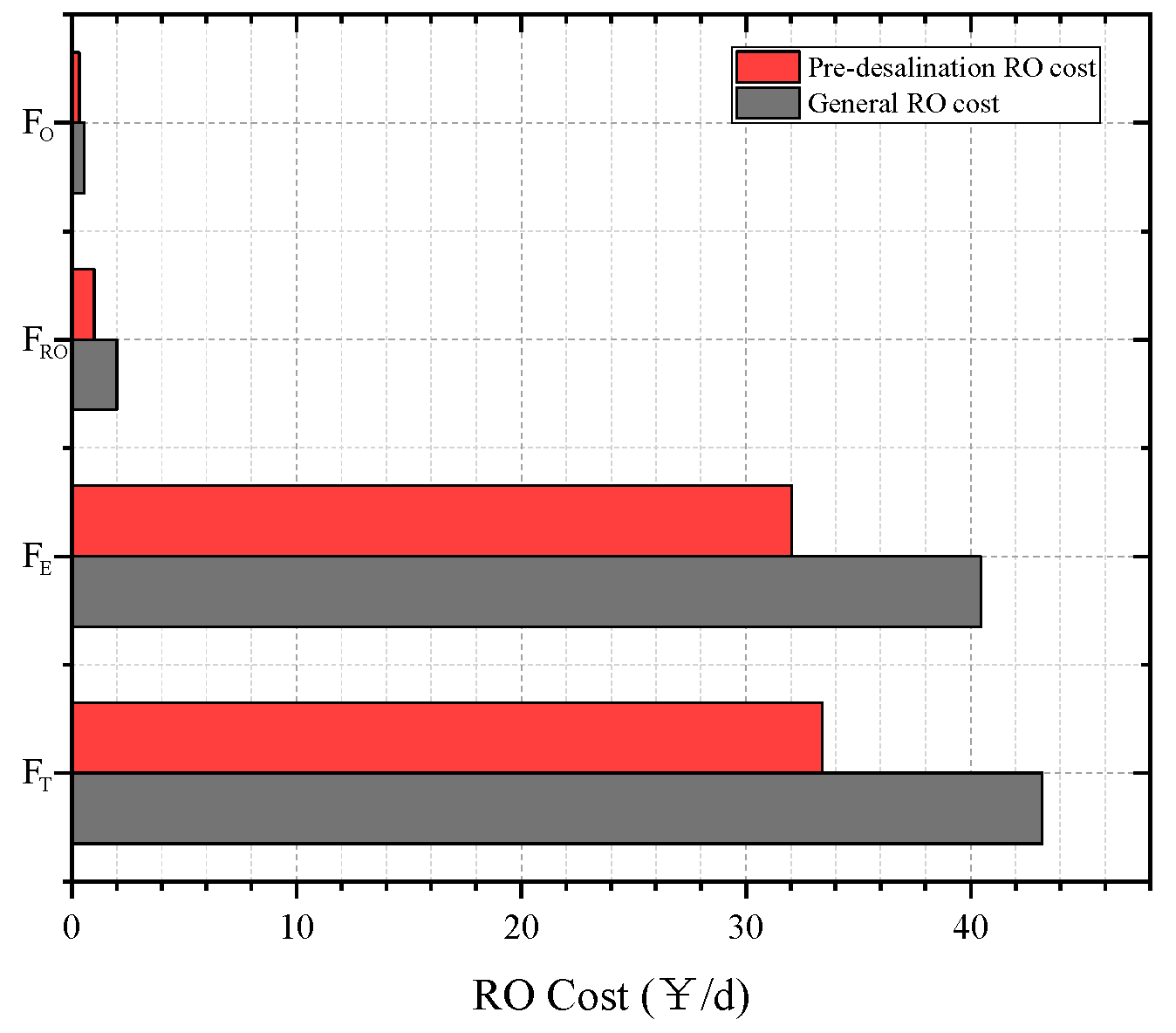
3.6. Economic Analysis of Desalination
4. Conclusions
- (1)
- The performance of CPDCC is significantly influenced by the mass fractions of ammonia–water solution. Opting for a higher concentration ammonia–water solution enhances the heat conversion performance and efficiency of the cycle. However, it also leads to an increase in the cycle absorption pressure, which necessitates the use of an additional air compressor to raise the vapor pressure, resulting in a reduction in the cycle’s net output work.
- (2)
- After conducting MOPSO multi-objective optimization, considerable improvement is achieved in CPDCC performance, with a thermal efficiency of 12.55%, a COP of 54.36%, and a comprehensive efficiency of 42.34%. Notably, there is still potential for further enhancing the output work by considering the heat exchanger area.
- (3)
- The main exergy losses in the CPDCC occur in the evaporators, generator, and absorber, accounting for 78.51% of the total exergy losses in the system.
- (4)
- After multi-objective optimization, the net output power of the CPDCC is 142.08 kW, the total heat exchange area of each heat exchange component is 863.32 m2, and it is expected that the maximum output of fresh water is about 7000 per day. The implementation of freezing desalination significantly reduces the cost of RO desalination by 22.69%, the cold recovery rate reaches 55.39%, and the power generated by CPDCC can meet the needs of RO desalination equipment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area, m3 |
| E | Exergy, kW |
| I | Exergy loss, kW |
| Q | Heat transfer rate, kW |
| T | Temperature, K |
| W | Output work, kW |
| c | heat capacity, J·K−1 |
| d | Feature length, m |
| h | Specific enthalpy, kJ·kg−1 |
| i | Intensity of solar radiation, W·m−2 |
| k | heat transfer coefficient, W·(m2·K)−1 |
| m | Mass flow rate, kg·s−1 |
| r | fouling resistance, m2·K·W−1 |
| s | Specific entropy, kJ·(kg·K)−1 |
| t | Temperature, °C |
| v | Velocity, m·s−1 |
| w | Solution concentration, kg/kg |
| y | Gas phase mass fraction |
| Greek symbols | |
| α | Convective heat transfer coefficient, W·(m2·K)−1 |
| δ | Thickness, m |
| η | Efficiency |
| λ | Thermal conductivity coefficient, W·(m·K) −1 |
| μ | Dynamic viscosity, Pa·s |
| ρ | Density, kg/m3 |
| Subscripts | |
| gen | Generator |
| re | Reheater |
| tur/t | Turbine |
| con | Condensation |
| eva | Evaporator |
| abs | Absorber |
| pump/p | Pump |
| in/out | Inlet/Outlet |
| com | Compressor |
| net | Net output work |
| hot/cold | Heat source/cold source |
| ce | Comprehensive efficiency |
| ref | Refrigeration |
| sp | Single-phase |
| tp | Two-phase |
| l | Liquid phase |
| lo | Assuming all mass as liquid |
| v | Vapor phase |
| vo | Assuming all mass as vapor |
| f | Freezing |
| fp | Freezing point |
| lat | Latent heat |
| ac | Air conditioner |
| rec | recovery |
| Acronyms | |
| ORC | Organic Rankine cycle |
| CPDCC | Cooling-power-desalination combined cycle |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| COP | Coefficient of performance |
| RO | Reverse osmosis |
References
- Mondejar, M.E.; Andreasen, J.G.; Pierobon, L.; Larsen, U.; Thern, M.; Haglind, F. A review of the use of organic Rankine cycle power systems for maritime applications. Renew. Sustain. Energy Rev. 2018, 91, 126–151. [Google Scholar] [CrossRef]
- MARPOL: Annex VI and NTC 2008 with Guidelines for Implementation; IMO: London, UK, 2013; Volume 258.
- International Convention for the Prevention of Pollution from Ships (MARPOL). 2005. Available online: https://www.imo.org/en/about/Conventions/Pages/International-Convention-for-the-Prevention-of-Pollution-from-Ships-(MARPOL).aspx (accessed on 30 October 2023).
- Song, J.; Song, Y.; Gu, C.-w. Thermodynamic analysis and performance optimization of an Organic Rankine Cycle (ORC) waste heat recovery system for marine diesel engines. Energy 2015, 82, 976–985. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H. Thermodynamic and economic performances optimization of an organic Rankine cycle system utilizing exhaust gas of a large marine diesel engine. Appl. Energy 2015, 149, 1–12. [Google Scholar] [CrossRef]
- Yang, M.-H. Thermal and economic analyses of a compact waste heat recovering system for the marine diesel engine using transcritical Rankine cycle. Energy Convers. Manag. 2015, 106, 1082–1096. [Google Scholar] [CrossRef]
- Yang, M.-H. Optimizations of the waste heat recovery system for a large marine diesel engine based on transcritical Rankine cycle. Energy 2016, 113, 1109–1124. [Google Scholar] [CrossRef]
- Mat Nawi, Z.; Kamarudin, S.K.; Sheikh Abdullah, S.R.; Lam, S.S. The potential of exhaust waste heat recovery (WHR) from marine diesel engines via organic rankine cycle. Energy 2019, 166, 17–31. [Google Scholar] [CrossRef]
- Feng, Y.; Du, Z.; Shreka, M.; Zhu, Y.; Zhou, S.; Zhang, W. Thermodynamic analysis and performance optimization of the supercritical carbon dioxide Brayton cycle combined with the Kalina cycle for waste heat recovery from a marine low-speed diesel engine. Energy Convers. Manag. 2020, 206, 112483. [Google Scholar] [CrossRef]
- Sakalis, G. Investigation of supercritical CO2 cycles potential for marine Diesel engine waste heat recovery applications. Appl. Therm. Eng. 2021, 195, 117201. [Google Scholar] [CrossRef]
- Gürgen, S.; Altın, İ. Novel decision-making strategy for working fluid selection in Organic Rankine Cycle: A case study for waste heat recovery of a marine diesel engine. Energy 2022, 252, 124023. [Google Scholar] [CrossRef]
- Ouadha, A.; El-Gotni, Y. Integration of an Ammonia-water Absorption Refrigeration System with a Marine Diesel Engine: A Thermodynamic Study. Procedia Comput. Sci. 2013, 19, 754–761. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Waste heat utilization from internal combustion engines for power augmentation and refrigeration. Renew. Sustain. Energy Rev. 2021, 152, 111629. [Google Scholar] [CrossRef]
- Demir, M.E.; Çıtakoğlu, F. Design and modeling of a multigeneration system driven by waste heat of a marine diesel engine. Int. J. Hydrogen Energy 2022, 47, 40513–40530. [Google Scholar] [CrossRef]
- Shafieian, A.; Khiadani, M. A multipurpose desalination, cooling, and air-conditioning system powered by waste heat recovery from diesel exhaust fumes and cooling water. Case Stud. Therm. Eng. 2020, 21, 100702. [Google Scholar] [CrossRef]
- Cao, Y.; Mihardjo, L.W.W.; Dahari, M.; Mustafa Mohamed, A.; Ghaebi, H.; Parikhani, T. Assessment of a novel system utilizing gases exhausted from a ship’s engine for power, cooling, and desalinated water generation. Appl. Therm. Eng. 2021, 184, 116177. [Google Scholar] [CrossRef]
- Tang, J.; Ni, H.; Peng, R.-L.; Wang, N.; Zuo, L. A review on energy conversion using hybrid photovoltaic and thermoelectric systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- Li, X.; Xu, B.; Tian, H.; Shu, G. Towards a novel holistic design of organic Rankine cycle (ORC) systems operating under heat source fluctuations and intermittency. Renew. Sustain. Energy Rev. 2021, 147, 111207. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Y.; Xie, J. Simulation analysis of dynamic cooling loads of ship air conditioning in summer. Chin. J. Ship Res. 2018, 13, 8. [Google Scholar]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Salajeghe, M.; Ameri, M. Thermodynamic analysis of single and multi-effect freeze desalination. Appl. Therm. Eng. 2023, 225, 120148. [Google Scholar] [CrossRef]
- Janajreh, I.; Zhang, H.; El Kadi, K.; Ghaffour, N. Freeze desalination: Current research development and future prospects. Water Res. 2023, 229, 119389. [Google Scholar] [CrossRef]
- Ali, U.; Zhang, H.; Abedrabbo, S.; Janajreh, I. Freeze desalination via thermoacoustic cooling: System analysis and cost overview. Energy Nexus 2023, 10, 100195. [Google Scholar] [CrossRef]
- Yuan, H.; Sun, P.; Zhang, J.; Sun, K.; Mei, N.; Zhou, P. Theoretical and experimental investigation of an absorption refrigeration and pre-desalination system for marine engine exhaust gas heat recovery. Appl. Therm. Eng. 2019, 150, 224–236. [Google Scholar] [CrossRef]
- Ni, N.; Yuan, H.; Zhang, Z.; Bai, Y.; Zhu, M. Theoretical research on ship desulfurization wastewater freezing desalination system driven by waste heat. Desalination 2023, 549, 116363. [Google Scholar] [CrossRef]
- Sun, P.; Yuan, H.; Zhang, J.; Sun, K.; Pang, H. Experimental investigation of a seawater freezing pre-desalination system. Period. Ocean Univ. China 2021, 51, 8. [Google Scholar]
- Song, R.; Wang, K.; Gong, M.; Yuan, H. Multi-physical field simulations of directional seawater freeze-crystallisation under a magnetic field. Desalination 2023, 560, 116687. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Yuan, H.; Mei, N. Theoretical analysis on extraction-ejection combined power and refrigeration cycle for ocean thermal energy conversion. Energy 2023, 273, 127216. [Google Scholar] [CrossRef]
- Qian, S. Heat Exchanger Design Handbook; Chemical Industry Press: Beijing, China, 2002. [Google Scholar]
- Shah, M.M. A general correlation for heat transfer during film condensation inside pipes. Int. J. Heat Mass Transf. 1979, 22, 547–556. [Google Scholar] [CrossRef]
- Bivens, D.B.; Yokozeki, A. Heat Transfer Coefficients and Transport Properties for Alternative Refrigerants. In Proceedings of the International Refrigeration and Air Conditioning Conference, Hannover, Germany, 10–13 May 1994. [Google Scholar]
- Churchill, S.W.; Bernstein, M. A Correlating Equation for Forced Convection From Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Du, S.; Li, Q.Y.; Cao, X.; Song, Q.L.; Wang, D.C.; Li, Y.H.; Li, L.S.; Liu, J. Investigation on heat transfer and pressure drop correlations of R600a air-cooled finned tube evaporator for fridge. Int. J. Refrig. 2022, 144, 118–127. [Google Scholar] [CrossRef]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flows. Int. Chem. Eng. 1976, 16, 359–367. [Google Scholar]
- E, W. Study on Calculation Method of Ammonia-Water Absorber Area with Heat and Mass Transfer Process. Master’s Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Yang, L. Research on Frequency Conversion Energy-Saving Technology of Ship Refrigerator. Master’s Thesis, Shanghai Maritime University, Shanghai, China, 2000. (In Chinese). [Google Scholar]
- Gao, S. Dynamic Cooling Loads of Ship Air-Condition. Master’s Thesis, Dalian University of Technology, Dalian, China, 2006. [Google Scholar]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the WCCI 2002, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Mhs95 Sixth International Symposium on Micro Machine & Human Science, Nagoya, Japan, 4–6 October 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Banzhaf, W.; Daida, J.; Eiben, A.E.; Garzon, M.H.; Honavar, V.; Jakiela, M.; E, R. A Comprehensive Survey of Evolutionary Based Multiobjective Optimization Techniques. Knowl. Inf. Syst. 1999, 1, 269–308. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple attribute decision making. Methods and applications. A state-of-the-art survey. In Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 1981; Volume 186. [Google Scholar]
- Xue, B. Performance Analysis of Ocean Thermal Energy Convention System Using Kalina Cycle an Uehara Cycle. Master’s Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Zhang, X. Experimental and Simulation Study on Ammonia-Water Absorption Refrigeration. Master’s Thesis, Qingdao University of Science & Technology, Qingdao, China, 2020. [Google Scholar]
- Gao, C.; Ruan, G. Chapter 4—Reverse osmosis and nanofiltration seawater desalination. In Seawater Desalination Technology and Engineering; American Water Works Association: Washington, DC, USA, 2016; pp. 294–301. [Google Scholar]
- Shen, B.; Pan, X.; Wang, W. Feasibility of absorption refrigeration air conditioner powered by west heat. Navig. China 2012, 35, 33–36. [Google Scholar]
- Luo, L.; Fan, Y.; Zhou, D.; Wang, L.; Chen, X.; Xi, G. Experimental study of waste heat recovery of diesel exhaust gas fromn small and medium-sized ships. Ship Eng. 2021, 12, 043. [Google Scholar]
- Climate Reanalyzer. Daily Sea Surface Temperature. Climate Change Institute, University of Maine. n.d. Available online: https://climatereanalyzer.org/ (accessed on 12 December 2023).
- Wang, J.; Dai, Y.; Gao, L. Parametric analysis and optimization for a combined power and refrigeration cycle. Appl. Energy 2008, 85, 1071–1085. [Google Scholar] [CrossRef]
- Yuan, H.; Mei, N.; Li, Y.; Yang, S.; Hu, S.Y.; Han, Y.F. Theoretical and experimental investigation on a liquid-gas ejector power cycle using ammonia-water. Sci. China Technol. Sci. 2013, 56, 2289–2298. [Google Scholar] [CrossRef]
- Yuan, H.; Zhou, P.; Mei, N. Performance analysis of a solar-assisted OTEC cycle for power generation and fishery cold storage refrigeration. Appl. Therm. Eng. 2015, 90, 809–819. [Google Scholar] [CrossRef]
- Bian, Y.; Pan, J.; Liu, Y.; Zhang, F.; Yang, Y.; Arima, H. Performance analysis of a combined power and refrigeration cycle. Energy Convers. Manag. 2019, 185, 259–270. [Google Scholar] [CrossRef]
- Gao, Q.; Yuan, H. Performance Analysis of Zeotropic Organic Rankine Cycle for Marine Diesel Exhaust Heat Recovery. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, IMECE 2021, Virtual, GA, USA, 1–5 November 2021; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2021. [Google Scholar]





| Parameters | Values |
|---|---|
| Maximum number of iterations | 1000 |
| Population size | 500 |
| Inertia factor | 0.5 |
| Inertia factor-damping rate | 0.99 |
| Personal learning coefficient | 0.5 |
| Global learning coefficient | 0.5 |
| Parameters | Values | Unit |
|---|---|---|
| Heat source temperature | 28 | °C |
| Evaporation temperature | 25 | °C |
| Cold source temperature | 4 | °C |
| Condensation temperature | 8.3 | °C |
| Pinch Point | 1.5 | °C |
| Mass fraction of ammonia | 94 | % |
| Pump isentropic efficiency | 80 | % |
| Turbine isentropic efficiency | 80 | % |
| Evaporation pressure | 900 | kPa |
| Results | Units | Results in This Paper | Ref. [43] | Relative Error |
|---|---|---|---|---|
| Net output work | kW | 9646.7 | 9637.12 | 0.10% |
| Thermal efficiency | % | 2.09 | 2.05 | 1.95% |
| Parameters | Values | Unit |
|---|---|---|
| Heat source temperature | 160 | °C |
| Cold source temperature | 32 | °C |
| Evaporator temperature | −15 | °C |
| Mass fraction of ammonia | 30.2 | % |
| Mass flow | 66.6 | kg/h |
| Results | Units | Results in This Paper | Ref. [44] | Relative Error |
|---|---|---|---|---|
| Cooling capacity | kW | 3.21 | 3.23 | 0.62% |
| COP | % | 42.16 | 42.5 | 0.8% |
| Parameters | Values | Unit | |
|---|---|---|---|
| Generation temperature | 200 | °C | |
| Seawater temperature | 25 | °C | |
| Ammonia mass fraction | 40 | % | |
| Reflux ratio | 3.5 | — | |
| Pump isentropic efficiency | 0.85 | — | |
| Turbine isentropic efficiency | 0.85 | — | |
| Desalination temperature | −18 | °C | |
| Air conditioning temperature | 10 | °C | |
| Temperature drops of distillation | 5 | °C | |
| Pinch point | Generator | 5 | °C |
| Absorber | 5 | °C | |
| Superheat | 5 | °C | |
| Evaporator | 2 | °C | |
| Condenser | 2 | °C | |
| LMTD | Heat exchange I | 5 | °C |
| Heat exchange II | 15 | °C | |
| Heat exchange III | 15 | °C | |
| State Points | Temperature | Pressure | Specific Enthalpy | Specific Entropy | Mass Flow | Mass Fraction |
|---|---|---|---|---|---|---|
| °C | MPa | kJ/kg | kJ/(kg·K) | kg/s | % | |
| 1 | 190 | 3.28 | 2007.68 | 6.28 | 0.5199 | 100 |
| 2 | 195 | 3.28 | 2021.33 | 6.31 | 0.5199 | 100 |
| 3 | 105.91 | 1.07 | 1839.14 | 6.40 | 0.5199 | 100 |
| 4 | 27 | 1.07 | 470.43 | 1.91 | 0.5199 | 100 |
| 5 | 27 | 1.07 | 470.43 | 1.91 | 0.1954 | 100 |
| 6 | 24.69 | 1.07 | 459.34 | 1.88 | 0.1954 | 100 |
| 7 | 8 | 0.57 | 459.34 | 1.89 | 0.1954 | 100 |
| 8 | 8 | 0.57 | 1613.43 | 5.99 | 0.1954 | 100 |
| 9 | 12 | 0.57 | 1624.52 | 6.03 | 0.1954 | 100 |
| 10 | −0.30 | 0.22 | 1624.52 | 6.47 | 0.1954 | 100 |
| 11 | 27 | 1.07 | 470.43 | 1.91 | 0.3245 | 100 |
| 12 | 11.31 | 1.07 | 396.11 | 1.66 | 0.3245 | 100 |
| 13 | −20 | 0.19 | 396.11 | 1.70 | 0.3245 | 100 |
| 14 | −20 | 0.19 | 1580.83 | 6.38 | 0.3245 | 100 |
| 15 | 12 | 0.19 | 1655.15 | 6.65 | 0.3245 | 100 |
| 16 | 21.75 | 0.22 | 1675.11 | 6.65 | 0.3245 | 100 |
| 17 | 195 | 3.28 | 803.52 | 2.57 | 1.2997 | 16 |
| 18 | 35.38 | 3.28 | 77.29 | 0.69 | 1.2997 | 16 |
| 19 | 36.00 | 0.22 | 77.29 | 0.70 | 1.2997 | 16 |
| 20 | 30 | 0.22 | 28.11 | 0.839 | 1.8196 | 40 |
| 21 | 30.38 | 3.28 | 32.32 | 0.841 | 1.8196 | 40 |
| 22 | 138.21 | 3.28 | 551.05 | 2.30 | 1.8196 | 40 |
| Components | Values | Unit | Components | Values | Unit |
|---|---|---|---|---|---|
| 1085.42 | kW | 6.48 | kW | ||
| 7.10 | kW | 94.72 | kW | ||
| 711.57 | kW | 80.58 | kW | ||
| 225.50 | kW | COP | 55.83 | % | |
| 383.79 | kW | 7.38 | % | ||
| 903.30 | kW | 19.94 | % | ||
| 7.66 | kW | 17.54 | % | ||
| — | — | 37.48 | % |
| Parameter | Values | Unit |
|---|---|---|
| Generation temperature | 150~250 | °C |
| Seawater temperature | 22~30 | °C |
| Ammonia mass fraction | 0.3~0.8 | - |
| Reflux ratio | 2.5~4 | - |
| Optimal Values | Design Variables | Optimize Goals | ||||||
|---|---|---|---|---|---|---|---|---|
| Th/°C | Tc/°C | w | Rreflux | Wnet/kW | ηce/% | Atotal/m3 | ||
| Wnet | max | 249.46 | 22.27 | 0.407 | 3.60 | 144.70 | 42.67 | 882.54 |
| min | 156.29 | 23.35 | 0.794 | 3.12 | 6.46 | 34.58 | 773.23 | |
| ηce | max | 248.54 | 22.01 | 0.498 | 3.42 | 125.96 | 43.25 | 865.77 |
| min | 156.29 | 23.35 | 0.794 | 3.12 | 6.46 | 34.58 | 773.23 | |
| Atotal | min | 156.29 | 23.35 | 0.794 | 3.12 | 6.46 | 34.58 | 773.23 |
| max | 249.46 | 22.27 | 0.407 | 3.60 | 144.70 | 42.67 | 882.54 | |
| TOPSIS results | 249.95 | 22.29 | 0.420 | 3.24 | 142.08 | 42.34 | 863.32 | |
| Years | Fluids | Thot | Tcold | Teva | ηpower | COP | ηce | Ref. |
|---|---|---|---|---|---|---|---|---|
| °C | °C | °C | % | % | % | |||
| 2008 | NH3-H2O | 300 | 20 | −5 | 14.96 | 5.49 | 36.60 | [49] |
| 2013 | NH3-H2O | 28 | 4 | 2.94 | 36.89 | [50] | ||
| 2015 | NH3-H2O | 75 | 4 | −18 | 2.27 | 18.00 | 22.29 | [51] |
| 2019 | NH3-H2O (Power) R600a (Refrigeration) | 122 | 4.85 | 8 | 8.00 | 24.00 | 50.34 | [52] |
| 2021 | Cyclopentane–Toluene | 200 | 5 | 23.00 | 49.21 | [53] | ||
| 2023 | NH3-H2O | 30 | 5 | −18 | 0.85 | 29 | 66.14 | [28] |
| 2023 | NH3-H2O | 249.95 | 22.29 | 10, −18 | 12.55 | 54.36 | 42.34 | CPDCC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Zhao, S.; Zhang, Z.; Zhang, J.; Zhao, Y.; Sun, Y.; Li, D.; Yuan, H. Performance Analysis and Multi-Objective Optimization of a Cooling-Power-Desalination Combined Cycle for Shipboard Diesel Exhaust Heat Recovery. Sustainability 2023, 15, 16942. https://doi.org/10.3390/su152416942
Gao Q, Zhao S, Zhang Z, Zhang J, Zhao Y, Sun Y, Li D, Yuan H. Performance Analysis and Multi-Objective Optimization of a Cooling-Power-Desalination Combined Cycle for Shipboard Diesel Exhaust Heat Recovery. Sustainability. 2023; 15(24):16942. https://doi.org/10.3390/su152416942
Chicago/Turabian StyleGao, Qizhi, Senyao Zhao, Zhixiang Zhang, Ji Zhang, Yuan Zhao, Yongchao Sun, Dezhi Li, and Han Yuan. 2023. "Performance Analysis and Multi-Objective Optimization of a Cooling-Power-Desalination Combined Cycle for Shipboard Diesel Exhaust Heat Recovery" Sustainability 15, no. 24: 16942. https://doi.org/10.3390/su152416942
APA StyleGao, Q., Zhao, S., Zhang, Z., Zhang, J., Zhao, Y., Sun, Y., Li, D., & Yuan, H. (2023). Performance Analysis and Multi-Objective Optimization of a Cooling-Power-Desalination Combined Cycle for Shipboard Diesel Exhaust Heat Recovery. Sustainability, 15(24), 16942. https://doi.org/10.3390/su152416942







