Supply Chains: Planning the Transportation of Animals among Facilities
Abstract
:1. Introduction
1.1. Background of the Problem
1.2. Literature Review
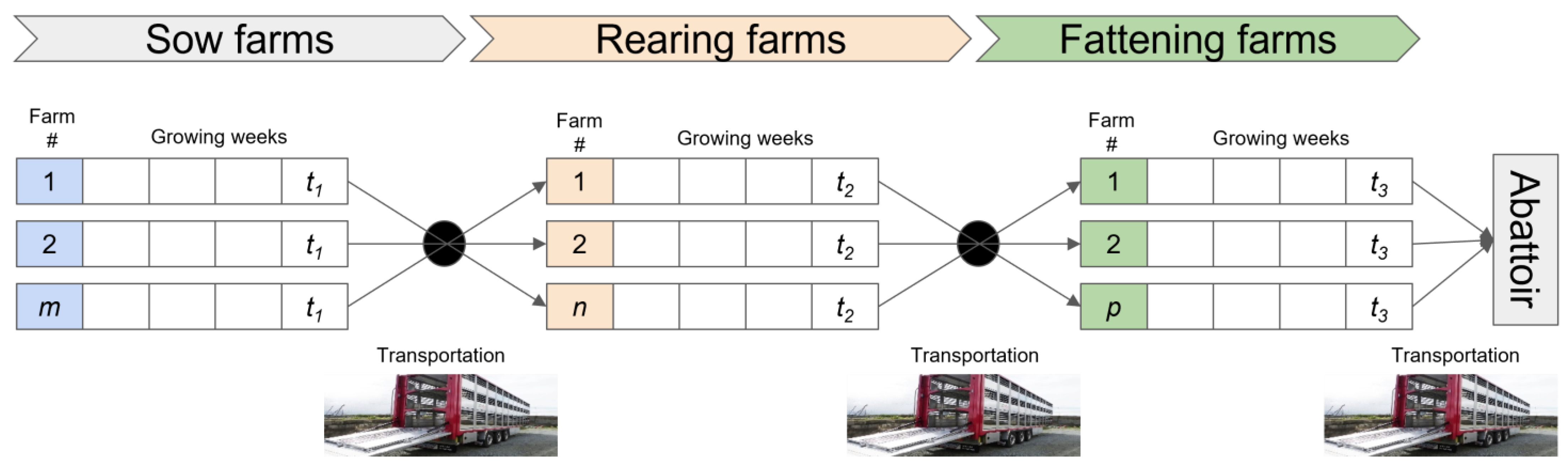
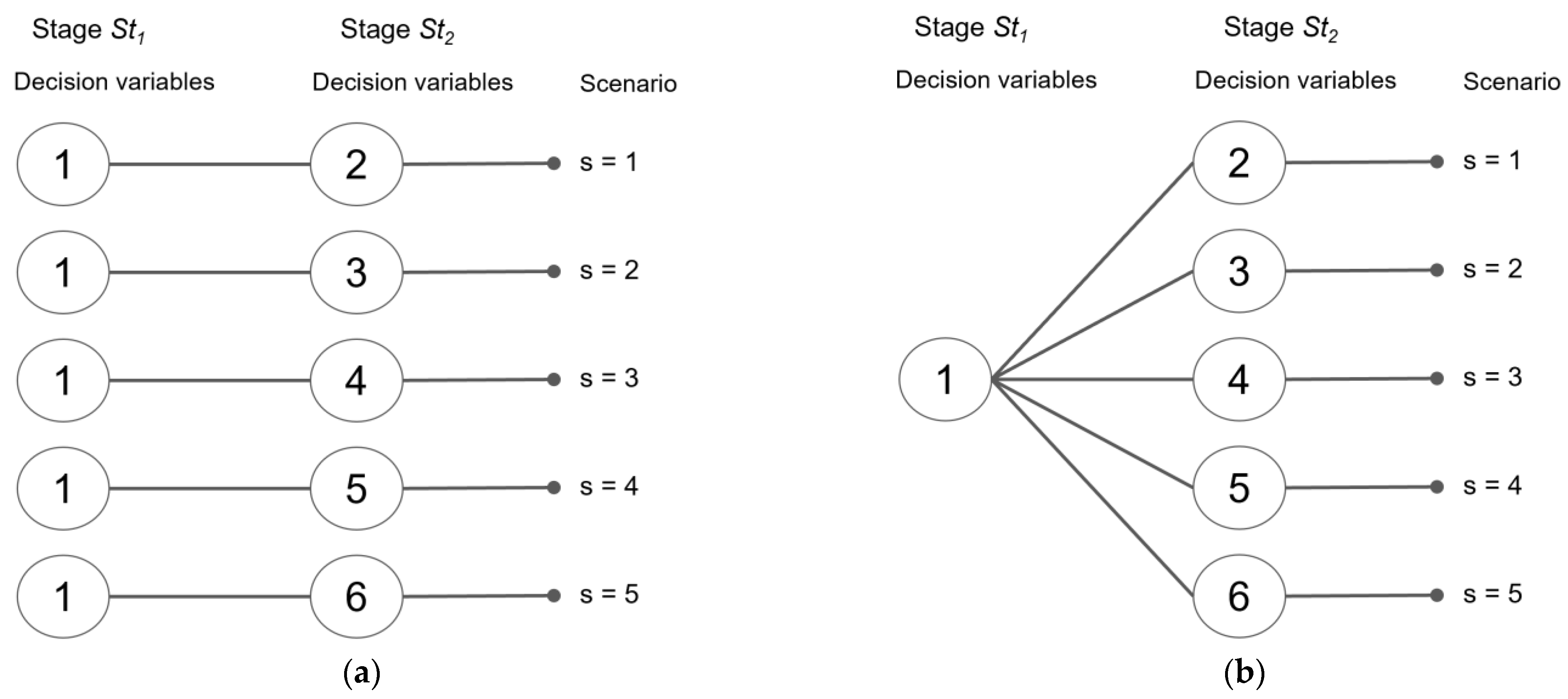
2. The Two-Stage Stochastic Model
2.1. The Deterministic Equivalent Model Formulation
2.2. Assumptions of the Model
- The sizes of sow farms are constant and house the same number of sows, producing a steady number of weaned piglets depending on seasonal fertility.
- The replacement rates of sows are constant, and this implies the weekly number of sows sent to the abattoir is the same.
- The mortality of pigs is the same per phase and computed at the end of each phase. The survival rate is 1 by default.
- The growth of animals over time is homogeneous among farms and exhibits equal conversion rate, feed intake, and growth rate.
- Transportation cost is considered constant per km covered regardless of the speed and load.
- The PSC includes only one abattoir where fattened pigs are delivered without capacity constraints.
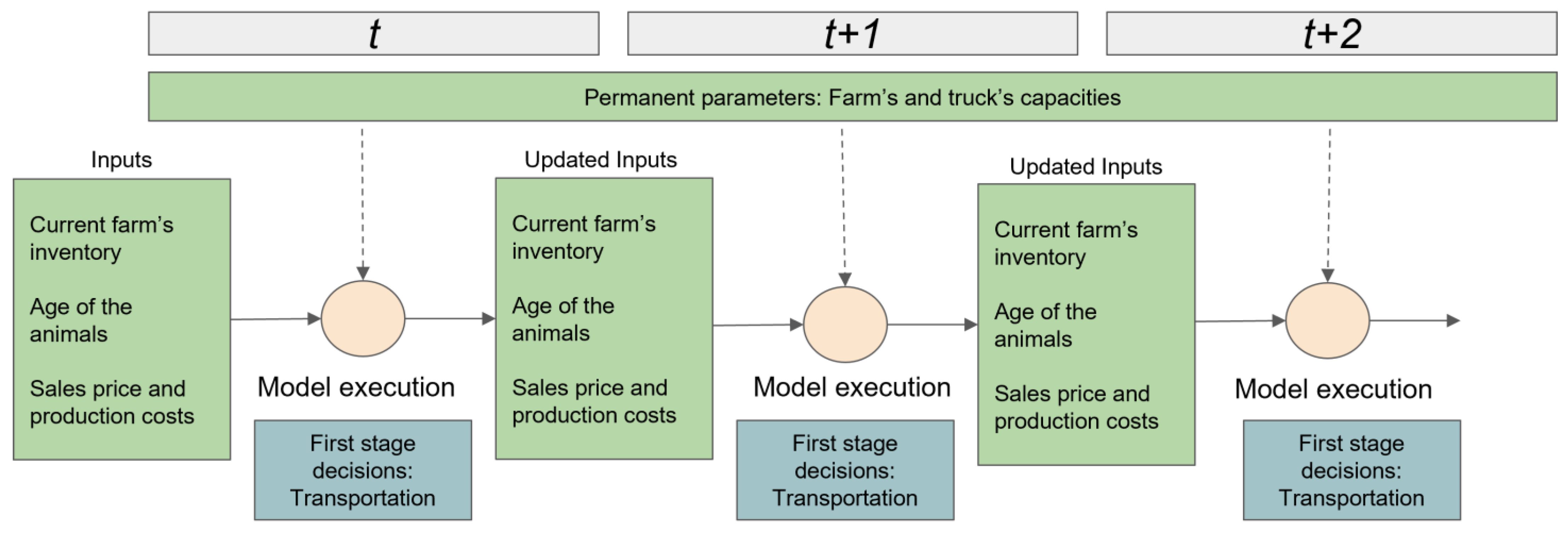
- The solution from this model is intended to be applied in a rolling horizon manner. Thereby, only first-stage decisions for the current period are made. The model with updated information is solved again for the next decision period and so on.
3. Empirical Analysis
3.1. Data and Scenario Generation
3.2. Heuristic Algorithm and Computational Results
4. Discussion
5. Study Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patidar, R.; Agrawal, S. Restructuring the Indian agro-fresh food supply chain network: A mathematical model formulation. Clean Technol. Env. Policy 2020, 22, 2053–2077. [Google Scholar] [CrossRef]
- Utama, D.M.; Santoso, I.; Hendrawan, Y.; Dania, W.A.P. Integrated procurement-production inventory model in supply chain: A systematic review. Oper. Res. Perspect. 2022, 9, 100221. [Google Scholar] [CrossRef]
- Rodríguez, S.V.; Faulin, J.; Plà, L.M. New opportunities of Operations Research to improve pork supply chain efficiency. Ann. Oper. Res. 2014, 219, 5–23. [Google Scholar] [CrossRef]
- Plà-Aragonès, L.M. The Evolution of DSS in the Pig Industry and Future Perspectives. In EURO Working Group on DSS; Integrated Series in Information Systems; Papathanasiou, J., Zaraté, P., de Sousa, F.J., Eds.; Springer: Cham, Switzerland, 2021; pp. 229–323. [Google Scholar] [CrossRef]
- van der Heijden, A.; Cramer, J.M. Change agents and sustainable supply chain collaboration: A longitudinal study in the Dutch pig farming sector from a sensemaking perspective. J. Clean. Prod. 2017, 166, 967–987. [Google Scholar] [CrossRef]
- Nadal-Roig, E.; Pagès-Bernaus, A.; Plà-Aragonès, L.M. Bi-objective optimization model based on profit and CO2 emissions for pig deliveries to the abattoir. Sustainability 2018, 10, 1782. [Google Scholar] [CrossRef] [Green Version]
- van der Gaag, M.A.; Vos, F.; Saatkamp, H.W.; van Boven, M.; van Beek, P.; Huirne, R.B.M. A state-transition simulation model for the spread of Salmonella in the pork supply chain. Eur. J. Oper. Res. 2004, 156, 782–798. [Google Scholar] [CrossRef]
- Beynon, M.; Rasmequan, S.; Russ, S. A new paradigm for computer-based decision support. Decis. Support Syst. 2002, 33, 127–142. [Google Scholar] [CrossRef]
- Plà, L.M.; Sandars, D.L.; Higgins, A.J. A perspective on operational research prospects for agriculture. J. Oper. Res. Soc. 2014, 65, 1078–1089. [Google Scholar] [CrossRef]
- Ohlmann, J.; Jones, P. A integer programming model for optimal pork marketing. Ann. Oper. Res. 2011, 190, 271–287. [Google Scholar] [CrossRef]
- Khamjan, S.; Piewthongngam, K.; Pathumnakul, S. Pig procurement plan considering pig growth and size distribution. Comput. Ind. Eng. 2013, 64, 886–894. [Google Scholar] [CrossRef]
- Cadero, A.; Aubry, A.; Dourmad, J.; Salaun, Y.; Garcia-Launay, F. Towards a decision support tool with an individual-based model of a pig fattening unit. Comput. Electron. Agric. 2018, 147, 44–50. [Google Scholar] [CrossRef]
- Davoudkhani, M.; Mahé, F.; Dourmad, J.; Gohin, A.; Darrigrand, E.; Garcia-Launay, F. Economic optimization of feeding and shipping strategies in pig-fattening using an individual-based model. Agric. Syst. 2020, 184, 102899. [Google Scholar] [CrossRef]
- Rodríguez, S.V.; Albornoz, V.M.; Plà, L.M. A two-stage stochastic programming model for scheduling replacements in sow farms. TOP 2009, 17, 171–189. [Google Scholar] [CrossRef]
- Plà, L.M.; Romero, D. Planning Modern Intensive Livestock Production: The Case of the Spanish Pig Sector; International Workshop in OR: La Havana, Cuba, 2008. [Google Scholar]
- Nadal-Roig, E.; Plà-Aragonès, L.M.; Alonso-Ayuso, A. Production planning of supply chains in the pig industry. Comput. Electron. Agric. 2019, 161, 72–78. [Google Scholar] [CrossRef]
- Brevik, E.; Lauen, A.Ø.; Rolke, M.C.B.; Fagerholt, K.; Hansen, J.R. Optimisation of the broiler production supply chain. Int. J. Prod. Res. 2020, 58, 5218–5237. [Google Scholar] [CrossRef]
- Solano-Blanco, A.; González, J.E.; Gómez-Rueda, L.O.; Vargas-Sánchez, J.J.; Medaglia, A.L. Integrated planning decisions in the broiler chicken supply chain. Int. Trans. Oper. Res. 2020; early view. [Google Scholar] [CrossRef]
- Han, J.-H.; Lee, J.-Y.; Jeong, B. Two-Level Supply Chain with Production-Time-Dependent Products. Appl. Sci. 2021, 11, 9687. [Google Scholar] [CrossRef]
- Nadal-Roig, E.; Plà-Aragonès, L.M.; Pagès-Bernaus, A.; Albornoz, V.M. A two-stage stochastic model for pig production planning in vertically integrated production systems. Comput. Electron. Agric. 2020, 176, 2020105615. [Google Scholar] [CrossRef]
- Wallace, S.; Ziemba, W.T. Applications of Stochastic Programming; MPS-SIAM Series in Optimization; Society for Industrial Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Birge, J.R.; Louveaux, F.V. Introduction to Stochastic Programming, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Escudero, L.F.; Kamesam, P.V.; King, A.J.; Wets, R. Production planning via scenario modeling. Ann. Oper. Res. 1993, 43, 311–355. [Google Scholar] [CrossRef]
- Mercolleida. Reference Price in the Market Lleida (Spain). 2022. Available online: https://www.mercolleida.com/es/la-lonja-last (accessed on 16 January 2023).
- Winters, P. Forecasting sales by exponentially weighted moving averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day Series in Time Series Analysis; Revised edition; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Gamberini, R.; Lolli, F.; Rimini, B.; Sgarbossa, F. Forecasting of sporadic demand patterns with seasonality and trend components: An empirical optimization between Holt-Winters and (S) ARIMA methods. Math. Probl. Eng. 2010, 2, 579010. [Google Scholar] [CrossRef]
- Kamble, S.S.; Gunasekaran, A.; Gawankar, S.A. Achieving sustainable performance in a data-driven agriculture supply chain: A review for research and applications. Int. J. Prod. Econ. 2020, 219, 179–194. [Google Scholar] [CrossRef]
- Chardine-Baumann, E.; Botta-Genoulaz, V. A framework for sustainable performance assessment of supply chain management practices. Comput. Ind. Eng. 2014, 76, 138–147. [Google Scholar] [CrossRef]
- Tseng, M.L.; Wu, K.J.; Lim, M.K.; Wong, W.P. Data-driven sustainable supply chain management performance: A hierarchical structure assessment under uncertainties. J. Clean. Prod. 2019, 227, 760–771. [Google Scholar] [CrossRef]
- Kamp, J.A.L.M. Knowledge based systems: From research to practical application: Pitfalls and critical success factors. Comput. Electron. Agric. 1999, 22, 243–250. [Google Scholar] [CrossRef]
- Wan, N.; Li, L.; Wu, X.; Fan, J. Coordination of a fresh agricultural product supply chain with option contract under cost and loss disruptions. PLoS ONE 2021, 16, e0252960. [Google Scholar] [CrossRef]
- Kungwalsong, K.; Cheng, C.-Y.; Yuangyai, C.; Janjarassuk, U. Two-Stage Stochastic Program for Supply Chain Network Design Under Facility Disruptions. Sustainability 2021, 13, 2596. [Google Scholar] [CrossRef]
- Juan, A.A.; Keenan, P.; Martí, R.; Jeong, A. A review of the role of heuristics in stochastic optimization: From metaheuristics to learnheuristics. Ann. Oper. Res. 2021, 320, 831–861. [Google Scholar] [CrossRef]
- Kruger, S.D.; Zanin, A.; Durán, O.; Afonso, P. Performance Measurement Model for Sustainability Assessment of the Swine Supply Chain. Sustainability 2022, 14, 9926. [Google Scholar] [CrossRef]

| Reference | Problem | Approach | Uncertainty | The Gap |
|---|---|---|---|---|
| [17] | Production planning of a broiler supply chain | MIP | - | Does not consider uncertainty |
| [12] | Flow of animals in the PSC | SIM | Live weight, mortality, loss and feed conversion rate, Number of shipments per batch | Does not optimize the transportation problem. Focused on a fattening farm |
| [13] | Feeding and transportation to the abattoir | BOP | Pig growth performance profile | Focused on a fattening farm |
| [19] | Production planning of a broiler supply chain | MIP | - | Does not consider uncertainty |
| [11] | Transportation to the abattoir | MIP | - | Does not consider uncertainty |
| [6] | Transportation to the abattoir | BOP | - | Does not consider uncertainty |
| [16] | Production planning of a PSC | MIP | - | Does not consider uncertainty |
| [20] | Production planning of a PSC | TSP | Sales prices | Does not propose a heuristic for solving the TSP model |
| this manuscript | Transportation planning of a PSC | TSP | Sales prices | Does propose a heuristic for solving the TSP model |
| [10] | Transportation to the abattoir | MIP | - | Does not consider uncertainty. Focused on a fattening farm |
| [14] | Flow of animals in a sow farm | TSP | Litter size, mortality, and fertility rates | Does not optimize the transportation problem. Focused on a sow farm |
| [18] | Production planning of a broiler supply chain | MIP | - | Does not consider uncertainty |
| [7] | Flow of animals in the PSC | SIM | Spread of a pathogen | Does not optimize the transportation problem |
| Indexes and Sets | |
|---|---|
| t ∈ T | Finite time planning horizon (in weeks), t = 1, …, |T| |
| h ∈ H | Farms belonging the PSC, h = 1, …, |H|. H = B∪R∪F: Disjoint partition of farms in three phases (sites), being B the set of sow farms, R the set of rearing farms and F the set of fattening farms |
| e ∈ E | Growing period in weeks, e = 1, …, |E|, where E = EB∪ER∪EF disjoint partition of the productive cycle, i.e., weeks spend by pigs in different facilities. |
| Parameters | |
| INhe | Initial inventory of pigs of age e in the farm h ∈ H |
| Kh | Housing capacity of facilities for h ∈ H. |
| LSbt | Litter size at farrowing in the b ∈ B sow farm per week t ∈ T. |
| CPthe | Unitary production cost on farm h, per week t ∈ T and stage e ∈ E per piglet. |
| CT(h,h*) | Transportation cost from farm h to another farm or to the abattoir, h* ∈ H∪{a} |
| CT(h,h*) | Transportation cost from farm h to another farm or to the abattoir, h* ∈ H∪{a} |
| KP(h,h*) | Truck capacity (# of animals) transported from farm h to another farm or to the abattoir, h* ∈ H∪{a} |
| Pte | Expected pork value of pigs at week t and fattening week e. |
| R(h+) | Cost of renting a farm not owned by the company |
| Decision Variables | |
| Ithe | Inventory of piglets of age e ∈ E at week t on the farm h. |
| Nte(h,h*) | Number of trips from farm h to another farm or to the abattoir, h* ∈ H∪{a} of pigs at age e, week t. |
| Xh+ | Binary variable for renting a farm not owned by the company |
| Z1th | Binary variable for batch control. Z1th = 1 if farm h ∈ F is not empty at week e and Z1th = 0 otherwise |
| Z2th | Binary variable for batch control. Z2th = 1 if farm h ∈ F is not empty at week e and Z2th = 0 otherwise |
| All Decision Variables, Integer | Trucks as Continuous Nte(h,h*) | Animals as Continuous Ithe | All Continuous | |
|---|---|---|---|---|
| # Integer Variables | 4,862,081 | 1,674,400 | 3,187,681 | -- |
| # Continuous Variables | -- | 3,187,681 | 1,674,400 | 4,862,081 |
| Constraints | 4,072,238 | 4,072,238 | 4,072,238 | 4,072,238 |
| Solving time | >48 h | >48 h | >48 h | 1502 s. |
| # Weeks in the First Stage/Second Stage | ||||
|---|---|---|---|---|
| 1/51 | 2/50 | 3/49 | 4/48 | |
| Solving time (s) | 1502 | 2407 | 7.987 | 11,563 |
| First Stage (# variables) | 9431 | 18,781 | 28,131 | 37,481 |
| Second Stage (# variables) | 6,199,131 | 6,077,581 | 5,956,031 | 5,834,481 |
| # Pigs sent 1st week | 22,840 | 34,829 | 18,232 | 18,232 |
| Benefit per pig 1st week (€) | 111 | 105.23 | 112.48 | 112.48 |
| # Pigs sent 1st stage | 22,840 | 65,548 | 76,336 | 79,268 |
| Benefit per pig 1st stage (€) | 111 | 109.49 | 108.84 | 113.33 |
| Total # Pigs sent | 321,491 | 356,621 | 358,430 | 339,598 |
| Total Benefit per pig (€) | 108.61 | 109.25 | 109,59 | 109,72 |
| Time Horizon (# Weeks) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | |
| Solving time (s) | 1502 | 2035 | 2641 | 6139 | 6281 | 6619 | 4982 | 4422 |
| Pigs sent 1st stage (#) | 22,840 | 22,840 | 22,840 | 22,840 | 22,840 | 18,230 | 18,230 | 18,230 |
| Benefit per pig (€) | 111.0 | 111.0 | 111.0 | 111.0 | 111.0 | 114.2 | 114.2 | 114.2 |
| Total # Pigs sent (thousands) | 321 | 345 | 369 | 391 | 415 | 448 | 493 | 519 |
| Benefit per pig (€) | 108.6 | 108.3 | 109.0 | 110.6 | 112.0 | 114.6 | 117.0 | 119.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadal-Roig, E.; Plà-Aragonès, L.M.; Albornoz, V.M. Supply Chains: Planning the Transportation of Animals among Facilities. Sustainability 2023, 15, 2523. https://doi.org/10.3390/su15032523
Nadal-Roig E, Plà-Aragonès LM, Albornoz VM. Supply Chains: Planning the Transportation of Animals among Facilities. Sustainability. 2023; 15(3):2523. https://doi.org/10.3390/su15032523
Chicago/Turabian StyleNadal-Roig, Esteve, Lluís Miquel Plà-Aragonès, and Víctor Manuel Albornoz. 2023. "Supply Chains: Planning the Transportation of Animals among Facilities" Sustainability 15, no. 3: 2523. https://doi.org/10.3390/su15032523
APA StyleNadal-Roig, E., Plà-Aragonès, L. M., & Albornoz, V. M. (2023). Supply Chains: Planning the Transportation of Animals among Facilities. Sustainability, 15(3), 2523. https://doi.org/10.3390/su15032523








