Experimental Approach for Enhancing the Natural Convection Heat Transfer by Nanofluid in a Porous Heat Exchanger Unit

Abstract

Natural convection heat transfer is a significant component in the energy transfer mechanism and plays an essential role in a wide range of scientific and industrial technologies. This research seeks to enhance the energy transfer by nanofluid, which is compatible with some applications, such as heat exchanger thermal energy storage (HXTES). For this purpose, a triplex tube heat exchanger (TTHX) is designed to receive the hot and cold flow by two pumps from two thermal baths, respectively. Samples of the Copper (Cu) nanoparticles were then carefully selected in a volume concentration range of 0.05 $\le$ $\varnothing$ $\le$ 0.5 to promote the thermal conductivity of the base fluid, which consists of 55% water and 35% ethylene glycol (EG), and to form nanofluid. On the other side, the effect of the porous medium of glass spheres inside a TTHX is considered. Experimentally, and after preparing the nanofluid, temperature readings of six various thermocouples locations have been investigated. The effects of Cu volume concentrations under different temperatures of 20 °C, 30 °C and 50 °C on nanofluid heat transfer are evaluated, respectively. One more result: the yields in the heat transfer coefficient of the hot tube were higher compared to those of the cold tube under Reynolds number (Re) between 200 and 7000. The efficiency of transition and turbulent flow through TTHX is clearly appointed. Overall, these findings support the supposition that the heat transfer enhancement is optimized by 0.05% nanoparticle volume concentration due to increasing thermal conductivity and fluid movement effectiveness. Ultimately, a natural progression of this work is to analyze more convective form using controlled trial applications, such as solar collectors.

1. Introduction

In addition to conduction and radiation, natural convection is a major area of interest concerning mechanisms of energy transfer. The process is defined by the transfer of heat from a solid surface to an adjacent fluid (liquid or gas), driven by buoyancy forces that cause fluid motion [1]. However, the use of nanofluid is essential for a wide range of technologies and industrial applications, such as heat exchangers, solar collectors, electronics, aeronautics, aeolian and geothermal industries [2,3], as a convective heat transfer medium, especially in thermal energy storage (TES) systems. This is because of enhanced thermal conductivity with the minimal increase in the viscosity of nanofluid, compared with conventional fluid [4].

There is a growing body of literature that recognizes and focuses on the preparation, characterization and measurement of thermal conductivity and viscosity of nanofluids used for heat transfer by convection. Most of the research confirmed that the enhancement of these properties has been achieved by the addition of nanoparticles in various concentrations. Putra et al. [5] presented, experimentally, a horizontal cylindrical enclosure filled with water alumina (Al₂O₃) as a base fluid and copper (C_u) nanoparticles as a nanofluid, with volume concentrations or 1% and 4%, respectively. In this cylinder, one side is heated by a hot bath and other side is cooled by a cold bath. The results showed the effective enhancement of the natural convection heat transfer process. Moradi et al. [6] used Al₂O₃ and titanium dioxide (TiO₂) with water as two nanofluids in a cylindrical enclosure. At volume concentrations of 0.2% Al₂O₃, the heat transfer by natural convection was improved. Moreover, there was no heat transfer enhancement with TiO₂. On the other side, the inclination angle, aspect ratio and heat flux effectiveness on this transfer have been considered. Nnanna et al. [7] enhanced the heat transfer rate by convection, employing a nanofluid of Al₂O₃ with water in a rectangular cavity. Experimentally, the heat flows inside vertical walls, while horizontal walls are insulated. The heat transfer rate improvement occurs when nanoparticle volume concentrations are 0.2% $<\varnothing <$ 2%. Omri et al. [8] experimentally used a vertical helical coil heat exchanger to distill water based on copper oxide (C_uO) and graphene (Gp) (80–20%) hybrid nanofluid. The results showed that the nanoparticles’ mass fractions (0% ≤ wt ≤ 1%) enhanced the thermal conductivity and thermal energy exchange rate. However, increasing the Reynolds number causes ab increase in the heat transfer coefficient. There is a relatively small body of literature that is concerned with the viscosity of nanofluid, compared to thermal conductivity [9]. Data from some studies, such as those of Wang et al. [10], Murshed et al. [11] and Liu et al. [12] show improvements in the viscosity measurement during the addition of nanoparticles of Al₂O₃ and C_uO to base fluids of water and ethylene glycol (EG), respectively. To address a major issue in many industrial fields, nanofluids with natural convection heat transfer have been considered, especially in the porous cavities. Bourantas et al. [13] evaluated numerically the performance of cooling units of square porous cavities filled with nanofluid. The thermophysical properties of the heat transfer nanofluid have been studied. One more, Sheremet et al. [14], employed Buongiorno’s mathematical model to study heat transfer by convection in a porous cavity filling with nanofluid. The model includes two slip modes: Brownian motion and thermophoresis. The findings illustrated that the coefficient of heat transfer is increased at the hot side by Brownian motion and reduced at the cold side by thermophoresis. Ghalambaz et al. [15] numerically reported viscous dissipation and radiation effectiveness in a square cavity during heat transfer by natural convection. The square cavity was filled with porous media and nanofluid. The Nusselt number (Nu) in the cold and hot walls was affected by viscous dissipation. Drag, lift, Brownian motion and thermophoresis are important parameters and have been studied by Bagheri et al. [16]. We can see the effectiveness of these parameters on the particle trajectories of the heat exchanger cavity. Further, thermophorosis and Rayleigh number (Ra) have a significant effect on heat transfer and particle deposition. On the other hand, the issue of Brownian motion has received considerable critical attention and effectiveness on thermal conductivity and viscosity. Sheikholeslami et al. [17] constructed a three-dimensional mesoscopic simulation by employing the magnetic field in heat transfer by natural convection. The researchers observed that this field reduces the velocity and creates a drag force, which causes a decrease in the convection currents. Ellahi et al. [18] studied the heat transfer by natural convection, which included the effect of magneto–hydrodynamics in nanotubes, which are suspended in salt-water solution. By increasing the nanotubes’ volume fraction, the heat transfer rate is improved. This paper gives a brief overview of nanofluids and some external effects, such as the magnetic field for enhancing heat transfer by conviction, especially in cavities. In addition, many of the models studied by this literature review predict an increase in thermal conductivity and viscosity of the nanofluids used; this is due to contribution of increased nanoparticle volume concentrations [19].

The scope of this study was limited in terms of heat transfer and fluid flow; that is, to the coefficient of heat transfer, heat exchanger and flow transition. The aim of this research is to improve the mechanism of convection heat transfer that is compatible with the triplex tube heat exchanger (TTHX) by employing nanofluid and porous media. The base fluid consists of water and EG, while C_u is nanoparticles are added in various volume concentrations to form the nanofluid. The hot and cold flow from hot and cold baths, respectively, have been considered in this study.

2. Experimental Approach

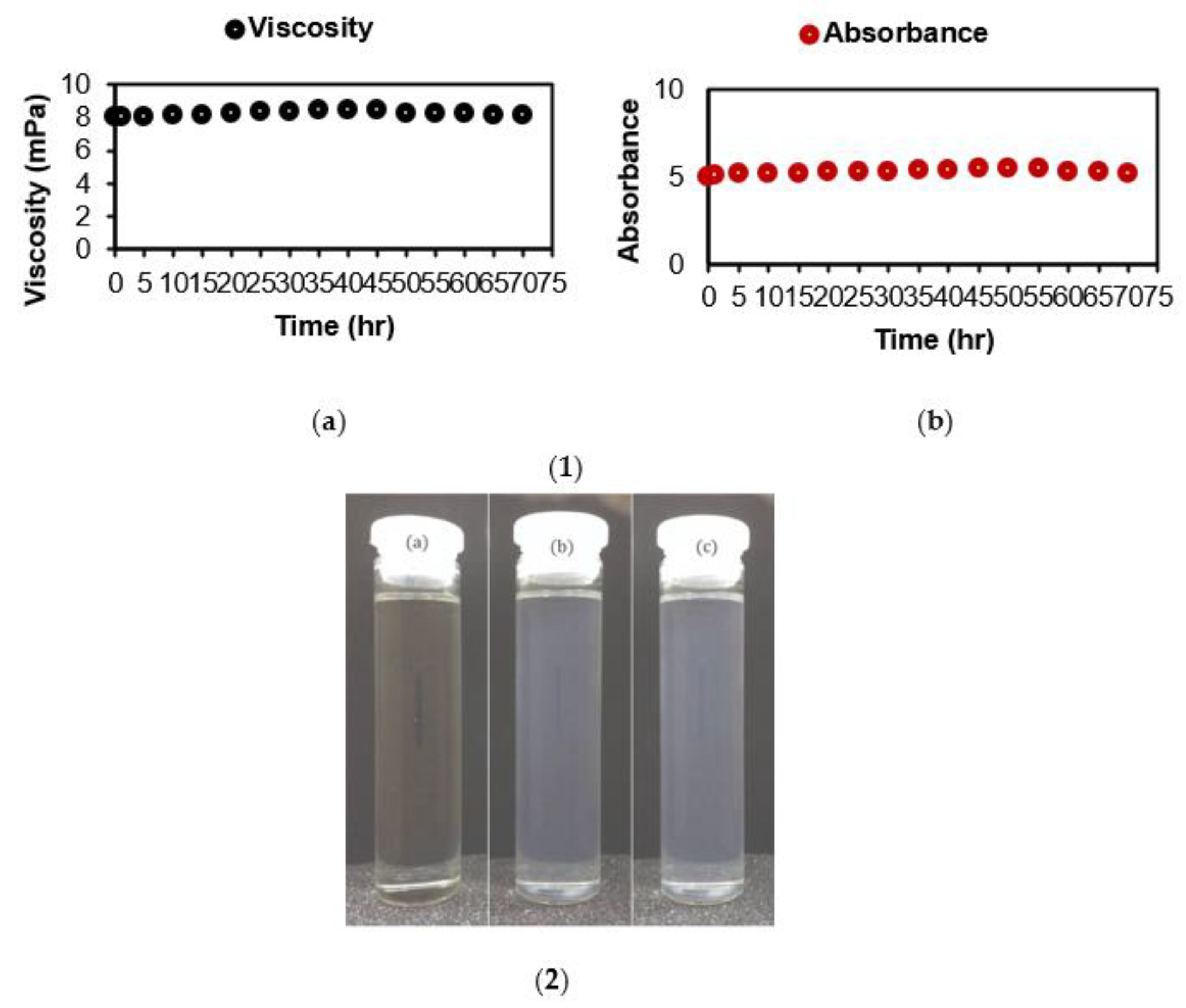
2.1. Preparation of Nanofluid

Stable concentrated C_u nanoparticles (stabilised with polyvinylpyrrolidone (PVP)) from US Nanomaterial Research (USA) are purchased and diluted with the base fluid. The base fluid consists of 35% EG and 65% water. This combination of working fluid is prepared due to its anti-freezing capability, which is effectively used in many industrial processes, such as heat exchanger applications. The nanoparticle size of C_u is 20 nm. In this work, volume concentrations of nanoparticles 0.05 $\le$ $\varnothing$ $\le$ 0.5 are added to base fluid to form the nanofluid; this is achieved by mixing these components and using an ultrasonic process (Qsonica-Q700) for the period of 30 to 40 min. For examining the nanofluid stability and reading and recording the viscosity, a UV-visible spectroscopy (Jenway-7315) unit is used at constant temperature. Figure 1(1) displays the stability of the nanofluid in terms of the UV-visible absorbance and viscosity of the fluids. However, to check the visual stability of the nanofluid at 0.5% volume concentration, the photo graph of the base fluid and nanofluid after preparation has been taken, see Figure 1(2).

2.2. Thermo–Physical Properties of Nanofluids

Traditionally, the thermal conductivity and viscosity of the nanofluid have been calculated by the correlations presented by Sunder et al. [20]. In this research, the base fluid is a mixture of water and EG of 65% and 35%, respectively. Moreover, nanoparticles (20 nm in diameter) used in various volume concentrations 0.05 $\le$ $\varnothing$ $\le$ 0.5 have been considered. These percentages are taken according to Sharifpur et al. [21], who reported that the volume concentrations of nanoparticles less than 1% are suitable for enhancing the thermal conductivity of nanofluids. First of all, we apply the Equation (1) to calculate the thermal conductivity of the naofluid as shown:

$$\frac{{\mathrm{k}}_{\mathrm{nanofluid} }}{{\mathrm{k}}_{\mathrm{basefluid}}}=1.0618+10.448\varnothing$$

(1)

where k is a thermal conductivity in W/m-°C and $\varnothing$ is the nanoparticles’ volume concentration. The viscosity ($\mathsf{\mu }$) in kg/m-s of the nanofluid is calculated by:

$$\frac{{\mathsf{\mu }}_{\mathrm{nanofluid}}}{{\mathsf{\mu }}_{\mathrm{basefluid}}}=1.1216{\mathrm{e}}^{77.56\varnothing }$$

(2)

The viscosity has been obtained by Equation (2). To validate this value, the nanofluid viscosity under nanoparticle volume concentrations of 0.05%—to take an example—is measured by sine-wave vibro viscometer (SV-10) at different temperatures. Then, the findings can be compared with those of Sunder et al. [20]. According to mixing theory defined by Ho et al. [22], the nanofluid density is calculated by:

$${\mathsf{\rho }}_{\mathrm{nanofluid}}={\varnothing }_{{\mathrm{nanofluid} \mathsf{\rho }}_{\mathrm{particles}}+(1-}{\varnothing }_{\mathrm{nanofluid}){ \mathsf{\rho }}_{\mathrm{basefluid}}}$$

(3)

where $\mathsf{\rho }$ is a density in kg/m³. The base fluid density is given by [23] at different temperatures. More properties of the nanofluid can be calculated by Equations (4) and (5). This is for the specific heat ${\mathrm{C}}_{\mathrm{p}}$ in kJ/kg-K and the coefficient of thermal expansion $\mathsf{\beta }$, respectively.

$${\mathsf{\rho }}_{\mathrm{nanofluid}}{ \mathrm{C}}_{\mathrm{p}}{}_{\mathrm{nanofluid}}={\varnothing }_{\mathrm{nanofluid} }{\mathsf{\rho }}_{\mathrm{particles}}{ \mathrm{C}}_{\mathrm{p}}{}_{\mathrm{particles}}+\left(1-{\varnothing }_{\mathrm{nanofluid} }\right){ \mathsf{\rho }}_{\mathrm{basefluid}}{ \mathrm{C}}_{\mathrm{p}}{}_{\mathrm{basefluid}}$$

(4)

$${ \mathsf{\rho }}_{\mathrm{nanofluid}}{ \mathsf{\beta }}_{\mathrm{nanofluid}}={\varnothing }_{\mathrm{nanofluid} }{ \mathsf{\rho }}_{\mathrm{particles}}{ \mathsf{\beta }}_{\mathrm{particles}}+\left(1-{\varnothing }_{\mathrm{nanofluid} }\right){ \mathsf{\rho }}_{\mathrm{basefluid}}{ \mathsf{\beta }}_{\mathrm{basefluid}}$$

(5)

The $\mathsf{\beta }$ of EG and water are identified by 5.4 $\times$ ${10}^{-4}$ and 2.14 $\times {10}^{-4}$, respectively. As a result, the base fluid (65% water + 35% EG) has $\mathsf{\beta }$ of 4.09 $\times {10}^{-4}$. The glass spheres used as the porous medium also has $\mathsf{\beta }$ of 0.9 $\times {10}^{-5}$ [24].

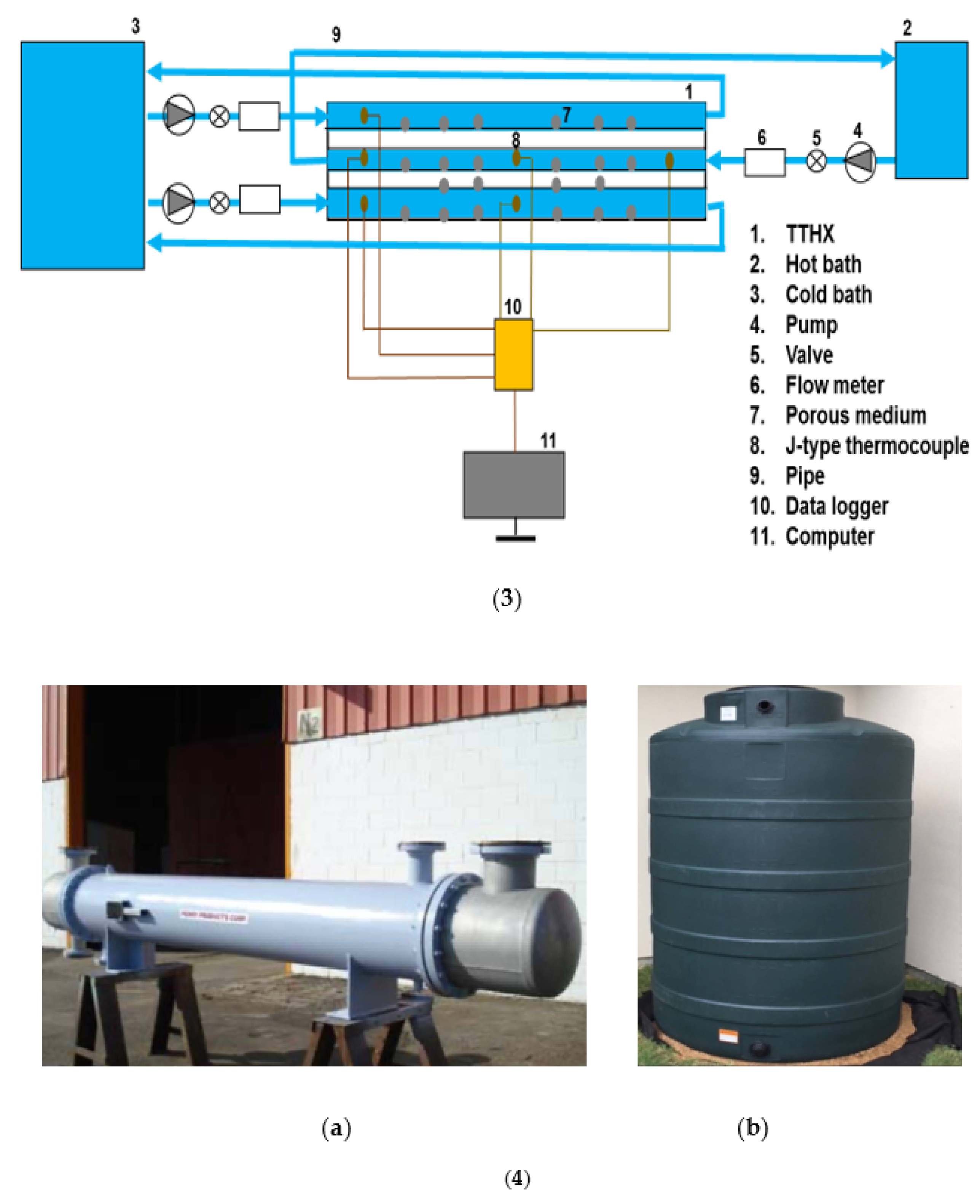
2.3. Experimental Setup and Procedure

Figure 1(3). demonstrates an experimental setup and procedure for the heat transfer process by convection. The major unit of the system is a TTHX. It consists of three tubes: inner, middle and outer with 10 mm, 17 mm and 30 mm diameters, respectively, and 490 mm length and 2 mm thickness for each one. However, the heat exchanger is totally made up of C_u (see Figure 1(4a)). The hot water flows through the inner tube, while the cold water flows through the outer tube. This is circulated by two pumps supplied the water from two thermal baths—hot and cold, respectively (see Figure 1(4b)). The specifications of these pumps were connections: ¾, 1 or 1¼ inch for unions and valves; system pressure: Max. 10 bar; liquid temperature: +2 °C to 110 °C. The middle, inner and outer tubes of TTHX contained glass spheres as a porous medium, 14 mm in diameter. The purpose is to enhance heat transfer through nanofluid where the thermal conductivity is 0.7 W/m-K (see

Table 1. Thermophysics properties of porous medium.

Properties	Values
Spherical glass diameter (mm)	16
Thermal conductivity (W/m-K)	0.7
Density (kg/m3)	2800
Specific heat (J/kg K)	13.96

). To avoid the heat losses to the surroundings, the TTHX is wrapped with a 60 mm thickness polyurethane sheet as an insulation. Two ball valves used for managing the flows enter the inner and outer tubes. In addition, two ultrasonic flow meters are accurately (±0.5% of actual value) used to measure the nanofluid volume flow rate in the pipes network. It comprises a tapered glass tube with a float inside. The specifications of flow meter were (Model: H612, 2-19 LPM flow range, port size 0.5 inches, SAE 10 and brass material). To minimize the thermal losses, all pipes are totally insulated. The temperatures were accurately measured to six locations using thermocouples. Three thermocouples were soldered into the inner and outer tubes of the heat exchanger, respectively, at desired locations (T₁ to T₆), as shown in Figure 1(3). The specifications of these thermocouples were J-type thermocouple; size: 4.8 mm diameter × 25 mm; C/W: ¼ inch BSP; 2 MTR PVC wire with an accuracy of ±0.2 °C. The Graphic (GL820) is a data acquisition system supplied with a color monitor and internal memory comprises compact, light-weight and multi-channel data loggers supplied with twenty channels. The GL820 is equipped with an internal flash memory to store data and transfer it to be saved in universal serial bus (USB) memory. The data logger is equipped with USB and ethernet interfaces to a personal computer. Practically, the variations in the temperature scale recorded for the inner and outer tubes, as well as working fluid under different temperatures, were constant (see

Table 2. Temperatures tests of the TTHX.

Inner Tube Temperatures (°C)	Outer Tube Temperatures (°C)	Temperatures Difference ΔT (°C)
55	5	50
45	15	30
40	20	20

). Therefore, the data can be recorded after 40 to 45 min. Ultimately and for all experiments, the error bar value did not exceed 0.5%.

2.4. Solution Methodology

After collecting the data, reading and recording the different temperatures at six different positions on the inner and outer tubes, the parameters of heat transfer by natural convection were used to evaluate the heat exchanger performance. Therefore, and by applying Newton’s law of cooling, the heat transfer rate through inner tube can be determined by:

$${\dot{\mathrm{q}}}_{\mathrm{hot}}={\dot{\mathrm{m}}}_{\mathrm{hot}}{ \mathrm{C}}_{\mathrm{p}} \mathrm{dTM}={\dot{\mathrm{m}}}_{\mathrm{hot}}{ \mathrm{C}}_{\mathrm{p}}\left({\mathrm{T}}_{\mathrm{hot},\mathrm{i} }-{\mathrm{T}}_{\mathrm{cold},\mathrm{o}}\right)$$

(6)

where $\dot{\mathrm{q}}$ is a heat transfer rate in W and $\dot{\mathrm{m}}$ is a mass flow rate in kg/s. dTM is a mean temperature difference in °C. Similarly, the heat transfer rate in outer tube can be calculated by:

$${\dot{\mathrm{q}}}_{\mathrm{cold}}={\dot{\mathrm{m}}}_{\mathrm{cold}}{ \mathrm{C}}_{\mathrm{p}} \mathrm{dTM}={\dot{\mathrm{m}}}_{\mathrm{cold} }{\mathrm{C}}_{\mathrm{p}}\left({\mathrm{T}}_{\mathrm{hot},\mathrm{o}}-{\mathrm{T}}_{\mathrm{cold},\mathrm{i}}\right)$$

(7)

However, the coefficient of natural convection heat transfer h in W/m²-K of the inner and outer tubes is calculated by Equations (8) and (9), respectively:

$${\mathrm{h}}_{\mathrm{hot}}=\frac{{\dot{\mathrm{q}}}_{\mathrm{hot}}}{\mathrm{dTM}}=\frac{{\dot{\mathrm{q}}}_{\mathrm{hot}}}{\left({\mathrm{T}}_{\mathrm{hot}}-{\mathrm{T}}_{\mathrm{fluid}}\right)}$$

(8)

$${\mathrm{h}}_{\mathrm{cold}}=\frac{{\dot{\mathrm{q}}}_{\mathrm{cold}}}{\mathrm{dTM}}=\frac{{\dot{\mathrm{q}}}_{\mathrm{cold}}}{\left({\mathrm{T}}_{\mathrm{fluid}}-{\mathrm{T}}_{\mathrm{cold}}\right)}$$

(9)

where T is a temperature in °C of the inner tube, outer tube and fluid. The Nu number is calculated by:

$$\mathrm{Nu}=\frac{\mathrm{hl}}{\mathrm{k}}$$

(10)

where $\mathrm{l}$ represents the characteristic length of stream in mm unit where the heat transfer takes place. The Re can be determined by:

$$\mathrm{Re}=\frac{{\mathsf{\rho }\mathrm{VD}}_{\mathrm{h}}}{\mathsf{\mu }}$$

(11)

where ${\mathrm{D}}_{\mathrm{h}}$ denotes the hydraulic diameter in mm and V denotes the average velocity of fluid in m/s. Totally, the coefficient of heat transfer of TTHX equals the average coefficients of the inner and outer tubes $\mathrm{h}=({\mathrm{h}}_{\mathrm{h}}+{ \mathrm{h}}_{\mathrm{c}})/2$. The efficiency of convection heat transfer $\mathsf{\eta }$ can be calculated by [25]:

$$\mathsf{\eta }=\frac{({\mathrm{Q}}_{\mathrm{conv} \mathrm{nanofluid}})/\left({\mathrm{P}}_{\mathrm{pump} \mathrm{nanofluid}}\right)}{({\mathrm{Q}}_{\mathrm{conv} \mathrm{basefluid}})/({\mathrm{P}}_{\mathrm{pump} \mathrm{basefluid}})}$$

(12)

where $\mathrm{Q}$ and $\mathrm{P}$ denote convection heat transfer and pumping power in W, respectively. This is for nanofluid and base fluid, respectively. In this study, this equation is used for the transition or turbulent flow regimes. The uncertainties of coefficient of heat transfer and Nu number were approximately 2% and 5%, respectively. However, the uncertainty analysis has been determined by two factors: random errors and systematic errors. The total uncertainty was calculated by the standard deviation method.

Table 3. The uncertainty analysis results.

Parameters	Device	Total Uncertainty (±%)
Temperature	J-thermocouple	1.7
Flow rate	Flow meter	2
Heat convection	-	3
Thermal efficiency	-	4.5

displays the uncertainty results of this study.

3. Results and Discussion

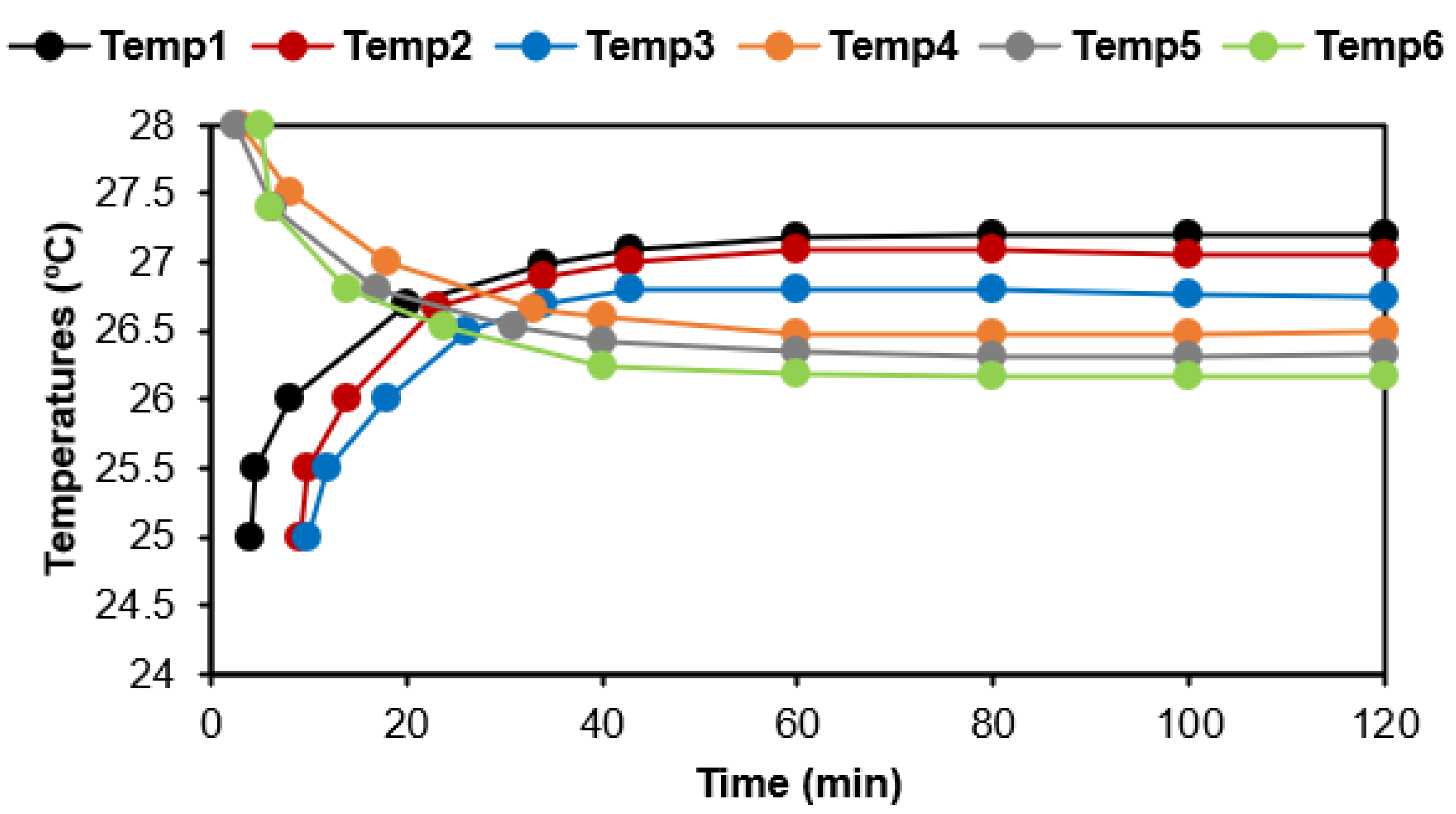
3.1. Temperatures Variation with Time

Figure 2 presents the experimental data from temperature readings of thermocouple locations T₁ to T₆ with time. The results were obtained over each tow-hour test period for nanoparticles’ volume concentration of zero ($\varnothing$ = 0%). Steady-state operations were attained after one hour and can widely be seen between the inner and outer tubes (hot and cold flow, respectively). As a result, the mean temperature approximately stays constant at 27 °C. An increase in fluctuations of the temperature scale at T₃ occurs when the volume concentration of nanoparticles reaches 0.5%. Further, other temperature readings maintained relatively similar fluctuations. This is because of increasing interactions between thermocouples’ junctions and volume concentrations of C_u nanoparticles. Certainly, from natural heat transfer experiments, it is significant to minimize the heat losses to the surroundings. This should provide the balance between the heat removal and the heat gain of hot and cold flow, respectively.

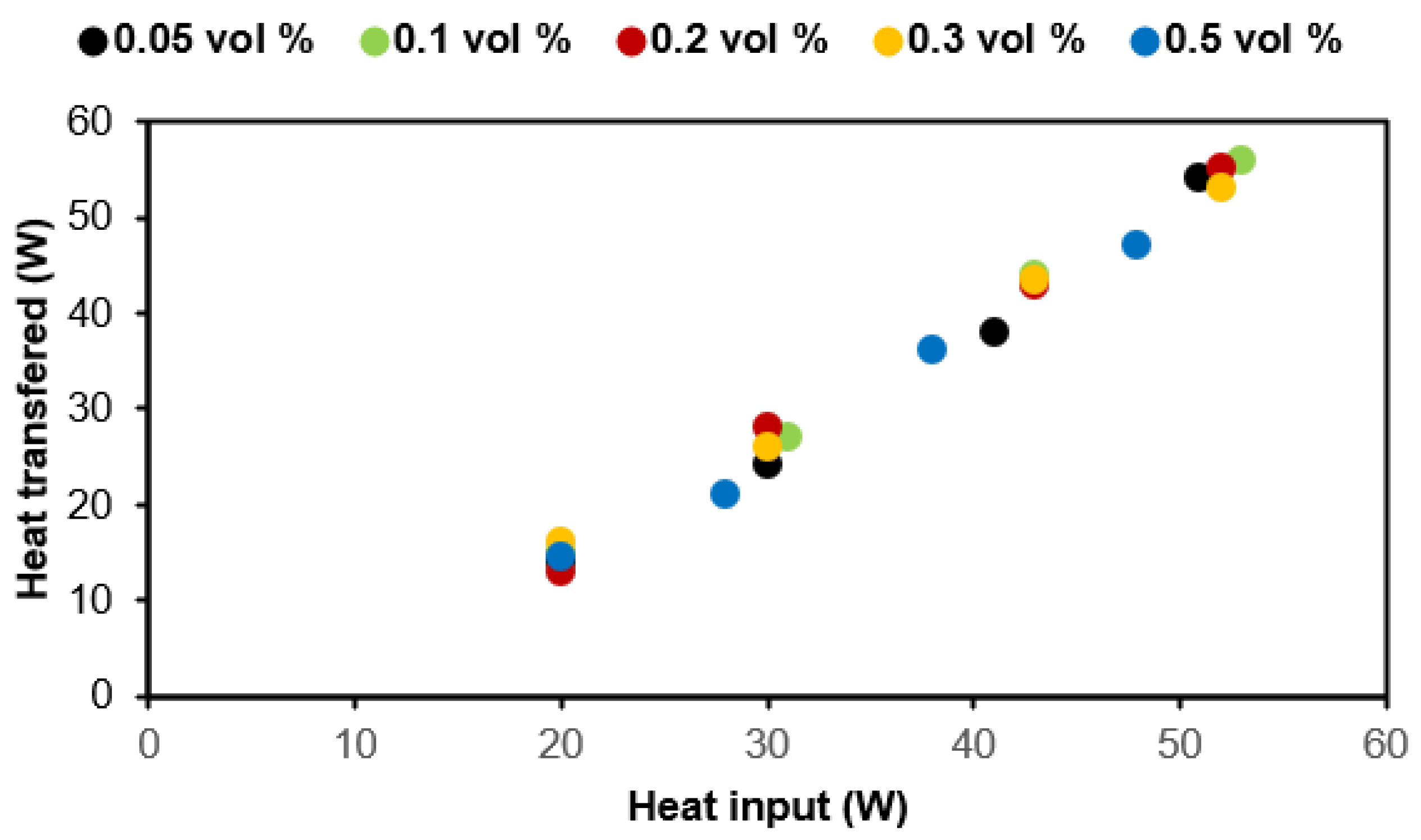
3.2. Heat Transfer Enhancement by Nanofluid

The relation between the convection heat transfer and different volume concentrations of C_u nanoparticles 0.05 $\le$ $\varnothing$ $\le$ 0.5 under different temperatures is shown in Figure 3. Enhancing the heat transfer is effective because it increases the temperature difference for all volume concentrations. For example, the addition of C_u volume concentration of 0.05% causes an approximate heat transfer enhancement of 10%, compared to base fluid with no particles. One of important reasons is the thermal conductivity improvement of working fluid. However, the biggest buoyancy forces, resulting from density variations of nanofluid, promoted the heat transfer as a result of the water circulation. Brownian motion and thermophoresis of C_u concentrations also play an important role in this issue. Another finding: the heat transfer is enhanced because of the increase in the volume concentrations of C_u nanoparticles to 0.05%. It is then slightly reduced up to 0.3% and, after that, it is totally dropped to 0.5%. This trend is observed when the temperature reached 50 °C. Therefore, maximum heat transfer by the nanofluid given is 54 W for the temperature of 50 °C and volume concentration of 0.05%. The question of heat input effectiveness into porous TTHX filled with nanofluid under various volume concentrations is addressed in Figure 4. The experiment’s findings illustrated that there is a linear heat transfer enhancement due to the heat input supplied to the inner tube of TTHX. This enhancement has been compared with the heat transferred through outer tube, showing a big difference. Therefore, more capacity of heat transfer can be noted during the increasing of the heat input by nanofluid, and the opposite is true. This is because of the thermal conductivity enhancement, which is leads to a high-speed fluid circulation.

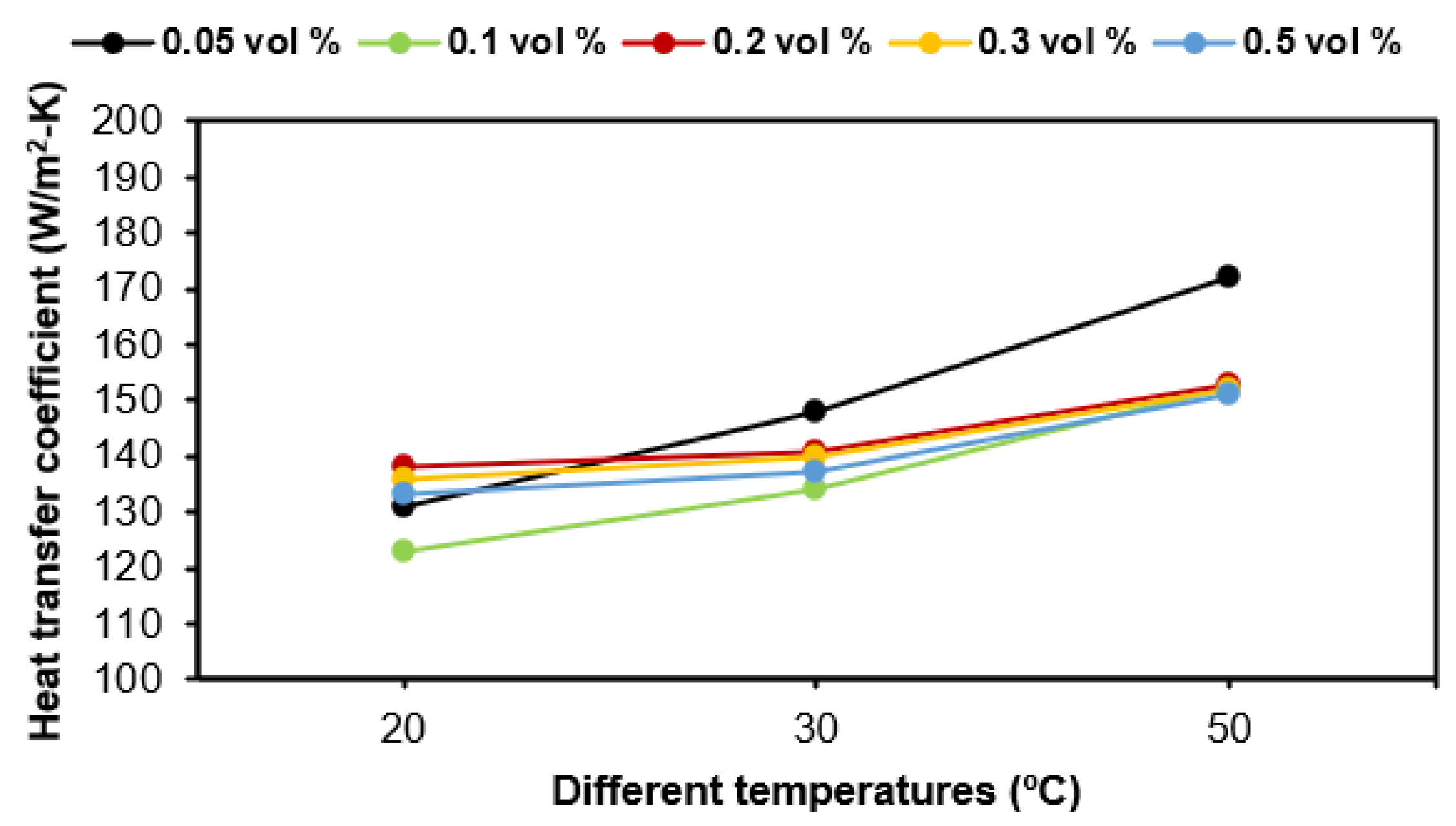
3.3. The Heat Transfer Coefficient of Hot and Cold Tubes

The hot inner and cold outer tubes play essentially roles in whether heat transfer by convection is considered. Figure 5 displays the heat transfer coefficient at the inner tube of porous TTHX under different temperatures and nanoparticle volume concentrations. It is somewhat surprising that the heat transfer coefficient was increased linearly in this part with the rise of different temperatures. For example, the heat transfer coefficient under C_u volume concentration of 0.05% is higher than other volume concentrations. Further, this coefficient reduces as a result of increasing particle concentrations. One more result: the addition of C_u concentrations of 0.1% to 0.3% leads to a decrease in the coefficient of heat transfer by nanofluid. These coefficients are still going up compared to the coefficient of base fluid (water + EG) because of the increasing Brownian motion of the fluid during different temperatures [14]. Similarity, the coefficient of heat transfer by convection at the outer tube of TTHX is gradually increased with different temperatures, as shown in Figure 6, but the behavior is so difference. A maximum heat transfer coefficient can be obtained at the outer tube (cold tube) when the temperature is decreased to 5 °C (see Table 2). This value is minimized at the lower temperature of 20 °C. At the different temperature of 50 °C, the cold and hot tube temperatures were 5 °C and 55 °C, respectively. Therefore, the maximum heat transfer coefficient can be seen at the inner tube (hot tube) when the temperature is increased to 55 °C. However, this coefficient decreases due to increasing particle concentrations. Therefore, the value of the heat transfer coefficient of the hot tube is higher than that of the cold tube. This reason concerns the thermal conductivity of nanofluid; the higher temperature increases the thermal conductivity property and the opposite is also true. On the other hand, the h in a porous TTHX under the same temperatures and C_u nanoparticle volume concentrations of nanofluid compared to pure water and against Re are presented in Figure 7. The range of Re number was between 200 to 7000. The results showed that an enhancement in the heat transfer in the turbulent flow regime was obtained when the Re number reached 6364. The enhancement ratios of h were 3.1%, 10% and 16% when nanoparticle volume concentrations were 0.05%, 0.3% and 0.5%, respectively. The thickness of the thermal boundary layer is reduced because of the random motion of the nanoparticles in the fluid. This is a biggest reason for enhancing the h rate in a turbulent flow [26,27]. In the transition regime, the flow fluctuates between laminar and turbulent flows. It can be seen to have two features: First, it started earlier at a critical Re number and occurred at a smaller Re number compared to pure water when higher nanoparticle volume concentrations were used. This is due to the higher viscosity of the nanofluid than pure water. The values of Re number were 1731, 1723 and 1705 when nanoparticle volume concentrations were 0.05%, 0.3% and 0.5%, respectively. These values decreased to 125, 110 and 105, respectively, and transition flow increased. Second, the enhancements in h values were 15%, 29% and 54% for C_u nanoparticle volume concentrations of nanofluid of 0.05%, 0.3% and 0.5%, respectively.

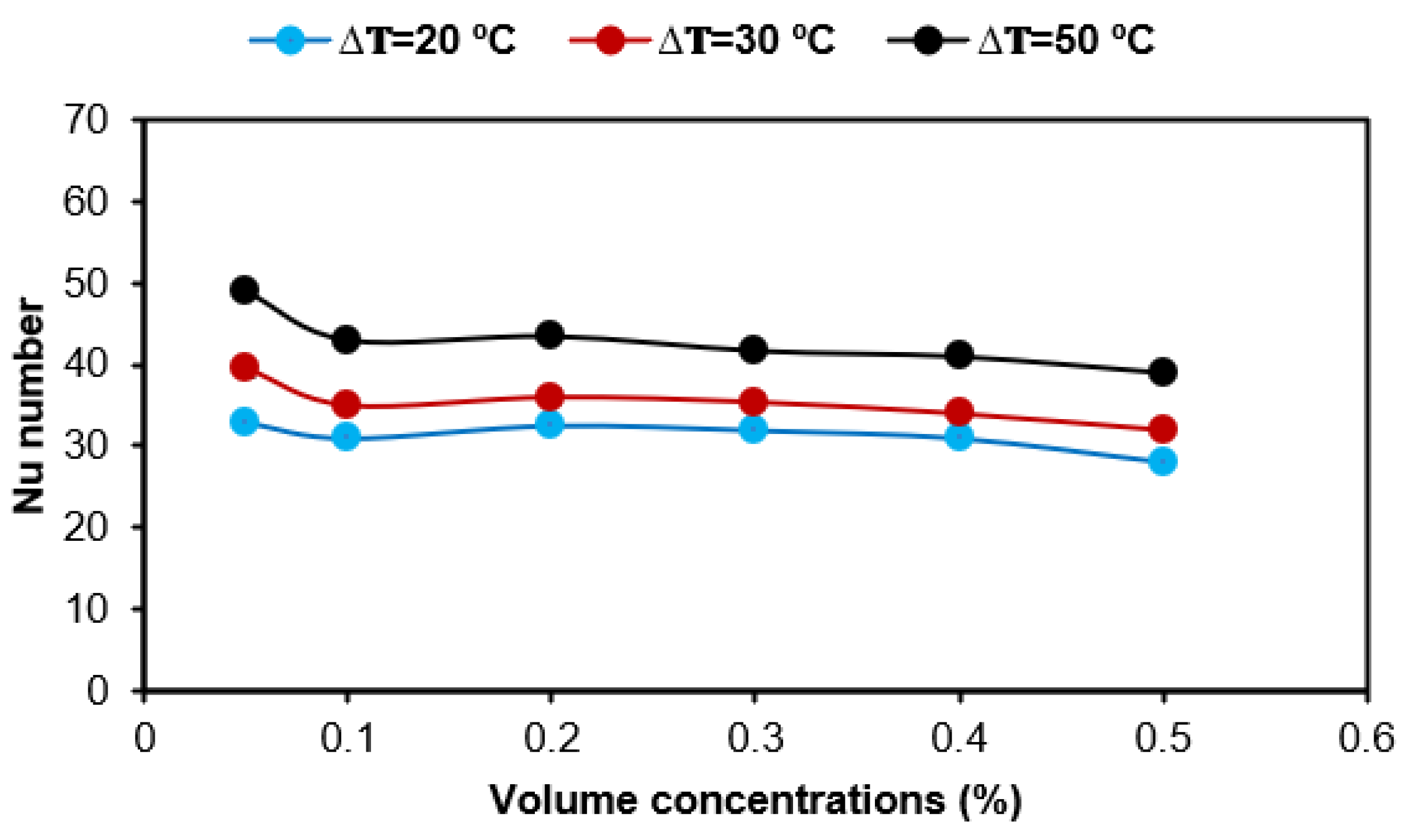
3.4. Variations of Nu Number in Clear and Porous TTHX with and without Nanoparticle Concentrations

Figure 8 shows Nu number variations of nanofluid at various volume concentrations of C_u nanoparticles in a porous TTHX. It confirms that the rise of Nu number is for all C_u volume concentrations, as well as the base fluid (water + EG). This is because of the increase in temperatures between hot and cold tubes. At 0.05% of C_u volume concentrations, the average Nu number increases then it starts to reduce gradually as the nanoparticle volume concentrations increase. One of the interesting results is that the Nu number of nanofluid is gradually lower according to increasing volume concentrations of C_u from 0.1% to 0.5%, respectively. This is also compared to the Nu number of base fluid. More analysis: the physical properties of the nanofluid, such as density and viscosity, are increased due to the increasing volume concentrations added. This leads to a reduction in buoyancy forces, resulting from slow fluid movement, which affects on flow circulation in TTHX. As a result, the heat transfer by convection is reduced. The explanation conforms to previously mentioned reasons during the discussions of Figure 4 and Figure 5. Theoretically, the Nu number is calculated by applying Equation (10) and the variations of this value are clear (TTHX and porous TTHX are represented in Figure 9). In the current study, comparing clear TTHX with porous TTHX showed that the Nu number increases gradually the increase in temperature. Furthermore, the density of the fluid is reduced, and buoyancy forces are increased because of the hottest inner tube. The fluid circulation was fastest. Therefore, the Nu number was increased. On the other side, and because of the resistance of the porous medium, the Nu number was lower in porous TTHX compared with clear TTHX. From the results, the Nu number is in the ranges of 45–59 and 34–45 for the clear and porous TTHX, respectively. It means that the difference was 24% less than that of clear TTHX. The buoyancy forces reduction and slow fluid circulation are caused by the porous structure. For these reasons, the Nu number is decreased in porous TTHX.

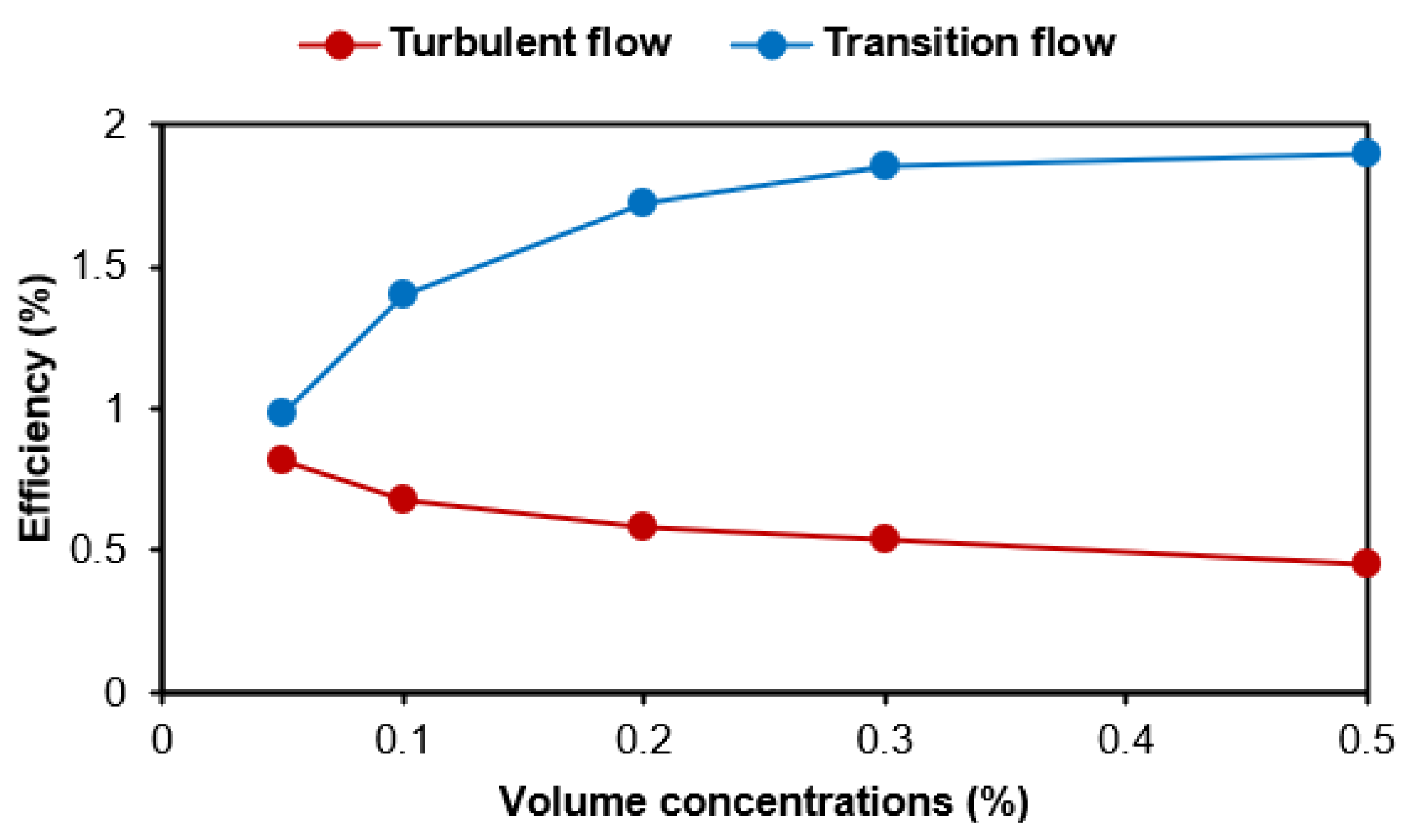
3.5. Efficiency of Convective Heat Transfer

The efficiency of convection heat transfer can be defined as the ratio of convection heat transfer by nanofluid to pumping power required where the flow is laminar, transition or turbulent. Figure 10 shows the efficiency of convection heat transfer during transition and turbulent flow in porous TTHX with C_u nanoparticle volume concentrations. This efficiency is determined by applying Equation (12), which is previously mentioned in this study. It can be seen that in the transition flow regime, the nanofluid efficiency is high when the C_u volume concentration is greater than 0.3%. Moreover, in the turbulent flow, the efficiency percentage is lower. Further, the maximum efficiency reached more than 100% when the nanoparticle volume concentrations increased by 0.5%. The efficiency is dropped in the turbulent flow to less than 70% due to increasing C_u concentrations with the same value. Clearly, the efficiency increased gradually in the flow transition and the performance was optimal, compared with turbulent flow. That is because of the dominance of heat transfer by convection as a result of the increase in the buoyancy forces of transition flow.

4. Conclusions

This study has identified a porous TTHX as one of TES systems which is designed to pass the hot and cold flow, as well as energy transfer through the inner and outer tubes, respectively. The main goal of this experimental work was to improve the mode of heat transfer by nanofluid according to a nanoparticle volume concentration range of 0.05 $\le$ $\varnothing$ $\le$ 0.5. On the other hand, the influence of the porous medium of glass spheres inside the TTHX is considered. The following conclusions can be drawn from the results obtained:

• Taken together, the findings confirm an important role for temperature differences of $\Delta$T = 20 °C, $\Delta$T = 30 °C and $\Delta$T = 50 °C, respectively, in promoting the heat transfer capacity for all C_u volume concentrations;
• The experiments confirmed that the coefficient of heat transfer was approximately 185 W/m²-K higher at the hot tube, compared with low value of 172 W/m²-K at the cold tube. The temperature rise to 50 °C enhances thermal conductivity and causes a minimal increase in the viscosity of the nanofluid.
• Although the current study is based on a small sample of C_u nanoparticles with 20 nm in diameter, the increase in the Nu number was for all C_u volume concentrations added to the base fluid. This is because of the increase in temperature between hot and cold tubes;
• The findings also shows that the Nu number is decreased in porous TTHX, compared with pure TTHX; the ratio was 24% less than that of clear TTHX. The reasons were the reduction in buoyancy forces and the slow fluid circulation caused by the porous structure;
• In this study, the enhancement to convection heat transfer for laminar flow was negligible. This is because, at a low Re number, an agglomeration of C_u nanoparticles occurred through the nanofluid, which decreased the heat transfer rate. However, the laminar flow was not fully developed in relation to the entrance length of TTHX. Therefore, one of the more significant findings to emerge from this research is that the efficiency of convective heat transfer increased gradually via the flow transition and the performance was optimal, compared with turbulent flow.

The present work has made effective steps towards enhancing energy transfer in TTHX-TES. This would be a fruitful foundation for further work aimed at the analysis of heat transfer in many applications, such as solar collectors.