Battery Power Control Strategy for Intermittent Renewable Energy Integrated Modular Multilevel Converter-Based High-Voltage Direct Current Network
Abstract
:1. Introduction
- A local voltage-based combined energy control approach for the battery (a) to regulate the HVDC-link voltage during the low-voltage faults at the PCC of AC grids, and (b) to address intermittency caused by the renewable energy generation fluctuation.
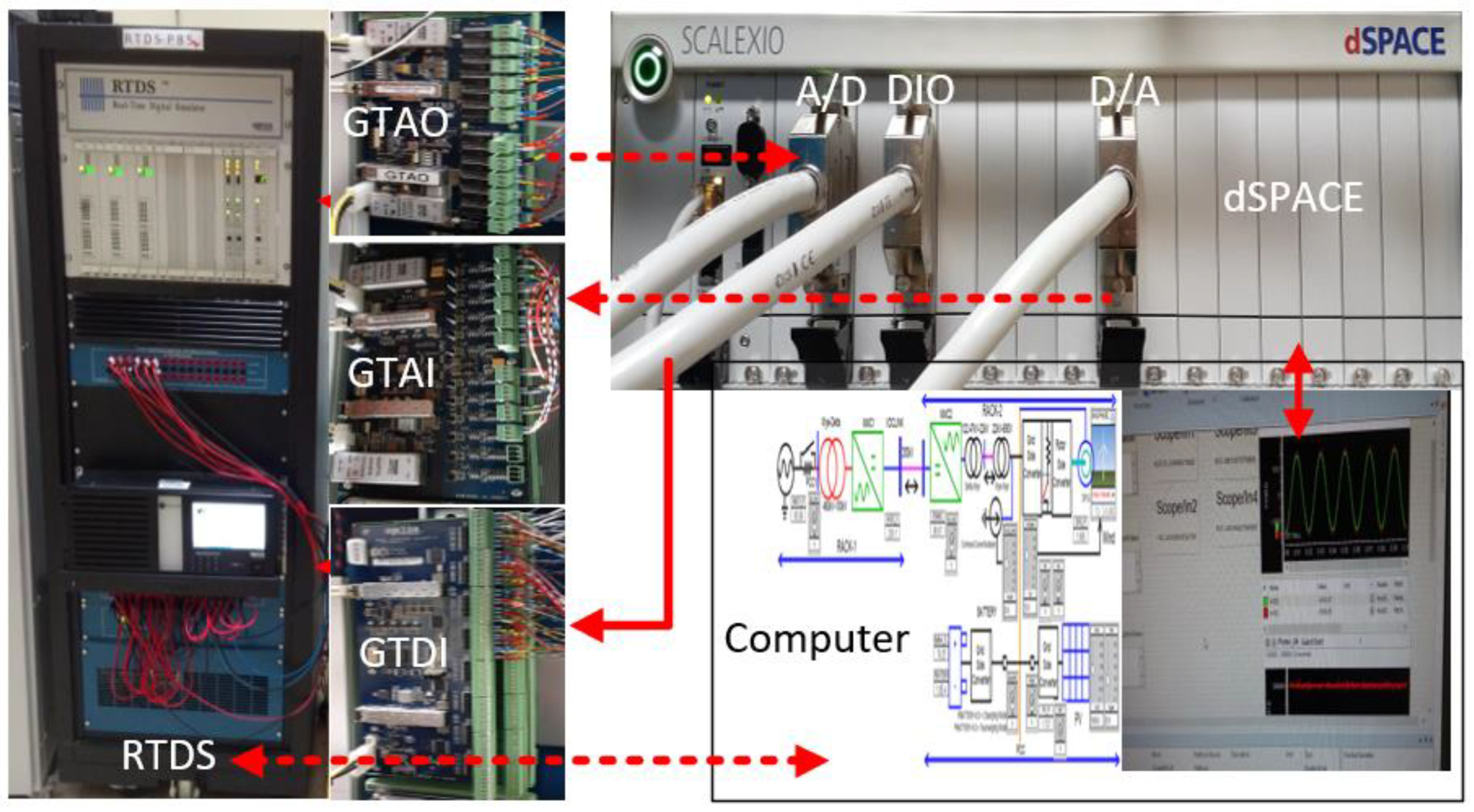
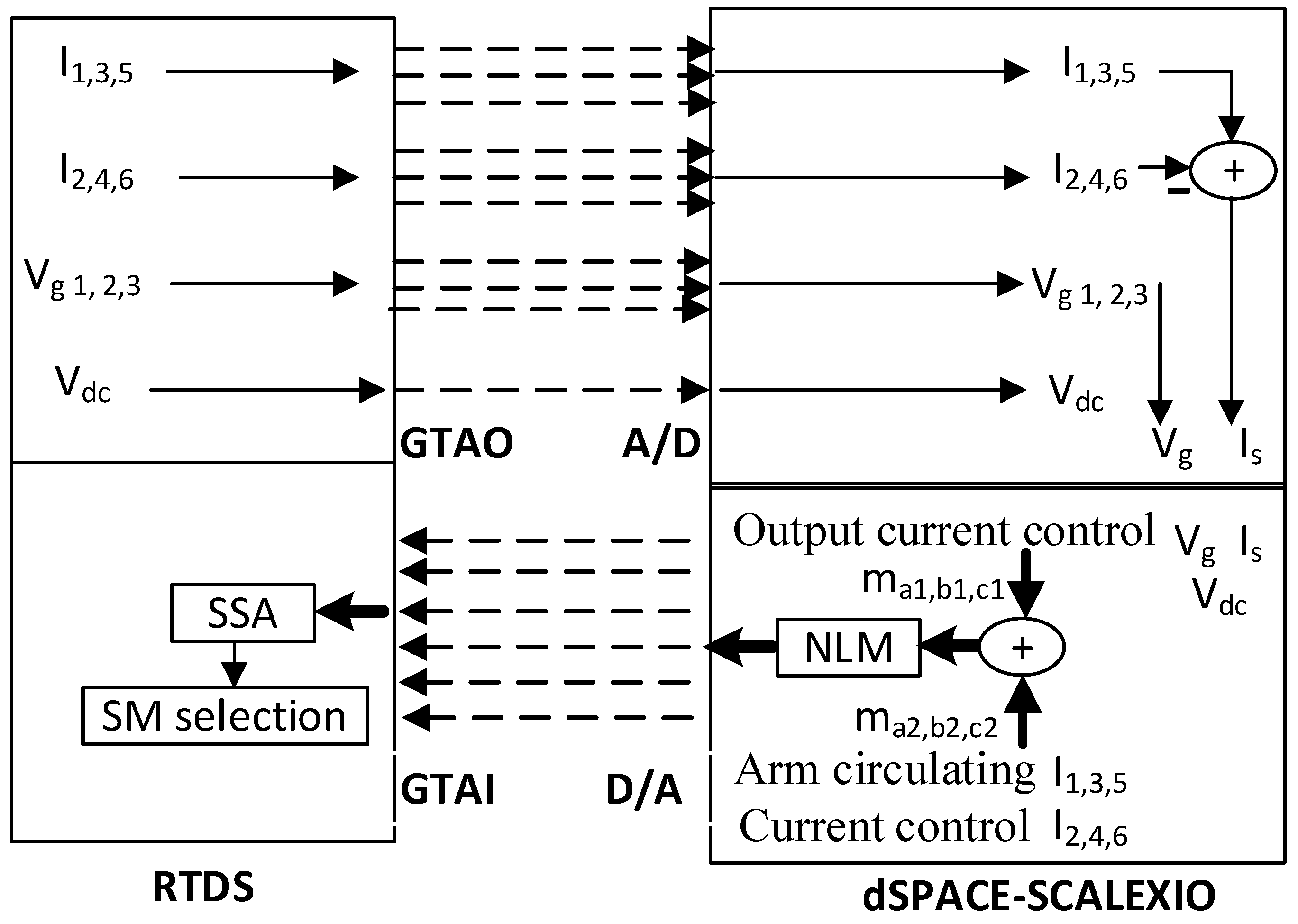
- Simulation and testing of the complete systems in a real-time digital simulator (RTDS) and dSPACE-based controller hardware in the loop (CHIL), with detailed converter models.
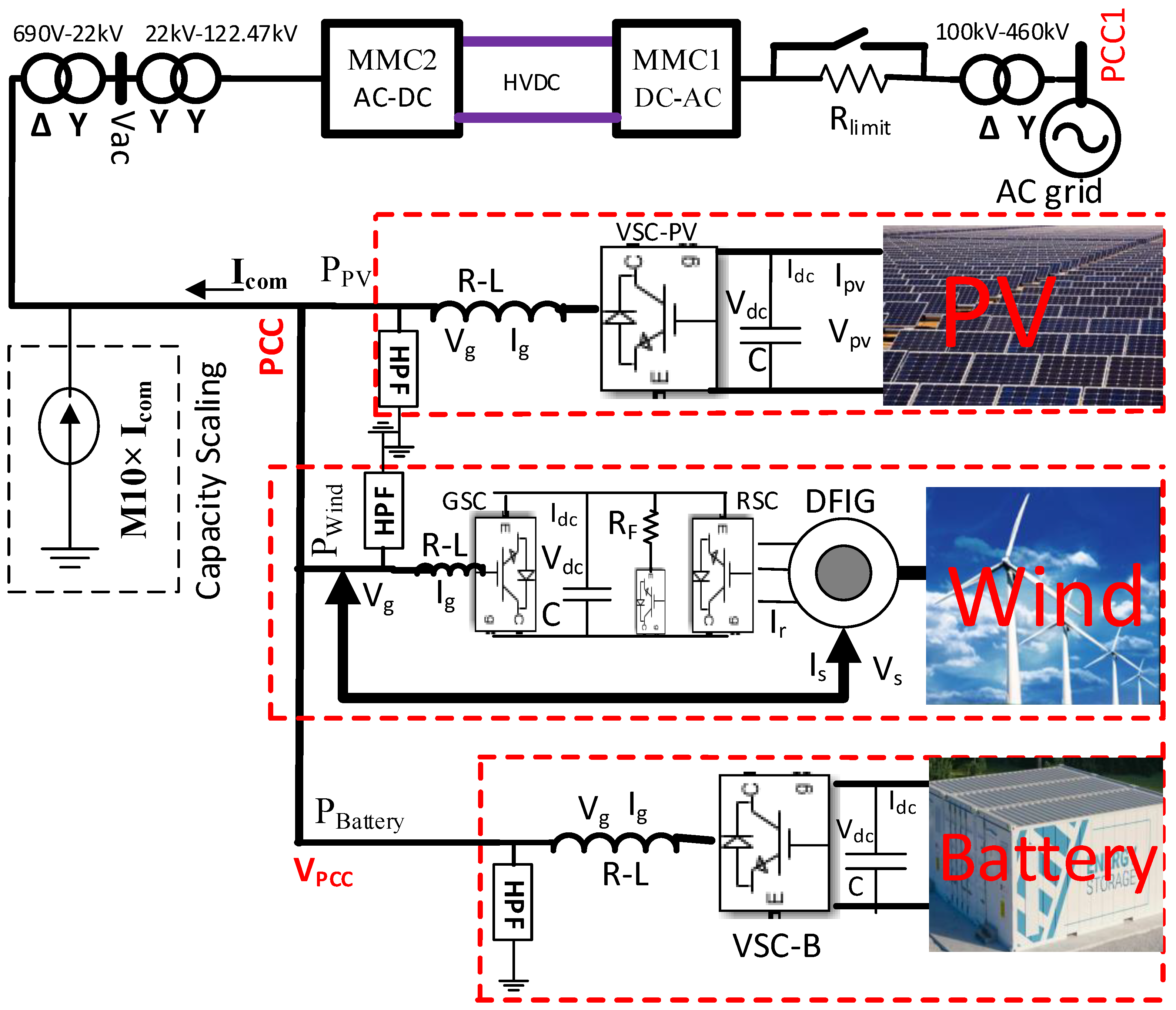
2. Modeling and Controller Design
2.1. Battery Modeling and Sizing
2.2. Solar and Wind Energy Grid Integration
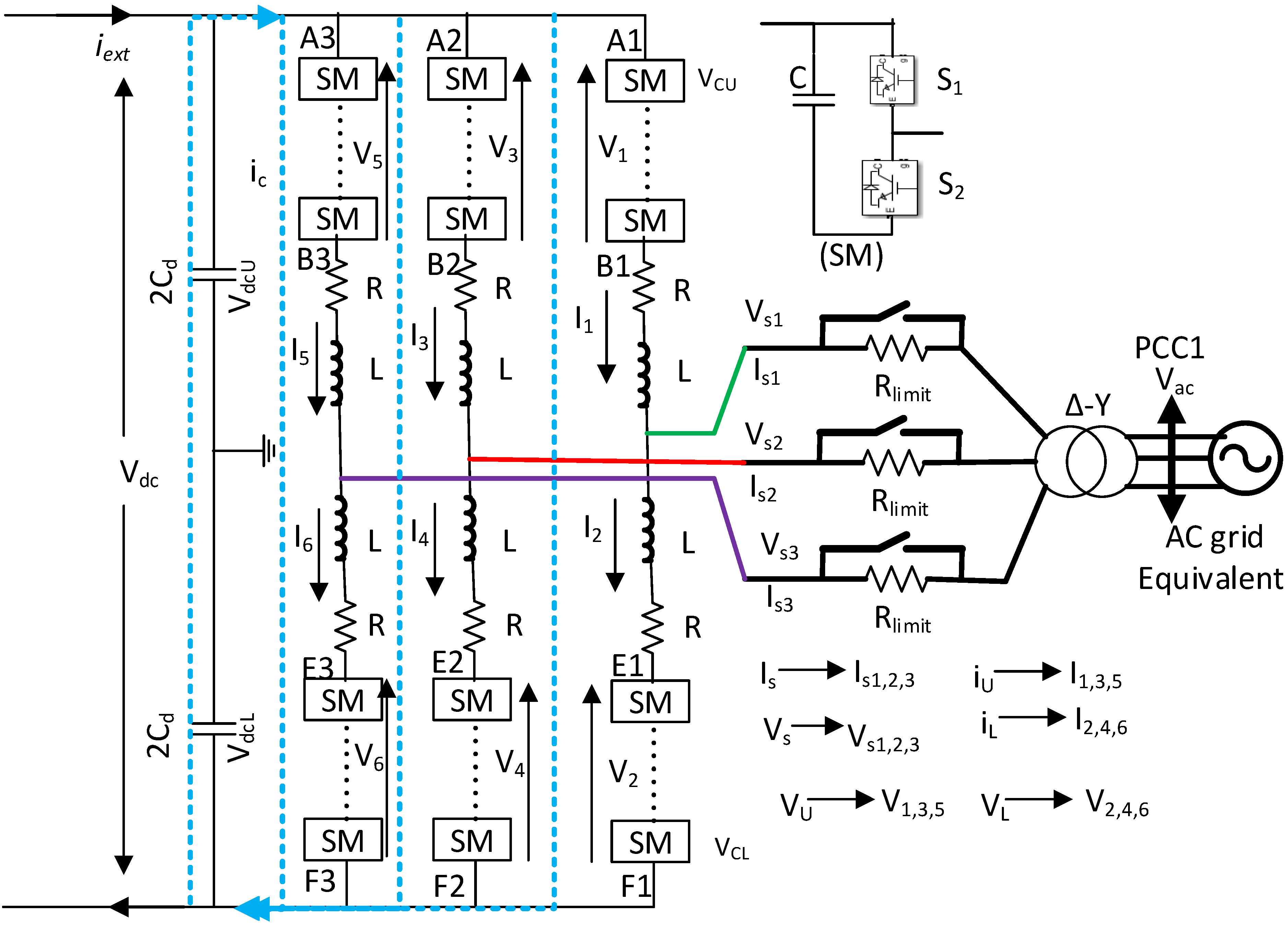
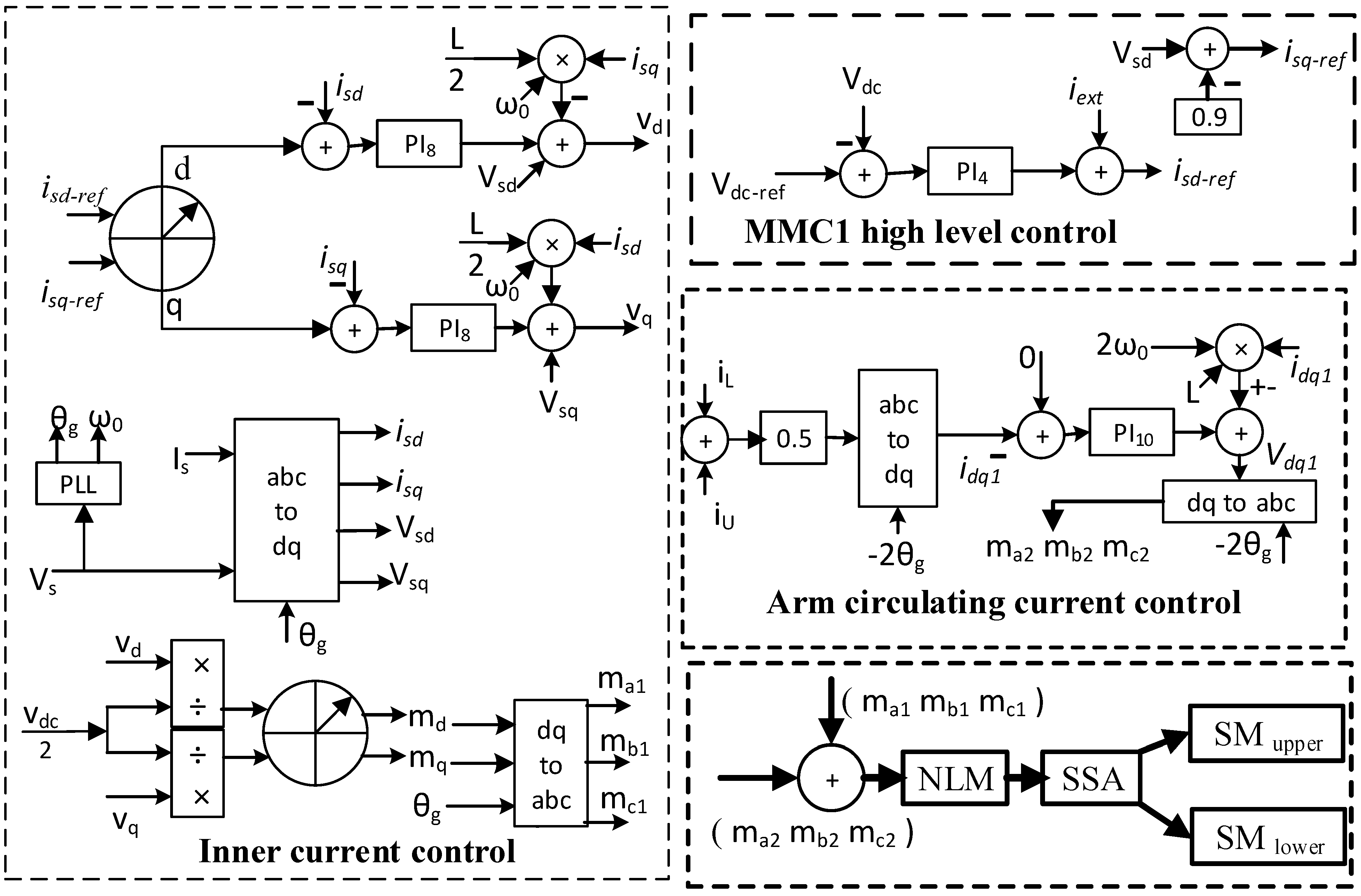
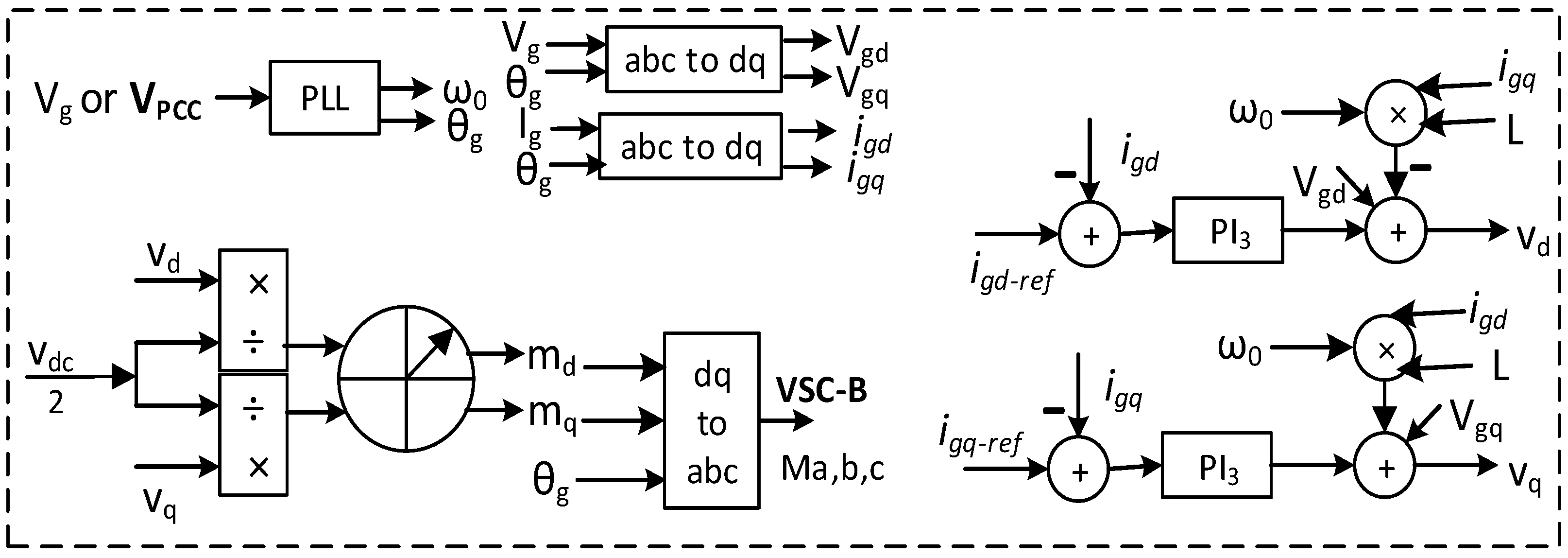
2.3. Modular Multilevel Converter Control
3. Proposed Energy Management System
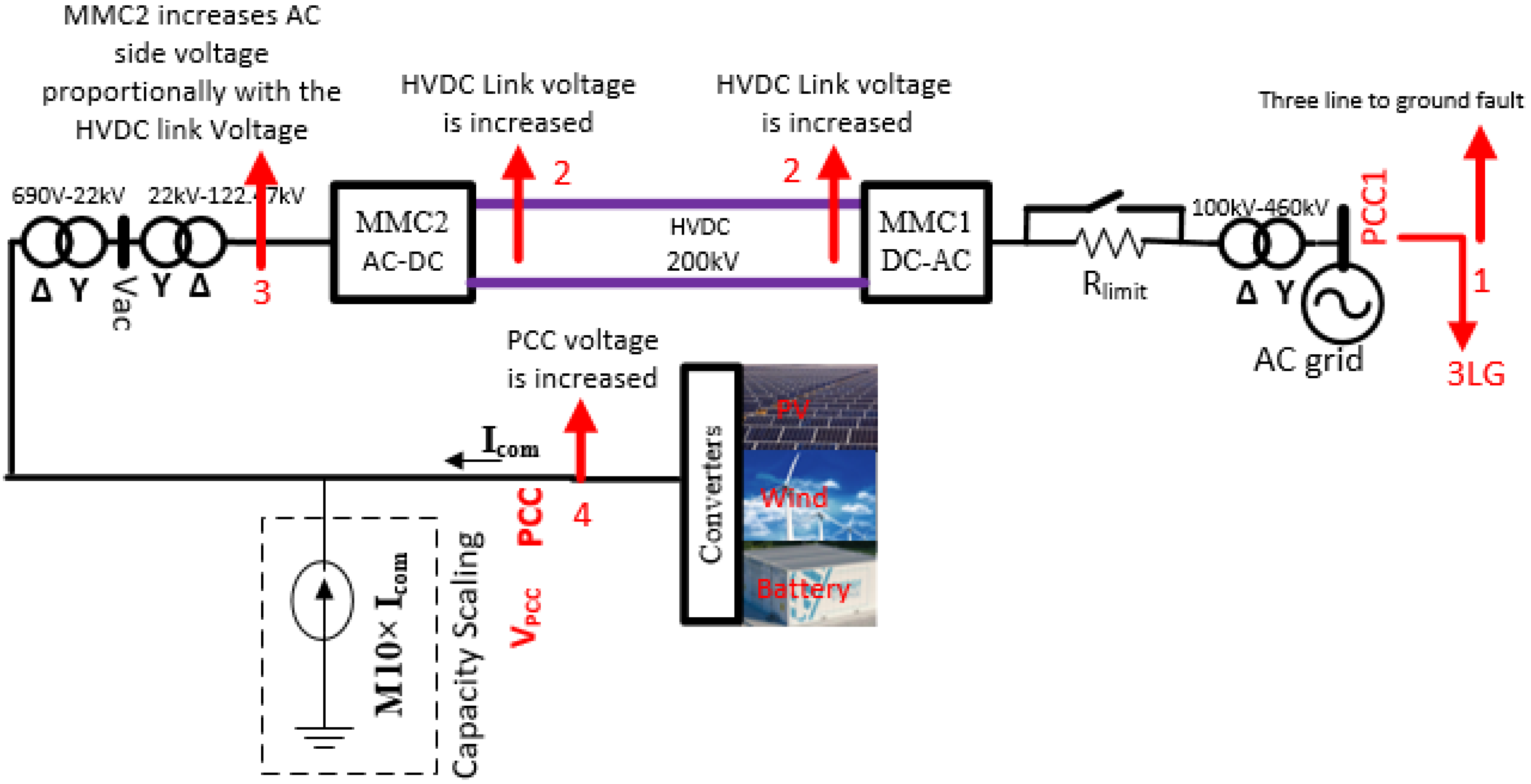
3.1. Surplus Energy Control Strategy in the HVDC Link during Low-Voltage Faults at PCC1
- (1)
- A Three-phase-to-ground low-voltage fault occurs at PCC1.
- (2)
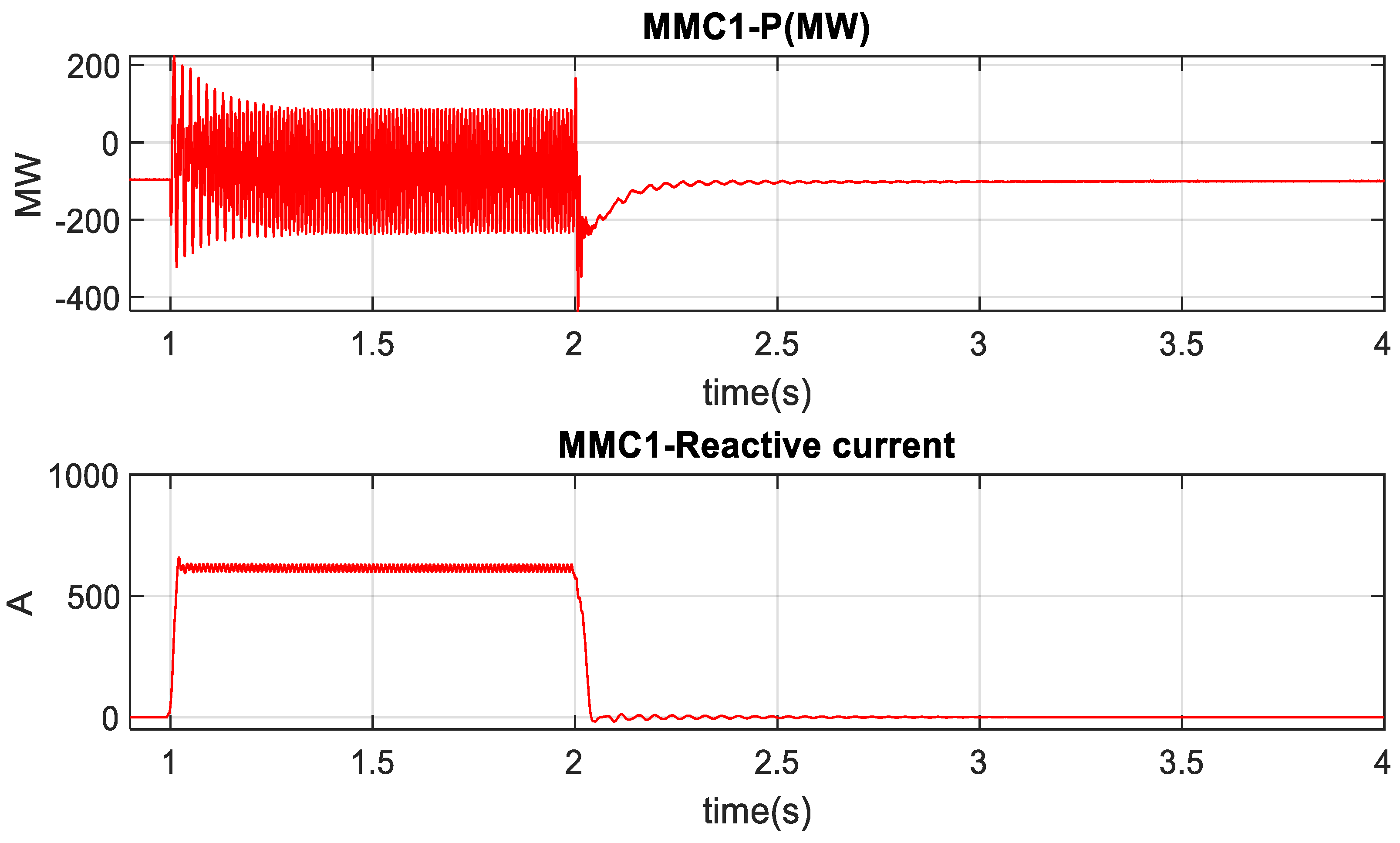
- This low-voltage fault reduces the power delivering capacity of MMC1, which in turn increases HVDC link voltage due to excess energy in the HVDC link.
- (3)
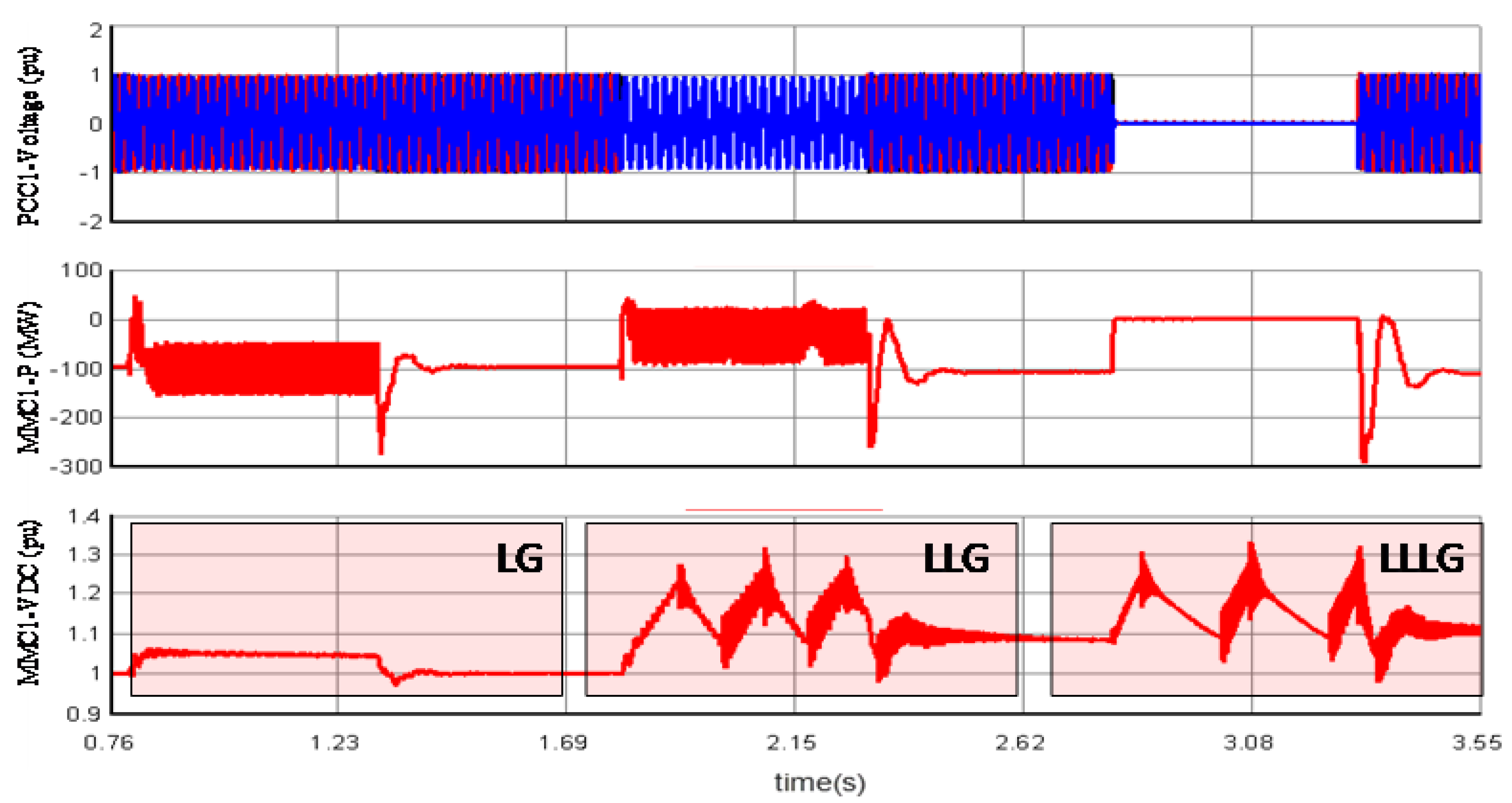
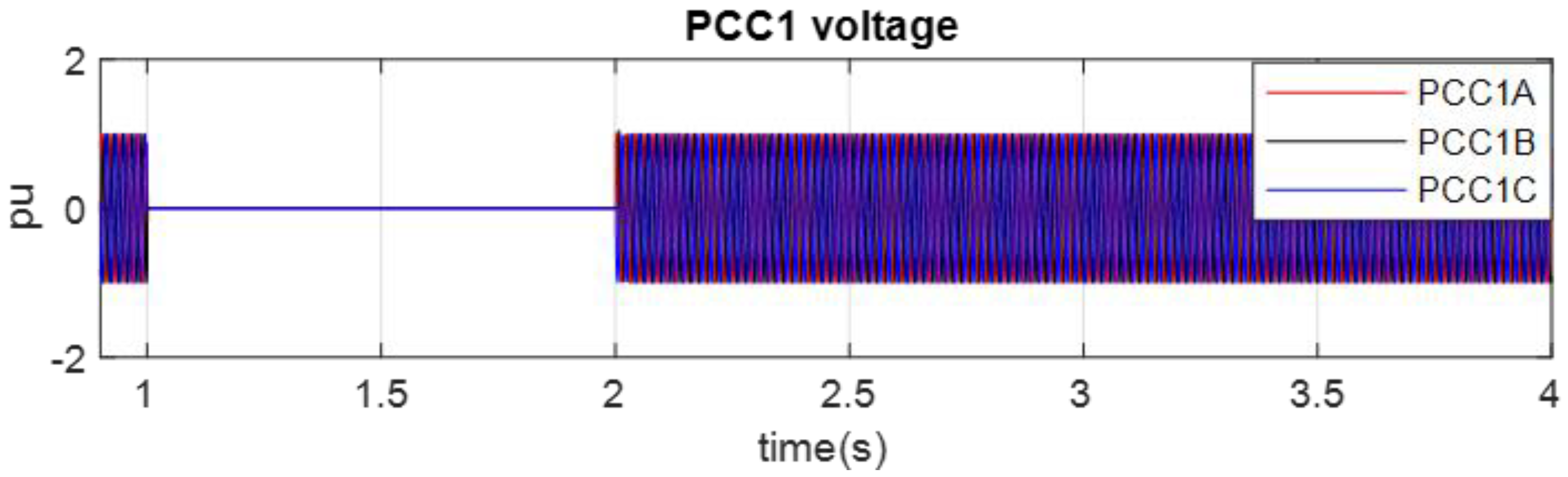
- The reference AC voltage for the MMC2 control loop changes from fixed to variable, and increases with the HVDC-link voltage. Consequently, the AC side voltage of the MMC2 rises. As can be seen from Figure 6a, the reference voltage for MMC2 AC link is changed from 100 kV to if the HVDC link voltage rises more than 210 kV. 200 kV is the nominal voltage for HVDC link (Vdc). During normal operating mode, the reference AC link voltage is 100 kV.
- (4)
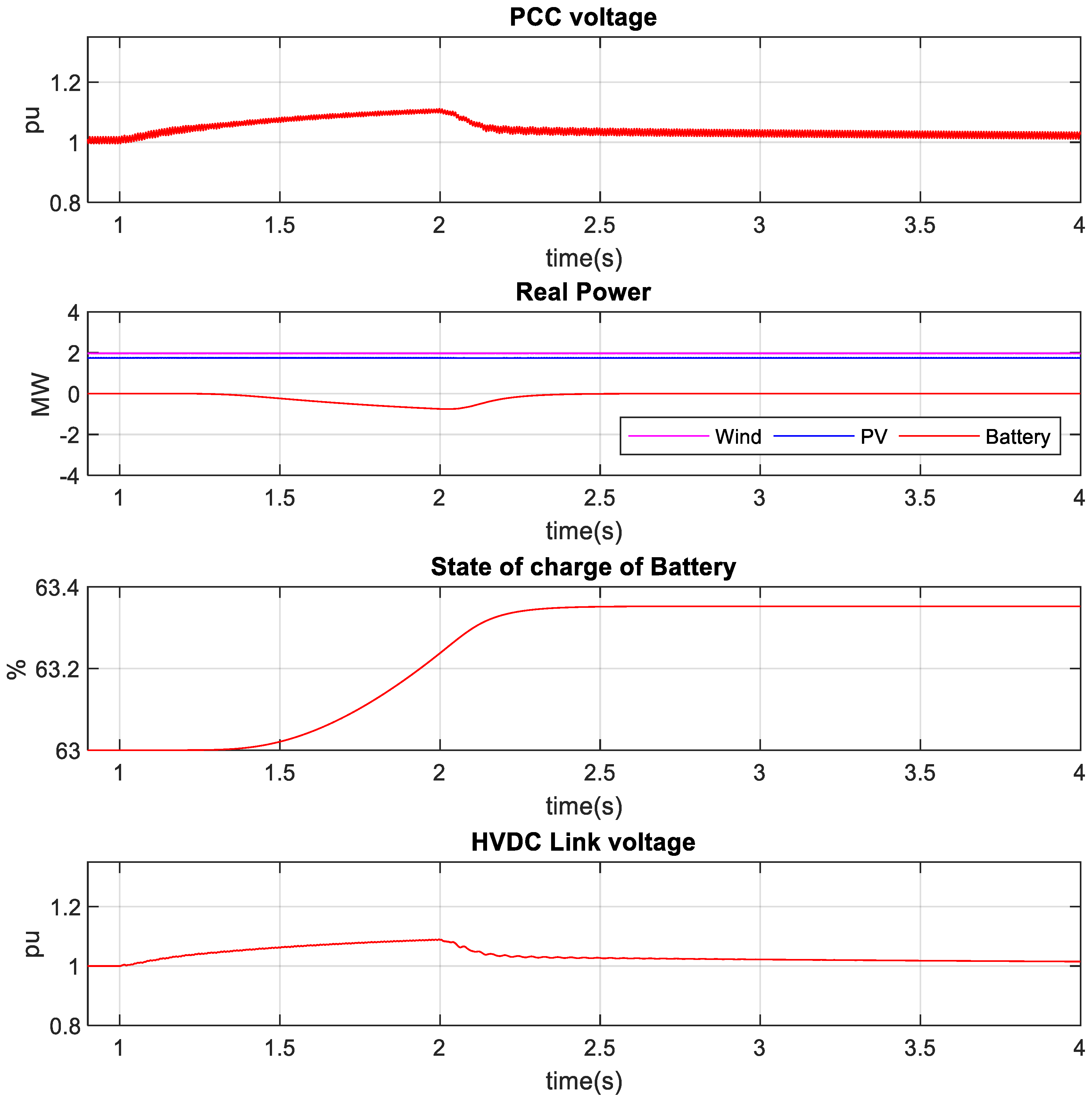
- The rise in the AC link voltage of MMC2 increases the AC voltage of the PCC point or the magnitude of VPCC. It provides the sensing signal for the charging and discharging controller of the BESS. As can be seen from Figure 6b, an increased VPCC (>1.05 pu) provides a negative real current command that means the battery is charged. Therefore, the solar and wind energy is delivered to the battery due to the charging command, instead of going to HVDC-link. Hence, the HVDC-link voltage remains regulated within its limit. The inner current control loop of MMC2 is the same as MMC1.
3.2. Renewable Energy Intermittency Improvement Control Strategy
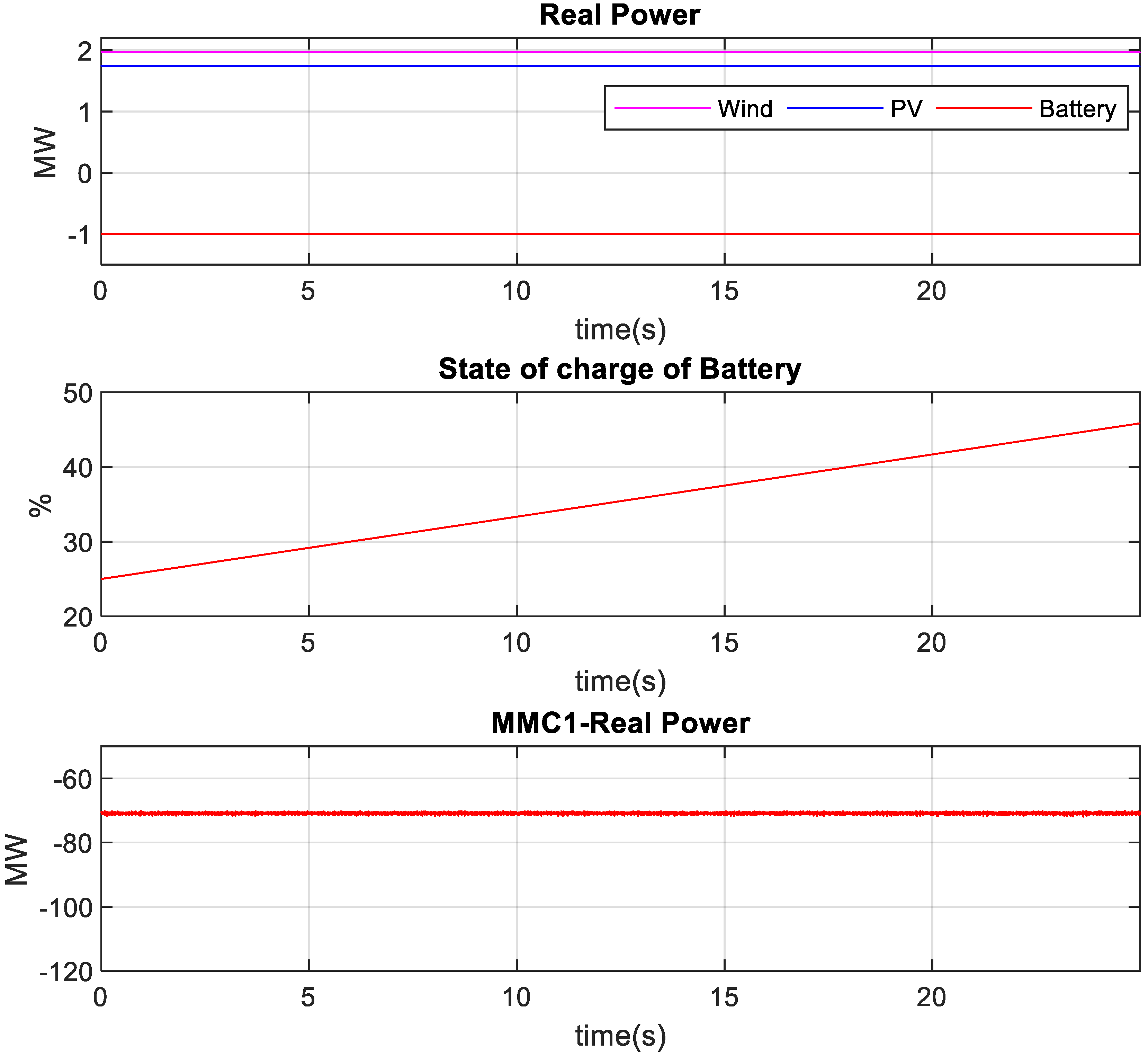
3.3. Charging and Discharging Control during Normal Voltage at PCC
4. Result and Discussion
4.1. HVDC-Link Voltage Control during Low-Voltage Faults at PCC1
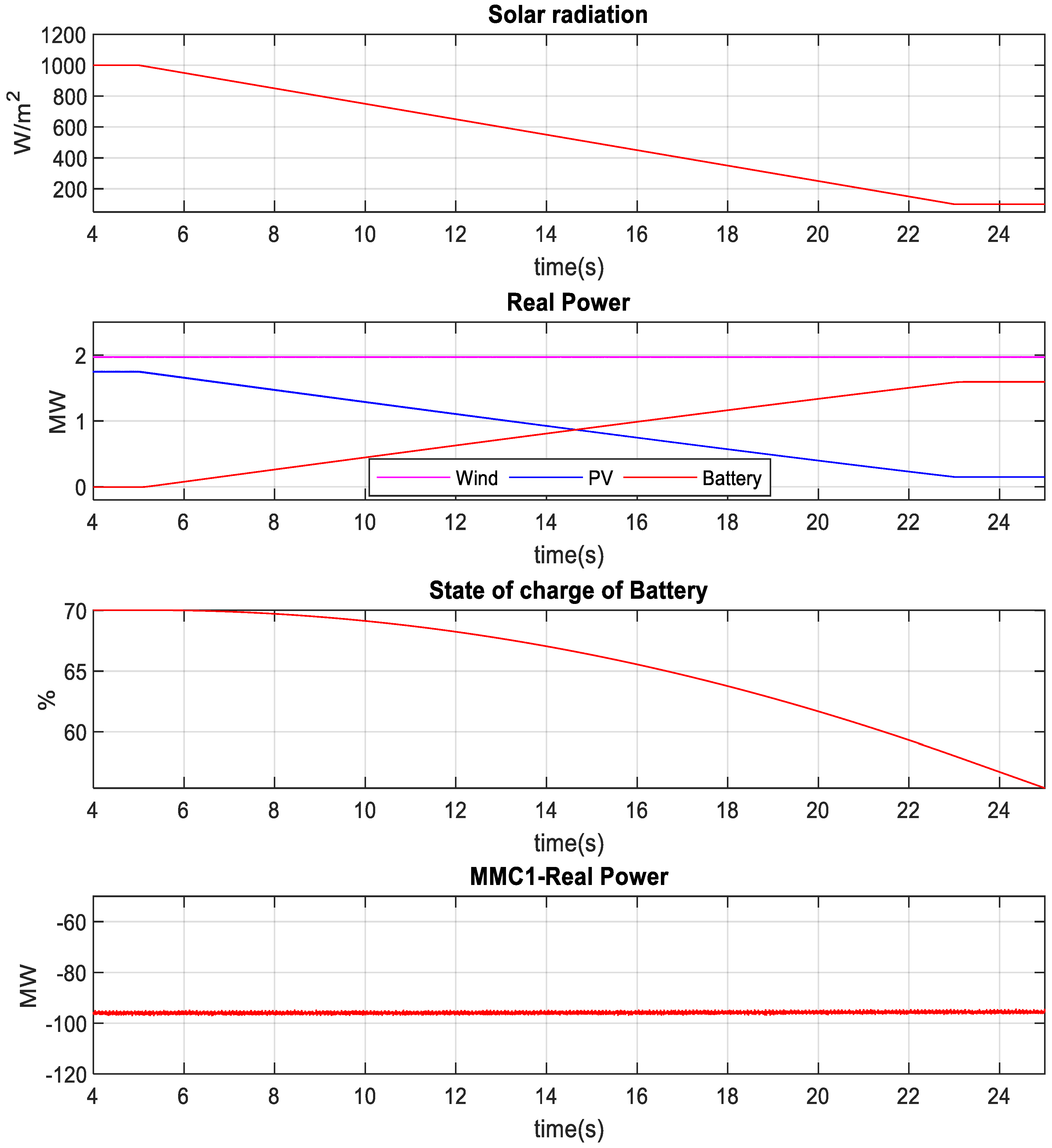
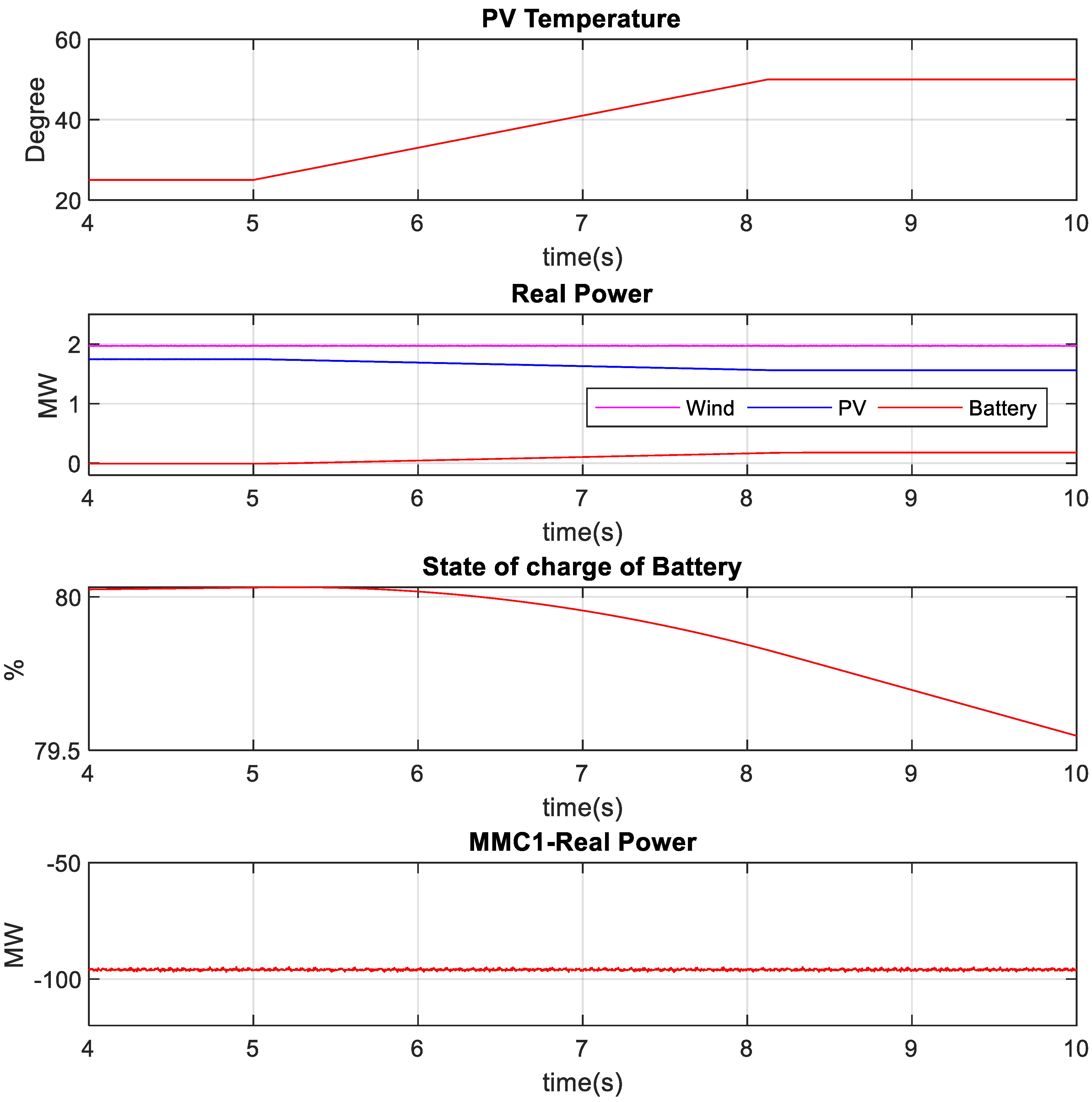
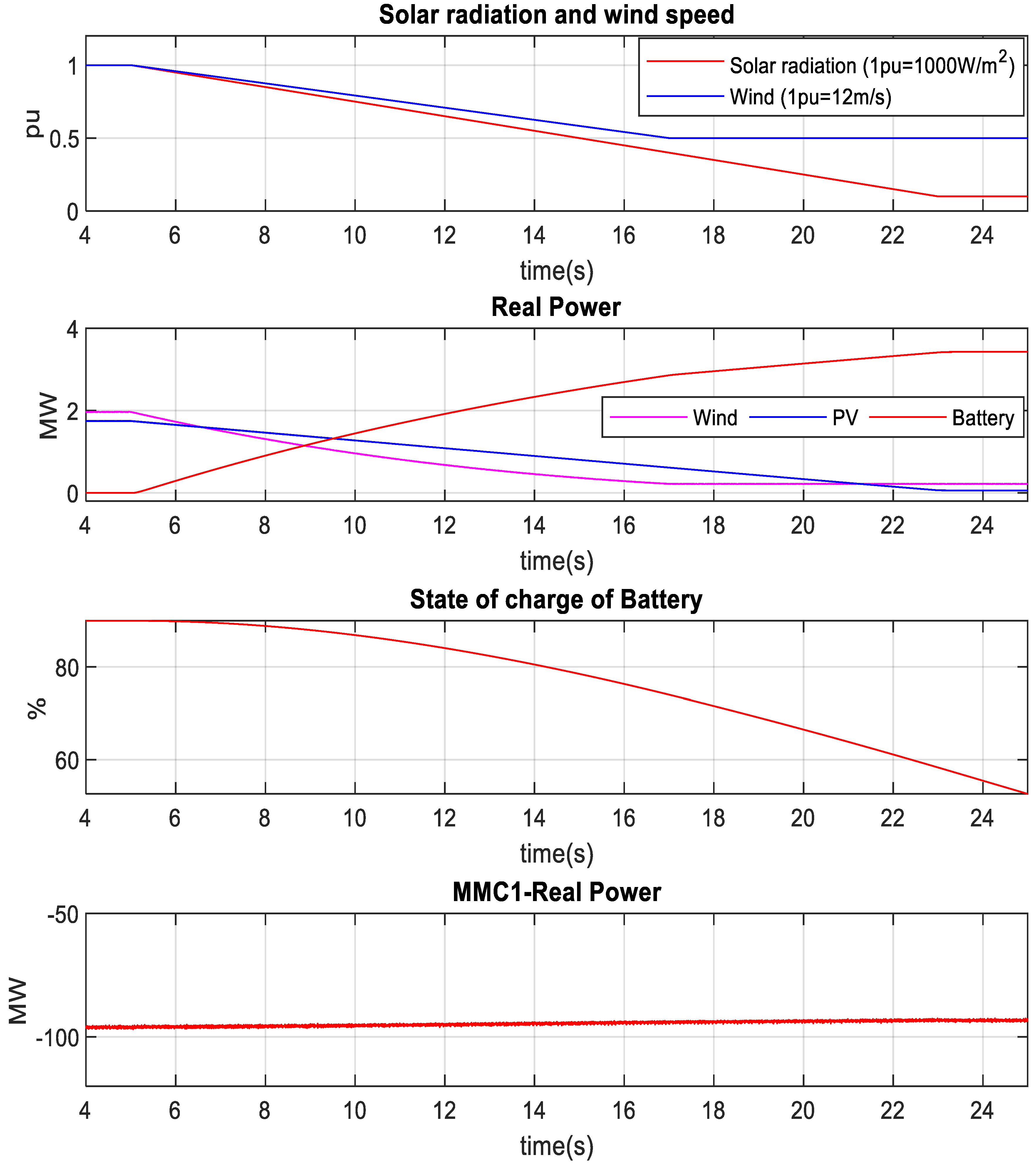
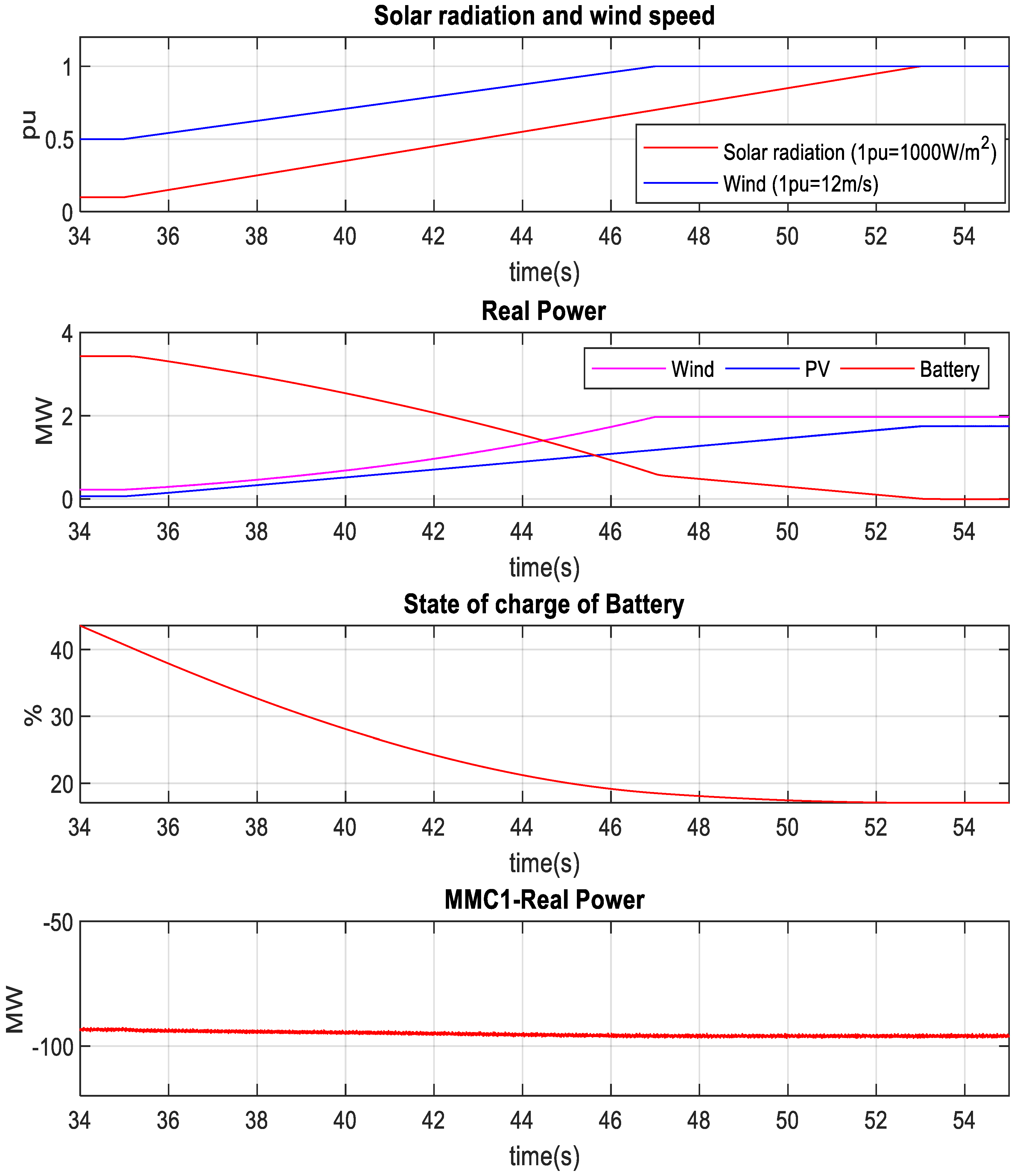
4.2. Power Smoothing for PV System under Solar Irradiance and Temperature Change
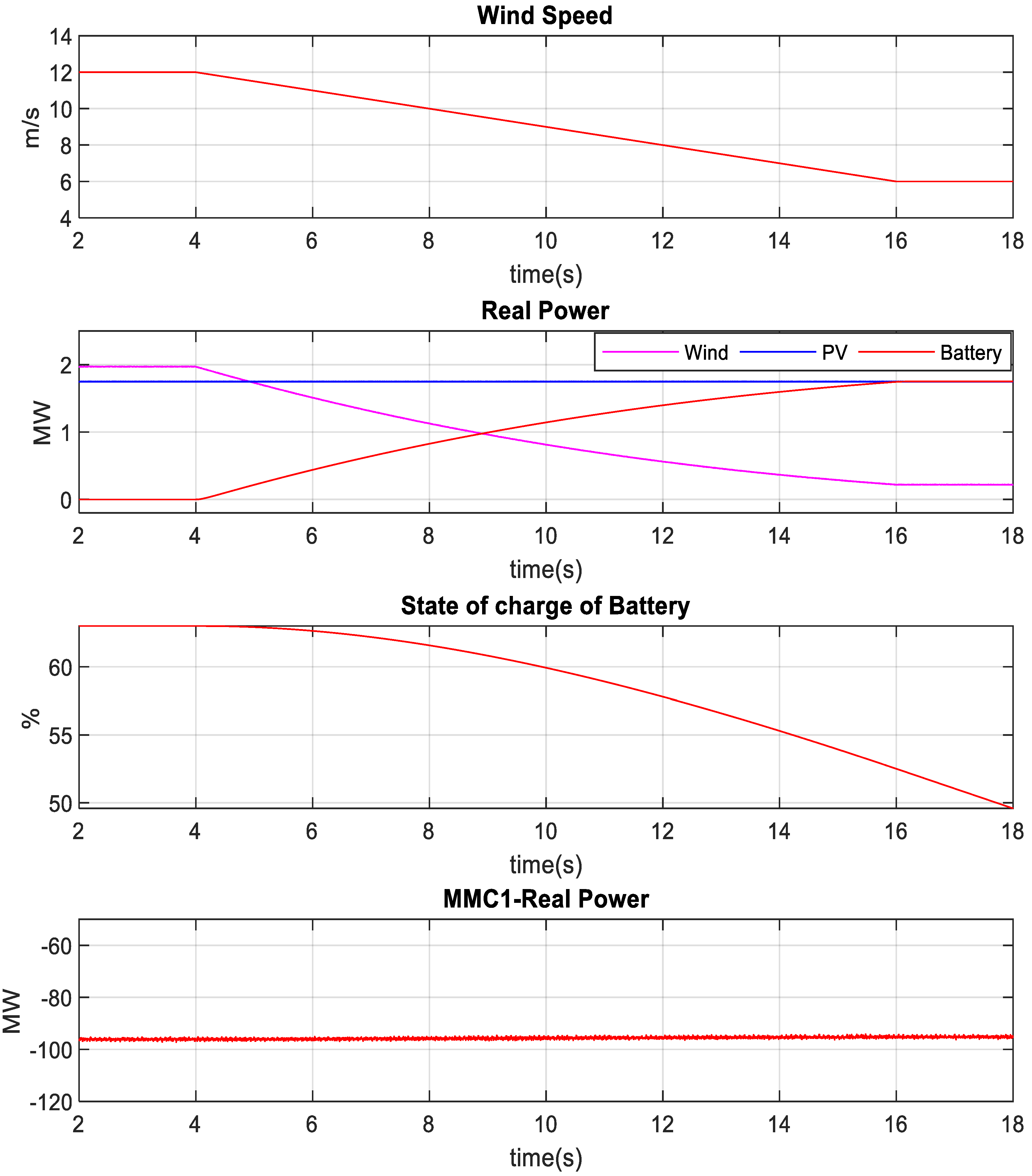
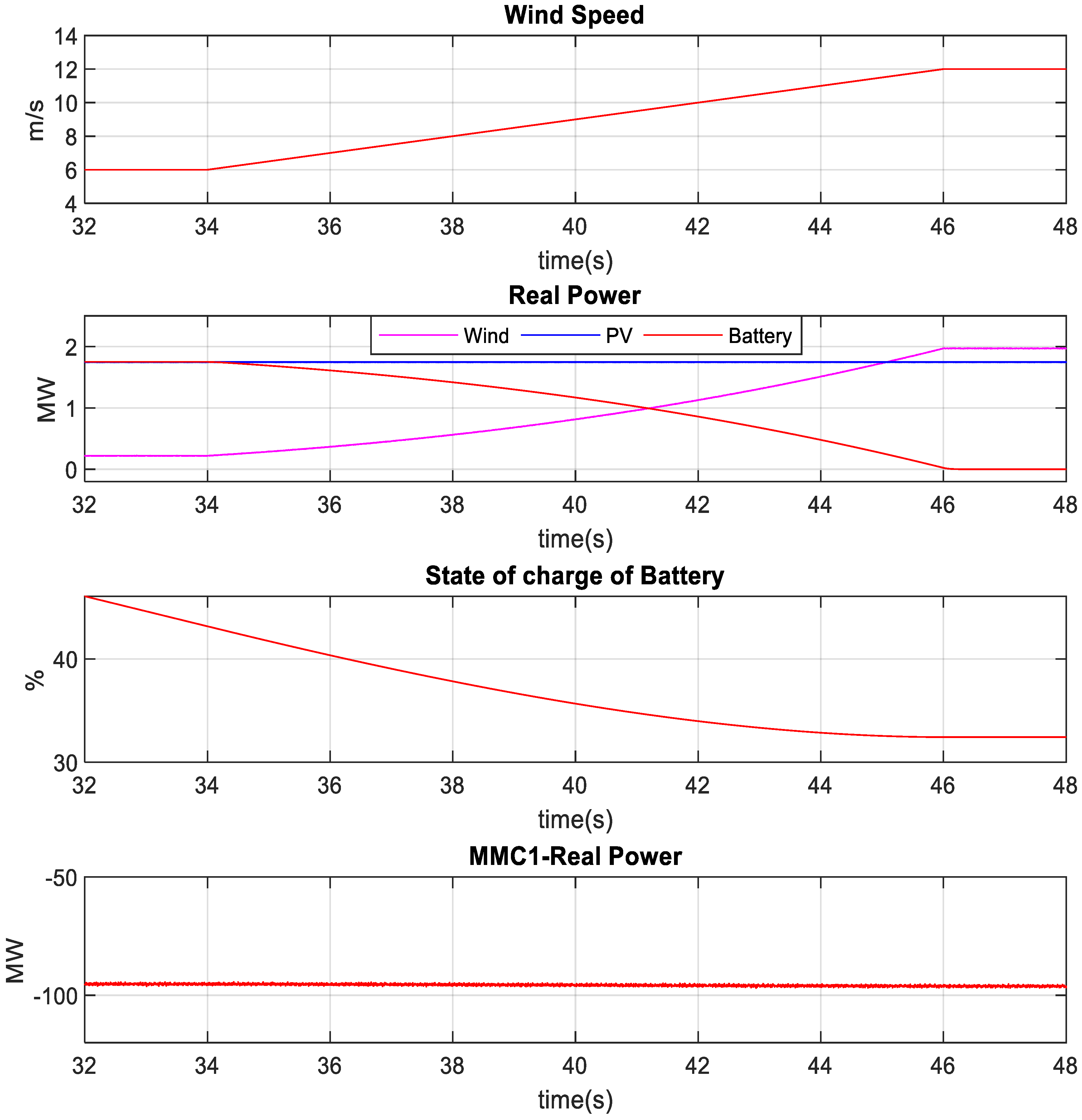
4.3. Battery-Based Power Smoothing under Wind Speed Variation
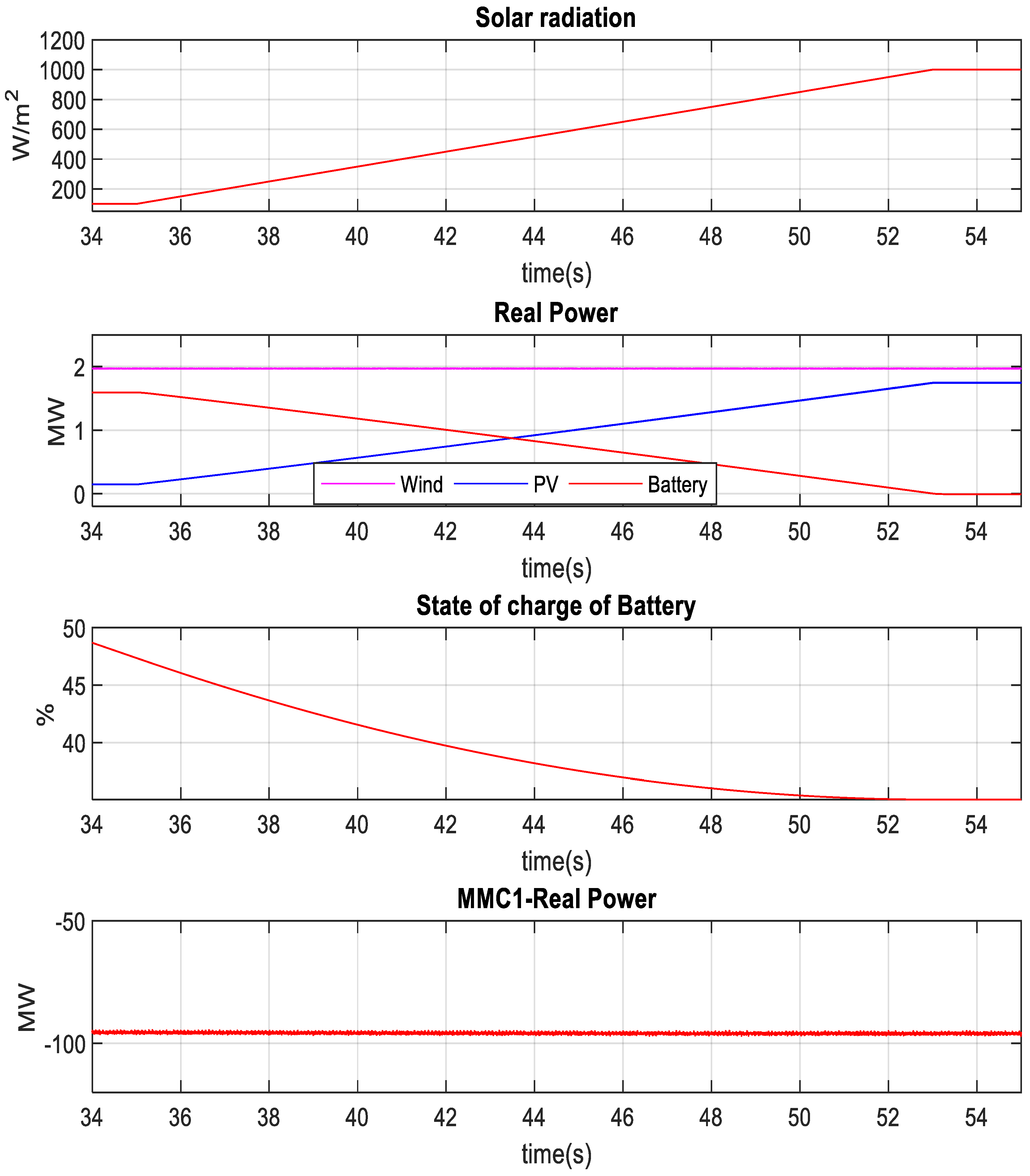
4.4. Power Smoothing under Solar Irradiance and Wind Speed Variation
4.5. Charging of Battery
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Battery Side Converter: | |
| R, L | Reactor resistance and inductance |
| PCC | Point of common coupling |
| PCC angular frequency | |
| PCC d-q axis current | |
| PCC d-q axis voltage | |
| VSC terminal d-q axis voltage | |
| C | DC link capacitance |
| VDC | DC link voltage |
| DC link current | |
| VSC-B | Battery side converter |
| Icom | Combined current of PV, wind and battery |
| M10 | Scaling factor |
| HPF | High pass filter (LF + RF // CF) |
| BESS | Battery energy storage system |
| Battery power | |
| MMC Converter: | |
| R, L | Arm reactor resistance and inductance, |
| PCC1 | Point of common coupling of AC grid 1 |
| Angular frequency at PCC1 | |
| 3-Ø voltage and current | |
| d-q axis voltage of PCC1 | |
| d-q axis current of PCC1 | |
| MMC terminal d-q axis voltage, | |
| VDC | HVDC-link voltage |
| HVDC-link DC current | |
| C | Submodule capacitance |
| DC link pole-to-pole capacitance | |
| N | Number of submodules |
| Negative sequence d-q axis current | |
| Negative sequence d-q axis voltage, | |
| LG | Single-line-to-ground |
| LLG | Double-line-to-ground |
| LLLG | Three-line-to-ground |
| DBR | Dynamic braking resistor |
| MMC | Modular multilevel converter |
| HVDC | High-voltage DC current |
| Others: | |
| PV panel array power | |
| Wind generator power | |
| Fault ride through | |
| Combined power of wind generator and solar array | |
| RER | Renewable energy resources |
| CHIL | Controller hardware in loop |
| RTDS | Real-time digital simulator |
References
- Hossain, I.; Abido, M.A. SCIG Based Wind Energy Integrated Multiterminal MMC-HVDC Transmission Network. Sustainability 2020, 12, 3622. [Google Scholar] [CrossRef]
- Hossain, I.; Abido, M.A. Positive-Negative Sequence Current Controller for LVRT Improvement of Wind Farms Integrated MMC-HVDC Network. IEEE Access 2020, 8, 193314–193339. [Google Scholar] [CrossRef]
- Hossain, I.; Abido, M.A. Active Power Control of PV-Battery Connected MMC-HVDC System for FRT Support. Appl. Sci. 2020, 10, 7186. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, X.; Hu, J. Inertia and Primary Frequency Provisions of PLL-Synchronized VSC HVDC When Attached to Islanded AC System. IEEE Trans. Power Syst. 2017, 33, 4179–4188. [Google Scholar] [CrossRef]
- Sakamuri, J.N.; Rather, Z.H.; Rimez, J.; Altin, M.; Goksu, O.; Cutululis, N.A. Coordinated Voltage Control in Offshore HVDC Connected Cluster of Wind Power Plants. IEEE Trans. Sustain. Energy 2016, 7, 1592–1601. [Google Scholar] [CrossRef]
- Moawwad, A.; El Moursi, M.S.; Xiao, W. Advanced Fault Ride-Through Management Scheme for VSC-HVDC Connecting Offshore Wind Farms. IEEE Trans. Power Syst. 2016, 31, 4923–4934. [Google Scholar] [CrossRef]
- Moawwad, A.; El Moursi, M.S.; Xiao, W. A Novel Transient Control Strategy for VSC-HVDC Connecting Offshore Wind Power Plant. IEEE Trans. Sustain. Energy 2014, 5, 1056–1069. [Google Scholar] [CrossRef]
- Egea-Àlvarez, A.; Aragüés-Peñalba, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Power reduction coordinated scheme for wind power plants connected with VSC-HVDC. Renew. Energy 2017, 107, 1–13. [Google Scholar] [CrossRef]
- Hossain, I.; Shafiullah; Al-Sulaiman, F.A.; Abido, M.A. Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network. Sustainability 2022, 15, 253. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.; Pathan, M.I. PMSG Based Wind Energy Integration into MMC Based HVDC Transmission Network in RTDS. In Proceedings of the 2020 IEEE Electric Power and Energy Conference EPEC, Edmonton, AB, Canada, 9–10 November 2020. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.; Pathan, M.I. MMC based PV energy integrated multiterminal HVDC transmission network. In Proceedings of the 2020 IEEE Electric Power and Energy Conference EPEC, Edmonton, AB, Canada, 9–10 November 2020. [Google Scholar] [CrossRef]
- Nanou, S.; Papathanassiou, S. Evaluation of a communication-based fault ride-through scheme for offshore wind farms connected through high-voltage DC links based on voltage source converter. IET Renew. Power Gener. 2015, 9, 882–891. Available online: https://digital-library.theiet.org/content/journals/10.1049/iet-rpg.2015.0017 (accessed on 20 September 2019). [CrossRef]
- Ndreko, M.; Popov, M.; van der Meijden, M.A. Study on FRT compliance of VSC-HVDC connected offshore wind plants during AC faults including requirements for the negative sequence current control. Int. J. Electr. Power Energy Syst. 2017, 85, 97–116. [Google Scholar] [CrossRef]
- Nanou, S.I.; Patsakis, G.N.; Papathanassiou, S.A. Assessment of communication-independent grid code compatibility solutions for VSC–HVDC connected offshore wind farms. Electr. Power Syst. Res. 2015, 121, 38–51. [Google Scholar] [CrossRef]
- Ndreko, M.; Bucurenciu, A.; Popov, M.; Van Der Meijden, M.A.M.M. On grid code compliance of offshore mtdc grids: Modeling and analysis. In Proceedings of the 2015 IEEE Eindhoven PowerTech, PowerTech 2015, Eindhoven, The Netherlands, 29 June—2 July 2015. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Z.; An, T. Fault ride-through strategy for fully rated converter wind turbines connected to the grid via MMC-HVDC transmission. IET Conf. Publ. 2016, 2016, CP696. [Google Scholar] [CrossRef]
- Liang, J.; Gomis-Bellmunt, O.; Ekanayake, J.; Jenkins, N.; An, W. A multi-terminal HVDC transmission system for offshore wind farms with induction generators. Int. J. Electr. Power Energy Syst. 2012, 43, 54–62. [Google Scholar] [CrossRef]
- Sun, W.; Torres-Olguin, R.E.; Anaya-Lara, O. Investigation on Fault-ride through Methods for VSC-HVDC Connected Offshore Wind Farms. Energy Procedia 2016, 94, 29–36. [Google Scholar] [CrossRef]
- Erlich, I.; Feltes, C.; Shewarega, F. Enhanced Voltage Drop Control by VSC–HVDC Systems for Improving Wind Farm Fault Ridethrough Capability. IEEE Trans. Power Deliv. 2013, 29, 378–385. [Google Scholar] [CrossRef]
- Jing, Y.; Li, R.; Xu, L.; Wang, Y. Enhanced AC voltage and frequency control on offshore MMC station for wind farm. J. Eng. 2017, 2017, 1264–1268. Available online: https://onlinelibrary.wiley.com/doi/full/10.1049/joe.2017.0532 (accessed on 12 October 2019). [CrossRef]
- Karaagac, U.; Mahseredjian, J.; Cai, L.; Saad, H. Offshore wind farm modeling accuracy and efficiency in MMC-based mul-titerminal HVDC connection. IEEE Trans. Power Deliv. 2016, 32, 617–627. [Google Scholar] [CrossRef]
- Nguyen, M.C.; Rudion, K.; Styczynski, Z.A. Improvement of stability assessment of VSCHVDC transmission systems. In Proceedings of the 2010 5th International Conference on Critical Infrastructure CRIS, Washington, DC, USA, 14–17 March 2010. [Google Scholar] [CrossRef]
- Mohammadi, M.; Avendano-Mora, M.; Barnes, M.; Chan, J.Y. A study on Fault Ride-Through of VSC-connected offshore wind farms. In Proceedings of the IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2013. [Google Scholar] [CrossRef]
- Adeuyi, O.D.; Cheah-Mane, M.; Liang, J.; Livermore, L.; Mu, Q. Preventing DC over-voltage in multi-terminal HVDC transmission. CSEE J. Power Energy Syst. 2015, 1, 86–94. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Egea-Alvarez, A.; Junyent-Ferre, A.; Liang, J.; Ekanayake, J.; Jenkins, N. Multiterminal HVDC-VSC for offshore wind power integration. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011. [Google Scholar] [CrossRef]
- Chen, R.; Jia, K.; Bi, T.; Liu, B.; Sun, Y. Coordinated Fault Ride through Strategy for Offshore Wind Integration System. IOP Conf. Series: Earth Environ. Sci. 2018, 170, 042124. [Google Scholar] [CrossRef]
- Arulampalam, A.; Ramtharan, G.; Caliao, N.; Ekanayake, J.; Jenkins, N. Simulated Onshore-Fault Ride through of Offshore Wind Farms Connected through VSC HVDC. Wind. Eng. 2008, 32, 103–114. [Google Scholar] [CrossRef]
- Xu, L.; Yao, L.; Sasse, C. Grid Integration of Large DFIG-Based Wind Farms Using VSC Transmission. IEEE Trans. Power Syst. 2007, 22, 976–984. [Google Scholar] [CrossRef]
- Hu, X.; Liang, J.; Rogers, D.J.; Li, Y. Power Flow and Power Reduction Control Using Variable Frequency of Offshore AC Grids. IEEE Trans. Power Syst. 2013, 28, 3897–3905. [Google Scholar] [CrossRef]
- Silva, B.; Moreira, C.L.; Leite, H.; Lopes, J.A.P. Control Strategies for AC Fault Ride Through in Multiterminal HVDC Grids. IEEE Trans. Power Deliv. 2014, 29, 395–405. [Google Scholar] [CrossRef] [Green Version]
- Göksu, Ö.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjær, P.C. Instability of Wind Turbine Converters During Current Injection to Low Voltage Grid Faults and PLL Frequency Based Stability Solution. IEEE Trans. Power Syst. 2014, 29, 1683–1691. [Google Scholar] [CrossRef]
- Penalba, M.A.; Gomis-Bellmunt, O.; Martins, M. Coordinated Control for an Offshore Wind Power Plant to Provide Fault Ride Through Capability. IEEE Trans. Sustain. Energy 2014, 5, 1253–1261. [Google Scholar] [CrossRef]
- Ma, S.; Geng, H.; Liu, L.; Yang, G.; Pal, B.C. Grid-Synchronization Stability Improvement of Large Scale Wind Farm During Severe Grid Fault. IEEE Trans. Power Syst. 2017, 33, 216–226. [Google Scholar] [CrossRef]
- Li, W.; Zhu, M.; Chao, P.; Liang, X.; Xu, D. Enhanced FRT and Postfault Recovery Control for MMC-HVDC Connected Offshore Wind Farms. IEEE Trans. Power Syst. 2019, 35, 1606–1617. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Shafiullah; Ahmed, S.D.; Al-Sulaiman, F.A. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar] [CrossRef]
- Ali, M.; Hossain, M.; Shafiullah, M. Fuzzy Logic for Energy Management in Hybrid Energy Storage Systems Integrated DC Microgrid. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications ICoPESA, Virtual, 25–27 February 2022; pp. 424–429. [Google Scholar] [CrossRef]
- Nair, S.G.; Senroy, N. Power smoothening using multi terminal DC based DFIG connection and flywheel energy storage system. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, Z.; Zou, X.; Duan, S.; Wei, H. Power conditioning system of Flywheel Energy Storage. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia: Green World with Power Electronics, ICPE 2011-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011; pp. 2763–2768. [Google Scholar] [CrossRef]
- Gadelrab, R.G.; Hamad, M.S.; Abdel-Khalik, A.S.; El Zawawi, A. Wind farms-fed HVDC system power profile enhancement using solid state transformer based flywheel energy storage system. J. Energy Storage 2015, 4, 145–155. [Google Scholar] [CrossRef]
- Daoud, M.I.; Massoud, A.M.; Abdel-Khalik, A.S.; Elserougi, A.; Ahmed, S. A Flywheel Energy Storage System for Fault Ride Through Support of Grid-Connected VSC HVDC-Based Offshore Wind Farms. IEEE Trans. Power Syst. 2015, 31, 1671–1680. [Google Scholar] [CrossRef]
- Ahmed, K.H.; Abdel-Khalik, A.S.; Elserougi, A.; Massoud, A.; Ahmed, S. Fault ride-through capability enhancement based on flywheel energy storage system for wind farms connected via VSC high voltage DC transmission. IET Conf. Publ. 2012, 2012, 610 CP. [Google Scholar] [CrossRef]
- Gowaid, I.A.; Elserougi, A.A.; Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. A series flywheel architecture for power levelling and mitigation of DC voltage transients in multi-terminal HVDC grids. IET Gener. Transm. Distrib. 2014, 8, 1951–1959. [Google Scholar] [CrossRef]
- Daoud, M.I.; Massoud, A.; Ahmed, S.; Abdel-Khalik, A.; Elserougi, A. Ride-through capability enhancement of VSC-HVDC based wind farms using low speed flywheel energy storage system. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition-APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 2706–2712. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Salkuti, S.R.; Jung, C.M. Comparative analysis of storage techniques for a grid with renewable energy sources. Int. J. Eng. Technol. 2018, 7, 970–976. [Google Scholar] [CrossRef]
- Nadeem, F.; Hussain, S.M.S.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Comparative review of energy storage systems, their roles, and impacts on future power systems. IEEE Access 2019, 7, 4555–4585. [Google Scholar] [CrossRef]
- Argyrou, M.C.; Christodoulides, P.; Kalogirou, S.A. Energy storage for electricity generation and related processes: Technologies appraisal and grid scale applications. Renew. Sustain. Energy Rev. 2018, 94, 804–821. [Google Scholar] [CrossRef]
- Swierczynski, M.; Teodorescu, R.; Rasmussen, C.; Rodriguez, P.; Vikelgaard, H. Overview of the energy storage systems for wind power integration enhancement. In Proceedings of the IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 3749–3756. [Google Scholar] [CrossRef]
- Ahmed, M.; Kuriry, S.; Shafiullah, M.; Abido, M.A. DC Microgrid Energy Management with Hybrid Energy Storage Systems. In Proceedings of the 2019 23rd International Conference on Mechatronics Technology (ICMT), Salerno, Italy, 23–26 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ribeiro, P.; Johnson, B.; Crow, M.; Arsoy, A.; Liu, Y. Energy storage systems for advanced power applications. Proc. IEEE 2001, 89, 1744–1756. [Google Scholar] [CrossRef]
- CNESA. Global Energy Storage Market Analysis–2020.Q1 (Summary)—China Energy Storage Alliance. Available online: http://en.cnesa.org/latest-news/2020/5/28/cnesa-global-energy-storage-market-analysis-2020q1-summary (accessed on 10 January 2021).
- Suberu, M.Y.; Mustafa, M.W.; Bashir, N. Energy storage systems for renewable energy power sector integration and mitigation of intermittency. Renew. Sustain. Energy Rev. 2014, 35, 499–514. [Google Scholar] [CrossRef]
- Battery Storage for Renewables: Market Status and Technology Outlook. Available online: https://www.irena.org/publications/2015/Jan/Battery-Storage-for-Renewables-Market-Status-and-Technology-Outlook (accessed on 22 June 2020).
- Hellesnes, M.N.; Sharifabadi, K.; Acevedo, S.A.S.S.; Hellesnes, M.N. Use of Battery Energy Storage for Power Balancing in a Large-Scale HVDC Connected Wind Power Plant. 2017. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2454582 (accessed on 10 January 2021).
- Reite, I.P. Battery Energy Storage System Connected to a Three-Phase 50 Hz-Grid. NTNU. 2017. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2453622 (accessed on 10 January 2021).
- Wang, G.; Konstantinou, G.; Townsend, C.D.; Pou, J.; Vazquez, S.; Demetriades, G.D.; Agelidis, V.G. A Review of Power Electronics for Grid Connection of Utility-Scale Battery Energy Storage Systems. IEEE Trans. Sustain. Energy 2016, 7, 1778–1790. [Google Scholar] [CrossRef]
- Soong, T.; Lehn, P.W. Evaluation of Emerging Modular Multilevel Converters for BESS Applications. IEEE Trans. Power Deliv. 2014, 29, 2086–2094. [Google Scholar] [CrossRef]
- Hagiwara, M.; Akagi, H. Control and Experiment of Pulsewidth-Modulated Modular Multilevel Converters. IEEE Trans. Power Electron. 2009, 24, 1737–1746. [Google Scholar] [CrossRef]
- Xiao, B.; Filho, F.; Tolbert, L.M. Single-phase cascaded H-bridge multilevel inverter with nonactive power compensation for grid-connected photovoltaic generators. In Proceedings of the IEEE Energy Conversion Congress and Exposition: Energy Conversion Innovation for a Clean Energy Future, ECCE, Phoenix, AZ, USA, 17–22 September 2011; pp. 2733–2737. [Google Scholar] [CrossRef]
- Chen, Q.; Li, R.; Cai, X. Analysis and Fault Control of Hybrid Modular Multilevel Converter with Integrated Battery Energy Storage System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 64–78. [Google Scholar] [CrossRef]
- Lachichi, A. Modular multilevel converters with integrated batteries energy storage. In Proceedings of the 3rd International Conference on Renewable Energy Research and Applications, ICRERA 2014, MilwaNuee, WI, USA, 19–22 October 2014; pp. 828–832. [Google Scholar] [CrossRef]
- Trintis, I.; Munk-Nielsen, S.; Teodorescu, R. A new modular multilevel converter with integrated energy storage. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Melbourne, Australia, 7–10 November 2011; pp. 1075–1080. [Google Scholar] [CrossRef]
- Soong, T. Modular Multilevel Converters with Integrated Energy Storage. 2015. Available online: https://tspace.library.utoronto.ca/handle/1807/71617 (accessed on 10 January 2021).
- Ma, Y.; Lin, H.; Wang, Z.; Ze, Z. Modified State-of-Charge Balancing Control of Modular Multilevel Converter with Integrated Battery Energy Storage System. Energies 2018, 12, 96. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Rincon-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Cicio, D. EssProTM-Battery Energy Storage. 2017, pp. 1–25. Available online: http://new.abb.com/docs/librariesprovider78/eventos/jjtts-2017/presentaciones-peru/(dario-cicio)-bess---battery-energy-storage-system.pdf?sfvrsn=2 (accessed on 25 December 2022).
- Tey, K.S.; Mekhilef, S. Modified incremental conductance MPPT algorithm to mitigate inaccurate responses under fast-changing solar irradiation level. Sol. Energy 2014, 101, 333–342. [Google Scholar] [CrossRef]
- Motahhir, S.; El Hammoumi, A.; El Ghzizal, A. The most used MPPT algorithms: Review and the suitable low-cost embedded board for each algorithm. J. Clean. Prod. 2019, 246, 118983. [Google Scholar] [CrossRef]
- Yazdani, A.; Dash, P.P. A Control Methodology and Characterization of Dynamics for a Photovoltaic (PV) System Interfaced with a Distribution Network. IEEE Trans. Power Deliv. 2009, 24, 1538–1551. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; IEEE Press/John Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control and Application of Modular Multilevel Converters for HVDC Transmission Systems; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Martinez-Rodrigo, F.; Ramirez, D.; Rey-Boue, A.B.; de Pablo, S.; Lucas, L.C.H.-D. Modular Multilevel Converters: Control and Applications. Energies 2017, 10, 1709. [Google Scholar] [CrossRef]
- Hossain, I.; Shafiullah; Abido, M. VSC Controllers for Multiterminal HVDC Transmission System: A Comparative Study. Arab. J. Sci. Eng. 2020, 45, 6411–6422. [Google Scholar] [CrossRef]








| Parameter | Value | |
|---|---|---|
| Discharge power | 1 MW | 0.5 MW |
| Maximum DC voltage | 1.2 kV | 1.2 kV |
| Battery current | 833.3 A | 416.7 A |
| Discharge time | 0.25 h | 0.25 h |
| Energy capacity | 0.25 MWh | 0.125 MWh |
| PV Module Parameters | Wind Turbine Parameters | ||
|---|---|---|---|
| Quantity | Value | Quantity | Value |
| Cells per module | 36 | Nominal wind speed | 12 m/s |
| Short circuit current | 3.35 A | Nominal generator speed, DFIG | 1.2 pu |
| Open circuit voltage | 21.7 V | Nominal turbine power | 2 MW |
| Current at MPP | 3.05 A | DFIG and controller parameters | |
| Voltage at MPP | 17.4 V | Quantity | Value |
| Temperature coefficient of Isc | 0.065%/degree | Stator voltage (L-L) | 690 V |
| Temperature coefficient of Voc | −0.56%/degree | Nominal frequency, f | 50 Hz |
| PV array parameter | Nominal power | 2.2 MVA | |
| Series connected modules per string | 115 | Stator resistance, | 1 mΩ |
| Parallel strings | 285 | Rotor resistance, | 1.3 mΩ |
| Grid side VSC parameters for battery | Inductance of stator, | 2.55 mH | |
| Quantity | Value | Inductance of rotor, | 2.56 mH |
| Nominal DC-link voltage | 2 kV | Magnetizing inductance, | 2.44 mH |
| Rated power | 2.2 MVA | High pass filter (HPF) parameters | |
| Resistance, R | 0.004 pu | Filter inductance, LF | 4.3 µH |
| Inductance, L | 0.15 pu | Filter capacitance, CF | 1.47 mF |
| PI3 | Filter resistance, RF | 0.054 Ω | |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rated power | 200 MW | C | 16 mF |
| Rated HVDC-link voltage | 200 kV | Cd | 100 µF |
| Rated AC voltage (L-L) | 100 kV | SM/arm | 200 |
| Nominal frequency | 50 Hz | DC line resistance per km | 1.39 mΩ |
| Reactor resistance, R | 0.002 pu | DC line inductance per km | 0.159 mH |
| Reactor inductance, L | 0.2 pu | DC line capacitance per km | 0.231 µF |
| Modulation | Nearest level | M10 | 26 |
| PI4 | Parameters of battery controller | ||
| PI7 | 0.6+6/s pu | Battery discharge power capacity | 4 MW |
| PI10 | 0.8+100/s pu | Duration | 15 min |
| PI8 | 0.6+6/s pu | PI51 | pu |
| AC grids’ short circuit ratio | 10 | PI52 | (3+10/s) pu |
| Number of cells in series in a stack | 325 | ||
| Number of stacks in parallel | 834 | ||
| Capacity of a single cell | 1.00 AH | ||
| Nominal cell voltage | 3.7 V | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.I.; Shafiullah, M.; Abido, M.A. Battery Power Control Strategy for Intermittent Renewable Energy Integrated Modular Multilevel Converter-Based High-Voltage Direct Current Network. Sustainability 2023, 15, 2626. https://doi.org/10.3390/su15032626
Hossain MI, Shafiullah M, Abido MA. Battery Power Control Strategy for Intermittent Renewable Energy Integrated Modular Multilevel Converter-Based High-Voltage Direct Current Network. Sustainability. 2023; 15(3):2626. https://doi.org/10.3390/su15032626
Chicago/Turabian StyleHossain, Md Ismail, Md Shafiullah, and Mohammad A. Abido. 2023. "Battery Power Control Strategy for Intermittent Renewable Energy Integrated Modular Multilevel Converter-Based High-Voltage Direct Current Network" Sustainability 15, no. 3: 2626. https://doi.org/10.3390/su15032626
APA StyleHossain, M. I., Shafiullah, M., & Abido, M. A. (2023). Battery Power Control Strategy for Intermittent Renewable Energy Integrated Modular Multilevel Converter-Based High-Voltage Direct Current Network. Sustainability, 15(3), 2626. https://doi.org/10.3390/su15032626












