The Nexus between Higher Education and Unemployment—Evidence from Romania
Abstract
:1. Introduction
2. Data and Variables
3. Methodological Approach
- The mean is constant and independent of time, ;
- The variance is constant over time, , ;
- The covariance is a function only of the time lag between variables.
3.1. Results of the Unit Root Tests
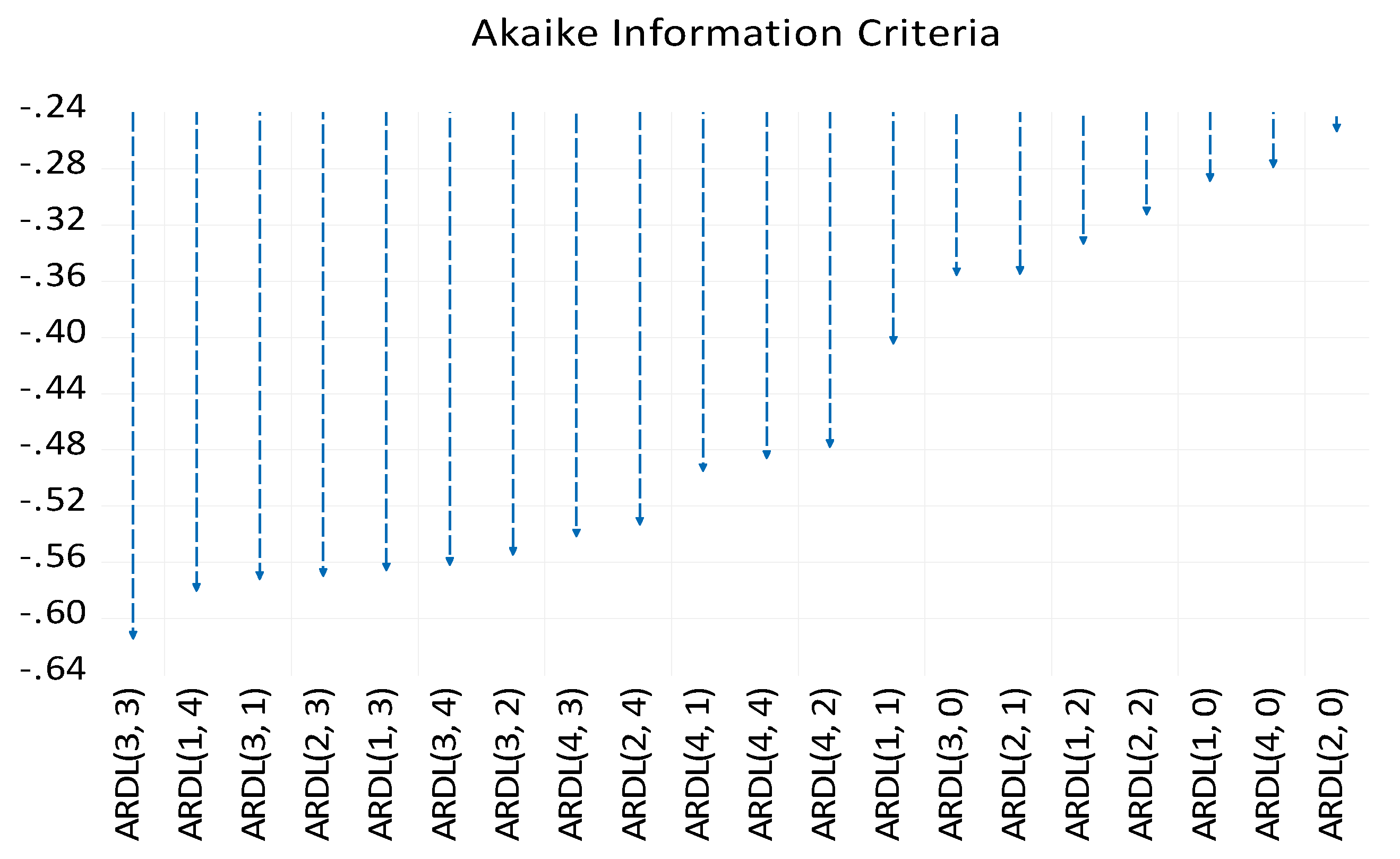
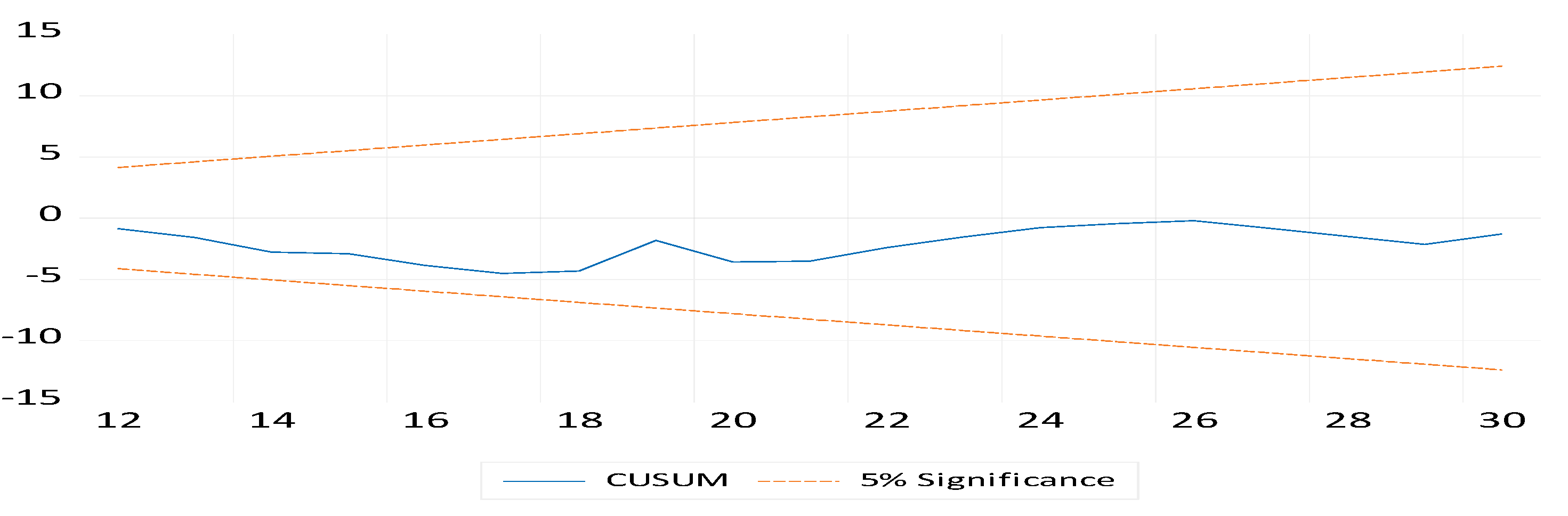
3.2. Results of the ARDL Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Denison, E. Why Growth Rates Differ? Postwar Experience in Nine Western Countries; The Brookings Institution: Washington, DC, USA, 1967; 494p. [Google Scholar]
- Mincer, J. Education and Unemployment. NBER Work. Pap. 1981, 3838, 1–34. [Google Scholar]
- Lucas, R.E. On the Mechanics of Economic Development. J. Monet. Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Barro, R.J. Economic Growth in a Cross-Section of Countries. Q. J. Econ. 1991, 106, 407–443. [Google Scholar] [CrossRef] [Green Version]
- Dickens, W.T.; Sawhill, I.; Tebbs, J. The Effects of Investing in Early Education on Economic Growth. Policy Brief, 153, The Brookings Institutions. 2006. Available online: https://www.brookings.edu/wp-content/uploads/2016/07/200604dickenssawhill.pdf (accessed on 21 November 2022).
- Núñez, I.; Livanos, I. Higher Education and Unemployment in Europe: An Analysis of the Academic Subject and National Effects. High. Educ. 2010, 59, 475–487. [Google Scholar] [CrossRef] [Green Version]
- Maneejuk, P.; Yamaka, W. The Impact of Higher Education on Economic Growth in ASEAN-5 Countries. Susteinability 2021, 13, 520. [Google Scholar] [CrossRef]
- Dănăcică, D.E. Employment and Unemployment of Highly Educated Labor Force in Romania; Academica Brâncuși Publishing House: Târgu-Jiu, Romania, 2022; pp. 25–75. [Google Scholar]
- Stevens, P.; Weale, M. Education and Economic Growth. NIESR Working Paper. 2003. Available online: http://cee.lse.ac.uk/conference_papers/28_11_2003/martin_weale.pdf (accessed on 15 November 2022).
- Lazic, Z.; Ðordevic, A.; Gazizulina, A. Improvement of Quality of Higher Education Institutions as a Basis for Improvement of Quality of Life. Sustainability 2021, 13, 4149. [Google Scholar] [CrossRef]
- Ram, R. Educational Expansion and Schooling Inequality: International Evidence and Some Implications. Rev. Econ. Stat. 1990, 72, 266–274. [Google Scholar] [CrossRef]
- McKenna, C.J. Education and the Distribution of Unemployment. Eur. J. Polit. Econ. 1996, 12, 113–132. [Google Scholar] [CrossRef]
- Domadenik, P.; Pastore, F. The Impact of Education and Training Systems on the Labour Market Participation of Young People in CEE Economies. A Comparison of Poland and Slovenia. GDN Research Report. 2004. Available online: https://www.cerge-ei.cz/pdf/gdn/rrc/RRCIII_50_paper_01.pdf (accessed on 21 November 2022).
- Niepel, V. The Importance of Cognitive and Social Skills for the Duration of Unemployment; ZEW Discussion Papers No. 10-104; Zentrum für Europäische Wirtschaftsforschung (ZEW): Mannheim, Germany, 2010. [Google Scholar]
- Podrecca, E.; Carmeci, G. Does Education Cause Economic Growth? DiSES Working Papers 96B; University of Trieste: Trieste, Italy, 2002. [Google Scholar]
- Gregorio, J.D. Economic Growth in Chile: Evidence, Sources and Prospects; Working Papers of Central Bank of Chile 298; Central Bank of Chile: Santiago, Chile, 2004. [Google Scholar]
- Erdem, E.; Tugcu, C.T. Higher Education and Unemployment: A Cointegration and Causality Analysis of the Case of Turkey. Eur. J. Educ. 2012, 47, 299–309. [Google Scholar] [CrossRef]
- Pillay, P. Higher Education and Economic Development. Literature Review; Centre for Higher Education Transformation: Cape Town, South Africa, 2011; pp. 1–7. Available online: https://www.borbolycsaba.ro/wp-content/uploads/2013/09/Higher-Education-and-Economic-Development-Literature-Review.pdf (accessed on 2 February 2023).
- Wolf, A. Does Education Matter? Myths about Education and Economic Growth; Penguin Publishing Group: London, UK, 2002; p. 3. [Google Scholar]
- UNESCO. Available online: https://www.unesco.org/en/higher-education (accessed on 2 February 2023).
- Bai, L. Graduate Unemployment: Dilemmas and Challenges in China’s Move to Mass Higher Education. China Q. 2006, 185, 128–144. [Google Scholar] [CrossRef]
- Li, S.; Whalley, J.; Xing, C. China’s Higher Education Expansion and Unemployment of College Graduates. China Econ. Rev. 2014, 30, 567–582. [Google Scholar] [CrossRef]
- Lubyova, M.; van Ours, J. Unemployment Dynamics and the Restructuring of the Slovak Unemployment Benefit System. Eur. Econ. Rev. 1997, 41, 925–934. [Google Scholar] [CrossRef]
- D’Agostino, A.; Mealli, F. Modeling Short Unemployment in Europe; ISER Working Paper; Institute for Social & Economic Research: Essex, UK, 2000. [Google Scholar]
- Grogan, L.; van den Berg, J. Determinants of Unemployment in Russia. J. Popul. Econ. 2001, 14, 549–568. [Google Scholar] [CrossRef] [Green Version]
- Farber, H.S. Job Loss in the United States, 1981 to 2001. In Accounting for Worker Well-Being, Research in Labor Economics; Polachek, S.W., Ed.; Emerald Group Publishing Limited: Bingley, UK, 2004; pp. 69–117. [Google Scholar]
- Ollikainen, V. Gender Differences in Unemployment in Finland. Doctoral Thesis, University of Jyvaskyla, Jyväskylän yliopisto, Finland, 2006. Chapter 4. pp. 82–110. Available online: https://jyx.jyu.fi/bitstream/handle/123456789/13191/9513925609.pdf (accessed on 24 November 2022).
- Kavkler, A.; Danacica, D.E.; Babucea, A.G.; Bicanic, I.; Bohm, B.; Tevdovski, D.; Tosevska, K.; Borsic, D. Cox Regression Models for Unemployment Duration in Romania, Austria, Slovenia, Croatia, and Macedonia. Rom. J. Econ. 2009, 6, 81–104. [Google Scholar]
- Dănăcică, D.E. The Impact of Factors Influencing Unemployment Duration and Exit Destinations of Higher Educated People in Romania and Hungary. Stud. UBB Oeconomica 2012, 57, 3–26. [Google Scholar]
- Dănăcică, D.E. The Effect of Factors Influencing Unemployment Duration and (Re)employment Probability (Cercetări Privind Impactul Factorilor ce Influenţează Durata Şomajului şi Probabilitatea (Re)angajării în România); Expert Publishing House: Bucharest, Romania, 2013; pp. 44–84. [Google Scholar]
- Foley, M.C. Determinants of Unemployment Duration in Russia; Center Discussion Paper No. 770; Yale University: New Haven, CT, USA, 1997; Available online: https://core.ac.uk/download/pdf/7056835.pdf (accessed on 23 November 2022).
- Kettunen, J. Education and Unemployment Duration. Econ. Educ. Rev. 1997, 2, 163–170. [Google Scholar] [CrossRef]
- Wolbers, M.H.J. The Effect of Education on Mobility between Employment and Unemployment in Netherlands. Eur. Sociol. Rev. 2000, 16, 185–200. [Google Scholar] [CrossRef]
- Woodley, A.; Brennan, J. Higher Education and Graduate Employment in the United Kingdom. Eur. J. Educ. 2000, 35, 239–249. [Google Scholar] [CrossRef]
- Schomburg, H. Higher Education and Graduate Employment in Germany. Eur. J. Educ. 2000, 35, 189–200. [Google Scholar] [CrossRef]
- Plümper, T.; Schneider, C.J. Too Much to Die, too Little to Live: Unemployment, Higher Education Policies and University Budgets in Germany. J. Eur. Public Policy 2007, 14, 631–653. [Google Scholar] [CrossRef]
- Qazi, W.; Ali Raza, S.; Sharif, A. Higher Education Development and Unemployment in Pakistan: Evidence from Structural Break Testing. Glob. Bus. Rev. 2017, 18, 1089–1110. [Google Scholar] [CrossRef]
- Florea, S.; Oprean, C. Towards an Integrated Project: Higher Education and Graduate Employment in Romania. Manag. Sustain. Dev. 2010, 2, 78–85. [Google Scholar]
- Naghi, D.I. Young Graduates Are Looking for Jobs! Between Education and the Labor Market. Eur. J. Soc. Sci. 2014, 1, 86–90. [Google Scholar] [CrossRef] [Green Version]
- Mirică, A. Higher Education—A Solution to Unemployment? Case Study: Romania. Rev. Rom. Stat. 2014, 3, 63–75. [Google Scholar]
- Mroz, T.A.; Savage, T.H. The Long-Term Effects of Youth Unemployment. J. Hum. Resour. 2006, 41, 259–293. [Google Scholar] [CrossRef] [Green Version]
- Bell, D.N.F.; Blanchflower, D.G. Young People and the Great Recession. IZA DP No. 5674. 2011. Available online: https://www.econstor.eu/bitstream/10419/52080/1/666568758.pdf. (accessed on 19 November 2022).
- Bartlett, W.; Uvalić, M.; Durazzi, N.; Monastiriotis, V.; Sene, T. From University to Employment: Higher Education Provision and Labour Market Needs in the Western Balkans; European Comission: Brussels, Belgium, 2006; Available online: http://www.lse.ac.uk/business-and-consultancy/consulting/assets/documents/From-University-to-Employment.pdf (accessed on 18 November 2022).
- Gagea, M. Identificarea transformărilor necesare staționarizării unei serii de timp. Ann. Alexandru Ioan Cuza Univ. Iași 2005, 50, 432–438. [Google Scholar]
- Gujarati, D.N.; Porter, D.C. Basics Econometrics, 5th ed.; McGraw-Hill Companies, Inc.: New York, NY, USA, 2009; pp. 737–773. [Google Scholar]
- Granger, C.W.J.; Newbold, P. Spurious Regressions in Econometrics. J. Econom. 1974, 2, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.S. An Investigation of Cointegration and Causality Between Fertility and Female Labour Force Participation. Appl. Econ. Lett. 1996, 3, 29–32. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y. An autoregressive distributed lag modelling approach to cointegration analysis. In Econometrics and Economic Theory in the 20th Century: The Ragnar Frisch Centennial Symposium 1998; Strom, S., Ed.; Cambridge University Press: Cambridge, UK, 1999; Chapter 11, Part V; pp. 371–413. [Google Scholar]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds Testing Approaches to the Analysis of Level Relationships. J. Appl. Econ. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Shrestha, M.B.; Bhatta, G.R. Selecting appropriate methodological framework for time series data analysis. J. Financ. Data Sci. 2018, 4, 71–89. [Google Scholar] [CrossRef]
- Bădulescu, A. Unemployment in Romania. A Retrospective Study. Theor. Appl. Econ. 2006, 2, 71–76. [Google Scholar]
- Zaman, G. Dezvoltarea Durabilă, Imperativ Pentru Prezentul şi Viitorul României. In Dezvoltarea Durabilă in Secolul XXI, Revista 22. 2006. Available online: https://revista22.ro/supliment/este-posibila-o-dezvoltare-durabila-in-romania (accessed on 2 February 2023).




| Variables | Order of Integration | Intercept | Trend and Intercept | ||||
|---|---|---|---|---|---|---|---|
| ADF | 5% Crit. Val. | Prob. | ADF | 5% Crit. Val. | Prob. | ||
| lnHE1 | 0 | −2.281579 | −2.971853 | 0.1845 | −1.645007 | −3.580622 | 0.7485 |
| 1 | −3.834070 * | −2.971853 | 0.0071 | −4.238627 * | −3.580622 | 0.0121 | |
| lnU1 | 0 | −0.909610 | −2.976263 | 0.7695 | −3.409562 | −3.580622 | 0.0703 |
| 1 | −4.964692 * | −2.976263 | 0.0004 | −4.848265 * | −3.587527 | 0.0031 | |
| Variables | Order of Integration | Intercept | Trend and Intercept | ||||
|---|---|---|---|---|---|---|---|
| ADF | 5% Crit. Val. | Prob. | ADF | 5% Crit. Val. | Prob. | ||
| lnHE2 | 0 | −1.929596 | −2.998064 | 0.3138 | −1.063119 | −3.612199 | 0.9147 |
| 1 | −3.384180 * | −2.998064 | 0.0224 | −3.552445 | −3.622033 | 0.0571 | |
| lnU2 | 0 | −1.507158 | −2.991878 | 0.5129 | −2.697055 | −3.632896 | 0.2468 |
| 1 | −5.222480 * | −2.998064 | 0.0003 | −5.446441* | −3.622033 | 0.0011 | |
| Dependent Variable: LNU1 | ||||
|---|---|---|---|---|
| Method: ARDL | ||||
| Included observations: 27 after adjustments | ||||
| Maximum dependent lags: 4 (Automatic selection) | ||||
| Model selection method: Akaike info criterion (AIC) | ||||
| Dynamic regressors (4 lags, automatic): LNHE1 | ||||
| Fixed regressors: C | ||||
| Number of models evaluated: 20 | ||||
| Selected Model: ARDL (3, 3) | ||||
| Note: final equation sample is larger than selection sample | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. * |
| LNU1(−1) | 1.172147 | 0.196250 | 5.972725 | 0.0000 |
| LNU1(−2) | −0.372685 | 0.274276 | −1.358795 | 0.1901 |
| LNU1(−3) | 0.045849 | 0.143830 | 0.318773 | 0.7534 |
| LNHE1 | −0.535249 | 0.206778 | −2.588515 | 0.0180 |
| LNHE1(−1) | 0.537946 | 0.315518 | 1.704962 | 0.1045 |
| LNHE1(−2) | 0.387757 | 0.318200 | 1.218596 | 0.2379 |
| LNHE1(−3) | −0.486963 | 0.189127 | −2.574788 | 0.0186 |
| C | 1.361299 | 1.161370 | 1.172148 | 0.2556 |
| R-squared | 0.868817 | Mean dependent var | 1.819248 | |
| Adjusted R-squared | 0.820487 | S.D. dependent var | 0.390585 | |
| S.E. of regression | 0.165487 | Akaike info criterion | −0.518654 | |
| Sum squared resid. | 0.520333 | Schwarz criterion | −0.134702 | |
| Log likelihood | 15.00183 | Hannan-Quinn criter. | −0.404485 | |
| F-statistic | 17.97657 | Durbin-Watson stat. | 2.060345 | |
| Prob(F-statistic) | 0.000000 | |||
| Breusch-Godfrey Serial Correlation LM Test: | ||||
|---|---|---|---|---|
| Null hypothesis: No serial correlation at up to 4 lags | ||||
| F-statistic | 0.751820 | Prob. F (4,15) | 0.5721 | |
| Obs * R-squared | 4.509098 | Prob. Chi-Square (4) | 0.3415 | |
| Test Equation: | ||||
| Dependent Variable: RESID | ||||
| Method: ARDL | ||||
| Included observations: 27 | ||||
| Pre-sample missing value lagged residuals set to zero. | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| LNU1 (−1) | 0.117850 | 0.368631 | 0.319697 | 0.7536 |
| LNU1 (−2) | 0.032952 | 0.483494 | 0.068154 | 0.9466 |
| LNU1 (−3) | −0.012376 | 0.193586 | −0.063931 | 0.9499 |
| LNHE1 | −0.068364 | 0.224329 | −0.304749 | 0.7647 |
| LNHE1 (−1) | 0.110929 | 0.345501 | 0.321067 | 0.7526 |
| LNHE1 (−2) | 0.087028 | 0.383704 | 0.226811 | 0.8236 |
| LNHE1 (−3) | −0.065983 | 0.211181 | −0.312450 | 0.7590 |
| C | −0.976691 | 1.428300 | −0.683814 | 0.5045 |
| RESID (−1) | −0.255598 | 0.443418 | −0.576427 | 0.5729 |
| RESID (−2) | −0.311934 | 0.339434 | −0.918982 | 0.3726 |
| RESID (−3) | −0.392935 | 0.316611 | −1.241066 | 0.2336 |
| RESID (−4) | −0.408892 | 0.301665 | −1.355450 | 0.1953 |
| R-squared | 0.167004 | Mean dependent var | 1.75 × 10−15 | |
| Adjusted R-squared | −0.443860 | S.D. dependent var | 0.141467 | |
| S.E. of regression | 0.169987 | Akaike info criterion | −0.405084 | |
| Sum squared resid. | 0.433435 | Schwarz criterion | 0.170844 | |
| Log likelihood | 17.46863 | Hannan-Quinn criter. | −0.233830 | |
| F-statistic | 0.273389 | Durbin-Watson stat. | 2.200375 | |
| Prob(F-statistic) | 0.982248 | |||
| ARDL Long Run Form and Bounds Test | ||||
|---|---|---|---|---|
| Dependent Variable: D(LNU1) | ||||
| Selected Model: ARDL (3, 3) | ||||
| Case 3: Unrestricted Constant and No Trend | ||||
| Included observations: 27 | ||||
| Conditional Error Correction Regression | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 1.361299 | 1.161370 | 1.172148 | 0.2556 |
| LNU1(−1) * | −0.154689 | 0.114509 | −1.350886 | 0.1926 |
| LNHE1(−1) | −0.096509 | 0.093427 | −1.032991 | 0.3146 |
| D(LNU1(−1)) | 0.326836 | 0.211174 | 1.547709 | 0.1382 |
| D(LNU1(−2)) | −0.045849 | 0.143830 | −0.318773 | 0.7534 |
| D(LNHE1) | −0.535249 | 0.206778 | −2.588515 | 0.0180 |
| D(LNHE1(−1)) | 0.099206 | 0.213831 | 0.463946 | 0.6480 |
| D(LNHE1(−2)) | 0.486963 | 0.189127 | 2.574788 | 0.0186 |
| * p-value incompatible with t-Bounds distribution. | ||||
| Levels Equation | ||||
| Case 3: Unrestricted Constant and No Trend | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| LNHE1 | −0.623890 | 0.627671 | −0.993977 | 0.3327 |
| EC = LNU1—(−0.6239*LNHE1) | ||||
| F-Bounds Test | Null Hypothesis: No levels relationship | |||
| Test Statistic | Value | Signif. | I(0) | I(1) |
| Asymptotic: n = 1000 | ||||
| F-statistic | 1.105916 | 10% | 4.04 | 4.78 |
| k | 1 | 5% | 4.94 | 5.73 |
| 2.5% | 5.77 | 6.68 | ||
| 1% | 6.84 | 7.84 | ||
| Actual Sample Size | 27 | Finite Sample: n = 35 | ||
| 10% | 4.225 | 5.05 | ||
| 5% | 5.29 | 6.175 | ||
| 1% | 7.87 | 8.96 | ||
| Finite Sample: n = 30 | ||||
| 10% | 4.29 | 5.08 | ||
| 5% | 5.395 | 6.35 | ||
| 1% | 8.17 | 9.285 | ||
| t-Bounds Test | Null Hypothesis: No levels relationship | |||
| Test Statistic | Value | Signif. | I(0) | I(1) |
| t-statistic | −1.350886 | 10% | −2.57 | −2.91 |
| 5% | −2.86 | −3.22 | ||
| 2.5% | −3.13 | −3.5 | ||
| 1% | −3.43 | −3.82 | ||
| VAR Lag Order Selection Criteria | ||||||
|---|---|---|---|---|---|---|
| Endogenous variables: LNU1 | ||||||
| Exogenous variables: C LNHE1 | ||||||
| Included observations: 26 | ||||||
| Lag | LogL | LR | FPE | AIC | SC | HQ |
| 0 | −10.24252 | NA | 0.150192 | 0.941732 | 1.038509 | 0.969600 |
| 1 | 6.715205 | 30.00212 * | 0.044041 | −0.285785 | −0.140620 * | −0.243983 |
| 2 | 7.257489 | 0.917711 | 0.045685 | −0.250576 | −0.057023 | −0.194840 |
| 3 | 9.587594 | 3.764016 | 0.041340 * | −0.352892 * | −0.110950 | −0.283221 * |
| 4 | 9.588468 | 0.001344 | 0.044804 | −0.276036 | 0.014294 | −0.192431 |
| * indicates lag order selected by the criterion | ||||||
| LR: sequential modified LR test statistic (each test at 5% level) | ||||||
| FPE: Final prediction error | ||||||
| AIC: Akaike information criterion | ||||||
| SC: Schwarz information criterion | ||||||
| HQ: Hannan-Quinn information criterion | ||||||
| Dependent Variable: D(LNU1) | ||||
|---|---|---|---|---|
| Method: Least Squares | ||||
| Included observations: 26 after adjustments | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | −0.067730 | 0.040039 | −1.691610 | 0.1071 |
| D(LNU1(−1)) | 0.000607 | 0.254456 | 0.002384 | 0.9981 |
| D(LNU1(−2)) | −0.337408 | 0.225269 | −1.497798 | 0.1506 |
| D(LNU1(−3)) | −0.030061 | 0.149172 | −0.201520 | 0.8424 |
| D(LNHE1(−1)) | −0.129429 | 0.243757 | −0.530975 | 0.6016 |
| D(LNHE1(−2)) | 0.232530 | 0.234392 | 0.992055 | 0.3336 |
| D(LNHE1(−3)) | 0.200845 | 0.241508 | 0.831629 | 0.4159 |
| R-squared | 0.319178 | Mean dependent var | −0.044807 | |
| Adjusted R-squared | 0.104181 | S.D. dependent var | 0.197082 | |
| S.E. of regression | 0.186534 | Akaike info criterion | −0.295605 | |
| Sum squared resid. | 0.661102 | Schwarz criterion | 0.043113 | |
| Log likelihood | 10.84287 | Hannan-Quinn criter. | −0.198066 | |
| F-statistic | 1.484571 | Durbin-Watson stat. | 2.028694 | |
| Prob(F-statistic) | 0.236315 | |||
| Breusch-Godfrey Serial Correlation LM Test: | ||||
|---|---|---|---|---|
| Null hypothesis: No serial correlation at up to 3 lags | ||||
| F-statistic | 0.196222 | Prob. F (3,16) | 0.8974 | |
| Obs * R-squared | 0.922639 | Prob. Chi-Square (3) | 0.8200 | |
| Test Equation: | ||||
| Dependent Variable: RESID | ||||
| Method: Least Squares | ||||
| Included observations: 26 | ||||
| Pre-sample missing value lagged residuals set to zero. | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 0.012866 | 0.052744 | 0.243941 | 0.8104 |
| D(LNU1(−1)) | 0.327742 | 0.826134 | 0.396718 | 0.6968 |
| D(LNU1(−2)) | −0.189657 | 0.467786 | −0.405435 | 0.6905 |
| D(LNU1(−3)) | 0.131410 | 0.239036 | 0.549751 | 0.5901 |
| D(LNHE1(−1)) | −0.086921 | 0.285957 | −0.303966 | 0.7651 |
| D(LNHE1(−2)) | 0.125100 | 0.320299 | 0.390574 | 0.7013 |
| D(LNHE1(−3)) | −0.194126 | 0.391400 | −0.495978 | 0.6267 |
| RESID(−1) | −0.403315 | 0.887549 | −0.454415 | 0.6556 |
| RESID(−2) | 0.255004 | 0.576876 | 0.442043 | 0.6644 |
| RESID(−3) | −0.185701 | 0.390728 | −0.475270 | 0.6410 |
| R-squared | 0.035486 | Mean dependent var | 1.71 × 10−17 | |
| Adjusted R-squared | −0.507053 | S.D. dependent var | 0.162616 | |
| S.E. of regression | 0.199631 | Akaike info criterion | −0.100967 | |
| Sum squared resid. | 0.637642 | Schwarz criterion | 0.382916 | |
| Log likelihood | 11.31257 | Hannan-Quinn criter. | 0.038374 | |
| F-statistic | 0.065407 | Durbin-Watson stat. | 1.896266 | |
| Prob(F-statistic) | 0.999874 | |||
| Dependent Variable: LNU2 | ||||
|---|---|---|---|---|
| Method: ARDL | ||||
| Included observations: 22 after adjustments | ||||
| Maximum dependent lags: 4 (Automatic selection) | ||||
| Model selection method: Akaike info criterion (AIC) | ||||
| Dynamic regressors (4 lags, automatic): LNHE2 | ||||
| Fixed regressors: C | ||||
| Number of models evaluated: 20 | ||||
| Selected Model: ARDL (3, 0) | ||||
| Note: final equation sample is larger than selection sample | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob.* |
| LNU2(−1) | 0.845471 | 0.231384 | 3.653977 | 0.0020 |
| LNU2(−2) | 0.233138 | 0.299229 | 0.779129 | 0.4466 |
| LNU2(−3) | −0.650798 | 0.312212 | −2.084474 | 0.0525 |
| LNHE2 | 0.062249 | 0.081792 | 0.761071 | 0.4570 |
| C | 0.351124 | 0.906013 | 0.387548 | 0.7032 |
| R-squared | 0.664251 | Mean dependent var | 1.846093 | |
| Adjusted R-squared | 0.585251 | S.D. dependent var | 0.193236 | |
| S.E. of regression | 0.124446 | Akaike info criterion | −1.133178 | |
| Sum squared resid. | 0.263275 | Schwarz criterion | −0.885214 | |
| Log likelihood | 17.46496 | Hannan-Quinn criter. | −1.074765 | |
| F-statistic | 8.408262 | Durbin-Watson stat | 2.140265 | |
| Prob(F-statistic) | 0.000622 | |||
| ARDL Long Run Form and Bounds Test | ||||
|---|---|---|---|---|
| Dependent Variable: D(LNU2) | ||||
| Selected Model: ARDL (3, 0) | ||||
| Case 3: Unrestricted Constant and No Trend | ||||
| Included observations: 22 | ||||
| Conditional Error Correction Regression | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 0.351124 | 0.906013 | 0.387548 | 0.7032 |
| LNU2(−1) * | −0.572189 | 0.252070 | −2.269964 | 0.0365 |
| LNHE2 ** | 0.062249 | 0.081792 | 0.761071 | 0.4570 |
| D(LNU2(−1)) | 0.417660 | 0.349311 | 1.195668 | 0.2482 |
| D(LNU2(−2)) | 0.650798 | 0.312212 | 2.084474 | 0.0525 |
| * p-value incompatible with t-Bounds distribution. | ||||
| ** Variable interpreted as Z = Z (−1) + D(Z). | ||||
| Levels Equation | ||||
| Case 3: Unrestricted Constant and No Trend | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| LNHE2 | 0.108792 | 0.134473 | 0.809023 | 0.4297 |
| EC = LNU2 − (0.1088 * LNHE2) | ||||
| F-Bounds Test | Null Hypothesis: No levels relationship | |||
| Test Statistic | Value | Signif. | I(0) | I(1) |
| Asymptotic: n = 1000 | ||||
| F-statistic | 2.576412 | 10% | 4.04 | 4.78 |
| K | 1 | 5% | 4.94 | 5.73 |
| 2.5% | 5.77 | 6.68 | ||
| 1% | 6.84 | 7.84 | ||
| Actual Sample Size | 22 | Finite Sample: n = 35 | ||
| 10% | 4.225 | 5.05 | ||
| 5% | 5.29 | 6.175 | ||
| 1% | 7.87 | 8.96 | ||
| Finite Sample: n = 30 | ||||
| 10% | 4.29 | 5.08 | ||
| 5% | 5.395 | 6.35 | ||
| 1% | 8.17 | 9.285 | ||
| t-Bounds Test | Null Hypothesis: No levels relationship | |||
| Test Statistic | Value | Signif. | I(0) | I(1) |
| t-statistic | −2.269964 | 10% | −2.57 | −2.91 |
| 5% | −2.86 | −3.22 | ||
| 2.5% | −3.13 | −3.5 | ||
| 1% | −3.43 | −3.82 | ||
| Dependent Variable: D(LNU2) | ||||
|---|---|---|---|---|
| Method: Least Squares | ||||
| Included observations: 21 after adjustments | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | −0.015203 | 0.030145 | −0.504334 | 0.6219 |
| D(LNU2(−1)) | −0.170020 | 0.276773 | −0.614292 | 0.5489 |
| D(LNU2(−2)) | 0.258713 | 0.258977 | 0.998981 | 0.3348 |
| D(LNU2(−3)) | −0.270626 | 0.289628 | −0.934394 | 0.3659 |
| D(LNHE2(−1)) | −0.209866 | 0.180369 | −1.163534 | 0.2641 |
| D(LNHE2(−2)) | 0.150385 | 0.192180 | 0.782523 | 0.4469 |
| D(LNHE2(−3)) | 0.199932 | 0.178820 | 1.118066 | 0.2824 |
| R-squared | 0.297285 | Mean dependent var | −0.013220 | |
| Adjusted R-squared | −0.003879 | S.D. dependent var | 0.133463 | |
| S.E. of regression | 0.133721 | Akaike info criterion | −0.924918 | |
| Sum squared resid. | 0.250339 | Schwarz criterion | −0.576744 | |
| Log likelihood | 16.71164 | Hannan-Quinn criter. | −0.849355 | |
| F-statistic | 0.987120 | Durbin-Watson stat | 1.954400 | |
| Prob(F-statistic) | 0.470095 | |||
| Breusch-Godfrey Serial Correlation LM Test: | ||||
|---|---|---|---|---|
| Null hypothesis: No serial correlation at up to 4 lags | ||||
| F-statistic | 1.344832 | Prob. F (4,10) | 0.3195 | |
| Obs * R-squared | 7.345306 | Prob. Chi-Square (4) | 0.1187 | |
| Test Equation: | ||||
| Dependent Variable: RESID | ||||
| Method: Least Squares | ||||
| Included observations: 21 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 0.008823 | 0.029116 | 0.303034 | 0.7681 |
| D (LNU2(−1)) | 0.516561 | 0.617798 | 0.836133 | 0.4226 |
| D (LNU2(−2)) | −0.115881 | 0.509028 | −0.227651 | 0.8245 |
| D (LNU2(−3)) | 0.502340 | 0.452597 | 1.109906 | 0.2930 |
| D (LNHE2(−1)) | 0.153330 | 0.198129 | 0.773891 | 0.4569 |
| D (LNHE2(−2)) | −0.051891 | 0.198374 | −0.261581 | 0.7990 |
| D (LNHE2(−3)) | −0.020397 | 0.190255 | −0.107207 | 0.9167 |
| RESID (−1) | −0.469628 | 0.598759 | −0.784337 | 0.4510 |
| RESID (−2) | 0.220297 | 0.571901 | 0.385201 | 0.7082 |
| RESID (−3) | −1.053741 | 0.567498 | −1.856818 | 0.0930 |
| RESID (−4) | −0.080005 | 0.538860 | −0.148471 | 0.8849 |
| R-squared | 0.349776 | Mean dependent var | −1.45 × 10−17 | |
| Adjusted R-squared | −0.300447 | S.D. dependent var | 0.111879 | |
| S.E. of regression | 0.127584 | Akaike info criterion | −0.974405 | |
| Sum squared resid | 0.162776 | Schwarz criterion | −0.427274 | |
| Log likelihood | 21.23125 | Hannan-Quinn criter. | −0.855663 | |
| F-statistic | 0.537933 | Durbin-Watson stat | 2.041976 | |
| Prob(F-statistic) | 0.828658 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dănăcică, D.-E.; Babucea, A.-G.; Paliu-Popa, L.; Bușan, G.; Chirtoc, I.-E. The Nexus between Higher Education and Unemployment—Evidence from Romania. Sustainability 2023, 15, 3641. https://doi.org/10.3390/su15043641
Dănăcică D-E, Babucea A-G, Paliu-Popa L, Bușan G, Chirtoc I-E. The Nexus between Higher Education and Unemployment—Evidence from Romania. Sustainability. 2023; 15(4):3641. https://doi.org/10.3390/su15043641
Chicago/Turabian StyleDănăcică, Daniela-Emanuela, Ana-Gabriela Babucea, Lucia Paliu-Popa, Gabriela Bușan, and Irina-Elena Chirtoc. 2023. "The Nexus between Higher Education and Unemployment—Evidence from Romania" Sustainability 15, no. 4: 3641. https://doi.org/10.3390/su15043641
APA StyleDănăcică, D.-E., Babucea, A.-G., Paliu-Popa, L., Bușan, G., & Chirtoc, I.-E. (2023). The Nexus between Higher Education and Unemployment—Evidence from Romania. Sustainability, 15(4), 3641. https://doi.org/10.3390/su15043641






