Optimal Prediction of Wind Energy Resources Based on WOA—A Case Study in Jordan

Abstract

The average wind speed in a given area has a significant impact on the amount of energy that can be harvested by wind turbines. The regions with the most attractive possibilities are typically those that are close to the seaside and have open terrain inland. There is also good potential in several mountainous locations. Despite these geographical restrictions on where wind energy projects can be located, there is enough topography in most of the world’s regions to use wind energy projects to meet a significant amount of the local electricity needs. This paper presents a new method of energy prediction of wind resources in several wind sites in Jordan, which can be used to decide whether a specific wind site is suitable for wind farm installation purposes. Three distribution models, Weibull, Gamma and Rayleigh, were employed to characterize the provided wind data. Different estimation methods were used to assign the parameters associated with each distribution model and the optimal parameters were estimated using whale optimization algorithms which reduce the error between the estimated and the measured wind speed probability. The distribution models’ performance was investigated using three statistical indicators. These indicators were: root mean square error (RMSE), coefficient of determination (R²), and mean absolute error (MAE). Finally, using the superlative distribution models, the wind energy for the chosen wind sites was estimated. This estimation was based on the calculation of the wind power density (E_D) and the total wind energy (E_T) of the wind regime. The results show that the total wind energy ranged from slightly under 100 kWh/m² to nearly 1250 kWh/m². In addition, the sites recording the highest estimated wind energy had the optimum average wind speed and the most symmetrical distribution pattern.

1. Introduction

Currently, renewable energy is a crucial and essential need to mitigate the hazards caused by fossil fuels. Although the global capacity of renewable energy in 2019 was 2588 GW, the percentage of electricity generation from renewable resources was about 27.3% versus 72.7% for traditional resources [1]. Therefore, all essential steps must be taken by governments worldwide to support these strategies.

One of the most highly developed sectors in the field of renewable energy is the wind energy sector. In 2015, 63.8 GW of wind power capacity was installed in networks throughout the globe, recording the greatest yearly increase in the capacity of wind power generation. In 2019, the second largest yearly increase in the capacity of wind power generation was recorded with a value of 60 GW [1,2].

The climate of Jordan enhances the utilization of renewable energy sources. It contains various locations that are appealing for wind energy investment. However, Jordan is still 93% dependent on its energy from gas and oil imported from other countries. In 2018, renewable energy contributed 10.7% of the total national energy production, in which the wind energy contribution was around 3.52% [1].

A wind energy prediction process can be accomplished by determining the speed and direction of the wind [3]. However, these two parameters cannot be specified precisely, due to the wind’s erratic behavior. The characteristics of wind should be established based on analyzing and recognizing the natural behavior of wind at the candidate site. The parts of the wind energy conversion system (WECS) can be efficiently designed once the wind characteristics have been established.

Any wind energy project has a lifecycle that consists of several phases and several steps. Accomplishing each phase properly leads to the success of the project. The prediction of wind resources is the first stage in the lifecycle of a wind energy project. Generally, wind resource prediction involves four main steps which are individually discussed as follows [3,4].

The first step is “site identification and data collection”: this step includes identifying one or more sites across countries, states, or provinces. Wind atlases or airport wind data are used to provide a preliminary prediction of the wind potential in those sites. Several aspects should be considered when identifying sites such as: market situations, local society and government support, transmission access and capacity, site constructability, and environmental aspects. Wind data are measured and collected from the metrological stations or airports near the candidate wind sites. Wind data are usually measured in ten minutes basis at 10 m height, which is considered the standard height.

The second step is “analyzing the collected data”: in this step, the collected data (mean wind speed) are analyzed by utilizing a statistical distribution model to obtain the frequency distribution of the average wind velocity for the candidate site over a certain period. Each distribution model includes several parameters that are assigned by utilizing a variety of estimation methods. Such methods can be classified into two main categories: the numerical methods and the optimization algorithms.

The third step is “choosing the best performance indicator model”: during this stage, a comparison between the selected distribution models must be carried out to choose the optimal distribution function. This is achieved by using various types of goodness of fit indicators such as the root mean square (RMS) error, the coefficient of determination (R²), chi-square (χ²), and others.

The fourth step is “estimating the wind energy”: this step involves evaluating the extracted energy from both the wind regime and wind turbines that are installed in the candidate sites based on the best distribution models. In this stage, the distribution model can be represented as a probability distribution function (PDF). Then, the power curve model (P-V characteristic) is utilized to evaluate the extracted wind energy from a specific wind turbine installed in a candidate wind site. By the end of this phase, it will be feasible to determine whether or not the potential wind site can support the installation of a wind turbine.

Several research studies have made great efforts in the evaluation of wind energy potential, attempting to find the optimum wind distributions and estimation methods [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Most of these studies focused on parametric distribution models and numerical estimation methods. However, some researchers considered the non–parametric distribution models [13]. Various parametric models were utilized to assess wind energy resources such as Weibull [4,5,6,7,9,10,11,12,13,14,15], Rayleigh [8,18,19,20,21], Lognormal [21,22,23,24,25,26], and others.

According to the literature, the Weibull distribution was the most widely utilized by researchers, especially when optimizing algorithms were used to determine their parameters. Based on wind data gathered for over a year from a measuring station built at the Atlm University campus area in Ankara, Turkey, Bilir et al. used the Weibull distribution as an assessment tool in [7]. Wang et al., in [11], showed that the Weibull model was the most suitable distribution among the five selected distribution models, which were tested according to the RMSE indicator. In [14], Li et al. conducted a comparison of onshore and offshore wind profiles and their potentials for generating wind energy in two sites in China’s southeast coastline area. The authors verified the reliability of utilizing the Weibull model in both candidate sites. The results showed that the wind energy at an offshore location was greater than onshore wind energy for a specified region. The Weibull distribution was compared with the Rayleigh, Gamma, and Lognormal distributions in [18] by Jiang et al. Afterward, considering the low wind profile, the Weibull model was utilized for evaluating the associated potentials in China.

An analysis of 46 studies released during the years of 2010–2018 was performed in [27]. This analysis demonstrated that in 44 studies, the Weibull distribution was the optimum method. The Weibull distribution has not always been thought to be the best option [22,24]. Wu et al., in [24], employed the Weibull, Logistic, and Lognormal distributions to assess wind energy at typical locations in Inner Mongolia, China. The Weibull performance was the weakest, and the Logistic and Lognormal performances were better. According to [28], a number of mixed distributions perform better than the traditional Weibull distribution, including the Gamma–Weibull function (GW), bimodal Weibull function (WW), mixture truncated normal function (NN), and truncated Normal–Weibull function (NW).

A variety of estimation techniques, including the maximum likelihood method (MLM) [4,7], moment method (MM) [10,12,13,14,15], least square estimation (LSE) [18,19], empirical method (EM) [10,11,12,15], power density method (PDM) [14,26], and energy pattern factor (EPF) [9,15], should be used to accurately value the parameters of the associated models. The modified maximum likelihood (MMLM) [25] and modified energy pattern method (MEPM) [12] are two examples of modified approaches that can also be used. The first four mentioned methods were most commonly used by many studies. In [9], authors found that the MLM was superior over the other methods according to three performance indicators, which were the root mean square error (RMSE), coefficient of determination (R²), and chi-square (χ²). The EM was the best choice for wind energy assessment in three candidate potential sites in Australia to allocate parameters of the Weibull distribution, as presented in [10]. Gugliani et al. [12] proposed a new estimation method that was compared with six common estimation methods via a Monte Carlo simulation study with sample sizes varying from 100 to 100,000. For each sample size, the MEPF achieved the best results and was superior over the other methods.

Some researchers proposed non-parametric distribution models to overcome the drawbacks of the parametric models. One of these drawbacks is the need of determining the values of the parameters appropriately by various types of estimation methods. According to [16,17,28,29,30], the Kernal density method is the well-known used method.

Wind energy exploration in Jordan began in 1979 via the Royal Scientific Society (RSS) [31], and various studies have been performed since then to analyze wind energy resources [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. The technical details of eight studies published between 2007 and 2022 as well as the proposed study are listed in

Table 1. The recent studies of wind energy assessment in Jordan.

Study	Candidate Site(s)		Study Period	Data Resolution	Distribution Model(s)	Estimation Method(s)	Performance Indicator(s)	Study Objective(s)
Study in Ref. [37]	Amman	Aqaba	9 years	Daily	Weibull	Graphical method	Kolmogorov–Smirnov	For wind regime: Annual power density.
	Irbid	Der Alla
	Ras Monief
Study in Ref. [38]	Hofa	Tafila	2–4 years 9 years (Fujaij)	Monthly	Rayleigh	Direct computing of parameter (c) based on mean speed	N/A	For proposed 4 models of WTs: Annual energy production; Capacity factor; Cost of energy.
	Ibrahimya	Fujaij
	Zabda	Aqaba
	Ras Monief
Study in Ref. [39]	Alhassan Industrial City		20 years	Monthly	N/A	N/A	N/A	For proposed wind farm: Annual energy production; Capacity factor; Cost of energy; Payback period; Annual net profit.
	Fujaij
	Safawi
	Ras Monief
Study in Ref. [31]	Azraq	Q. A. Airport *	5 years	6 h	Weibull	Standard deviation method	N/A	For proposed 5 models of WTs: Annual and seasonal energy pro-duction; Capacity factor.
	Safawi	K. H. Airport **
	Ras Monief
Study in Ref. [40]	Amman		9 years	Daily	Weibull	Graphical method	N/A	For proposed 4 models of WTs: Annual energy production; Capacity factor. No. of WT units; Cost of energy.
	Irbid
	Aqaba
	Der Alla
	Ras Monief
Study in Ref. [41]	Amman		7 years	N/A	Weibull	Trend of k vs. $\overline{V}$	N/A	For wind regime: Annual power density; Annual energy density.
Study in Ref. [42]	Ma’an		1 year	Daily	Weibull Rayleigh	Graphical method Empirical method Moment method Energy pattern factor method	RMSE X2 test R2 MPE MAPE	For wind regime: Monthly power density.
Study in Ref. [43]	Ma’an		1 year	10 min	Weibull Rayleigh	Empirical method Moment method Energy pattern factor method	N/A	For wind regime: Annual power density; Annual energy density. For proposed 4 models of WTs: Annual energy production.
	Aqaba
	Batn Elghol
Proposed Study	Q. A. Airport *	Mafraq	1 year	1 h, 3 h and 6 h	Gamma Weibull Rayleigh	Artificial intelligent method (WOA) Moment method Maximum likelihood method	RMSE R2 MAE	For wind regime: Annual power density; Annual energy density.
	K. H. Airport **	Ma’an
	A. C. Airport ***	Safawi
	Irbid	Irwaished
	Ghor El Safai

* Queen Alia Airport; ** King Hussein Airport; *** Amman Civil Airport.

. Markedly, the available span for wind data is between one and 20 years; nevertheless, there was an inverse relationship between the length of the study and the precision of the data available, as shown in the table. These studies were reported to be restricted to the implementation of the Weibull or Rayleigh distribution models. Moreover, it is noticeable that numerical methods dominated the estimation of model parameters in these studies.

Different wind locations in Jordan were examined as study objects in this work to investigate various types of distribution functions for wind energy evaluation. The following were the primary objectives of this study in comparison to those presented by other studies in the same scope:

• In this paper, the mathematical model of wind analysis based on the Gamma distribution, which was infrequently utilized in the literature, has been derived;
• Using real examples, this paper provides technical comparisons between several types of wind distribution models: Weibull, Gamma, and Rayleigh distribution functions;
• The wind energy has been estimated for the designated wind sites using Weibull, Gamma, and Rayleigh distribution models.

The body of this article is structured as follows: Section 2 provides the measured wind data. The direction of the collected wind data is also presented in Section 2. The estimation of these wind data based on Weibull, Rayleigh, and Gamma distribution functions and their parameters is presented in Section 3. The results are discussed in Section 4 before concluding in Section 5.

2. Wind Data

The wind data should be assembled from the nearest meteorological stations to the potential wind site in order to perform an accurate wind resource evaluation. Such information is typically collected at 10 m above ground level and can be extrapolated to a higher altitude (usually the turbine’s installation height). This gives a precise evaluation of the wind for big wind projects. Key wind statistics, such as average wind speed and direction, may be categorized into 10 min, hourly, daily, monthly, and annual time intervals. The most typical time scale, a 10 min basis, can offer enough resolution to provide an accurate wind potential estimation [3,49,50,51,52]. Jordan is divided geographically into three main regions: Jordan Valley region, Western Highlands Range, and the Desert Regions. Jordan Valley is a narrow region along the western strip considered a low-lying agricultural land that can reach up to 400 m below sea level; thus, it is a poor region in terms of wind energy resources. Western Highlands Range is a mountain range along Jordan’s western facade representing an encouraging environment for investment in wind energy projects, as well as the Desert Regions which are vast areas including the eastern and southern parts of Jordan [31,38,39,40]. The wind data were collected and recorded for this study, at a height of 10 m above ground, from nine wind stations in Jordan: Queen Alia Airport, Civil Amman Airport, King Hussein Airport, Irbid, Mafraq, Ma’an, Ghor El-Safi, Safawi, and Irwaished. The geographical distribution of these sites across Jordan is depicted in Figure 1. In this work, the wind data were collected for a one-year period, sufficiently representing all the year’s seasons. The geographic position of the meteorological stations at these sites are shown in

Table 2. Topographical information and technical details of wind data for each designated wind site.

	Latitude	Longitude	Elevation	Number of Data	Sampling Rate	Period
Queen Alia Airport	31.43° N	35.59° E	722 m	7173	1 h	01/2019–12/2019
Amman Civil Airport	31.59° N	35.59° E	767 m	6910	1 h	09/2018–08/2019
King Hussein Airport	29.33° N	35.00° E	51 m	6711	1 h	01/2018–12/2018
Irbid	32.33° N	35.51° E	618 m	899	6 h	03/2018–02/2019
Mafraq	32.22° N	36.15° E	686 m	1909	3 h	09/2018–08/2019
Ma’an	30.10° N	35.47° E	1069 m	1014	6 h	03/2018–02/2019
Safawi	32.09° N	37.12° E	647 m	1703	3 h	01/2018–12/2018
Irwaished	32.30° N	38.12° E	686 m	764	6 h	09/2017–08/2018
Ghor El-Safi	31.02° N	35.28° E	−350 m	790	6 h	01/2018–12/2018

. Additionally, Table 1 includes the wind data time spans, data sampling rate, and the number of obtained data for each wind station.

2.1. Wind Speed Analysis

The direct statistical analysis of wind speed data to find the mean value and standard deviation are illustrated in Figure 2. This chart demonstrates that the average wind speed at all sites was roughly 5 m/s. A deeper look at this data reveals that the average wind speed for all sites ranged between 2.5 m/s and slightly above 6 m/s. The minimum standard deviation regarding wind speed data across all locations was approximately 1 m/s in Irbid, while the maximum values are around 2.7 m/s in Ghor El-Safi. The distribution patterns of wind data are illustrated in Figure 3. Wind data skewness was positive at all locations. Ghor El-Safi had the highest skewness value for wind speed data, with a value of about 12.5. This result shows that its distribution curve had a noticeable asymmetry. The smallest kurtosis values were found at King Hussein Airport and Safawi, with a value of less than one for both sites. Remarkably, Ghor El-Safi had the highest kurtosis value compared to the other sites, indicating a significant difference. The distribution curve for this site was very steep compared to the typical distribution as a result.

The wind speed was split across many divisions in order to be organized. Each division had a speed interval of 1 m/s. The observed probability of each class was calculated for all sites, as shown in

Table 3. The observed probabilities of wind speeds for all sites.

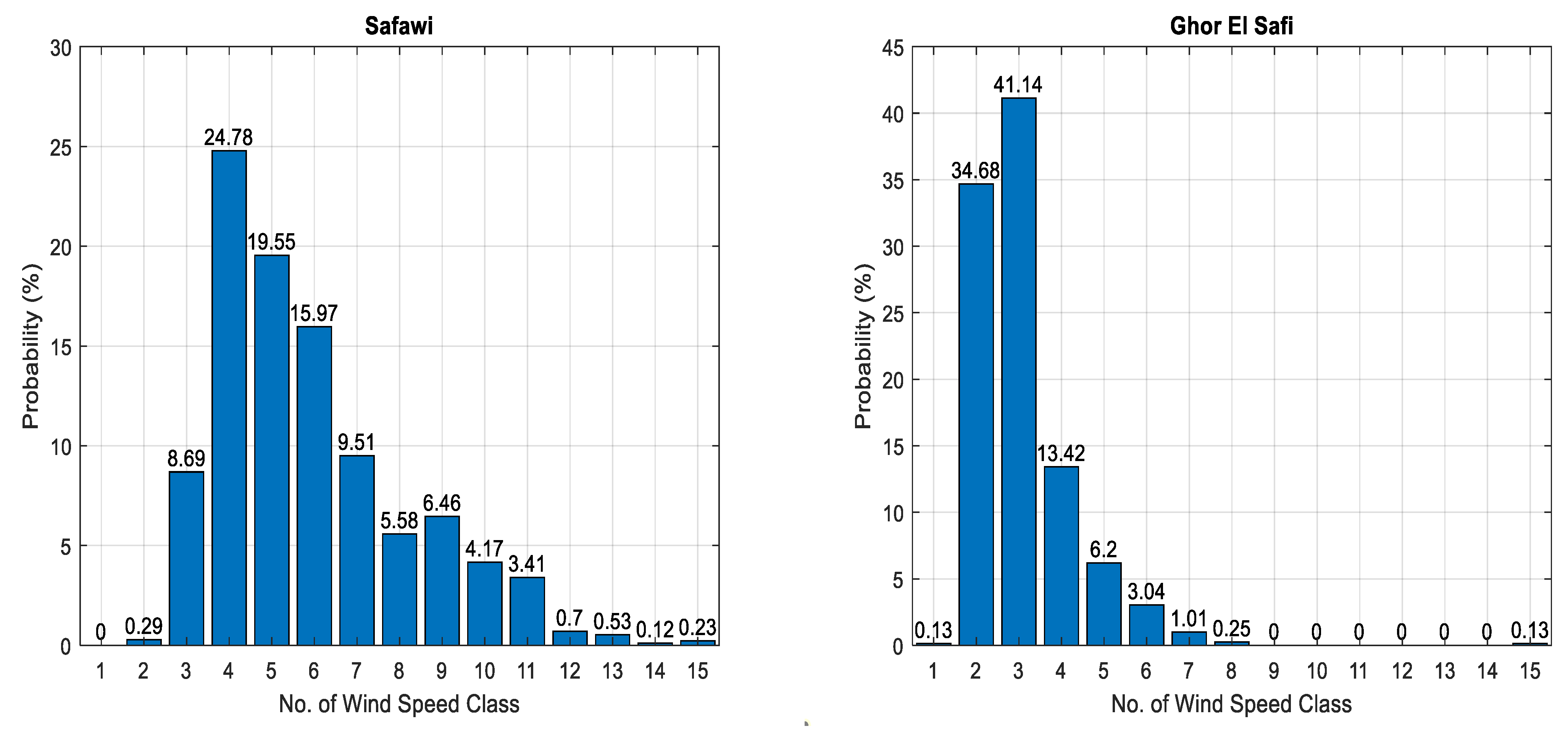
No. of Class	Speed Class (m/s)	Wind Speed Observations (%)
		Queen Alia Airport	Amman Civil Airport	King Hussein Airport	Irbid	Mafraq	Ma’an	Safawi	Irwaished	Ghor El-Safi
1	$0\le V_i<1$	0.04	0.04	0.00	0.11	0.00	0.00	0.00	0.13	0.13
2	$1\le V_i<2$	3.14	14.20	0.58	43.60	5.08	1.68	0.29	6.15	34.68
3	$2\le V_i<3$	23.67	23.00	12.71	40.04	31.53	18.84	8.69	26.05	41.14
4	$3\le V_i<4$	16.94	18.47	16.36	11.12	20.53	32.64	24.78	20.29	13.42
5	$4\le V_i<5$	12.46	13.98	16.41	3.67	15.61	18.93	19.55	14.27	6.20
6	$5\le V_i<6$	16.23	12.59	16.38	1.22	12.05	10.06	15.97	13.09	3.04
7	$6\le V_i<7$	10.25	7.71	16.87	0.11	7.86	3.55	9.51	8.64	1.01
8	$7\le V_i<8$	8.43	4.60	13.80	0.00	4.66	4.44	5.58	3.53	0.25
9	$8\le V_i<9$	2.89	2.14	3.89	0.11	1.10	5.92	6.46	3.53	0.00
10	$9\le V_i<10$	2.27	1.19	2.21	0.00	0.79	1.18	4.17	1.44	0.00
11	$10\le V_i<11$	1.74	0.90	0.52	0.00	0.26	0.79	3.41	0.26	0.00
12	$11\le V_i<12$	0.70	0.64	0.18	0.00	0.10	0.79	0.70	0.65	0.00
13	$12\le V_i<13$	0.50	0.41	0.01	0.00	0.26	0.39	0.53	0.92	0.00
14	$13\le V_i<14$	0.25	0.07	0.00	0.00	0.05	0.49	0.12	0.65	0.00
15	$14\le V_i$	0.49	0.07	0.09	0.00	0.10	0.30	0.23	0.39	0.13

. A closer inspection of this table shows that class (3) recorded the highest probability value in five wind sites, followed by class (4) with two wind sites. The highest probability values achieved by classes (2) and (3) were in the Irbid wind site with around 84%. This indicates that the prevailing wind speed in the Irbid site is within these classes, which is considered as low wind speeds. The same observation was made for the Ghor El-Safi wind site. It is clear from Table 3 that the classes of (11) and above recorded the lowest probability values in all wind sites, as they did not exceed 5% (see the Safawi wind site). Figure 4 represents the histograms of the observed probabilities for two wind sites, one was classified as richly endowed with wind resources (Safawi site) while the other was a resource-poor site, such as Ghor El Safi, according to Table 2 and Figure 2 and Figure 3. In general, the data shown in Table 2 and Table 3 show significant disparities in the features and specifications of the proposed wind sites. This was due to the differences in geography between these areas.

2.2. Wind Direction Analysis

The available data were utilized to determine the wind directions. The frequency of each wind direction at each wind station is well described in

Table 4. The occurrence rate of each wind direction for each site.

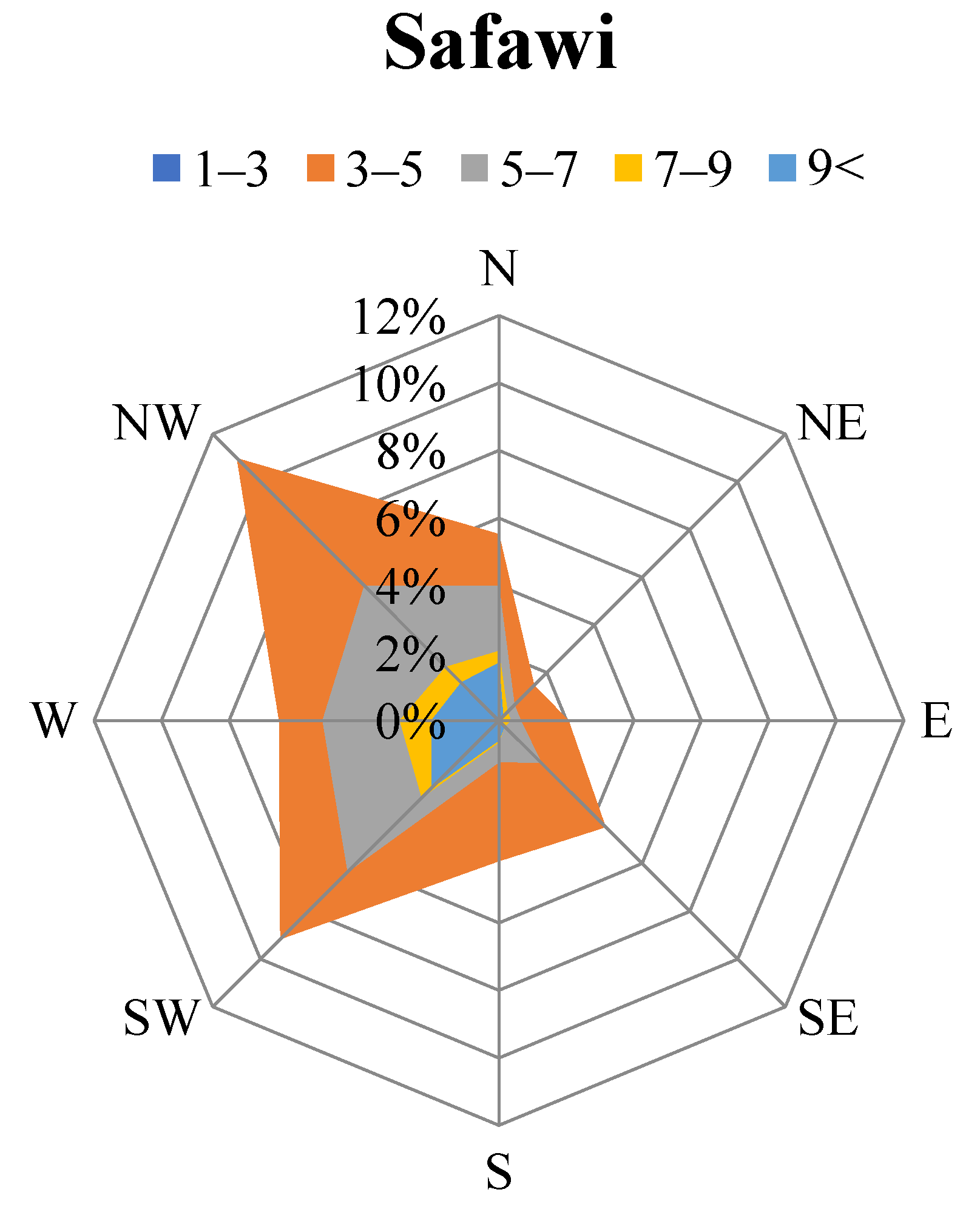
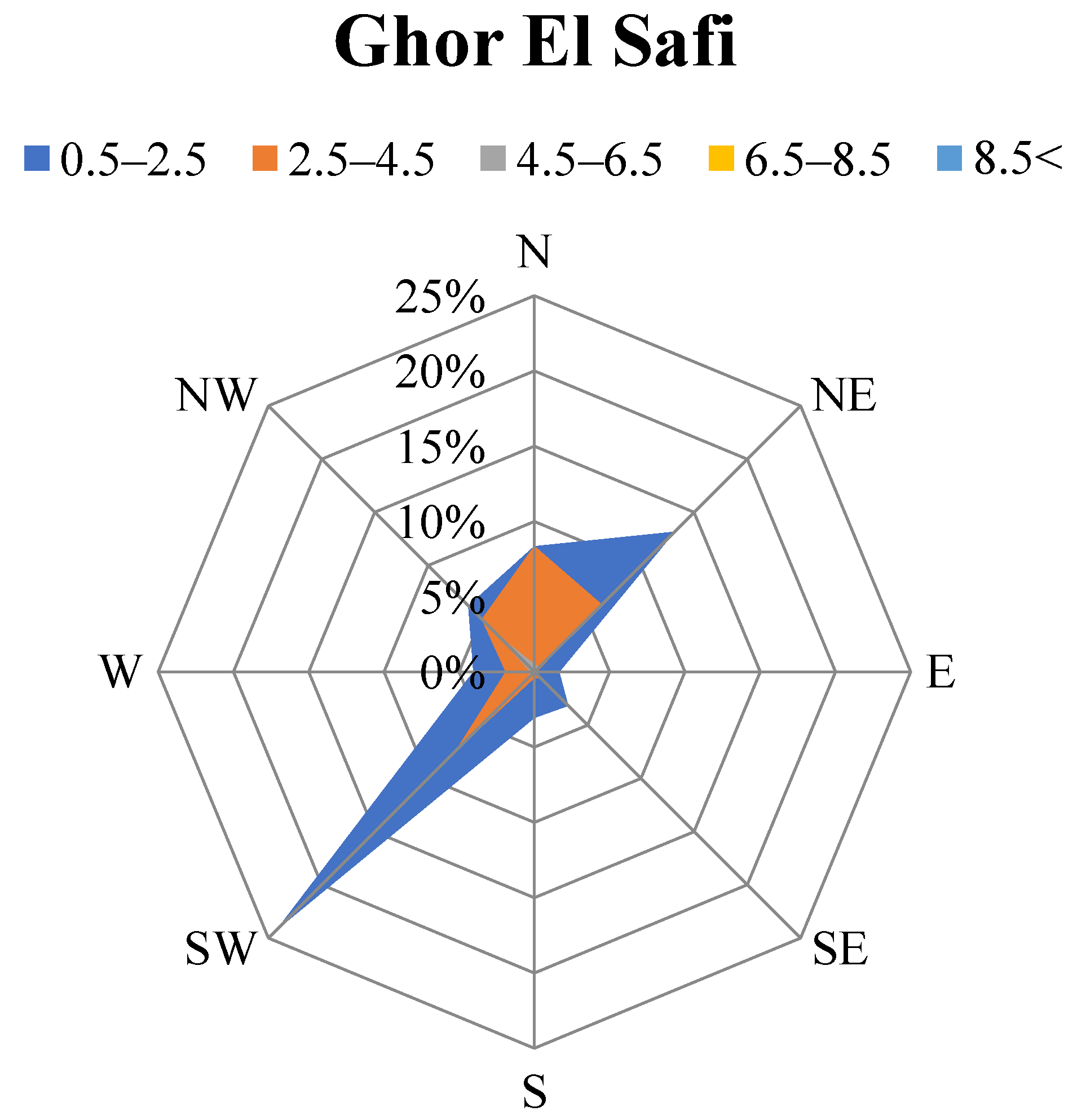
Site	Occurrence Rate (%)								Overall (%)
	N	NW	W	SW	S	SE	E	NE
Queen Alia Airport	1.87	26.20	27.42	17.50	2.17	8.02	7.17	9.66	100
Amman Civil Airport	4.15	29.32	21.49	26.66	0.87	4.67	5.70	7.13	100
King Hussein Airport	68.55	16.69	1.00	4.04	3.46	2.09	0.36	3.82	100
Irbid	3.67	14.24	33.93	25.14	2.00	15.68	4.12	1.22	100
Mafraq	5.61	51.23	7.44	16.66	2.83	14.35	1.20	0.68	100
Ma’an	7.50	41.32	15.38	15.98	8.19	6.31	2.27	3.06	100
Safawi	14.15	22.49	18.03	24.13	7.11	7.69	3.35	3.05	100
Irwaished	7.46	20.55	15.71	16.36	12.30	11.65	8.90	7.07	100
Ghor El-Safi	17.22	14.56	6.20	32.53	3.42	4.43	1.77	19.87	100
Average	14.46	26.29	16.29	19.89	4.70	8.32	3.87	6.17	100

. This table clearly shows that the north-west direction showed the highest recurrence rate across all sites (26.29%). With a mere 3.87% chance of occurring, the eastward wind had the lowest frequency of any direction. Surprisingly, King Hussein Airport had the largest percentage of times that wind was coming from the north (68.55%). In general, knowing the predominant wind direction at a particular wind site gave an indicator of the wind turbine’s proper direction. In most locations, their range should be from northwest to southwest. The wind roses were drawn for both Safawi and Ghor El-Safi sites, as presented in Figure 5.

3. Methodology

In this section, a comprehensive description of the developed models and methods is provided. The work plan of the suggested wind energy prediction is represented in step-wise-step style, graphically, as shown in Figure 6.

3.1. Wind Energy Fundamentals

The time-rate of the flow of wind energy across certain space is called wind power, which is a function of air’s volume, speed and mass. The fundamental equation for wind power can be written as follows [53,54].

$$P_W= \frac{1}{2} \rho A v^3$$

(1)

where v is the wind speed, $\rho$ is the air density and A is the cross-sectional area of wind flow. This equation clearly shows that wind speed is the most important factor in wind energy calculations. When the wind speed doubled, the available power increased eightfold. Furthermore, wind power is directly related to air density and implicitly related to radius squared.

3.2. Wind Distribution Models

Three distinct distribution functions were employed in this study to illustrate the wind behavior of the specified sites. Many wind researchers are familiar with and employ Weibull and Rayleigh. The Gamma function, which is infrequently applied in the field of wind, was chosen as the third function in this study.

3.2.1. Weibull Model

The Weibull model’s probability distribution function is described as follows: [55,56,57].

$$f_W\left(v\right)=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}{e}^{-{\left(\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)}^k}$$

(2)

where k and c are the Weibull shape and scale parameters, respectively. Integrating Equation (2), the cumulative distribution of the Weibull function, F_w(v), is given by:

$$F_W\left(v\right)=1-e^{-{\left(\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)}^k}$$

(3)

3.2.2. Rayleigh Model

The probability distribution function f_R(v) of the Rayleigh model is stated as follows [3,58].

$$f_R\left(v\right)=\frac{v}{c^2}{e}^{-\left(\raisebox{1ex}{$v^2$}\!\left/ \!\raisebox{-1ex}{$2c^2$}\right.\right)}$$

(4)

3.2.3. Gamma Model

Gamma distribution, f_G(v), can be used to evaluate wind energy. Gamma’s probability distribution function is written as follows [59].

$$f_G\left(v\right)={\left(\frac{v}{c}\right)}^k\frac{e^{-\left(\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)}}{\mathsf{\Gamma }\left(k\right)v}$$

(5)

where $\mathsf{\Gamma }\left(\mathrm{a}\right)$ is the gamma function.

3.3. Wind Distribution Models Parameters Estimation

The distribution models were used to represent the probability distribution functions of a set of wind speed data for the candidate wind sites. Each distribution model had several parameters which were estimated by numerical and artificial intelligent (AI) techniques. The numerical techniques used in this study were the maximum likelihood method and the moment method, while the artificial intelligent technique was the whale optimization. The mathematical formulas of the numerical methods utilized in this study are presented in [59]. The whale optimization algorithm will be discussed in the following subsection.

Whale Optimization Algorithm

Mirjilalili et al. proposed the whale optimization algorithm in 2016 [60]. The bubble-net feeding approach, a distinguishing social behavior of humpback whales when foraging, served as the model for this algorithm. By forming several bubbles along a circular or 9-shaped path, this approach works well. The statistical foraging behavior of the humpback whale is demonstrated using the procedures below.

Step one: Encircling the prey

The humpback whale can properly identify and encircle its prey. The location of the prey is considered to be the best option. The other whales (search agents) must, therefore, change their positions in accordance with the position of the ideal whale. As shown below, encircling behavior can be represented by:

$$\overline{D}=\left|\overline{C}·\overline{X^{*}}\left(t\right)-\overline{X}\left(t\right)\right|$$

(6)

$$\overline{X}\left(t+1\right)=\overline{X^{*}}\left(t\right)-\overline{A}·\overline{D}$$

(7)

where $\overline{X^{*}}$ refers to the best position vector of the optimal solution, $\overline{X}$ represents the position vector of a search agent, and the current iteration is defined by t. $\overline{A}$ and $\overline{C}$ are both coefficient vectors that can be expressed by the following equations:

$$\overline{A}=2\overline{a}·\overline{r}-\overline{a}$$

(8)

$$\overline{C}=2\overline{r}$$

(9)

where $\overline{a}$ is a component that decreases linearly from 2 to 0 throughout the iterations, $\overline{r}$ is a random vector defined as $rϵ\left[0,1\right]$.

Step two: Method of bubble-net attacking

Two approaches represent this method, as follows.

A. Shrinking encircling mechanism

The mechanism of this approach lowers the value of $\overline{a}$. Consequently, this results in a reduction in the $\overline{A}$ coefficient’s fluctuation range, i.e., $\overline{A} \in \left[-a,a\right]$. Setting the range of $\overline{A}=\left[-1,1\right]$ or $\left|A\right|<1$ leads to locate the new position of a search agent anywhere in-between the original position and the optimal current position.

B. Spiral updating position

In this approach, the whale attacks the prey in a helix-shaped path. This can be expressed as follows.

$$\overline{D^{\prime }}=\left|\overline{X^{*}}\left(t\right)-\overline{X}\left(t\right)\right|$$

(10)

$$\overline{X}\left(t+1\right)=\overline{D^{\prime }}·e^{bl}·\cos \left(2\pi l\right)+\overline{X^{*}}\left(t\right)$$

(11)

where $\overline{D^{\prime }}$ represents the distance of the $i^{th}$ whale to the prey (optimal solution obtained), $l$ is a random number defined as $lϵ\left[-1,1\right]$, $b$ is constant value related to the shape of the logarithmic spiral.

It is noteworthy that the humpback whale employs both strategies simultaneously when attacking and encircling its prey. The algorithm, therefore, considers there to be an equal chance of selecting either of the two strategies. As a result, the updated position of the whales can be represented using the following model.

$$\overline{X}\left(t+1\right)=\{\begin{array}{c}Equation \left(6\right), p<0.5\\ Equation \left(11\right), p\ge 0.5\end{array}$$

(12)

where $p$ represents the probability and is a random number defined as $pϵ\left[0,1\right]$.

Step three: Searching for prey

Actually, humpback whales randomly search for prey based on where they are in relation to one another. To encourage the whales (search agents) to separate in pursuit of better prey, a coefficient might be utilized. Making the vector A’s norm bigger than 1 or less than −1 might be used to model this, i.e., $\left|A\right|>1$. The new position is obtained at this stage by selecting a random search agent rather than the optimal agent selected. This can be stated as follows.

$$\overline{D}=\left|\overline{C}·\overline{X_{rand}}\left(t\right)-\overline{X}\left(t\right)\right|$$

(13)

$$\overline{X}\left(t+1\right)=\overline{X_{rand}}\left(t\right)-\overline{A}·\overline{D}$$

(14)

where $\overline{X_{rand}}$ is the random position vector.

The following steps summarize the whale optimization algorithm.

• Establish the necessary parameters (N, Population size, Iter_max) and then, initialize the population X_i (i = 1, 2..., N), as well as the coefficients a, A, C, l, and p;
• Assess the fitness of each search agent, and then choose X* as the ideal candidate;
• Update the following coefficients $a$, $A$, $C$, $l$ and $p$;
• Determine the $p$ value. (I) If p < 0.5, then determine the $\left|A\right|$ value. (i) If $\left|\mathrm{A}\right|<1$, update the position by (7). (ii) Otherwise, if $\left|A\right|\ge 1$, select a random search agent X_rand and then, update the position by (14). (II) Otherwise, if p > 0.5, then update the position by (11);
• Verify that all whales (search agents) are taken into account. If not, move on to the next search agent; if yes, determine which search agents go over the search space and make the appropriate adjustments;
• Calculate the fitness for all search agents;
• Save the best solution X*.;
• Verify that the stopping criteria are met. If not, move on to step three; if yes, provide the optimal solution X* and its corresponding fitness score.

3.4. Performance Indicators

The efficient distribution model was identified using three statistical performance tests. These tests were: RMSE, R², and MAE. Each test is discussed in the following subsections.

3.4.1. Root Mean Square Error

The discrepancy between the estimated values of the distribution model and the actual values was computed using the root mean square error (RMSE). Therefore, RMSE is defined as follows [12]:

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-x_i\right)}^2}$$

(15)

where the $y_i and x_i$ are i^th measured and estimated value, respectively, while $n$ is the total number of observations. The minimum RMSE value shows that the estimating technique utilized achieved the best results.

3.4.2. Coefficient of Determination

This test assesses the level of agreement between observable and theoretical values predicted by distribution models. R² is expressed as follows [61,62,63]:

$$R^2=1-\frac{{\sum }_{i=1}^n{\left(y_i-x_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}$$

(16)

where the $\overline{y}$ represents the average value of the observations. The greater the R² value, the stronger the performance of the estimating approach.

3.4.3. Mean Absolute Error

This test evaluates the absolute difference between the actual and expected values. Corresponding to RMSE, the lower the MAE value, the better the result. MAE is expressed as follows [64,65,66]:

$$\mathrm{MAE}=\frac{1}{n}{\sum }_{i=1}^n\left|y_i-x_i\right|$$

(17)

3.5. Wind Energy Estimation

In this section, the Weibull, Gamma, and Rayleigh distribution models were used to evaluate the energy potential of wind regimes. This evaluation was based on an investigation of the two primary components of any wind regime: total annual wind energy (E_T) and wind power density (E_D).

$$E_D={\int }_0^{\infty }{P}_{v}f\left(v\right) dv$$

(18)

where P_v represents the available wind power per unit area of the wind regime expressed in W/m², while f(v) is the distribution function. The wind power can be expressed as [66,67]:

$$P_v= \frac{1}{2} \rho v^3$$

(19)

where ρ is the air density in kg/m³. In terms of kWh/m², the total energy for a certain wind regime at a definite time (T) can be calculated as follows:

$$E_T=T{E}_D$$

(20)

The wind power density of Weibull and Rayleigh functions, (E_DW)and (E_DR,), can be expressed by (21) and (22), respectively [44].

$$E_{DW}=\frac{\rho c^3}{2}\Gamma \left(1+\frac{3}{k}\right)$$

(21)

$$E_{DR}=\frac{\rho c^3}{2}\sqrt{\frac{\pi }{2}}$$

(22)

By substituting (5) and (19) in (18), the wind power density of the gamma function was calculated.

$$E_{DG}=\frac{\rho }{2\Gamma \left(k\right)}{\int }_0^{\infty }{v}^2{\left(\frac{v}{c}\right)}^k{e}^{-\left(\frac{v}{c}\right)}dv$$

(23)

Let x = v/c, therefore dv = cdx. Substitute in (23), yields:

$$E_{DG}=\frac{\rho c^3}{2\Gamma \left(k\right)}{\int }_0^{\infty }{x}^{k+2}{e}^{-x}dx$$

(24)

The standard Gamma integral is stated as follows:

$${\Gamma }_n={\int }_0^{\infty }{x}^{n-1}{e}^{-x}dx$$

(25)

Comparing (24) with (25), hence, using the Gamma distribution function, the wind power density can be written as follows:

$$E_{DG}=\frac{\rho c^3\Gamma \left(k+3\right)}{2\Gamma \left(k\right)}$$

(26)

3.6. Objective Function and Constraint

Each distribution model included several parameters, which can be determined using different estimation methods. Two numerical methods and one Metaheuristic algorithm were applied to determine the parameters of these distribution functions. By reducing the error between the measured wind speed and the predicted values, the objective function utilized in this work aimed to maximize the estimated energy of the wind regime. The objective function in this study and its constraint can be written in a compact format by the following representations [19]:

Objective function:

$$\mathrm{Maximize}(E_T=T{E}_D)$$

(27)

Subject to:

$$\mathrm{Error}\left(v_i\right)=\frac{1}{2}{\displaystyle \sum }_{i=1}^n{\left[f_m\left(v_i\right)-f_c\left(v_i,{\varnothing }_i\right)\right]}^2<{\epsilon }_o$$

(28)

where f_m(v_i) represents the measured frequency distribution of i^th wind data, f_c (v_i, ф_i) is the predicted values obtained by the distribution functions which include the parameters ф_i, and n is the number of wind speed data.

4. Results and Discussion

In this study, two numerical estimating methods (MM and MLM) and one artificial intelligent optimization (WOA) were used to estimate the parameter values for all indicated models, i.e., Weibull, Rayleigh, and Gamma, for the prospective wind sites. As was already indicated, the goal of this study was to minimize the error between the likelihood of the observed wind speed and the estimated values while also maximizing the estimated energy of the wind regime. The accuracy of the anticipated wind speed in comparison to the measured values offered by Taqs Alarab Weather Forecasting Company were tested using three different performance indicators. The estimated parameters and accuracy indicators for each approach are listed in

Table 5. Distribution function parameters and performance indicators results.

Site	Parameter and Indicator	Estimation Methods
		W-MM	W-MLM	W-WOA	R-MM	R-MLM	R-WOA	G-MM	G-MLM	G-WOA
Queen Alia Airport	K	2.326	2.075	2.013	2.000	2.000	2.000	4.771	4.172	4.051
	C	6.564	5.272	5.012	4.641	3.697	3.369	1.219	1.114	1.013
	RMSE	0.03919	0.02846	0.0254	0.03738	0.02904	0.02690	0.03620	0.02488	0.02223
	R2	0.68313	0.83287	0.88272	0.71169	0.82599	0.87527	0.72965	0.87232	0.90230
	MAE	0.02157	0.01502	0.01312	0.02201	0.01546	0.01446	0.01768	0.01417	0.01140
Amman Civil Airport	K	3.609	4.277	1.503	2.000	2.000	2.000	1.940	2.191	0.541
	C	5.750	4.492	4.231	4.063	3.201	4.903	1.190	1.098	1.034
	RMSE	0.03796	0.01848	0.01548	0.03537	0.01809	0.01711	0.03454	0.01082	0.01013
	R2	0.73523	0.93727	0.95721	0.77006	0.93985	0.94912	0.78082	0.97849	0.98836
	MAE	0.02514	0.00900	0.00700	0.02368	0.00944	0.00821	0.02161	0.00725	0.00425
King Hussein Airport	K	3.011	2.806	2.515	2.000	2.000	2.000	7.636	6.339	5.323
	C	6.397	5.640	3.550	4.559	3.800	2.98500	0.748	0.791	0.6820
	RMSE	0.02012	0.01760	0.01588	0.02886	0.03012	0.02746	0.02147	0.02257	0.01734
	R2	0.91378	0.93402	0.94362	0.82265	0.80674	0.84612	0.90186	0.89149	0.92164
	MAE	0.01092	0.00993	0.00793	0.02192	0.01663	0.01561	0.01272	0.01201	0.01002
Irbid	K	2.795	2.462	2.122	2.000	2.000	2.000	6.664	6.588	6.211
	C	2.798	2.379	2.139	1.988	1.618	1.521	0.374	0.320	0.282
	RMSE	0.06894	0.04226	0.03226	0.08108	0.07409	0.05409	0.04504	0.02086	0.01883
	R2	0.83109	0.93653	0.94631	0.76638	0.80491	0.84123	0.92790	0.98453	0.99123
	MAE	0.03991	0.02789	0.02289	0.06006	0.04231	0.02385	0.02457	0.01490	0.01291
Mafraq	K	2.361	2.090	1.890	2.000	2.000	2.000	4.904	4.757	4.451
	C	5.385	4.269	4.166	3.808	2.987	2.612	0.973	0.792	0.721
	RMSE	0.04008	0.03073	0.02661	0.03933	0.03214	0.03014	0.03464	0.02310	0.02011
	R2	0.72736	0.83973	0.86952	0.73735	0.82462	0.84455	0.79629	0.90938	0.92912
	MAE	0.01718	0.01169	0.01069	0.01751	0.01246	0.01146	0.01311	0.01062	0.00805
Ma’an	K	2.279	2.033	2.012	2.000	2.000	2.000	4.595	4.592	4.582
	C	6.183	4.868	4.561	4.370	3.428	3.122	1.192	0.934	0.832
	RMSE	0.06074	0.04812	0.03322	0.05982	0.04869	0.03511	0.05256	0.03512	0.03222
	R2	0.54047	0.71168	0.79451	0.55439	0.70478	0.78422	0.65602	0.84639	0.91539
	MAE	0.03774	0.02848	0.02122	0.03806	0.02873	0.02273	0.03076	0.01889	0.01711
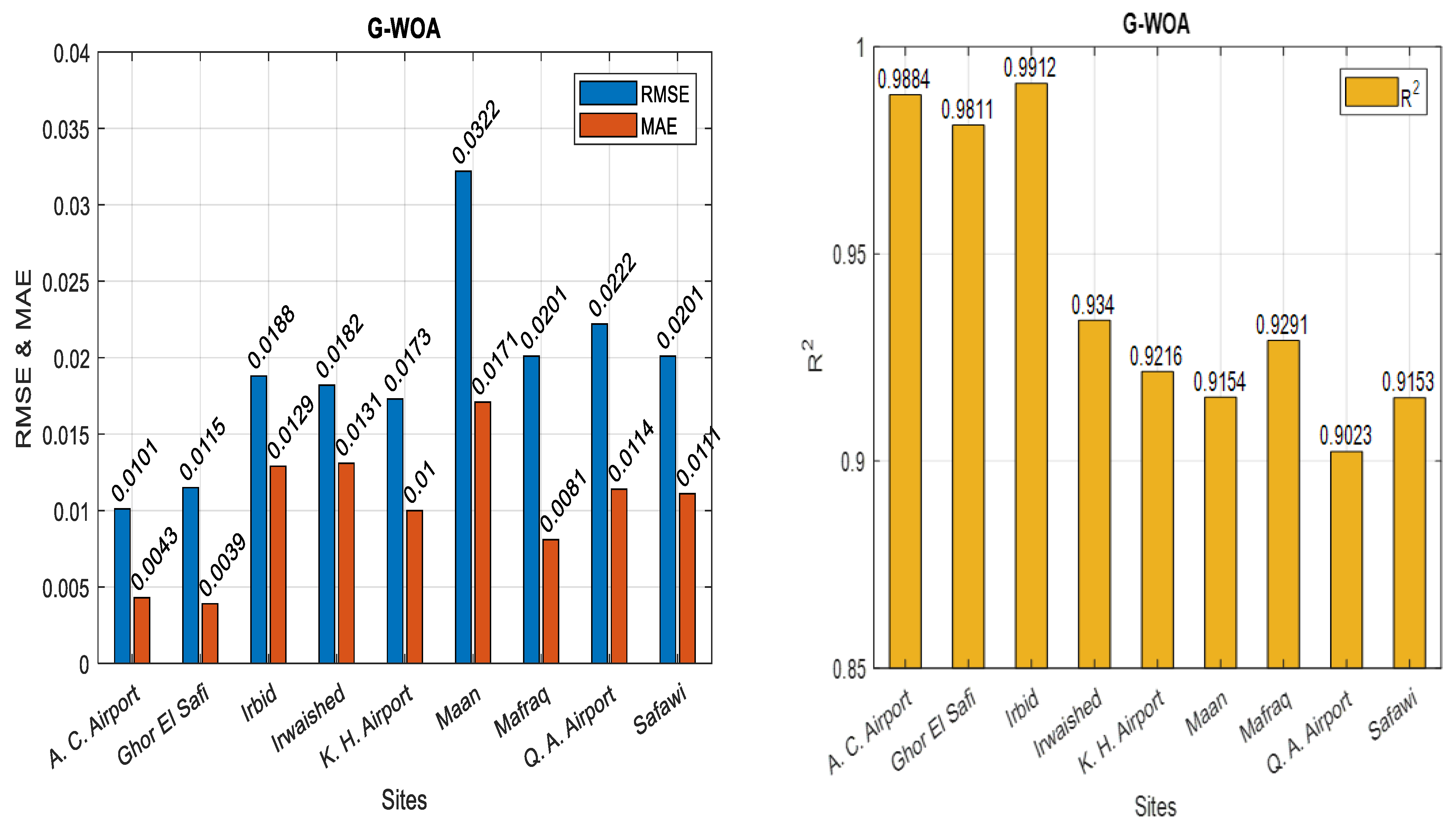
Safawi	K	2.566	2.312	2.212	2.000	2.000	2.000	5.704	5.276	5.076
	C	6.917	5.783	5.645	4.900	3.974	3.734	1.077	0.967	0.912
	RMSE	0.04550	0.03341	0.03134	0.04481	0.03832	0.02823	0.03743	0.02301	0.02014
	R2	0.63002	0.80052	0.82023	0.64109	0.73750	0.85712	0.74963	0.90537	0.91533
	MAE	0.02877	0.02152	0.01812	0.03046	0.02536	0.01501	0.02198	0.01515	0.01112
Irwaished	K	2.150	1.908	1.815	2.000	2.000	2.000	4.135	3.797	3.297
	C	6.216	4.764	4.264	4.393	3.412	3.112	1.332	1.107	1.007
	RMSE	0.04821	0.03268	0.03034	0.04692	0.03135	0.03134	0.04243	0.02286	0.01823
	R2	0.62109	0.82588	0.83512	0.64098	0.83977	0.83912	0.70653	0.91482	0.93401
	MAE	0.02869	0.01941	0.01701	0.02854	0.01859	0.01801	0.02517	0.01388	0.01312
Ghor El-Safi	K	1.729	1.676	1.476	2.000	2.000	2.000	2.779	4.757	4.351
	C	5.087	2.683	2.483	3.617	2.065	2.012	1.631	0.503	0.493
	RMSE	0.06149	0.04152	0.03834	0.06466	0.03221	0.02821	0.05802	0.01457	0.01150
	R2	0.48583	0.76558	0.73523	0.43145	0.85895	0.91895	0.54215	0.97114	0.98110
	MAE	0.02501	0.01203	0.01012	0.02592	0.01091	0.00991	0.02363	0.00481	0.00388

. Generally, the WOA method outperformed the traditional methods (MM and MLM) in all sites based on all indicators results; therefore, this supports the fact that artificial intelligent methods are better than traditional methods. Specifically, the Gamma model employing the whale optimization algorithm (G-WOA) achieved the best results among other models (W-WOA and R-WOA), according to RMSE, R2, and MAE outcomes. Amman Civil Airport had the lowest RMSE value, which was 0.01013, while the worst value recorded by Ma’an with 0.03222. The findings of the RMSE test, which demonstrated the dominance of G-WOA over the other approaches, were supported by the MAE test values. A closer look at the accuracy analysis results revealed that for all wind sites, values greater than 0.9 for the results generated by R² techniques imply that the observations and the expected PDFs were very consistent. In contrast to other wind locations, where the accuracy of the Weibull model employing the whale optimization algorithm (W-WOA) was the superlative model and the indicator values of the RMSE, R², and MAE tests were, respectively, 0.0176, 0.934, and 0.0093, the results for King Hussein Airport were different. In Figure 7, the accuracy indicator results of the best model (G-WOA) are represented graphically. Figure 8 represents the probability distribution function (PDF) and the observation histograms for each site. These graphs confirm that G-WOA offered the best fit. In comparison to the other methods, the figure generally showed that the PDFs associated with the G-WOA method matched the observed data histograms efficiently.

Table 6. Total Wind Energy for the Selected Wind Sites based MM, MLM, and WOA.

	ET (kWh/m2)
Method	Numerical		AI	Numerical		AI	Numerical		AI
	MM	MLM	WOA	MM	MLM	WOA	MM	MLM	WOA
Site	Queen Alia Airport			Amman Civil Airport			King Hussein Airport
Weibull	1002.32	1006.72	1150.85	634.64	668.45	809.34	910.87	992.54	1066.74
Rayleigh	1005.82	1019.06	1319.76	653.56	661.49	792.66	1080.98	1106.81	1228.51
Gamma	930.56	988.21	1070.26	622.21	662.62	862.92	1002.21	1029.35	1140.65
Site	Irbid			Ma’an			Mafraq
Weibull	76.55	80.38	109.58	488.60	530.80	630.93	780.64	809.05	915.65
Rayleigh	81.21	85.47	113.77	502.45	537.65	577.55	802.88	812.81	890.41
Gamma	70.3	75.7	98.51	420.22	493.92	603.73	705.23	739.93	825.12
Site	Safawi			Irwaished			Ghor El-Safi
Weibull	1190.99	1209.17	1369.33	164.89	172.17	194.25	165.74	172.17	192.84
Rayleigh	1202.65	1265.83	1295.95	158.92	177.7	201.22	155.56	177.70	189.52
Gamma	1121.43	1170.33	1250.82	116.22	126.36	192.71	122.76	126.36	168.71

summarizes the entire scenarios of wind energy outcomes for wind regime in all sites. It is noteworthy that the total wind energy calculated by WOA models were greater than the MM and MLM related models; this was because of the optimal performance of WOA according to accuracy indicators. Figure 9 illustrates the total available wind energy based on the G-WOA model. As can be seen from the figure, the Safawi and King Hussein Airport wind sites both produced high total wind energy values with 1250.82 kWh/m² and 1140.65 kWh/m², respectively. On the other hand, Irbid and Ghor El-Safi obtained the lowest energy values with 98.51 kWh/m² and 168.71 kWh/m², respectively. The mean value and the distribution of wind speeds, effectively, affected the outcomes of energy assessment. It is clear that if the mean value was high and the distribution of wind was closer to symmetry (i.e., skewness and kurtosis approach to zero), the amount of extracted energy from wind regime was high and vice versa. Both the Safawi and Irbid cases support this claim, evidently.

5. Conclusions

In this work, a novel method for evaluating the wind energy potential of nine wind sites in Jordan—Queen Alia Airport, Civil Amman Airport, King Hussein Airport, Irbid, Mafraq, Ma’an, Ghor El-Safi, Safawi, and Irwaished—was provided. The Weibull, Rayleigh, and Gamma distribution functions were used to analyze the wind energy potential. The estimation of wind power density and total wind energy—two essential wind regime parameters—formed the basis of this evaluation. It is possible to determine whether or not a wind farm may be built at a particular wind site by applying this assessment to any wind site in the world.

Three distribution models—the Weibull, Rayleigh, and Gamma distributions—were used to implement the available wind speed data in order to evaluate the created method’s correctness. Estimating the parameters for each distribution model involved using the maximum likelihood and moment methods. The root mean square error, coefficient of determination, and mean absolute error were three performance measures that were examined in order to select the best distribution model. The total wind energy varied from slightly less than 100 kWh/m² to approximately 1250 kWh/m². Particularly, the King Hussein Airport and Safawi wind sites both attained the maximum wind power density, whereas Irbid and Ghor El-Safi recorded the lowest wind power densities. Furthermore, the sites with the greatest estimated wind energy showed the highest average wind speed and the most symmetrical distribution pattern.