Analysis of Content Knowledge Categories in Preservice Teachers When Teaching the Concept of Number in Preschool

Abstract

This paper analyzes a cohort of 128 pre-service educators teaching the concept of numbers to 4–5 year old children. Through a professional practice report, which educators elaborate on during the last year of teaching training, we have constructed a dichotomous guide to examine content knowledge, pedagogical content knowledge, curricular content knowledge, and reflective practice categories in their teaching practice. A Bernoulli statistical analysis and the k-means algorithm applied to a sample of 51 lesson plans collected from practice reports leads us to conclude that there is a weak integration of knowledge categories in educators’ practice and suggests how to improve their teaching–learning process.

1. Introduction

Under a formal instructional approach [1], mathematics teaching strictly depends on ontological, epistemological, and methodological elements inherent to the subject who teaches [2]. Understanding the close relationship between these elements within the mathematics teaching process favors the effective teaching of mathematical objects [3]. This teaching discipline is consistent when considering social and cognitive nature elements, such as the curriculum [4] and learning [5]. In general, the ontological and epistemological elements in the teaching function are combined to give particular answers to the question, what can I teach?

The question about how to teach immediately follows, which marks the learner’s socio-cognitive conflict [6]. Under this premise and within the framework of a formal educational process, teaching mathematics means, in the first place, giving meaning to the teaching object in the context defined by the set of individuals who are attached to the learning object previously mentioned, conditioned by a formal curricular structure. Coupled with this, a teacher can teach mathematics if they can continually re-signify the teaching object based on the learning process [7].

This last aspect considers a pedagogy to establish a communication channel between the subject who teaches and the subject who learns through specific didactics of that knowledge [8]. The mechanism of continuous resignification is implemented through the reflection [9] of said educational practice and, in the long term, allows partially answering the question, what does teaching mean? [10,11]. In this research, the elements described above will be considered categories of analysis within the mathematics teaching–learning process.

In particular, a mixed analysis of the integration of the dimensions of content knowledge (CK), pedagogical content knowledge (PCK), curricular content knowledge (CCK), and reflective practice (RP) was performed with a statistical sample of 51 lesson plans taken from 128 educators in pre-service when they taught the concept of numbers to children who were 4–5 years old. These lesson plans were taken from the “professional practice report”, a document written by educators in pre-service during the last semester of professional practice [12].

This consists of preparing a manuscript that integrates and organizes the evidence that is considered essential to represent the competencies established in the graduation profile of an educator in Mexico who is enrolled in a program of Normal Education [13]. This evidence must indicate the knowledge of what is being performed, why it should be completed, and what to do if the context changes in addition to the performance of the competencies considered in the teacher’s graduation profile [14].

This kind of report can be understood as an intellectual exercise derived from reflections on practice to analyze in depth and explain, based on experience and relevant theoretical contributions, a specific educational problem that accounts for the real conditions in which it is developed, the factors that intervene and influence it, the relationships between these factors, and how the school works and is organized. The professional practice reports used as analysis units in this investigation were taken from [15].

This document is structured as follows. Section 2 sets out the contextual coordinates in which this research was performed–namely, a description of the curricular structure of the normal Mexican school and the school mathematics taught in Mexico’s preschool education. In Section 3, the authors present our conception of this research, from which the objectives and central questions to be answered in this work emanate, all related to the analysis of the teaching practice of educators in training when they teach mathematics.

To do this, in Section 4, we present the conceptual framework that we use as an interpretive basis for the results of this work. This section closes by defining content knowledge, pedagogical content knowledge, curricular content knowledge, and reflective practice as categories of analysis. In Section 5, we detail the construction of a first analysis guide to account for the situation of the population analyzed about the above content categories to help us show how reflective practice amalgamates the three other categories of study.

In this section, a clustering method is suggested that helps simplify the content analysis performed, giving rise to a shorter second analysis guide that preserves the same theoretical links found by the first guide. In Section 6, we discuss the results found via both analysis guides, and finally in Section 7, we give our main conclusions for this work as well as recommendations for practitioners about the teaching of mathematics at the preschool level and the perspectives of future work to follow after this work.

2. Context

2.1. A Brief Description of the Normal Education in Mexico

The training of teachers, through the Normal Education in Mexico, are based on competency-based education and the learning-centered approach [16]. On the one hand, competence is the ability to identify, select, coordinate, and mobilize, in an articulated and interrelated manner, diverse knowledge within the framework of an educational situation in a specific context. On the other hand, the learning-centered approach implies an active and conscious process whose purpose is the construction of meanings and attributing meaning to the contents and experiences of the person who learns. This approach implies a highly reflective approach, which is also social, affective, and interactive within a community of socio-cultural practices.

From the structural perspective of an educational system [17], the curricular purpose of Normal Education is to generate graduation profiles that ensure adequate linkage and synergy with Basic Education (mandatory in the 3–15 years stage in Mexico) to guarantee coherence between the curricular approaches, the teaching style and the learning that is desired to be developed in the study plans and programs from the preschool level (3–5 years) to the secondary level (13–15 years) [18].

The curriculum of Normal Education conceives each course as nodes of a complex network that articulates knowledge, purposes, methodologies, and practices that give meaning to the training paths. To fulfill the training purposes, the curriculum was structured with 55 courses (100%) scattered over eight semesters, organized into five training paths and one more curricular space assigned to degree work.

The training paths of the Normal Education plan have a theoretical–practical nature and correspond to (i) the psycho-pedagogical path (∼29.1%); (ii) the path of preparation for teaching and learning (∼36.4%), (iii) the path of additional language and information and communication technologies (∼12.7%), (iv) the path of elective courses (∼7.3%), and (v) the professional practice path (∼14.5%), in which seven courses articulate theoretical–practical activities, with emphasis on the gradual approach to professional activity in specific contexts and its analysis, which are located in the first to the seventh semester.

The last course of this path, in which we focus the analysis population of this work, is located in the eighth semester and is a curricular space of intensive professional practice in preschool with a duration of 20 h for 16 weeks [12]. During this period, educators in training choose a specific topic to make up their professional practice report, which—in this research—corresponds to those documents that deal with the construction of the concept of numbers with children aged 4–5 years.

2.2. Learning Numerical Knowledge in Mexican Preschool Education

According to Mexico’s curriculum [19], the graduation profile in basic education points that students have to achieve progressively throughout their school career are defined from a formative perspective [20]. The graduation profile is organized into several academic areas, of which—in the present study—we only consider mathematical thinking, critical thinking, and problem-solving. Their scope at the preschool level (stages 3–5) and the first cycle of primary school (stages 6–8) are described in

Table 1. Academic areas of the basic education graduate profile considered in this research, according to [18].

Academic Area	At the End of the Preschool Education	At the End of the Primary Education
Mathematical thinking	The child counts to at least 20. The child reasons with quantity problems, builds structures with geometric figures and bodies, and organizes information in simple shapes in simple ways (for example, in tables).	The child understands concepts and procedures to solve mathematical problems and can apply them in other contexts. He/she has a favorable attitude towards mathematics.
Critical thinking and problem solving	The child has ideas and proposes actions to play, learn, and know their environment, solve simple problems and express the steps he/she followed to do it.	The child solves problems applying different strategies, observes, analyzes, reflects, and poses in order. He/she obtains evidence to support the solution he/she proposes. He/she explains their thought processes.

. When developing the graduation profile in these two areas, teaching is assumed as a model that allows the solution of many problems that arise throughout the training through mathematical language. This type of teaching is a productive way of encouraging the student to generate interest through which he/she develops knowledge [18].

Through the above academic areas, we obtain learning constructions for the mathematical field. Within the preschool education learning program [21], expected learning targets are grouped according to different types of problems that require different mathematical knowledge for their treatment and resolution.

Therefore, they are classified according to the discipline itself in three curricular organizers, namely: (i) numbers, algebra, and variation; (ii) form, space, and measure; and (iii) probability and statistics. The expected learning goals related to the curricular organizers (i) and (iii) are described in

Table 2. Expected learning goals from the curricular organizers (i) and (iii) through stages 3–5 in Mexico. See references [21,22].

Expected Learning Goals
Compare, match, and classify collections based on the number of items.
Communicate orally and write the numbers from 1 to 10 in various situations and ways, including conventional.
Count collections of no more than 20 items.
Relate the number of elements in a collection with the written number sequence from 1 to 30.
Identify some currency equivalence relationships of $1, $2, $5, and $10 in real or fictitious buying and selling situations.
Solve problems through counting and actions on the collections.
Answering questions in which it needs to collect data, organize them through tables and pictograms, and make interpretations.

[22]. Based on this, the pre-service educators design their lesson plans.

The educator’s understanding of mathematics demands the structures and functions of basic knowledge (expected learning) to develop them and see how they are transformed during educational practice. This is why it is necessary to establish knowledge from a teaching conviction regarding how to achieve learning results.

3. The General Approach to the Investigation

This study’s importance lies in discussing the conception of teaching practice that pre-service educators have from the ontological, epistemological, and reflective dimensions simultaneously. Once these dimensions have been determined in the practices analyzed, they are contrasted with the curricular dimension that governs, institutionally, the exercise of teaching practice. As part of the subject who teaches, these theoretical elements induce appropriate conditions to acquire specific knowledge for the subject who learns.

The described positioned thesis is that the teacher performs a better pedagogical intervention based on their understanding of this construct. For this reason, it is essential to study the work in the classroom since, reflecting on the practice [23], it is possible to understand the scope of the curricular defined purposes in a particular educational level. The instrumentation of teacher reflection, through the planning process, reflects a dynamic work that regulates student learning [24]. This metacognitive process allows the in-training-educators to answer the question partially, how do my students learn? Moreover, what does it mean to teach the concept of numbers in stages 3–5? This directly impacts the design of the teacher’s class plan [25].

However, discontinuous reflection may be responsible for formulating teacher intervention non-aligned plans with the learning process that are characterized by a lack of intentionality in their structure [26]. This condition depends, strictly speaking, on the extent to which the teacher develops their teaching activity based on CK, PCK, and CCK. From this perspective, it is legitimate to ask ourselves: Do the in-training-educators adequately integrate the dimensions of CK, PCK, and CCK during their teaching intervention in the pre-service stage? Let us place this question in the academic field of Mathematical Thinking at the preschool stage [27].

To teach mathematics to preschool children, we must first know about mathematics at this level, understand how this school mathematics works, know how to build a communication channel between the children and the teacher, and reflect on the intervention itself. Attempting to understand how children learn leads us to reformulate what it means to teach mathematics in early childhood education [28].

Reflective practice is the basis for constructing partial responses to the previous questions, which immediately prompts us to think about those critical aspects within an educator’s academic and professional training. The CK is the engine that makes teaching functional. However, pure knowledge is insufficient to lead a class in early childhood education if pedagogical channels are not created that establish a dialogue with children. In this way, we can say that the PCK is the essence of the teaching activity; however, it is also necessary to know the conditions under which teaching is congruent, that is, to have the CCK.

Continuous reflection on these three dimensions lets us ask whether integrating the CK, PCK, and CCK dimensions into teaching practice favors the teacher’s educational intervention. This question is the backbone of this research. Answering this question, at least partially, will allow us to approach the particular teaching structure that pre-service educators utilize when they work on mathematics in preschool education.

In this way, we will have elements to determine the situation (CK, PCK, and CCK) through the lesson plans of a group of educators selected under specific criteria to conclude their process of reflection on educational practice. These criteria are: (i) being a teacher in training for the eighth semester of Normal Education in Mexico, (ii) studying a Bachelor’s degree in Preschool Education, and (iii) preparing a report on professional practices on the construction of the concept of numbers with children at 4–5 years of age.

4. Conceptual Framework

4.1. Intentional and Reflective Planning as a Methodological Approach That Comes from the Epistemological and Ontological Positions of the Teacher

The implementation of reflective practice (RP) in education falls on the planning of teacher intervention [29]. This, in turn, is the product of a close relationship between the ontological and epistemological positions of the teacher. These positions combine what is believed to be researchable and what is known about what is taught. All this entails adopting a methodological approach to understanding the impact of said teaching ontology and epistemology.

The elements that were considered in this work, in each of the dimensions mentioned, correspond to the teaching of the concept of numbers as a didactic object added to the game in an early childhood education as a didactic means within the context of preschool education. Methodologically, the central product of this approach is an instrument that we call reflective and intentional planning that, in the long run, allows the teacher-in-training to partially answer the following questions: How to teach the concept of numbers in early childhood education? How do children learn their first numerical knowledge?

These constructs will not be produced until the teachers in training reflect on their pedagogical practice. Pedagogy and knowledge are dimensions of teaching that allow one to communicate with students (in this case, children) about the object of knowledge proposed to them [30]. The latter awakens one of the essential elements for the teacher to understand how students learn: the permanent reflection mediated by practice on the educational process immersed in a specific social system [31]. Moreover, this reflection would not make sense unless a social frame of reference indicates that what it teaches has a purpose [32]. Curricular knowledge is a reference system connecting the isolated classroom with society [33]. The curriculum implementation is educational planning, and its premises are educational institutions.

From this social perspective of educational phenomena [34], the epistemological and ontological positions provide quality and meaning to teaching intervention, ensuring the quality of the teaching–learning process through a (teaching) method. The combination of these types of knowledge (content, pedagogy, and curriculum) allows us to glimpse the construct of teaching. However, the motor of the intervention falls on a metacognitive process that implies a reflection on the disciplinary fields, a reflection on the didactic and pedagogical knowledge of the discipline, and a curricular reflection on the knowledge taught [30].

Here, symbolic interactionism [33] is translated as a pragmatic understanding of educational facts [34], regardless of the scale of the analyzed phenomenon. The teacher’s formulation of what it means to teach is a natural product of this process. Reflection on this construction makes it possible to modify (and eventually improve) the teaching intervention. The reflection arises from the educational practice to improve the teaching intervention, giving value to the teacher’s experiences in training. To achieve a true RP, this position must be inscribed in an analytical relationship with the action.

For this reason, recording teaching experiences is a fundamental tool that allows the construction of one’s own teaching styles, fostering a close relationship between theory and practice [35]. The practical–theory relationship enables the teacher to correct and improve the teaching–learning process. In general terms, RP is based on an intentional and systematic analysis. Due to this feature, it can be implemented and, therefore, learned. A natural reflection can become an RP if it promotes a learning outcome that helps with knowledge created through theoretical foundations.

Teachers who practice and exercise RP continuously assume classroom observation, planning, action, and reflection cycles. They are usually nested with future sessions, thus, acting as an upward spiral in which there is no interruption, thereby, achieving continuous improvement in the teaching–learning process. From this frame of reference, we understand RP as a particular form of reasoning that teachers must use during (i) knowledge of the action, (ii) in action, and (iii) about the action [36].

In this way, educational research from a qualitative paradigm is responsible for solving pedagogical problems through critical thinking that arises from the socio-critical method [37]. This method assumes a crucial position towards educational phenomena (whatever their scale), considering action from reflection, self-learning, reasoning, and analysis of reality (see an example in [38]).

4.2. The General Conception of the Teaching–Learning in This Research

The theoretical perspective of the PCK is the conceptual frame of reference [39,40] that we used in this work to describe teaching mathematics in early childhood education [41,42] performed by a group of 128 pre-service educators who worked on constructing the natural number concept with children of 4–5 years old. Qualitatively, the content analysis built on the lesson plans deposited in the professional practice report is the route to understand various aspects of the studied practices. Through a process of constant comparison [43], we identify features of the structure underlying these practices.

Describing learning [44] requires understanding (i) the nature of the knowledge that is learned, (ii) how that knowledge is acquired, and (iii) the meaning of knowing. The first of these elements is subject to the discipline in which that knowledge was conceived, an abstract space in which all objects have a logical order and are entirely related to each other. In reality, this element alone does not involve teaching or learning. The latter are processes associated with subjects that exert some action on the abstract objects that make up the knowledge structure. Interpreting the knowledge objects is the most frequent process performed either by the subject who learns or the subject who teaches [45].

To establish a hierarchy within the teaching–learning process, we will say that the first interpretation made about knowledge is performed by the subject who teaches. This assumption is based on the idea that the teaching–learning process occurs within the socially recognized institution known as School [46,47].

This implies that the object of teaching and learning mediates between both processes. Despite this, the path followed by the subject who teaches to reaches the discipline’s objects could be completely different from the path followed by the learner. A priori, the subject who teaches has some experience with the objects of knowledge that he/she intends to teach. However, the School is regulated through the curriculum, which, at its formal structural level, dictates what, when, and how. This subordination is regulated by educational practice planning, which originates, from a certain point of view, the hidden curriculum [48].

In this way, it can be said that there is a specific method to teach a given specific discipline. For its part, the learner establishes their mechanisms to acquire knowledge under a second interpretation. It is well accepted that one of these mechanisms is the constructivism theory, whose functioning is well described at the cognitive level of the subject [49]. The methods (or trajectories) to access the epistemology of knowledge within the School context coexist permanently. This engenders an inevitable social mediation that can only be regulated, from the teacher’s perspective, by reflection on educational practice and, from the learner’s perspective, by the construct they create about the meaning of knowledge [50].

To facilitate the reading of this work, we will say that knowledge is the subject’s ability to create relationships between the objects that make up the whole within a specific discipline. More precisely, we will say that a subject who knows can create new relationships between the objects that make up their cognitive structure, around a specific knowledge, and the latest information that integrates this structure. In general, learning is significant if it stimulates the acquisition of new relationships, establishes connections between objects, and creates new knowledge within that cognitive structure.

In this way, it is not difficult to assume that “good" teaching promotes analyzing the processes that originate from the study objects’ relationships. We will say then that we are facing dynamic teaching if the subject who teaches identifies, in the subject who learns, the execution of processes that lead him/her to create new relationships in their cognitive structure. On the contrary, static teaching prioritizes the acquisition of objects of knowledge and despises the creation of new relationships.

Teaching and learning from a dynamic approach never end. We begin to weave a graph whose nodes are the concepts of a specific discipline and whose links are the relationships between those objects. A subject knows how large the cognitive graph that he/she constructs in a specific discipline is. With this in mind, we will say that the ability to solve problems lies in the amplitude and nodal density of that cognitive graph.

Suppose the elements described above are located in the specific context of teaching the concept of numbers in preschool education. In that case, we must combine children’s logic, the development of the concept of numbers in stages 3–5, the curriculum of preschool education concerning mathematical thought, the teaching intervention at this level, and the reflection of the mathematical educator, which are described in the following.

4.3. On the Acquisition of the Concept of Numbers in Preschool Education

The development of numerical thinking is based, to a great extent, on the acquisition of the concept of the numerical structure, and, from this, the use of arithmetic [51] naturally follows. However, from a less formal perspective and considering cognitive development, numerical entities’ learning is born informally when we are children. Informal learning is the fundamental basis for understanding and learning the mathematics studied in school.

Children tend to approach formal mathematics based on the informal mathematics they know [52]. In this sense, the childhood stage’s enormous importance in the subsequent mathematics learning that a person will have is postulated. One of the first ideas, and probably the most important one that comes into play during the preschool years, is the concept of quantity. It is here that number words are placed into a variety of contexts that make them practical [53].

Without a doubt, the first abstract object that is learned is the number sequence. This one does not necessarily have to be associated with external objects, unlike the count, where each number is associated with an element of a set of discrete objects. Both objects are designed for counting. However, the second process adds complexity to this activity since it implies the correct use of a one-to-one correspondence between objects and numbers. The counting process concludes with the acquisition of the cardinal concept, becoming aware that the last number in the count indicates the number of objects in the set and enables the child immediately to answer the question, how many are there? It is recognized that the coordination rule is reached around 4 years of age [54].

Thus, counting implies the establishment of a principle of term–object pairing through the action of pointing. In fact, this action creates a space–time unit that connects the object (existing in space) with the numerical entity (existing in time). Within this process, five logical principles implicit in the counting process [55] have been determined: stable order, correspondence, univocity, cardinality, and irrelevance of order. Sometimes a principle known as the principle of abstraction is attached, and, mathematically, this means that any set is countable. Often, this principle is also interpreted as the ability that children acquire to understand that a numeral serves to represent the cardinal of a set formed by any class of objects. The latter seems more than a principle of counting—a mastery level in counting [56,57].

Thus far, we have only described the process of counting, having established a terminology underlying the action of counting. However, we have not established a definition or conception of numbers. The counting process is indispensable in the development of the notion of numbers.

In Ref. [58], J. Sarama (2009) conducted a study that highlights the multidisciplinary nature of research on the construction of the concept of numbers and the implications of those sets that are naturally ordered—that is, a characteristic is added to the objects of the set that they previously did not have: they adopted a position within the group. This means that the objects in the set, when labeled with the numerical entities when a count is made, automatically acquire one (and only) position within that count—that is, an ordinal has been associated with them. In other words, we say that, when a child masters the cardinal notion and the ordinal notion within the counting processes, he/she has acquired the concept of natural numbers.

This small section rescues a conceptual nucleus that in-training educators must understand. Note that there are both theoretical and practical aspects and that they are not exclusive to the field of mathematics but rather strongly intersect with aspects of the educator’s professional practice [59]. We must bet on the conceptual mastery that the student possesses about the disciplinary contents so that, based on this, he/she can adequately project pedagogical intervention activities in preschool [60]. In other words, the knowledge of this conceptual structure allows one to discern which are the appropriate games and activities to develop mathematical concepts in children that encourage them to develop true mathematical thinking.

4.4. Child Logic

In childhood, mathematical thinking is configured by deduction or generalization of the child’s thoughts when solving mathematics learning problems. The development of this thinking is key to the development of mathematical intelligence as this reflects the ability to understand concepts and techniques within reasoning itself.

Logic investigates the relationship of consequences between a series of premises and the conclusion of a correct (valid) argument if its conclusion follows or is a consequence of its premises. Therefore, it is essential to introduce thought processes before results that allow abstracting significant conclusions. From childhood, children reflect on the need to find logical–mathematical reasoning about actions in daily life. This lies the essence of planning educational activities focused on developing mathematical thinking at the preschool level [61].

Logical thinking is dynamic because it is developed at critical moments within the learning of objects. The school context seeks that students develop both that form of logical reasoning and unconventional reasoning. On the one hand, reasoning processes, such as abstraction, justification, visualization, estimation, and reasoning, under our hypotheses are a particular form of human activity that we can understand as mathematical thinking [62]. On the other hand, mathematics is part of the culture transmitted by the organized social training system, which is called the educational system [17].

Mathematics education ranges from the first notions about numbers, form, reasoning, proof, and structure to a set of ideas, knowledge, and processes involved in the construction, representation, and transmission within school education [63]. According to this, if mathematics is the teachers’ study object, the intention of their actions must include performing new practices that involve new generations to achieve mathematics as the object of student learning [64].

In particular, within the acquisition of the concept of numbers, it is necessary to understand the numerical relationships that, from the didactic point of view, combine an aspect of the structure of the concept of numbers with the previous notions that the child acquires in their environment or social context [65]. Numbers and their uses are learned in a social context, hence, the importance of children recognizing the value of the representation of numbers and what can be communicated with them.

As a reflective abstraction, the number is a synthesis of two types of relationships that the child has to establish between objects: order and the other, that of hierarchical inclusion [66]. The child’s notion of numbers is achieved from the direct action that this exerts on objects. In this way, he/she will be able to assimilate each other’s characteristics, linking the ability to conduct correspondences, classifications, and series with the objects in their environment. The acquisition of these relationships in children occurs through concrete experiences—sometimes natural and other times induced.

The mathematical educator’s approach to numbers with children occurs through the game, a fundamental element in early childhood education. In addition to being an innate activity for the child, the game allows the implementation of a variety of didactic strategies. However, school planning should always be adjusted to children’s needs to achieve the purpose that is expected or desired for them to learn [67].

4.5. Reflection on Educational Practice

The reflection arises from the educational practice to improve the teaching intervention, thereby, giving value to the teaching experiences [68]. This is a process of routine action aimed at personal growth in awareness of one’s educational actions. To specify a proper reflective practice (RP), it is necessary that this position becomes something almost permanent and is inscribed within an analytical relationship with the action. This makes it possible to correct and improve the teaching–learning process [9].

Generally speaking, RP is based on an intentional and methodical analysis [69,70]. Since it is systematic, it can be implemented in practice and, therefore, learned. Then, it is possible that a natural reflection can become an RP if it seeks to promote a learning outcome that helps the knowledge created through theoretical foundations. We assume that a reflective attitude contributes to accepting a greater variety of options to help achieve, as already mentioned, learning in students.

Teachers who practice and exercise RP continuously assume cycles of observation, planning, action, and reflection in the classroom [71]. These are usually nested with future sessions, thereby, acting as an upward spiral in which there is no interruption, thus, achieving continuous improvement in the teaching–learning process. The RP must serve to optimize the teaching response so that, effectively, the real needs are satisfied within the classroom. RP, understood as a particular type of reasoning, highlights the importance of practical thinking [72].

Teaching practice is a complex action that inevitably requires reflection on practice to learn from it, which is the appropriate way to improve it. When the teacher learns from their experience, he/she recognizes their knowledge. He/she mobilizes it according to theoretical support, aiming to act in a conscious, comprehensive, and critical way of doing and being in the teaching–learning process [73].

4.6. Dimensions of Knowledge in Teaching Practice

In research focused on teaching practice, it is common to ask: How are content knowledge and general pedagogical knowledge related? In what way are the domains and dimensions of knowledge represented in teachers? How could the acquisition and development of this knowledge be improved? The complexities of understanding and transmitting content knowledge can be addressed according to four dimensions that will be taken as a reference within this work to simplify the analysis of pre-service educators’ teaching practice:

1.

Content Knowledge (CN). This refers to the quantity and organization of knowledge per se in the mind of the teacher. Thinking correctly about content knowledge requires going beyond the knowledge of the facts or concepts of a domain. It requires understanding the structures of the subject in a defined way. This knowledge is understood as the amount of knowledge and method in which the teacher organizes it to achieve better transmission, while having a clear outline of what he/she wants the students to receive.

2.

Pedagogical Content Knowledge (PCN). This refers to the representation of knowledge through ideas, analogies, illustrations, examples, explanations, and more powerful demonstrations, which allow it to be understood by others. It is closely related to the topic’s content within the teaching moment and the materials and support resources in the classroom.

3.

Curricular Content Knowledge (CCN). The curriculum is represented by the full range of programs designed to teach particular subjects and topics at a given level, the variety of instructional materials available concerning those programs, and the set of characteristics that serve as indications and contraindications for using study plans or materials from particular programs. In specific circumstances, the teacher draws out those teaching tools that present or exemplify certain content and remedy or assess student achievement’s adequacy. This type of knowledge marks the teacher’s congruence when deciding what kind of materials or methods he/she will use to transmit curricular knowledge. This knowledge is continuously developing because it must improve with experience during practice.

4.

Reflective Practice (RP). This is a final dimension that is implicit in all the others. Reflection is the process that the teacher uses to realize what is happening in the classroom and self-evaluate its performance to improve their educational practice. Although it may be true that, within the action research that the teacher performs regarding their practice, these dimensions will help them achieve a more profound teacher thinking within the understandable teaching representations. The cognitive process that teachers perform in this type of exercise aims to recover a forgotten aspect during research and didactic practice that is part of the practical wisdom of a teacher’s tradition and their trade of knowledge.

5. Methodology

In this work, we analyzed a sample of 51 lesson plans derived from the professional practices report made by a group of 128 pre-service preschool educators teaching mathematics classes in Mexico. This cohort graduated between 2018 and 2020 under the same study plan, namely, the educational model of Normal Schools in Mexico that was in force from 2012 to 2018. In this way, a semiempirical approach [74] is offered for the methodologically controlled analysis of texts within their communication contexts following analytical rules of content and step-by-step models initially without quantification involved. The purpose of this type of content analysis is to prepare and process relevant data on the conditions in which said texts had been produced or on the conditions that may arise for their subsequent use.

We adjusted the dimensions CK, PCK, and CCK before the specific teaching of the concept of numbers in preschool, obtaining the categories numerical content knowledge in preschool (NCKP), pedagogical knowledge of numerical content in preschool (PKNCP), curricular knowledge of numerical content in preschool (CKNCP), and reflective practice (RP), and the main features are presented in

Table 3. Characterization of the dimensions NCKP, PKNCP, CKNCP, and RP.

Category	Main Features
NCKP	This refers to the quantity and organization of knowledge per se in the mind of the teacher. Think adequately about content knowledge and understand thematic structures.
PKNCP	Include within the topics that are taught most frequently in the subject area the most useful forms of representation of ideas, such as analogies and illustrations, that help the explanations and demonstrations to become representations of the topic in a way that is understandable to all.
CKNCP	The curriculum is represented by the full range of programs designed to teach particular subjects and topics at a given level, including the variety of instructional materials available concerning those programs and the set of characteristics that serve as indications and contraindications for the use of particular curricula or program materials in particular circumstances. The teacher extracts those teaching tools that present or exemplify particular content and remedy or evaluate the adequacy of student achievements.
RP	Reflection on the teacher’s process to realize what is happening in the classroom and self-evaluate their performance to find areas of opportunity that can improve their educational practice.

.

We judged the in-training educator’s group under the conceptual elements of reference and the content analysis—in particular, on whether they integrated the NCKP, PKNCP, and CKNCP categories of teaching intervention and the particular way in which the RP dimension regulated said integration. The final integration of the findings constitutes a synthesis that makes use of the dimensions, and, if the axial codes have been used productively, it will be possible to glimpse new links between classes or between their properties, thereby, allowing the analytical results to be framed on a comparison and relation of the thematic emphasis of interest to the study [75].

The memos or units of analysis were initially filtered, as shown in

Table 4. Questions were used to analyze the features of the NCKP, PKNCP, CKNCP, and RP dimensions. Each feature is mapped to a 0 or 1 value only.

Category	Question (YES/NO)/Feature
NCKP	Q1: Does it include a detailed discussion about the acquisition of the concept of numbers in preschool education?
	Q2: Do your lesson plans call for the child to apply the basic principles of counting?
	Q3: Do your lesson plans call for the child to do numerical reasoning?
	Q4: Do your lesson plans call for the child to use graphic representations to communicate mathematical information?
	Q5: In your teaching intervention proposal, do you consider the development of children’s logical thinking?
PKNCP	Q1: In your experience, do you describe how your students learn mathematics?
	Q2: Does your teaching intervention proposal relate to the development of numerical thinking after stages 3–5 (the first cycle of primary education)?
	Q3: Did you document the child’s prior knowledge before your intervention?
	Q4: Do you take the game as an instructional base in the development of your teaching?
	Q5*: Do your teaching support materials impact your learning purposes? * Specific didactics of content knowledge.
CKNCP	Q1: Do you know the curriculum in which your teaching intervention is framed?
	Q2: Are your lesson plans in accordance with the curricular organization and the pedagogical approaches of the current educational plan and programs?
	Q3: Is there a relationship between the purpose and content of learning within your lesson plans?
RP	Q1: Do you show a reflective practice throughout your intervention proposal? (Substantial or noticeable changes in your lesson plans.)
	Q2: Do you write a notion about the meaning of teaching math at the preschool level?

, which reduces the four dimensions of interest to a set of dichotomous questions that facilitate their assessment. In this way, we managed to articulate a qualitative basis that seeks a better understanding and interpretation of educational reality in teaching the concept of numbers in preschool education. The teaching practice that is performed and expressed is a process that requires teacher–student interaction in line with the curriculum. This research finds the importance of relating the work curriculum with the specific knowledge taught through deliberate and thoughtful planning.

Aimed by specific assignment criteria for each of the questions that make up each category of analysis, it is possible to take, as a basis, the qualitative methodology described above and attempt to associate a statistical measure with the set of results for each of the 51 lesson plans that have been selected as a statistical sample. The binomial character that results from the allocation process allows us to map the qualitative analysis (not shown in this brief report) in a quantitative analysis governed by variables whose values are restricted to the set $\{1,0\}$, “it is observed”, or some of the criteria defined in Table 4 are “not observed”.

In statistics, these variables are known as Bernoulli variables [76]. Given that this study seeks to determine the integration of the NCKP, PKNCP, CKNCP, and RP categories in the teaching intervention observed in the educators’ pre-service period, from the questions in Table 4, our objective was to estimate the proportion of the population that conducted integrated practice through their lesson plans and teacher intervention reports based on the sample of $N=51$ individuals.

If we define the population proportion of reports for which the NCKP-P1 question is observed as $p_1$, then the parameter $p_1$ can be estimated employing a quotient of the form $X/N$, where X represents the sum over the 51 responses (coding “observed” as 1 and “not observed” as 0) to question NCKP-P1. This estimator allows us to infer the proportion of analyzed subjects that reflect having the NCKP-P1 trait. This same methodology applies to each of the 15 questions (features of an integrated practice) listed in Table 4, with which we have 15 estimators on the different features of interest.

Furthermore, it is possible to determine a confidence interval on these proportions and to measure our measurements’ certainty. The latter is essential for the study because it allowed us to migrate from a point estimator to one for which the margin over the estimate grows and carries a degree of confidence (95% is generally used). It is already known that, for a proportion, a confidence interval is given by the point estimator with a correction that, as is typical in Statistics, is obtained as a function of the standard deviation and the reliability, which depend on the distribution of the events.

In our case, we use $n_p\ge 5$ and $n(1-p)\ge 5$ as an empirical rule to conclude the normality in the sample distribution. Finally, it should be mentioned that this empirical rule implies that it was not possible to assume normality for the 15 random variables that result from the sampling. In this case, this same rule will help us to determine those key questions for statistical analysis and inference.

6. Results and Discussion

Using the statistic method described above, we analyzed whether the educators’ population had an integrated practice based on the 15 features of population proportions described in the last section. The results are shown in

Table 5. Population proportions per question.

Category	Question	p	q
NCKP–	P1	0.00	1.00
	P2	0.86	0.14
	P3	0.25	0.75
	P4	0.02	0.98
	P5	0.76	0.24
PKNCP–	P1	0.00	1.00
	P2	0.02	0.98
	P3	0.12	0.88
	P4	0.84	0.16
	P5	0.16	0.84
CKNCP–	P1	1.00	0.00
	P2	1.00	0.00
	P3	0.43	0.57
RP–	P1	0.51	0.49
	P2	0.00	1.00

.

Due to the above empirical rule and as shown in the shaded columns of Table 5, for questions NCKP-P1, NCKP-P4, PKNCP-P1, PKNCP-P2, CKNCP-P1, CKNCP-P2, and RP-P2, it was not possible to assume normality. In these cases, the proportions tended to take extreme values. In this situation, it is natural to discard these categories because this demarcates a trend as to whether these practices were “observed” (∼1) or “not observed” (∼0).

For the rest of the categories, it was possible to assume normality, and this allows us to reinforce the point estimate shown in Table 5. Therefore, we calculated the eight confidence intervals using, as is usual, 95% confidence. The results of this are shown in

Table 6. Confidence intervals for the population proportions per question with a normal distribution.

i	Question	${\mathit{L}}_{\mathit{inf}}$	${\mathit{p}}_{\mathit{i}}$	${\mathit{L}}_{\mathit{sup}}$
2	NCKP-P2	0.7683	0.86	0.9572
3	NCKP-P3	0.1353	0.25	0.3745
5	NCKP-P5	0.6483	0.76	0.8811
8	PKNCP-P3	0.0292	0.12	0.2061
9	PKNCP-P4	0.7433	0.84	0.9429
10	PKNCP-P5	0.0571	0.16	0.2567
13	CKNCP-P3	0.2954	0.43	0.5673
14	RP-P1	0.3726	0.51	0.6470

, where we detail the point estimates $p_i$ (where i = 1,…,15 are the features of each category, labeled from up to down in Table 5) and the lower limits $L_{inf}$ and upper $L_{sup}$ for each of them. Once the confidence intervals were calculated, the margins for the confidence intervals were within reasonable values.

The NCKP-1 and NCKP-4 features were not integrated into the NCKP category of teachers’ teaching practice. This could imply that pre-service educators do not have enough solid formal structure of the school knowledge that they are teaching. In particular, the reported practice does not reflect discussions on building the concept of numbers in preschool mathematics. Similarly, the communication of mathematical results through multiple representations, both concrete and abstract, is not an activity that educators demand of children. However, most lesson plans reflect good work with children on the basic principles of counting and number reasoning, considering the child’s logical thinking. These last features correspond to NCKP-2, NCKP-3 (weakly integrated), and NCKP-5 of the NCKP category.

Once the organization of (scholar) math objects is clear to the subject who teaches, he/she must build multiple representation schemes that help design communication channels with the subject who learns. At the preschool level, a vital vehicle to achieve a level of understanding with the child is the game’s didactic strategy, which must be regulated into the design class structures to keep accurate records of the child’s learning. A frequently used alternative applied by teachers is qualitative analysis through observation guides in the classroom on activities with specific intentions about what the educator wants to observe and how he wants to relate it in their general intervention plan.

This corresponds to PKNCP-3 (weakly integrated) and PKNCP-4 features. The multiple representations of the mathematical objects are integrated into the child’s games, and the educator will present them. Here, the tangible materials that the educator designs are part of the communication channel that the child establishes with the object of knowledge and not only with the educator or with other children. The teaching materials’ function should be aligned with the educator’s purposes in his/her lesson plan. The connectivity and relationship between these elements must be transparent within the lesson plan and, particularly, in the didactic sequence described by the educator as indicated by the PKNCP-5 (weakly integrated) feature.

In the medium or long term, the educator’s records about their teaching intervention place them in a suitable position to describe and understand how their students learn. In other words, he/she empirically has constructs and theories about learning induced by their teaching practice that are still in an unconsolidated development of PKNCP-1 and PKNCP-2 features.

In a way, both the NCKP category and PKNCP maintain certain independence until analyzed together with the CKNCP category. It is possible to assume that the educators’ practice is dominated by intuition and the experience accumulated in their (short) teaching practice but not by considering theoretical positions that help them adequately develop their intervention. Likewise, it is observed that an intervention is performed without a registered (in the teaching practice reports) work methodology that places them in a position to improve the practice itself.

The congruence of educational practice is strictly determined by the curriculum that governs the teaching–learning process when we speak of socially schooled systems. Through the curriculum that pre-service educators use to conduct their practice, the instrumentation of the curriculum requires compliance with specific control standards as set out in the profile of graduation from preschool education. Therefore, it is essential to consider that the hidden (or lived) curriculum plays a fundamental role in teacher development when innovating their educational practice.

However, for this to happen, the educator must bring together the NCKP and PKNCP categories and align them with CKNCP, but how is it possible to perform such an undertaking if there is no evident integration of the NCKP, PKNCP, and CKNCP categories? This inevitably leads to a practice detached from the philosophical foundations and principles of a given curricular proposal as reflected by the absence of CKNCP-P1 and CKNCP-P2 features in their teaching practice.

Despite this, the organization of learning within the class plans of the analyzed educators shows that the structural aspects of the study plan with which the practice is accompanied are known, highlighting that, in general, they have CKNCP-P3 features. This indicates correct use of the curricular organizers and moderately acceptable use of the expected learning targets.

The conscious integration and alignment of the NCKP, PKNCP, and CKNCP categories cannot occur without the RP category. To describe how pre-service educators understand and interpret RP, we must address three fundamental questions: (i) How do they understand and perceive the process of reflection during educational practice? (ii) Do they describe how they learn to reflect on their practice? (iii) Under what context does the reflection occur?

Reflection proceeds the intelligent, active, persistent, and careful action of any supposed form of knowledge considering the motives that support it and the consequences to which it leads. If we refer to question (i), we immediately notice that the construct of educational reflection depends, to a great extent, on the discipline that is taught. This is because the NCKP category’s domain determines the educational intervention’s perception based on what is observed by the educator about the children’s mathematical reasoning. This, in turn, allows him/her to modify the practice of it.

The iterative cycles that can occur within a sequence made up of numerous lesson plans would eventually make the educator perceive a reflection process if he/she notices and records changes in their educational practice. Thus, he/she would gain awareness about the educational process and would be able to perceive educational reflection. However, this implies having the ability to look back in practice critically and imaginatively, performing task analysis, and looking ahead through purposeful planning. This intelligent action that defines the RP is a social object that results from interpreting the teaching–learning dynamic processes.

In other words, a reflection occurs in the action of attempting to understand the relationship of the teaching object, the learning subject, and their role as a teaching subject. These features would help pre-service educators to describe how they reflect, based on the integration of the NCKP and PKNCP. The teaching experiences, situated in socially specific contexts, incorporate the CKNCP dimension to synthesize the educational act’s understanding, thus, originating a personal vision of the entire teaching–learning process.

The RP allows understanding and controlling the content and processes of their work in the classroom, helping the educator to control what happens in the teaching process and to make decisions that define the educational path in which he/she is immersed. The reflection occurs in specific space–time coordinates that give rise to a reflection linked to the concrete action that the educator performs in their working environment. In this way, question (iii) brings us closer to thinking that the RP is a deliberate and systematic investigation of practice that impacts the detection and development of students and of itself.

Hence, the RP is of great interest and importance. It is the amalgamation between teaching and learning or, in other words, of the NCKP, PKNCP, and CKNCP categories. In the context of teaching the concept of numbers in preschool, the RP added to the NCKP makes it possible for the educator to adequately reason regarding their lesson plans and to make them intentional and reflective, linking them to the preschool graduation profile and the entry profile of primary education. Let us not lose sight of the fact that the dimensions mentioned at the beginning of this document are general and that, here, the only example under discussion is the construction of the concept of numbers in preschool at its various levels of development.

The content analysis results that were shown are based on the categories CK, PCK, CCK, and RP defined a priori in this study. These categories applied to the context of teaching the concept of numbers in preschool allowed us to understand the integration of these elements in the teaching practice of the pre-service educators that composed our study sample. However, within the content analysis technique, the analysis guide that emanates from these categories is not governed by any rule that allows deeper investigation. In this study, the said guide mapped each lesson plan analyzed to a row vector of 15 entries with values 1 or 0 depending on whether the previously established traits for each category were observed or not in the units of analysis.

In this way, a certain number of those 15 entries corresponded to a specific category that, in short, accounted for the level of integration of that category of knowledge in the educator. From now on, what we propose in this additional analysis of our results is (i) to determine, under an objective criterion, if the length of the vector associated with each study plan is the most appropriate for the study we propose and (ii) if the order of inputs may be different. The second approach is the most important in this analysis since it implies that the categories can be analyzed in more than one way but with similar or equivalent results to those that the “pure" content analysis already yielded.

In addition to reducing the previous analysis by contracting the original vector, this also reformulates the established categories, thereby, giving a second aligned analysis guide with greater affinity for the analyzed sample in response. In addition to the contraction of the vectors, this analysis could project the set of vectors into a smaller number of categories that are more robust and consistent than those with which the study began. The interest in conducting this analysis is to establish a method that helps us to objectively filter the content analysis to obtain results that are likely to be interpreted more quickly without losing the consistency of the previous results. To do this, we submitted the data to the algorithm known as k-means, which constitutes an objective and robust analysis of our original data.

Below, we make a simple and brief description of this method. The algorithm’s goal is to cluster data, given an input consisting of a sample of N data, to generate k subgroups of this sample (clusters) as output. To achieve this, k centroids or means are initially randomly proposed, then the distance of each of the data to each of these k centroids is determined, and they are grouped with the centroid closest to the data in question. Generally, an exploration is conducted on the number of clusters—that is, the number of clusters is increased, and the one that minimizes the WCSS (within-cluster sums of squares) parameter, or inertia, is chosen, seeking that the number of clusters is not too high. A more detailed description of this method can be found in [77].

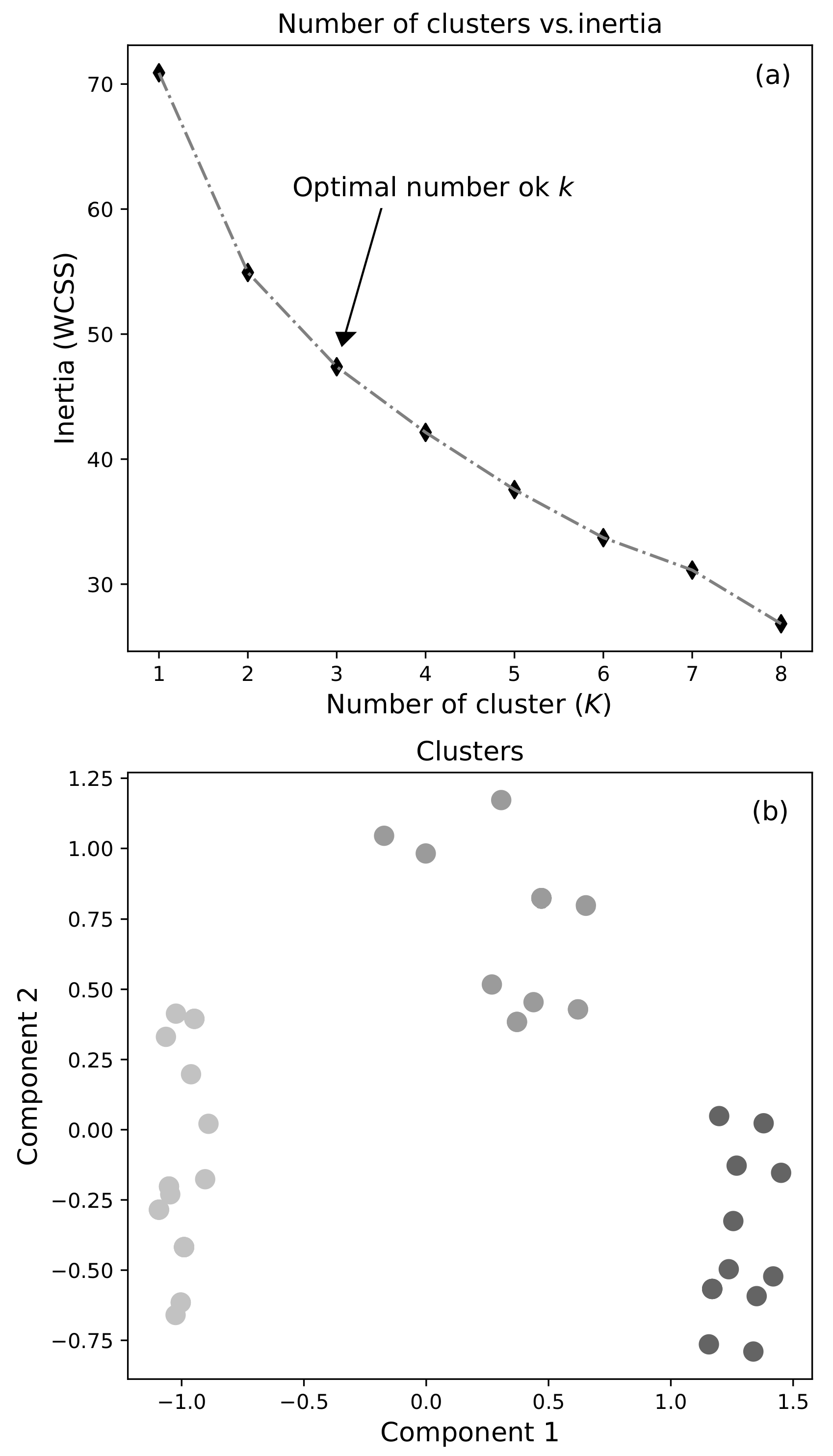
Our data was subjected to the k-means method implemented in the scikit learn library [78] within the python programming language, and then a principal component analysis (PCA was performed and implemented in scikit learn [79]), using only two components (to be able to visualize these groups in a diagram). Analyzing the WCSS parameter, we determined that the best compromise between the least variation and the number of desired clusters was 3 as seen in Figure 1a. It should be noted that, each time the algorithm is executed, the choice of centroids can change. This can be controlled by setting the value of the seed; in our case, we set different values for the seed, and, in Figure 1b, some of the results obtained are visualized.

Our ensemble consists of a sample of $N=51$ data, each consisting of a vector formed by the values 0 or 1 (corresponding to the total of the 15 questions, which were initially grouped in one of the content knowledge categories showed in Table 4). The objective was to know if there is a way to reduce the number of subgroups and whether this is consistent with the current grouping—that is, if any of the new groups completely absorbs any of the categories that were already discussed, or if, on the contrary, it takes elements (questions) from both categories.

Despite the random character present in the algorithm, after performing several simulations with different seed values, we can conclude that, in effect, it is possible to reduce the number of categories (clusters) to 3 because, despite what the image may suggest, detailed analysis allowed us to conclude that, if between one seed and another, the apparent structure of the groups changes, then, on average, the data grouped in cluster 1 in another simulation migrate to group 2 or 3 (similarly for the other two subgroups), and this is only conclusive evidence of the inherent closeness of the data.

Regarding the vector length approach, this methodology tells us that 3 of the 15 questions in the analysis guide can be discarded because they are not significant in the study population, which leads to new vectors of 12 entries. Regarding the second approach, namely a new possible ordering of the entries of the vectors to compose new categories (clusters), we find that these can be reduced to three categories. One of the results that this method yields and confirms the results discussed in section above is that the NCKP-P1, PKNCP-P1, and RP-P1 traits are not integrated in any way in the sample of lesson plans analyzed. For this reason, in

Table 7. The second analysis guide resulting from the k-means algorithm is grouped into three new categories that can reveal new theoretical links about the categories of the guide shown in Table 4.

Category	#	Question	Cluster
NCKP-P2	2	Do your lesson plans call for the child to apply the basic principles of counting?	1
NCKP-P4	4	Do your lesson plans call for the child to use graphic representations to communicate mathematical information?	1
NCKP-P5	5	Do your lesson plans call for the child to use graphic representations to communicate mathematical information?	1
PKNCP-P2	7	Does your teaching intervention proposal relate to the development of numerical thinking after stages 3–5? (the first cycle of primary education.)	1
PKNCP-P4	9	Do you take the game as an instructional base in the development of your teaching?	1
PKNCP-P5	10	Do your teaching support materials impact your learning purposes? Specific didactics of content knowledge.	1
CKNCP-P1	11	Do you know the curriculum in which your teaching intervention is framed?	1
CKNCP-P2	12	Are your lesson plans in accordance with the curricular organization and the pedagogical approaches of the current educational plan and programs?	1
NCKP-P3	3	Do your lesson plans call for the child to do numerical reasoning?	3
PKNCP-P3	8	Did you document the child’s prior knowledge before to your intervention?	3
CKNCP-P3	13	Is there a relationship between the purpose and content of learning within your lesson plans?	3
RP-P1	14	Do you show a reflective practice throughout your intervention proposal? (Substantial or noticeable changes in your lesson plans.)	2

, the questions corresponding to these traits do not appear in any of the clusters shown. However, Table 7 shows the questions that comprise the second analysis guide grouped into the new categories that the described method yielded. The gray scale is in correspondence with the colors of the clusters shown in Figure 1b.

As can be seen, the questions that were not included in any of the clusters found by the algorithm correspond to constructs that the educator forms throughout their practice as a teacher—namely, the meaning of teaching mathematics (RP-P2) and its learning process in preschool (PKNCP-P1) once there is a defined knowledge structure around the concept of numbers (NCKP-P1). These three traits are developed on time scales depending on the work experience in the classroom, adding to a solid conceptual architecture of the numerical knowledge it teaches. Given that the population of educators analyzed is still in the process of teacher training, their experience with the group is expected to be low; and we can say that the abstraction processes necessary in the reflection process have not matured enough.

However, in Group 1, pedagogical and curricular aspects can be observed that organize the educator’s work session around the concept of numbers, according to their class plan: the key learning goals around the development of number sense (NCKP-P2, NCKP-P3, and NCKP-P4), the pedagogy that is known to respond effectively to children’s logic (NCKP-P5, PKNCP-P4, and PKNCP-P5), and elements of curricular understanding, such as the approach and the graduation profile defined for children in the formative field of mathematical thinking (CKNCP-P1, CKNCP-P2, and PKNCP-P2). All these aspects are those that are typically taught during the teacher training stage.

Under the competency development approach in the training plan, the educator constantly practices the knowledge or educational theory that is taught. Therefore, this second cluster (Group 1) has a sense of basic training for teaching and learning. Group 2 refers to the use of the curriculum by requiring the educator to consider the children’s prior knowledge and to align the objective and purposes of the intervention around what is stated in the curriculum used (PKNCP-P3 and CKNCP- P3). Finally, Group 3 resulted in a single-trait cluster (RP-P1), which refers to the permanent process of reflection on educational practice as a modifying agent of constructs that the subject who teaches forms and transforms throughout their practice.

Likely, this new organization of the analysis guide allows us to see theoretical links that were previously were not obvious. For example, Group 1 consists of the pedagogical, instructional, and curricular aspects in which the in-service teacher has been prepared; Group 2 links the curricular organization of the session with the curricular presuppositions of the preschool training path in its entirety and even before it, and finally Group 3 exclusively contains reflective practice as a motor of change and construction of meanings by the teacher in the classroom for continuous improvement.

In this new order, the analysis guide allows us to judge the curriculum under which an educator is trained in Mexico to teach at the preschool level. A substantial load of instructional pedagogical elements is detected in the analyzed population together with general structural elements of the preschool curriculum that it uses (operational aspects) but with a weak understanding of the approaches and vision framed in the basic education curriculum added to a fragile mathematical construction of the number concept. This second analysis is identical to our first discussion of results, which tells us that the implemented method can not only reduce the content analysis technique but also uncover theoretical links that may not have been seen once a new order is detected.

In other words, it shows another face of the same object, making it easier to have a more robust interpretation of the analyzed phenomenon. The method can be used in the same way as shown here with discussion guides leading to vectors of 1s and 0s either for problems similar to the one discussed here or for essentially different ones. Therefore, the PCA used here is valid in populations similar to the one analyzed regardless of the curriculum under which the educator is trained, which constitutes one of the most relevant results of this study.

Finally, for the selected study sample, the questions that make up the only features integrated into the practice of the teachers analyzed are the questions NCKP-P2, NCKP-P5, PKNCP-P4, CKNCP-P1, and RP-P1; grouped into three categories. This reduction of the analysis vector indicates the integrated elements and the categories in which these elements are projected. It is evident that the teacher’s school training, or rather, the curricular response of the study plan in which preschool educators are trained, is responding to minimal needs in the face of the educational reality they face.

Although this vector of 5 entries describes this sample of educators in pre-service, there are 13 entries corresponding to the second analysis guide, and this requires modifications, either in the implementation or in the redesign of the curriculum in normal education, to obtain graduation profiles that, instructionally, are capable of conducting the teaching (in the case at hand) of the concept of numbers in preschool education (the stage of 3–5 years). The proper analysis of Mexican Normal Education curricula is far from the scope of this work; however, it is aligned with our research perspectives.

7. Concluding Remarks

This research focused specifically on mathematics educator’s teaching activities in their practices with children from 4 to 5 years old through analysis of the “professional practice report manuscript”. The CK, PCK, and CCK dimensions of teaching practice bring us closer to understanding the ontological, epistemological, and reflective positions of the analyzed group of educators. The categories of analysis used in the specific context of teaching the number in preschool were NCKP, PKNCP, and CKNCP. The features that define each study category were integrated through a complementary analysis based on the k-means algorithm.

The results of this methodological approach allowed us to understand that the conceptual situation in content, pedagogy, curriculum, and reflection of pre-service teachers was given by the reduced vector {2, 5, 9, 13, 14} about the number of features presented in Table 4. Conducting this procedure yielded a second analysis guide (Table 7) that “decanted” the first analysis guide (Table 4) formulated from the theoretical constructs established a priori in this research. This provides a valuable contribution to synthesizing the common techniques of content analysis—as long as we can reduce the description of the units of analysis to vectors of dichotomous inputs.

The interpretation of this second phase of results maintains reasonable agreement with that derived exclusively from elements of statistical inference from Bernoulli-type variables. Finally, we can say that the simultaneous work of content, pedagogy, curriculum, and reflection produce effective instruction in the classroom through demarcating domain categories that emerge directly or else building an ontological and epistemological position that results in an efficient teaching method regardless of the scholar context where this process is located.

7.1. About the Reflection of the Teaching Practice: General Recommendations

Math educators must have a good command and understanding of the mathematical objects that he/she intends to teach. In this way, he/she can organize a pedagogical intervention through multiple representations of said objects. In preschool education, it is well known that games are the instructive basis of teaching. However, these must be consistent with the purpose of math sessions and their relevance within the curriculum in which the teaching–learning process is conducted.

From the findings of this research, it is clear that the RP dimension governs, in a metacognitive sense, the integration of the other three dimensions. Particularly, regarding the NCKP category, we found that the analysis population does not have a precise organization of the math objects, which induces sequences of classes that do not promote adequate numerical knowledge in children. In addition, we found that most activities focus solely on teaching the basic principles of counting and, to a lesser extent, on number reasoning activities. On the other hand, teaching information processing and communication is almost nil.

This implies that the didactic sequence design lacks intentionality, which derives from a weak mastery of the construction of the concept of numbers in early childhood education. However, according to the study plan, many of the analyzed class plans adequately organized the proposed activity. Despite this, the use of didactic materials, games, and worksheets, among others (that is, the multiple representations that are the product of the use of a good pedagogy) is not necessarily congruent with the exposed curricular organization.

Statistically, it is possible to infer that the RP category is weak. This is possibly due to the short experience of the educators in training. Superfluous reflection leads to scattered didactic plans and sequences about given expected learning. The category RP is the key to acquiring a construct about the meaning of teaching math in preschool and reaching a degree of understanding about how students learn. The RP implementation is the plan that an educator will formulate only if he/she makes a meticulous record of the children’s response behaviors to the proposed activities. The analysis of this study’s dimensions confirms that the teaching intervention’s quality is a direct function of the conscious integration of the dimensions mentioned above.

7.2. Future Research

Finally, we mention the expectations and future work aligned with this research. Concerning the training of the mathematics educator in the infant stage, it is possible to build a curricular proposal that prioritizes the construction of the concept of numbers in the context of pure mathematics, then reinterprets them as school mathematics, and finally is organized within a curricular structure. This type of curriculum would allow teachers in training, during their practice periods, to begin deeper reflection processes that will eventually enable them to build notions of the teaching–learning process of mathematics at a specific educational level.

This reflective practice must always be accompanied by the theoretical frameworks that underlie the contexts where teaching takes place and where learning will occur. The proposal of a curriculum governed by these aspects is a challenge for the community of educational researchers and teachers in front of a group. On the other hand, research work in mathematics applied to the systematization of the content analysis methodology relies on the numerical coding of the analysis guides in scales that are not necessarily dichotomous. In this way, with the adaptation of certain clustering methods, it would be possible to obtain analysis categories that are well defined by data-analysis techniques.

Once this is finished, the coding and categorization processes would preserve highly reliable analytical methods that would help the social science researcher discover theoretical links in the units of analysis collected in a given population that come from a phenomenon of specific interest. The method suggested here is independent of the subject of study as long as the analysis guides can be vectorized in the way we present here. Despite the existence of software specialized in performing this type of analysis, this proposal is cheaper.

This method is versatile in proceeding with an analysis that descends from the heights of the established theoretical precepts to the analysis units collected. Still, it can also reconstruct a theory from the base where the units of analysis are rooted. Proceeding in both directions embodies a method of triangulation that would confirm the coding processes and open up opportunities to extend the theories used in a given problem.