Forecast of the Evolution Trend of Total Vehicle Sales and Power Structure of China under Different Scenarios
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contribution and Organization
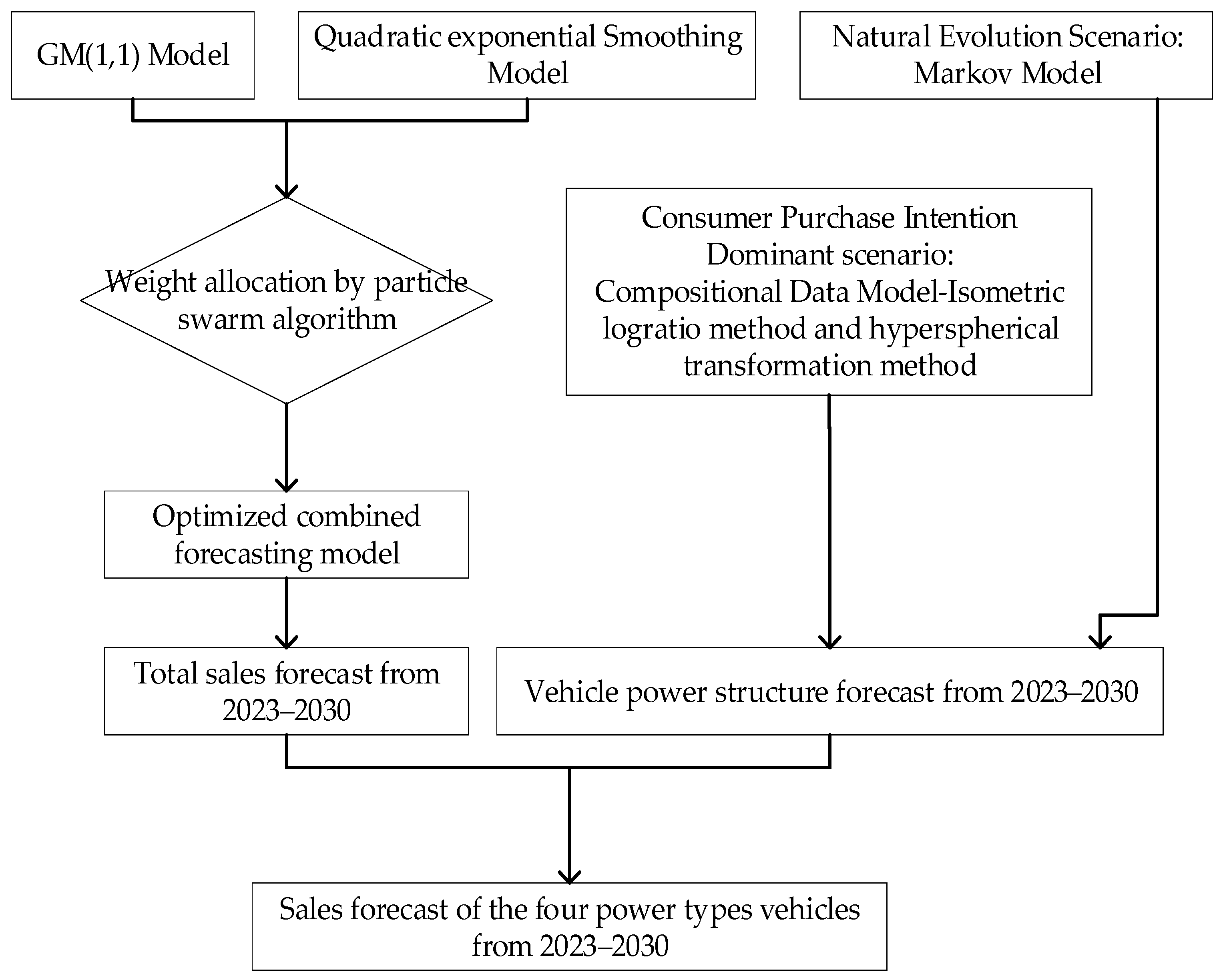
2. Methodology
2.1. Forecast Models for Total Car Sales in China
2.1.1. Grey Model
2.1.2. Quadratic Exponential Smoothing Model
2.1.3. Combinatorial Prediction Model Optimized by Particle Swarm Algorithm
2.1.4. Model Evaluation
2.2. Forecast Models for China’s Vehicle Power Structure
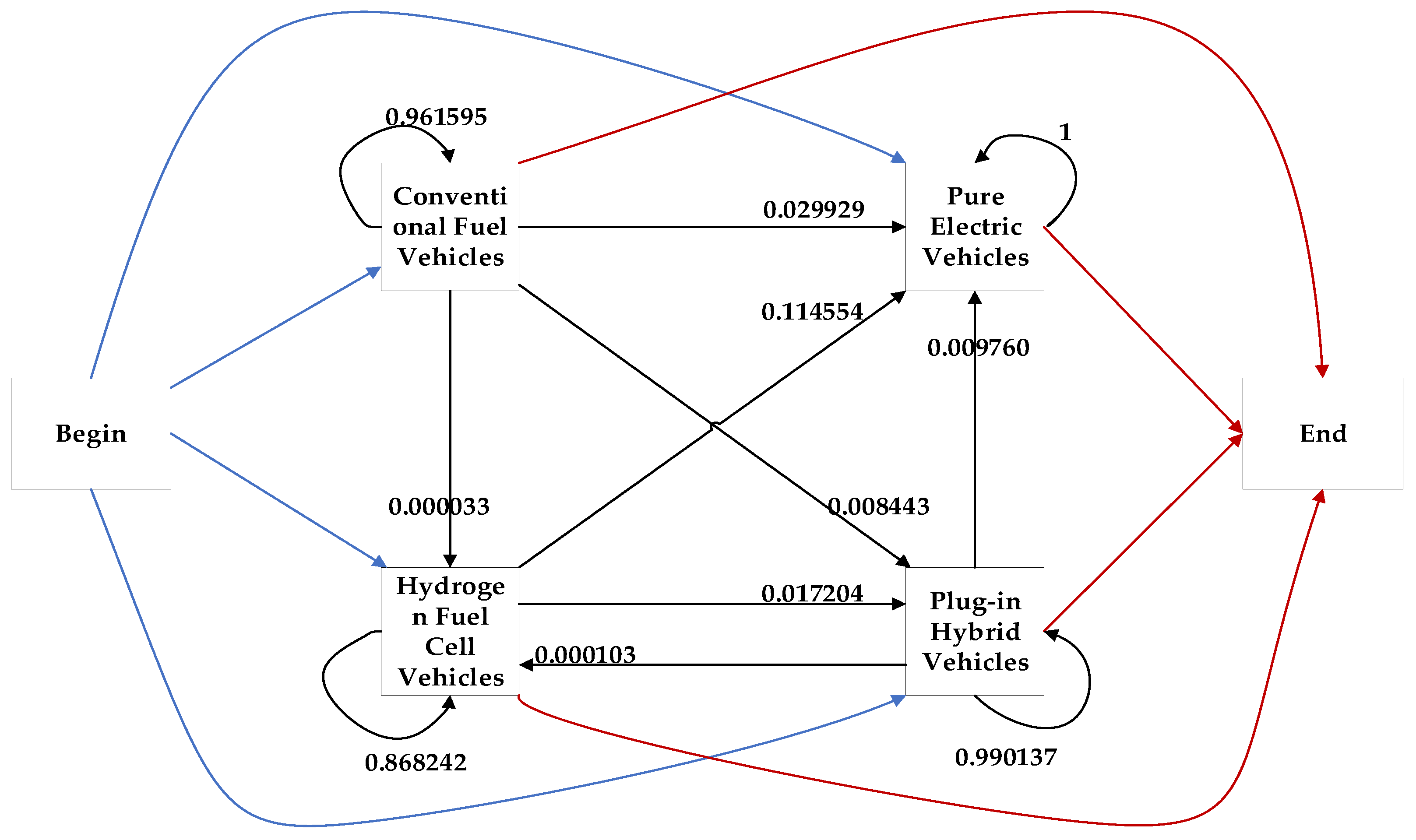
2.2.1. Markov Model
2.2.2. Compositional Data Model
2.2.3. Model Evaluation
2.3. Scenario Analysis
2.3.1. Natural Evolution Scenario
2.3.2. Consumer Purchase Intention Dominant scenario
3. Results and Discussion
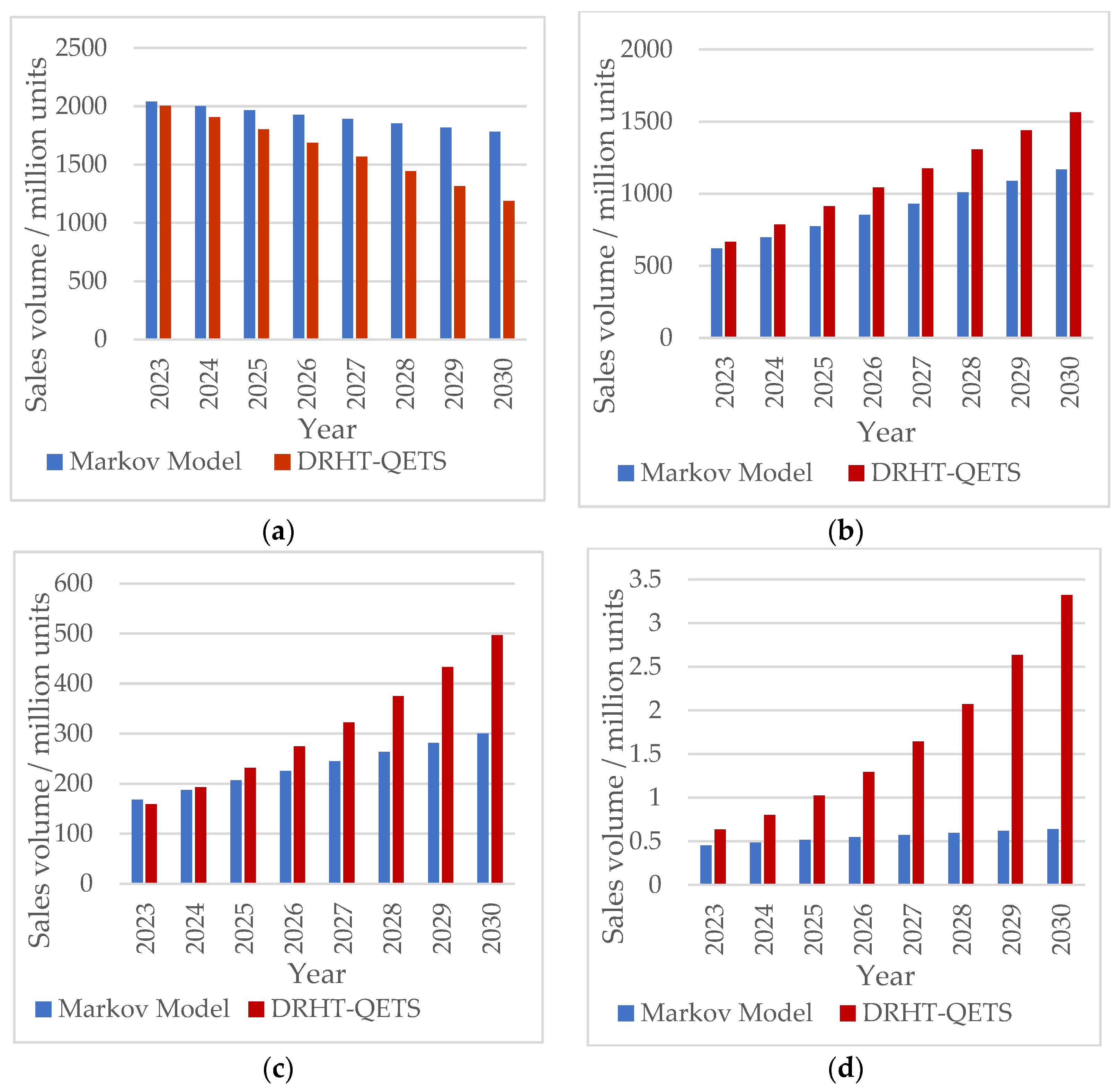
3.1. Total Vehicle Sales Forecast Results
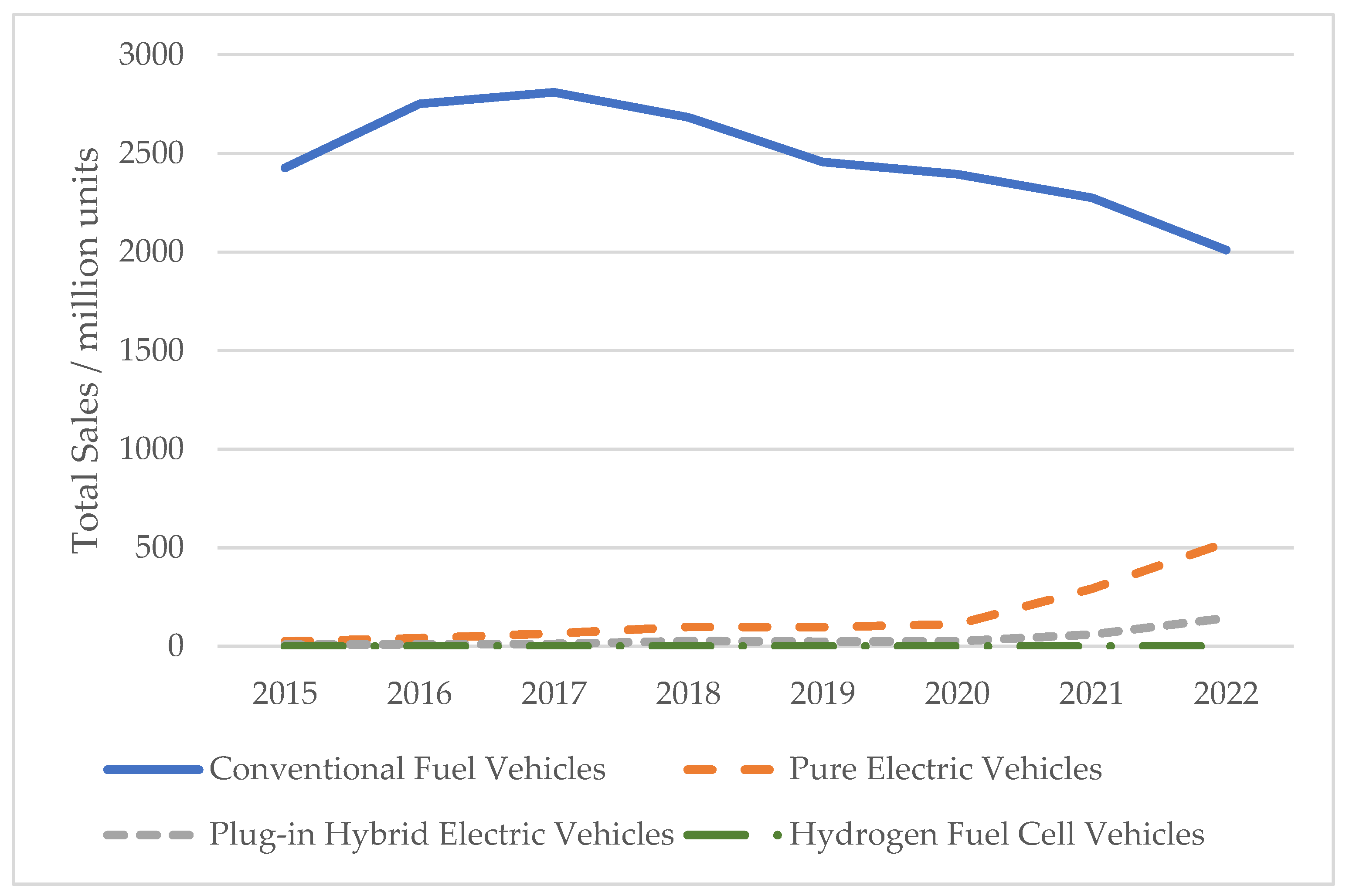
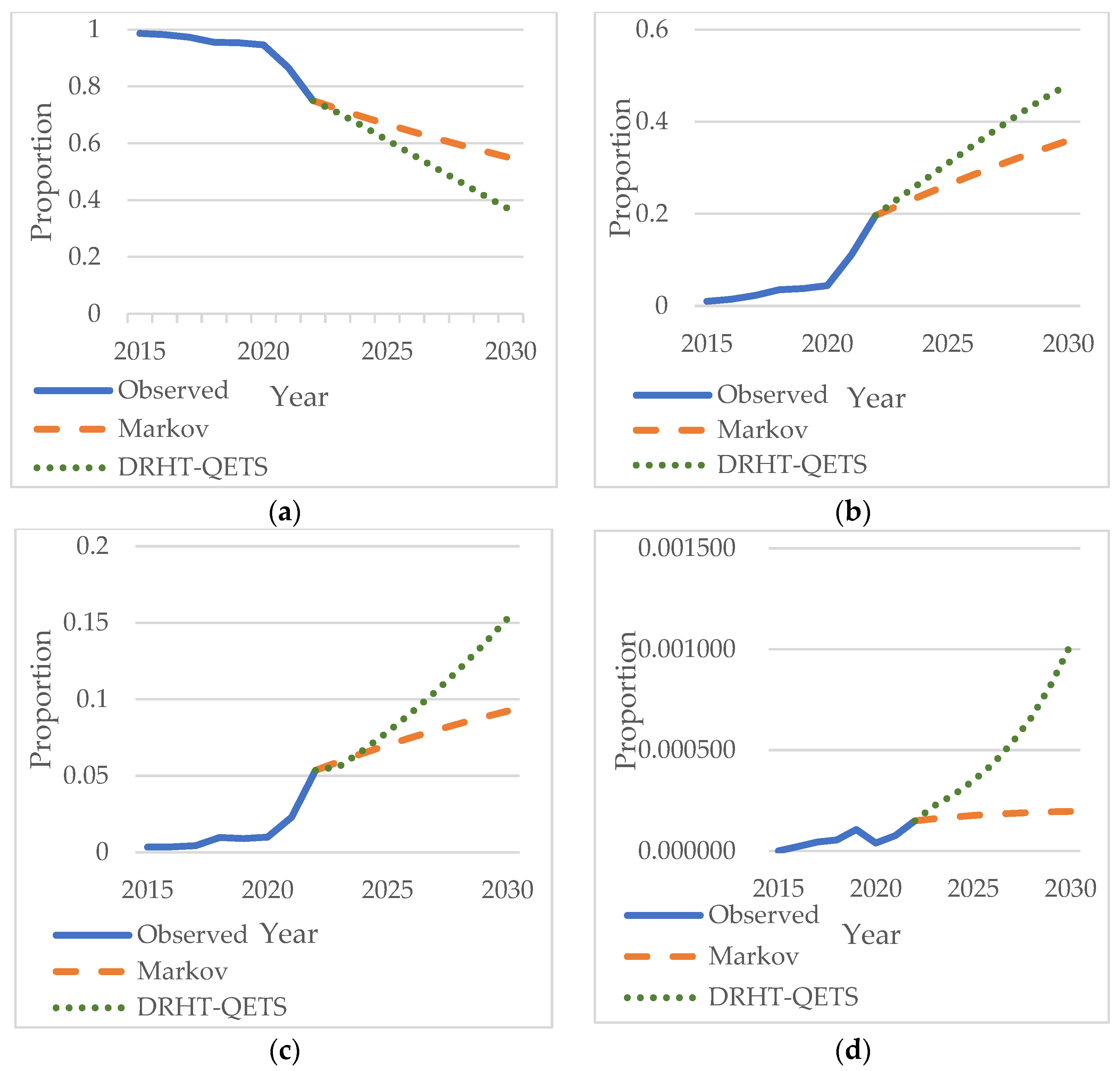
3.2. Vehicle Power Structure Prediction Results
3.2.1. Calculation Result of Transition Probability Matrix
3.2.2. Comparison of Models
3.2.3. Prediction Results of Vehicle Power Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, L.; Wu, M.H.; Tian, X.J.; Zheng, G.H.; Du, Q.C.; Wu, T. China’s provincial vehicle ownership forecast and analysis of the causes influencing the trend. Sustainability 2019, 11, 3928. [Google Scholar] [CrossRef]
- Pichler, M.; Krenmayr, N.; Maneka, D.; Brand, U.; Hogelsberger, H.; Wissen, M. Beyond the jobs-versus-environment dilemma? Contested social-ecological transformations in the automotive industry. Energy Res. Soc. Sci. 2021, 79, 11. [Google Scholar] [CrossRef]
- Zhao, M.; Sun, T.; Feng, Q. A study on evaluation and influencing factors of carbon emission performance in china’s new energy vehicle enterprises. Environ. Sci. Pollut. Res. 2021, 28, 57334–57347. [Google Scholar] [CrossRef]
- Du, Z.L.; Lin, B.Q.; Guan, C.X. Development path of electric vehicles in china under environmental and energy security constraints. Resour. Conserv. Recycl. 2019, 143, 17–26. [Google Scholar]
- Chen, W.W.; Xu, M.Z.; Xing, Q.S.; Cui, L.G.; Jiao, L.D. A fuzzy demand-profit model for the sustainable development of electric vehicles in china from the perspective of three-level service chain. Sustainability 2020, 12, 6389. [Google Scholar] [CrossRef]
- Wang, X.L.; Huang, L.C.; Daim, T.; Li, X.; Li, Z.Q. Evaluation of China’s new energy vehicle policy texts with quantitative and qualitative analysis. Technol. Soc. 2021, 67, 11. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Xu, H.Y.; Ma, N.; Pan, X.L. Intelligent vehicle sales prediction based on online public opinion and online search index. Sustainability 2022, 14, 344. [Google Scholar] [CrossRef]
- Yuan, X.D.; Cai, Y.C. Forecasting the development trend of low emission vehicle technologies: Based on patent data. Technol. Forecast. Soc. Chang. 2021, 166, 9. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczynski, D.; Robak, S.; Kopyt, M.; Piekarz, M.; Polewaczyk, M. Comprehensive forecast of electromobility mid-term development in poland and its impacts on power system demand. Bull. Pol. Acad. Sci.-Tech. Sci. 2020, 68, 697–709. [Google Scholar]
- Mao, J.; Hong, D.; Ren, R.W.; Li, X.Y. The effect of marine power generation technology on the evolution of energy demand for new energy vehicles. J. Coast. Res. 2020, 103, 1006–1009. [Google Scholar] [CrossRef]
- Akbar, K.; Zou, Y.; Awais, Q.; Baig, M.J.A.; Jamil, M. A machine learning-based robust state of health (soh) prediction model for electric vehicle batteries. Electronics 2022, 11, 1216. [Google Scholar] [CrossRef]
- Gibson, E.; van Blommestein, K.; Kim, J.; Daim, T.; Garces, E. Forecasting the electric transformation in transportation: The role of battery technology performance. Technol. Anal. Strateg. Manag. 2017, 29, 1103–1120. [Google Scholar] [CrossRef]
- Sato, F.E.K.; Nakata, T. Recoverability analysis of critical materials from electric vehicle lithium-ion batteries through a dynamic fleet-based approach for japan. Sustainability 2020, 12, 147. [Google Scholar] [CrossRef]
- Zou, Y.J.; Ding, L.S.; Zhang, H.; Zhu, T.; Wu, L.T. Vehicle acceleration prediction based on machine learning models and driving behavior analysis. Appl. Sci.-Basel 2022, 12, 5259. [Google Scholar] [CrossRef]
- Liu, Y.T.; Cheng, D.; Wang, Y.R.; Cheng, J.J.; Gao, S.C. A novel method for predicting vehicle state in internet of vehicles. Mob. Inf. Syst. 2018, 2018, 9728328. [Google Scholar] [CrossRef]
- Tang, L.; Wang, H.Y.; Zhang, W.H.; Mei, Z.Y.; Li, L. Driver lane change intention recognition of intelligent vehicle based on long short-term memory network. IEEE Access 2020, 8, 136898–136905. [Google Scholar] [CrossRef]
- Hsieh, I.Y.L.; Kishimoto, P.N.; Green, W.H. Incorporating multiple uncertainties into projections of chinese private car sales and stock. Transp. Res. Record 2018, 2672, 182–193. [Google Scholar] [CrossRef]
- Lian, L.; Tian, W.; Xu, H.F.; Zheng, M.L. Modeling and forecasting passenger car ownership based on symbolic regression. Sustainability 2018, 10, 2275. [Google Scholar] [CrossRef]
- Pai, P.F.; Liu, C.H. Predicting vehicle sales by sentiment analysis of twitter data and stock market values. IEEE Access 2018, 6, 57655–57662. [Google Scholar] [CrossRef]
- Ou-Yang, C.; Chou, S.C.; Juan, Y.C. Improving the forecasting performance of taiwan car sales movement direction using online sentiment data and cnn-lstm model. Appl. Sci.-Basel 2022, 12, 1550. [Google Scholar] [CrossRef]
- Wang, K.L.; Zheng, L.J.; Zhang, J.Z.; Yao, H.J. The impact of promoting new energy vehicles on carbon intensity: Causal evidence from china. Energy Econ. 2022, 114, 12. [Google Scholar] [CrossRef]
- Pei, L.L.; Li, Q. Forecasting quarterly sales volume of the new energy vehicles industry in china using a data grouping approach-based nonlinear grey bernoulli model. Sustainability 2019, 11, 1247. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, M.; Geng, N.N.; Jiang, Y.J. Forecasting electric vehicles sales with univariate and multivariate time series models: The case of china. PLoS ONE 2017, 12, 15. [Google Scholar] [CrossRef]
- Wang, M.X.; Wang, Y.J.; Chen, L.; Yang, Y.Q.; Li, X. Carbon emission of energy consumption of the electric vehicle development scenario. Environ. Sci. Pollut. Res. 2021, 28, 42401–42413. [Google Scholar] [CrossRef]
- Wu, M.F.; Chen, W. Forecast of electric vehicle sales in the world and china based on pca-grnn. Sustainability 2022, 14, 2206. [Google Scholar] [CrossRef]
- Rietmann, N.; Hugler, B.; Lieven, T. Forecasting the trajectory of electric vehicle sales and the consequences for worldwide co2 emissions. J. Clean Prod. 2020, 261, 16. [Google Scholar] [CrossRef]
- Bitencourt, L.; Abud, T.; Santos, R.; Borba, B. Bass diffusion model adaptation considering public policies to improve electric vehicle sales-a brazilian case study. Energies 2021, 14, 5435. [Google Scholar] [CrossRef]
- Guo, D.; Yan, W.; Gao, X.B.; Hao, Y.J.; Xu, Y.; Wenjuan, E.; Tan, X.C.; Zhang, T.Q. Forecast of passenger car market structure and environmental impact analysis in china. Sci. Total Environ. 2021, 772, 17. [Google Scholar] [CrossRef]
- Islam, M.R.; Ali, S.M.; Fathollahi-Fard, A.M.; Kabir, G. A novel particle swarm optimization-based grey model for the prediction of warehouse performance. J. Comput. Des. Eng. 2021, 8, 705–727. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Liu, H.T.; Hsieh, H.L. Time series interval forecast using gm(1,1) and ngbm(1,1) models. Soft Comput. 2019, 23, 1541–1555. [Google Scholar] [CrossRef]
- Yao, T.X.; Wang, Z.H. Crude oil price prediction based on lstm network and gm (1,1) model. Grey Syst. 2021, 11, 80–94. [Google Scholar] [CrossRef]
- Qian, W.Y.; Wang, J. An improved seasonal gm(1,1) model based on the hp filter for forecasting wind power generation in china. Energy 2020, 209, 15. [Google Scholar] [CrossRef]
- Zor, C.; Cebi, F. Demand prediction in health sector using fuzzy grey forecasting. J. Enterp. Inf. Manag. 2018, 31, 937–949. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.J.; Liu, S.F. A new method to mitigate data fluctuations for time series prediction. Appl. Math. Model. 2019, 65, 390–407. [Google Scholar] [CrossRef]
- Barrow, D.; Kourentzes, N.; Sandberg, R.; Niklewski, J. Automatic robust estimation for exponential smoothing: Perspectives from statistics and machine learning. Expert Syst. Appl. 2020, 160, 14. [Google Scholar] [CrossRef]
- Sbrana, G.; Silvestrini, A. Random switching exponential smoothing: A new estimation approach. Int. J. Prod. Econ. 2019, 211, 211–220. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.H.; Zhang, Q.; Huang, C.Y. Empirical mode decomposition based hybrid ensemble model for electrical energy consumption forecasting of the cement grinding process. Measurement 2019, 138, 314–324. [Google Scholar] [CrossRef]
- Lin, L.; Handley, J.C.; Gu, Y.M.; Zhu, L.; Wen, X.J.; Sadek, A.W. Quantifying uncertainty in short-term traffic prediction and its application to optimal staffing plan development. Transp. Res. Pt. C-Emerg. Technol. 2018, 92, 323–348. [Google Scholar] [CrossRef]
- Miao, K.; Mao, X.L.; Li, C. Individualism of particles in particle swarm optimization. Appl. Soft. Comput. 2019, 83, 13. [Google Scholar] [CrossRef]
- Liu, E.C.; Li, J.; Zheng, A.N.; Liu, H.R.; Jiang, T. Research on the prediction model of the used car price in view of the pso-gra-bp neural network. Sustainability 2022, 14, 8993. [Google Scholar] [CrossRef]
- Sun, L.Q.; Yang, Y.L.; Ning, T.; Zhu, J.D. A novel grey power-markov model for the prediction of china’s electricity consumption. Environ. Sci. Pollut. Res. 2022, 29, 21717–21738. [Google Scholar] [CrossRef]
- Zhu, B.Z.; Wang, K.F.; Chevallier, J.; Wang, P.; Wei, Y.M. Can china achieve its carbon intensity target by 2020 while sustaining economic growth? Ecol. Econ. 2015, 119, 209–216. [Google Scholar] [CrossRef]
- Wei, Y.G.; Wang, Z.C.; Wang, H.W.; Li, Y.; Jiang, Z.Y. Predicting population age structures of china, india, and vietnam by 2030 based on compositional data. PLoS ONE 2019, 14, 42. [Google Scholar] [CrossRef]
- Wei, Y.G.; Wang, Z.C.; Wang, H.W.; Yao, T.; Li, Y. Promoting inclusive water governance and forecasting the structure of water consumption based on compositional data: A case study of beijing. Sci. Total Environ. 2018, 634, 407–416. [Google Scholar] [CrossRef]
- Lin, B.Q.; Shi, L. Do environmental quality and policy changes affect the evolution of consumers’ intentions to buy new energy vehicles. Appl. Energy 2022, 310, 9. [Google Scholar] [CrossRef]

| Primary Indicators | Secondary Indicators | Type |
|---|---|---|
| A1 Cost Factors | A11 Purchase Price | Negative |
| A12 Cost of Using | Negative | |
| A2 Technical Factors | A21 Range | Positive |
| A22 Charging Speed | Positive | |
| A23 Battery Durability | Positive | |
| A3 Infrastructure Factors | A31 Construction of charging stations, hydrogen refueling stations, etc | Positive |
| A32 After Sales Service | Positive | |
| A4 Policy Factors | A41 Promotion Policy | Positive |
| A42 Vehicle Purchase Policy | Positive | |
| A43 Right-of-way Policy | Positive | |
| A44 Supporting Services Policy | Positive |
| Scale | Scale Meaning |
|---|---|
| 1 | Both factors are equally important |
| 3 | One factor is slightly more important than the other |
| 5 | One factor is significantly more important than the other |
| 7 | One factor is more strongly important than the other |
| 9 | One factor is more important than the other in calculation |
| 2, 4, 6, 8 | Median of the above two adjacent judgment |
| Primary Indicators | 2023: A1 | A2 | A3 | A4 | Weight | CR | 2030: A1 | A2 | A3 | A4 | Weight | CR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1/3 | ½ | ¼ | 0.10 | 1 | 1/5 | ½ | ¼ | 0.08 | ||
| A2 | 3 | 1 | 2 | ½ | 0.28 | 0.012 | 5 | 1 | 3 | 2 | 0.48 | 0.008 |
| A3 | 2 | ½ | 1 | 1/3 | 0.16 | 2 | 1/3 | 1 | ½ | 0.15 | ||
| A4 | 4 | 2 | 3 | 1 | 0.46 | 4 | ½ | 2 | 1 | 0.29 |
| Primary Indicators | Secondary Indicators | Weight | CR | Consistency Check |
|---|---|---|---|---|
| A1 | A11 | 0.75 | / | Passed |
| A12 | 0.25 | |||
| A2 | A21 | 0.54 | 0.009 | Passed |
| A22 | 0.30 | |||
| A23 | 0.16 | |||
| A3 | A31 | 0.25 | / | Passed |
| A32 | 0.75 | |||
| A4 | A41 | 0.16 | 0.012 | Passed |
| A42 | 0.10 | |||
| A43 | 0.28 | |||
| A44 | 0.46 |
| Primary Indicators | Weight | Value | Secondary Indicators | Weight | Value | |||
|---|---|---|---|---|---|---|---|---|
| 2023 | 2030 | 2023 | 2030 | 2023(2030) | 2023 | 2030 | ||
| A1 | 0.100 | 0.080 | 0.125 | 0.225 | A11 | 0.750 | 0.100 | 0.200 |
| A12 | 0.250 | 0.200 | 0.300 | |||||
| A2 | 0.280 | 0.480 | 0.123 | 0.269 | A21 | 0.540 | 0.100 | 0.300 |
| A22 | 0.300 | 0.150 | 0.250 | |||||
| A23 | 0.160 | 0.150 | 0.200 | |||||
| A3 | 0.160 | 0.150 | 0.125 | 0.225 | A31 | 0.250 | 0.200 | 0.300 |
| A32 | 0.750 | 0.100 | 0.200 | |||||
| A4 | 0.460 | 0.290 | 0.260 | 0.390 | A41 | 0.160 | 0.250 | 0.500 |
| A42 | 0.100 | 0.300 | 0.600 | |||||
| A43 | 0.280 | 0.350 | 0.400 | |||||
| A44 | 0.460 | 0.200 | 0.300 | |||||
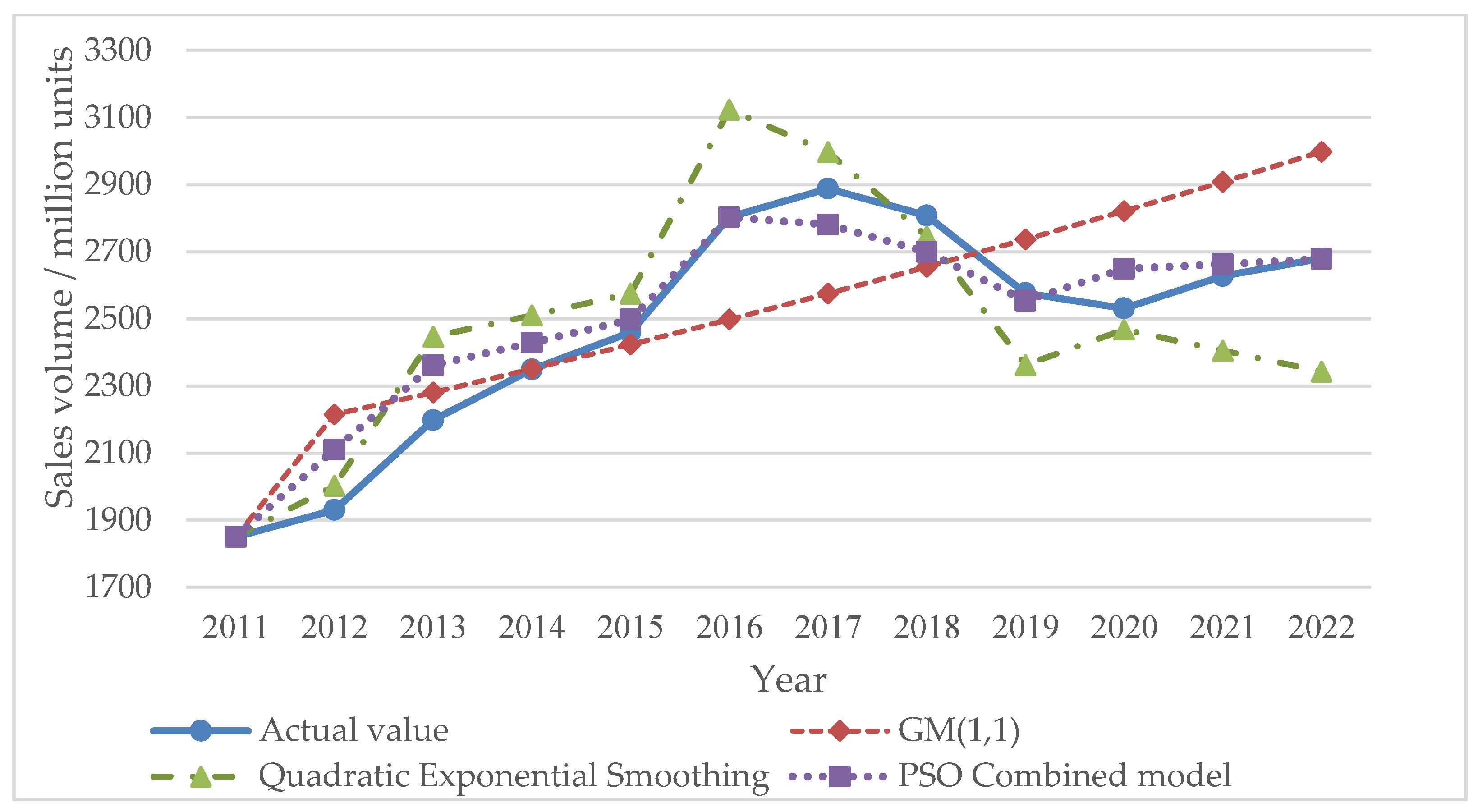
| Year | Actual Value | GM (1,1) | Quadratic Exponential Smoothing Model | PSO Combined Model |
|---|---|---|---|---|
| 2011 | 1850.51 | 1850.51 | 1850.51 | 1850.51 |
| 2012 | 1930.64 | 2215.50 | 2002.80 | 2110.30 |
| 2013 | 2198.41 | 2280.70 | 2446.80 | 2361.70 |
| 2014 | 2349.19 | 2351.10 | 2510.20 | 2428.70 |
| 2015 | 2459.76 | 2423.60 | 2575.10 | 2497.50 |
| 2016 | 2802.80 | 2498.30 | 3122.90 | 2802.80 |
| 2017 | 2887.89 | 2575.40 | 2997.10 | 2780.90 |
| 2018 | 2808.10 | 2654.80 | 2746.60 | 2699.60 |
| 2019 | 2576.90 | 2736.70 | 2362.20 | 2554.10 |
| 2020 | 2531.10 | 2821.10 | 2468.00 | 2649.00 |
| Fitting MAPE | 6.470% | 5.480% | 3.476% | |
| 2021 | 2627.50 | 2908.10 | 2405.30 | 2663.00 |
| 2022 | 2680.00 | 2997.80 | 2342.60 | 2678.40 |
| Predicting MAPE | 11.269% | 10.523% | 0.705% |
| Model | Error Evaluation Method | ILR | DRHT |
|---|---|---|---|
| GM (1,1) | MAPE | 41.645 | 40.826 |
| CMAPE | 11.800 | 11.832 | |
| DGM (1,1) | MAPE | 41.282 | 40.798 |
| CMAPE | 11.707 | 11.822 | |
| GM (1,1) Power Model | MAPE | 40.669 | 55.437 |
| CMAPE | 11.520 | 18.585 | |
| QETS | MAPE | 42.227 | 36.429 |
| CMAPE | 19.599 | 11.461 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Fang, Y.; Dai, D. Forecast of the Evolution Trend of Total Vehicle Sales and Power Structure of China under Different Scenarios. Sustainability 2023, 15, 3985. https://doi.org/10.3390/su15053985
Zhao M, Fang Y, Dai D. Forecast of the Evolution Trend of Total Vehicle Sales and Power Structure of China under Different Scenarios. Sustainability. 2023; 15(5):3985. https://doi.org/10.3390/su15053985
Chicago/Turabian StyleZhao, Min, Yu Fang, and Debao Dai. 2023. "Forecast of the Evolution Trend of Total Vehicle Sales and Power Structure of China under Different Scenarios" Sustainability 15, no. 5: 3985. https://doi.org/10.3390/su15053985
APA StyleZhao, M., Fang, Y., & Dai, D. (2023). Forecast of the Evolution Trend of Total Vehicle Sales and Power Structure of China under Different Scenarios. Sustainability, 15(5), 3985. https://doi.org/10.3390/su15053985







