A Multi-Objective Optimization Model for Multi-Facility Decisions of Infectious Waste Transshipment and Disposal

Abstract

Infectious waste disposal is a crucial concern in many areas. Not only is the waste obnoxious, but it can also pose a vital risk to human health. Disposal of infectious waste incurs higher costs than general waste disposal and must abide by stricter regulations. In this paper, the infectious waste disposal is formulated as a multi-objective optimization model. The objectives encompass economic, social, and environmental concerns. To save cost, waste transshipment facilities to function as consolidation points are proposed and integrated in the model. The economic objective includes construction and operational costs of the transshipment and disposal facilities. The social objective considers the communities surrounding the disposal facilities, while carbon dioxide emission is used as the measure in the environmental objective. The model is reformulated based on the lexicographic weighted Tchebycheff method to ensure that the Pareto frontier of the solutions is obtained. Then the model is applied to a health region in Thailand. Daily and every-other-day waste collection intervals are compared to examine additional benefits. Certain sensitivity of the solutions is also analyzed. After comparing several solutions, a compromise among all three objectives is suggested. It is composed of three transshipment and two disposal facilities, each with 1000 kg capacity. Moreover, if the solution is executed with the every-other-day waste collection interval, the overall costs can be saved. A sensitivity analysis of the solution on fuel price found that the solution was not very sensitive against an increase in the fuel price, in that when the fuel price increased by 20% the overall costs only increased by 7%. Lastly, when the daily infectious wastes are doubled, all the objective function values rise, ranging from 56% to 163%. The new solution suggests an increase in the number of the disposal facilities to four, but a decrease of the transshipment ones to only two.

1. Introduction

Medical waste management has become a prominent concern in recent years. Increasing demands for single-use medical devices together with the growth in the medical sector have led to a rise in medical wastes [1,2,3]. Infectious waste is described as any material containing pathogens that, with sufficient concentration and quantity, can pose a risk of disease transmission [4]. Because of the associated risk and legal requirements in handling and disposal of infectious waste, the cost of managing infectious waste could be as high as 20 times more than that of solid waste [5]. For example, the vehicles to transport infectious waste are required to be a close storage, and equipped with antibacterial injection and a temperature control system to reduce pathogen transmission during transportation [6]. The infectious waste incinerators themselves must combust the waste at a temperature of at least 1000 degrees Celsius to eliminate any pathogenic activity. There must be sufficient air intake to the incinerators to ensure complete combustion. This is to reduce air pollution emission and meet pollution control standards [7,8,9], as well as lower environmental contamination from micro/nano plastics used in medical components [10]. To avoid high management cost, infectious waste is sometimes improperly and illegally disposed of in the environment [5]. It is thus an urgent need to reduce the cost of infectious waste management in order to reduce its associated risks.

Cost minimization is a common objective for businesses and governmental services involved in infectious and hazardous waste management. Several cost components often appear, such as transportation cost, fixed cost of opening various facilities, operational or handling cost, inventory or storage cost, freight and fuel cost, waste treatment cost, human resource cost, as well as penalty cost for partially utilized trucks [11,12,13,14,15,16,17]. For example, Mantzaras and Voudrias [14] proposed an optimization model to minimize the cost for collection and disposal of infectious medical waste; Boyer et al. [18] used a weighted sum method to lower the cost in managing hazardous wastes for local communities; Melachrinoudis et al. [19] addressed the expense to the local government to manage waste disposal; and Nema and Gupta [20] focused on transport routes for either waste treatment or disposal and attempted to lower the cost through integer programming.

Moreover, social and environmental concerns should be taken into consideration when dealing with waste management. Yapicioglu et al. [21] modelled undesirable effects of the (semi)obnoxious facilities—such as airports, garbage dump sites, and power plants that are both desirable and undesirable at the same time—as a nonincreasing concave function from the facility. Samanlioglu [12] and Zhao and Zhu [22] included a risk of population exposure along the transportation routes and around the waste disposal centers. Farrokhi-Asl et al. [15] quantified health and environmental impacts as the number of people who might be impacted by the hazardous waste, and the total emission incurred from the distance travelled and technology deployed. Luo and Liao [23] optimized locations and routing of mobile medical waste collection units by considering both economic and environmental impacts. Entezaminia et al. [13] assessed several environmental criteria using scores for those which they wanted to minimize. Zhao and Huang [24] measured the risk of their hazardous waste management system based on the amount of waste processed. Azadeh et al. [25] combined health, safety, environmental, and economic indicators as a single objective by the weighted sum method, and optimized this objective. Torkayes et al. [26] modelled a multi-objective healthcare waste management problem using goal programming. They measured the social impact as job creation opportunities. Other approaches and applications in medical waste and medical service management are such as Etim et al. [27] and Wichapa and Khokhajaikiat [28] who utilized a multi-criteria decision-making approach to assess a medical waste management system and to solve a transshipment problem of infectious waste management, respectively; Sivakumar et al. [29] reformulated a multi-criteria decision making problem to a multi-objective optimization problem to improve medical service quality in which several concerns of physicians and patients are considered. However, no economic or environmental issues were covered. Wang et al. [30] rewrote a multi-objective optimization problem of urban healthcare waste transportation to a single-objective problem using important weights of the objectives from experts.

To solve a multi-objective optimization problem, an approach that has recently been gaining popularity is a lexicographic weighted Tchebycheff method. The method was first introduced by Steuer and Choo [31] and Steuer [32]. It has been lately applied to various applications, despite it being one of the most effective methods in solving multi-objective optimization problems [32]. For instance, Samanlioglu [12] applied the method in solving industrial hazardous waste location-routing problem; Lui and Tsai [33] in parallel machine scheduling; Zhao and Zhu [22] in multi-depot explosive waste recycling; Khalilpourazari and Khalilpourazary [34] in optimizing a surface grinding process; Ito et al. [35] in reducing backup capacity due to random failure for a cloud service provider; Aydin et al. [36] in determining car sharing points for sustainable transportation; and Kaoud et al. [37] in maximizing the total costs and minimizing the carbon dioxide emissions of a transportation system. The method determines non-dominated efficient points on the Pareto optimal frontier by reformulating the initial optimization problem and solving with several weight vectors [32].

In managing infectious waste, the transportation network is a critical issue. The locations and capacities of the disposal facilities influence the total costs and other impacts. The facility location problem is traditionally to determine a single proper site of the desired facility. Recently, the problem has been extended to consider several locations of the needed facilities at the same time. This multi-facility location problem has been modelled in many applications, such as in determining collection and recycling centers in green supply chain by Entezaminia et al. [13], deciding the locations of explosive waste recycling depots by Zhao and Zhu [22], and locating proper sites for mobile infectious waste processing centers by Luo and Liao [23]. Each of these studies also considers two competing objectives simultaneously in optimizing their problems.

In this research, we propose a multi-objective, multi-facility optimization model to minimize economic, social, and environmental impacts, which are the three pillars of sustainability. To save costs, transshipment locations are introduced as options to accumulate the wastes prior to transporting them to the disposal locations; unless the waste source locates close to a disposal facility than a transshipment one, then a direct transport to the disposal facility should be executed. The cost of establishing a new facility, operational cost, as well as transportation cost are included in the problem formulation. The social impact is modelled as the number of the population within a certain radius of all the disposal sites. Carbon dioxide (CO₂) emissions from the transportation and waste incineration are employed as the measure in the environmental objective function. These objectives are then reformulated using the lexicographic weighted Tchebycheff method, while retaining the same network and operational constraints. A daily waste collection is examined against every-other-day collection to explore any further saving through a different management strategy. A sensitivity analysis of certain constants is also tested.

The objective and the contribution of this research are:

• This research proposes a mathematical model to alleviate the high cost of infectious waste disposal which sometimes leads to illegal infectious waste dumping. The model encompasses multiple objectives of a multi-facility decision making problem in which these objectives are based on the three pillars of sustainability for infectious waste disposal.
• The model includes options to consolidate the infectious wastes at transshipment facilities prior to transporting them to the disposal facilities to save the transportation cost. However, the cost of establishing and operating these transshipment facilities must be considered as well. Hence, if the solution reveals that the transshipment facilities should be established, then it implies that their existence can lower the overall costs.
• The model that integrates multiple objectives covering all sustainability pillars, and multi-facility decision making of infectious waste disposal facilities with transshipment options, to our knowledge, has not be proposed elsewhere.
• Moreover, the solution of the numerical application suggests that improvement of the economic objective is possible through management. Specifically, the daily waste collection is compared with a prolonged collection interval of every other day. The results reveal that the every-other-day collection can further save the overall costs.

The remainder of the paper is as follows. The next section introduces the infectious waste transportation network model where transshipment and disposal locations as well as their capacities must be determined under multiple objectives. This multi-objective, multi-facility location problem is then reformulated according to the lexicographic weighted Tchebycheff method. Section 3 is a case study in which the model is applied to obtain numerical results. Section 4 compares the results of the sensitivity analysis and the change in collection strategy. Section 5 concludes the paper.

2. Mathematical Model

2.1. Problem Description

In a multi-facility location problem, the aim is to determine the locations in which the needed facilities should be established. In this paper, there are requests to transport infectious waste from individual hospitals to disposal facilities. Let $H_1$ be the set of hospitals that only generate infectious waste, and $H_2$ be the set of hospitals that are candidates for being transshipment facilities. The hospital in $H_2$ must satisfy a few criteria which are the number of beds greater than 30, convenient access to a public road, and a sufficiently large area to construct a transshipment facility. The hospitals in $H_2$ also generate infectious waste. The candidate locations for constructing disposal facilities are in set $K$, where all the three sets are mutually exclusive, or $H_1\cap H_2\cap K=\varnothing$. The disposal facilities are assumed to situate in areas legally operational by local municipalities, and not generating any infectious waste.

The waste from any hospital must be either sent to a transshipment facility or a disposal one, whichever is closer. The waste at any transshipment facility must be transported and processed by an incinerator at a disposal facility within a few days after it is collected. It is assumed that there is no splitting of waste due to transportation. Specifically, if the waste from a hospital or a transshipment facility is to be transported to a destination site, the whole amount must be transported in a single trip. The amount of daily waste needed to be disposed is assumed to be approximately constant, but may vary among the hospitals. The waste at any hospital shall be collected every day or every two days. There are costs associated with constructing and operating the facilities, depending upon their types and capacities. The carbon dioxide emission is considered at the transshipment and disposal facilities. Even though the incinerators at the disposal facilities must completely combust the infectious waste, there are still certain pollutants emitted. The people included in this problem are only those affected by these pollutants and therefore only the people surrounding the disposal sites are considered. However, the coverage areas of different disposal facilities could differ depending on the capacities of the incinerators.

2.2. Problem Formulation

Objective function:

$$\begin{array}{ll}\mathrm{Min}{Z}_1=& {\sum }_{i=1}^I{\sum }_{j=1}^{J}t{c}_{ij}{X}_{ij}+{\sum }_{i=1}^I{\sum }_{k=1}^{K}t{c}_{ik}{X}_{ik}+{\sum }_{j=1}^J{\sum }_{k=1}^{K}t{c}_{jk}{X}_{jk}+\\ & {\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{\sum }_{j=1}^{J}t{c}_{j^{\prime }}{X}_{j^{\prime }j}+{\sum }_{j=1}^J{\sum }_{m=1}^{M}f{c}_m{Y}_{jm}+{\sum }_{k=1}^K{\sum }_{n=1}^{N}f{c}_n{Y}_{kn}\end{array}$$

(1)

$$\mathrm{Min}{Z}_2={\sum }_{k=1}^K{\sum }_{n=1}^N{\rho }_k{A}_n{Y}_{kn}$$

(2)

$$\mathrm{Min}{Z}_3={\sum }_{j=1}^J{\sum }_{m=1}^M{e}_m{Y}_{km}+{\sum }_{k=1}^K{\sum }_{n=1}^N{e}_n{Y}_{kn}$$

(3)

Subject to:

$${\sum }_{i=1}^I{d}_i{X}_{ij}+{\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{d}_{j^{\prime }}{X}_{j^{\prime }j}+d_j=D_j,\forall j$$

(4)

$${\sum }_{i=1}^I{d}_i{X}_{ij}+{\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{d}_{j^{\prime }=1}{X}_{j^{\prime }j}+d_j={\sum }_{k=1}^K{D}_j{X}_{jk},\forall j$$

(5)

$${\sum }_{i=1}^I{d}_i{X}_{ij}+{\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{d}_{j^{\prime }}{X}_{j^{\prime }j}+d_j\le ca{p}_m{Y}_{jm}, \forall j$$

(6)

$${\sum }_{i=1}^I{d}_i{X}_{ik}+{\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{d}_{j^{\prime }}{X}_{j^{\prime }k}+{\sum }_{j=1}^J{D}_j{X}_{jk}\le ca{p}_n{Y}_{kn},\forall k$$

(7)

$${\sum }_{i=1}^I{X}_{ij}+{\sum }_{i=1}^I{X}_{ik}=1,\forall i$$

(8)

$${\sum }_{j^{\prime }=1,j^{\prime }\ne j}^J{X}_{j^{\prime }j}+{\sum }_{j^{\prime }=1}^J{X}_{j^{\prime }k}=1,\forall j^{\prime }$$

(9)

$${\sum }_{k=1}^K{X}_{jk}=1,\forall j$$

(10)

$${\sum }_{m=1}^M{Y}_{jm}\le 1,\forall j$$

(11)

$${\sum }_{n=1}^N{Y}_{kn}\le 1,\forall k$$

(12)

$$X_{ij},X_{ik},X_{jk},X_{j^{\prime }j,j^{\prime }\ne j},X_{j^{\prime }k}\in \left\{0,1\right\},\forall i,\forall j^{\prime },\forall j,\forall k, j^{\prime }\ne j$$

(13)

$$Y_{jm},Y_{kn}\in \left\{0,1\right\},\forall j,\forall k,\forall m,\forall n$$

(14)

Equation (1) is the economic objective function whereby it is calculated from the transportation cost and facility establishment cost. This facility establishment cost includes construction and operational costs with more details in the next section. Equation (2) is the social objective function. The waste disposal facility must be operated with safety measures. In case of an accident or with normal operations, the surrounding communities could be affected by the disposal process and related activities of the facility. Therefore, this objective is measured by the number of the neighboring population within a certain radius of disposal facilities. This radius depends upon the capacity of the incinerators. Equation (3) is the environmental objective function where it is to minimize the total CO₂ emission based on the capacity of the transshipment and disposal facilities. This is because the operations of both types of facility emit CO₂.

Equation (4) is an aggregated amount of all infectious waste that a transshipment facility needs to service. Equation (5) ensures that all infectious waste of a transshipment facility is transferred to a disposal facility. Equation (6) indicates that the capacity of a transshipment facility suffices to service the aggregated infectious waste. Likewise, Equation (7) shows that the capacity of a disposal facility is adequate to service in-coming infectious waste. Equation (8) enforces that any hospital in $H_1$ must send its infectious waste to only one facility (either a transshipment facility or a disposal one). Equation (9) imposes that all infectious waste from a transshipment location candidate (but is not selected to establish a transshipment facility) must be sent to either a transshipment facility or a disposal one. Similarly, Equation (10) indicates that any disposal facility must send its waste to merely one disposal facility. These latter three constraints (Equations (8)–(10)) imply no splitting of the waste during transportation. Equation (11) ensures that if a transshipment location candidate is selected to establish a facility, only one capacity is utilized. This same concept is applied to the disposal location candidates in Equation (12). However, these capacities could differ among the facilities. Equations (13) and (14) indicate that the decision variables are binary.

2.3. Lexicographic Weighted Tchebycheff Reformulation

Prior to solving the multi-objective optimization problem in the previous section, the model was reformulated using the lexicographic weighted Tchebycheff method. Following the notation in Steuer [23], the lexicographic weighted Tchebycheff reformulation of the problem can be written as:

$$lex\mathrm{Min}\left\{\alpha ,e^T\left(Z-Z^{*}\right)\right\}$$

(15)

Subject to:

$$\alpha \ge {\lambda }_1\left(Z_1-Z_1^{*}\right)$$

(16)

$$\alpha \ge {\lambda }_2\left(Z_2-Z_2^{*}\right)$$

(17)

$$\alpha \ge {\lambda }_3\left(Z_3-Z_3^{*}\right)$$

(18)

and (1)–(14), where ${\lambda }_i>0$ (i = 1, 2, 3) are weights and ${\sum }_{i=1}^3{\lambda }_i$ = 1. The notation $Z_i^{*}$ is the utopia point defined by $Z_i^{*}$ = Min $Z_i-{\delta }_i$ for i = 1, 2, 3 and ${\delta }_i>0$; and $e^T$ is a vector of ones ($e^T$ = [1 1 1]). The lexicographic weighted Tchebycheff method guarantees obtaining efficient optimal solutions on the Pareto frontier, as discussed in [32]. Through the reformulation, all the objectives can be optimized simultaneously. However, the method must be resolved with different weight vectors to sufficiently represent the solutions. In this study, the reformulated problem is solved several times, each with a different set of weights to obtain representative efficient solutions. This approach follows the implementation in [12].

3. Numerical Application

The above problem was applied to Health Region 7 in northeastern Thailand. Details of the data input into the model are given in Section 3.1. Results of the application are provided in Section 3.2.

3.1. Input Information

Health Region 7 is composed of 36 small hospitals in Set $H_1$, 25 hospitals as transshipment location candidates (which themselves are hospitals as well) in Set $H_2$, and four disposal location candidates in Set $K$. Hence, there are, in total, 36 + 25 = 61 hospitals with daily infectious wastes to dispose. The amounts of their daily infectious wastes were acquired from [38]. Their daily infectious waste and from-to distances were obtained from the Bureau of Environmental Health, Thailand [38], and Google map, respectively.

Figure 1 depicts the transshipment and disposal problem in which the locations of the hospitals (in yellow), the transshipment location candidates (in red), and the disposal location candidates (in orange) are superimposed onto the map. Transportation cost is roughly 4.5 Baht per kilometer. The costs involved in constraction and operating (at full capacity) the transshipment and disposal facilities are shown in

Table 1. Cost details.

Costs	Transshipment		Incinerator
	Capacity (kg/Day)		Capacity (kg/Day)
	1000	2000	1000	2000
1. Fixed cost per day 1.1 Construction 1.2 Labor cost	1267 2000	2000 1500	6333 3000	10,000 5000
2. Variable cost per day 2.1 Infectious solid treatment 2.2 Infectious waste treatment 2.3 Landfill 2.4 Maintenance cost	55 14 - 19	75 18 - 30	198 76 58 95	274 152 115 150
Total cost (Baht/day)	2355	3623	9760	15,691

. The depreciation of both types of facilities is assumed to be 10 years. All the costs are recomputed to be based on a daily basis. The density of the people around disposal location candidates are displayed in

Table 2. Density of people around disposal location candidates.

Disposal Location Candidate	Density (People/km2)
Maha Sarakham (K1)	1648
Kalasin (K2)	3107
Khon Kaen (K3)	888
Roi Et (K4)	2038

. We note that the radius $r_n$ of the area affected by the incinerator depend on the capacity of the incinerator. Specifically, $r_1$ = 1.5 and $r_2$ = 3.0 km when the capacity of the incinerator is 1000 and 2000 kg, orderly. This follows the model in Delfani et al. [39]. CO₂ emissions based on the type of facilities and the capacity are shown in

Table 3. CO₂ emission by type and capacity of facility.

Type of Facility and Capacity	CO2 Emission (kg of CO2)
Transshipment facility with 1000 kg capacity	356
Transshipment facility with 2000 kg capacity	712
Incinerator with 1000 kg capacity	1074
Incinerator with 2000 kg capacity	2148

.

To apply the lexicographic weighted Tchebycheff approach, the objective functions Z₁, Z₂, and Z₃ must first be solved individually to obtain their optimal values. The problem was solved using LINGO software version 12, on an Intel I7 6500U 2.5 GHz with 8 gigabyte RAM, and the results are shown in

Table 4. Optimal values obtained when individual objective function is solved.

Objective	Min Z1	Min Z2	Min Z3
Z1	36,619	62,684	36,619
Z2	57,646	17,933	57,646
Z3	2860	3572	2860

. Please note that both $j$ and $j^{\prime }$ denoted in the nomenclature represent the transshipment location candidates. However, j are the candidates that are selected to establish the transshipment facilities. The selection which is a part of the solution is performed by the LINGO software.

From the table, the optimal values of Z₁, Z₂, and Z₃ are 36,619, 17,933, and 2860, respectively.

Representatives of the efficient solutions at the Pareto frontier are obtained according to dispersed weight vectors ${\lambda }_i$, where ${\lambda }_i$ > 0 and ∑i ${\lambda }_i$ = 1 for i = 1, 2, 3 as given in

Table 5. Weight vectors of lexicographic weighted Tchebycheff method.

Solution	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
${\lambda }_1$	0.10	0.10	0.10	0.10	0.20	0.20	0.25	0.25	0.30	0.33	0.40	0.40	0.50	0.60	0.70	0.80
${\lambda }_2$	0.10	0.60	0.70	0.80	0.10	0.40	0.25	0.50	0.10	0.33	0.20	0.40	0.25	0.30	0.20	0.10
${\lambda }_3$	0.80	0.30	0.20	0.10	0.70	0.40	0.50	0.25	0.60	0.33	0.40	0.20	0.25	0.10	0.10	0.10

. This approach follows a similar execution performed by Samanlioglu [12]. These vectors were used in the lexicographic weighted Tchebycheff reformulation of the problem. The corresponding solutions are exhibited in

Table 6. Representative efficient solutions.

Objective	Solution
	1	2	3	4
$Z_1$	37,902	62,684	62,684	62,684
$Z_2$	46,614	17,933	17,933	17,933
$Z_3$	2860	3572	3572	3572
CPU(s)	852	54	185	1341
	5	6	7	8
$Z_1$	36,619	38,959	37,902	39,503
$Z_2$	57,646	25,118	46,614	20,691
$Z_3$	2860	2860	2860	3216
CPU(s)	3869	3622	2972	267
	9	10	11	12
$Z_1$	36,619	38,959	36,619	38,298
$Z_2$	57,646	26,065	57,646	26,065
$Z_3$	2860	3216	2860	2860
CPU(s)	619	1614	3053	1673
	13	14	15	16
$Z_1$	36,619	38,959	38,999	36,619
$Z_2$	57,646	26,065	26,065	57,646
$Z_3$	2860	3216	3216	2860
CPU(s)	586	504	4641	172

.

From Table 6, the minimal value of $Z_1$ is 36,619 and it occurred in Solutions 5, 9, 11, 13, and 16. The minimal value of $Z_2$ is 17,933 and appeared in Solutions 2, 3, and 4. Likewise, the minimal value of $Z_3$ is 2806 which exists in Solutions 1, 5, 6, 7, 9, 11, 12, 13, and 16. The table also shows the CPU time (in second) needed to acquire each solution.

Notice that the minimal values of both $Z_1$ and $Z_3$ emerge in Solutions 5, 9, 11, and 13. In fact, the values of the three objectives are exactly the same in these four solutions. The details of this solution are shown in

Table 7. Optimal solution of $Z_1$ and $Z_3$.

Hospital	Transshipment	Disposal
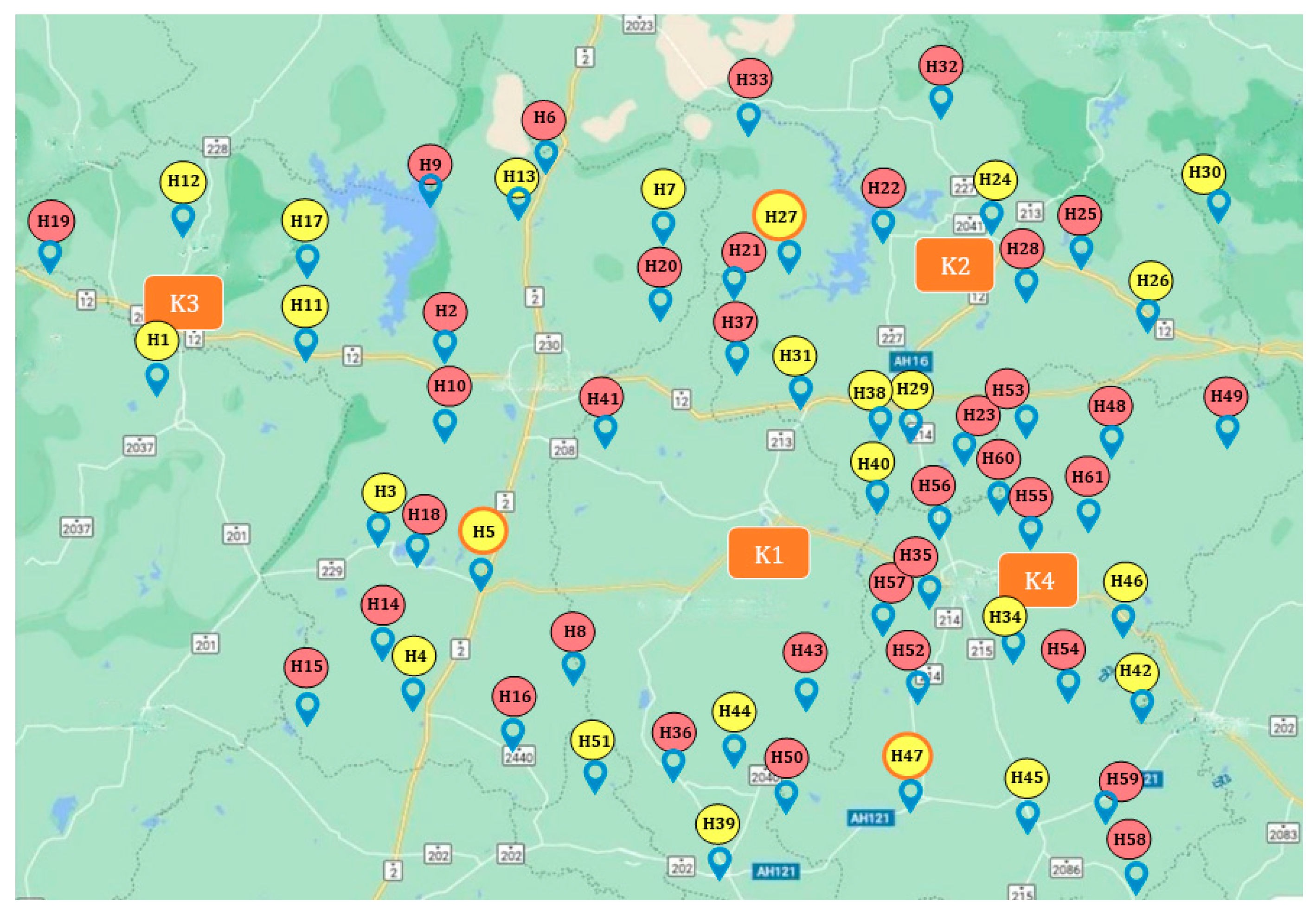
H1, H2, H3, H4, H5, H8, H10, H11, H12, H14, H15, H16, H17, H18, H19, H34, H36 H39, H41	H5 (1000 kg)	K4 (2000 kg)
H6, H7, H9, H13, H20, H21, H22, H24, H25 H27, H28, H31, H32, H33, H37, H40	H27 (1000 kg)
H23, H26, H29, H30, H35, H38, H42, H43 H44, H45, H46, H47, H48, H49, H50, H51, H52, H53, H54, H55, H56, H57, H58, H59 H60, H61	Direct to K4

. Solutions 2, 3, and 4 are also essentially the same, and are specified in

Table 8. Optimal solution of $Z_2$.

Hospital	Transshipment	Disposal
H3, H4, H5, H8, H14, H15, H16, H18, H36, H40, H42	H5 (1000 kg)	K3 (1000 kg)
H7, H20, H21, H22, H27, H31, H32, H33, H37, H38	H7 (1000 kg)
H1, H2, H6, H9, H10, H11, H12, H13, H17, H19	Direct to K3
H24, H25, H26, H28, H30, H48, H49, H53	H26 (1000 kg)	K1 (1000 kg)
H39, H44, H45, H47, H50, H51, H54, H58, H59	H47 (1000 kg)
H23, H29, H34, H35, H41, H43, H46, H52 H55, H56, H57, H60, H61	Direct to K1

. Solution 8 was selected to represent a compromising solution in which its individual objective function values are not the lowest, but they are relatively small. The details of Solution 8 are described in

Table 9. Compromising solution among the objective functions.

Hospital	Transshipment	Disposal
H2, H3, H4, H8, H10, H14, H15, H16, H18, H36, H41, H51	H5 (1000 kg)	K3 (1000 kg)
H6, H7, H9, H13, H20, H21, H22, H24, H31, H32, H33, H37	H27 (1000 kg)
H1, H11, H12, H17, H19	Direct to K3
H43, H44, H45, H50, H52, H58, H59	H47 (1000 kg)	K4 (1000 kg)
H23, H25, H26, H28, H29, H30, H34, H35 H38, H39, H40, H42, H46, H48, H49, H53, H54, H55, H56, H57, H60, H61	Direct to K4

.

Table 9 shows that there should be establishment of two disposal facilities at K3 and K4, each with 1000 kg capacity. Three transshipment facilities should be placed at H5, H27, and H47 with 1000 kg capacity each. Transportation of the wastes from individual hospitals to either a transshipment facility or a disposal one is provided in the table.

3.2. Solution

Table 7 indicates that only one incinerator is needed and should be placed at Roi-et or K4 with 2000 kg capacity, while two transshipment facilities are required at H5 and H27, each with 1000 kg capacity. Moreover, the infectious waste from hospitals H1 to H5, H8, H10 to H12, H14 to H19, H34, H36, H39, and H41 should be transported to the transshipment facility at H5; and the waste from hospitals H6, H7, H9, H13, H20 to H22, H24, H25, H27, H28, H31 to H33, H37, and H40 to the transshipment facility at H27. However, the waste from hospitals H23, H26, H29, H30, H35, H38, H43 to H61 should be sent directly to the disposal facility at K4.

Table 8 specifies that the solution suggests establishing the disposal facilities at K1 and K3, each with an incinerator of 1000 kg capacity. The transshipment facilities should be established at H5, H7, H26, and H47, each with 1000 kg capacity.

The infectious waste from these facilities should be transported to particular disposal facility as shown in the table. In this solution, there are some hospitals that should directly send their wastes to disposal facilities as well.

Comparing Solution 8 to the other extreme solutions of which can minimize certain objectives but perform badly on the other ones, this solution is trading off extreme performances with merely good performance in all of the objectives. Traditionally, businesses emphasize heavily on the economic objective. As the regulations and pressure from the society progress, environmental and social considerations must also be addressed together with the economic performance. Hence, the solution that should be selected must fulfill all the objectives, not only some of them.

Solution 8, as shown in Table 9, is depicted in Figure 2. The figure also shows the directions of the infectious waste transportation. This solution is a compromising solution among the three objective functions. Specifically, the solution is not the minimum in any of the objectives, but it yields relatively low values in all of the objectives. However, it is noticed that the total capacity of the three transshipment facilities is 3000 kg, which exceeds the total capacity of 2000 kg of the two disposal facilities. Since the transshipment facilities act as consolidation points and all the in-coming wastes are sent out to the destinations at the disposal facilities, this implies that the total capacity of the transshipment facilities is not fully utilized.

Alleviating this partial utilization problem leads us to explore whether any change in waste management from daily to every-other-day collection would be beneficial, specifically in cost saving. This examination, along with an increase in the daily quantify of infectious wastes as well as an increase in fuel price, is to be investigated in the next section.

4. Sensitivity Analysis

Three scenarios are explored in this section. First, the infectious waste collection interval is changed from operating daily to every-other-day in the first scenario. This scenario is motivated by the unbalanced of the capacities between the transshipment and disposal facilities in Solution 8. The second scenario investigates when the amounts of daily wastes from individual hospitals are doubled. This scenario reflects the trend mentioned earlier that there is a rise in the medical waste due to the growth in single-use medical devices. It could also simulate when there is a small outbreak of disease. The last scenario considers an increase in the fuel price and its effect to the economic objective function. This scenario echoes fluctuations of fossil fuel prices in recent years.

4.1. Prolonged Collection Interval

When the time between two consecutive waste collections is prolonged, the amount of the waste collected in a single trip increases (assuming that the amount of the daily waste is approximately unchanged). To ensure that the network in Solution 8 (Table 9) implementable, the network is divided into two zones. The collection occurs every day but alternates between these two zones. In other words, the wastes of each zone would be collected every other day. However, the disposal facilities remain operating every day, although their in-coming wastes alternate between the two zones. The first zone comprises of (i) H5 and the hospitals of its in-coming wastes (H2, H3 to H51), (ii) H11, H12, H17, and H19, and (iii) H47 and the hospitals of in-coming wastes (H43, H44 to H59). The other zone includes (i) H27 and the hospitals of its in-coming wastes (H2, H3 to H51), (ii) H1, and (iii) H23, H25 to H61. Note that the hospitals that used to send their wastes directly to K3 are divided into two groups (H1 and the rest) in the prolonged collection interval from daily to every-other-day. This is to ensure sure that the capacity of the incinerator is sufficient. The hospital H1 is a large hospital with a large amount of daily infectious waste, while the rest (H11, H12, H17, and H19) is small hospitals with small amounts of daily wastes.

Resolving the model based on the new collection frequency, the results as shown in

Table 10. Values of the three objectives with different collection frequencies.

Objective	Current Value	Every-Other-Day Collection	Change	%
Cost (THB)	39,503	31,882	−6621	−17%
Social (Number of people)	20,691	20,691	0	0%
CO2 (kg of CO2)	3216	3216	0	0%

reveal that the total costs could be reduced by approximately 17 percent. The primary reduction is due to cost saving in transportation fuel. The values of the other two objectives are unchanged. Another benefit of this every-other-day collection strategy is a smaller size of vehicle fright since the number of hospitals needed to visit and collect the wastes are reduced. The cost of managing the freight is not included in the model formulation, but its benefit is to be expected in the new collection strategy.

4.2. Increase of Infectious Waste Quantify

When the quantity of the daily waste from the hospitals increases twice that in Solution 8, the effects encompass all the objective functions. First, it is expected that the total capacity of the disposal facilities must be extended to accommodate this rise in the total amount of waste. Increasing the total capacity of the disposal facilities by either increase the capacity of the existing facilities or establish additional disposal facilities, certainly heighten the impact to surrounding communities which is measured in $Z_2$. Likewise, the increase in the total capacity of the disposal facilities leads to an increase in the environmental objective function $Z_3$. This is because the areas under the consideration of this objective partially depend on the capacity of the incinerators.

Resolving Solution 8 with the doubly increase in the daily quantity of the infectious wastes, a new solution is found and its objective function values are shown in

Table 11. Values of the three objectives with doubled daily infectious waste.

Objective	Current Value	+100% Waste	Change	%
Cost (THB)	39,503	81,101	+42,598	+111%
Social (Number of people)	20,691	54,315	+33,624	+163%
CO2 (kg of CO2)	3216	5008	+1793	+56%

. In the new solution, additional disposal facilities at K1 and K2 are required. Each of the added disposal facilities is required to install an incinerator of capacity 1000 kg, while the previous disposal facilities at K3 and K4 remain the same. However, the transshipment facilities needed in the new solution are reduced to be only at H5 and H27, each with the same capacity of 1000 kg as before. This reduction in the transshipment facilities is because many hospitals choose to bypass the transshipment facility and send their infectious wastes directly to the new nearby disposal facilities. Although the transportation cost is reduced, the cost of establishing new facilities increases.

The impact of surrounding communities also rises because the new disposal facilities locate in crowded locations. However, this rise in the social impact is still smaller than increasing the capacity of the disposal facilities in Solution 8; otherwise, the social impact would be quadrupled due to the way the impacted areas is calculated. The new solution yields an increase in the total carbon dioxide emission from the additional disposal facilities, but a decrease from having only two transshipment facilities instead of three. However, the net emission still rises.

4.3. Increase in Fuel Price

The economic objective function is composed of two groups of cost components and one of them is transportation cost. The price of fuel has been fluctuating in recent years. For example, from the crude oil price data for the past 5 years (Jul 2017–Jun 2022) the price has been varied around ±20% of the average price [40]. This research only considers when the fuel price increases approximately 20%, or from 4.5 to 5.5 Baht per kilometer. The other two objective functions values remain unchanged.

As expected, there is an increase in the total costs as shown in

Table 12. The crude oil price and the cost, social, and CO₂ emission.

Objective	Current Value	+20% Fuel Price	Change	%
Cost (THB)	39,503	42,096	+3593	+9%
Social (Number of people)	20,691	20,691	0	0%
CO2 (kg of CO2)	3216	3216	0	0%

. However, the increase is merely 9% compared to that in Solution 8. This shows that the total costs are robust against a small rise in the fuel price.

Table 13. Summary of sensitivity analysis in terms of solutions and objective function values.

Scenario	Transshipment Facility	Disposal Facility				Cost	Social	CO2
		K1	K2	K3	K4
Base scenario: Compromising solution	H5: 1000 kg H27: 1000 kg H47: 1000 kg	-	-	1000 kg	1000 kg	39,503	20,691	3216
Scenario 1: Every-other-day collection interval	H5: 1000 kg H27: 1000 kg H47: 1000 kg	-	-	1000 kg	1000 kg	31,882 (−19%)	20,691 (0%)	3216 (0%)
Scenario 2: +100% waste	H5: 1000 kg H27: 1000 kg	1000 kg	1000 kg	1000 kg	1000 kg	81,101 (+111%)	54,315 (+163%)	5008 (+56%)
Scenario 3: +20% fuel price	H5: 1000 kg H27: 1000 kg H47: 1000 kg	-	-	1000 kg	1000 kg	42,096 (+9%)	20,691 (0%)	3216 (0%)

summarizes the findings from all three scenarios of sensitivity analysis. Comparing their solutions, particularly the decision variable values, we notice that the solutions of every-other-day waste collection interval in Scenario 1 and 20% fuel price increase in Scenario 3 are the same as that of the compromising solution scenario. The only difference is in the value of the cost objective function. The number in the parenthesis under the objective function values in the three scenarios indicate the changes in their objectives relative to those of the base scenario (Solution 8). This difference shows twofold implications. First, through proper management of the collection interval, this waste transportation network can save cost. Second, the increase in the fuel price affects only the cost objective, but not the other two objectives. However, an increase in the amounts of infectious wastes in Scenario 2 changes the locations of the transshipment and disposal facilities. In this scenario, only two transshipment facilities are required, but the disposal facilities are now needed in all the disposal location candidates. This leads to changes in the destinations of the infectious wastes of some hospitals and more direct transportation to the disposal facilities without having to pass through the transshipment facilities. This is to be expected, however. As there are sufficient amounts of waste to be transported from the sources, the need for the wastes to be consolidated at the transshipment facilities is being diminished.

5. Conclusions

The infectious waste management has been a global issue recently because of an increasing trend in medical waste. The cost of managing infectious waste is unfortunately higher than that of regular waste. This has prompted several studies to strategically reduce costs. In the meanwhile, infectious waste disposal procedures could pose a risk to the surrounding communities and affect the environment. These concerns are considered and modelled as a mathematical optimization problem. Three objective functions encompassing economic, social, and environmental impacts are proposed. To reduce cost, transshipment facilities to aggregate nearby wastes are introduced. The aggregated waste at each of the transshipment facilities is to be transported to a disposal facility. This aggregation mechanism can reduce the total distance needed to transport all the wastes, and is also integrated into the mathematical model. The problem is reformulated through lexicographic weighted Tchebycheff method to ensure acquisition of optimal solutions on the Pareto frontier.

The model is applied to a case study of Health Region 7 in Thailand to determine the locations to establish the transshipment and disposal facilities. The region comprises 61 hospitals [38] and four disposal location candidates. Three solutions are discussed in more detail, as described in Section 3.2. The discussion shows the advantages and disadvantages of those solutions. A compromise solution is chosen as it represents a solution that, even though it may not be best in any of the objective functions, well satisfies all of them. From another perspective, this implies that this solution does not perform badly in any of the objective functions. In this solution, establishment of three transshipment and two disposal facilities, each with 1000 kg capacity, is suggested.

This compromise solution is further discussed through sensitivity analysis in three scenarios. The first scenario shows that, through management of zoning and collection intervals, the overall costs of the problem could be reduced by 19%, while the locations of the facilities remain unchanged. This reduction is due to the daily fuel consumption that is decreased from 258 L/day to a half of this amount in the every-other-day collection interval. The total distance that is used to travel on the daily basis in the daily waste collection needs to be completed in a two-day period in the every-other-day collection. Hence, the total distance in the every-other-day collection is reduced to a half if we are to compare the total distance of the two collection intervals on the daily basis. However, other operating and fixed costs are not affected by the collection interval. The transshipment and disposal facilities must still be processing the incoming wastes every day. Therefore, the change in the collection interval can lead to only 19% reduction in the overall costs.

The second scenario explores the impacts of an increase in the daily infectious waste. The results show that this increase greatly affects all three objective functions. The objective function values rise, ranging from 56% to 163%. The last scenario examines the impact of the rise of the fuel price. The results reveal that the increase of the cost objective function of 9% is relatively small compared to the rise of the fuel price of 20%. This means that the selected solution (Solution 8) is not too sensitive to small increases in the fuel price.

This model, however, is not without a disadvantage. Since the variables in the model are binary, as the number of variables grow the time needed to solve the problem could increase greatly. A heuristic may be required to solve this model in high dimensions. Moreover, if the number of objective functions increases, more weight vectors are recommended to represent the solutions. This implies more effort to solve the solutions corresponding to those vectors. Future research could explore the benefit of collecting the infectious waste in a milk-run manner. This could possibly reduce trucks with partial loads.