Effect of Loading and Unloading Rates on Sandstone Deformation and Dilatancy under True Triaxial Condition
Abstract
:1. Introduction
2. Test Device and Sample
3. Test Program
- (1)
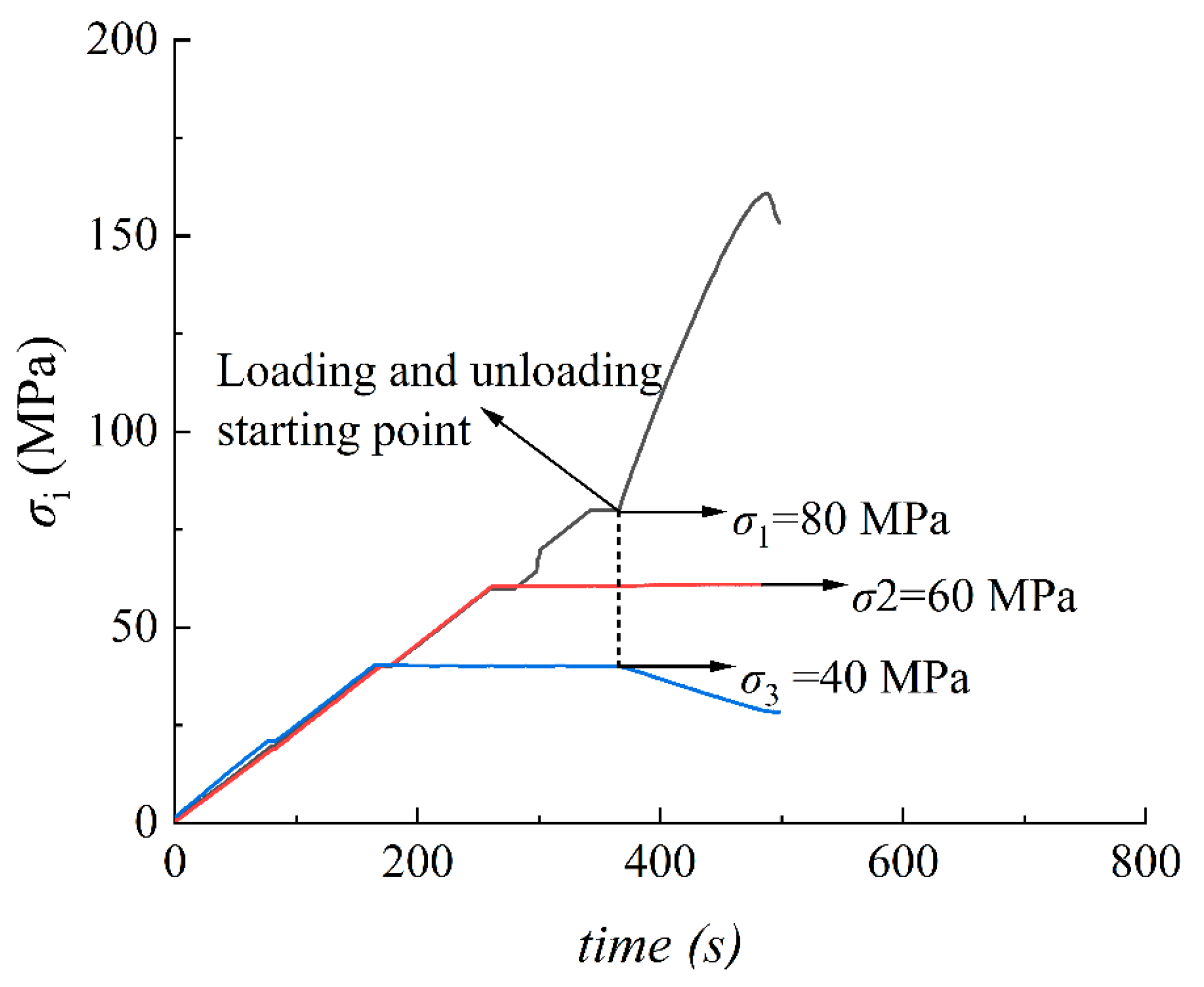
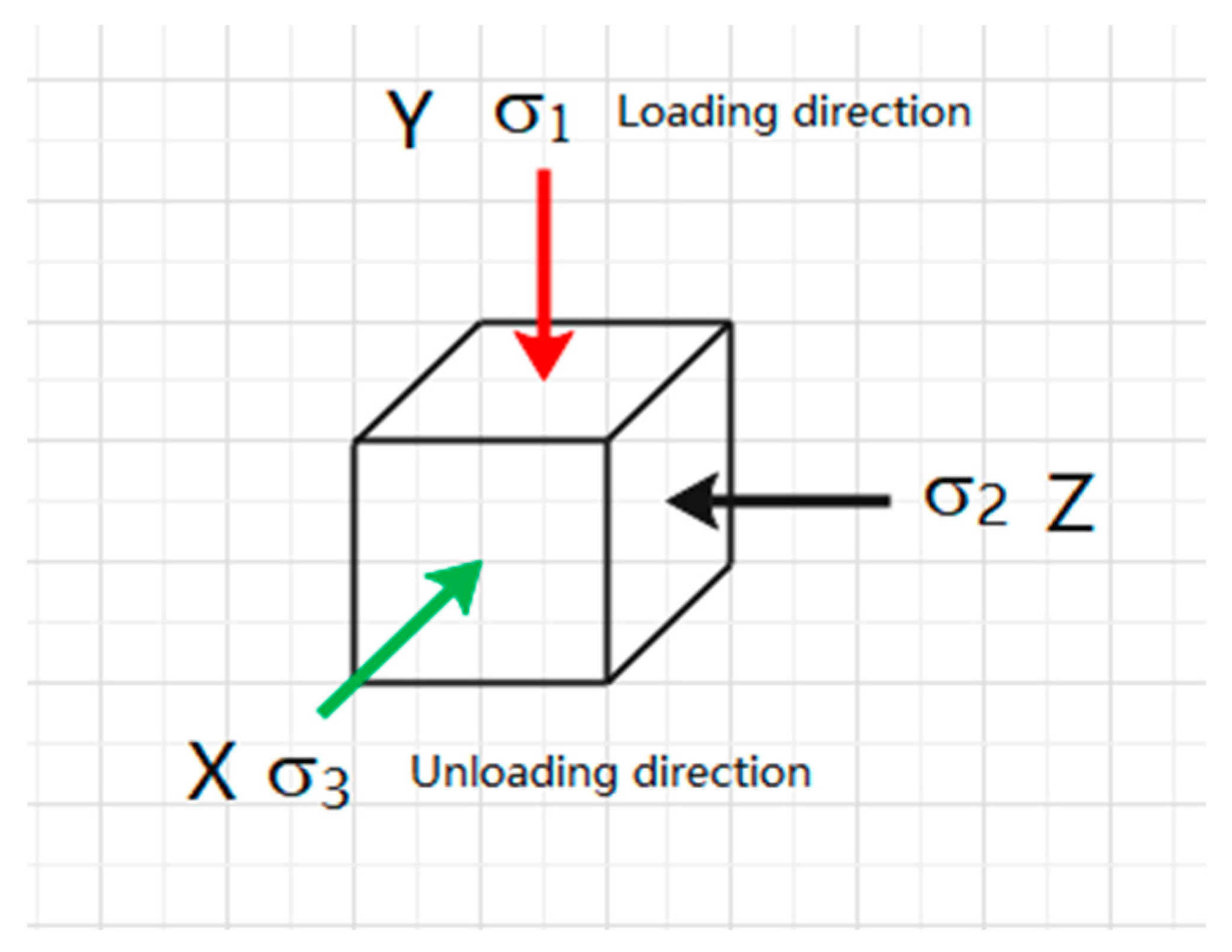
- Tests at different loading rates: load σ1, σ2, and σ3 to 40 MPa at a rate of 2 kN/s, load σ1 and σ2 to 60 MPa at a rate of 2 kN/s while σ3 remains unchanged, and load σ1 to 80 MPa at a rate of 2 kN/s while σ3 and σ2 remains unchanged. After maintaining the stress state (i.e., after loading and unloading starting point), unload σ3 at a constant 1 kN/s on one side, σ2 remains unchanged, and increase σ1 at different loading rates (displacement control mode) until sandstone sample failure. The experiment group is named group G, as shown in Table 1.
- (2)
- Tests at different loading rates: load σ1, σ2, and σ3 to 40 MPa at a rate of 2 kN/s, load σ1 and σ2 to 60 MPa at a rate of 2 kN/s while σ3 remains unchanged, and load σ1 to 80 MPa at a rate of 2 kN/s while σ3 and σ2 remains unchanged. After maintaining the stress state (i.e., after loading and unloading starting point), unload σ3 from one side at a constant unloading rate (force control mode), remain σ2 unchanged, and increase σ1 at a constant 0.003 mm/s until the sandstone sample failure. The experiment group is named group H, as shown in Table 1.
4. Experimental Results and Analysis
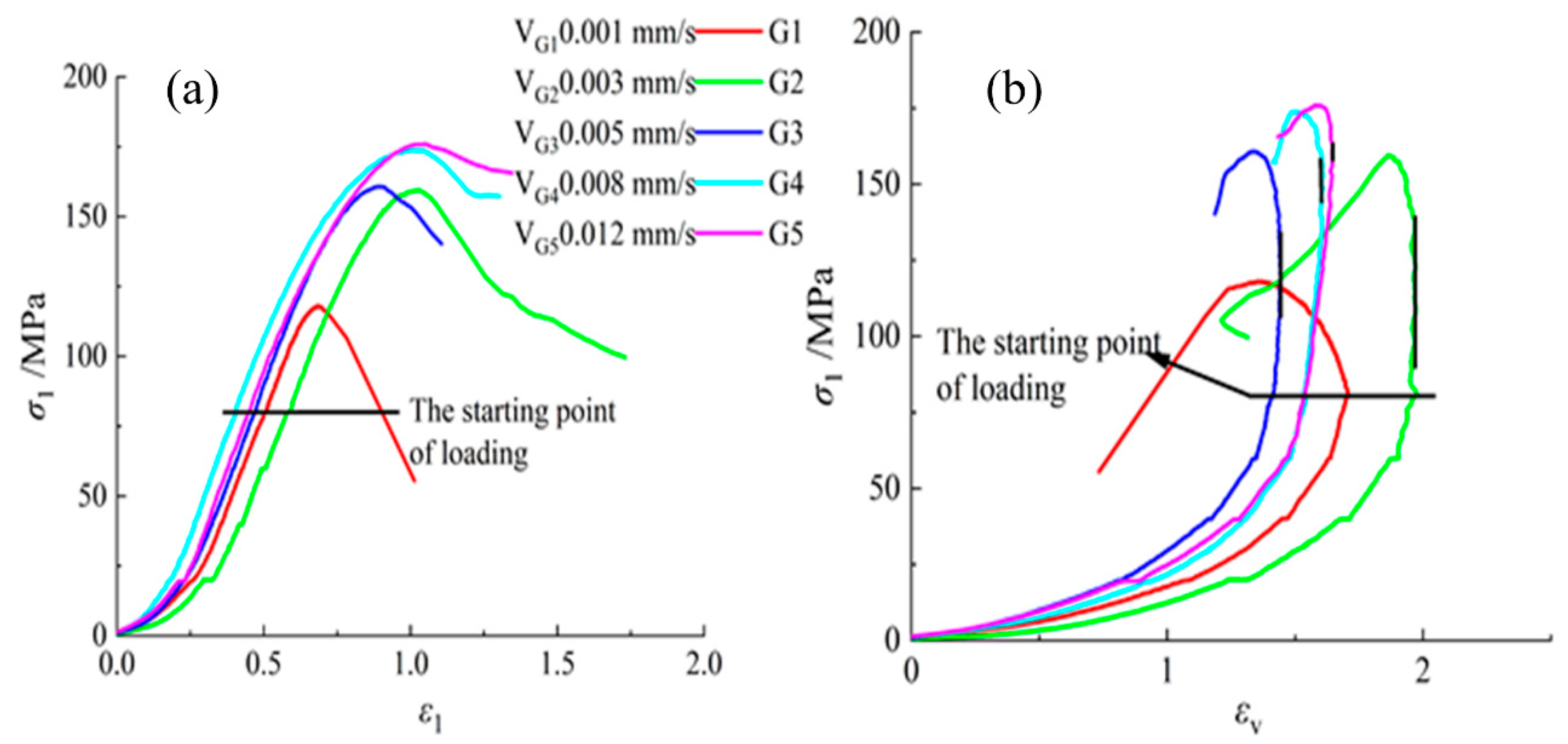
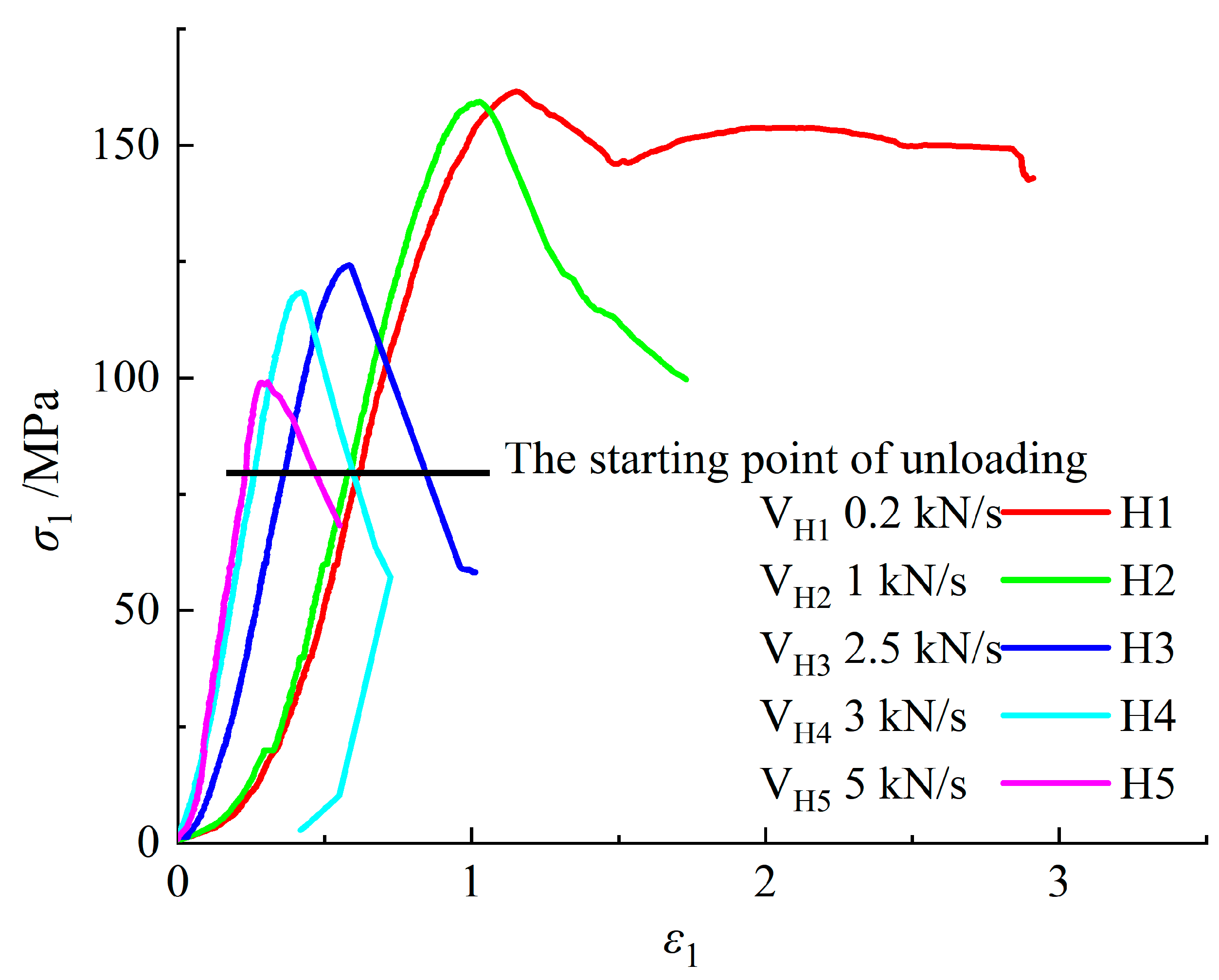
4.1. Mechanical Properties of Sandstone under True Triaxial Loading Rates
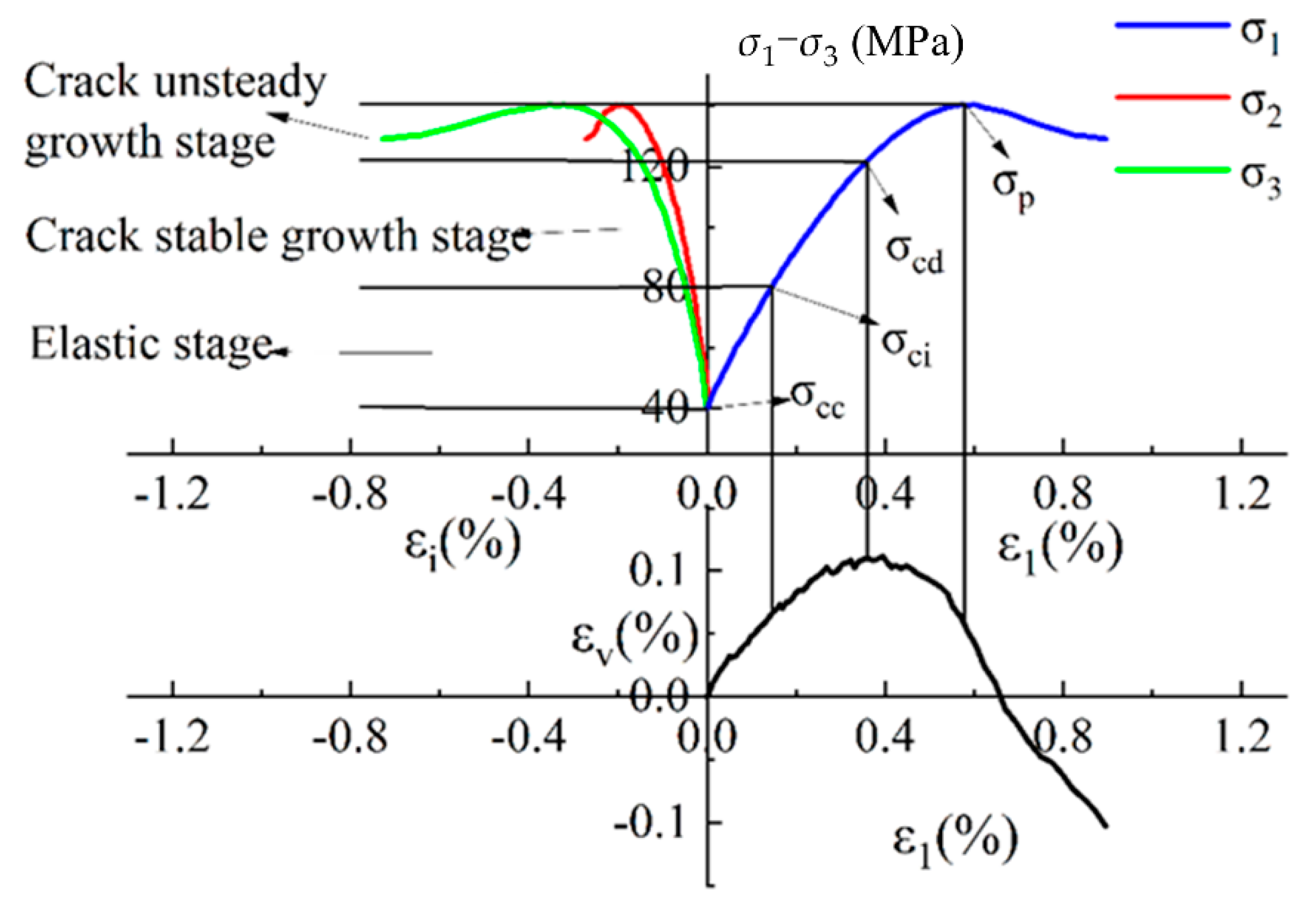
- (1)
- Elastic deformation stage: the sandstone rapidly begins the elastic deformation stage with the loading of σ1 and unloading of σ3.
- (2)
- The stage of steady crack growth: with the loading time increase, σ1 reaches the crack initiation stress σci, and the crack increases gradually and enters the stage of steady crack growth.
- (3)
- The stage of fracture unstable propagation: with continuous loading of σ1 and unloading of σ3, the crack expands rapidly, and the volume expands. In this case, the corresponding axial stress is the damage stress σcd, which is the long-term strength of the rock.
4.2. Mechanical Properties of Sandstone under True Triaxial Conditions with Different Unloading Rates
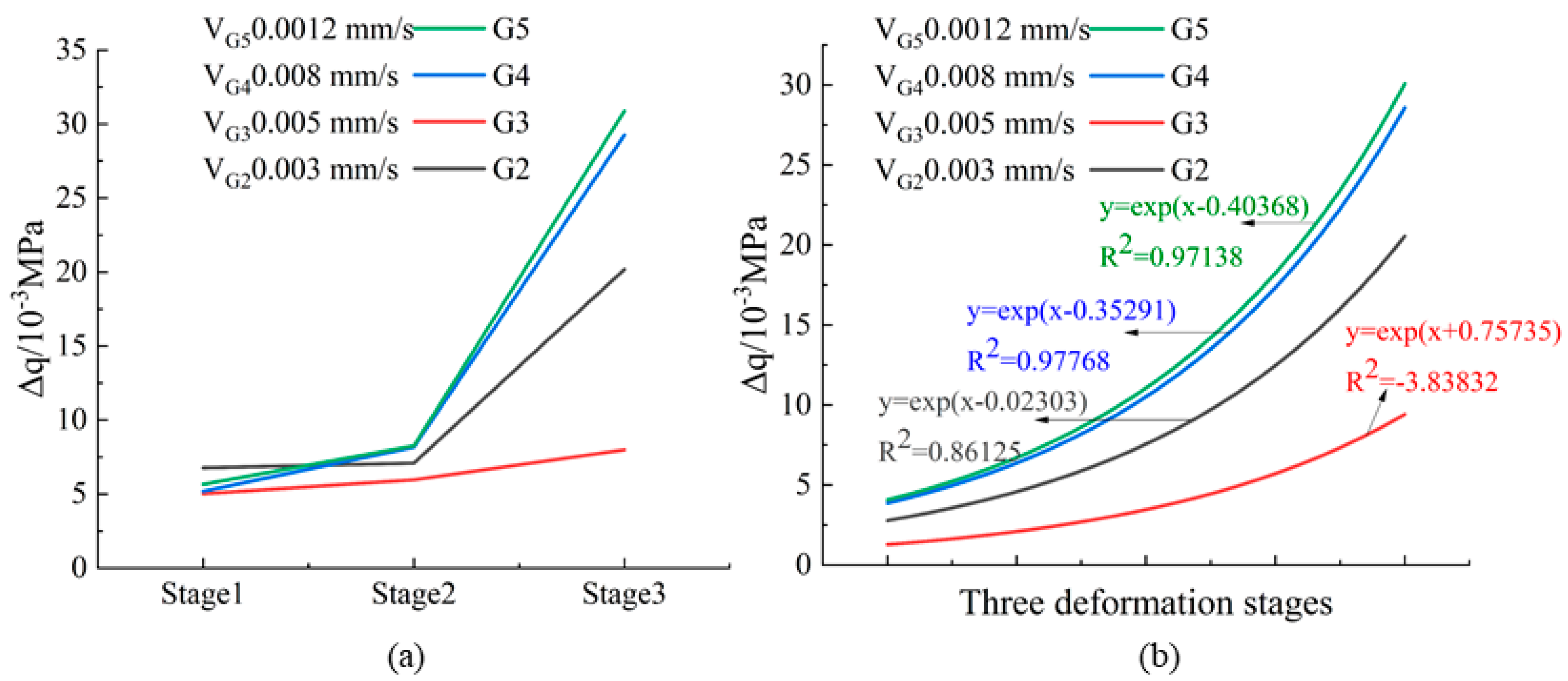
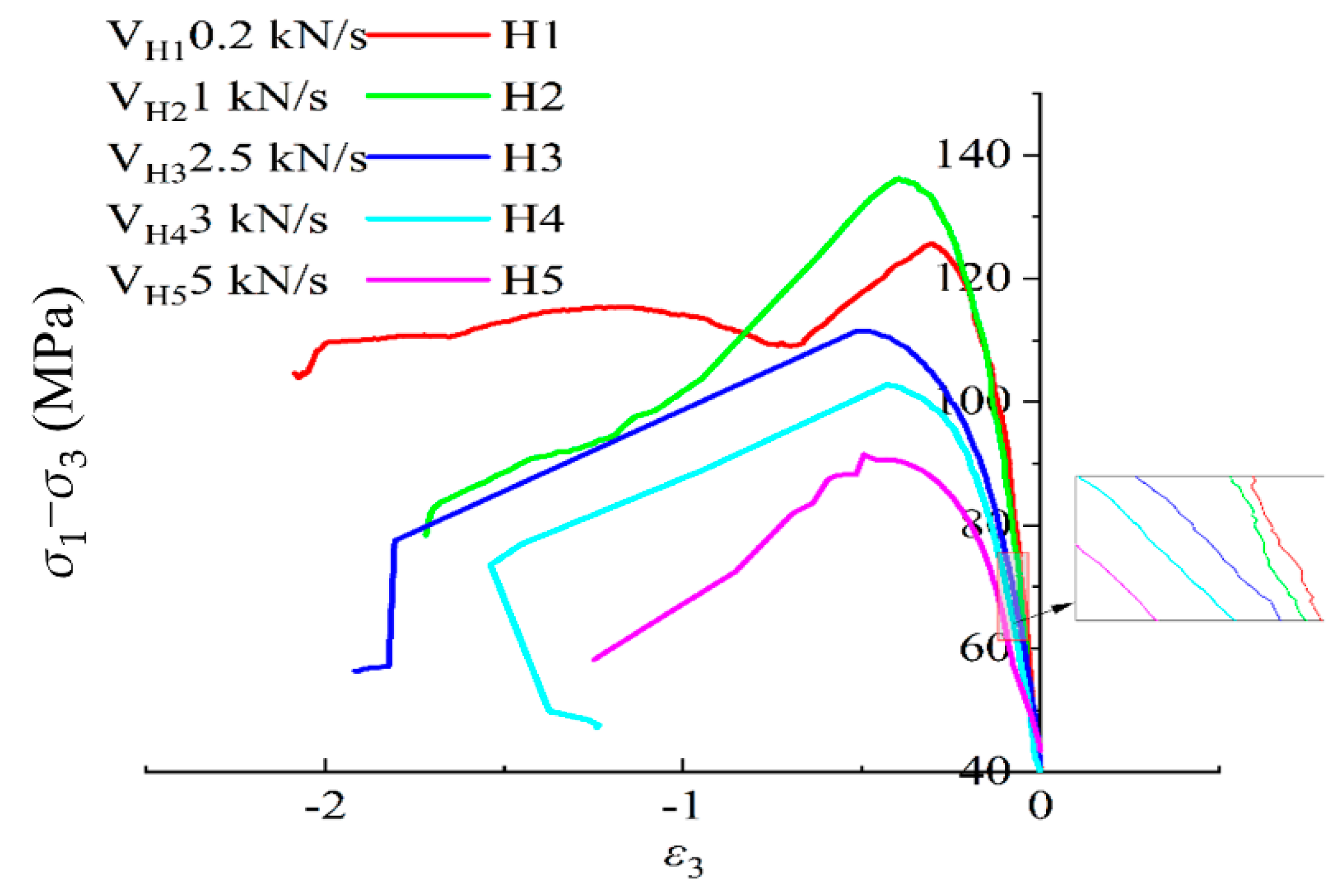
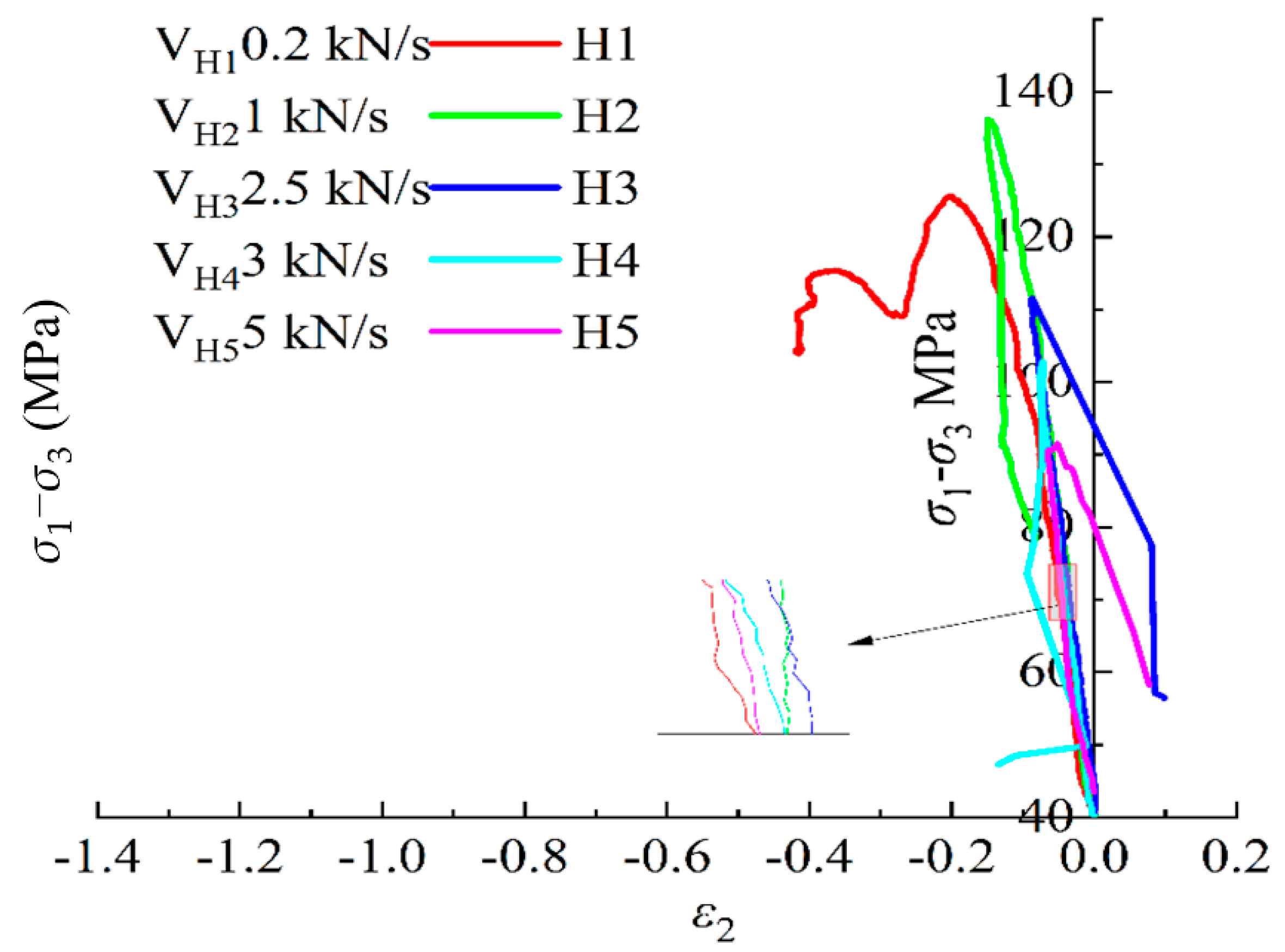
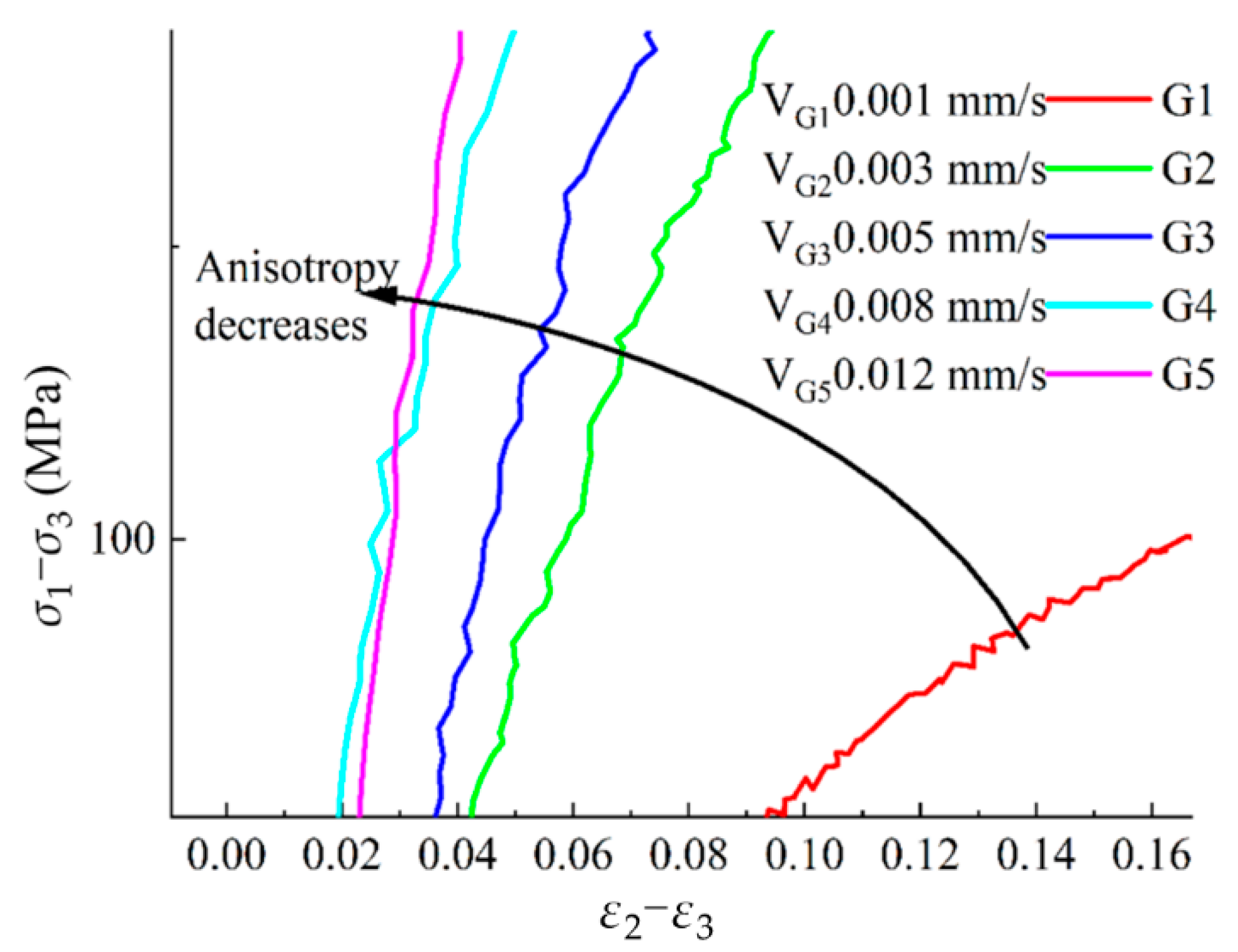
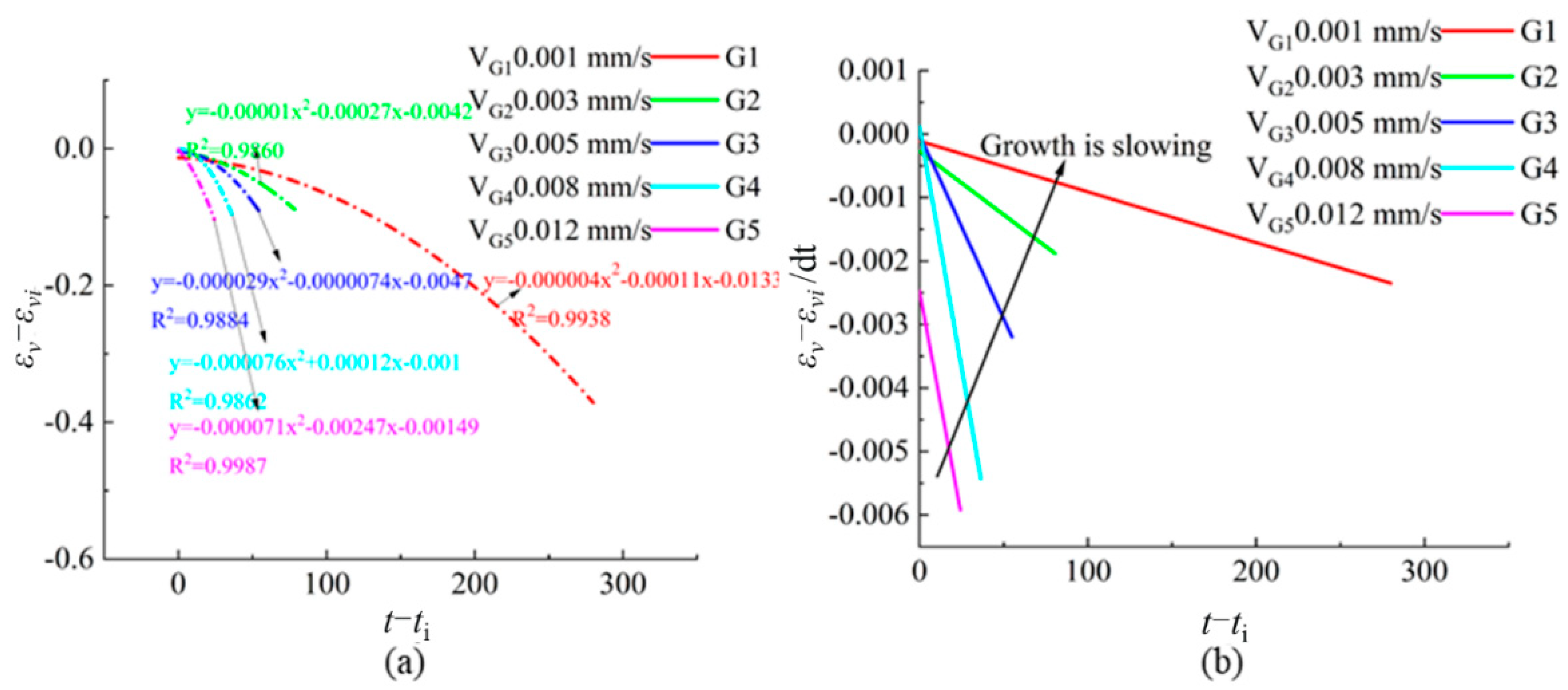
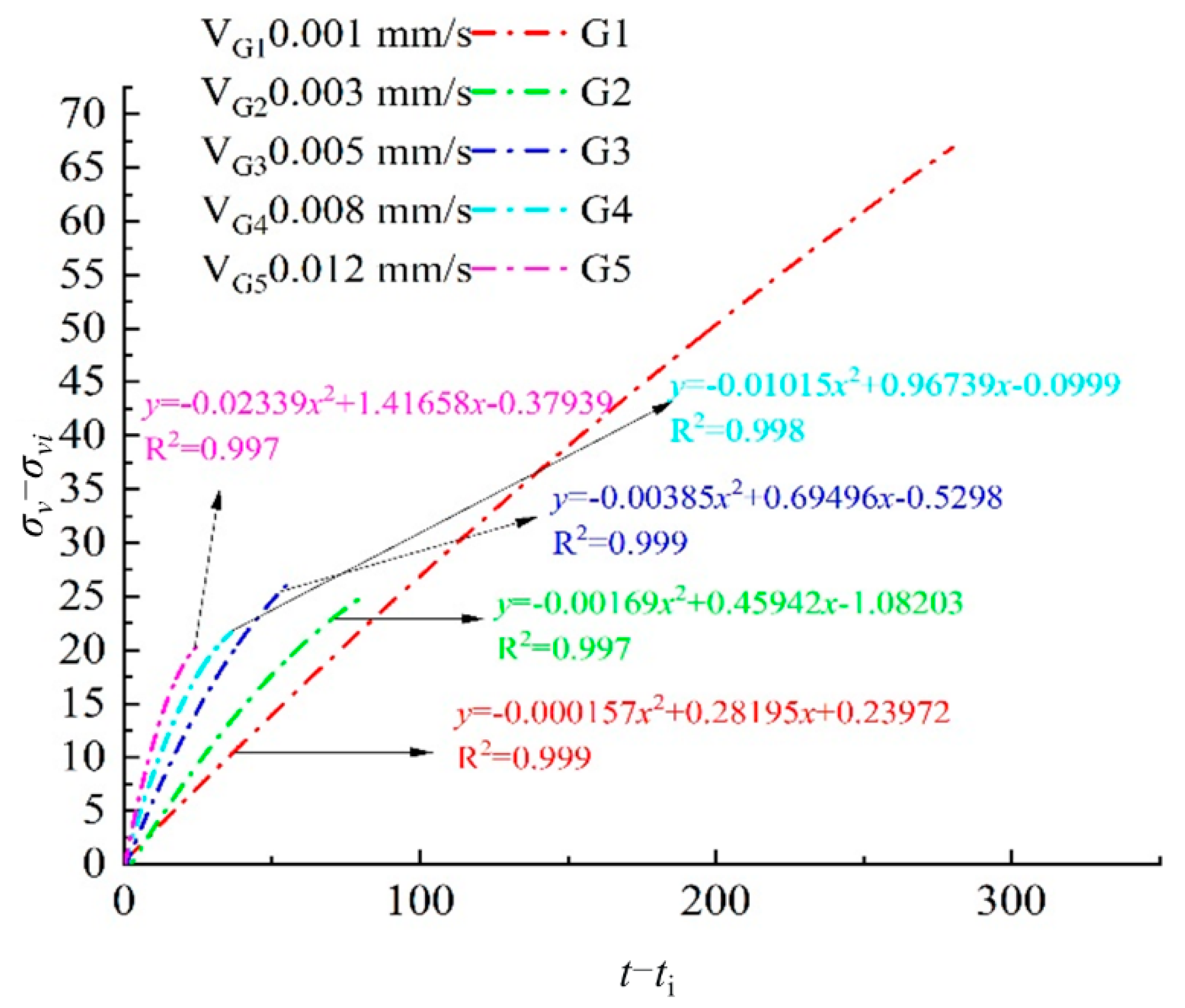
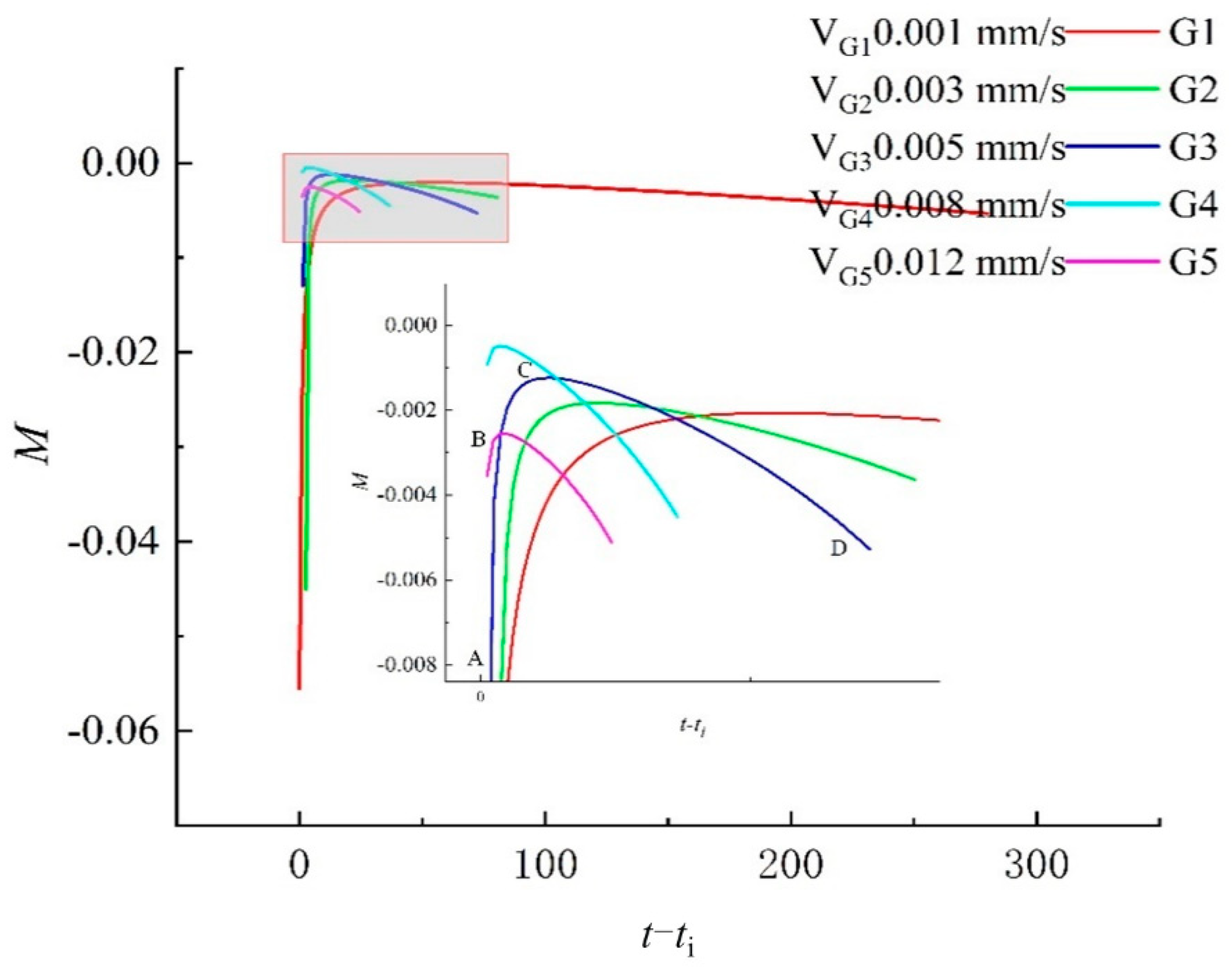
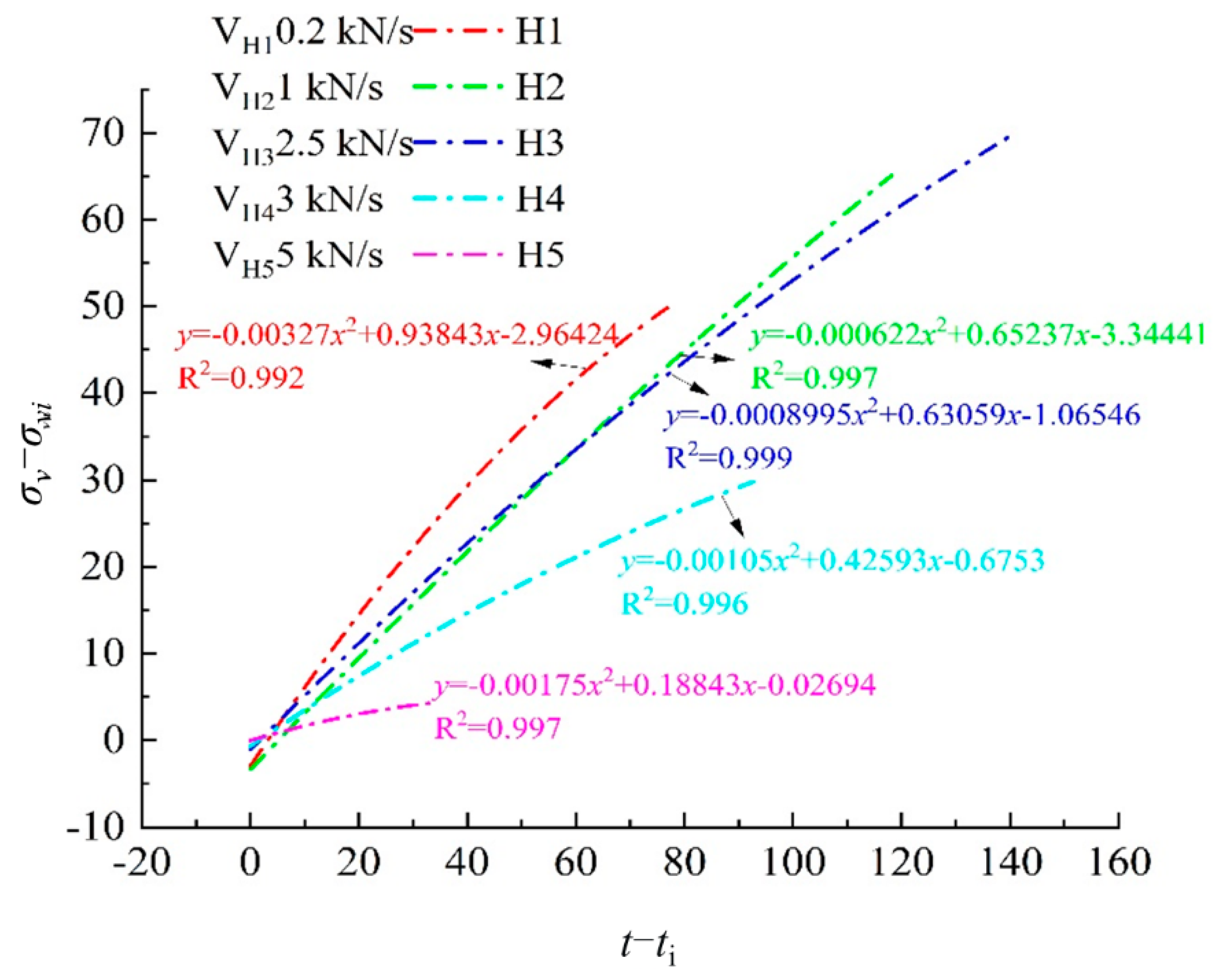
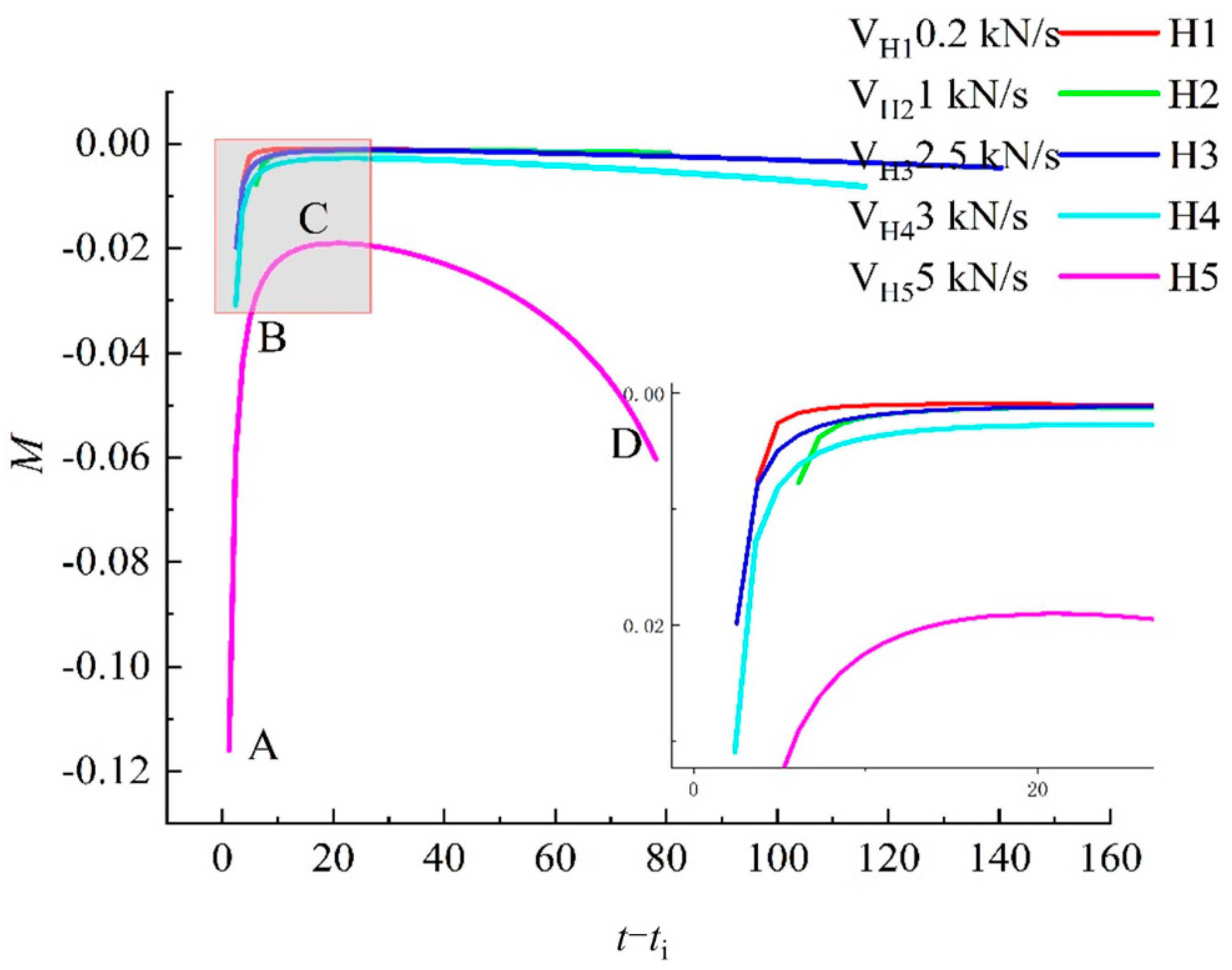
4.3. Dilatancy Characteristics and Deformation Anisotropy of Rock under Different True Triaxial Loading and Unloading Conditions
4.3.1. Deformation Anisotropic Characteristics of Rocks
4.3.2. Dilatancy Characteristics
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, M.C.; Xie, H.P.; Peng, S.L.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 16, 2803–2813, (In Chinese with English abstract). [Google Scholar]
- Gao, M.Z.; Ye, S.Q.; Yang, B.G.; Liu, Y.T.; Li, J.H.; Liu, J.J.; Xie, H.P. Research progress of deep in-situ rock mechanics. China Sci. Found. 2021, 6, 895–903, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Guo, Y.T.; Yang, C.H. Experimental investigation on strength and deformation properties of anhydrite under conventional triaxial compression. Rock Soil Mech. 2010, 35, 1776–1780, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Huo, L.; Yang, C.H.; Liu, J.; Mao, H.J.; Huang, W.G. Experimental Research on the Failure of Mudstone Cap Rock of Western HubeiEastern Chongqing Suffered Uplift and Erosion. Chin. J. Undergr. Space Eng. 2018, 14, 33–42, (In Chinese with English abstract). [Google Scholar]
- Zhou, H.W.; Xie, H.P.; Zuo, J.; Du, S.; Man, K.; Yan, C.Y. Experimental study of the effect of depth on mechanical parameters of rock. Chin. Sci. Bull. 2010, 55, 3276–3284, (In Chinese with English abstract). [Google Scholar]
- Xie, H.P.; Gao, M.Z.; Fu, C.; Lu, Y.Q.; Yang, M.Q.; Hu, J.J.; Yang, B.G. Mechanical behavior of brittle-ductile transition in rocks at different depths. J. China Coal Soc. 2021, 46, 701–715, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Xie, H.P.; Lu, J.; Li, C.B.; Li, M.H.; Gao, M.Z. Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int. J. Min. Sci. Technol. 2022, 32, 915–950. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L.M.; Cong, Y.; Wang, Z.Q. Research on the mechanical characteristics of granite failure process under true triaxial stress path. Rock Soil Mech. 2021, 42, 2069–2077, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Yin, G.Z.; Ma, B.; Liu, C.; Li, M.H.; Li, J. Effect of loading and unloading rates on mechanical properties and energy characteristics of sandstone under true triaxial stress. J. China Coal Soc. 2019, 42, 454–462, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Li, M.; Yin, G.; Xu, J.; Li, W.; Song, Z.; Jiang, C. A Novel True Triaxial Apparatus to Study the Geomechanical and Fluid Flow Aspects of Energy Exploitations in Geological Formations. Rock Mech. Rock Eng. 2016, 49, 4647–4659. [Google Scholar] [CrossRef]
- Zhao, H.G.; Song, Z.L.; Zhang, D.M.; Liu, Y.B. True triaxial experimental study on mechanical characteristics and energy evolution of sandstone under various loading and unloading rates. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–17. [Google Scholar] [CrossRef]
- Zhang, J.W.; Fan, W.B.; Song, Z.X.; Huo, Y.H.; Ding, L.J. Mechanical characteristics of deep sandstone under true triaxial stress paths. J. China Univ. Min. Technol. 2021, 50, 106–114, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Hu, J.; He, M.C.; Li, Z.H.; Feng, J.L. Experimental study of strain rockburst of anisotropic bedded sandstone. J. China Univ. Min. Technol. 2021, 48, 735–741, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, H.; Pan, P.Z.; Shen, L.F.; Feng, X.T. Characteristics of strength of rocks under different unloading rates. Rock Soil Mech. 2010, 31, 2072–2078, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- He, M.C.; Miao, J.L.; Li, J.D.; Wang, C.G.W. Experimental study on rockburst process of deep granite samples. Chin. J. Rock Mech. Eng. 2007, 5, 865–876, (In Chinese with English abstract). [Google Scholar]
- Qiu, S.L.; Feng, X.T.; Zhang, C.Q.; Zhou, H. Experimental study on mechanical properties of deep buried marble under different unloading rates of confining pressure. Chin. J. Rock Mech. Eng. 2010, 29, 1807–1817, (In Chinese with English abstract). [Google Scholar]
- Guo, J.Q.; Huang, W.F.; Liu, X.R.; Chen, J.X.; Jiang, J.G. Rock dilatancy criterion based on releasable strain energy. J. China Coal Soc. 2019, 44, 2094–2102, (In Chinese with English abstract). [Google Scholar]
- Hou, W.S.; Li, S.D.; Li, X.; He, H.M.; Pan, L.; Liu, Y.H.; Wang, R.Q. Comparison between initial and peak dilatancy characteristics of rock. J. Geotech. Eng. 2013, 35, 1478–1485, (In Chinese with English abstract). [Google Scholar]
- Zhang, W.L.; Feng, M.; Jiang, Y. Study on Triaxial Compression Test of Sandstone Dilatancy Based on PFC3D. Coal Technol. 2019, 38, 23–25, (In Chinese with English abstract). [Google Scholar]
- Cong, Y.; Cong, Y.; Zhang, L.M.; Jia, L.X. 3D particle flow simulation of loading-unloading failure process of marble. Rock Soil Mech. 2019, 40, 1179–1186+1212, (In Chinese with English abstract). [Google Scholar]
- Li, X.B.; Chen, Z.H.; Weng, L.; Li, C.J. Unloading responses of pre-flawed rock specimens under different unloading rates. Trans. Nonferrous Met. Soc. China 2019, 29, 1516–1526, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Li, Z.Y.; Wu, P.; Jiang, D.Y.; Xiao, F.; Liu, W. Study on True Triaxial Mechanical Characteristics with Hole Defects of Sandstone. Chin. J. Undergr. Space Eng. 2022, 18, 120–128, (In Chinese with English abstract). [Google Scholar]
- Kang, D.A.; Wei, W.B. Unloading-induced failure of brittle rock and implications for excavation-induced strain burst—ScienceDirect. Tunn. Undergr. Space Technol. 2019, 84, 495–506. [Google Scholar]
- Zhao, Y.; Bi, J.; Wang, C.; Liu, P. Effect of Unloading Rate on the Mechanical Behavior and Fracture Characteristics of Sandstones Under Complex Triaxial Stress Conditions. Rock Mech. Rock Eng. 2021, 54, 4851–4866. [Google Scholar] [CrossRef]
- Dai, B.; Zhao, G.; Dong, L.; Yang, C. Mechanical Characteristics for Rocks under Different Paths and Unloading Rates under Confining Pressures. Shock. Vib. 2015, 1, 1–8. [Google Scholar] [CrossRef]
- Li, J.Z.; Lin, F.; Zhang, Z. Triaxial Experimental Study on Changes in the Mechanical Properties of Rocks Under Different Rates of Confining Pressures Unloading. Soil Mech. Found. Eng. 2019, 56, 246–252. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.S.; Liu, B.; Liu, X.; Pan, Y.; Liu, J. Experimental Study on the Dilatancy and Fracturing Behavior of Soft Rock Under Unloading Conditions. Int. J. Civ. Eng. 2017, 15, 921–948. [Google Scholar] [CrossRef]
- Hu, X.W.; Yi, X.J.; Wang, S.Y.; Huang, R.Q. Experimental study on mechanical properties of red sandstone under different triaxial stress paths. Hydrogeol. Eng. Geol. 2009, 36, 57–61. [Google Scholar]
- Young, R.P.; Nasseri, M.H.B. The effect of true-triaxial stress path on induced fracturing in anisotropic gneiss. In Proceedings of the ISRM 2nd International Conference on Rock Dynamics, Suzhou, China, 18–19 May 2016. [Google Scholar]
- Yin, G.Z.; Lu, J.; Li, X.; BIan, G.; Song, Z.L.; Liu, Y.B. Influence of intermediate principal stress on dilatancy and strength characteristics of sandstone. J. China Coal Soc. 2017, 42, 879–885, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Wu, G. Comparative analysis of failure effect of rock mass under loading and unloading conditions. Rock Soil Mech. 1997, 2, 13–16, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Du, K. Fracture Characteristics of Deep Rock Mass under True Triaxial Unloading and Mechanism of Induced Rockburst; Central South University: Changsha, China, 2013; (In Chinese with English abstract). [Google Scholar]
- Chu, Y.P.; Sun, H.; Zhang, D.M. Experimental study on evolution in the characteristics of permeability, deformation, and energy of coal containing gas under triaxial cyclic loading-unloading. Energy Sci. Eng. 2019, 7, 2112–2123. [Google Scholar] [CrossRef] [Green Version]
- Wen, T.; Tang, H.M.; Fan, Z.Q.; Cai, Y.; Wang, J.D. Mechanical properties and unloading constitutive model of Padong Formation rocks. J. China Univ. Min. Technol. 2018, 47, 768–779, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Jia, P.; Yang, N.; Liu, D.; Liu, D.; Wang, S.; Zhao, Y.; Tong, X. Failure mechanism of combined rock under true triaxial loading and unloading conditions. J. Cent. South Univ. (Nat. Sci. Ed.) 2021, 52, 2867–2875. [Google Scholar]
- Liang, Y.; Ran, Q.; Zou, Q.; Hong, Y. Experimental Study of Mechanical Behaviors and Failure Characteristics of Coal Under True Triaxial Cyclic Loading and Unloading and Stress Rotation. Nat. Resour. Res. 2022, 31, 971–991. [Google Scholar] [CrossRef]
- Chen, G.Q.; Liu, D.; Xu, P.; Qin, C.A. Experimental study on true triaxial excavation unloading of jointed rock bridge. Chin. J. Rock Mech. Eng. 2018, 37, 325–328, (In Chinese with English abstract). [Google Scholar]
- Fan, P.X.; Li, Y.; Zhao, Y.T.; Wang, M.Y.; Wang, D.R.; Shi, H.J. Experimental study on unloading failure strength characteristics of red sandstone. Chin. J. Rock Mech. Eng. 2018, 37, 852–861, (In Chinese with English abstract). [Google Scholar]
- Ma, X.; Rudnicki, J.W.; Haimson, B.C. The application of a Matsuoka-Nakai-Lade-Duncan failure criterion to two porous sandstones. Int. J. Rock Mech. Min. Sci. 2017, 92, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Haimson, B.C.; Rudnicki, J.W. True triaxial failure stress and failure plane of two porous sandstones subjected to two distinct loading paths. Porous Rock Fract. Mech. 2017, 285–307. [Google Scholar]
- Miao, J.L.; He, M.C.; Li, D.J.; Zeng, F.J.; Zhang, Q. Acoustic emission characteristics and fracture mechanism of granite strain rock burst. Chin. J. Rock Mech. Eng. 2009, 28, 1593–1603, (In Chinese with English abstract). [Google Scholar]
- Gong, Q.M.; Yin, L.J.; Wu, S.Y.; Zhao, J.; Ting, Y. Rock burst and slabbing failure and its influence on TBM excavation at headrace tunnels in Jinping II hydropower station. Eng. Geol. 2012, 124, 98–108. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, J.; Cai, M.; Cheng, C. Influence of Unloading Rate on the Strainburst Characteristics of Beishan Granite Under True-Triaxial Unloading Conditions. Rock Mech. Rock Eng. 2014, 47, 467–483. [Google Scholar] [CrossRef]
- Zhao, X.G.; Cai, M. Influence of specimen height-to-width ratio on the strainburst characteristics of Tianhu granite under true-triaxial unloading conditions. Can. Geotech. J. 2014, 52, 890–902. [Google Scholar] [CrossRef]
- Huang, L.; Liang, J.; Ma, J.; Chen, W. A dynamic bounding surface plasticity damage model for rocks subjected to high strain rates and confinements. Int. J. Impact Eng. 2022, 168, 104306. [Google Scholar] [CrossRef]
- Ma, J.; Yin, P.; Huang, L.; Liang, Y. The application of distinct lattice spring model to zonal disintegration within deep rock masses. Tunn. Undergr. Space Technol. 2019, 90, 144–161. [Google Scholar] [CrossRef]
- Huang, L.; Liang, J.; Ma, J.; Yang, H.; Gui, Y. Spherical cavity expansion in porous rock considering plasticity and damage. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 2235–2259. [Google Scholar] [CrossRef]
- Yin, G.Z.; Li, M.H.; Xu, J.; Wang, W.Z.; Li, W.P.; Li, X.; Song, Z.L.; Deng, B.Z. Development and application of multifunctional true triaxial fluid-structure coupling test system. J. Rock Mech. Eng. 2015, 34, 2436–2445. [Google Scholar]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Zhou, H.; Meng, Z.F.; Zhang, C.Q.; Lu, J.J. Quantitative evaluation method of rock brittleness characteristics based on stress-strain curve. Chin. J. Rock Mech. Eng. 2014, 33, 1114–1122, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Li, Z.L. Study on Mechanical Properties and FailureMechanism of Rock under True TriaxialLoading and Unloading Conditions. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2015. (In Chinese with English abstract). [Google Scholar]





| Specimen Number | Loading Rate/ (mm/s) | Unloading Rate/ (kN/s) | Specimen Number | Loading Rate/ (mm/s) | Unloading Rate/ (kN/s) |
|---|---|---|---|---|---|
| H1 | 0.003 | 0.2 | G1 | 0.001 | 1 |
| H2 | 0.003 | 1 | G2 | 0.003 | 1 |
| H3 | 0.003 | 2.5 | G3 | 0.005 | 1 |
| H4 | 0.003 | 3 | G4 | 0.008 | 1 |
| H5 | 0.003 | 5 | G5 | 0.012 | 1 |
| Specimen Number | Crack Initiation Deviatoric Stress /σcip | Damage Deviatoric Stress /σcdp | Peak Deviating Stress /σfp |
|---|---|---|---|
| G2 | 41.11 MPa | 113.22 MPa | 136.17 MPa |
| G3 | 48.84 MPa | 106.55 MPa | 132.09 MPa |
| G4 | 53.75 MPa | 119.42 MPa | 140.94 MPa |
| G5 | 60.30 MPa | 120.84 MPa | 140.48 MPa |
| Specimen Number | B1 | B2 | Bd | σr/100 MPa | σp/100 MPa | εr | εp |
|---|---|---|---|---|---|---|---|
| H1 | 0.1322 | 0.4709 | 0.0623 | 1.090 | 1.256 | 0.8757 | 0.5232 |
| H2 | 0.2372 | 1.4062 | 0.3336 | 1.039 | 1.362 | 0.6653 | 0.4356 |
| H3 | 0.4941 | 1.2838 | 0.6343 | 0.564 | 1.115 | 0.6454 | 0.2162 |
| H4 | 0.2850 | 0.9918 | 0.2826 | 0.735 | 1.028 | 0.4081 | 0.1638 |
| H5 | 0.3639 | 1.4051 | 0.5113 | 0.582 | 0.915 | 0.3186 | 0.0816 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Du, W.; Zhang, D.; Yu, B. Effect of Loading and Unloading Rates on Sandstone Deformation and Dilatancy under True Triaxial Condition. Sustainability 2023, 15, 5105. https://doi.org/10.3390/su15065105
Wang Y, Du W, Zhang D, Yu B. Effect of Loading and Unloading Rates on Sandstone Deformation and Dilatancy under True Triaxial Condition. Sustainability. 2023; 15(6):5105. https://doi.org/10.3390/su15065105
Chicago/Turabian StyleWang, Yingwei, Weihang Du, Dongming Zhang, and Beichen Yu. 2023. "Effect of Loading and Unloading Rates on Sandstone Deformation and Dilatancy under True Triaxial Condition" Sustainability 15, no. 6: 5105. https://doi.org/10.3390/su15065105
APA StyleWang, Y., Du, W., Zhang, D., & Yu, B. (2023). Effect of Loading and Unloading Rates on Sandstone Deformation and Dilatancy under True Triaxial Condition. Sustainability, 15(6), 5105. https://doi.org/10.3390/su15065105







