Numerical Simulation of Assembly Process and Sealing Reliability of T-Rubber Gasket Pipe Joints
Abstract
:1. Introduction
2. Computational Model
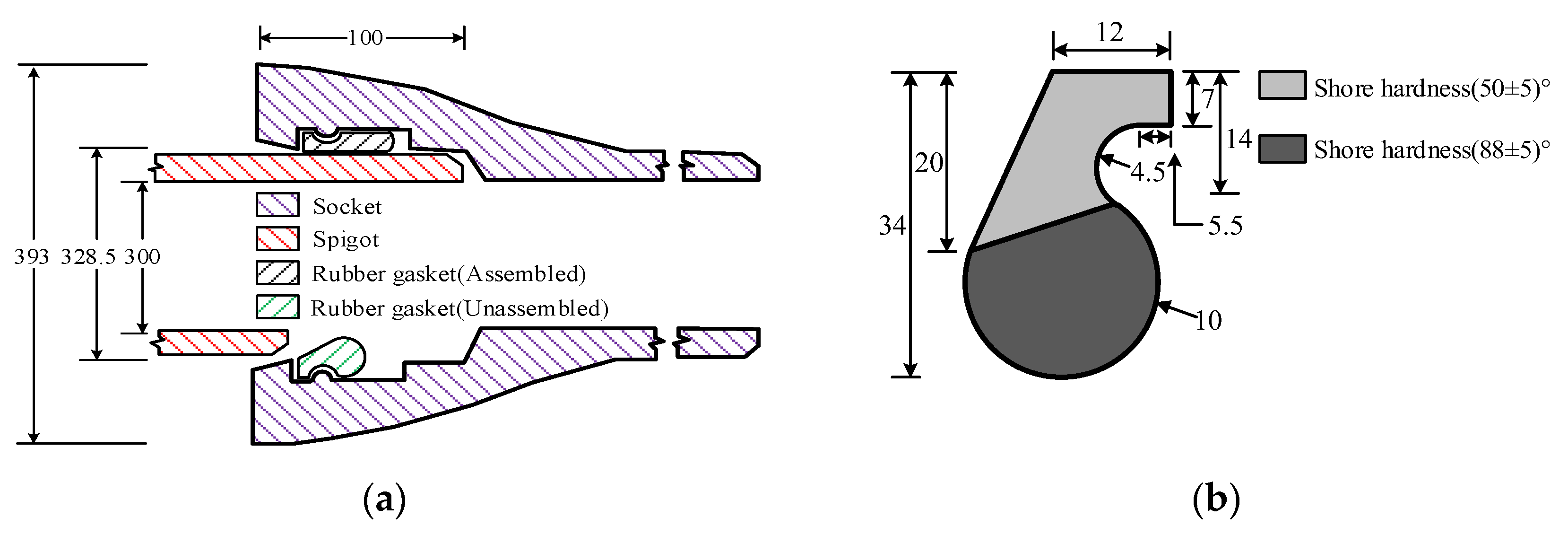
2.1. Model Parameters
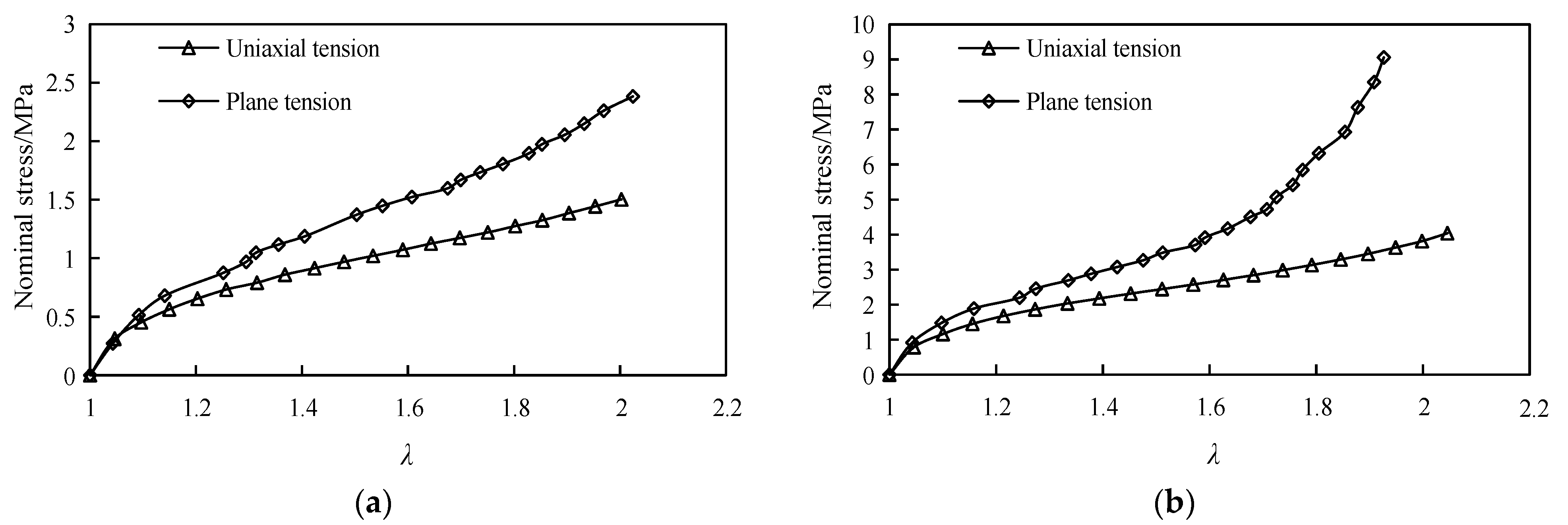
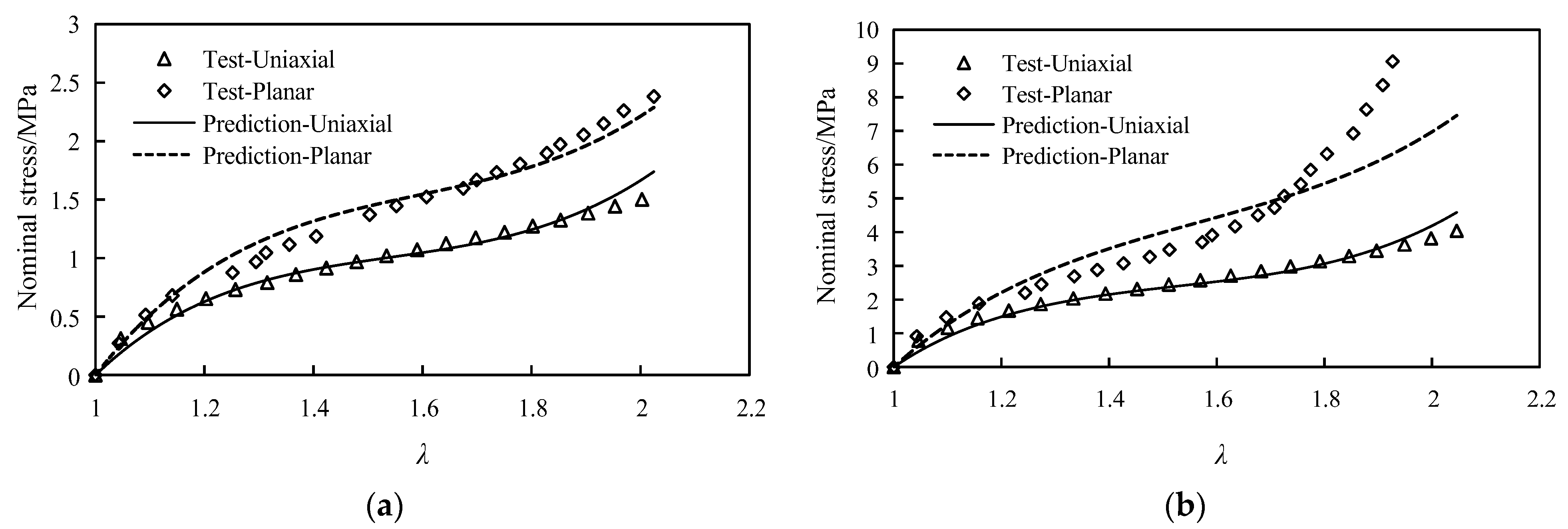
2.2. Constitutive Parameters of T-Rubber Gasket Materials
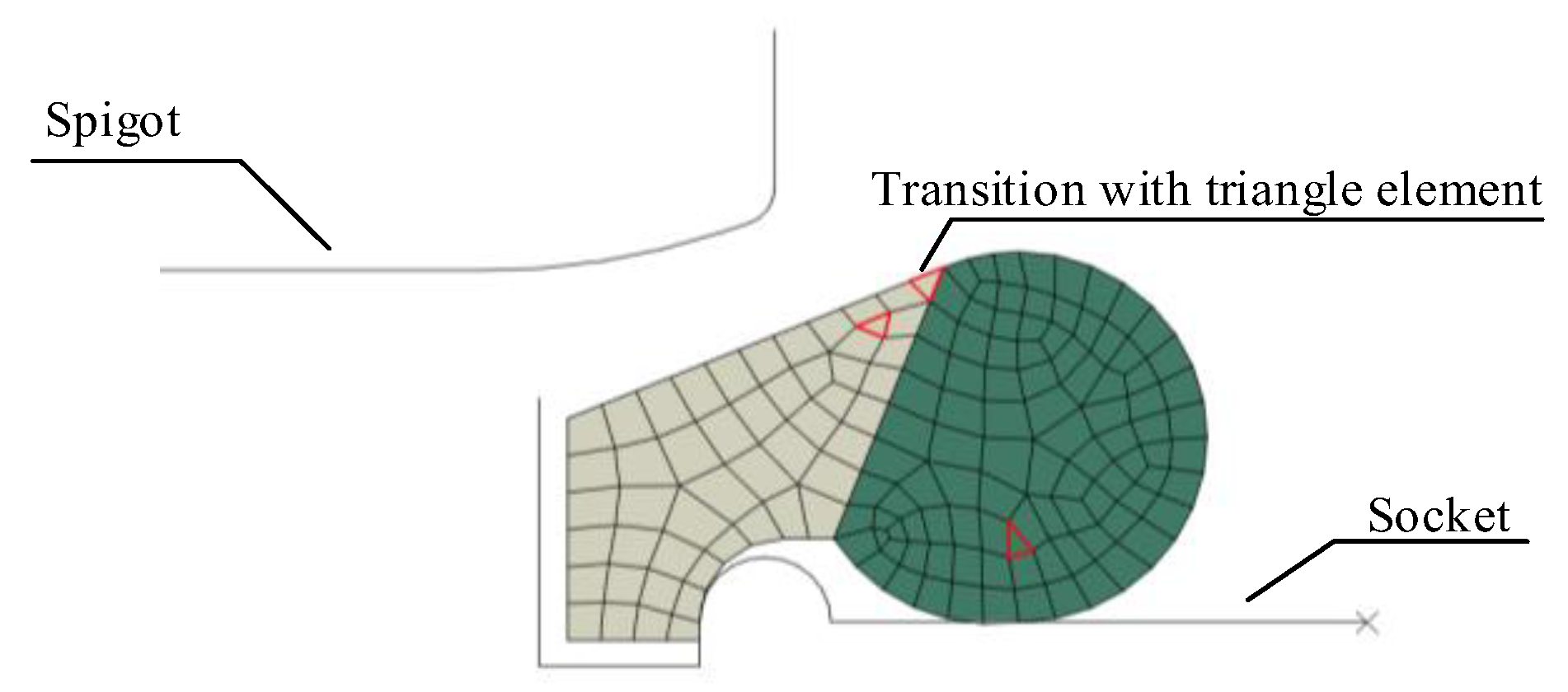
2.3. Simulation Scheme
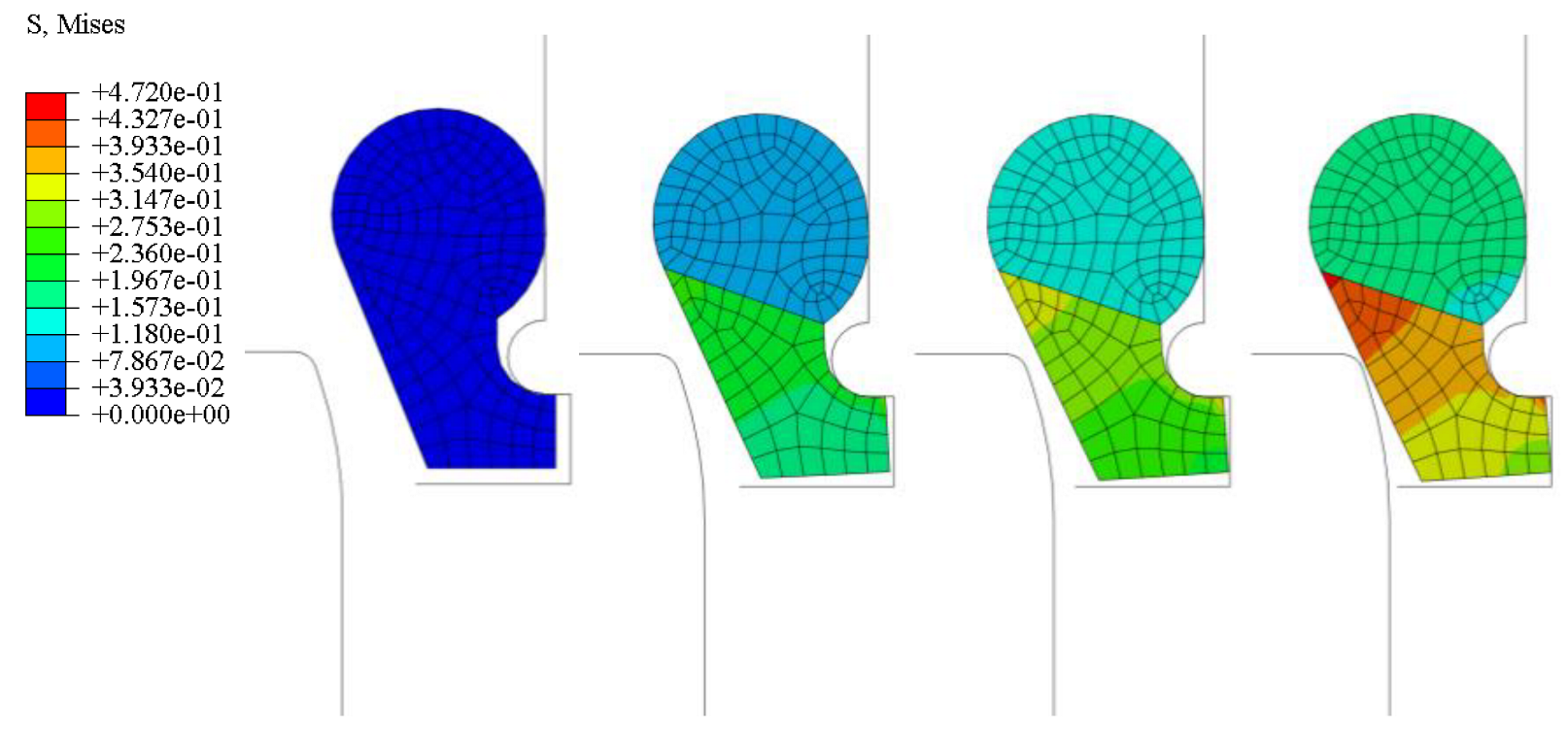
3. Results
4. Analysis and Discussion
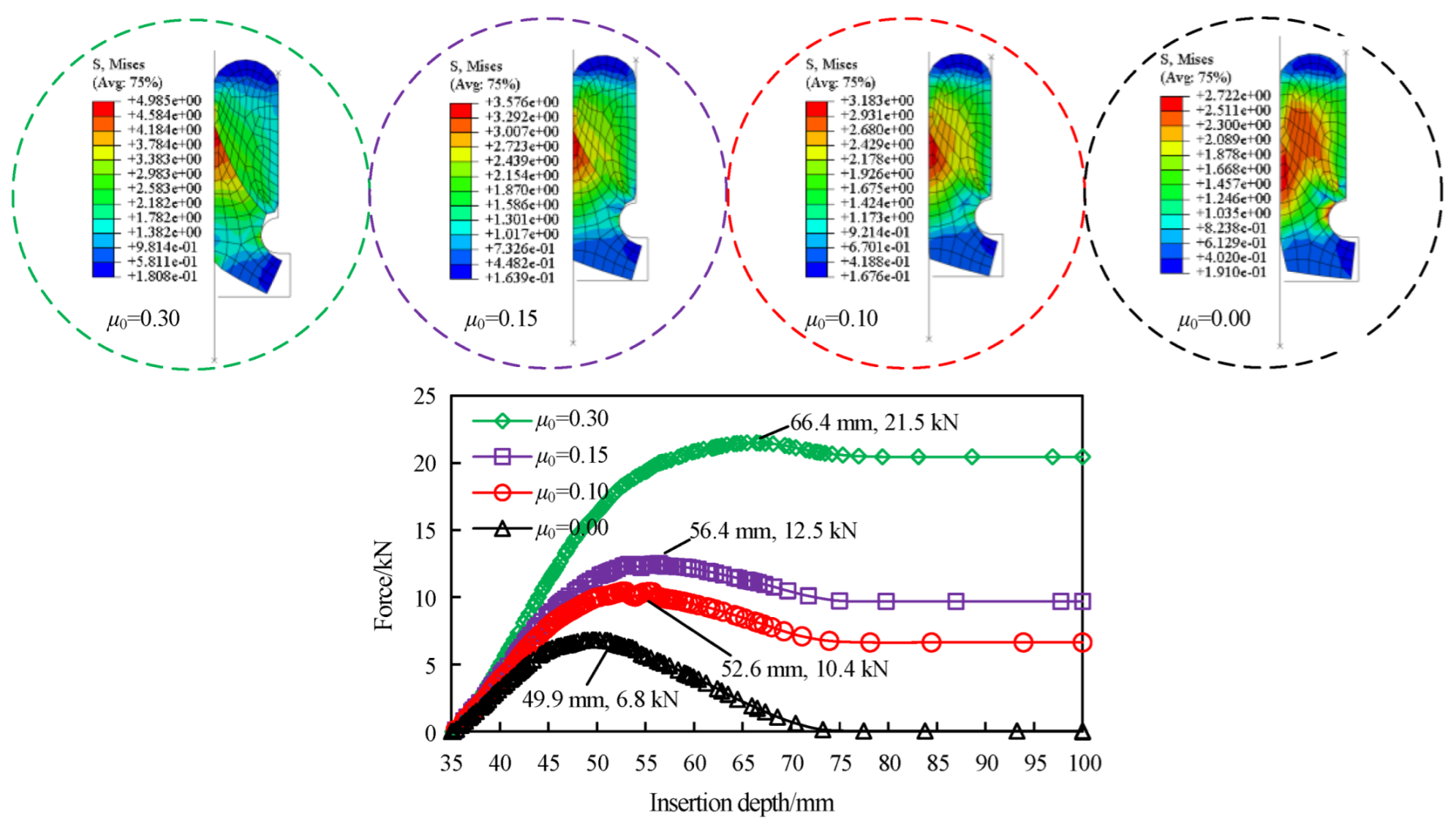
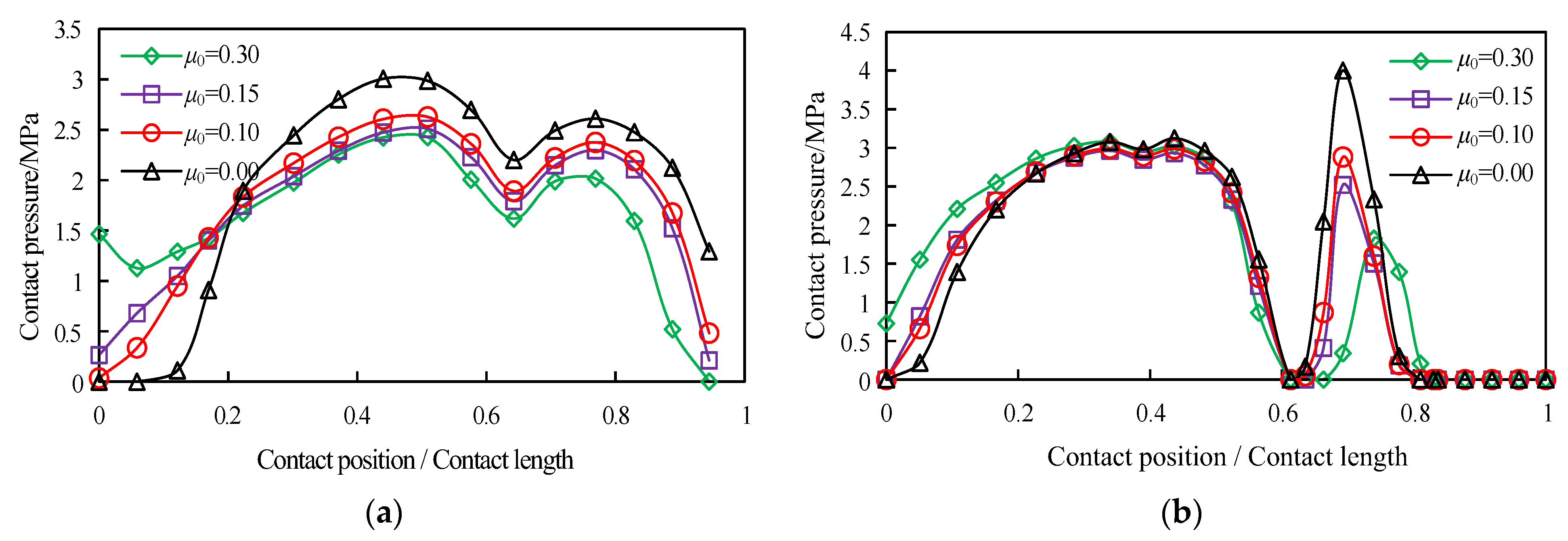
4.1. Effect of Friction Coefficient μ0 between Spigot and Rubber Gasket
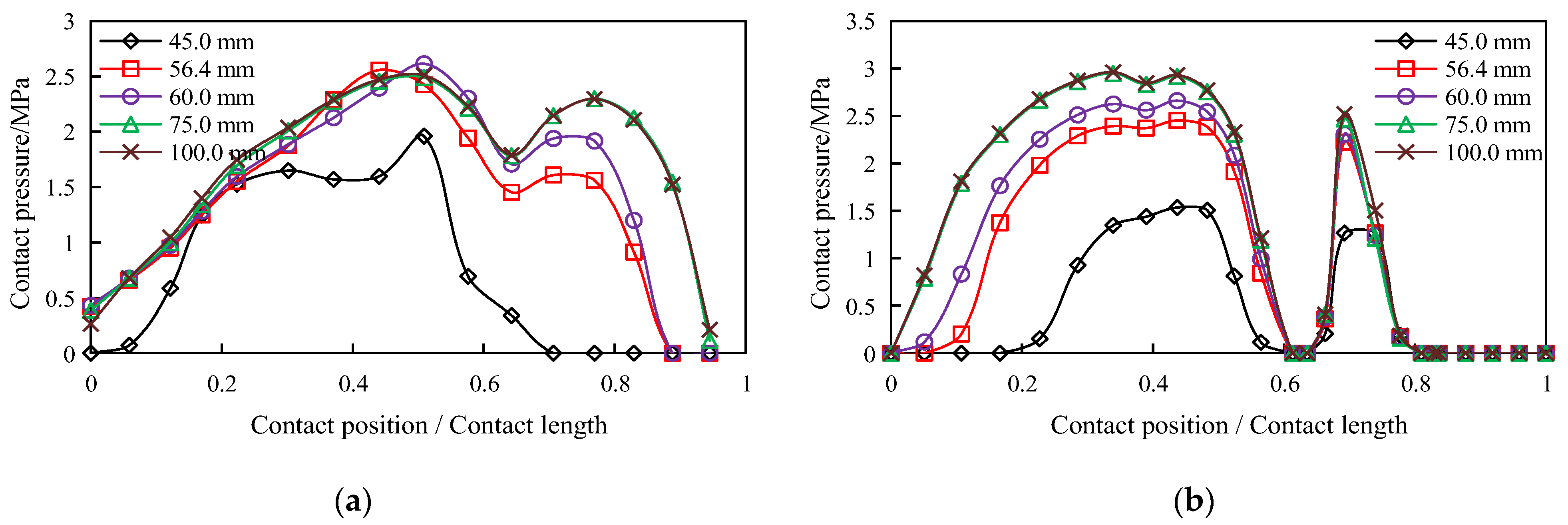
4.2. Effect of Depth of Spigot Assembly
4.3. Effect of Radial Clearance Deviation of Socket and Spigot
5. Conclusions
- (1)
- The interference fit between the T-rubber gasket and socket formed the initial assembly stress of the rubber gasket. The subsequent socket assembly was completed based on the initial assembly stress, and the deformation of the rubber gasket exhibited a certain historical accumulation.
- (2)
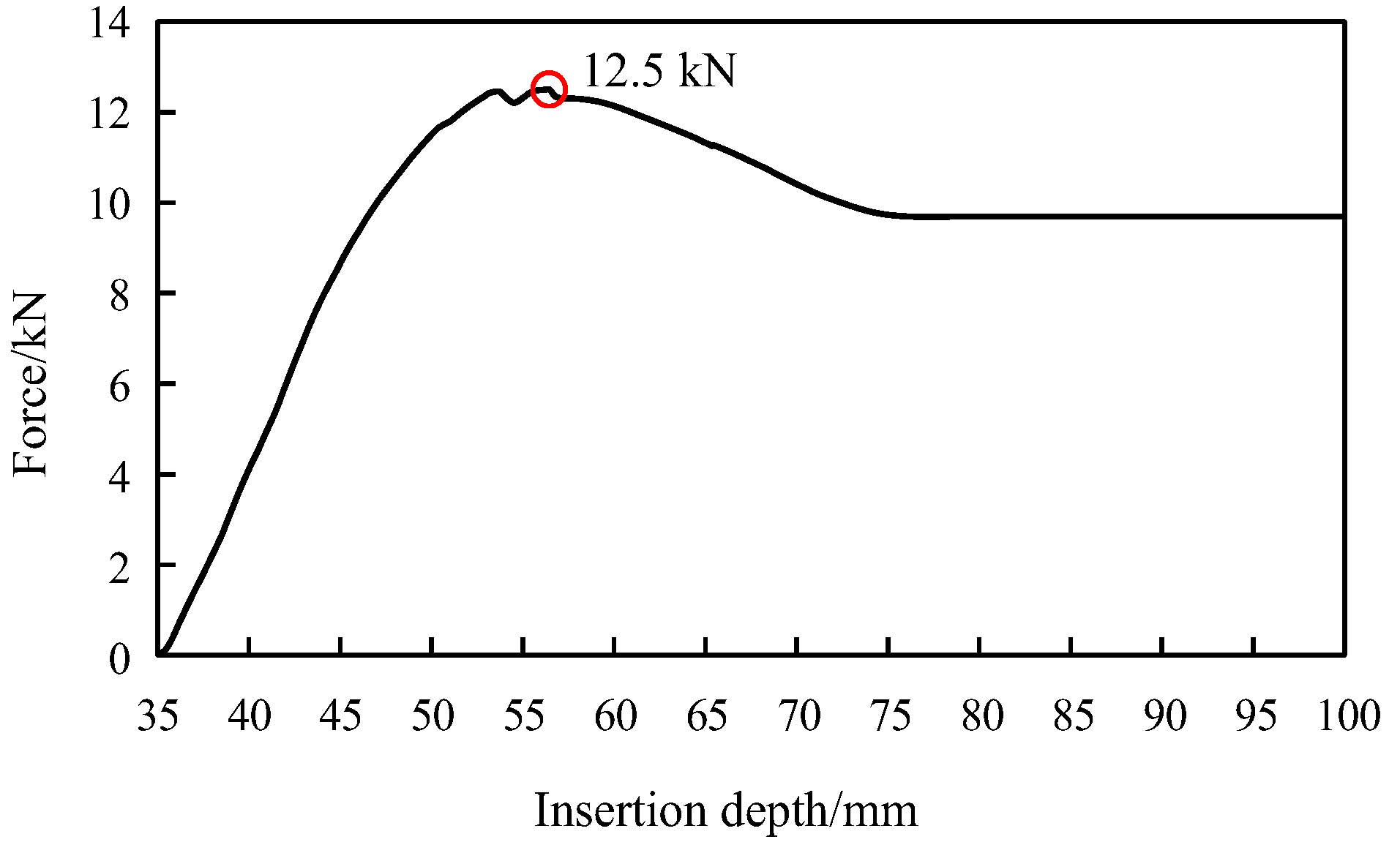
- During the assembly of the socket, the peak propulsive force required by the assembly pipe joint increased with the friction coefficient of the seepage surface, thus indicating that the lubricant selection and coating process significantly affect the installation thrust control of the rubber gasket joint. For the different friction coefficients, the assembly depth corresponding to the sliding friction condition of the spigot pipe was 74 mm. Based on the ideal situation with a friction coefficient of 0, the minimum pushing force required to assemble the T-rubber gasket joint of a DN300 ductile iron pipe was 6.8 kN.
- (3)
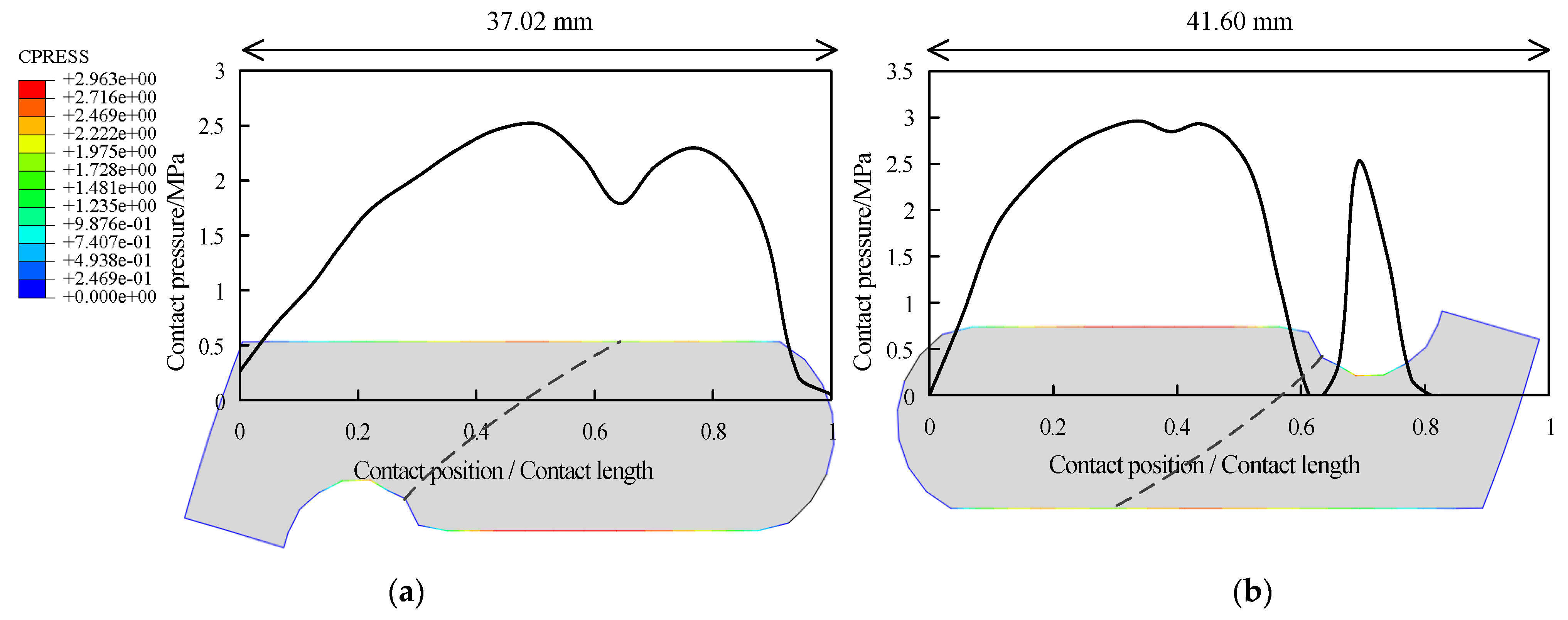
- After the T-rubber gasket joint was assembled, two contact pressure peaks were indicated on the two seepage surfaces, and the trough was located at the interface of the two types of rubber. Under the effects of different factors, the effective contact pressure on the two seepage surfaces of the T-rubber gasket was significantly greater than the maximum operating pressure of the urban municipal pipeline. The results indicate that the T-rubber gasket joint affords high-quality sealing and the ability to adapt to a small axial displacement.
- (4)
- The large deformation and stress change history of the rubber gasket was clearly visualized in the simulation. The method could be applied to the design of the rubber gasket joint and sealing rubber gasket of municipal pipelines to reduce the test cost. The obtained results can serve as a reference for the sustainable design of rubber components.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.R.L.; Sun, S.; Shen, S. Seismic Damage Behavior of Buried Lifeline Systems during Recent Severe Earthquakes in USA, China and Other Countries. In Technical Report No.ODULEE-02 In Lifeline Earthquake Engineering Research Series; National Science Foundation: Washington, DC, USA, 1985. [Google Scholar]
- Nair, G.S.; Dash, S.R.; Mondal, G. Review of Pipeline Performance during Earthquakes since 1906. J. Perform. Constr. Facil. 2018, 32, 11–18. [Google Scholar] [CrossRef]
- Wang, M. Discussion on sealing design of flexible interface of water supply pipeline. Munic. Eng. Technol. 2000, 4, 43–46. (In Chinese) [Google Scholar]
- Hou, L.; Tan, W. Design of the rubber gasket ring for concrete sewer pipes. China Concr. Prod. 2021, 4, 42–44. (In Chinese) [Google Scholar]
- Lin, A.; Wu, J.; Li, H.; Li, Z.; Su, B.; Wang, Y. Effect of geometric error on friction behavior of cylinder seals. Polymers 2021, 13, 3438. [Google Scholar] [CrossRef]
- Vieira, J.C.; Mendes, A.O.; Ribeiro, M.L.; Vieira, A.C.; Carta, A.M.; Fiadeiro, P.T.; Costa, A.P. FEM analysis validation of rubber hardness impact on mechanical and softness properties of embossed industrial base tissue papers. Polymers 2022, 14, 2485. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wang, C.; Fan, P.; Kuang, Y.; Dong, Z. The Sealing effect improvement prediction of flat rubber ring in roller bit based on Yeoh_Revised Model. Materials 2022, 15, 5529. [Google Scholar] [CrossRef] [PubMed]
- Draganová, K.; Semrád, K.; Blišťanová, M.; Musil, T.; Jurč, R. Influence of Disinfectants on Airport Conveyor Belts. Sustainability 2021, 13, 10842. [Google Scholar] [CrossRef]
- Cheon, K.-M.; Akpudo, U.E.; Kareem, A.B.; Nwabufo, O.C.; Jeon, H.-R.; Hur, J.-W. An FEA-Assisted decision-making framework for PEMFC gasket material selection. Energies 2022, 15, 2580. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X. A novel structure of rubber ring for hydraulic buffer seal based on numerical simulation. Appl. Sci. 2021, 11, 2036. [Google Scholar] [CrossRef]
- Theiner, Y.; Lehar, H.; Hofstetter, G. Numerical and experimental investigation of a pipe-joint system for high operating pressures. J. Pipeline Syst. Eng. 2012, 3, 77–83. [Google Scholar] [CrossRef]
- Zhong, J. Waterproof stress analysis of pipeline double O-shaped rubber Seal. China Munic. Eng. 2016, 5, 30–32+98–99. (In Chinese) [Google Scholar]
- Wang, F.; Fang, H.; Li, B.; Chen, C. Dynamic response analysis of drainage pipes with gasketed bell and spigot joints subjected to traffic loads. Chin. J. Geotech. Eng. 2018, 40, 2274–2280. (In Chinese) [Google Scholar]
- Dong, S.; Yan, X.; Zhang, H.; Ma, B. Numerical study of restrained joint and pulling load for ductile iron pipe in horizontal directional drilling. J. Pipeline Syst. Eng. 2018, 9, 04018012.1–04018012.8. [Google Scholar] [CrossRef]
- Treloar, L.R.G. Stress-strain data for vulcanized rubber under various types of deformation. Trans Faraday Soc. 1944, 40, 59–70. [Google Scholar] [CrossRef]
- GB/T 13295-2019; Ductile Iron Pipes, Fitting and Accessories for Water or Gas Applications. Standards Press of China: Beijing, China, 2019. (In Chinese)
- Singhai, A.C. Behavior of jointed ductile iron pipelines. J. Transp. Eng. 1984, 110, 235–250. [Google Scholar] [CrossRef]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformation of isotropic material—IV. Further developments of the general theory. Philos. Trans. R. Soc. 1948, A241, 379–397. [Google Scholar]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Gent, A.N.; Thomas, A.G. Forms for the stored(strain) energy function for vulcanized rubber. J. Polym. Sci. Part A 1958, 28, 625–637. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: A review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Han, Y.; Chen, J.; Wang, S. Characterisation of hyper-elastic materials by non-equibiaxial extension test based on dual-variable method. Plast. Rubber. Compos. 2017, 46, 103–109. [Google Scholar] [CrossRef]
- Seibert, D.J.; Schöche, N. Direct comparison of some recent rubber elasticity models. Rubber Chem. Technol. 2000, 73, 366–384. [Google Scholar] [CrossRef]
- Marckmann, G.; Verron, E. Comparison of hyperelastic models for rubber-like materials. Rubber Chem. Technol. 2006, 79, 835–858. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Hongling, S.; Lei, Z.; Duan, J. Experimental Research on Ductile Iron Pipes with Rubber Gasketed Joints. In Proceedings of the Pipelines 2010: Climbing New Peaks to Infrastructure Reliability—Renew, Rehab, and Reinvest, Keystone, CO, USA, 28 August–1 September 2010. [Google Scholar]



| Shore Hardness | μ1 (MPa) | μ2 (MPa) | μ3 (MPa) | α1 | α2 | α3 |
|---|---|---|---|---|---|---|
| 50 | −3.783 | 1.229 | 4.047 | 3.407 | 4.927 | 1.222 |
| 88 | −3.924 | 3.136 | 4.428 | 5.468 | 5.911 | −1.155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Han, G.; Li, D.; Duan, J.; Yan, Y. Numerical Simulation of Assembly Process and Sealing Reliability of T-Rubber Gasket Pipe Joints. Sustainability 2023, 15, 5160. https://doi.org/10.3390/su15065160
Han Y, Han G, Li D, Duan J, Yan Y. Numerical Simulation of Assembly Process and Sealing Reliability of T-Rubber Gasket Pipe Joints. Sustainability. 2023; 15(6):5160. https://doi.org/10.3390/su15065160
Chicago/Turabian StyleHan, Yang, Guoqi Han, Dongqiao Li, Junfeng Duan, and Yewen Yan. 2023. "Numerical Simulation of Assembly Process and Sealing Reliability of T-Rubber Gasket Pipe Joints" Sustainability 15, no. 6: 5160. https://doi.org/10.3390/su15065160
APA StyleHan, Y., Han, G., Li, D., Duan, J., & Yan, Y. (2023). Numerical Simulation of Assembly Process and Sealing Reliability of T-Rubber Gasket Pipe Joints. Sustainability, 15(6), 5160. https://doi.org/10.3390/su15065160







