Operating Multi-Purpose Reservoirs in the Red River Basin: Hydropower Benefit Optimization in Conditions Ensuring Enough Water for Downstream Irrigation

Abstract

Operational management of multiple reservoirs and hydropower plants in the Red River Basin (RRB) in Vietnam was investigated for optimal benefit of hydropower generation and to ensure the water supply for agricultural and social–economic development downstream during the dry season. This research will investigate the operation of three hydropower reservoirs, including Hoa Binh, Thac Ba, and Tuyen Quang reservoirs. Those reservoirs are managed under the operating Decision No. 740 of the Prime Minister in 2019, which stipulates the dry season and water - enhanced discharge period to supply water for agriculture and ensures that the minimum water level in Hanoi is above 2.2 m, which may lead to lack of water for hydropower plants. To do this, I used the optimization approach to determine the optimal water discharge scenario in these three reservoirs during the enhanced discharge period (irrigation water supply). Based on the optimal scenario, I calculated the amount of saved water which is then compared with the standard discharge scenario under Decision No. 740. This study also found that there is an increasing economic benefit from saved water and hydropower generation during peak hours (after the winter–spring crop). Addtionally, the results demonstrated that the economic value added by the power generation of three reservoirs is about 401.7 billion VND. If compared with using thermal power plants, it saves 858.0 billion VND.

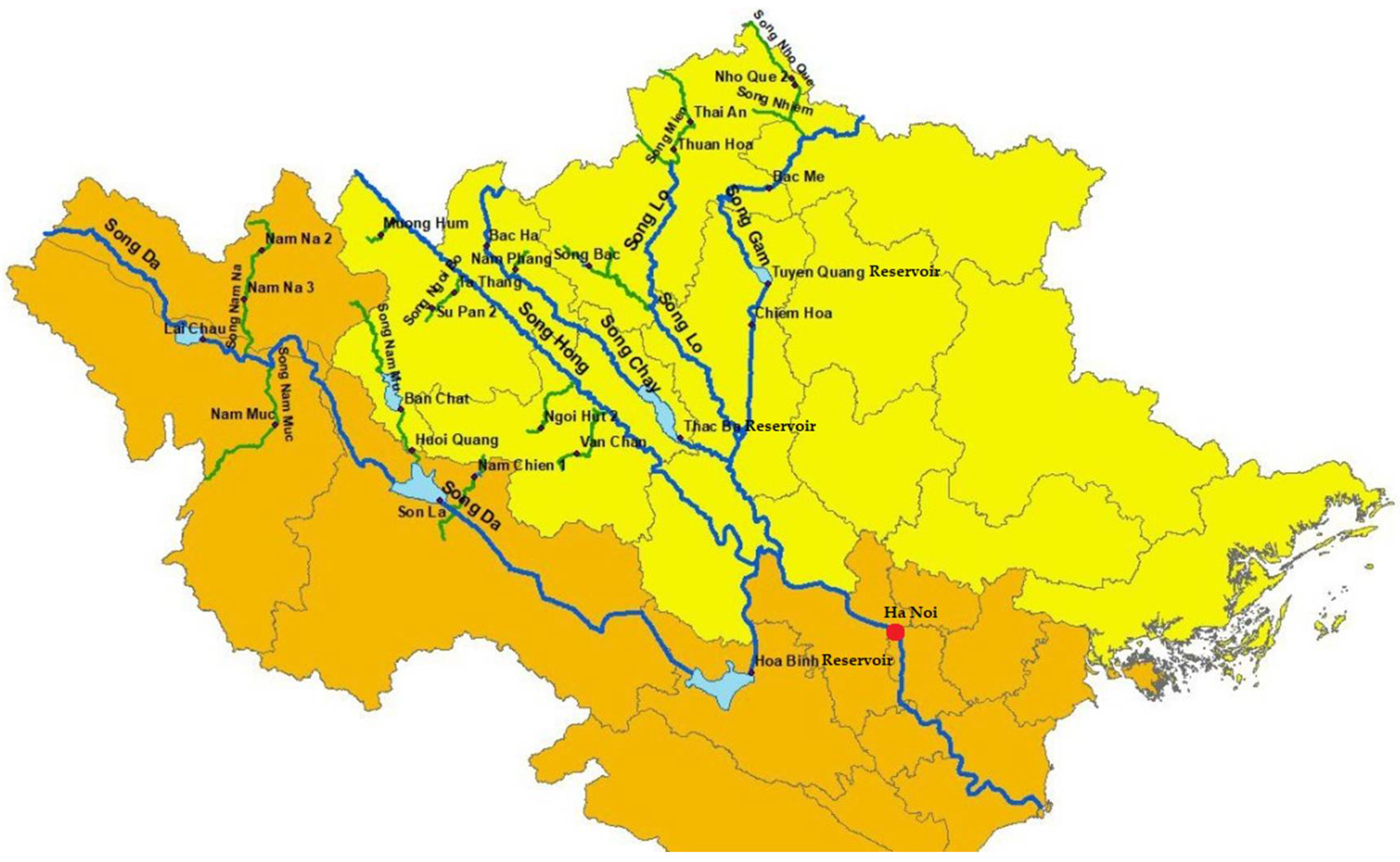
1. Introduction

Vietnam is among the few countries in Southeast Asia with a relatively comprehensively developed irrigation system, with thousands of large, medium, and small irrigation structures for water supply and drainage systems for agricultural production, aquaculture, domestic and industrial use, as well as for flood, inundation, and drought prevention. They contribute significantly to environmental protection. However, due to the influence of climate change and socioeconomic development activities, irrigation work is facing tremendous difficulties and challenges. Indeed, water resources are increasingly scarce and water pollution is becoming more and more serious. Additionally, natural disasters such as floods, droughts, and saltwater intrusion frequently occur with more and more severely. Furthermore, there have been numerous shortcomings to be properly addressed in the coordination mechanism and irrigation policies, which significantly affect water use efficiency in the river basins.

Currently, Vietnam has more than 1700 irrigation reservoirs and 330 hydropower reservoirs in operation, with water reserves of hundreds of billions of cubic meters for hydropower generation and supplying water for agricultural production. The sustainable integrated management of water resources is always the goal of the optimal exploitation and use of water resources through the optimal operation of reservoirs [1]. If not well-performed, the operation and management of hydroelectric and irrigation reservoirs would cause great harm. For instance, if the hydroelectric and irrigation reservoirs discharge water inappropriately in the rainy season, they can cause even more floods. In the dry season, if the reservoirs fail to reserve sufficient water, they will not be able to ensure enough water for downstream irrigation, causing saltwater intrusion. To properly manage water resources in a reservoir-regulated basin, in addition to building a scientific operation process, it is necessary to have a specific policy mechanism that can help to strengthen the coordination among all parties in reservoir operation. This is extremely important for the safety of the reservoirs and dams while providing sufficient electricity and water for agricultural production, domestic and industrial use, and the safety of the downstream areas.

The Red River Basin (RRB) is the second largest river basin in Vietnam. RRB is a transboundary river basin of which Vietnam is located downstream and accounts for only 51% of the total 169,000 km²—the rest is in China and Lao. Thus, the water source management in the RRB depends on activities upstream. Water sources in the RRB are used for multiple purposes such as water supply for agriculture, hydropower, industry, domestic use, environmental flow maintenance, the flood prevention construction system, and downstream safety. With the socioeconomic development in the RRB, integrated water resources management has become more complex [2,3].

Currently, in the Red River system, the reservoirs are operated under Decision No. 740/QD-TTg, dated 17 June 2019 [4], in which downstream water regulation (Hanoi hydrological control point) is directly operated by three large reservoirs: Hoa Binh, Thac Ba, and Tuyen Quang. However, there has been an issue with balancing between the power shortage and the need to ensure the water supply for downstream agricultural irrigation. Suppose there is an electricity shortage in the national power system in a certain year. In that case, the increased discharge of water in the irrigation period (January and February) will cause the hydroelectric system to lack water to generate electricity in the remaining months of the dry season. This adjusted output will be evenly distributed for the months of March through June according to the corresponding shortage rate for each month. If the national electricity system has enough electricity in that year, the increase in water discharge in January and February for agricultural irrigation will indirectly change the structure of the power source. In the context of the operation of the electricity market, this makes the system’s marginal price decrease during January and February and increase in the months of March through June. Therefore, this study re-examines the scenarios during the intensive discharge period, using the model approach that optimizes the operation of the hydropower reservoirs to find a more water-saving discharge plan while still meeting the water intake requirements for agriculture.

Alongside the single-purpose reservoirs working for either electricity generation or agricultural irrigation, many large multi-purpose reservoirs are operating for flood prevention and control, agricultural irrigation, domestic and industrial water supply, and waterway transport all at once [5,6,7].

In the context of restructuring the economic and agricultural sectors towards the direction of increasing added value and sustainable development, it is required that fundamental changes in irrigation activities be made to fulfill the requirements of diversified and modern agricultural production services. In this regard, it is necessary to have appropriate solutions to coordinate and manage water resources reasonably to effectively exploit and use water resources, ensuring the harmony of interests among all stakeholders while achieving sustainable development goals [8,9]. These are undoubtedly important issues in the exploitation and management of water resources in the present time.

The problem is becoming more complex with the existence of multiple reservoir systems in which the practice of generating power can contribute substantially to diverse societal applications [10]. Among the methods of buidlding and solving the multi-objective reservoir operation problem was initially undertaken by linear programming [11,12,13], and then using the applied nonlinear algorithm [14,15]. The optimal multi-purpose reservoir operation has become increasingly important for sustainable water management because it must balance many conflicting purposes, such as irrigation, domestic supply, industrial supply, salinity control and environmental requite flows, etc.

In 2001, Ben Abdelaziz Foued and Mejri Sameh [16] used purpose planning to define a multi-purpose reservoir operation model in Tunisia. The problem consists of finding the corresponding discharge from different reservoirs in the system to satisfy many conflicting purposes, such as requirements for salinity, minimum pumping cost, etc. The authors considered two features—multi-purpose and random parameters—to solve this problem. The method used was based on the application of stochastic purpose planning approximation.

In 2001, Ximing Cai, Daene C. McKinney, and Leon S. Lasdon [17] provided solutions to nonlinear water resource management models using a combination of genetic algorithms and linear programming approximation. The gradient nonlinear programming method can solve problems, smoothing objective functions and nonlinear constraints. However, in large nonlinear models, these algorithms may not find viable solutions or have yet to converge to local solutions.

Several works have been conducted for reservoir and hydropower operation in Vietnam [18,19] and in the RRB [20] based on streamflow synthesis and reservoir regulation programs to approximate the river flow, and based on general purpose software, the HEC–ResSim, to simulate the reservoir operation. Among the suggested methods were modeling the optimal operation of hydropower systems to maximize the entire energy production of reservoir systems by using dynamic programming algorithms [21] or using a genetic algorithm [22,23,24].

In this study, three large hydropower reservoirs in the RRB are studied and operated in conjunction with the discharge of water downstream with a water level control point in Hanoi of above 2.2 m during the enhanced shot (discharge period for agricultural irrigation), this is the most stressful period in the operation of these reservoirs, they need to ensure an adequate supply of agricultural irrigation water and to storage of water for hydropower generation, especially during the electricity shortage during the summer. The purpose of the study is to use the power generation optimization problem model to test and calculate the selection of the optimal water discharge scenario while still ensuring the requirement of sufficient water supply for agriculture and the amount of water saved compared to the discharge according to the regulations. The process according to Decision No. 740 [4], will be optimally used for power generation at the peak time in summer. The model’s time step is used by days during the enhanced discharge.

Reservoir operation is carried out with a close mathematical relationship in the operation process. This is a system of mathematical equations that helps the system management agency, or each reservoir, to decide whether to keep the reservoir water level, to determine to what extent the discharge from each pool is based on data on the condition of each reservoir and to determine the state of other components in the system during the dry season. This study applies two methods of independent reservoir operation and coordinated operation in the design of three hydropower reservoirs Hoa Binh, Thac Ba and Tuyen Quang (Figure 1). Two methods of closely relating operational decisions to system conditions have been developed in GAMS (General Algebraic Modeling System) program code. The inputs of the models are: the system of hydrological boundary data, water use data, water requirement data downstream of the Hanoi control point and the system of constraints on reservoir characteristics and optimal model of the hydroelectric power plant. The model will process the series of hydrological data for the typical year.

2. Methodology

2.1. Set Up Operation Scenarios

According to Clause 2, Article 15, Decision No. 740/QD-TTg, dated 17/6/2019 [4], by the Prime Minister on the procedure of inter-reservoir system operation in the Red River Basin, the water level in Hanoi during the discharge period should be no less than 2.2 m. In the period before 2015, the water level of Ha Noi was maintained at 2.2 m, ensuring that all irrigation structures in both downstream and upstream areas of Hanoi hydrological station could collect water at approximately the designed capacity. However, in the fact, two problems arose:

• The water level in Hanoi: There are times when the reservoirs have discharged at their total capacity (through turbines), yet the water level in Hanoi still could not reach 2.2 m. This meant that keeping the water level in Hanoi continuously at 2.2 m or above during increased water discharge was technically or practically not feasible. The leading cause of this issue is that the water level in Hanoi was greatly affected by the range of tides. Indeed, when the tide was low, even though the reservoirs have discharged at total capacity, the water level in Hanoi was still low, corresponding to the tidal level;
• The water level in Son Tay and in the upstream area of the Hanoi hydrological station: In 2018 and 2019, when the water level in Hanoi reached 2.2 m, the level in Son Tay was 4.3 m, making irrigation structures in the upstream of Hanoi station inoperable. The regions that were affected were Cam Dinh, Phu Sa, Thanh Diem, Ap Bac, Bach Hac (old), and Dai Dinh (old). To ensure irrigation water supply for these pumping stations, the local authorities had to allow the use of small pumping stations.

The results of water discharge over the past 10 years show that in phase 1 (the first water discharge period), the system mainly serves the coastal provinces, while the midland regions do not have a high water demand. Thus, in phase 1, it is not necessary to maintain the water level in Hanoi at 2.2 m. Instead, Hanoi’s flow (water level) should be maintained sufficiently to prevent saltwater intrusion. Therefore, the water level to be maintained for Hanoi should be calculated according to different scenarios (with option H_Hanoi < 2.2 m). During the third water discharge period, the system mainly serves the provinces in the upstream area of the Hanoi hydrological station, including Hanoi, Vinh Phuc, and Bac Ninh. In contrast, the downstream provinces would have enough water during this period. Before 2015, when the water level in Hanoi reached 2.2 m, all the works in this area could collect water at approximately the designed capacity. However, currently (after 2015) all the works in this area, except for renovated ones, can‘t collect water; hence, the above provinces must use small pumping stations. Therefore, maintaining the water level at 2.2 m is not practical in this phase. The water level in phase 3 to be maintained for field pumping stations to operate should be calculated according to other scenarios.

With regard to the above issues, in this study, in addition to the original scenario (the scenario of water discharge with the desire to maintain the water level in Hanoi at 2.2 m), calculations are conducted according to scenarios for maintaining the Hanoi water level as follows.

Period 1	Period 2	Period 3
Option 1.2 m Option 1.4 m Option 1.6 m Option 1.8 m Option 2.0 m Option 2.2 m	Only Option 2.2 m	Option 1.2 m Option 1.4 m Option 1.6 m Option 1.8 m Option 2.0 m Option 2.2 m

2.2. Optimal Simulation of Hydropower Generation in the Period of Increased Discharge

Based on the calculation of the water balance and the actual flow measurement, whenever starting to take water into the irrigation system the upstream lakes need to discharge 3 days before and stop releasing water 1 day before the irrigation system is stopped. As the request of the Department of Water Resources, in the winter–spring crop, water is usually collected in 3 periods with the corresponding number of days 4-4-8. For example, the first phase of water intake into the irrigation system is 4 days. The upstream reservoir will need to discharge 3 days before and finish discharging 1 day before the water intake into the irrigation system is finished. Then, the total number of discharge days of the 3 lakes is 6 days (3 + 3 = 6 days). With the same second phase watering period also discharging for 6 days, and the third phase water intake (8 days), we have a total discharge time of 10 days (3 + 7 = 10 days). If all 3 phases are counted, the total number of days is 22. The problem of optimal operation of hydroelectricity is only for the time of water discharge to enhance agricultural irrigation.

2.2.1. Objective Function

The objective function determination is important for optimizing the benefit of hydropower generation. This research used a multi-objective function to solve the issue. These objectives include:

(1)

The maximum benefit of hydropower generation during the increased discharge period of three reservoirs;

(2)

The maximal hydropower benefit from the amount of total saved water by using at peak hours in the summer.

$$Maximize Obj=Max\left\{B_1+B_2\right\}$$

(1)

where:

• B₁: Hydropower generation benefit in the period of increased discharge;
• B₂: Hydropower benefit from the amount of total saved water for hydropower generation at Peak hours in the summer.

$$B_1={\displaystyle \sum }_1^{n}Bi={\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{t=1}^m{\mathsf{\eta }}_i\times R_{it}\times H_i\times T\times (P_E-C_E)$$

(2)

where ${\mathsf{\eta }}_i$: hydropower generation constant of reservoir number i; B_i: power generation benefit of reservoir i (i = 1…n); R_it: discharge flow through reservoir i in the calculation period t (m³/s); H_i: calculating water column for power generation of reservoir i (m); T: total computation time unit of T (hours) so if calculation period is in hours then T = m. If m is in days, then T = m × 24. P_E: the selling price of electricity per 1 kWh; C_E: Unit cost of producing 1 kWh of electricity.

Since hydroelectric plants are connected to the national grid, the selling price, and the cost of producing one unit of electricity are assumed to be the same. In addition, without loss of generality, we convert the maximum benefit (2) to the maximum revenue from selling electricity at the average price $\overline{P}$(VND per kWh). The electricity revenue objective function is as follows:

$$B_1={{\displaystyle \sum }}_1^{n}Bi={{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{t=1}^m{\mathsf{\eta }}_i\times R_{it}\times H_i\times T\times \overline{P}.$$

(3)

After finding the optimal solution for the hydropower generation of three reservoirs regarding increased discharge period to ensure enough water for downstream irrigation. I continued optimal hydropower generation benefits by maximizing hydropower generation and only used at peak hours in summer (The time with the highest price of electricity). I assumed that the total amount of saved water was W*. Then, based on the equations above, reservoir with a lower hydropower generation level will prioritize discharge first (or account for a large proportion of the total release) in order to increase the volume of water stored in reservoirs with higher Hydropower generation level. Then, this storage capacity will be prioritized for hydropower generation during the peak hours of the dry season (the summer season), thus increasing the economic value of water through higher electricity prices. Based on the optimal calculation for three lakes Hoa Binh, Thac Ba and Tuyen Quang, the amount of water saved will be stored in the Hoa Binh hydropower reservoir because in three reservoirs, H_0,HoaBinh = 88.0 m > H_0,TuyenQuang = 55.0 m > H_0,ThacBa = 30.0 m.

$$B_2=B_{HB}={\mathsf{\eta }}_{HB}\times R_{HB}\times H_{oHB}\times T^{*}\times \left(P_{Peak hour }-\overline{P}\right)$$

(4)

Where ${\mathsf{\eta }}_{HB}:$ hydropower generation constant of Hoa Binh reservoir; R_HB: water release through Hoa Binh reservoir during peak hours (m³/s); H_0HB: hydropower generation level of Hoa Binh reservoir (m); T*: total hours of electricity being generated (hours); T* is calculated as a function of W* as follows:

$$T*=\frac{W^{*}}{R_{HB}\times 3600}$$

(5)

where: W*: total amount of water saved in Hoa Binh reservoir due to optimal distribution of power generation; P_{Peak hour}: electricity price at peak hour (VND per kWh); $\overline{P}$: average electricity price of day (VND per kWh).

2.2.2. Constraints of Optimal Simulation

(i)

Reservoir storage balance constraints:

S_i,t+1 = S_i,t + Q_i,t − R_i,t − E_i,t − O_i,t

(6)

where Q_i,t: inflow in the reservoir i for the time period t; S_i,t+1 = final storage of the reservoir i for the time period t; E_i,t = Loss due to evaporation from the reservoir i for the time period t; and O_i,t = Overflow for the reservoir i during the time period t.

(ii)

Constraints of water release from reservoirs:

$${{\displaystyle \sum }}_i{R}_{i,t} \ge D_t$$

(7)

where: D_t represents the water demand at time t (time step t). When included in the model, D_t is expressed as a flow rate of m³/s. In the simulation model, the downstream control point can be represented as water level elevationn; this is entirely based on the relation H_t = f(R_t) at the control point. The function f is determined based on measured data.

(iii)

Reservoir storage- Capacity constraints:

S_i,min ≤ S_i,t ≤ S_i,max.

(8)

(iv)

Constraints when overloads water reservoirs:

O_i,t = S_I,t+1 − S_i,max.

(9)

When operating the reservoir in the dry season, there is no overflow phenomenon; it only discharges during the flood season, or the reservoir operates in series in case of special incidents.

(v)

The limit of the Plant’s electricity capacity:

$${\mathsf{\eta }}_i{R}_{i,t}·H_{i,\mathrm{t}} \le E_i.$$

(10)

(vi)

Constraints on discharge requirements of reservoirs according to the issued operating procedures water level downstream of the hydropower plant; Constraint on the power generation efficiency coefficient according to the difference in the water column upstream and downstream of the dam (determined from charts of turbine efficiency, generator efficiency, loss…); Constraint on maximum power transmission corresponding to calculated head differences; Constraint on power transmission should not be greater than the installed capacity; Constraint on power transmission must not be less than guaranteed power.

Constraints on navigation and constraints on environmental flows are only included in the model for the section from behind the reservoir to the Ha Noi control point. The total water demand in the downstream after Son Tay, Hanoi, is calculated according to the cumulative dynamics method. Hanoi is considered a control node, flow control according to the period calculated in the model.

3. Result and Analysis

3.1. Determination of Optimal Operation of Reservoirs According to Different Scenarios

According to specific calculations for each water collection, the principle of water discharge to serve the winter–spring crop irrigation in the Red River basin is calculated. To ensure that water can be supplied to the irrigation systems, the water level in Hanoi must reach a height of over 2.2 m. To ensure the above water intake level (flow), the three reservoirs operate in parallel and discharge water.

Given the discharge volume required to meet the water demand and the requirements of saltwater intrusion prevention and increased water efficiency, a discharge scenario has been determined due to the following reasons: (i) It is unnecessary to maintain the water level in Hanoi above 2.2 m continuously; (ii) In phase 1, water discharge is mainly for cleaning fields and providing water for coastal provinces such as Ninh Binh, Nam Dinh, Thai Binh, Hai Phong, and Hai Duong; other provinces have almost no or minimal access to water. Therefore, it is enough for the system to discharge a limited water volume to the extent that it can prevent saltwater intrusion in the downstream area. There is no need to discharge water to the level of 2.2 m for Hanoi; (iii) in phase 3, the system mainly serves three provinces, Vinh Phuc, Bac Ninh, and Hanoi, which are the city and provinces that collect water later than the others (most other provinces have already taken enough water). Thus, the system needs to discharge a certain amount of water to ensure enough water for crops and for submersible pumping stations in Hanoi, Vinh Phuc, and Bac Ninh. There is no need to discharge water to the level of 2.2 m for Hanoi (Figure 2 and Figure 3).

Additionally, with the investment in irrigation systems to adapt to lower water levels in the Red River system, the capacity to collect water has been increasingly improved. It is less dependent on the increase of discharge water. The determination of the discharge volume of these reservoirs is presented as follows. (See

Table 1. Optimal operation scenario of reservoirs.

No.	Released Day	Hoa Binh Reservoir	Tuyen Quang Reservoir	Thac Ba Reservoir	Total
		(m3/s)	(m3/s)	(m3/s)	(m3/s)
	Phase 1
1	Before period 1	838	690	444	1972
2	Before period 1	838	690	444	1972
3	Before period 1	838	690	444	1972
4	Period 1	838	690	444	1972
5	Period 1	838	690	444	1972
6	Period 1	838	690	444	1972
	Phase 2
1	Before period 2	2176	690	444	3310
2	Before period 2	2176	690	444	3310
3	Before period 2	2176	690	444	3310
4	Period 2	2176	690	444	3310
5	Period 2	2176	690	444	3310
6	Period 2	2176	690	444	3310
	Phase 3
1	Before period 3	1049	690	444	2183
2	Before period 3	1049	690	444	2183
3	Before period 3	1049	690	444	2183
4	Period 3	1049	690	444	2183
5	Period 3	216	690	444	1350
6	Period 3	216	690	444	1350
7	Period 3	216	690	444	1350
8	Period 3	216	690	444	1350
9	Period 3	216	690	444	1350
10	Period 3	216	690	444	1350

).

Given the above analysis, the economic benefits of the optimal discharge scenario are very significant compared to that of the 2.2 m scenario. In addition to economic benefits, the issue of energy security is also significant. (See

Table 2. Benefit of Optimal operation scenario of reservoirs.

No.	Released Day	Option 2.2 m	Optimal Option	Different	Total Amount of Saved Water	Benefit
		(m3/s)	(m3/s)	(m3/s)	(Million m3)	(Billion VND)
	Phase 1
1	Before period 1	2845	1972	873	75.4	18.9
2	Before period 1	2845	1972	873	75.4	18.9
3	Before period 1	2845	1972	873	75.4	18.9
4	Period 1	2845	1972	873	75.4	18.9
5	Period 1	2845	1972	873	75.4	18.9
6	Period 1	2845	1972	873	75.4	18.9
	Phase 2
1	Before period 2	3310	3310	0	0.0	0.0
2	Before period 2	3310	3310	0	0.0	0.0
3	Before period 2	3310	3310	0	0.0	0.0
4	Period 2	3310	3310	0	0.0	0.0
5	Period 2	3310	3310	0	0.0	0.0
6	Period 2	3310	3310	0	0.0	0.0
	Phase 3
1	Before period 3	3019	2183	836	72.2	18.1
2	Before period 3	3019	2183	836	72.2	18.1
3	Before period 3	3019	2183	836	72.2	18.1
4	Period 3	3019	2183	836	72.2	18.1
5	Period 3	3019	1350	1669	144.2	36.1
6	Period 3	3019	1350	1669	144.2	36.1
7	Period 3	3019	1350	1669	144.2	36.1
8	Period 3	3019	1350	1669	144.2	36.1
9	Period 3	3019	1350	1669	144.2	36.1
10	Period 3	3019	1350	1669	144.2	36.1
	Total				1606.7	401.7

).

3.2. Calculate Added Economic Value from Using Electricity at Peak Hours

Calculation results show that to ensure maximum power generation benefits in each scenario, I find that:

(i)

Water discharge from Thac Ba reservoir should be the highest priority (discharged at total capacity and upon water discharge demand);

(ii)

Water discharge from Tuyen Quang reservoir should be the second highest priority;

(iii)

Even when the above two reservoirs (Thac Ba and Tuyen Quang) have discharged at their total capacity, they still do not meet the discharge demand.

The above results also suggested that water from the Hoa Binh reservoir should be reserved for power generation during peak hours (after the winter–spring crops).

Furthermore, the distribution of discharge water among the three reservoirs in different scenarios can be determined (Table 1 and Figure 4).

The above results suggests that water from the Hoa Binh reservoir should be reserved for power generation during peak hours (after the winter–spring crops). Furthermore, the distribution of discharge water among the three reservoirs in different scenarios can be determined. The choice of the optimal scenarios and still ensures meeting water demand in downstream. The total amount of saved water compared with the standard scenario (H_Hanoi = 2.2 m) during 22 days is 1,607 million metric meters of water. (See Table 2).

With the above optimal operation plan, the system can satisfy water demand in downstream areas and prevent saltwater intrusion and increase water savings. This is much better than the 2.2 m scenario. The saved water during the increased discharge period is assumed to be used for hydropower generation during the peak hours of the period of high electricity demand (peak power generation occurs in summer).

The economic value of hydropower generation from 1 m³ of water from Hoa Binh reservoir during the increased discharge period (irrigation supply) is 500 VND/m³ (average electricity price in a day is 1,692 VND/kWh)

The power generation economic value from 1 m³ of water from Hoa Binh reservoir during summer at peak hour is 750 VND/m³ (electricity unit price at peak hour is 2,702 VND/kWh). The savings for each 1 m³ of water is 250 VND/m³. With the above optimal discharge scenario, the water savings can be determined, and the power generation value increases by 401.7 billion VND. (See Table 2). Suppose the economic efficiency is determined by comparing power generation from water and oil (minimum unit price = 3500 VND/kWh). The value of each m³ of water saved is 534 VND/m³. The economic value calculated using this method is 858.0 billion VND.

According to the above calculations, with the optimization of power generation during the increased discharge period and the water savings for power generation during peak hours, the benefits of power generation can increase by about 20%; the increase in value gained from saving water during the increased discharge period for power generation during peak hours is 3–4% of the total value of power generation, compared to the conventional discharge scenario (Option H_Hanoi = 2.2 m).

4. Conclusions

Due to the coordinated nature of operations of Hoa Binh, Thac Ba, and Tuyen Quang multiple-reservoir systems, satisfying the water requirements downstream and meeting the water requirements in Son Tay and Hanoi as described above is not a simple task. This is due to the irregularity of the flow process to the reservoirs and also the flow of the middle basins.

This result is consistent with world research on the operation of the multi-purpose inter-reservoir system in Vietnam. The findings call for a more integrated water resource management in RRB with the goal of optimal water resources use.

In particular, research shows that there is an increase in economic efficiency when energy-saving water is used to generate electricity during the peak hours of summer and there is a difference in the economic value of electricity between different times in seasons. The study shows that with the optimal solution, the economic benefits increased by 401.7 billion VND. If compared with the price of electricity products from oil, the benefit increases by 858.0 billion VND. Based on the calculations above, it is necessary to adjust Clause 1, Article 15 of Decision No. 740 as follows:

(a)

Phase 1: Only discharge to ensure salinity, to serve coastal provinces and to maintain the Hanoi water level at 1.8 m with the lowest water level at 1.2 m;

(b)

Phase 2: Maintain the average water level in Hanoi at 2.0 m, with the lowest water level at 1.6 m;

(c)

Phase 3: Maintain the water level in Hanoi at 1.4 m so that the upstream provinces can transport deep-rooted labor and field labor. The lowest water level is 1.2 m.

However, the system optimization calculation results only considering the optimization of power generation benefits does not reflect the simulation problem of the optimal allocation of water resources in downstream, the water demand was excellent for many purposes. This research has only been conducted based on the aggregate demand and determined the Hanoi water level as a flow control point with the requirement of Q_min not highlighting the optimization problem hear when there must be a trade-off between the economic value of electricity generation and the irrigation benefit, as well as other economic benefits such as industry, domestic, tourism, and the environment.

The study has shown that the benefit of hydropower generation increases by about 20% compared to the actual operations. It is calculated under the assumption that the discharge capacity of the 3 reservoirs is optimized and the amount of water stored is maximized so that the amount of electricity generation during peak hours is the largest. The study showed that the benefit of coordinating between reservoirs to save capacity for peak time increased by 3–4% of the total profit value of electricity generation.