Abstract
A novel computational model is proposed in this paper considering reliability analysis in the modelling of reinforced concrete beams at elevated temperatures, by assuming that concrete and steel materials have random mechanical properties in which those properties are treated as random variables following a normal distribution. Accordingly, the reliability index is successfully used as a constraint to restrain the modelling process. A concrete damage plasticity constitutive model is utilized in this paper for the numerical models, and it was validated according to those data which were gained from laboratory tests. Detailed comparisons between the models according to different temperatures in the case of deterministic designs are proposed to show the effect of increasing the temperature on the models. Other comparisons are proposed in the case of probabilistic designs to distinguish the difference between deterministic and reliability-based designs. The procedure of introducing the reliability analysis of the nonlinear problems is proposed by a nonlinear code considering different reliability index values for each temperature case. The results of the proposed work have efficiently shown how considering uncertainties and their related parameters plays a critical role in the modelling of reinforced concrete beams at elevated temperatures, especially in the case of high temperatures.
1. Introduction
Concrete can be considered as one of the mostly used materials in construction projects due to some important aspects, such as its strength, durability, and fire resistance. Several studies have been conducted to investigate the behavior of reinforced concrete beams under different loading and environmental conditions. A new shear reinforcement configuration was proposed by Demir et al. [1] by adapting a nonlinear finite element study to investigate the improvement of shear capacity in reinforced concrete beams. Salih and Zhou [2] studied the behavior of concrete beams reinforced with fiber polymer bars by conducting a series of finite element models, while Kytinou et al. [3] analyzed the steel fiber’s effects on the flexural performance of steel fiber-reinforced concrete. Chalioris et al. [4] developed a new structural health monitoring system by demonstrating its use and efficiency. This method could evaluate structural damage caused by concrete cracking and steel yielding under monotonic and cyclic loading. In addition, by using ferrocement composite as transverse reinforcement, Megarsa and Kenea [5] presented the results of a comprehensive analytical examination of the beams’ shear performance. Kytinou et al. [6] performed numerical analysis using ABAQUS 2018 finite element software for predicting the cyclic lateral response of reinforced concrete (RC) beam–column connections using composite carbon fiber-reinforced polymer (CFRP) bars as a longitudinal reinforcement in the beam.
However, in the cases of high temperatures, concrete’s mechanical properties are changed. Thus, in the case of elevated temperatures, failure might occur due to the presence of cracks which are parallel to the heat surface [7,8,9,10,11,12]. Consequently, concrete properties after fire exposure are still significant for estimating the load-carrying capacity [12,13]. Furthermore, it has been concluded that under high temperatures, the changes in chemical and physical properties of the concrete are not only dependent on the matrix composition, but also on the water/cement ratio, age of concrete, and the aggregate’s type [14,15,16].
In fact, the idea of investigating the mechanical properties of concrete at elevated temperatures has attracted many researchers recently, which was resulted in different experimental tests [17,18,19,20].
Carbon fiber-reinforced polymer (CFRP) bars were used in the reinforcement of a concrete beam, and the behaviour of the beam was numerically examined while being subjected to high temperatures in the study of Ilango and Mahato [21]. Kakae et al. [22] investigated the obtained physical properties of concrete, such as Young’s modulus, compressive strength and strain, and thermal properties, when it was exposed to high temperatures. Xiao and König [23] presented a general overview of the mechanical behavior of concrete when it is exposed to high temperatures by making a comparative analysis of prior research. By utilizing thermo-chemical reactions of the concrete, Cioni et al. [24] presented an assessment of fire damage of reinforced concrete elements. In addition, by replacing cement with finely ground pumice (FGP) of the concrete mix with different proportions of weight, the properties of concrete were investigated at elevated temperatures by Demirel and Keleştemur [25]. Savva et al. [26] also showed in their study how high temperatures affect the mechanical properties of pozzolanic concrete, in which the findings of the study concluded that the concrete’s residual properties crucially depend on the type of aggregates and binder. By considering different heating loads, the mechanical properties of residual fracture, such as stress intensity factor and fracture energy, were analyzed by Hlavička et al. [27]. Song et al. [28] determined that longitudinal reinforcement and proper stirrup reinforcement designs may enhance the fire resistance performance of simply supported reinforced concrete beams. Fire testing followed by bending tests on reinforced concrete specimens were conducted by Cai et al. [29], where the proposed work showed a sufficient agreement between the theoretical calculation and FEA results. Furthermore, Agrawal and Kodur [30] proposed valuable information about the residual capacity of high-strength concrete beams after exposure to fire, indicating that such beams can recover a significant portion of their flexural capacity provided they survive the fire exposure. The effects of fire exposure on the residual shear and flexural behavior of reinforced concrete beams were analyzed by Yuye et al. [31], who proposed a practical calculation method for assessing shear performance after fire.
Li and Purkiss [32] investigated the mechanical properties of concrete at elevated temperatures in their study, and one of their findings was that stress–strain diagrams in EN 1992-1-2 [33] are risky in the existence of high axial loads due to high peak strains. Furthermore, Kim et al. [34] tested the impact of high temperatures on concrete’s strength, and they contrasted their findings with those of ACI [35] model values.
Additionally, there are several research works which were conducted to study the effect of temperatures on the properties of reinforcing steels. For instance, Felicetti et al. [36] investigated how steel bars react after being exposed to high temperatures. Furthermore, Dotreppe [37] showed in his study how quenched and self-tempered steels’ mechanical characteristics may be impacted by temperature.
By considering the aim of structural engineering of proposing structural models that meet the safety and serviceability conditions, uncertainties that might be related to the material properties and the applied loading conditions should be considered in the design process [38,39,40,41]. Thus, the reliability-based algorithm was introduced into deterministic designs of concrete structures [42,43]. Rakoczy and Nowak [44] presented a reliability analysis for prestressed concrete where sensitivity functions were developed to consider the effect of reliability indices on the concrete girders. Reinforced concrete beams were considered for the reliability analysis in the study of Słowik et al. [45], where the experimental findings were used to determine the safety margins of the designed shear resistance. Additionally, Olmati et al. [46] introduced a framework of probabilistic design for flat slab punching due to accidental loads, such as a slab falling from above, column removal, or a blast load. By taking into account uncertainties when analyzing reinforced concrete beams, Schlune et al. [47] used the reliability level in which a safety format was proposed based on the nonlinear analysis and a resistance safety factor. Eamon and Jensen [48] explained in detail a way to figure out how reliable RC beams are under a fire load by assuming concrete compressive strength, steel yielding strength, and other important parameters as random variables. Li et al. [49] provided valuable insights into the reliability of HSC beams under elevated temperatures that could inform the design and assessment of these structures in fire conditions.
Many researchers have investigated the physical and mechanical properties of concrete at high temperatures, including Young’s modulus, compressive strength, and strain. However, the variability of material properties has created uncertainties in the results of previous research.
To address this issue, this paper aims to examine the effect of considering reliability design in the numerical analysis of reinforced concrete beams at elevated temperatures. The proposed work seeks to provide insights into the behavior of concrete and its reliability under high temperatures, informing the design and assessment of concrete structures in fire conditions. Taking into consideration that the proposed work in this paper considers EN 1992-1-2 [33] to show the proficiency of the proposed method. In addition, to achieve the desired aim, a written nonlinear programming code is developed to perform the reliability analysis by considering that the introduced reliability index (β) plays as a limit when the concrete properties are considered as random variables which follow normal distribution. Moreover, the Monte Carlo sampling method is considered in order to determine reliability indices based on the statistics of the concrete properties.
The rest of the paper is constructed as follows. Section 2 provides an overview of the reliability analysis. The considered constitutive concrete model is presented in Section 3. Section 4 demonstrates the experimental program of the considered reinforced concrete beam, while the numerical modelling including the model validation, considering the effect of elevated temperatures and introducing the reliability design, are presented in Section 5. Lastly, Section 6 includes the conclusions and remarks of the proposed work.
2. Reliability Analysis
By recalling the basic concept of reliability analysis and assuming that stands for non-negative bound, the failure is defined by , taking into consideration that and are independent random variables in which their probability density functions are and, respectively. Therefore, for the estimation failure probability, the following equation is used [50]:
where and denote the cumulative distribution functions (CDFs) of and , respectively. For most distributions of and , the above integrals will have to be evaluated numerically.
Equation (1) can be alternatively written in the case of considering limit state function, as follows:
where the failure domain is described by . Hence, can be determined by:
In fact, can be expressed as follows:
The Monte Carlo sampling technique is considered in this study for estimating . The very basic concept of this technique is about generating the expression of the random vector depending on probability density function . By determining the ratio of points inside the to the total generated points, can be calculated using the Monte Carlo technique. This assumption is formulated by writing an equation considering indicator function of , as follows:
Accordingly, can be rewritten as follows:
The distribution of random variable points are as follows:
where . Bearing in mind that is random variable following normal distribution which has mean value and variance:
To calculate , the estimator of the mean value is utilized as follows:
where indicates the independent random vectors, and are accompanied with probability density functions.
In order to consider uncertainties in our work, material properties of concrete and steel are assumed as random variables following a Gaussian distribution where the estimator of the mean value and variance ) are determined as follows:
Because of some difficulties in the process of computing accurately, the first-order reliability methods were utilized, where the reliability index (β) is used. The benefits of utilizing (β) are that as there are many applications of reliability analysis in engineering designs, the desired (β) controls more regular engineering practices and, thus, engineering standards, especially structural ones, offer an extensive set of target values (e.g., EN1990 [51]).
By utilizing , the reliability limit can be constructed as follows:
Lastly, the following expressions are used to determine and :
3. The Adopted Constitutive Model
In the accessible scientific papers, the explanations of this model can be deeply tracked. However, a short and brief description is introduced here. By adopting the Prandtl–Reuss concept regarding the elastoplastic deformation, the overall strain tensor consists of an elastic part () and a plastic one () as explained in Equation (19):
Furthermore, the scalar damage elasticity formula governs the internal stress–strain relationships as follows:
where , indicating the degraded elastic stiffness, is written as follows:
where represents the initial (elastic) stiffness of the material, and d indicates the stiffness degradation.
It is important to take into consideration that d might vary from (0) in the case of undamaged material to (1) in the case of fully damaged material. The stiffness reduction here is isotropic, taking into consideration that a single variable of degradation (d) is used to describe it. According to the concept of damage mechanics of continuum structures, the effective internal force is described as follows:
The relationship between the internal force and the effective internal force by adopting scalar reduction relation can be constructed as follows:
In the case of d = 0, . Nonetheless, the effective internal force turns out to be more illustrative than internal force due to the resistance of the external loads by the area of the effective internal force. By considering the nominal stress and the reduced elastic tensor which is shown in Equation (22), Equation (20) can be rewritten as follows:
The constitutive model of damaged plasticity is illustrated by the internal force–strain relationship:
where and represent the variables of compression and tension damage, respectively, taking into consideration that these variables are varying from 0 to 1 for undamaged and fully damaged cases, respectively. Furthermore, is the effective tension internal force and represents the effective compression internal force. In general, the damage model of concrete considers the compressive crushing and tensile cracking failures. Furthermore, it is assumed that plasticity damage affects the uniaxial compressive and tensile response of concrete, as can be seen in Figure 1; this can be calculated as follows:
where represents the initial Young’s modulus, is the equivalent tension plastic strain, and is the equivalent compression plastic strains. Therefore, the effective uniaxial compressive and tensile stresses are computed as follows:
where tensile strain , and compressive strain . Thus, it can be said that represents the equivalent elastic strains for tension and represents the equivalent elastic strains for compression.
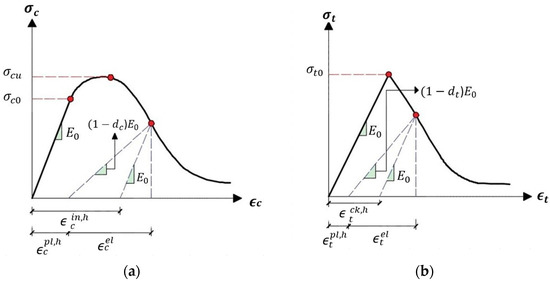
Figure 1.
Uniaxial loading condition. (a) Compression; (b) tension.
To sum up, the concrete damage plasticity (CDP) constitutive model is adopted to show the tension and compression behaviors of concrete within the validated model.
4. Experimental Tests
Experimental tests of three simply supported reinforced concrete beams are utilized in this section; these tests were held in the laboratory of Széchenyi István University. Furthermore, four samples were equipped for the tests on the properties of concrete. The standard cube test, which involves compressing a cubic sample of concrete under controlled conditions, was utilized for determining the compressive behavior of the concrete in this study, as it is a widely accepted method for measuring the compressive strength of concrete. The split cylinder test was adopted for concrete tensile behavior, taking into consideration that it is a reliable and widely accepted method for determining the tensile strength of concrete and is used in many design codes and standards for reinforced concrete structures. It was appropriate as the samples were stored at standard conditions of temperature = 20 °C.
After 28 days of curing, the samples were tested, and the compression and tension properties were assessed and shown in Figure 2, taking into consideration that Young’s modulus and Poisson’s ratio 0.2. The used reinforcing steel in this study was hot-rolled B500 reinforcing steel. Taking into account that a tensile test was performed, the obtained mechanical properties of the steel reinforcement are represented in Table 1. The geometry of the beams was , with a cross-sectional area of . The layout of the experiments, including the geometry, the boundary conditions, and the applied load for the considered reinforced concrete beams, is shown in Figure 3, considering that the beams were tested by applying one concentrated monotonic loading up to failure.
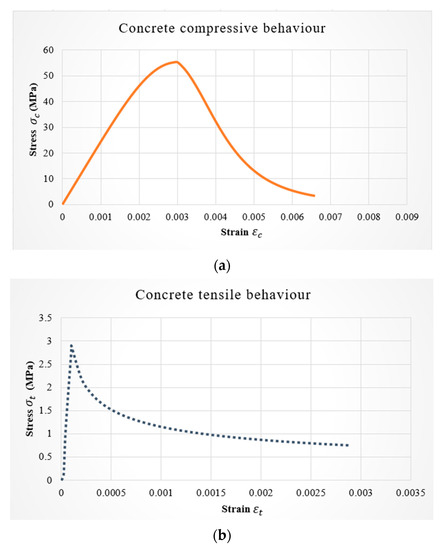
Figure 2.
The obtained concrete properties. (a) Compression; (b) tension.

Table 1.
Properties of the considered steel bars.
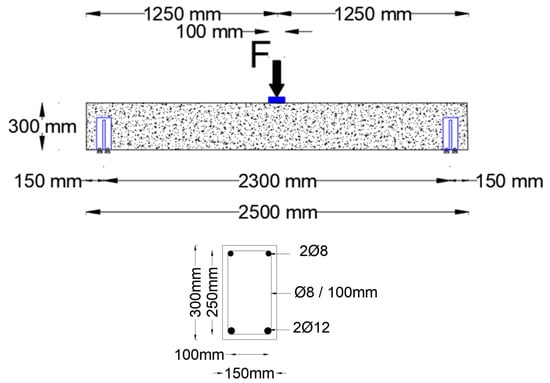
Figure 3.
Geometry, loading condition, and cross-section of the beam.
5. Numerical Modelling
5.1. Finite Element Model
In this section, validation of the model using 3D finite element analysis (FEA) based on the experimental tests is proposed. A finite element (FE) model of the reinforced concrete (RC) beam is made for this study using the commercially available software ABAQUS® [52]. ABAQUS is a finite element analysis (FEA) software package widely used for simulating the behavior of engineering structures and materials under various loading conditions. It is capable of handling complex geometric and material models, and provides a range of analysis capabilities including structural, thermal, acoustic, and electromagnetic analysis.
ABAQUS software has the capability to predict the failure of concrete by implementing a concrete damage plasticity model for material properties. This model considers the process of damage that occurs through micro-cracking, which initially starts on a specific beam section and gradually widens before coalescing to ultimately cause failure. The plasticity behavior can be described by various phenomena, such as strain softening, gradual deterioration, and volumetric expansion, which result in a decrease in both the strength and stiffness of concrete. The degradation of stiffness is typically indicative of the damage sustained. Failure is assumed to result from two primary factors: tensile cracking and compression crushing of the concrete material.
A parametric study was carried out to figure out the right mesh size for the finite element model. As a result, the best mesh size was found to be 25 mm, in which the element mesh sizes were carefully chosen so that the result could be reached with proper computational time. The reinforced concrete beam was modelled by using eight-node first-order hexahedral (C3D8) elements for concrete, and truss elements for steel, as is shown in Figure 4. Furthermore, the geometry, boundaries, and loading conditions of the beams are represented in Figure 5. Here, a single concentrated loading was applied at the middle of the top flange and approximately elements were used to generate the finite element mesh of the concrete, while elements were used for the mesh of steel reinforcement. Furthermore, a constraint of an embedded region was applied for the purpose of simulating the bond between the reinforcements with the concrete. The nonlinear behavior and the adoption of the damage plasticity model were carried out by utilizing finite element analysis for the beams.
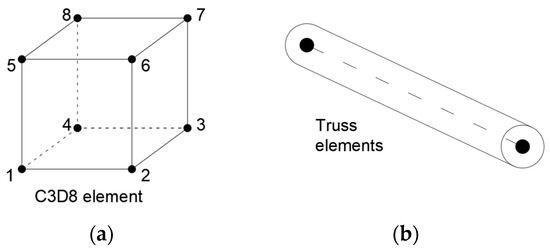
Figure 4.
Considered elements for modelling. (a) Concrete modelling; (b) Steel modelling.
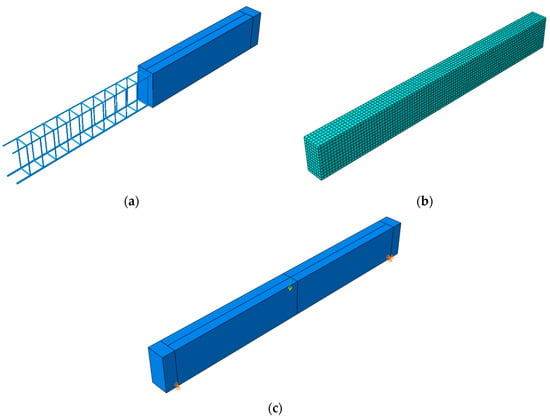
Figure 5.
Numerical reinforced concrete model. (a) Model assembly; (b) finite element mesh of the model; (c) loading and support conditions of the model.
5.2. Model Validation
According to the mechanical properties of the tested specimens (Figure 2), the (CDP) data, which contains the compressive crushing, as well as the tensile cracking, were recorded, then these data were imported to the FEA 2018 software to obtain CDP parameters that reveal the damage behavior of concrete. The CDP parameters which were assumed in this study are illustrated in Table 2, considering that the CDP parameters were kept constant during the reliability-based analysis process later. Furthermore, it should be noted that in this work, a variety of dilation angle values were investigated. Only the value that best predicts the deflection response of the experimental tests is presented here.

Table 2.
Concrete damage plasticity data.
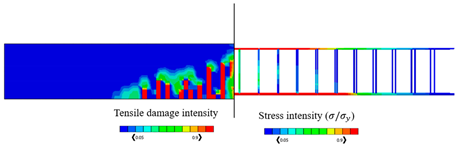
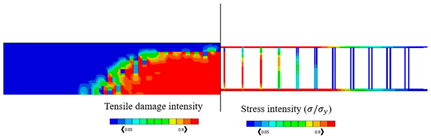
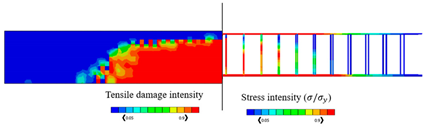
The numerical results of the models were verified according to the experimental results. It is worth mentioning that since the load is applied at the middle of the top flange of the beam, the damage pattern is within the area around the point of applied load which can be obviously seen from Figure 6 where the experimental model and numerical model have almost the same concrete damage patterns (tension damage), where the intensity of the damaged zones ranges from the blue color that represents the undamaged zones (dt = 0), to the red color which represents the fully damaged zones (dt = 1).
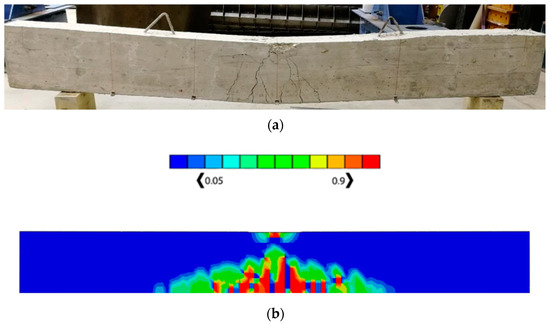
Figure 6.
Failure mechanism of the beam. (a) Experimental model; (b) numerical model.
Moreover, load–deflection diagrams of the numerical and experimental tests are shown in Figure 7, where the measured ultimate load capacity was about 74 kN in the case of the numerical model, while it was approximately 72 kN for the average experimental results.
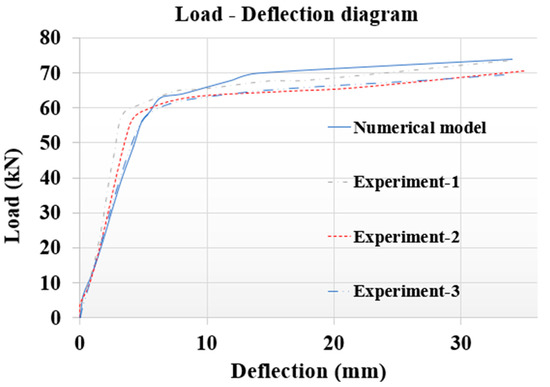
Figure 7.
Load–deflection diagrams of numerical and experimental tests.
5.3. Reinforced Concrete at Elevated Temperatures
In this part, the effect of temperature is considered for the reinforced concrete beam according to the stress–strain curves which was mentioned in the study of Schneider [53] for concrete material and according to the work of Meda et al. [54] for steel. It is worth mentioning that there are many available papers and monographs which can be referred to in order to find detailed descriptions and it is an open question between researchers, but as was mentioned earlier, this study aims to validate the proposed method.
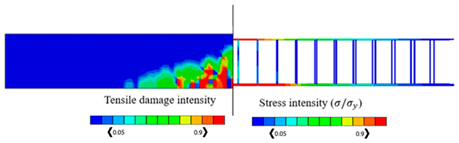
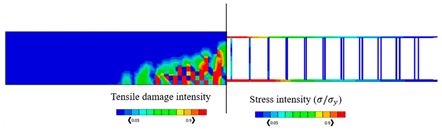
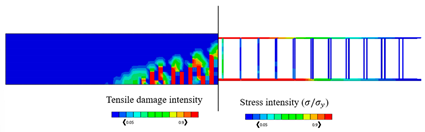
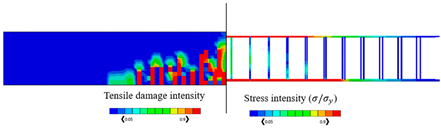
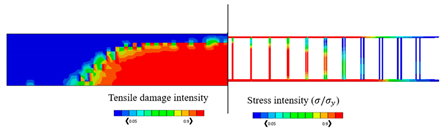
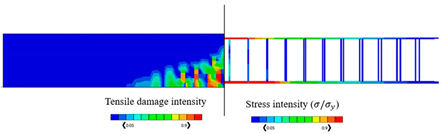
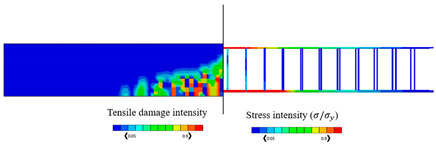
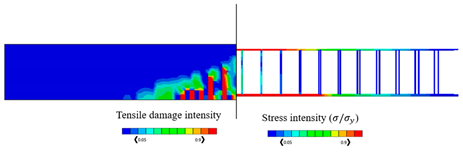
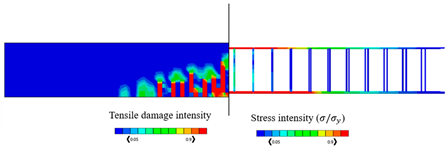
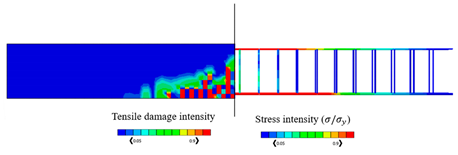
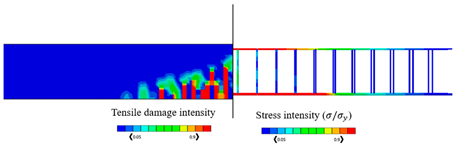
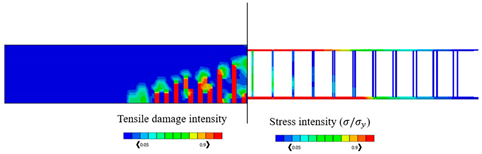
The validated reinforced concrete beam model is considered in this part, where it is modelled by the commercially FEA software ABAQUS [52] according to different temperature values which are , , , , and , and the corresponding mechanical properties of concrete are shown in Table 3. The used bars were assumed as hot-rolled reinforcing steel, taking into consideration that the stress–strain diagrams of the steel at elevated temperatures which are represented in Figure 8 were utilized according to Eurocode [55]. The proposed material properties of concrete and steel are used in the numerical analysis for the different considered temperatures. Thus, the results of the corresponding ultimate values of load and displacements are given in Table 4, in which the CDP constitutive model is adopted. Table 4 also represents the results of stress and tension damage intensities in case of deterministic designs, taking into consideration that the value of the applied load is (the ultimate load value in the case of ). It can be noted from Table 4 that as temperature increases, the corresponding values of ultimate load and displacements decrease. For instance, the displacement value is decreased by from in the case of to in the case of Additionally, the ultimate load value is decreased by from in the case of to in the case of . Furthermore, it can obviously be shown that the yielded stress zones which are represented by the red color within the steel reinforcement and the resultant tension damaged area of concrete increase as the temperature values increase, taking into consideration that the blue color represents the undamaged areas, and the red color reflects the damaged areas. Furthermore, it can be noticed that when the temperature increases, the damage pattern and stress intensity distributions are extended away from the middle area of the model.

Table 3.
Mechanical properties of concrete.
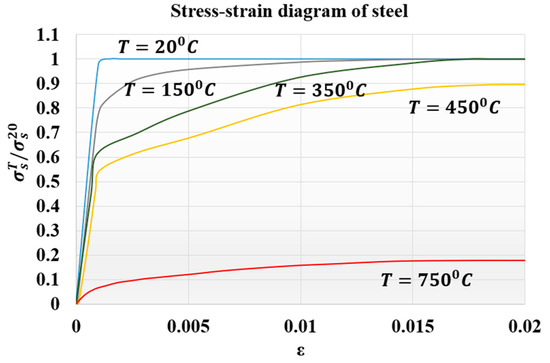
Figure 8.
Stress–strain diagrams of steel according to Eurocode [55].

Table 4.
Maximum load capacities, displacements, and stress and tensile damage intensity of the beam.
By considering the same value of the applied load (), Table 4 represents the obtained results of the percentage of the tensile damaged elements within the model for each temperature case. It should be noted that the percentage increases as the temperature increases. For instance, the percentage value is increased from in the case of temperature to in the case of .
5.4. Introducing Reliability Analysis
The properties of the concrete and steel materials are selected as the parameters affecting the performance of the reinforced concrete beam at increased temperatures. Due to the unpredictability inherent in the microstructure of the material, it is possible that the stress–strain curves for the same material strength cannot be replicated exactly, resulting in a considerable variation in the real capacity of the structure. To obtain a more accurate response for the compressive strength and elasticity modulus of concrete, some researchers have used the normal or lognormal distribution as the best match.
As was mentioned previously, a nonlinear code was written to perform the reliability analysis by considering that the introduced reliability index governs the process as well as playing a role as a limit by assuming the concrete and steel properties which were given in Table 3 and Figure 8 (Section 5.3) as random variables following a normal distribution. In order to determine , the Monte Carlo method is used by considering that the total samples number (). The considered concrete material’s probabilistic parameters are shown in Table 5. Furthermore, the deterministic steel material’s properties, which were mentioned earlier in Figure 8, are considered as mean values with standard deviation for the probabilistic case. It is worth mentioning that the corresponding CDP parameters are changed accordingly.

Table 5.
Probabilistic parameters of the concrete material.
Table 6, Table 7, Table 8, Table 9 and Table 10 represent the obtained results of the probabilistic analysis of different considered temperatures, where each table shows a comparison between the resulting load, displacement, stress and tensile damage intensity, and the percentage of the damaged elements within the model according to the values of the reliability index () for each temperature case. It can be noted for each temperature case that as (β) increases, the corresponding load and displacement values decrease. For instance, by considering the case of , the displacement value is decreased by from when to when Furthermore, it is also noted that the red zones of the model for each temperature case decrease as ( increases, which means less plastic behavior in the beam. To be more specific, by considering , the percentage of the tensile damaged elements was decreased from when to when . Furthermore, in the case of the damaged elements percentage was decreased from when to when .

Table 6.
Probabilistic results—.

Table 7.
Probabilistic results—.

Table 8.
Probabilistic results—.

Table 9.
Probabilistic results—.

Table 10.
Probabilistic results—.
According to the results of reliability-based design, we can say that in the case of high temperatures, the percentage of damaged zones within the model is higher than those which were observed in lower temperature cases. Furthermore, the considerations of mechanical properties of concrete and steel materials as random variables successfully proved that the results are changed in the probabilistic design compared to the deterministic designs according to the resulting displacement, load, and the tensile damage and the stress intensities. Therefore, we can say that (β) efficiently worked as a limit to control the nonlinear plastic state of the models.
6. Conclusions
In this paper, reliability nonlinear finite element models were considered for analyzing reinforced concrete beams at elevated temperatures. A concrete damage plasticity constitutive model was adopted to calibrate the numerical model according to generated data from laboratory tests. Moreover, the procedure of introducing the reliability analysis of the nonlinear mathematical problems was proposed by a nonlinear written code considering different reliability index value for each temperature case. This took into consideration that the concrete and steel materials’ properties were considered random variables with a mean value and standard deviation.
Accordingly, the main points which conclude the proposed work are as follows:
- In cases of deterministic design, when temperature is increased, the damage pattern, and stress intensity distributions are extended away from the middle area of the model.
- For all models with different temperature cases, it was shown that by considering β, the corresponding loads and displacements were changed from the resulting values in deterministic designs due to considering concrete properties as random variables.
- The intensity of the tensile damage pattern and intensity of stresses in cases of reliability-based design are less than was observed in cases of deterministic models for each temperature case.
- The results showed that as β increases, the corresponding load and displacement values decrease for each temperature case in the case of probabilistic analysis.
- The pattern of tensile damage and the stress intensities become less intensive as β increases for each temperature case in the case of probabilistic approach. Therefore, β can work as a controlling bound for producing a safe plastic design.
Based on the findings of this study, the following recommendations for practice and prospective work are suggested:
- Design codes and guidelines for reinforced concrete structures should incorporate probabilistic approaches to account for the uncertainties in material properties and loading conditions. This can help to ensure more reliable and safer designs.
- The proposed approach can be extended to other types of reinforced concrete structures, such as columns and slabs, to investigate their behavior under elevated temperatures.
- Future research can focus on investigating the effect of other parameters on the reliability of reinforced concrete structures at high temperatures, such as the effect of different types of reinforcements, different loading conditions, and the effect of cooling methods.
- The developed approach can be combined with other methods, such as fire resistance tests, to validate and improve the accuracy of the numerical models.
By implementing these recommendations, it is possible to advance the design and analysis of reinforced concrete structures under elevated temperatures and enhance their safety and reliability.
Author Contributions
Methodology, J.S. and M.M.R.; conceptualization, J.L. and M.M.R.; investigation, M.M.R.; writing—original draft preparation, M.H. and M.M.R.; software, M.H.; writing—review and editing, J.S.; formal analysis, M.H.; validation, J.S.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets created and analyzed during the present work are provided in the main publication; more information is available from the authors.
Conflicts of Interest
The authors state that they have no known conflicting financial interest or personal relationship that might seem to have influenced the research presented in this study.
Nomenclature
| Variable | Full Variable Description |
| The effective compression internal force | |
| The effective uniaxial compressive stress | |
| Effective internal force | |
| Internal force | |
| The effective tension internal force | |
| The effective uniaxial tensile stress | |
| Elastic stiffness of the material | |
| Failure domain | |
| Degraded elastic stiffness | |
| The initial Young’s modulus | |
| Probability of failure | |
| Independent random vectors | |
| Variable of compression damage | |
| Variable of tension damage | |
| Probability density function | |
| Compressive strain | |
| The equivalent compression plastic strains | |
| Strain tensor | |
| Elastic part of strain tensor | |
| Plastic part of strain tensor | |
| Tensile strain | |
| The equivalent tension plastic strain | |
| d | Stiffness degradation |
| fb0/fc0 | The ratio of initial equi-biaxial compressive yield stress to initial uniaxial compressive yield stress |
| K | Softening parameter |
| Number of sample points | |
| Mean value | |
| Variance | |
| Reliability index |
References
- Demir, A.; Caglar, N.; Ozturk, H.; Sumer, Y. Nonlinear Finite Element Study on the Improvement of Shear Capacity in Reinforced Concrete T-Section Beams by an Alternative Diagonal Shear Reinforcement. Eng. Struct. 2016, 120, 158–165. [Google Scholar] [CrossRef]
- Salih, R.; Zhou, F.Y. Numerical Investigation of the Behavior of Reinforced Concrete Beam Reinforced with FRP Bars. Civ. Eng. J. 2019, 5, 2296–2308. [Google Scholar]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of Residual Flexural Stiffness of Steel Fiber-Reinforced Concrete Beams with Steel Reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef] [PubMed]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Karayannis, C.G. Flexural Damage Diagnosis in Reinforced Concrete Beams Using a Wireless Admittance Monitoring System—Tests and Finite Element Analysis. Sensors 2021, 21, 679. [Google Scholar] [CrossRef] [PubMed]
- Megarsa, E.; Kenea, G. Numerical Investigation on Shear Performance of Reinforced Concrete Beam by Using Ferrocement Composite. Math. Probl. Eng. 2022, 2022, 5984177. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Kosmidou, P.-M.K.; Chalioris, C.E. Numerical Analysis Exterior RC Beam-Column Joints with CFRP Bars as Beam’s Tensional Reinforcement under Cyclic Reversal Deformations. Appl. Sci. 2022, 12, 7419. [Google Scholar] [CrossRef]
- Georgali, B.; Tsakiridis, P.E. Microstructure of Fire-Damaged Concrete. A Case Study. Cem. Concr. Compos. 2005, 27, 255–259. [Google Scholar] [CrossRef]
- Janotka, I.; Nürnbergerová, T. Effect of Temperature on Structural Quality of the Cement Paste and High-Strength Concrete with Silica Fume. Nucl. Eng. Des. 2005, 235, 2019–2032. [Google Scholar] [CrossRef]
- Ali, F.; Nadjai, A.; Silcock, G.; Abu-Tair, A. Outcomes of a Major Research on Fire Resistance of Concrete Columns. Fire Saf. J. 2004, 39, 433–445. [Google Scholar] [CrossRef]
- Sakr, K.; El-Hakim, E. Effect of High Temperature or Fire on Heavy Weight Concrete Properties. Cem. Concr. Res. 2005, 35, 590–596. [Google Scholar] [CrossRef]
- Luccioni, B.M.; Figueroa, M.I.; Danesi, R.F. Thermo-Mechanic Model for Concrete Exposed to Elevated Temperatures. Eng. Struct. 2003, 25, 729–742. [Google Scholar] [CrossRef]
- Arioz, O. Effects of Elevated Temperatures on Properties of Concrete. Fire Saf. J. 2007, 42, 516–522. [Google Scholar] [CrossRef]
- Hertz, K.D. Concrete Strength for Fire Safety Design. Mag. Concr. Res. 2015, 57, 445–453. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Kaplan, M.F.; Haslach, H.W. Concrete at High Temperatures: Material Properties and Mathematical Models. Appl. Mech. Rev. 1997, 50, B75. [Google Scholar]
- Zhang, B.; Bicanic, N.; Pearce, C.J.; Balabanic, G. Residual Fracture Properties of Normal- and High-Strength Concrete Subject to Elevated Temperatures. Mag. Concr. Res. 2015, 52, 123–136. [Google Scholar] [CrossRef]
- Ismail Ahmed Ali, S.; Lublóy, E. Effect of Elevated Temperature on the Magnetite and Quartz Concrete at Different W/C Ratios as Nuclear Shielding Concretes. Nucl. Mater. Energy 2022, 33, 101234. [Google Scholar] [CrossRef]
- Esfahani, M.; Hoseinzade, M.; Shakiba, M.; Arbab, F.; Yekrangnia, M.; Pachideh, G. Experimental Investigation of Residual Flexural Capacity of Damaged Reinforced Concrete Beams Exposed to Elevated Temperatures. Eng. Struct. 2021, 240, 112388. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Dwaikat, M.B.; Fike, R.S. An Approach for Evaluating the Residual Strength of Fire-Exposed RC Beams. Mag. Concr. Res. 2010, 62, 479–488. [Google Scholar] [CrossRef]
- Abid, S.R.; Abbass, A.A.; Murali, G.; Al-Sarray, M.L.J.; Nader, I.A.; Ali, S.H. Repeated Impact Response of Normal-and High-Strength Concrete Subjected to Temperatures up to 600 C. Materials 2022, 15, 5283. [Google Scholar] [CrossRef]
- Cho, H.-C.; Han, S.-J.; Heo, I.; Kang, H.; Kang, W.-H.; Kim, K.S. Heating Temperature Prediction of Concrete Structure Damaged by Fire Using a Bayesian Approach. Sustainability 2020, 12, 4225. [Google Scholar] [CrossRef]
- Ilango, S.; Mahato, S. Behaviour of Polypropylene Fibre-Reinforced Concrete Beam with CFRP Reinforcement under Elevated Temperature. Asian J. Civ. Eng. 2020, 21, 677–694. [Google Scholar] [CrossRef]
- Kakae, N.; Miyamoto, K.; Momma, T.; Sawada, S.; Kumagai, H.; Ohga, Y.; Hirai, H.; Abiru, T. Physical and Thermal Properties of Concrete Subjected to High Temperature. J. Adv. Concr. Technol. 2017, 15, 190–212. [Google Scholar] [CrossRef]
- Xiao, J.; König, G. Study on Concrete at High Temperature in China—An Overview. Fire Saf. J. 2004, 39, 89–103. [Google Scholar] [CrossRef]
- Cioni, P.; Croce, P.; Salvatore, W. Assessing Fire Damage to r.c. Elements. Fire Saf. J. 2001, 36, 181–199. [Google Scholar] [CrossRef]
- Demirel, B.; Keleştemur, O. Effect of Elevated Temperature on the Mechanical Properties of Concrete Produced with Finely Ground Pumice and Silica Fume. Fire Saf. J. 2010, 45, 385–391. [Google Scholar] [CrossRef]
- Savva, A.; Manita, P.; Sideris, K.K. Influence of Elevated Temperatures on the Mechanical Properties of Blended Cement Concretes Prepared with Limestone and Siliceous Aggregates. Cem. Concr. Compos. 2005, 27, 239–248. [Google Scholar] [CrossRef]
- Hlavička, V.; Hlavicka-Laczák, L.E.; Lublóy, É. Residual Fracture Mechanical Properties of Quartz and Expanded Clay Aggregate Concrete Subjected to Elevated Temperature. Constr. Build. Mater. 2022, 328, 126845. [Google Scholar] [CrossRef]
- Song, Y.; Fu, C.; Liang, S.; Yin, A.; Dang, L. Fire Resistance Investigation of Simple Supported RC Beams with Varying Reinforcement Configurations. Adv. Civ. Eng. 2019, 2019, 8625360. [Google Scholar] [CrossRef]
- Cai, B.; Li, B.; Fu, F. Finite Element Analysis and Calculation Method of Residual Flexural Capacity of Post-Fire RC Beams. Int. J. Concr. Struct. Mater. 2020, 14, 58. [Google Scholar] [CrossRef]
- Agrawal, A.; Kodur, V. Residual Response of Fire-Damaged High-Strength Concrete Beams. Fire Mater. 2019, 43, 310–322. [Google Scholar] [CrossRef]
- Yuye, X.; Bo, W.; Ronghui, W.; Ming, J.; Yi, L.U.O. Experimental Study on Residual Performance of Reinforced Concrete Beams after Fire. J. Build. Struct. 2013, 34, 20. [Google Scholar]
- Li, L.Y.; Purkiss, J. Stress–Strain Constitutive Equations of Concrete Material at Elevated Temperatures. Fire Saf. J. 2005, 40, 669–686. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures-Part 1.2 General Rules-Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Kim, J.K.; Han, S.H.; Song, Y.C. Effect of Temperature and Aging on the Mechanical Properties of Concrete: Part I. Experimental Results. Cem. Concr. Res. 2002, 32, 1087–1094. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Reinforced Concrete; American Concrete Institute: Farmington Hills, MI, USA, 1995. [Google Scholar]
- Felicetti, R.; Gambarova, P.G.; Meda, A. Residual Behavior of Steel Rebars and R/C Sections after a Fire. Constr. Build. Mater. 2009, 23, 3546–3555. [Google Scholar] [CrossRef]
- Dotreppe, J.C. Mechanical Properties of Quenched and Self-Tempered Reinforcing Steel at Elevated Temperatures Compared with Recommendations of Eurocode 2-Part 1–2. Mater. Struct. 1997, 30, 430–438. [Google Scholar] [CrossRef]
- Qiu, Z.; Huang, R.; Wang, X.; Qi, W. Structural Reliability Analysis and Reliability-Based Design Optimization: Recent Advances. Sci. China Phys. Mech. Astron. 2013, 56, 1611–1618. [Google Scholar] [CrossRef]
- Arangio, S. Reliability Based Approach for Structural Design and Assessment: Performance Criteria and Indicators in Current European Codes and Guidelines. Int. J. Lifecycle Perform. Eng. 2012, 1, 64–91. [Google Scholar] [CrossRef]
- Van Cao, V. Reliability-Based Moment Capacity Assessment of Reinforced Concrete Beams in Fire. Int. J. Civ. Eng. 2022, 20, 1291–1308. [Google Scholar] [CrossRef]
- Van Dao, D.; Adeli, H.; Ly, H.-B.; Le, L.M.; Le, V.M.; Le, T.-T.; Pham, B.T. A Sensitivity and Robustness Analysis of GPR and ANN for High-Performance Concrete Compressive Strength Prediction Using a Monte Carlo Simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Benyahi, K.; Kachi, M.S.; Bouafia, Y.; Barboura, S.; Li, J. Reliability Assessment of the Behavior of Reinforced and/or Prestressed Concrete Beams Sections in Shear Failure. Frat. Integr. Strutt. 2021, 15, 195–222. [Google Scholar] [CrossRef]
- Roy, A.; Robuschi, S.; Hendriks, M.A.N.; Belletti, B. Safety Assessment of Existing Reinforced Concrete Beams Using Probabilistic Methods at Different Levels. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2016; Volume 711, pp. 958–965. [Google Scholar]
- Rakoczy, A.M.; Nowak, A.S. Reliability-Based Sensitivity Analysis for Prestressed Concrete Girder Bridges. PCI J. 2013, 58, 81–92. [Google Scholar] [CrossRef]
- Słowik, M.; Skrzypczak, I.; Kotynia, R.; Kaszubska, M. The Application of a Probabilistic Method to the Reliability Analysis of Longitudinally Reinforced Concrete Beams. Procedia Eng. 2017, 193, 273–280. [Google Scholar] [CrossRef]
- Olmati, P.; Sagaseta, J.; Cormie, D.; Jones, A.E.K. Simplified Reliability Analysis of Punching in Reinforced Concrete Flat Slab Buildings under Accidental Actions. Eng. Struct. 2017, 130, 83–98. [Google Scholar] [CrossRef]
- Schlune, H.; PLoS, M.; Gylltoft, K. Safety Formats for Non-Linear Analysis of Concrete Structures. Mag. Concr. Res. 2012, 64, 563–574. [Google Scholar] [CrossRef]
- Eamon, C.D.; Jensen, E. Reliability Analysis of RC Beams Exposed to Fire. J. Struct. Eng. 2013, 139, 212–220. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, J.; Xie, Q. Reliability Analysis of the Residual Moment Capacity of High-Strength Concrete Beams after Elevated Temperatures. Struct. Concr. 2021, 22, 1586–1599. [Google Scholar] [CrossRef]
- Haldar, A.; Mahadevan, S. Probability, Reliability, and Statistical Methods in Engineering Design; John Wiley & Sons Incorporated: New York, NY, USA, 2000. [Google Scholar]
- ICS 91.010.30; Others Eurocode—Basis of Structural Design. CEN: Brussels, Belgium, 2002.
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Mayfield Heights, OH, USA, 2009. [Google Scholar]
- Schneider, U. Concrete at High Temperatures—A General Review. Fire Saf. J. 1988, 13, 55–68. [Google Scholar] [CrossRef]
- Meda, A.; Gambarova, P.G.; Bonomi, M. High-Performance Concrete in Fire-Exposed Reinforced Concrete Sections. Struct. J. 2002, 99, 277–287. [Google Scholar] [CrossRef]
- Narayanan, R.S. EN1992 Eurocode 2: Design of Concrete Structures. In Institution of Civil Engineers-Civil Engineering; Thomas Telford Ltd.: London, UK, 2001; Volume 144, pp. 23–28. [Google Scholar]
- Wiśniewski, D.F.; Cruz, P.J.S.; Henriques, A.A.R.; Simões, R.A.D. Probabilistic Models for Mechanical Properties of Concrete, Reinforcing Steel and Pre-Stressing Steel. Struct. Infrastruct. Eng. 2009, 8, 111–123. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).