Water Shortage Simulation Using a System Dynamics Approach: A Case Study of the Rafsanjan City
Abstract
:1. Introduction
- Which factors affect the water crisis in Rafsanjan?
- Which factors are sensitive and key?
- What are the optimal values of the factors affecting the water crisis?
- What scenarios can be defined for better management of water resources and related problems?
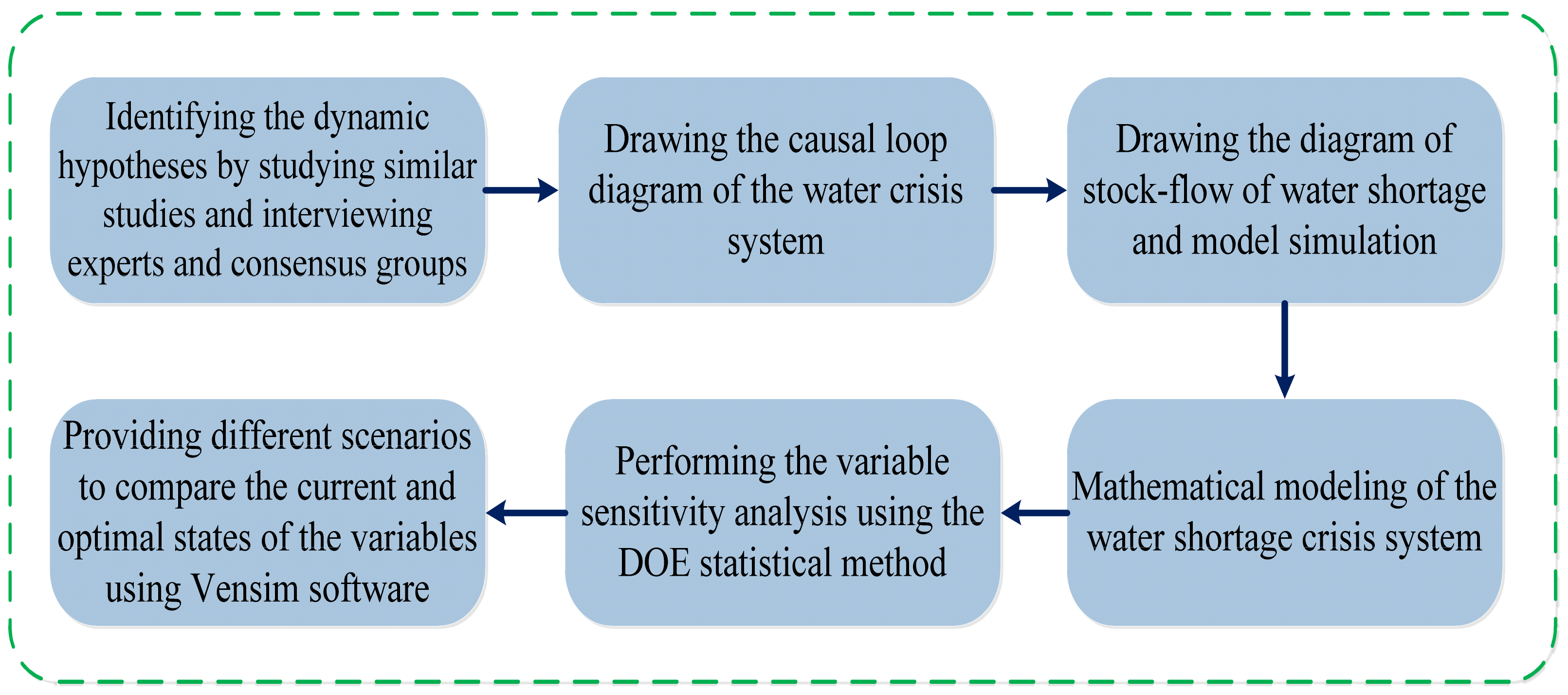
2. Research Methodology
- i.
- The factors affecting water shortage and their relationship are hypothesized. A series of factors affecting water shortage are identified by studying similar studies and interviewing experts and consensus groups.
- ii.
- The causal loop diagram of the whole system is depicted using the dynamic hypotheses extracted from step i.
- iii.
- The stock-flow diagram is provided and the model is simulated. State-flow diagrams as a practical tool to show accumulations and flows within a model are presented. An abbreviation is considered for each variable to reveal equations showing the relationship of each variable.
- iv.
- Formulating the model and developing the mathematical model: this step shows the mathematical relationships used in the simulation of the dynamic model of the water shortage crisis system in Rafsanjan. Validation of system dynamics models should be performed to ensure the validity and usefulness of the model. The validation is a combination of activities starting from the beginning steps of modeling in the system dynamics approach. During these steps, investigating the model structure of a real system is considered based on the different dimensions and their agreement with each other, and whether the proposed model is suitable to accomplish the desired objective. On the other hand, testing the model and its validity increases the reliability of the model and raises confidence in its applicability. In this paper, experts’ opinions and multiple tests of the model by experts were used to assess the validity of the model.
- v.
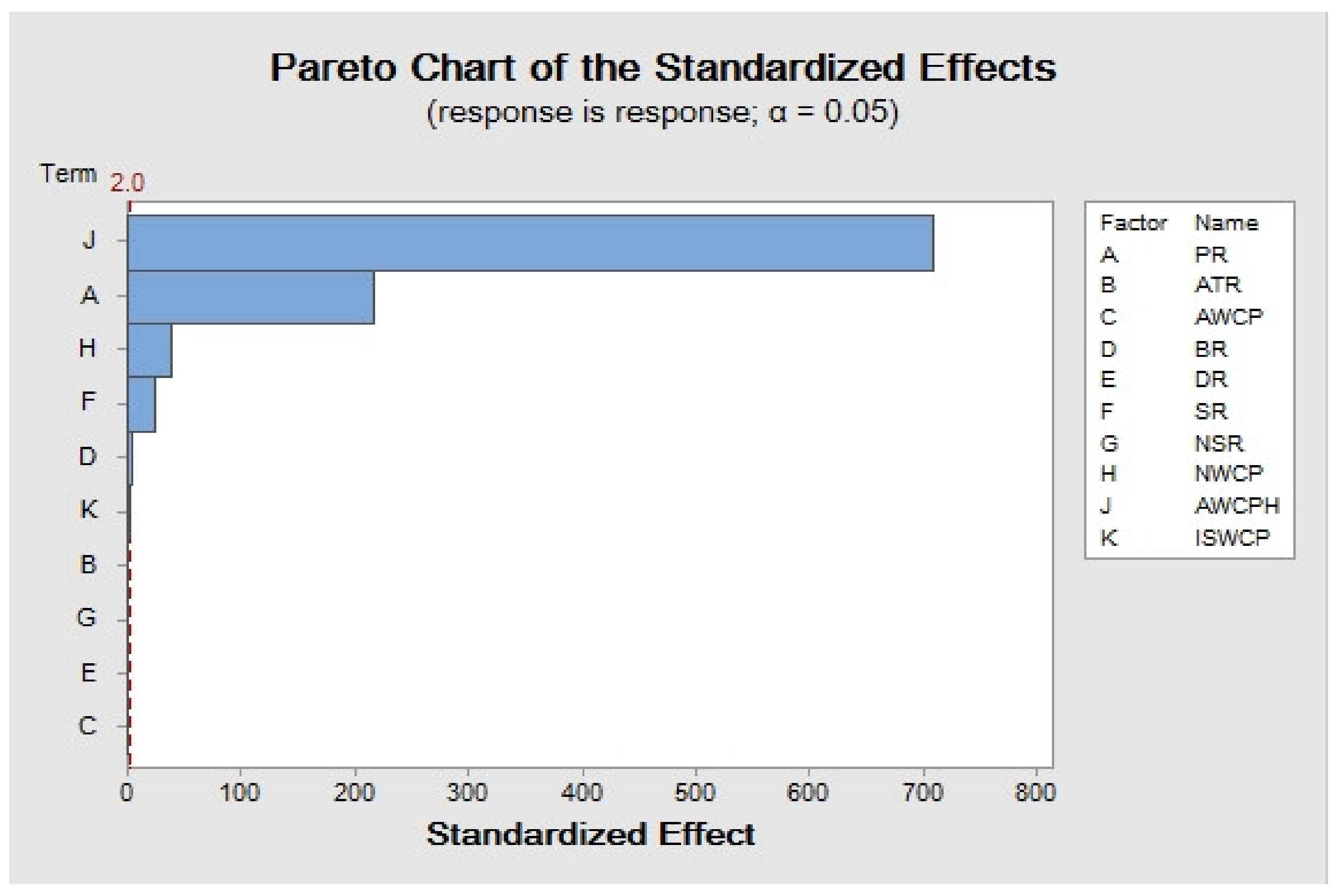
- The sensitivity analysis of the variables is performed using DOE. DOE is a statistical method to obtain maximum information from a process by performing the minimum possible experiments. By DOE implementation, the optimal value of measurement results (i.e., solutions) or the conditions can be determined in which conflicting solutions are compatible. In this work, the importance of the key variables affecting the water shortage in Rafsanjan was identified by DOE. A comparison of the current and optimal status of the variables was then discussed, and solutions were provided to reach the optimal status of the variables.
- vi.
- Vensim software is considered to illustrate the simulations of five scenarios aimed at better managing the water resources and dealing with the water shortage crisis in this city.
3. Results and Discussions
- -
- The amount of water penetration to underground aquifers (Equation (2))
- -
- The amount of water transferred to the system (Equation (4))
- -
- The amount of water consumption in agriculture (Equation (20))
- -
- The amount of water waste in the agricultural sector (Equation (18))
- -
- The amount of drinking water consumed each year (Equation (6))
- -
- The amount of water used for non-potable water consumption (Equation (10))
- -
- The amount of non-potable water waste (Equation (8))
- -
- The amount of water consumption in industry and services (Equation (26))
- -
- The amount of water waste in industry and services (Equation (28))
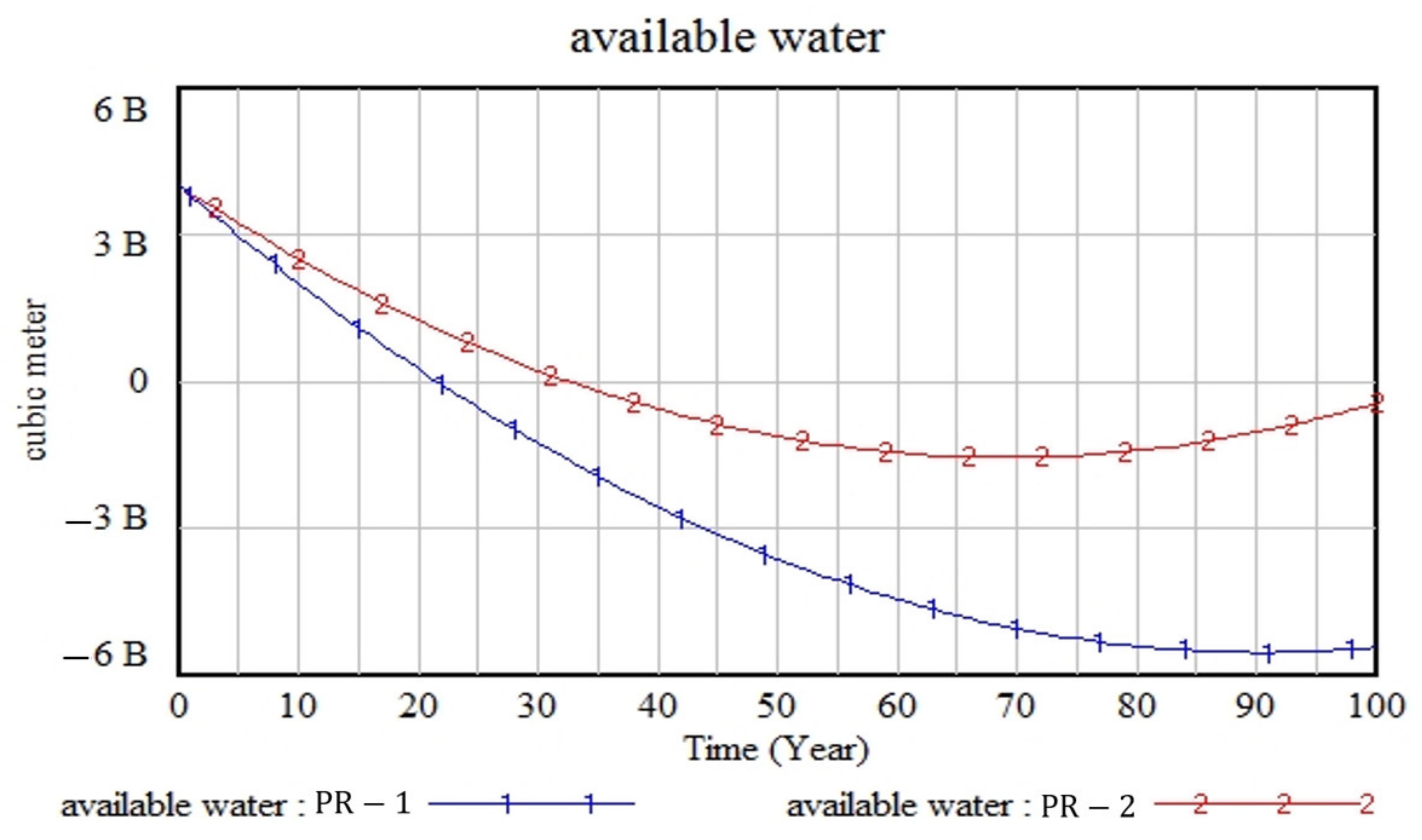
3.1. Results Obtained by the First Scenario
3.2. Results Obtained by the Second Scenario
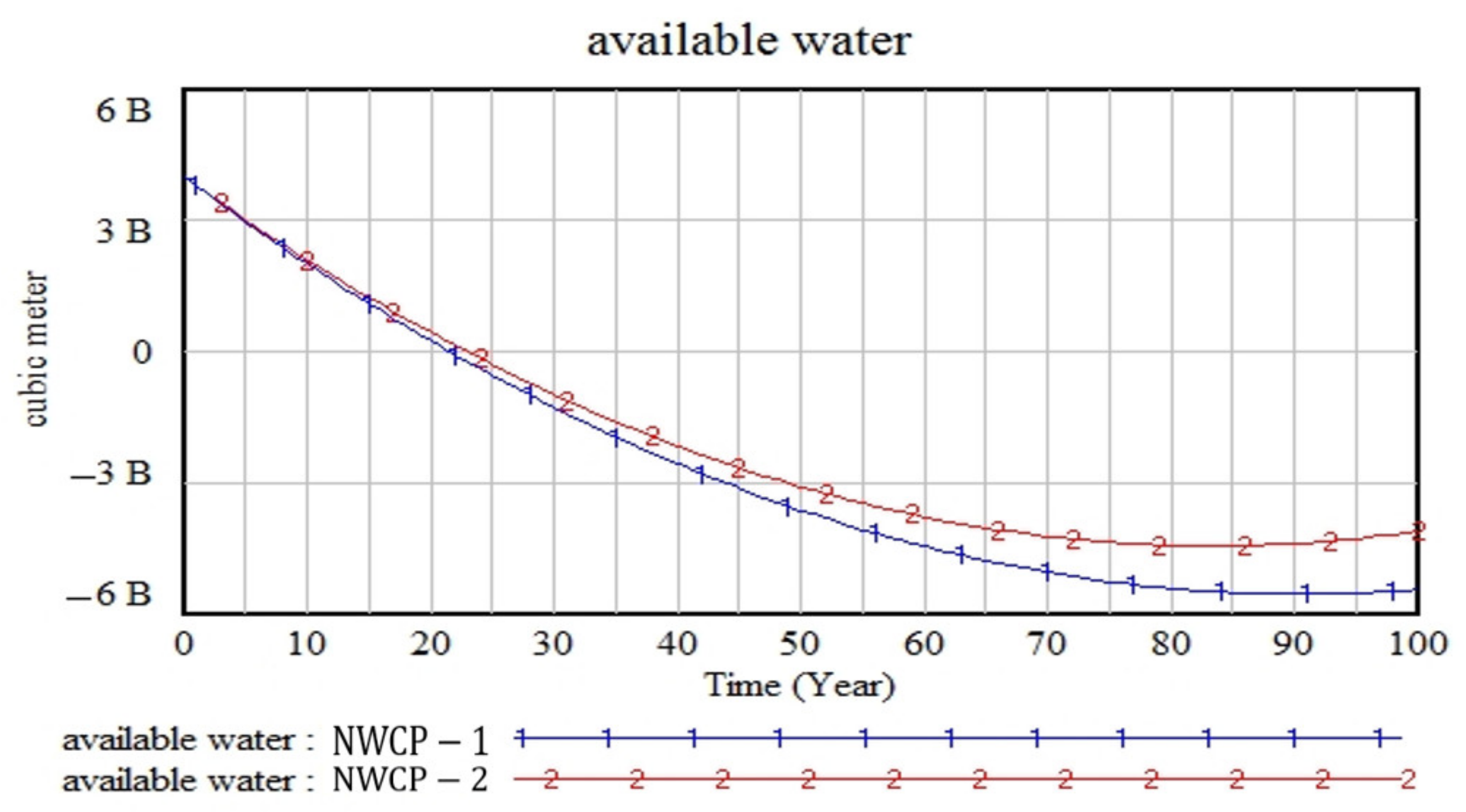
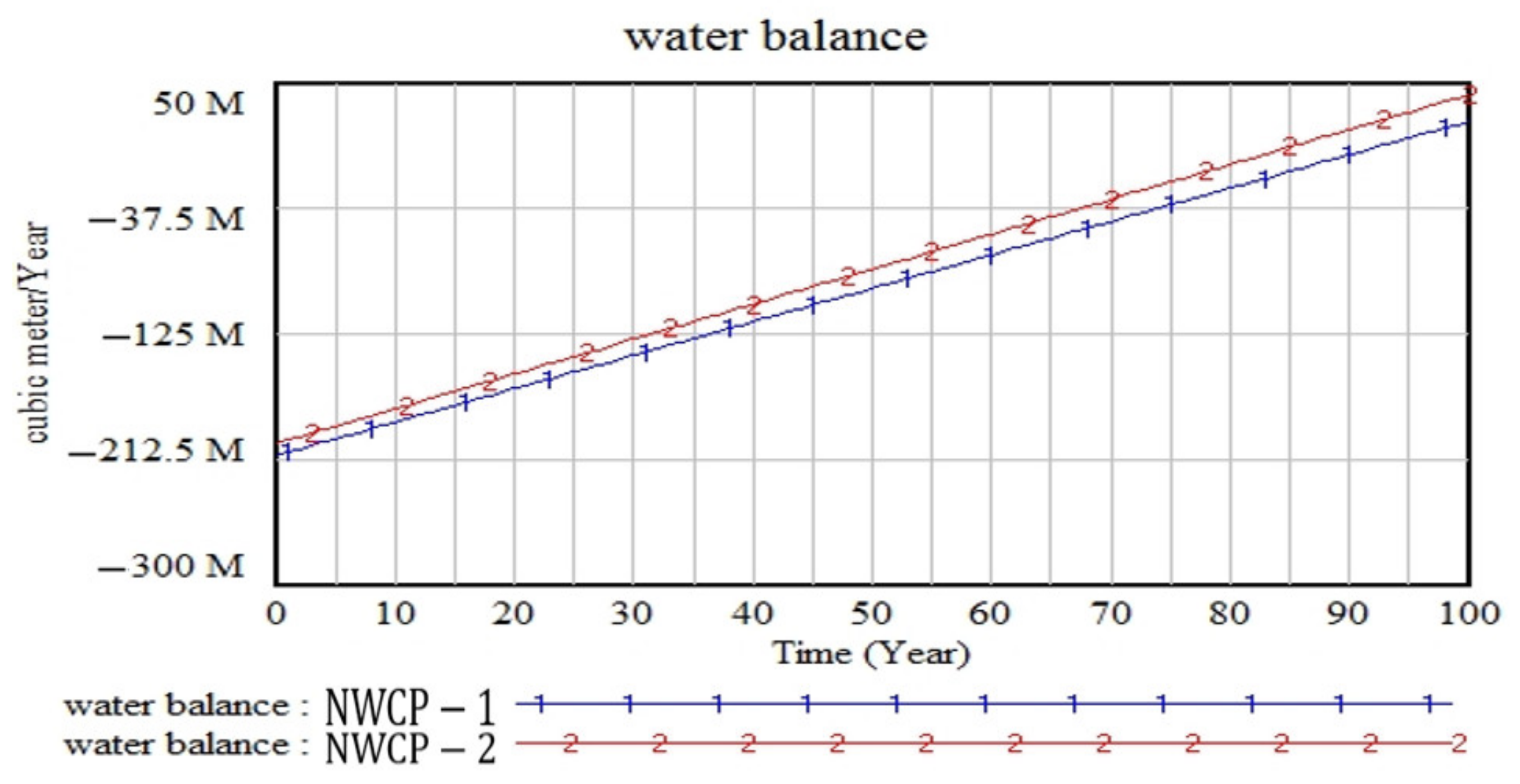
3.3. Results Obtained by the Third Scenario

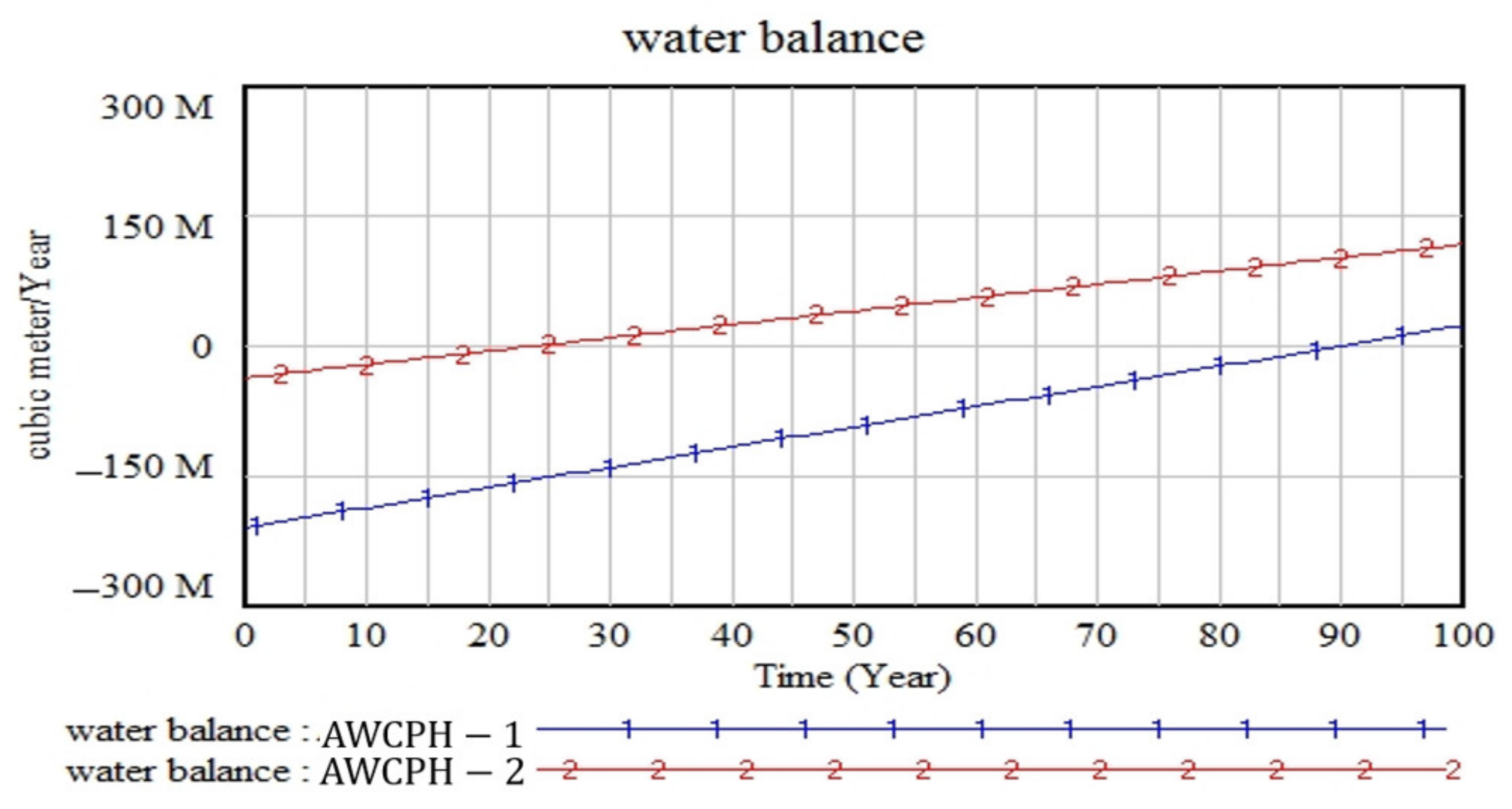
3.4. Results Obtained by the Fourth Scenario
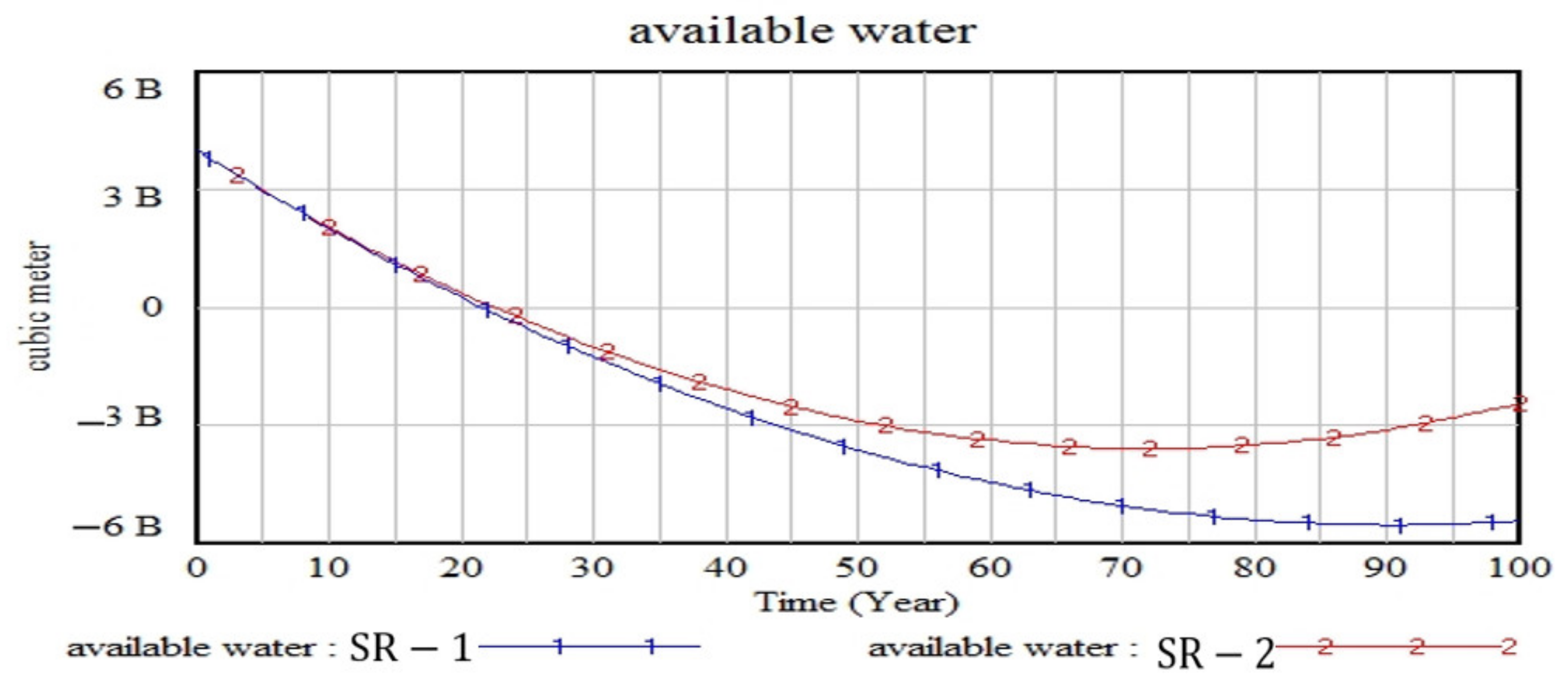
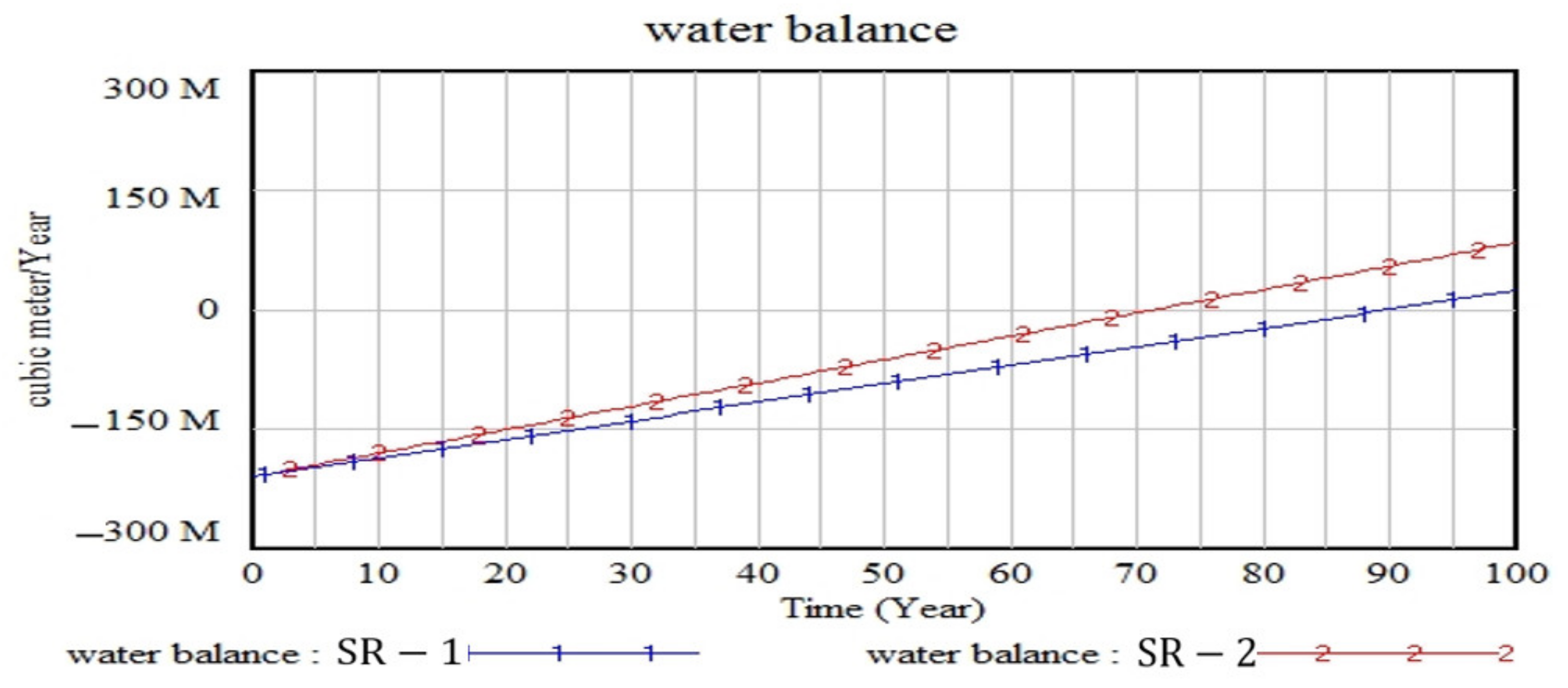
3.5. Results Obtained by the Fifth Scenario
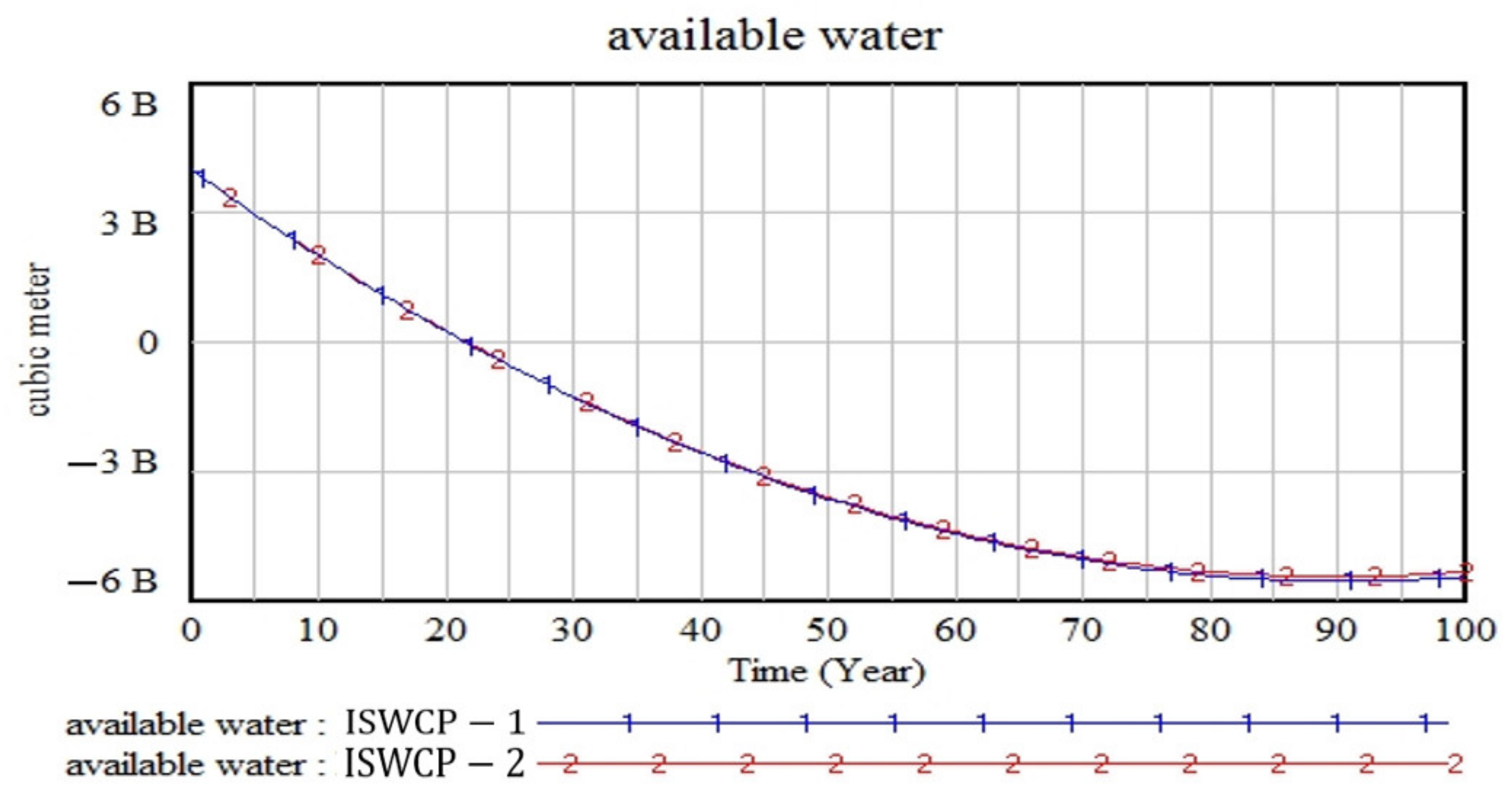
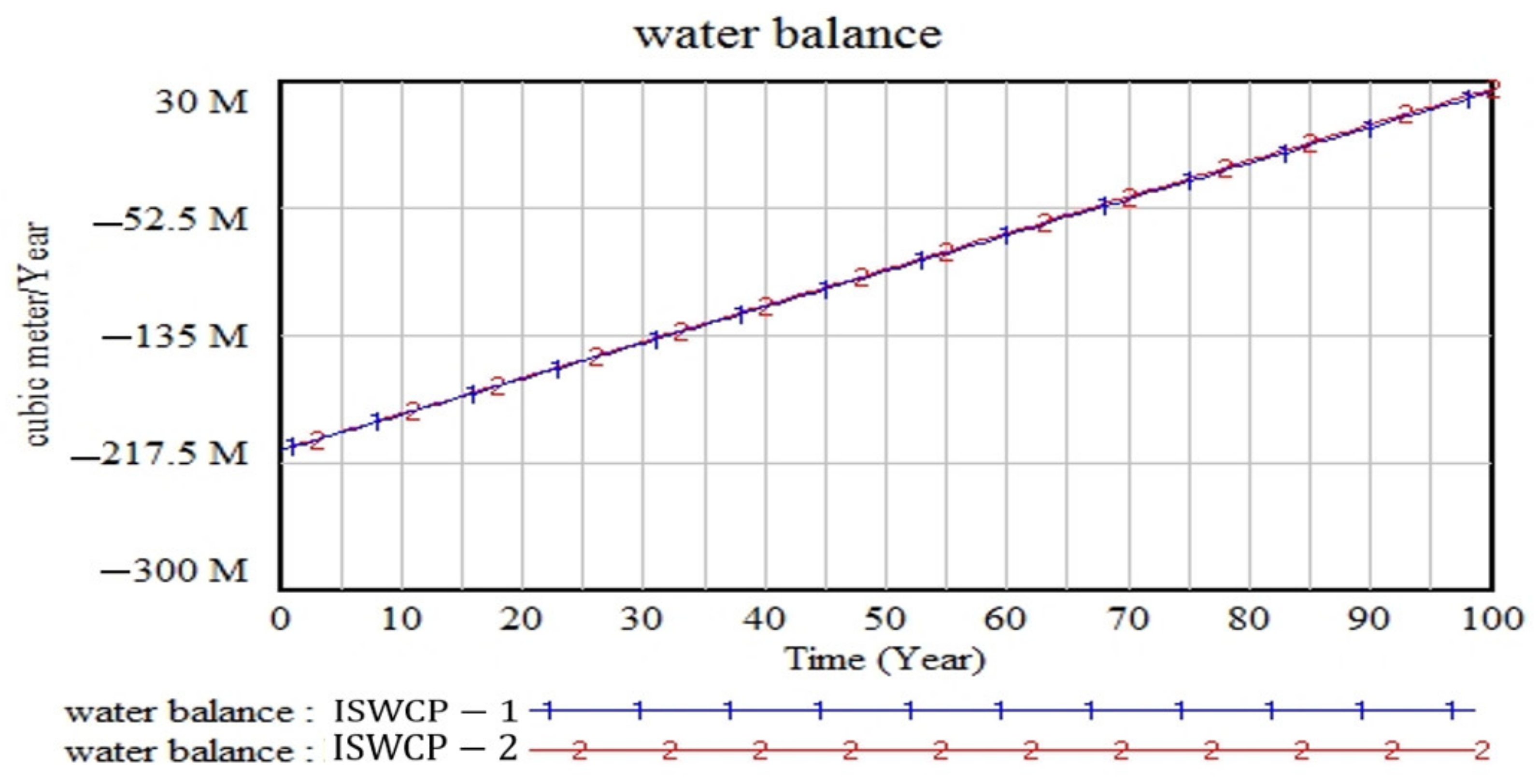
- At some times of the year, industrial and service units (i.e., schools, universities, etc.) are closed and do not consume water;
- Industrial and service units pay more attention to the problem of efficiency and effectiveness or productivity in general;
- Industrial and service units have better capital to update water consumption equipment and use facilities for less water consumption.
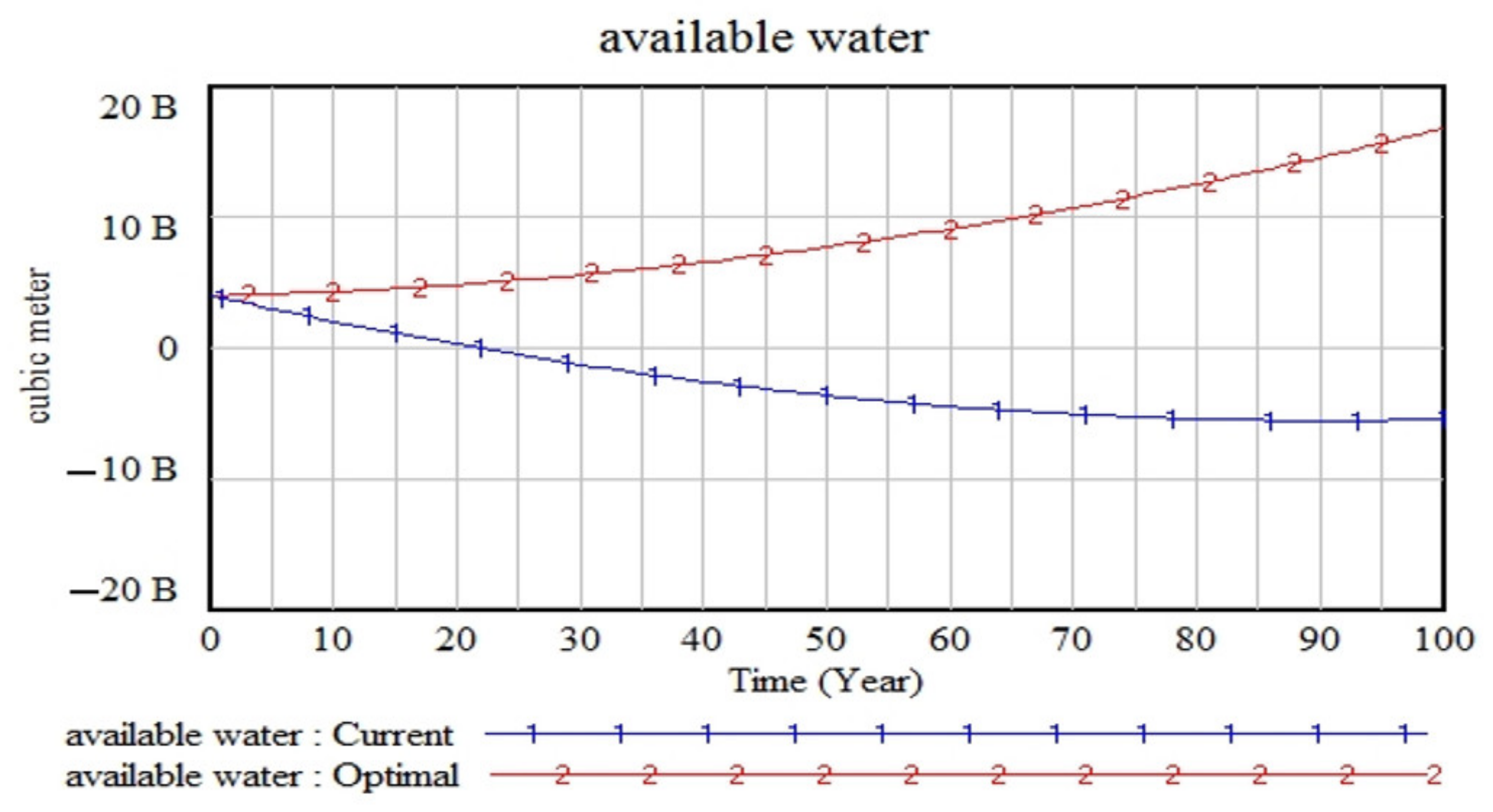
3.6. The System Describes the Optimality of All Variables
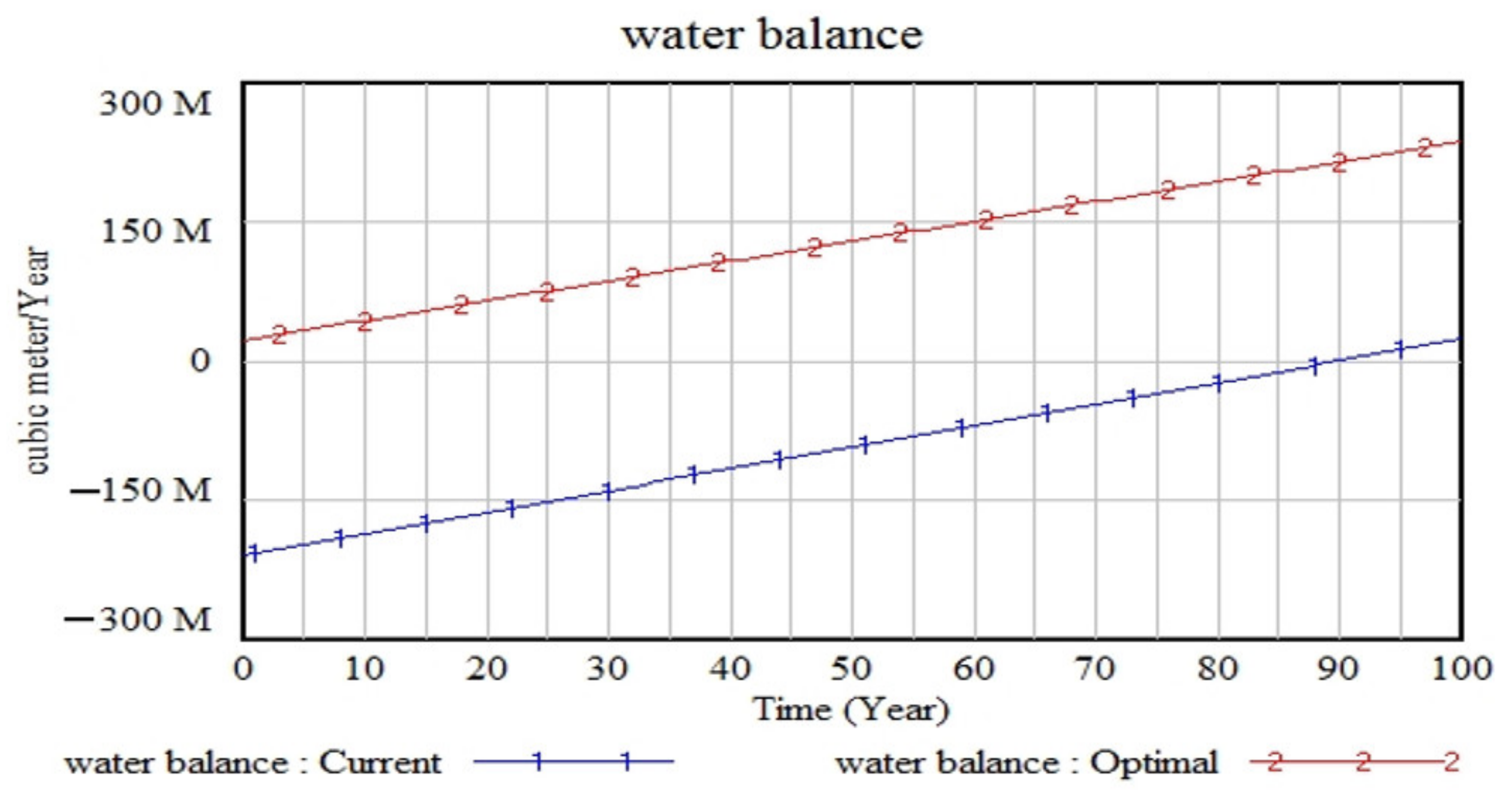
4. Conclusions and Future Suggestions
- As the most sensitive variable of the proposed system was the amount of water consumption per hectare of cultivated area, the boundary of the system should be developed by the agricultural sector, in which the factors and variables of the agricultural system should be identified and then optimized.
- This paper utilized a DOE statistical method to determine and optimize the system variables. It is suggested to use other methods such as multi-criteria decision-making (MCDM) techniques to optimize the variables in future studies.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xi, X.; Poh, K.L. Using system dynamics for sustainable water resources management in Singapore. Procedia Comput. Sci. 2013, 16, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Abdiyev, K.Z.; Maric, M.; Orynbayev, B.Y.; Toktarbay, Z.; Zhursumbaeva, M.B.; Seitkaliyeva, N.Z. Flocculating properties of 2-acrylamido-2-methyl-1-propane sulfonic acid-co-allylamine polyampholytic copolymers. Polym. Bull. 2022, 79, 10741–10756. [Google Scholar] [CrossRef]
- Kojiri, T.; Hori, T.; Nakatsuka, J.; Chong, T.S. World continental modeling for water resources using system dynamics. Phys. Chem. Earth Parts A/B/C 2008, 33, 304–311. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, N.; Shang, J.; Zhang, J. Sustainable utilization of water resources in China: A system dynamics model. J. Clean. Prod. 2017, 142, 613–625. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, H.W.; Chen, B.; Chen, G.Q.; Zhao, X.H. Water resources planning based on complex system dynamics: A case study of Tianjin city. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2328–2336. [Google Scholar] [CrossRef]
- Kerimkulova, A.R.; Azat, S.; Velasco, L.; Mansurov, Z.A.; Lodewyckx, P.; Tulepov, M.I.; Kerimkulova, M.R.; Berezovskaya, I.; Imangazy, A. Granular rice husk based sorbents for sorption of vapors of organic and inorganic matters. J. Chem. Technol. Met. 2019, 54, 578–584. [Google Scholar]
- Srinivasan, V.; Lambin, E.F.; Gorelick, S.M.; Thompson, B.H.; Rozelle, S. The nature and causes of the global water crisis: Syndromes from a meta-analysis of coupled human-water studies. Water Resour. Res. 2012, 48, W10516. [Google Scholar] [CrossRef]
- Guo, H.C.; Liu, L.; Huang, G.H.; Fuller, G.A.; Zou, R.; Yin, Y.Y. A system dynamics approach for regional environmental planning and management: A study for the Lake Erhai Basin. J. Environ. Manag. 2001, 61, 93–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ho, C.C.; Yang, C.C.; Chang, L.C.; Chen, T.W. The application of system dynamics modeling to study impact of water resources planning and management in Taiwan. In Proceedings of the 23rd International Conference of the System Dynamics Society, Boston, MA, USA, 17–21 July 2005; pp. 17–21. [Google Scholar]
- Feng, L.H.; Zhang, X.C.; Luo, G.Y. Application of system dynamics in analyzing the carrying capacity of water resources in Yiwu City, China. Math. Comput. Simul. 2008, 79, 269–278. [Google Scholar] [CrossRef]
- Dai, D.; Sun, M.; Lv, X.; Hu, J.; Zhang, H.; Xu, X.; Lei, K. Comprehensive assessment of the water environment carrying capacity based on the spatial system dynamics model, a case study of Yongding River Basin in North China. J. Clean. Prod. 2022, 344, 131137. [Google Scholar] [CrossRef]
- Cheng, L.I. System dynamics model of Suzhou water resources carrying capacity and its application. Water Sci. Eng. 2010, 3, 144–155. [Google Scholar]
- Wei, S.; Yang, H.; Song, J.; Abbaspour, K.C.; Xu, Z. System dynamics simulation model for assessing socio-economic impacts of different levels of environmental flow allocation in the Weihe River Basin, China. Eur. J. Oper. Res. 2012, 221, 248–262. [Google Scholar] [CrossRef]
- Madani, K.; AghaKouchak, A.; Mirchi, A. Iran’s socio-economic drought: Challenges of a water-bankrupt nation. Iran. Stud. 2016, 49, 997–1016. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial dynamics. J. Oper. Res. Soc. 1997, 48, 1037–1041. [Google Scholar] [CrossRef]
- Rahanandeh, R.; Langroodi, P.; Amiri, M. A system dynamics modeling approach for a multi-level, multi-product, multi-region supply chain under demand uncertainty. Expert Syst. Appl. 2016, 51, 231–244. [Google Scholar] [CrossRef]
- Towill, D.R. Industrial dynamics modelling of supply chains. Int. J. Phys. Distrib. Logist. Manag. 1996, 26, 23–42. [Google Scholar] [CrossRef]
- Chen, C.; Liu, W.; Liaw, S.; Yu, C. Development of a dynamic strategy planning theory and system for sustainable river basin land use management. Sci. Total Environ. 2005, 346, 17–37. [Google Scholar] [CrossRef] [PubMed]
- Vlachos, D.; Georgiadis, P.; Iakovou, E. A system dynamics model for dynamic capacity planning of remanufacturing in closed-loop supply chains. Comput. Oper. Res. 2007, 34, 367–394. [Google Scholar] [CrossRef]
- Turner, B.L.; Menendez, H.M.; Gates, R.; Tedeschi, L.O.; Atzori, A.S. System dynamics modeling for agricultural and natural resource management issues: Review of some past cases and forecasting future roles. Resources 2016, 5, 40. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]




| No | Variable | Reference | Data Collection Resource |
|---|---|---|---|
| 1 | Population–Birth–Death | Statistical yearbook of Kerman province | Management and planning organization of Kerman province |
| 2 | Cultivated area—shrinking cultivated area | Expert from Jihad Agricultural Department | Department of Agricultural Jihad in Rafsanjan |
| 3 | Industrial and services actual consumption—new subscriber | Rafsanjan Water and Wastewater Company | http://abfarafsanjan.ir/ (accessed on: 10 June 2017) |
| 4 | Drinking water consumption | According to the global standard | |
| 5 | The amount of underground water | Expert from Rafsanjan Regional Water Company | Rafsanjan Regional Water Company |
| 6 | Penetration in the underground aquifer | Statistics of Rafsanjan Regional Water Company | Rafsanjan Regional Water Company |
| Abbreviation | Description | Unit |
|---|---|---|
| PR | Penetration rate | cubic meter/Year |
| P | Penetration | cubic meter/Year |
| AW | Available water | cubic meter |
| DU | Drinking use | cubic meter/Year |
| ADWCP | Annual drinking water consumption per person | (cubic meter/person)/Year |
| STW | Supply through transferred water | cubic meter/Year |
| ATR | Annually transfer rate | cubic meter/Year |
| NDW | Non-drinking waste | cubic meter/Year |
| ANU | Actual non-drinking use | cubic meter/Year |
| NWW | Non-drinking wastewater | cubic meter/Year |
| NAC | Non-drinking actual consumption | cubic meter/Year |
| NWCP | Non-drinking water consumption per person | (cubic meter/person)/Year |
| POP | Population | person |
| B | Birth | person/Year |
| BR | Birth rate | person/Year |
| D | Death | person/Year |
| DR | Death rate | person/Year |
| AGW | Agricultural waste | cubic meter/Year |
| AAU | Actual agricultural use | cubic meter/Year |
| AAC | Agricultural actual consumption | cubic meter/Year |
| AWW | Agricultural wastewater | cubic meter/Year |
| AWCPH | Agricultural water consumption per hectare | (cubic meter/hectare)/Year |
| CA | Cultivated area | hectare |
| SCA | Shrinking cultivated area | hectare/Year |
| SR | Shrinking rate | hectare/Year |
| AISU | Actual industrial and services use | cubic meter/Year |
| ISW | Industrial and service waste | cubic meter/Year |
| ISAC | Industrial and services actual consumption | cubic meter/Year |
| ISWW | Industrial and services wastewater | cubic meter/Year |
| ISWCP | Industrial and services water consumption per subscriber | (cubic meter/subscriber)/Year |
| ISS | Industrial and services subscribers | subscriber |
| NS | New subscriber | subscriber/Year |
| NSR | New subscriber rate | subscriber/Year |
| WS | Water supply | cubic meter/Year |
| WD | Water demand | cubic meter/Year |
| WB | Water balance | cubic meter/Year |
| Abbreviation of Variable | Unit | Current | Down | Up |
|---|---|---|---|---|
| PR | cubic meter/Year | 500 million | 450 million | 550 million |
| ATR | cubic meter/Year | 315,576 | 315,576 | 500,000 |
| AWCP | cubic meter/Year | 1.095 | 1.04 | 1.14 |
| BR | person/Year | 4550 | 4300 | 5000 |
| DR | person/Year | 913 | 820 | 1000 |
| SR | hectare/Year | 400 | 320 | 480 |
| NSR | subscriber/Year | 439 | 415 | 460 |
| NWCP | cubic meter/Year | 138.53 | 110 | 166 |
| AWCPH | cubic meter/Year | 7568 | 5600 | 9500 |
| ISWCP | cubic meter/Year | 429.36 | 390 | 470 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahsavari-Pour, N.; Bahador, S.; Heydari, A.; Fekih, A. Water Shortage Simulation Using a System Dynamics Approach: A Case Study of the Rafsanjan City. Sustainability 2023, 15, 6225. https://doi.org/10.3390/su15076225
Shahsavari-Pour N, Bahador S, Heydari A, Fekih A. Water Shortage Simulation Using a System Dynamics Approach: A Case Study of the Rafsanjan City. Sustainability. 2023; 15(7):6225. https://doi.org/10.3390/su15076225
Chicago/Turabian StyleShahsavari-Pour, Nasser, Sadegh Bahador, Azim Heydari, and Afef Fekih. 2023. "Water Shortage Simulation Using a System Dynamics Approach: A Case Study of the Rafsanjan City" Sustainability 15, no. 7: 6225. https://doi.org/10.3390/su15076225
APA StyleShahsavari-Pour, N., Bahador, S., Heydari, A., & Fekih, A. (2023). Water Shortage Simulation Using a System Dynamics Approach: A Case Study of the Rafsanjan City. Sustainability, 15(7), 6225. https://doi.org/10.3390/su15076225









