Scanning Scheme for Underwater High-Rise Pile Cap Foundation Based on Imaging Sonar
Abstract
:1. Introduction
- Analyzed the effect of scanning position on the accuracy of sonar imaging experimentally, which provides a basis for the placement of IS measurement points in Section 2;
- Designed a sonar-carried platform suitable for HRPCF scanning and field tested in Section 3;
- Tested the proposed scheme in the field at the Wulong River New Bridge, and verified the theoretical feasibility in Section 5.
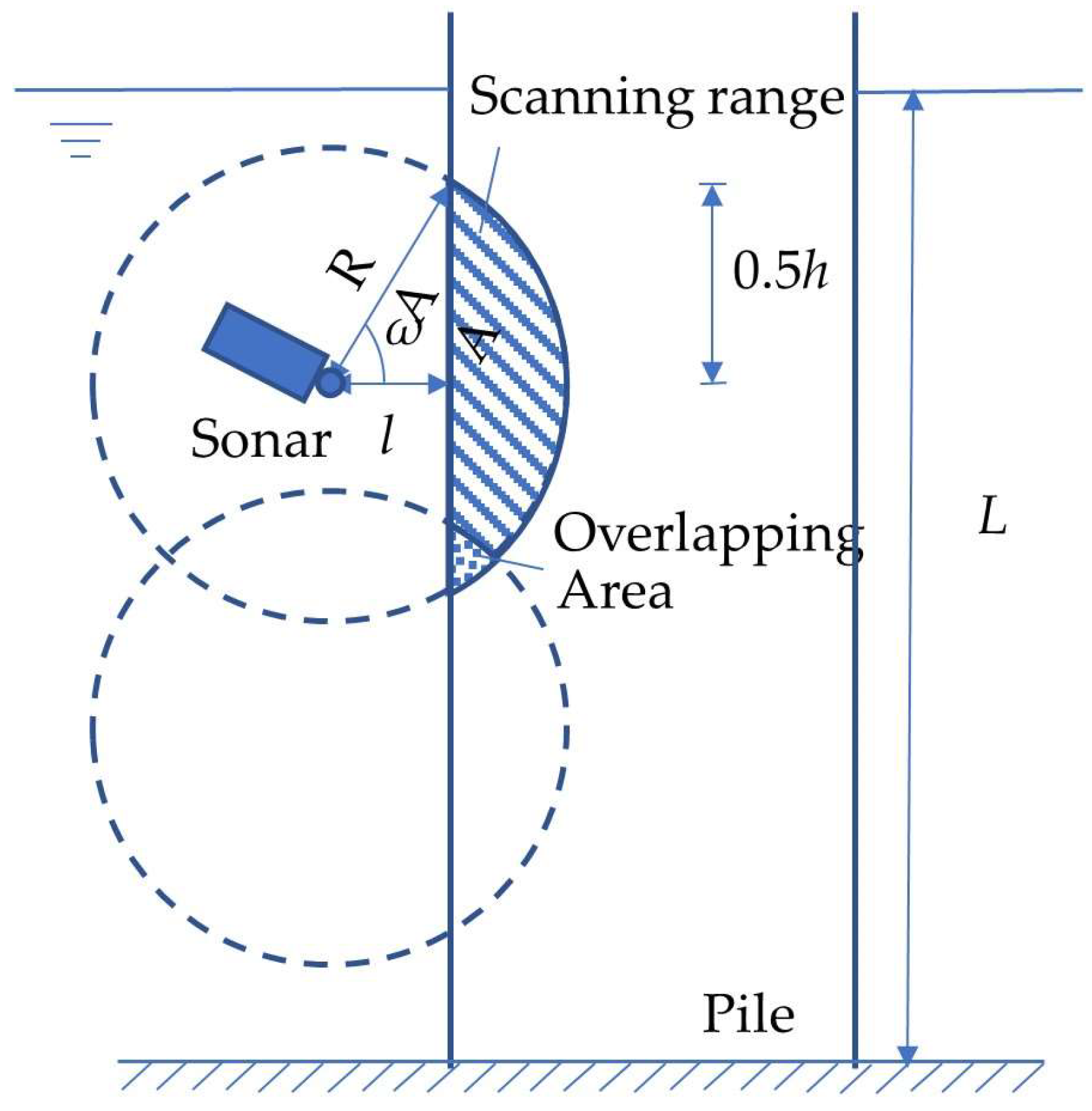
2. Relationship between the Measuring Accuracy of IS and the Scan Distance, and the Pitch Angle
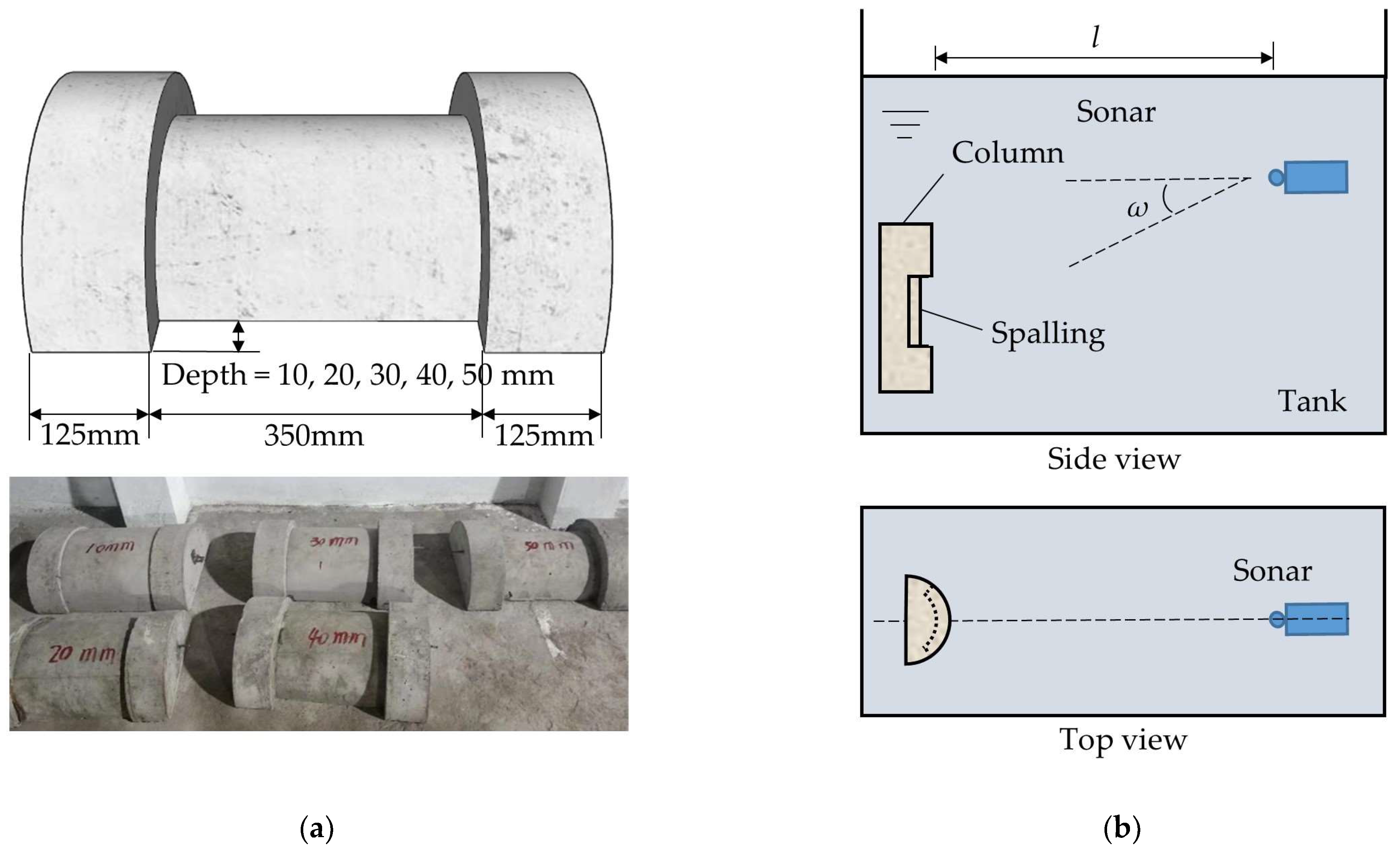
2.1. Experiment Design and Operation
2.2. Results and Discussion
3. Design and Manufacture of an Assembled Sonar-Carried Platform
3.1. The Assembled Floating Island
3.2. The Lifting Device to Carry the IS Device
3.3. Onsite Testing of the Platform
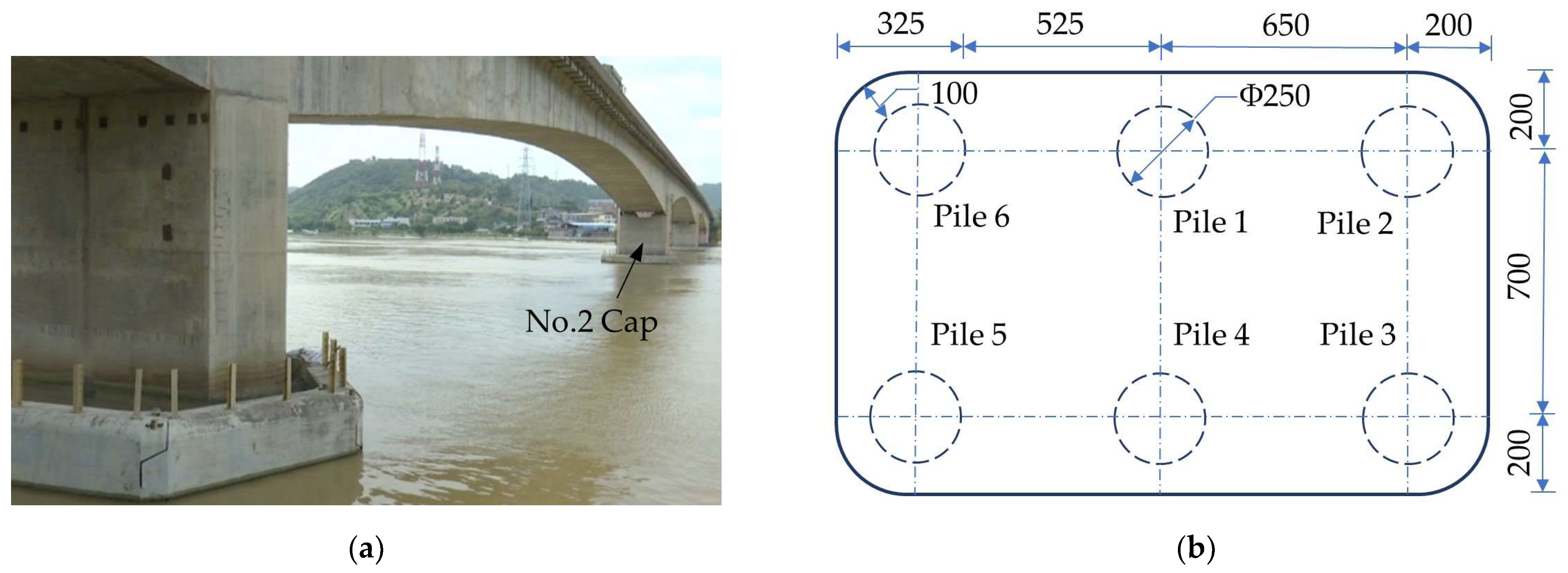
3.3.1. Overview of the Substructure of the Onsite Bridge
3.3.2. Test Procedure and Results
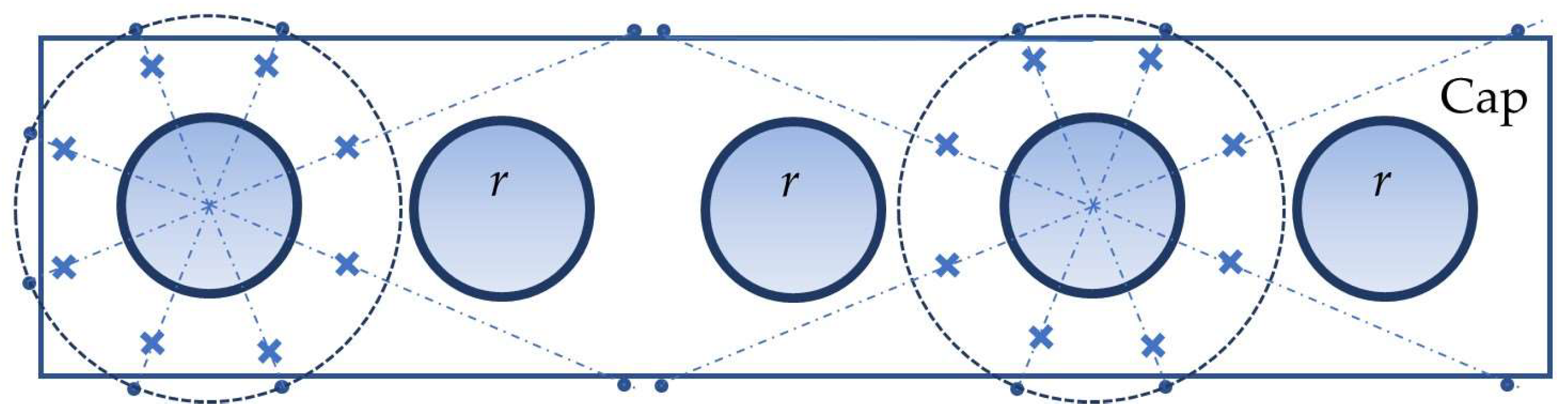
4. Measuring Point Arrangement
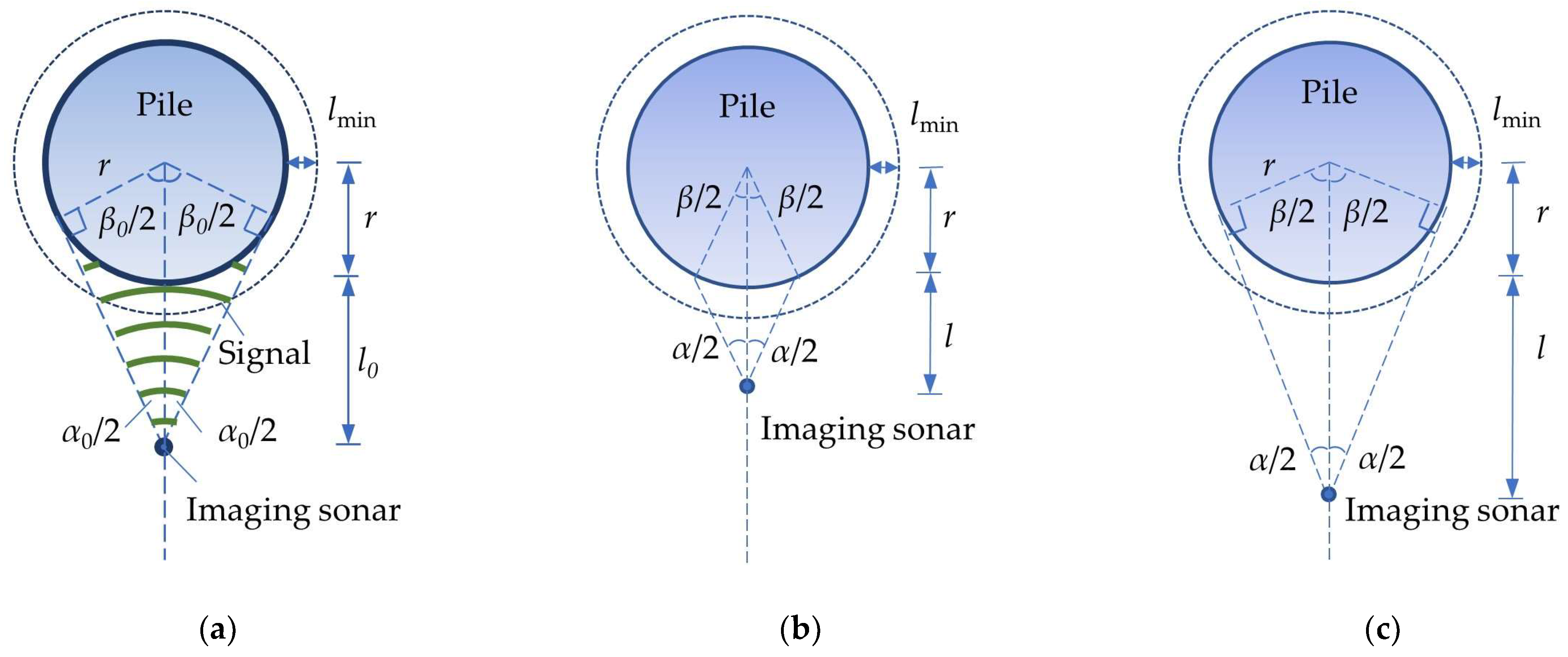
4.1. Absence of a Pile Cap
4.2. Existence of a Pile Cap
4.2.1. A Monopile
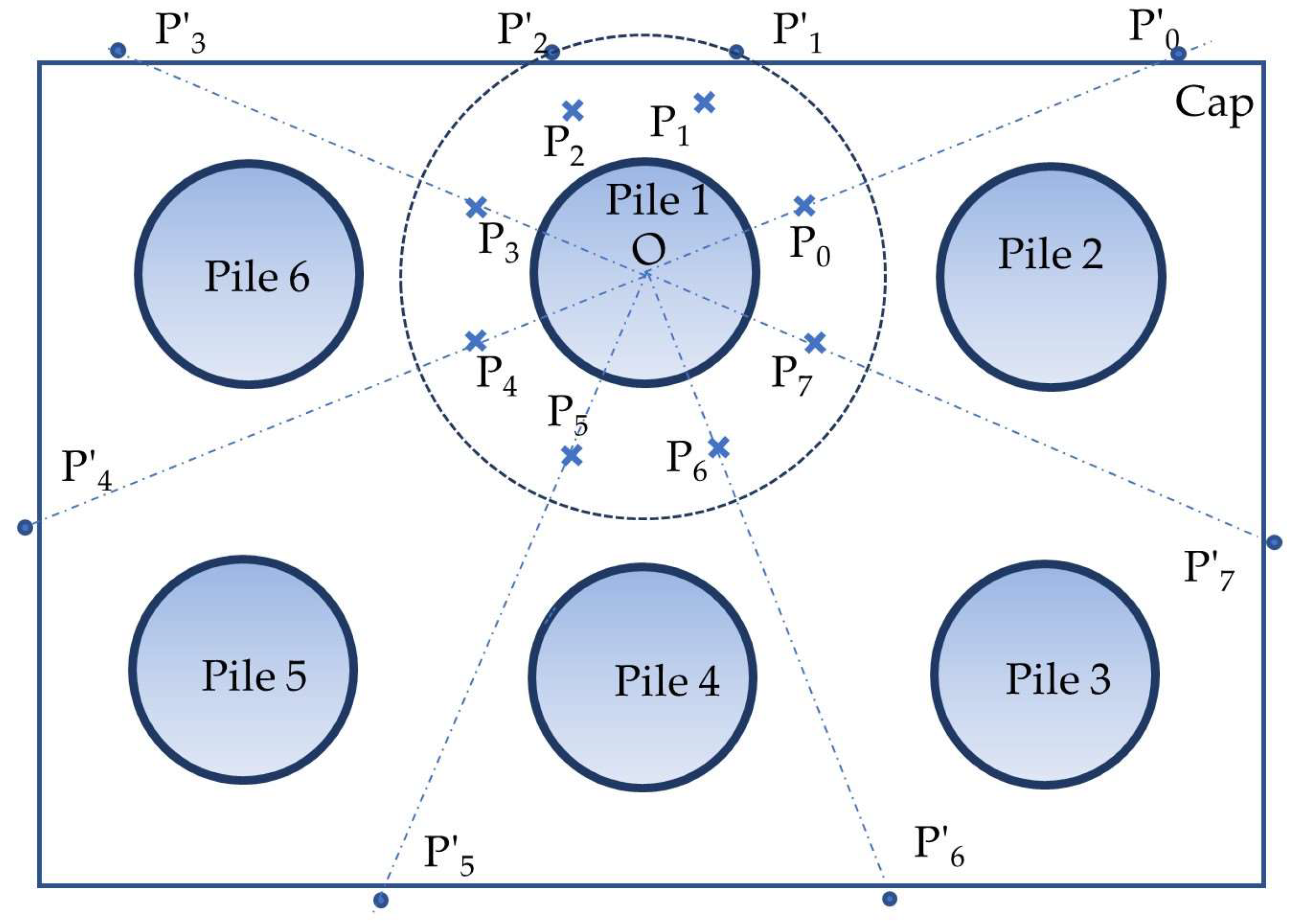
4.2.2. Four Piles (2 × 2) in a Pile Cap
4.2.3. N Piles Arranged in a Row in a Pile Cap
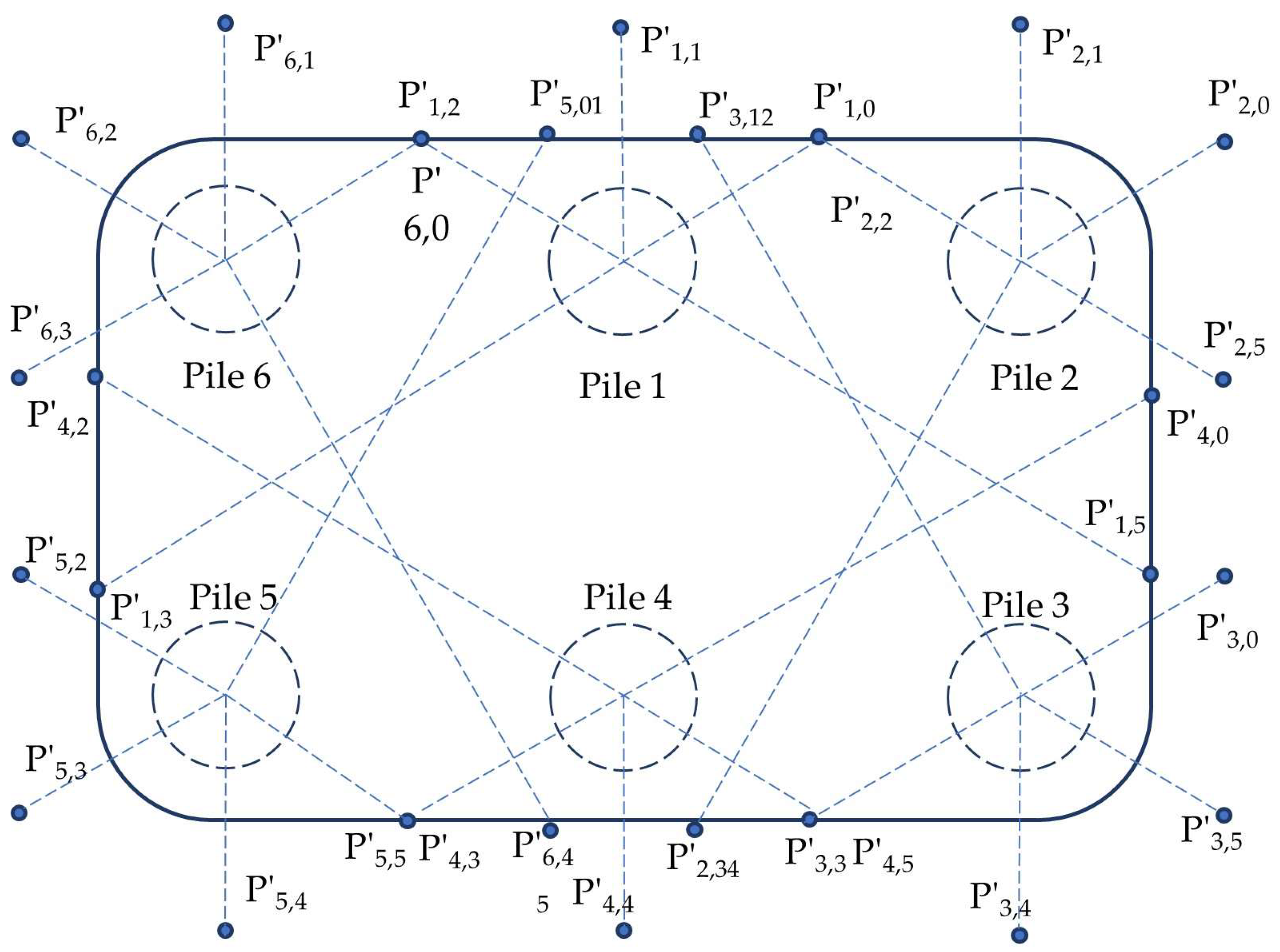
4.2.4. Six Piles (2 × 3) in a Pile Cap
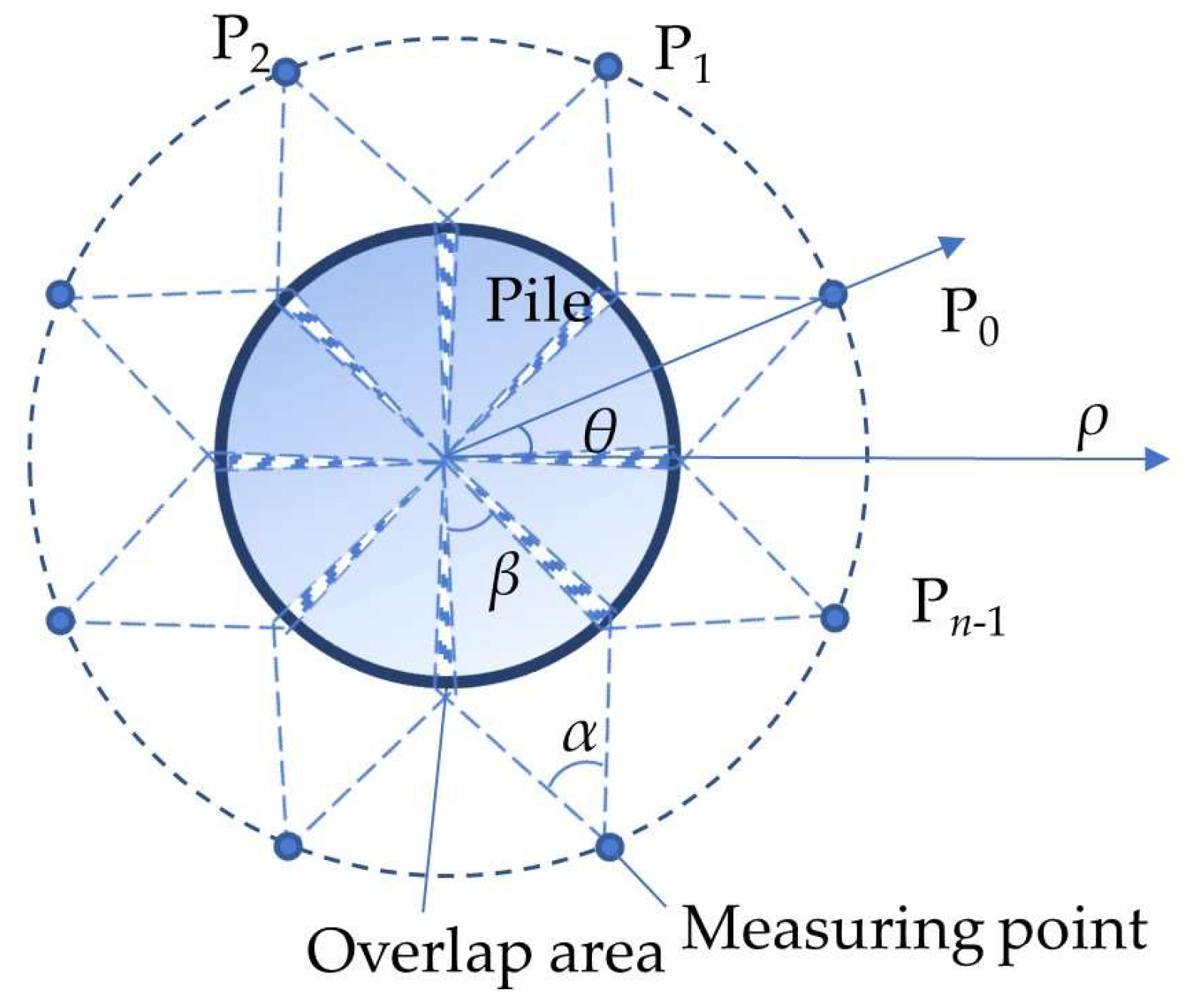
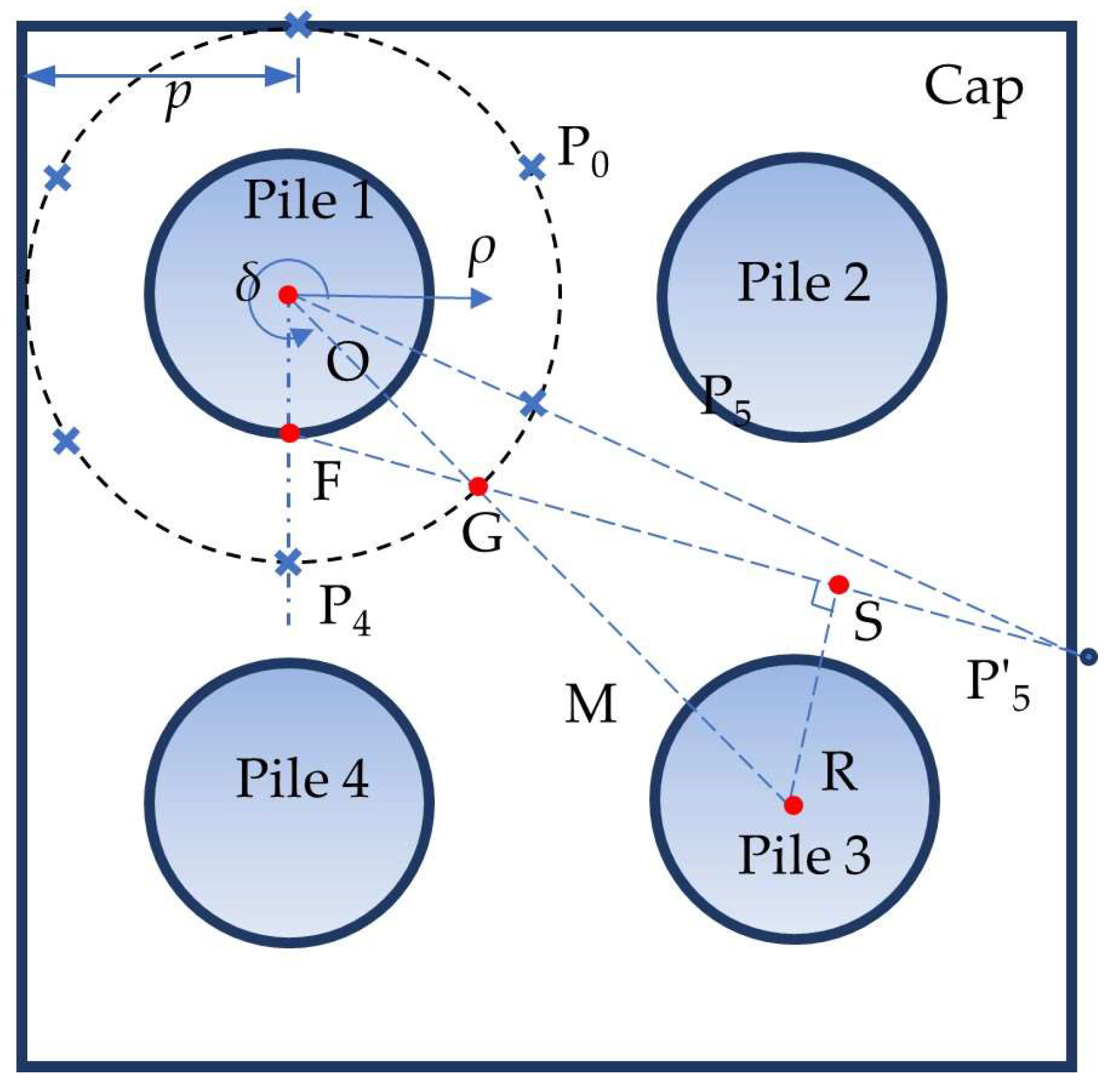
4.3. Replacement of Unmovable Measuring Point
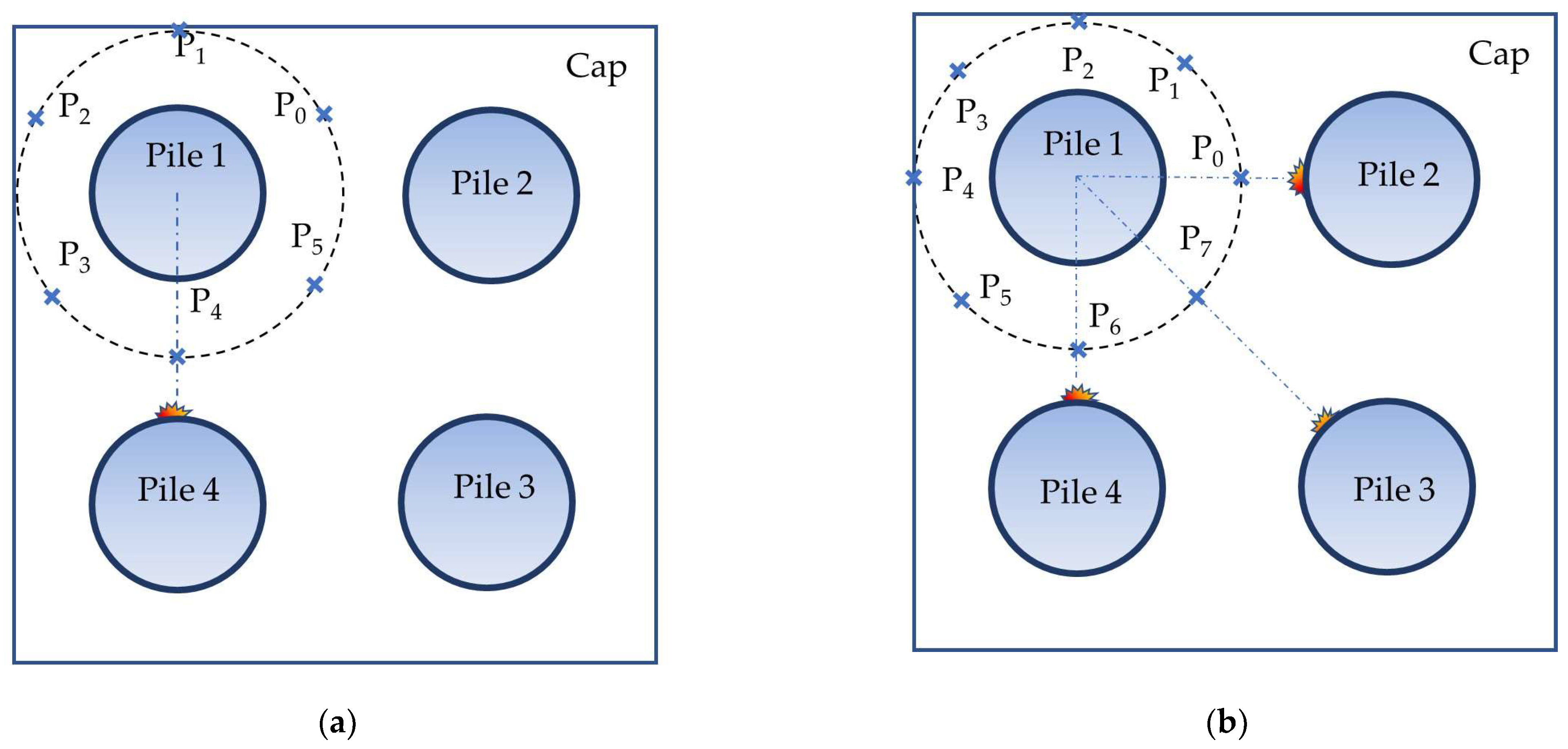
4.3.1. Feasibility of Replacing One Point
4.3.2. Feasibility of Replacing More Than One Point
- Feasibility of replacing P0 with P′70
- 2.
- Feasibility of replacing P7 with P′70
4.4. Layout of the Vertical Position of the Measuring Point
5. Onsite Test for the Proposed Arrangement of Measuring Points
5.1. Overview of the Substructure of an Onsite Bridge
5.2. Arrangement of the Measuring Points
5.3. Analysis of the Obtained Images
6. Conclusions
- The appropriate preset value ranges of two key parameters for the design of measuring point placement, including the horizontal measuring distance l and the pitch angle ω, are experimentally summarized as 1.0 m ≤ l ≤ 3.0 m and 0° ≤ ω ≤ 50°.
- The proposed assembled sonar-carried platform can provide a 13 m deep stable scan in a strong current with a flow speed close to 2.0 m/s. This provides a feasible alternative for solving the problem of unstable scans by AUVs in strong currents.
- Theoretical derivations and onsite tests show that the obstruction of the sonar signal by adjacent piles can be avoided by moving outward, adding, and replacing the obstructed measuring points. The obtained measuring point arrangement is helpful for the IS to scan the entire surface of each pile in the pile group without obstruction.
7. Scope for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Gong, X.; Duan, Y.; Guo, P. Load-Bearing Performance of Caisson-Bored Pile Composite Anchorage Foundation for Long-Span Suspension Bridge: 1-g Model Tests. Acta Geotech. 2023, 1–21. [Google Scholar] [CrossRef]
- Avent, R.R.; Alawady, M.; Guthrie, L. Underwater Bridge Deterioration and the Impact of Bridge Inspection in Mississippi. Transp. Res. Rec. 1997, 1597, 52–60. [Google Scholar] [CrossRef]
- Avent, R.R.; Alawady, M. Bridge Scour and Substructure Deterioration: Case Study. J. Bridge Eng. 2005, 10, 247–254. [Google Scholar] [CrossRef]
- Sweeney, R.A.P.; Unsworth, J.F. Bridge Inspection Practice: Two Different North American Railways. J. Bridge Eng. 2010, 15, 439–444. [Google Scholar] [CrossRef]
- Browne, T.M.; Collins, T.J.; Garlich, M.J.; O’Leary, J.E.; Stromberg, D.G.; Heringhaus, K.C. Underwater Bridge Inspection; United States, 2010; p. 54. Available online: https://rosap.ntl.bts.gov/view/dot/44391 (accessed on 12 March 2023).
- Stromberg, D.G. New Advances in Underwater Inspection Technologies for Railway Bridges over Water. Railw. Track Struct. 2011, 107, 1–29. [Google Scholar]
- Zhang, X.F.; Li, Q.N.; Ma, Y.; Jia, Y.S. Dimensional Imaging Sonar Damage Identification Technology Research On Sea-Crossing Bridge Main Pier Pile Foundations. In Proceedings of the 2016 5th International Conference on Energy and Environmental Protection (ICEEP 2016), Shenzhen, China, 17–18 September 2016. [Google Scholar]
- Mueller, C.A.; Fromm, T.; Buelow, H.; Birk, A.; Garsch, M.; Gebbeken, N. Robotic Bridge Inspection within Strategic Flood Evacuation Planning. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017. [Google Scholar]
- Hou, S.T.; Jiao, D.; Dong, B.; Wang, H.C.; Wu, G. Underwater Inspection of Bridge Substructures Using Sonar and Deep Convolutional Network. Adv. Eng. Inf. 2022, 52, 101545. [Google Scholar] [CrossRef]
- Zheng, S.W.; Xu, Y.J.; Cheng, H.Q.; Wang, B.; Lu, X.J. Assessment of Bridge Scour in the Lower, Middle, and Upper Yangtze River Estuary with Riverbed Sonar Profiling Techniques. Environ. Monit. Assess. 2018, 190, 15. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.R.; Steimle, E.; Hall, M.; Lindemuth, M.; Trejo, D.; Hurlebaus, S.; Medina-Cetina, Z.; Slocum, D. Robot-Assisted Bridge Inspection. J. Intell. Robot Syst. 2011, 64, 77–95. [Google Scholar] [CrossRef]
- Topczewski, Ł.; Cieśla, J.; Mikołajewski, P.; Adamski, P.; Markowski, Z. Monitoring of Scour Around Bridge Piers and Abutments. Transp. Res. Procedia 2016, 14, 3963–3971. [Google Scholar] [CrossRef] [Green Version]
- Clubley, S.; Manes, C.; Richards, D. High-Resolution Sonars Set to Revolutionise Bridge Scour Inspections. Proc. Inst. Civ. Eng. -Civ. Eng. 2015, 168, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Fadool, J.C.; Francis, G.; Clark, J.E.; Liu, G.; De Brunner, V. Robotic Device for 3D Imaging of Scour Around Bridge Piles. In Proceedings of the ASME International Design Engineering Technical, Chicago, IL, USA, 12–15 August 2013. [Google Scholar]
- Shi, P.F.; Fan, X.N.; Ni, J.J.; Wang, G.R. A Detection and Classification Approach for Underwater Dam Cracks. Struct. Health Monit. 2016, 15, 541–554. [Google Scholar] [CrossRef]
- Shi, P.F.; Fan, X.N.; Ni, J.J.; Khan, Z.; Li, M. A Novel Underwater Dam Crack Detection and Classification Approach Based on Sonar Images. PLoS ONE 2017, 12, e0179627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, B.; Yang, Y.; Zhou, J.; Zhuang, Y.Z.; McFarland, M. Damage Detection of Underwater Foundation of a Chinese Ancient Stone Arch Bridge via Sonar-Based Techniques. Measurement 2021, 169, 108283. [Google Scholar] [CrossRef]
- Helminen, J.; Dauphin, G.J.R.; Linnansaari, T. Length Measurement Accuracy of Adaptive Resolution Imaging Sonar and a Predictive Model to Assess Adult Atlantic Salmon (Salmo Salar) into Two Size Categories with Long-Range Data in a River. J. Fish Biol. 2020, 97, 1009–1026. [Google Scholar] [CrossRef]
- Wei, B.; Li, H.S.; Zhou, T.; Xing, S.Y. Obtaining 3D High-Resolution Underwater Acoustic Images by Synthesizing Virtual Aperture on the 2D Transducer Array of Multibeam Echo Sounder. Remote Sens. 2019, 11, 2615. [Google Scholar] [CrossRef] [Green Version]
- Burwen, D.L.; Fleischman, S.J.; Miller, J.D. Accuracy and Precision of Salmon Length Estimates Taken from DIDSON Sonar Images. Trans. Am. Fish. Soc. 2010, 139, 1306–1314. [Google Scholar] [CrossRef]
- Daroux, A.; Martignac, F.; Nevoux, M.; Bagliniere, J.L.; Ombredane, D.; Guillard, J. Manual Fish Length Measurement Accuracy for Adult River Fish Using an Acoustic Camera (DIDSON). J. Fish Biol. 2019, 95, 480–489. [Google Scholar] [CrossRef]
- Cook, D.; Middlemiss, K.; Jaksons, P.; Davison, W.; Jerrett, A. Validation of of Fish Length Estimations from a High Frequency Multi-Beam Sonar (ARTS) and Its Utilisation as a Field-Based Measurement Technique. Fish Res. 2019, 218, 59–68. [Google Scholar] [CrossRef]
- Carreras, M.; David Hernandez, J.; Vidal, E.; Palomeras, N.; Ribas, D.; Ridao, P. Sparus II AUV-A Hovering Vehicle for Seabed Inspection. IEEE J. Ocean. Eng. 2018, 43, 344–355. [Google Scholar] [CrossRef]
- Zhang, H.W.; Zhang, S.T.; Wang, Y.H.; Liu, Y.H.; Yang, Y.N.; Zhou, T.; Bian, H.Y. Subsea Pipeline Leak Inspection by Autonomous Underwater Vehicle. Appl. Ocean Res. 2021, 107, 102321. [Google Scholar] [CrossRef]
- Zacchini, L.; Franchi, M.; Ridolfi, A. Sensor-Driven Autonomous Underwater Inspections: A Receding-Horizon RRT-Based View Planning Solution for AUVs. J. Field Robot. 2022, 39, 499–527. [Google Scholar] [CrossRef]
- Song, Y.; He, B.; Liu, P. Real-Time Object Detection for AUVs Using Self-Cascaded Convolutional Neural Networks. IEEE J. Ocean. Eng. 2021, 46, 56–67. [Google Scholar] [CrossRef]
- Dai, G.B.; Ji, G.Y. Optimization of Measurement Point Layout for Large Size Structures. Noise Vib. Control. 2015, 35, 185–190+206. [Google Scholar]
- Ruan, J.A.; Li, C.J.; Li, M.; Wang, M.; Sun, F.; Lu, Y.Q. Determination of Safety Early Warning Value of Underwater Shield Tunnel Structural Health Monitoring Based on Probability Statistical Method. Saf. Environ. Eng. 2022, 29, 147–155. [Google Scholar]
- Lança, R.; Fael, C.; Maia, R.; Pêgo, J.P.; Cardoso, A.H. Clear-Water Scour at Pile Groups. J. Hydraul. Eng. 2013, 139, 1089–1098. [Google Scholar] [CrossRef]
- Amini, A.; Parto, A.A. 3D Numerical Simulation of Flow Field around Twin Piles. Acta Geophys. 2017, 65, 1243–1251. [Google Scholar] [CrossRef]


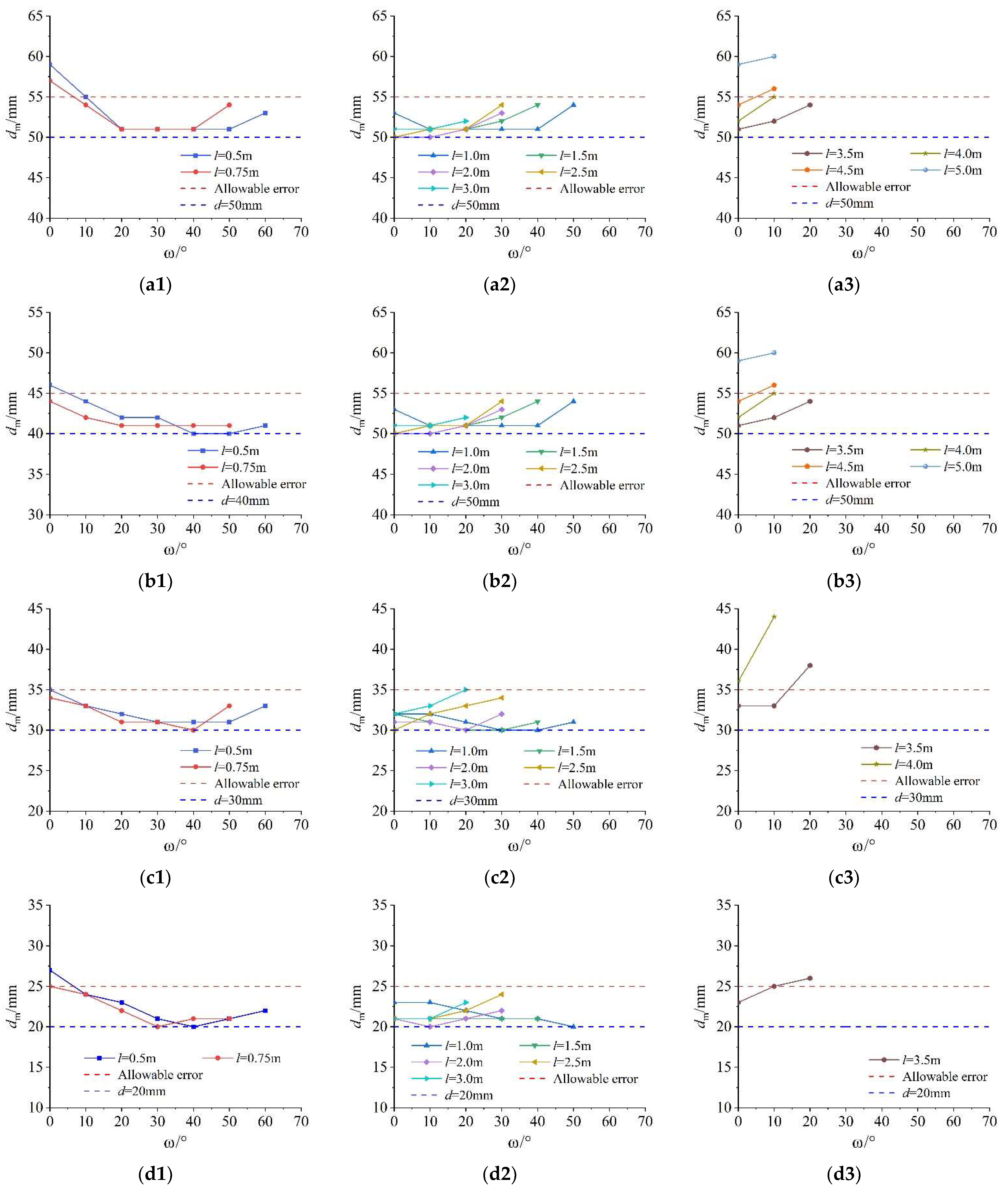









| d/mm | l/m | ω | d/mm | l/m | ω | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 0° | 10° | 20° | 30° | 40° | 50° | 60° | ||||
| 50 | 0.5 | 59 | 55 | 51 | 51 | 51 | 51 | 53 | 40 | 0.5 | 46 | 44 | 42 | 42 | 40 | 40 | 41 |
| 0.75 | 57 | 54 | 51 | 51 | 51 | 54 | - | 0.75 | 44 | 42 | 41 | 41 | 41 | 41 | - | ||
| 1.0 | 53 | 51 | 51 | 51 | 51 | 54 | - | 1.0 | 41 | 41 | 40 | 41 | 41 | 42 | - | ||
| 1.5 | 51 | 51 | 51 | 52 | 54 | - | - | 1.5 | 40 | 42 | 42 | 44 | 45 | - | - | ||
| 2.0 | 50 | 50 | 51 | 53 | - | - | - | 2.0 | 40 | 42 | 42 | 43 | - | - | - | ||
| 2.5 | 50 | 51 | 51 | 54 | - | - | - | 2.5 | 40 | 41 | 42 | 44 | - | - | - | ||
| 3.0 | 51 | 51 | 52 | - | - | - | - | 3.0 | 41 | 43 | 45 | - | - | - | - | ||
| 3.5 | 51 | 52 | 54 | - | - | - | - | 3.5 | 41 | 43 | 45 | - | - | - | - | ||
| 4.0 | 52 | 55 | - | - | - | - | - | 4.0 | 42 | 44 | - | - | - | - | - | ||
| 4.5 | 54 | 56 | - | - | - | - | - | 4.5 | 43 | 46 | - | - | - | - | - | ||
| 5.0 | 59 | 60 | - | - | - | - | - | 5.0 | 46 | 47 | - | - | - | - | - | ||
| d/mm | l/m | ω | d/mm | l/m | ω | ||||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 0° | 10° | 20° | 30° | 40° | 50° | 60° | ||||
| 30 | 0.5 | 35 | 33 | 32 | 31 | 31 | 31 | 33 | 20 | 0.5 | 27 | 24 | 23 | 21 | 20 | 21 | 22 |
| 0.75 | 34 | 33 | 31 | 31 | 30 | 33 | - | 0.75 | 25 | 24 | 22 | 20 | 21 | 21 | - | ||
| 1.0 | 32 | 32 | 31 | 30 | 30 | 31 | - | 1.0 | 23 | 23 | 22 | 21 | 21 | 20 | - | ||
| 1.5 | 32 | 31 | 30 | 32 | - | - | - | 1.5 | 21 | 21 | 21 | 21 | 21 | - | - | ||
| 2.0 | 31 | 31 | 30 | 32 | - | - | - | 2.0 | 21 | 20 | 21 | 22 | - | - | - | ||
| 2.5 | 30 | 32 | 33 | 34 | - | - | - | 2.5 | 21 | 21 | 22 | 24 | - | - | - | ||
| 3.0 | 32 | 33 | 35 | - | - | - | - | 3.0 | 21 | 21 | 23 | - | - | - | - | ||
| 3.5 | 33 | 33 | 38 | - | - | - | - | 3.5 | 23 | 25 | 26 | - | - | - | - | ||
| 4.0 | 36 | 44 | - | - | - | - | - | 4.0 | * | * | - | - | - | - | - | ||
| 4.5 | * | * | - | - | - | - | - | 4.5 | * | * | - | - | - | - | - | ||
| 5.0 | * | * | - | - | - | - | - | 5.0 | * | * | - | - | - | - | - | ||
| d/mm | l/m | ω | |||||||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | |||||||||||
| 10 | 0.5 | * | * | * | * | * | * | * | |||||||||
| 0.75 | * | * | * | * | * | * | - | ||||||||||
| 1.0 | * | * | * | * | * | * | - | ||||||||||
| 1.5 | * | * | * | * | * | - | - | ||||||||||
| 2.0 | * | * | * | * | - | - | - | ||||||||||
| 2.5 | * | * | * | * | - | - | - | ||||||||||
| 3.0 | * | * | * | - | - | - | - | ||||||||||
| 3.5 | * | * | * | - | - | - | - | ||||||||||
| 4.0 | * | * | - | - | - | - | - | ||||||||||
| 4.5 | * | * | - | - | - | - | - | ||||||||||
| 5.0 | * | * | - | - | - | - | - | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Cao, Z.; Lai, C. Scanning Scheme for Underwater High-Rise Pile Cap Foundation Based on Imaging Sonar. Sustainability 2023, 15, 6402. https://doi.org/10.3390/su15086402
Shen S, Cao Z, Lai C. Scanning Scheme for Underwater High-Rise Pile Cap Foundation Based on Imaging Sonar. Sustainability. 2023; 15(8):6402. https://doi.org/10.3390/su15086402
Chicago/Turabian StyleShen, Sheng, Zheng Cao, and Changqin Lai. 2023. "Scanning Scheme for Underwater High-Rise Pile Cap Foundation Based on Imaging Sonar" Sustainability 15, no. 8: 6402. https://doi.org/10.3390/su15086402
APA StyleShen, S., Cao, Z., & Lai, C. (2023). Scanning Scheme for Underwater High-Rise Pile Cap Foundation Based on Imaging Sonar. Sustainability, 15(8), 6402. https://doi.org/10.3390/su15086402






