Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China
Abstract
1. Introduction
2. Literature Review
2.1. Research on the Current Situation of Beijing-Tianjin-Hebei Region
2.2. Research on Node Importance
2.3. Research on HSR Network Planning
2.4. Research on DBSCAN
2.5. Literature Analysis
- (1)
- Most of the literature analyzes the importance of nodes in a qualitative way and provides suggestions and guidance for the development direction. In the research of this paper, on the basis of the analysis of the current situation, the quantitative calculation is carried out, and the importance value of the city node is given. The conclusion is more accurate and targeted.
- (2)
- In the literature on the development status and network planning of the Beijing–Tianjin–Hebei region, it is found that the core cities in the Beijing–Tianjin–Hebei region drive the development trend of small- and medium-sized cities, the synergy between railway transportation capacity and economic development is poor. The existing literature raises questions after introducing the current situation, while there is very little content in high-speed rail network planning for the development status of urban agglomerations. Therefore, in the selection of indices and line network planning, we pay attention to the establishment of models based on the actual development situation and policy requirements, which is of great practical significance.
- (3)
- In the part of the city hierarchy division, this paper innovatively uses density-based noise to apply the spatial clustering method instead of the traditional clustering algorithm so that the calculation process does not use pre-labeled targets to cluster data points. The calculation results are not affected by outliers.
3. Beijing–Tianjin–Hebei Node Importance and Line Urgency
3.1. Evaluation Model
3.1.1. Evaluating Indices
3.1.2. Node Importance Model
3.1.3. Line Urgency Model
3.2. Node Importance and Line Urgency Solution
3.2.1. Index Weight
- (1)
- Initial data statistics. Seven characteristics of urban nodes are selected as the comprehensive evaluation index of node importance. The initial data are calculated and are obtained as shown in Table 1. The unit of passenger railway mileage is passenger–kilometer.
- (2)
- In order to eliminate the influence of different dimensions on the index calculation, they need to be processed forward. Therefore, it needs to be forward processed after the forward processing and then normalization of the index.
- (3)
- Calculate the mean () and standard deviation () of the initial data for any metric q. Additionally, m is the number of city nodes. The equation is as follows:
- (4)
- Let the correlation coefficient matrix of the sample matrix be R. The corresponding eigenvalues and eigenvectors are calculated. Calculating the eigenvalues () and eigenvectors (), and n is the number of indexes.
- (5)
- KMO statistics and Bartlett’s sphericity test.
- (6)
- Common factor variance and component coefficient score calculation.
- (7)
- Determining eigenvalues, eigenvectors and selecting principal components.
- (8)
- Principal component factor gravel diagram analysis.
- (9)
- Determination of weight coefficient.
3.2.2. Node Importance
3.2.3. Line Urgency
4. Beijing–Tianjin–Hebei HSR Network Planning
4.1. City Node Classification
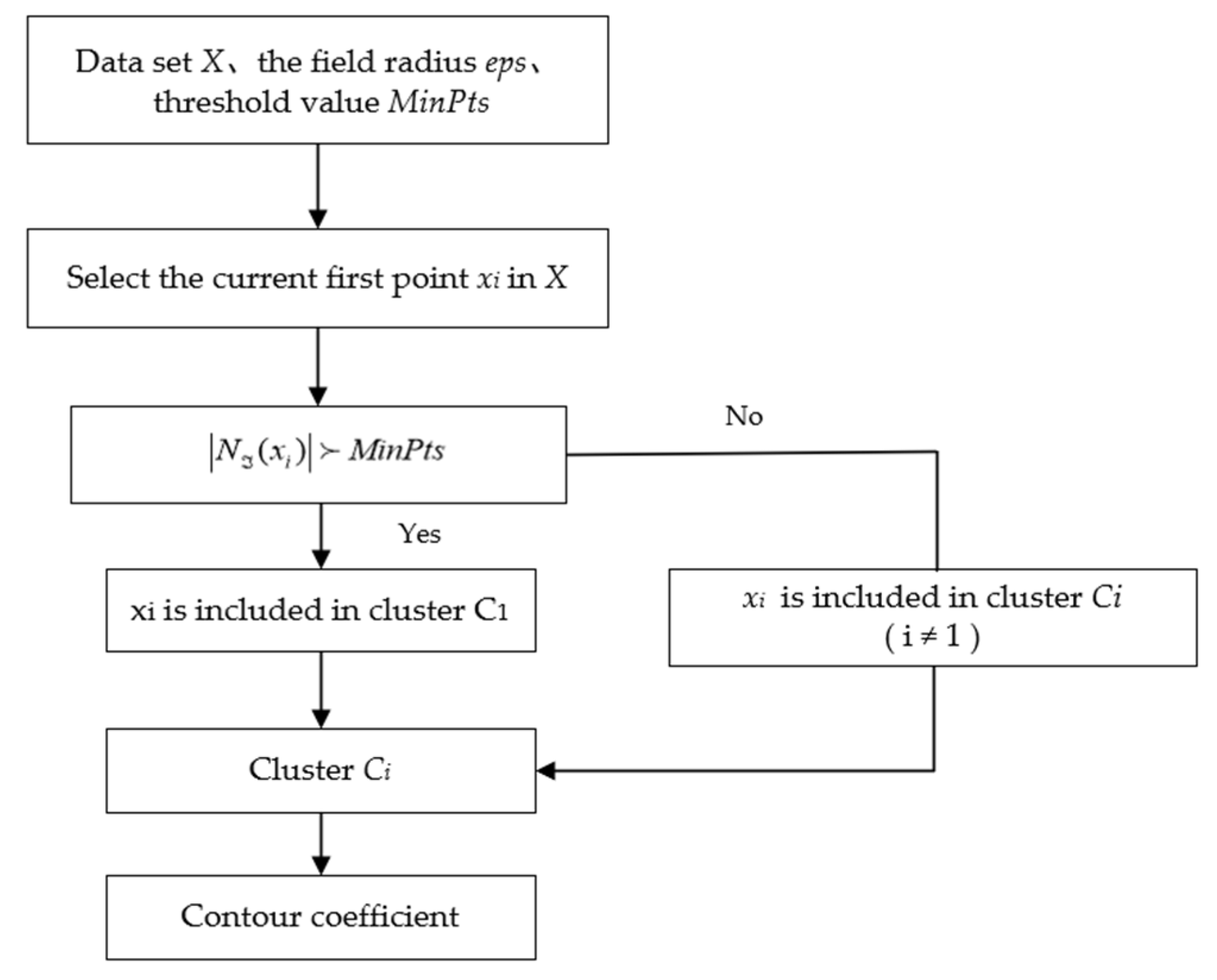
- (1)
- Let the sample set be T, .
belongs to the set T. If the neighborhood
corresponds
and contains at least the
.
- (2)
- The distance between the samples is measured. The radius distance between the core object and each sample is calculated. Through the sensitivity test, it is found that when the sample radius () is 0.09. The minimum sample size is two, which can be selected.
- (3)
- Find a set of nodes whose density can reach all the core objects, which is a cluster.
- (4)
- Then, continue to repeat the steps of (3), there is no category of core objects to find the density of the node set.
- (5)
- Finally, all clusters are obtained. Using phyton software, until all core objects have categories. Its operation steps are shown in the Figure 3 algorithm flow chart.
4.2. Main Backbone Line Planning Model
- (1)
- Coverage Constraints Between Adjacent Nodes.
- (2)
- Number Constraint of Main Backbone Lines.
- (3)
- Node Level Constraint.
- (4)
- Main Backbone Line Number Constraint.
- (5)
- Primary Network Size Constraints.
- (6)
- Non-Linear Coefficient.


 .
.4.3. DBSCAN Design
4.4. Analysis of Planning Results
- (1)
- Road Network Density.
- (2)
- The Proportion of Node GDP on the Main Trunk.
- (3)
- Population Coverage Rate.
- (4)
- HSR Coverage.
5. Conclusions
- (1)
- Through the quantitative analysis of the characteristics of urban nodes, the relative importance values of 13 urban nodes are calculated by means of node importance and line urgency model. Among them, Beijing and Tianjin are the highest, ranking first and second. At the same time, the urgency value of the HSR lines between any two cities among the 13 city nodes can be obtained.
- (2)
- Based on the value of node importance and line urgency, the DBSCAN is used to cluster the 13 urban nodes. It is found that the 13 cities in the Beijing–Tianjin–Hebei urban agglomeration can be divided into four levels, among which Beijing and Tianjin are located in the first-level urban nodes. Shijiazhuang, Qinhuangdao, Handan, Tangshan, Chengde and Cangzhou are located in the secondary city nodes. Additionally, the remaining cities are located in the third and fourth city nodes, which is in line with the relative situation of the comprehensive development level of cities in the urban agglomeration and intuitively reflects the relative status of each city node.
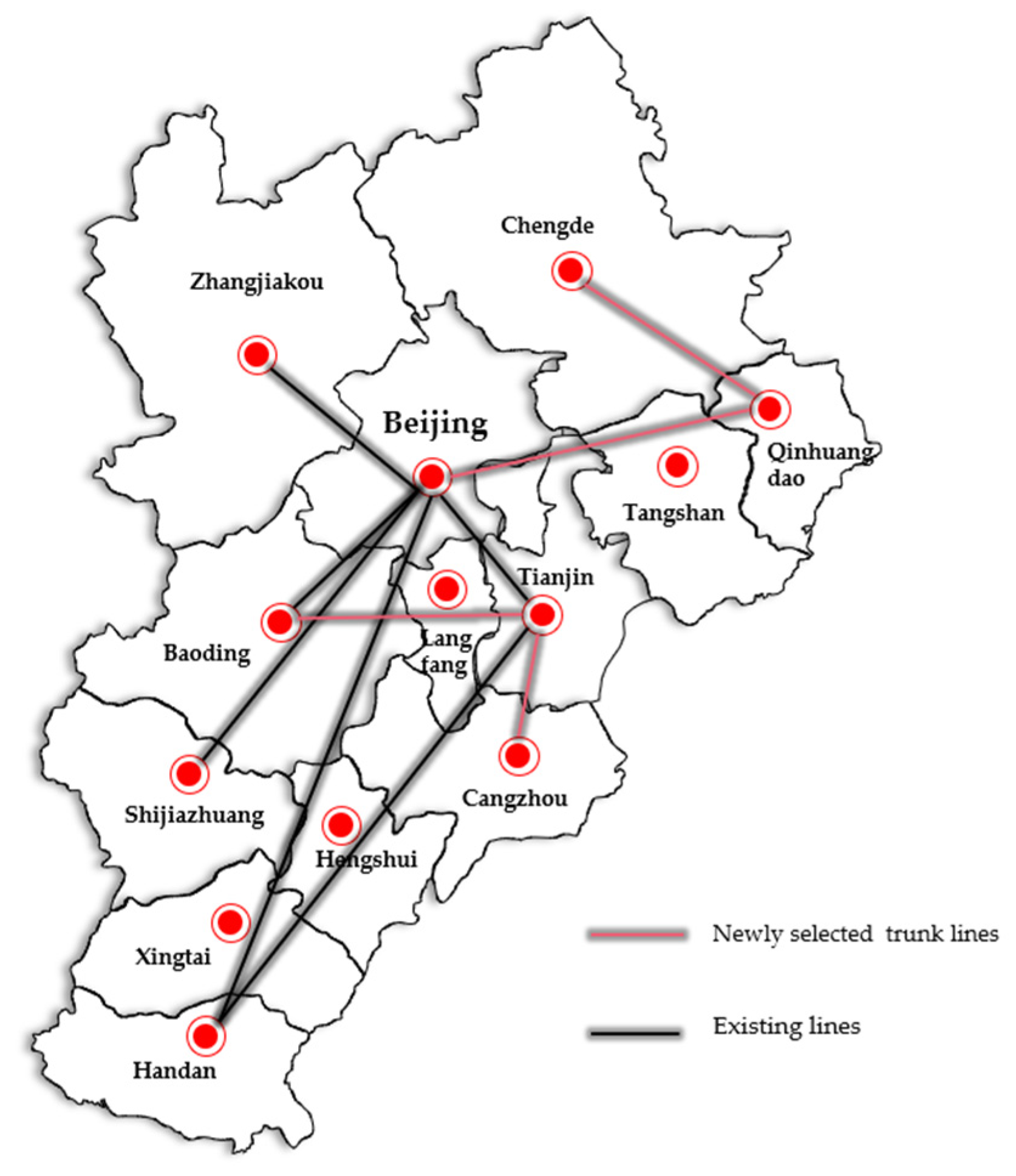
- (3)
- Combined with the development status of HSR network nodes and lines in urban agglomerations, a backbone selection model was constructed with the greatest urgency of the line. From the calculation results, it can be found that there are seven backbone lines in the Beijing–Tianjin–Hebei urban agglomeration, mainly covering eight secondary nodes, such as Beijing, Tianjin and Shijiazhuang. The line covers the existing lines, such as Beijing–Guangzhou, Beijing–Shanghai, Tianjin–Qinhuangdao and other major HSR lines in China. It basically covering the main development axes, such as Beijing–Tianjin, Beijing–Baoshi and Beijing–Tangshan, which can basically meet the railway transportation that attracts existing passenger flow. The four backbone lines of Beijing–Cangzhou, Beijing–Shijiazhuang-Baoding and Beijing–Tangshan selected in the new plan can take into account the passenger flow of the backbone line. At the same time, it realizes the role of driving and alleviating the operation of the branch line and realizes the backbone line as the core to accelerate the development of the internal traffic of the urban agglomeration and realize the construction goal of the hourly HSR.
- (4)
- The contribution of the adjusted main trunk line selection scheme. It can not only determine the layout of the railway network in the Beijing–Tianjin–Hebei urban agglomeration, alleviate the congestion of the branch passenger flow and ensure the stability of the operation but also improve the accessibility and coverage of the overall HSR network in the urban agglomeration. It provides direction and foreshadowing for the future urban spatial structure and economic development. In particular, when selecting the backbone line. This paper considers the importance of the node and the urgency of the line and innovatively uses the BDSCAN to comprehensively cluster the urban nodes to explore the potential development potential of the nodes. It is of surreal significance to supplement the branch lines and refine the line direction.
- (5)
- This paper has certain innovation and comprehensiveness in the method selection and factor consideration of the backbone line network planning of the urban agglomeration. However, due to the relatively high level of the selected 13 urban nodes, there are some limitations in the further site selection and feeder passenger flow distribution in the future. Considering the specific urban nodes at the county level and below, further refinement and supplement can be made in the node selection.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, F.; Li, Q.Y.; Yang, M. The impacts of high-speed rail on the transformation of resource-based cities in China: A market segmentation perspective. Resour. Policy 2022, 9, 78. [Google Scholar]
- Nurhidayat, A.Y.; Widyastuti, H.; Sutikno; Upahita, D.P. Research on Passengers’ Preferences and Impact of High-Speed Rail on Air Transport Demand. Sustainability 2023, 15, 3060. [Google Scholar] [CrossRef]
- Gu, H.Y.; Wan, Y.L. Airline reactions to high-speed rail entry: Rail quality and market structure. Transp. Res. Part A Policy Pract. 2022, 165, 511–532. [Google Scholar] [CrossRef]
- Wu, S.P.; Han, D. Accessibility of high-speed rail (HSR) stations and HSR–air competition: Evidence from China. Transp. Res. Part A Policy Pract. 2022, 166, 262–284. [Google Scholar] [CrossRef]
- Mattia, B.; Daniel, A. On the modal shift from motorway to high-speed rail: Evidence from Italy. Transp. Res. Part A Policy Pract. 2019, 137, 145–164. [Google Scholar]
- Suchithra, R.; Maximilian, P. Evaluating the substitutability of short-haul air transport by high-speed rail using a simulation-based approach. Transp. Res. Interdiscip. Perspect. 2022, 15, 100632. [Google Scholar]
- Liu, N.Y.; Zhang, Y.; Li, Y.X.; Wang, X.J. From city to urban agglomeration: Analysis of material metabolism characteristics and influencing factors in Beijing-Tianjin-Hebei. Ecol. J. 2022, 189, 1–11. [Google Scholar]
- Xu, J.M. Research on the coordinated development of transportation infrastructure and economy in Beijing-Tianjin-Hebei region. North China Financ. 2020, 11, 33–44. [Google Scholar]
- Wang, J.; Deng, Y.; Kumari, S.; Song, Z. Research on the Spatial Spillover Effect of Transportation Infrastructure on Urban Resilience in Three Major Urban Agglomerations in China. Sustainability 2023, 15, 5543. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, L.; Xu, Q.; Fu, J.; Lin, Y.; Sun, L.; He, S.; Yuan, S. A Comparative Analysis of Farmland Occupation by Urban Sprawl and Rural Settlement Expansion in China. Land 2022, 11, 1738. [Google Scholar] [CrossRef]
- Wang, H.; Zhan, M.Q. The impact of high-speed rail on accessibility and economic linkages in the Beijing-Tianjin-Hebei region. Geogr. Sci. 2021, 41, 1615–1624. [Google Scholar]
- Xu, Y.; Ou, G. Does High-Speed Railway Promote the Level of Human Capital an Empirical Analysis Based on Three Urban Agglomerations in China. Sustainability 2022, 14, 12631. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, K. Analysis of Spatial Differences and the Influencing Factors in Eco-Efficiency of Urban Agglomerations in China. Sustainability 2022, 14, 12611. [Google Scholar] [CrossRef]
- Li, X.Y.; Lu, Z.H. Quantitative measurement on urbanization development level in urban Agglomerations: A case of JJJ urban agglomeration. Ecol. Indic. 2021, 133, 108375. [Google Scholar] [CrossRef]
- Su, Q.Y.; Huang, C.C.; Xin, L.J. Interval Trend Rank method for grid node importance assessment considering new energy. Appl. Energy 2022, 324, 119647. [Google Scholar] [CrossRef]
- Mester, A.; Pop, A.; Mursa, B.-E.-M.; Greblă, H.; Dioşan, L.; Chira, C. Network Analysis Based on Important Node Selection and Community Detection. Mathematics 2021, 9, 2294. [Google Scholar] [CrossRef]
- Tian, X.J.; Liang, C.Y.; Feng, T.J. Dynamic Control Subarea Division Based on Node Importance Evaluating. Math. Probl. Eng. 2021, 11, 9923514. [Google Scholar] [CrossRef]
- Tiwari, S.; Sanjeev, K.J.; Ankit, S. Quantification of node importance in rain gauge network: Influence of temporal resolution and rain gauge density. Sci. Rep. 2020, 6, 9761. [Google Scholar] [CrossRef]
- Ji, F.; Shi, J.; Zhu, T.; Hu, X. Risk Assessment in the Industry Chain of Industrialized Construction: A Chinese Case Study. Buildings 2022, 12, 1688. [Google Scholar] [CrossRef]
- Liu, Z.M.; Qiu, H.; Guo, W.; Zhu, J.H.; Wang, Q.X. Node importance evaluation method for inter-domain routing network based on graph attention network. J. Comput. Sci. 2022, 65, 101885. [Google Scholar] [CrossRef]
- Ren, C.; Chen, B.; Xie, F.; Zhao, X.; Zhang, J.; Zhou, X. Understanding Hazardous Materials Transportation Accidents Based on Higher-Order Network Theory. Int. J. Environ. Res. Public Health 2022, 19, 13337. [Google Scholar] [CrossRef]
- Ma, Z.; Fan, M.; Su, J.; Ouyang, C.; Wu, M. Impact of Differential Leadership on Employee Zheng Chong Behavior: A Complex Network’s Perspective. Sustainability 2022, 14, 13238. [Google Scholar] [CrossRef]
- Blöcker, C.; Nieves Juan, C.; Rosvall, M. Map equation centrality: Community-aware centrality based on the map equation. Appl. Netw. Sci. 2022, 7, 56. [Google Scholar] [CrossRef]
- Claessens, M.T.; Van Dijk, N.M.; Zwaneveld, P.J. Cost optimal allocation of rail passenger lines. Eur. J. Oper. Res. 1998, 110, 474–489. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, R.F.; Shi, F. A line planning approach for high-speed railway network with time-varying demand. Comput. Ind. Eng. 2021, 160, 107547. [Google Scholar] [CrossRef]
- David, C.; Alicia, D.L.S.; Gilbert, L.; Juan, A.M. Integrated Railway Rapid Transit Network Design and Line Planning problem with maximum profit. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 1–30. [Google Scholar]
- Sharma, S.; Ram, S. Investigation of Road Network Connectivity and Accessibility in Less Accessible Airport Regions: The Case of India. Sustainability 2023, 15, 5747. [Google Scholar] [CrossRef]
- Liu, S.; Gao, H. The Self-Information Weighting-Based Node Importance Ranking Method for Graph Data. Entropy 2022, 24, 1471. [Google Scholar] [CrossRef]
- He, D.; Chen, Z.; Pei, T.; Zhou, J. The Regional and Local Scale Evolution of the Spatial Structure of High-Speed Railway Networks—A Case Study Focused on Beijing-Tianjin-Hebei Urban Agglomeration. ISPRS Int. J. Geo-Inf. 2021, 10, 543. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, F.; Lei, L. Dynamic Path Planning Based on Service Level of Road Network. Electronics 2022, 11, 3267. [Google Scholar] [CrossRef]
- Ding, R.; Fu, J.; Du, Y.; Du, L.; Zhou, T.; Zhang, Y.; Shen, S.; Zhu, Y.; Chen, S. Structural Evolution and Community Detection of China Rail Transit Route Network. Sustainability 2022, 14, 12342. [Google Scholar] [CrossRef]
- Lu, X.C. A Study of Beijing-Tianjin-Hebei Industrial Adjustment and Pollution Control from the Perspective of World-Class City Cluster. In Analysis of the Development of Beijing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 357–374. [Google Scholar]
- Deng, L.; Chen, H.; Zhang, L.J.; Li, X. Research on the High and New Technology Development Potential of China City Clusters Based on China’s New OTC Market. In Big Data–BigData 2018; Lecture Notes in Computer Science; Springer: Cham, Germany, 2018; Volume 10968, pp. 291–303. [Google Scholar]
- Fang, C.; Liu, X. Comprehensive measurement for carrying capacity of resources and environment of city clusters in central China. Chin. Geogr. Sci 2010, 20, 281–288. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.; Duan, X. Understanding Accessibility Changes from the Development of a High-Speed Rail Network in the Yangtze River Delta, China: Speed Increases and Distance Deductions. Appl. Spat. Anal. 2019, 12, 1011–1029. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd ACM International Conference on Knowledge Discovery and Data Mining (KDD), Oregon, Portland, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Schubert, E.; Koos, A.; Emrich, T.; Züfle, A.; Schmid, K.A.; Zimek, A. A framework for clustering uncertain data. Proc. VLDB Endow 2015, 8, 1976–1979. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Arlia, D.; Coppola, M. Experiments in Parallel Clustering with DBSCAN. In Euro-Par 2001 Parallel Processing. Euro-Par 2001; Lecture Notes in Computer Science; Sakellariou, R., Gurd, J., Freeman, L., Keane, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2150. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor 2009, 1, 10–18. [Google Scholar] [CrossRef]
- Limwattanapibool, O.; Arch-int, S. Determination of the appropriate parameters for K-means clustering using selection of region clusters based on density DBSCAN (SRCD-DBSCAN). Expert Syst. 2017, 34, e12204. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.; Zhang, S.; Jiang, X. Demand Response Transit Scheduling Research Based on Urban and Rural Transportation Station Optimization. Sustainability 2022, 14, 13328. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, H.T.; Deng, Y. Identification of influential nodes in complex networks: A local degree dimension approach. Inf. Sci. 2022, 610, 994–1009. [Google Scholar] [CrossRef]
- Wang, X. Optimization of Intercity Train Stop Scheme Based on Node Importance. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Li, Q.L.; Han, H.; Ma, Y.Y.; Zeng, Q.; Li, Q.L. Node Importance Evaluation Algorithm based on Gravity Model and Relative Path Number. Appl. Res. Comput. 2022, 39, 764–769. [Google Scholar]
- Raffaele, G.; Daniele, G.; Francesco, L.; Simona, E.; Rombo. Network Centralities and Node Ranking. In Encyclopedia of Bioinformatics and Computational Biology; Academic Press: Cambridge, MA, USA, 2019; pp. 950–957. [Google Scholar]
- Rodrigo, G.S.; M, R.O.; Lina, O. Theoretical derivation of interval principal component analysis. Inf. Sci. 2023, 621, 227–247. [Google Scholar]
- Colin, J.; Sergey, N. Gravity models and the Law of Large Numbers. Econ. Lett. 2022, 221, 110911. [Google Scholar]
- Gao, Y.; Wang, J. Study on urban spatial Interaction based on gravity model in Shanxi Province. Urban Archit. 2022, 19, 57–60. [Google Scholar]
- Liu, X. Research on Passenger Flow of Chengmianle Intercity Railway. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Zhao, J.; Xiao, Y.; Zhu, X.; Zhao, Y. A routing optimization method for emergency vehicles considering demand urgency. J. Harbin Inst. Technol. 2022, 54, 27–34. [Google Scholar]
- Xu, C.; Li, T.; Li, X.; Yang, G. Compaction Uniformity Evaluation of Subgrade in Highway Based on Principal Components Analysis and Back Propagation Neural Networks. Sustainability 2023, 15, 1067. [Google Scholar] [CrossRef]
- Han, X.; Armenakis, C.; Jadidi, M. Modeling Vessel Behaviours by Clustering AIS Data Using Optimized DBSCAN. Sustainability 2021, 13, 8162. [Google Scholar] [CrossRef]
- Xiao, T.; Wan, Y.; Jin, R.; Qin, J.; Wu, T. Integrating Gaussian Mixture Dual-Clustering and DBSCAN for Exploring Heterogeneous Characteristics of Urban Spatial Agglomeration Areas. Remote Sens. 2022, 14, 5689. [Google Scholar] [CrossRef]
- Liu, T.; Song, T.; Ou, Y.C.; Shi, F.Q. Research on target clustering and sorting technology based on DBSCAN algorithm. Technol. Wind 2022, 22, 65–67. [Google Scholar]




| Index | Degree Centrality | Closeness Centrality | Betweenness Centrality | Flow Betweenness Centrality | Economic Relations | Transportation Capacity | Passenger Railway-Mileage | |
|---|---|---|---|---|---|---|---|---|
| City | ||||||||
| BJ | 219 | 53.62 | 13 | 0.49 | 1478.44 | 5.75 | 1012.9 | |
| TJ | 270 | 5.12 | 11 | 0.15 | 129.82 | 1.82 | 278.82 | |
| SJK | 111 | 4.43 | 10 | 0.14 | 95.43 | 0.93 | 7.8 | |
| TS | 95 | 4.48 | 10 | 0.02 | 15.86 | 0.53 | 11 | |
| QHD | 85 | 2.79 | 10 | 0.07 | 1.04 | 0.48 | 6.2 | |
| HD | 105 | 10.74 | 10 | 0.07 | 36.94 | 0.94 | 1 | |
| XT | 56 | 5.17 | 9 | 0.05 | 3.5 | 0.29 | 13.2 | |
| BD | 40 | 0.17 | 9 | 0.01 | 6.29 | 0.75 | 8.5 | |
| ZJK | 6 | 0 | 2 | 0.01 | 0.28 | 0.69 | 4.9 | |
| CD | 6 | 0 | 2 | 0.02 | 2.83 | 0.45 | 3.2 | |
| CZ | 24 | 1.5 | 5 | 0.01 | 0 | 0.4 | 10.8 | |
| LF | 8 | 0 | 2 | 0.01 | 0.3 | 0.62 | 4.9 | |
| HS | 12 | 0 | 0 | 0 | 0 | 0.27 | 3 | |
| KMO Sampling Suitability Quantity | 0.725 | |
| Bartlett Sphericity Test | Approximate Chi-square | 158.586 |
| Degree of Freedom | 21 | |
| Significance | 0.000 | |
| Initialization Value | Extraction Rate | |
|---|---|---|
| Var00001 | 1 | 0.613 |
| Var00002 | 1 | 0.924 |
| Var00003 | 1 | 0.436 |
| Var00004 | 1 | 0.974 |
| Var00005 | 1 | 0.914 |
| Var00006 | 1 | 0.956 |
| Var00007 | 1 | 0.936 |
| Component | Initial Eigenvalue | Extract the Load Sum of Squares | ||||
|---|---|---|---|---|---|---|
| Grand total | Variance Proportion | Accumulative (%) | Grand Total | Variance Proportion | Accumulate (%) | |
| 1 | 5.755 | 82.221 | 82.221 | 5.755 | 82.221 | 82.221 |
| 2 | 0.947 | 13.524 | 95.746 | 0.000 | 0.000 | 0.000 |
| 3 | 0.231 | 3.294 | 99.040 | 0.000 | 0.000 | 0.000 |
| 4 | 0.034 | 0.490 | 99.530 | 0.000 | 0.000 | 0.000 |
| 5 | 0.021 | 0.302 | 99.832 | 0.000 | 0.000 | 0.000 |
| 6 | 0.010 | 0.143 | 99.975 | 0.000 | 0.000 | 0.000 |
| 7 | 0.002 | 0.025 | 100.000 | 0.000 | 0.000 | 0.000 |
| Index () | Degree Centrality | Closeness Centrality | Betweenness Centrality | Flow betweenness Centrality | Economic Relations | Transportation Capacity | Railway Passenger Turnover |
|---|---|---|---|---|---|---|---|
| Weight | 0.33 | 0.40 | 0.28 | 0.41 | 0.40 | 0.40 | 0.41 |
| City | BJ | TJ | SJZ | TS | QHD | HD | XT | BD | ZJK | CD | CZ | LF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Importance Value | 2.21 | 0.73 | 0.41 | 0.26 | 0.26 | 0.37 | 0.23 | 0.17 | 0.07 | 0.06 | 0.11 | 0.07 |
| BJ | TJ | SJZ | TS | QHD | HD | XT | BD | ZJK | CD | CZ | LF | HS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BJ | 0.00 | 67,435.35 | 3884.26 | 6199.29 | 475.94 | 696.74 | 319.76 | 3057.71 | 386.19 | 209.60 | 997.91 | 8650.94 | 59.52 |
| TJ | 67,435.35 | 0.00 | 396.84 | 1661.57 | 88.49 | 113.93 | 49.99 | 332.70 | 16.53 | 17.28 | 612.57 | 400.36 | 12.03 |
| SJZ | 3884.26 | 396.84 | 0.00 | 36.96 | 4.88 | 140.62 | 111.21 | 126.65 | 3.55 | 1.16 | 24.32 | 9.07 | 9.86 |
| TS | 6199.29 | 1661.57 | 36.96 | 0.00 | 52.09 | 12.10 | 5.10 | 22.25 | 2.49 | 7.31 | 20.84 | 24.54 | 0.90 |
| QHD | 475.94 | 88.49 | 4.88 | 52.09 | 0.00 | 1.87 | 0.76 | 2.35 | 0.34 | 1.21 | 1.98 | 1.54 | 0.11 |
| HD | 696.74 | 113.93 | 140.62 | 12.10 | 1.87 | 0.00 | 300.89 | 14.68 | 0.81 | 0.37 | 7.10 | 2.17 | 2.39 |
| XT | 319.76 | 49.99 | 111.21 | 5.10 | 0.76 | 300.89 | 0.00 | 7.88 | 0.37 | 0.67 | 3.21 | 0.99 | 1.32 |
| BD | 3057.71 | 332.70 | 126.65 | 22.25 | 2.35 | 14.68 | 7.88 | 0.00 | 0.74 | 0.24 | 5.78 | 3.65 | 0.73 |
| ZJK | 386.19 | 16.53 | 3.55 | 2.49 | 0.34 | 0.81 | 0.37 | 0.74 | 0.00 | 0.16 | 0.46 | 0.64 | 0.05 |
| CD | 209.60 | 17.28 | 1.16 | 7.31 | 1.21 | 0.37 | 0.67 | 0.24 | 0.16 | 0.00 | 0.85 | 1.24 | 0.05 |
| CZ | 997.91 | 612.57 | 24.32 | 20.84 | 1.98 | 7.10 | 3.21 | 5.78 | 0.46 | 0.85 | 0.00 | 4.53 | 1.17 |
| LF | 8650.94 | 400.36 | 9.07 | 24.54 | 1.54 | 2.17 | 0.99 | 3.65 | 0.64 | 1.24 | 4.53 | 0.00 | 0.20 |
| HS | 59.52 | 12.03 | 9.86 | 0.90 | 0.11 | 2.39 | 1.32 | 0.73 | 0.05 | 0.05 | 1.17 | 0.20 | 0.00 |
| Urban Hierarchy | Name of City Node |
|---|---|
| Primary City Node | BJ, TJ |
| Secondary City Node | SJZ, QHD, HD, TS, CD, CZ |
| Three-Level City Node | XT, HS |
| Four-Level City Node | BD, ZJK, LF |
| City | BJ | TJ | SJZ | QHD | HD | TS | CD | CZ | BD | Mean Value |
|---|---|---|---|---|---|---|---|---|---|---|
| region | 36,102.60 | 14,083.73 | 5935.1 | 1685.8 | 3636.6 | 7210.9 | 1550.3 | 3699.9 | 3954.3 | 10,799.14 |
| City | BJ | TJ | SJZ | QHD | HD | TS | CD | CZ | BD | Mean Value |
|---|---|---|---|---|---|---|---|---|---|---|
| Population | 2153.6 | 1373 | 1124.15 | 313.98 | 941.49 | 771.85 | 335.15 | 730.22 | 1154.63 | 1112.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Rong, W.; Liu, D. Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China. Sustainability 2023, 15, 6450. https://doi.org/10.3390/su15086450
Zhao J, Rong W, Liu D. Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China. Sustainability. 2023; 15(8):6450. https://doi.org/10.3390/su15086450
Chicago/Turabian StyleZhao, Jun, Wenyu Rong, and Di Liu. 2023. "Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China" Sustainability 15, no. 8: 6450. https://doi.org/10.3390/su15086450
APA StyleZhao, J., Rong, W., & Liu, D. (2023). Urban Agglomeration High-Speed Railway Backbone Network Planning: A Case Study of Beijing-Tianjin-Hebei Region, China. Sustainability, 15(8), 6450. https://doi.org/10.3390/su15086450






