Multiple Virtual Power Plants Transaction Matching Strategy Based on Alliance Blockchain

Abstract

Virtual power plants can aggregate distributed energy resources and interruptible loads in a region for coordinated regulation and unified transaction. However, with the diversification of competition in the electricity market, the distributed operation mechanism between multiple virtual power plants (multi-VPPs) has gradually become a research focus. Based on this, this paper proposes a new type of distributed transactions strategy between multi-VPPs, i.e., the transaction matching mechanism. A two-stage transaction model based on the transaction matching is constructed for multi-VPPs to participate in the day-ahead and intraday electricity trading markets. In the first stage, each VPP optimizes its own internal units’ output and external interaction power through a cooperative game; in the second stage, it is the transaction matching among multi-VPPs that can match the most suitable counterpart by flexible price setting to increase the benefits of all the VPPs. Considering the efficiency and security of blockchain technology, we choose to complete the transaction matching between multi-VPPs with the support of alliance blockchain technology to improve the speed of system solution.

1. Introduction

With a large number of distributed energy resources (DERs) connected to the grid, such as wind turbine (WT) and photovoltaic (PV) power generation [1], their intermittent nature not only poses a great challenge to the safe and stable operation of the grid [2] but also limits the flexibility to participate in market bidding due to the uncertainty of power generation forecasts [3]. A virtual power plant (VPP) can integrate distributed energy sources, energy storage systems (ESS), and interruptible loads (IL) in the region and conduct market trading and operation scheduling as a whole [4]. Meanwhile, a VPP can regulate the flexible resources in the system to compensate for the uncertainty of distributed power generation and adjust its optimization strategy according to internal and external demands to maximize economic benefits [5]. Therefore, a large number of research studies have been launched on the trading mechanism and coordination optimization of virtual power plants [6].

Among these studies, the trading mechanism of a VPP is the main research direction of most scholars. The power trading market is becoming more and more diversified and competitive, so a VPP should no longer focus only on its own bidding strategy [7] but should also fully consider the pricing and market behavior of the rest of its competitors [8]. Therefore, there is more and more research on the alliance and game mechanism between multiple virtual power plants (multi-VPPs) so as to make up for the shortcomings of the past single VPP participating in the market trading only as a price receiver. Ref. [9] studied the trading strategy of multi-VPPs participating in the power market by using the non-cooperative game method and proposed the concept of day-ahead intraday two-stage trading. However, it is not developed in the introduction, and the difference between the two stages is not clearly distinguished in the modeling. Ref. [10] chose the alliance game approach for the study of multi-VPPs, that is, multi-VPPs are jointly considered and the strategy of each VPP is formulated with the goal of maximizing the overall benefits; therefore, in order to maximize the benefit of each VPP itself, a suitable method of income distribution must be adopted, otherwise the coalition is unstable. In order to ensure that each VPP does not satisfy only its own interests in the alliance game, [11] we established a game algorithm with a cooperation-split rule. Firstly, VPPs that can be merged are merged according to the merging rule, taking the minimum utility function of the whole into account. Then, the coalition is split, with the objective of minimizing the utility function of each coalition after the split, and so on in a cycle until no new coalition can be formed. Ref. [12] conducted a multi-VPPs day-ahead dynamic pricing game model with real-time rolling coordinated optimization in the intraday stage. A two-layer game model with multi-VPPs is also proposed, and the two layers of the game iterate with each other to finally reach game equilibrium. However, the nested relationship between the two layers of the game makes the iterative speed slow and diffuse. It can be seen that the trading strategy among multiple virtual power plants has become a hot research topic nowadays, and it is necessary to choose an appropriate trading strategy in order to improve the overall benefit of virtual power plants. The game methods used in the previous literature are generally cooperative games, non-cooperative games, and master–slave games [13]; however, these methods have some limitations in terms of revenue distribution and solution speed [14]. In addition, these strategies do not classify the status of virtual power plants well, but rather, they trade uniformly. To our knowledge, there is no literature on the pricing mechanism among multi-VPPs.

In summary, to solve the limitations mentioned above, this paper establishes a two-stage game trading strategy for multi-VPPs based on the transaction matching mechanism, which is firstly proposed in this paper. In this trading strategy, priority is given to direct transactions between multiple VPPs in order to reduce the power supply pressure of the power grid and discard the monopoly position of the grid in the traditional model. At the same time, in order to improve the flexibility of trading among multi-VPPs and to set reasonable electricity prices to ensure the benefits of all VPPs, an electricity price game strategy is proposed for the first time in this paper. Each VPP can set the electricity price comprehensively, no longer accepting the high price of electricity from the grid. Because effective pricing involves the unified coordination of multi-VPPs in multiple regions, each node has a certain data processing capability and needs to grasp the global information. Therefore, we consider introducing blockchain technology to construct a multi-VPPs trading framework. This paper compares the current commonly used blockchains: private chain, public chain, and alliance chain [15]; it then chooses to use the alliance chain for multi-VPPs to participate in and complete the multiperiod unified transaction of the day-ahead market and intraday market of electricity. This can improve the lack of flexibility caused by full centralization and the security problems caused by decentralization. Finally, by setting different scenarios, the accuracy and rationality of the proposed method are verified. The main contributions are:

(1)

We firstly propose a transaction matching mechanism among multi-VPPs to make VPPs achieve a power balance through direct transactions among VPPs as much as possible. Moreover, the pricing update strategy of VPPs is designed to make VPPs have higher trading flexibility.

(2)

We introduce the alliance blockchain technology where each VPP node has a certain amount of computation, thus avoiding the traditional problem of large computations and improving the system efficiency.

(3)

We analyze the coordinated operation of multiple VPPs in multiple time scales and their market trading behavior.

This article is organized as follows: Section 2 focuses on the integrated carbon–electricity trading market for VPPs; Section 3 introduces the proposed multiple game model in this paper; Section 4 is the solution method of this paper; Section 5 performs the simulation analysis; and Section 6 draws conclusions.

2. Two-Stage Game Model

The first stage is a cooperative game among the units within the VPP, considering the lowest total cost of the VPP, while ensuring that the respective interests of each unit are not compromised [16]; the second stage is a game process among multiple VPPs, dividing all VPPs into power-shortage VPPs and power-surplus VPPs. Each VPP needs to fully consider the market price of electricity and the trading strategies of the remaining VPPs to formulate its own market behavior [17].

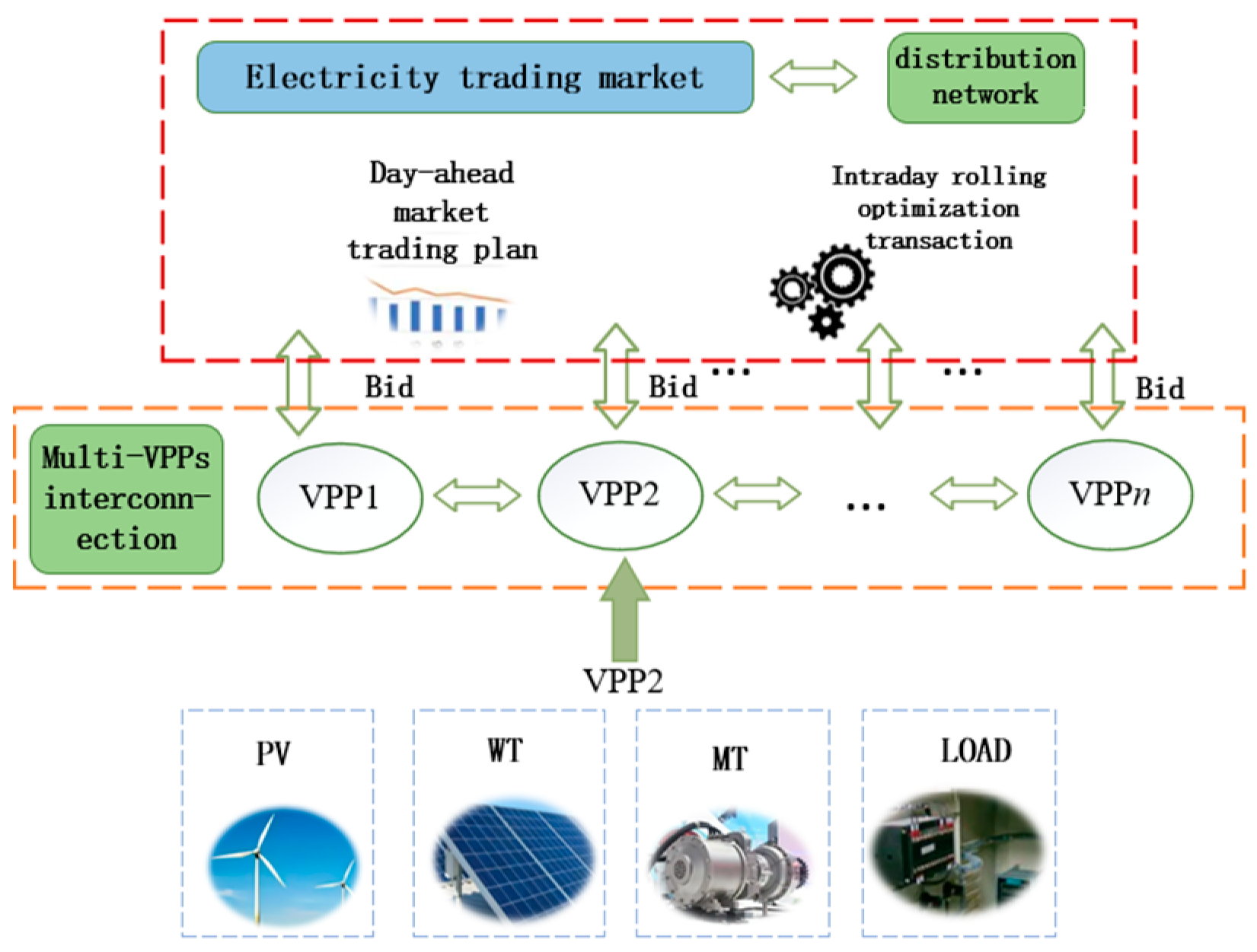
2.1. Multi-VPPs System Framework

Distributed energy resources cannot flexibly participate in power market transactions alone due to their uncertain output and small capacity [18], while a VPP can integrate all distributed energy resources in a region to flexibly formulate its trading strategy while ensuring maximum benefits. With the continuous improvement of VPP technology, more and more VPPs participate in market trading in a certain region, which also enables each VPP to have more trading options. Each VPP can set its own electricity price and is not limited to a single purchase or sale of electricity with the grid, which gives it greater incentive to participate. Figure 1 shows the structure of multi-VPPs unified trading.

• All stakeholders in the region, including wind power (WT), photovoltaic (PV), and various loads and micro gas turbines (MT), create their own power generation and consumption behavior through a cooperative game to minimize the total cost of the virtual power plant according to their own demand and forecast, while ensuring that the interests of each device are not compromised, and they then report the information to a VPP after the game is completed.
• Each VPP integrates the information of all units in its own region, calculates the interactive power with the outside, determines its initial offer, and then updates its trading price according to current trading status until it reaches the trading goal. After all the power-shortage VPPs have purchased the corresponding power or all the power-surplus VPPs have sold the corresponding power, the remaining power will be traded within the distribution network.
• Each VPP will submit its respective trading strategy to the power market for review and approval, and the trading will be completed after the review is approved.

2.2. Day-Ahead Two-Stage Game Model

2.2.1. First Stage of Game Model

The first stage is a cooperative game of all units in a VPP with the objective function of minimizing the total cost of the VPP. The final decision variable is its power generation and consumption strategy $e=\left[e_1^t,e_2^t,\dots ,e_n^t\right]$ at a certain time; then, the costs of all stakeholders in a VPP are:

$$\left\{\begin{array}{cc}{C}_{wt}=k_{wt}{e}_i^t+{\lambda }_{wt}\left(P_{wt}^t-e_i^t\right),\hfill & i\in n_{pv}\hfill \\ C_{pv}=k_{pv}{e}_i^t+{\lambda }_{pv}\left(P_{pv}^t-e_i^t\right),\hfill & i\in n_{pv}\hfill \\ C_{MT}=a_{MT}{\left(e_i^t\right)}^2+b_{MT}{e}_i^t+c_{MT},\hfill & i\in n_{MT}\hfill \\ C_{IL}=a_{IL}{\left(e_i^t\right)}^2+b_{IL}{e}_i^t,\hfill & i\in n_{IL}\hfill \end{array}\right.$$

(1)

where C is the cost of each unit; k is the generation cost of WT and PV, respectively; λ is the cost of wind and light cessation, respectively; P is the planned generation capacity at time t; $a_{MT}$, $b_{MT}$, and $c_{MT}$ are the cost factors of MT; $a_{IL}$ and $b_{IL}$ are the cut-off cost factors of IL.

Because the final result of the cooperative game is generally the maximization of the function value, the objective function of its cooperative game is established as:

$$\max F=\left(-\sum _{i=1}^{n_{wt}}{C}_{wt}-\sum _{i=1}^{n_{pv}}{C}_{pv}-\sum _{i=1}^{n_{MT}}{C}_{MT}-\sum _{i=1}^{n_{IL}}{C}_{IL}+Q\right)$$

(2)

$$Q={\lambda }_{\mathrm{load}}^t\left(L^t-e_{IL}^t\right)$$

(3)

where ${\lambda }_{load}$ is the price of electricity sold to the load at time t; Q is the income from selling electricity to the load; $L^t$ is the original scheduled electricity consumption of the load at time t; $e_{IL}^t$ is the amount of load that is cut off at time t.

Because the objective function of the first-stage game is convex, there is a game equilibrium point so that $F\left(e_i^{*},e_{-i}^{*}\right)\ge F\left(e_i,e_{-i}^{*}\right)$; then, the optimal strategy of the first-stage cooperation game is:

$$e^{\ast }=argmax\sum _{i\in n}F\left(e_i,e_{-i}\right)$$

(4)

where $e_i$ is the strategy choice of the ith DER in the VPP; $e_{-i}$ is the set of decisions of DERs other than participant i.

The total amount of electricity traded by a VPP in the day-ahead market can eventually be determined based on the results of the internal cooperative game, namely:

$$P_{VPP}^t=\sum _{i=1}^{n_{wt}}{e}_i^t+\sum _{i=1}^{n_{pv}}{e}_i^t+\sum _{i=1}^{n_{MT}}{e}_i^t-\left(L^t-\sum _{i=1}^{n_{IL}}{e}_i^t\right)$$

(5)

If $P_{VPP}^t$ is positive, it means that the VPP has surplus electricity and can sell electricity to the outside, which is defined as a power-surplus VPP; if $P_{VPP}^t$ is negative, it means that the VPP has insufficient internal electricity supply and needs to purchase electricity from the outside, which is defined as a power-shortage VPP.

The reason for participating in the cooperative game is to ensure that the economy after the game is better than that without participating in the game so that the game equilibrium point can be stable [19]. Therefore, after the cooperative game is completed, the overall income should be distributed to the game participants according to the Shapley value method [20]. The income $u_i\left(f\right)$ allocated to player i of the game is:

$$u_i(f)=\sum _{S\subseteq N\backslash \left\{i\right\}}\left[\frac{\left|S\right|!(n-|S|-1)!}{n!}(f(S\cup \{i\})-f(S))\right]$$

(6)

where $\left|S\right|$ is the total number of games in alliance S; $f\left(S\cup \left\{i\right\}\right)-f\left(S\right)$ is the marginal contribution of participant i to alliance S.

The Shapley value is actually the average expected value of marginal contribution of game player i in alliance S.

2.2.2. Second Stage of Game Model

After the first stage is over and each VPP has determined its market behavior, buying or selling electricity, it enters the second stage of the game between multi-VPPs.

In view of the common deficiency of game methods among multi-VPPs in previous studies, that is, VPPs can only be used as price receivers to formulate their own power purchase and sale strategies based on current electricity prices, in this paper, we therefore design a game strategy based on the transaction matching mechanism between buyers and sellers so that virtual power plants can set their own electricity prices based on their own power generation and consumption, as shown in Figure 2. Firstly, all VPPs calculate initial prices according to their own situation, at which time the selling price of all power-surplus VPPs and the purchasing price of all power-shortage VPPs are ranked from the lowest to highest. The lowest selling price ${\lambda }_{\min ,s}$ and the highest purchasing price ${\lambda }_{\max ,p}$ are selected as the optimal quotation. If ${\lambda }_{\min ,s}>{\lambda }_{\max ,p}$, as is shown in Figure 2a, both the purchase and sale of electricity meet the conditions for transaction matching. Then, they can reach a deal in which the final trading price is the middle value of the quotation mentioned above, and the trading electricity is the smaller value of the planned trading electricity of both parties. For the remaining virtual plants, they need to update their own quotations for the next round based on the current round’s best price so that they can participate in the trade matching. Similarly, if no VPP meets the trade matching condition in this round, as is shown in Figure 2b, a VPP will reformulate its own trade quotation according to the following formula based on the best quotation in the last round.

$$\left\{\begin{array}{l}{\lambda }_s(k)={\lambda }_s(k-1)-\frac{P_{VPPj,k}^t}{{\displaystyle \sum _j^{N_S}{P}_{VPPj,k}^t}}\left[{\lambda }_s(k-1)-{\lambda }_{\min ,s}(k-1)\right]\hfill \\ {\lambda }_p(k)={\lambda }_p(k-1)+\frac{P_{VPPi,k}^t}{{\displaystyle \sum _i^{N_p}{P}_{VPPi,k}^t}}\left[{\lambda }_p(k-1)-{\lambda }_{\max ,p}(k-1)\right]\hfill \end{array}\right.$$

(7)

where k is the number of rounds of aggregation performed. ${\lambda }_s$(k) and ${\lambda }_p$(k) are selling price and purchasing price in round k.

The adjustment factor in the equation is the ratio of the pre-trading volume of a VPP in the kth round to the total volume of the same type of trade, respectively.

If there is more than one VPP quote similarly in the process of one round of trading, which is the best quotation, they can all enter the current round of transaction matching. The reported trading power is ranked in order of high to low, of which the higher power will be prioritized for transaction matching until there is no tradable power and the current round of transaction matching ends.

In addition, the completion of trading between multi-VPPs requires the payment of a cross-grid fee to the grid. At the same time, the trading is matched on the blockchain’s platform, so a block fee must be paid to the blockchain recorder. The more rounds of trading experienced, the higher the corresponding block fee cost will be. Moreover, under the transaction matching mechanism, this additional cost is shared equally between the buyer and seller. Therefore, it can be concluded that the income of electricity sales for power-surplus VPPj is:

$$u_{vppj}=\sum _{i=1}^{N_p}{\lambda }_{ji}\cdot P_{ji}^t+d_p\cdot \left(P_{VPPj}^t-\sum _{i=1}^{N_p}{P}_{ji}^t\right)-\frac{1}{2}\sum _{i=1}^{N_p}{\lambda }_{ser}\cdot P_{ji}^t$$

(8)

The cost of electricity purchase for power-shortage VPPi is:

$$u_{vppj}=\sum _{i=1}^{N_s}{\lambda }_{ji}\cdot P_{ji}^t+d_p\cdot \left(P_{VPPj}^t-\sum _{i=1}^{N_s}{P}_{ji}^t\right)+\frac{1}{2}\sum _{i=1}^{N_s}{\lambda }_{ser}\cdot P_{ji}^t$$

(9)

where ${\lambda }_{ji}$ is the final trading price between VPPj and VPPi; $P_{ji}^t$ is the volume of electricity traded between VPPj and VPPi; N_p and N_s are the number of power-surplus VPPs and power-shortage VPPs, respectively; d_p and d_s are the prices for electricity purchased and sold by the distribution network to VPPs, respectively, and the relationship between them needs to satisfy d_p < d_s.

2.2.3. Constraint Condition

• MT output and climbing constraint

$$0\le e_{MT}^t\le P_{MT}^{\max }$$

(10)

$$P_{MT}^{\mathrm{down}}\le \left|e_{MT}^t-e_{MT}^{t-1}\right|\le P_{MT}^{up}$$

(11)

where $P_{MT}^{max}$ and $P_{MT}^{min}$ are the upper and lower limits of MT unit output, respectively; $P_{MT}^{down}$ and $P_{MT}^{down}$ are the downward and upward climbing power of the MT unit, respectively.

2.

IL cut-off volume and duration constraints

$$0\le e_{IL}^t\le {\eta }_{\max }{I}_L^t$$

(12)

$$\sum _{t=1}^T{\theta }_{IL}^t\le T_{\max }$$

(13)

where ${\eta }_{\max }$ is the maximum cut-off rate of IL; ${\theta }_{IL}^t$ is the cut-off state of IL at moment t, and 1 means there is a cut-off, but 0 means there is no cut-off.

3.

The operating constraints of the renewable energy units are the same as those of the conventional model and are not repeated in this paper.

2.3. Intraday Trading

In the intraday trading phase, since the forecast results of wind and light generation as well as load will be more accurate, it is only necessary to trade them with the generation deviation of the day-ahead phase at this period. Therefore, the game model in the first stage is the same as that in the day-ahead stage. It only needs to update the prediction data and formulate the latest strategy. However, the power of a VPP’s external interaction has changed, so it is necessary to subtract the trading power of the day-ahead stage so that the forecast deviation can be compensated, namely:

$$P_{VPP}^{RT}={\left[\sum _{i=1}^{n_{wt}}{e}_i^t+\sum _{i=1}^{n_{pv}}{e}_i^t+\sum _{i=1}^{n_{MT}}{e}_i^t-\left(L^t-\sum _{i=1}^{n_{IL}}{e}_i^t\right)\right]}^{RT}-P_{VPP}^{DA}$$

(14)

The constraint conditions are the same as those in the day-ahead stage. In addition, in the intraday phase, VPPs need to meet opportunity constraints.

Considering the reliability and security of the system, additional chance constraints are needed to ensure that the probability of reaching power balance after considering the prediction error is above a certain confidence level, namely:

$$P\left[{\displaystyle \sum _{i=1}^{n_{WT}}\left(e_i^t-{\delta }_i^t\right)}+{\displaystyle \sum _{i=1}^{n_{pv}}\left(e_i^t-{\delta }_i^t\right)}+{\displaystyle \sum _{i=1}^{n_{MT}}{e}_i^t}\ge P_{VPP}^t+{\displaystyle \sum _{i=1}^{n_{IL}}\left(L^t-e_i^t\right)}\right]\ge \alpha$$

(15)

where ${\delta }_i$ is forecast errors of wind, photovoltaic, and load, as obtained by the Monte Carlo simulation method with random sampling. The Weibull distribution model is generally chosen for wind speed prediction, while light intensity usually obeys the Beta distribution model. After getting the wind speed and light intensity prediction, the WT and PV output prediction can be obtained according to the corresponding power calculation formula; the load prediction is relatively more complicated and has many influencing factors, so the method of artificial neural network is chosen to train the historical data of similar days to predict the load situation of each time period of that day. The prediction errors of all three can be described by a normal distribution with an expectation of 0, namely: ${\delta }_i^t~N(0,{\sigma }_i^{t^2}),i\in \left\{wt,pv,load\right\}$.

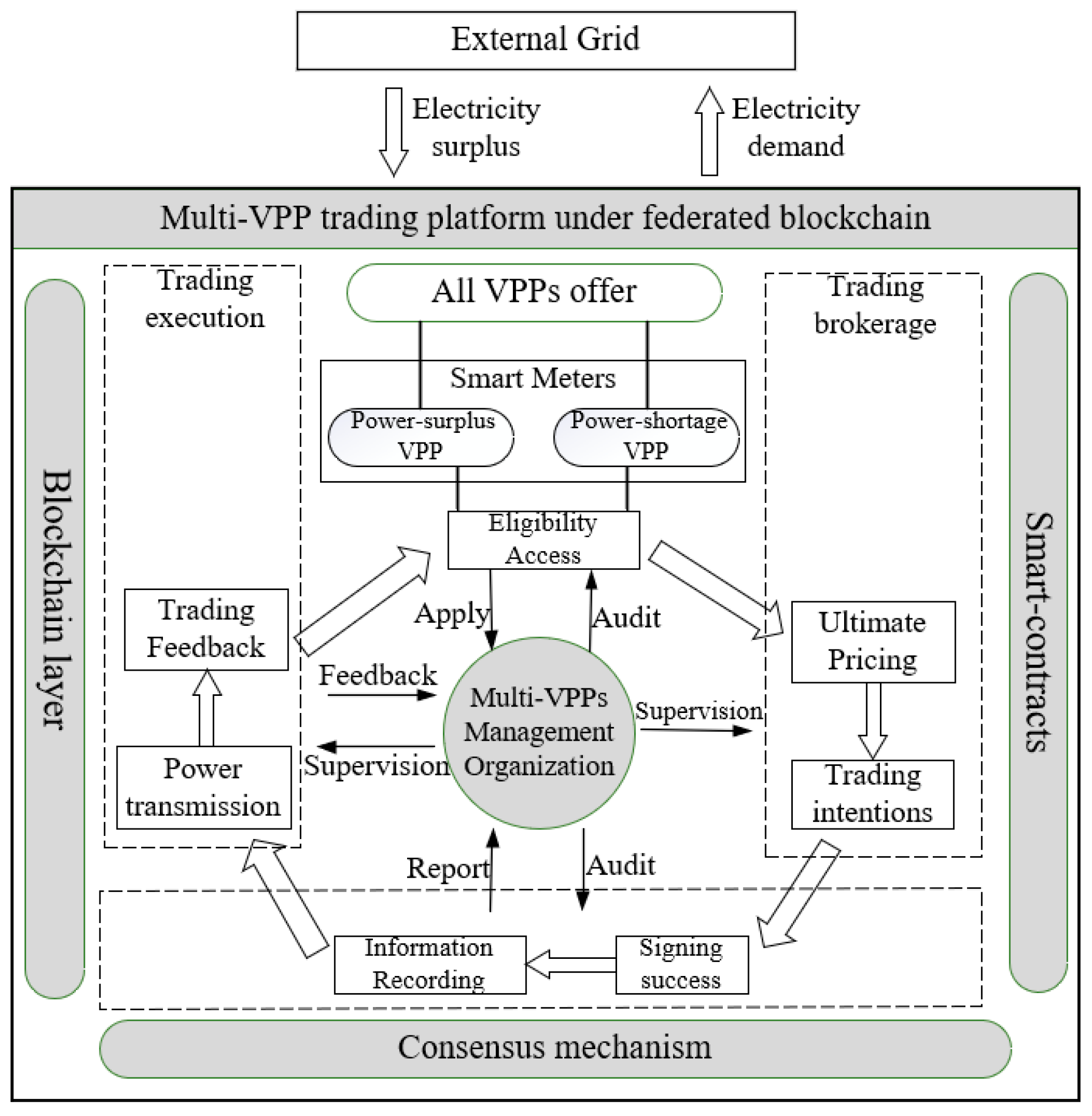
3. Transaction Process under Alliance Blockchain

Blockchain is an emerging technology similar to a distributed ledger, which is a peer-to-peer distributed management technology connected by a series of data blocks, combining smart contracts, private key encryption, consensus algorithms, and massive data storage to ensure the security and stable operation of information within the block, and has obvious advantages for dealing with decentralized and multi-regional coordination [21]. According to edge computing capability, the original computation that needs to be centralized is handed over to each node, which has the characteristic of “decentralization”. Blockchain technology applied in the field of multi-regional trading can ensure that any node in the system can access and read the global trading information, grasp the market behavior and trustworthiness of all interested parties, and choose their own trading partners [22]. Therefore, this is a great fit with the multi-VPPs trading strategy in this paper, which improves trading efficiency and ensures information security [23].

As shown in

Table 1. Classification of blockchain.

Evaluation Dimension	Public Chain	Alliance Chain	Private Chain
Node Access	No license required	License required	License required
Read Permissions	All nodes	All nodes	Central node only
Modify Permissions	All nodes	Pre-selected Nodes	Central node only
Centrality	Decentralized	Weakly centralized	Fully centralized
Efficiency	Low	Higher	Low
Security	Low	Higher	High

, the blockchains commonly used at present are classified into three types: public chains, private chains, and alliance chains. The public chain is the earliest and most commonly used blockchain, characterized by a completely public and decentralized blockchain, which leads to the lowest security among the three; the private chain still emphasizes the importance of the central node, such as the traditional centralized model, and all information is supervised by the central node; the alliance chain combines the advantages of the above two chains and can achieve weak centralization but not complete decentralization. Any node in the blockchain can grasp the global information under the supervision of pre-selected nodes, and the security and efficiency are guaranteed. Therefore, this paper introduces an alliance blockchain to complete the unified trading among multi-VPPs. Moreover, the alliance blockchain has the following characteristics:

• Weak centralization. For multi-regional VPPs coordinated trading, if fully decentralized, each VPP will set its own electricity price and trading behavior with the goal of maximizing its own economic benefits. Similarly disadvantageous, full centralization brings a large amount of computation to the central node and reduces the efficiency of the system. Therefore, this paper establishes a multi-VPPs management organization as a pre-selected node, whose role is to review node qualifications, supervise the entire transaction, write information and provide follow-up feedback.
• Each VPP in the alliance blockchain can join the blockchain as a node by the consensus mechanism and participate in the block writing process after the review of the preselected node. Likewise, each VPP can read the block data, which is convenient for multi-VPPs to grasp the trading information of other subjects and make their own correct gaming choices.
• Smart contract. On the platform of a blockchain, after the trading is completed between multi-VPPs, the trading settlement can be automatically executed on the smart contract using electronic signature, thus improving efficiency.

As shown in Figure 3, the process of transaction matching for multi-VPPs under the alliance blockchain is as follows:

• Firstly, each VPP internally determines its own market trading behavior and electricity price after gaming, joins the blockchain platform through a consensus mechanism, and uploads its own trading information through smart meters to build a global trading information database. At this point, the multi-VPPs management organization is required to audit its historical creditworthiness as well as power generation capacity, and after the audit is passed, it obtains an electronic signature to register as a block.
• Secondly, under the supervision of the multi-VPPs management organization and according to the trading aggregation mechanism in this paper, direct trading is completed between VPPs, and after reaching the trading, both parties provide their own electronic signatures, sign smart contracts and obtain keys, and the multi-VPPs management organization stores all the smart contracts.
• Finally, both parties of the trading only need to carry out power transmission according to the contract requirements. If there is a breach of contract during the execution of the trading, the multi-VPPs management organization will record it on the record and deduct some of its credit scores. In the future, scrutiny in the future qualification access reviews will be strengthened.

For all VPPs participating in blockchain unified transactions, they are required to receive creditworthiness scores to judge their contract performance ability. For a power-shortage VPP, if the actual power required is less than the contracted power and the deviation between the two is beyond a certain range, it will affect the power sales income of the VPP with which it signed the smart contract, and it will need to pay a certain compensation to the VPP and deduct a certain credit score. Similarly, for a power-surplus VPP, if the actual electricity sold is less than the contracted electricity, and the deviation between the two is beyond a certain range, the corresponding power-shortage VPP needs to purchase additional electricity from the grid, which increases its cost, so it also needs to deduct a certain credit score and pay compensation. In addition, if the actual power is greater than the contracted power, the excess part can receive the grid quotation and trade with the grid so as to obtain more income, without default.

Then, the credit score of VPPj in the kth trading is:

$$H_j^k=\left\{\begin{array}{c}100,\frac{P_{{VPP}_j}^k-E_j^k}{P_{VPPj}^k}\le 0.2\\ 100\left(1-\beta \frac{P_{VPPj}^k-E_j^k}{P_{VPPj}^k}\right),\frac{P_{VPPj}^k-E_j^k}{P_{VPPj}^k}>0.2\end{array}\right.$$

(16)

where $E_j^k$ is the actual traded electricity of VPPj in the kth trading; $\beta$ is the credibility factor.

4. Solving Method

Due to the presence of nonlinear terms in the cooperative game model and constraints for each unit within the upper single virtual power plant, it is a nonlinear convex optimization problem. To facilitate the solution, this paper chooses to use a genetics algorithm to solve the optimization problem in the first stage. After obtaining the trading strategies of all the VPPs in that time period, the second stage of the transaction matching game is conducted at the same time. The two sides of the VPPs that reach the trading intention withdraw from the game process, and the remaining VPPs update their pricing strategies based on this price and enter a new game stage until all transactions are completed.

5. Case Study

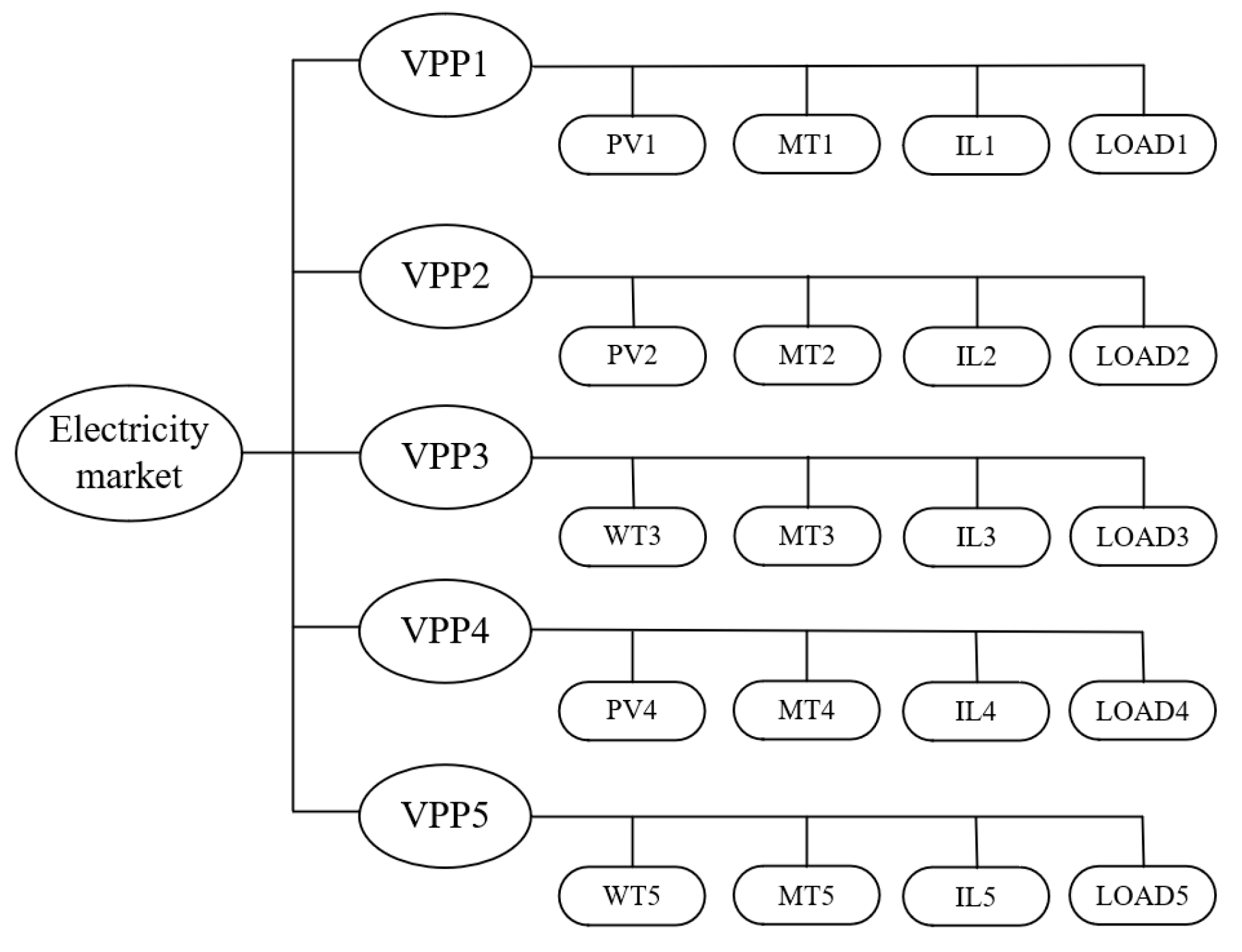
5.1. Illustrations

To verify the reliability of the proposed method in this paper, a multi-VPPs system consisting of five VPPs is set up, as shown in Figure 4. The price of electricity sold by the distribution network to a VPP is stepped, i.e., d_s = 1.2 CNY/MW during the peak of electricity consumption period (9:00–12:00; 18:00–22:00) and 1.0 CNY/MW at all other moments; the price of electricity purchased from a VPP by the distribution network is a fixed value of d_p = 0.4 CNY/MW. Therefore, the quoted price as well as the trading price between VPPs must be guaranteed to be within the interval [0.4, 1] CNY/MW. The integrated service charge cost λ_ser = 0.03 CNY/MW.

Firstly, after each VPP determines its own transaction strategy, the blockchain coordination center uses the method proposed in this paper to aggregate the transactions among multiple VPPs. Secondly, the overall transaction results of all VPPs can be concluded by observing the convergence process. Finally, the effectiveness of this strategy is verified by comparing the benefits of this paper’s method with the traditional method as well as the speed of solving.

5.2. Analysis of Simulation Results

5.2.1. Optimization Results in the First Stage

Firstly, the CPLEX solver is used to solve the first-stage optimal dispatch problem. According to the internal cooperation game of the VPP in the first stage, the optimal output results of its internal units can be obtained. Taking VPP1 as an example, the scheduling results of its units are shown in Figure 5 and Figure 6, and the same is true for other VPPs. Because VPP1 contains PV generation, there is no light during the 22:00–5:00 h, so all the internal electricity is provided by the MT at this time, and the shortfall electricity needs to be purchased from outside. Moreover, since the electricity price is not at its peak at this time, IL does not need to call too much and reduce the load demand; between 5:00 and 9:00, PV generation gradually rises, and at this time, in order to promote the renewable resources consumption, the pressure on the micro gas turbine units to supply electricity is reduced, so most of the electricity demand is provided by PV. The demand for electricity from the load at this stage also rises significantly, so the call of IL shows an upward trend at this stage; between 9:00 and 16:00, the light intensity is the highest, and the PV output reaches the peak. Since the total load in VPP1 is small, the load demand can be met by photovoltaic supply alone, so the output of MT reaches valley. VPP1 can sell the surplus electricity during the peak electricity price period to improve the benefits; between 16:00 and 21:00, the photovoltaic output is 0, but the load is about to reach the peak. At this time, MT units are required to take the full pressure of the supply. Similarly, the number of IL calls have reached the highest at this stage. Although the electricity price is at its peak at this time, VPP1 has to purchase power from external so that it can meet its internal demand.

After the above analysis, as well as the unit dispatch results shown in Figure 5 and Figure 6, the expected trading electricity quantity of VPP1 in the day-ahead trading market at each time can be derived from Equation (5) and is shown in Figure 7. It can be seen that at different times, different VPPs show different trading behaviors, which not only can sell electricity to the outside but can also purchase electricity from the outside. When $P_{VPP}^t>0$, i.e., the curve is above the x-axis, it means that the VPP sells electricity to the outside as a power-surplus VPP, and when $P_{VPP}^t<0$, i.e., the curve is below the x-axis, it means that the VPP purchases electricity from the outside as a power-shortage VPP. From Figure 8, it can be seen that less electricity is traded in the intraday trading market because, as the forecast value is updated, the amount of electricity interacted between a VPP and external will also change, and only the deviation is traded in the intraday trading, i.e., it is supplementary to the trading in the day-ahead phase.

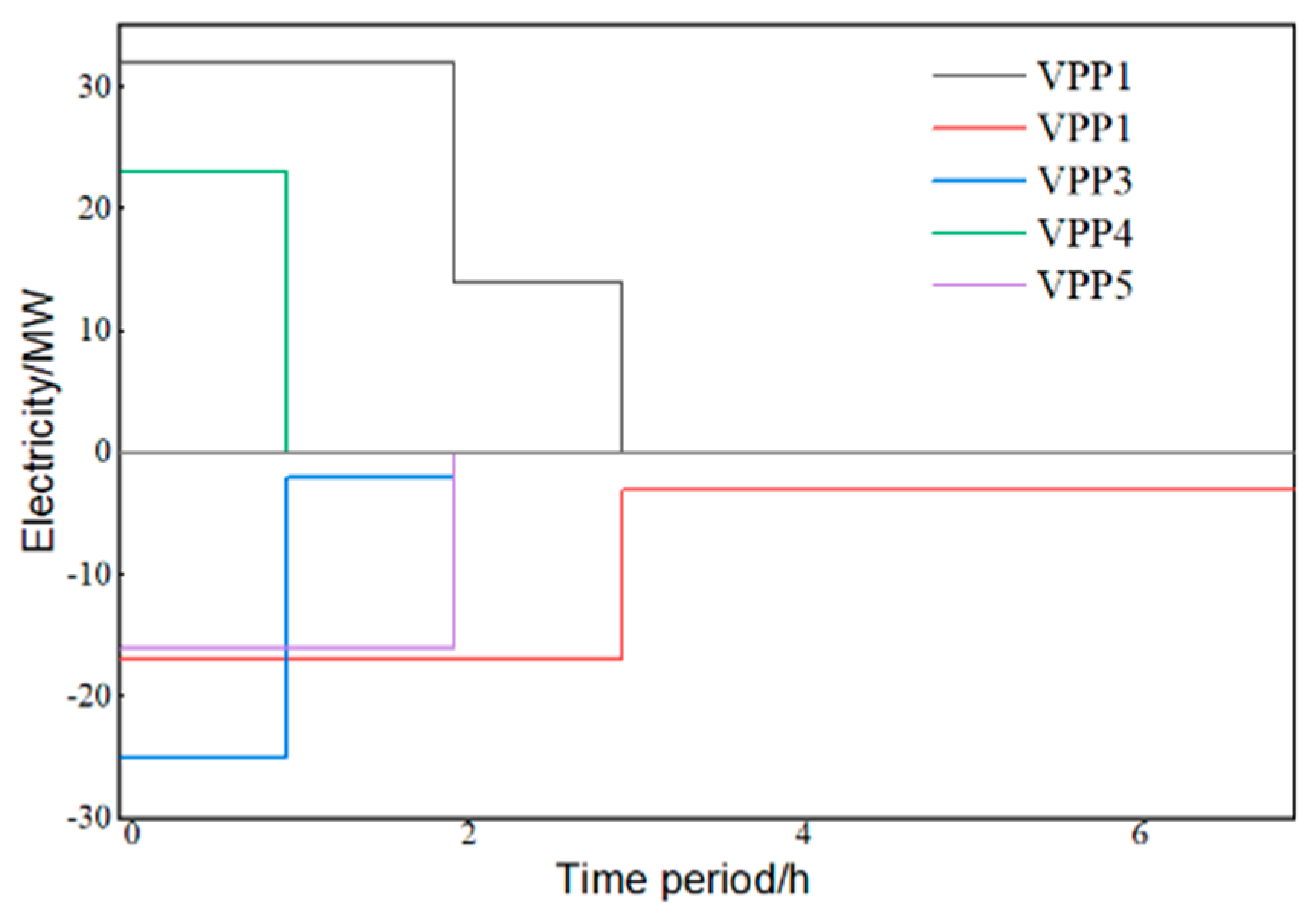
5.2.2. Analysis of the Transaction Matching Process

Taking the day-ahead transaction matching process at t = 12 as an example, Figure 9 shows the convergence process of the trading power variation among VPPs. At the beginning, each VPP reports its expected total power of trading to the multi-VPPs management organization in the blockchain and makes an initial quotation, as shown in

Table 2. Trading information of each VPP.

VPP	The First Round		The Second Round
	Expected Trading Power (MW)	Trading Quotation (CNY/MW)	Expected Trading Power (MW)	Trading Quotation (CNY/MW)
VPP1	32	0.82	32	0.82
VPP2	−17	0.71	−17	0.71
VPP3	−2	0.72	−2	0.72
VPP4	0	0	0	0
VPP5	−16	0.72	−16	0.72

. At this time, VPP1 and VPP4 are power-surplus VPPs selling electricity to the outside; VPP2, VPP3, and VPP5 are power-shortage VPPs purchasing electricity from the outside. The price of VPP4 is lower than that of VPP1, so ${\mathit{\lambda }}_{\mathit{min},\mathit{s}}$ is chosen to be 0.85; the price of VPP3 is higher than that of VPP2 and VPP5, so ${\mathit{\lambda }}_{\mathit{max},\mathit{p}}$ is chosen to be 0.72. Therefore, in the first round of transaction matching, the two sides of the trading are VPP3 and VPP4, respectively, and the traded electricity is 23 MW.

After the first round of matching, each VPP redetermines its own quotation for this round according to Equation (7), and the updated VPP market behavior is also shown in Table 2. Since VPP3 has been selected as the best quotation in the previous round of matching, its quotation remains unchanged. Meanwhile, the quotation of VPP2 and VPP5 have changed to 0.71 and 0.72, respectively, so ${\lambda }_{max,p}$ is chosen to be 0.72, and both corresponding power-shortage VPPs are entered into this round of transaction matching. After sorting by power, VPP5—with more expected trading power—will trade firstly. In this round of matching, there is only one power-surplus VPP left in the system, VPP1, whose quotation is updated to 0.82 and enters the current round of transaction matching.

By analogy, we can finally obtain the trading behavior of all the VPPs at the moment t = 12, as shown in

Table 3. Trading behavior of each VPP at t = 12.

Matching Round	Trading Participants	Trading Power (MW)	Trading Price (CNY/MW)
1	VPP4–VPP3	23	0.785
2	VPP1–VPP3	2	0.77
	VPP1–VPP5	16	0.77
3	VPP1–VPP2	14	0.8
4	Distribution network–VPP5	−16	0.72

. Since all the power-surplus VPPs in the system have already finished trading their excess power, the transaction matching is over. However, VPP2 still needs to buy 3 MW power from outside at this time, so it can only choose to trade with the grid at a price of 1.2, and its trading cost is much higher than the direct trading between VPPs. Therefore, all VPPs will improve the rationality of their own quotations and participate in direct trading between VPPs as much as possible. Thus, the effectiveness and convergence of the transaction matching strategy are verified.

5.2.3. Comparative Analysis of Methods

In order to fully validate the economy and efficiency of the proposed multi-VPPs transaction matching mechanism considering the alliance blockchain in this paper, four different scenarios are simulated for comparative validation. Scenario 1: Using alliance blockchain technology, multiple VPPs determine their respective market behaviors through a non-cooperative game model to maximize their respective benefits; this model cannot set electricity prices. Scenario 2: Using alliance blockchain technology, multi-VPPs determine their respective market behaviour through a cooperative game model to maximize all of the benefits of the multi-VPPs; this model also cannot set electricity prices. Scenario 3: Using the transaction matching mechanism proposed in this paper to conduct multi-VPPs trading under the alliance blockchain technology, each VPP can set its own quotation. Scenario 4: Using the transaction matching mechanism proposed in this paper but without using blockchain technology.

• Economic analysis

As can be seen from

Table 4. Multi-VPPs system trading benefits in each scenario.

VPP	Scenario 1	Scenario 2	Scenario 3
VPP1	173,684	190,122	190,936
VPP2	155,389	175,638	157,256
VPP3	177,529	180,537	187,235
VPP4	186,239	195,891	217,439
VPP5	142,234	179,025	147,682
Total	835,075	921,213	900,548

, in Scenario 1, both the overall trading benefits of the multi-VPPs system and the benefits of each VPP are reduced compared with the transaction matching mechanism proposed in this paper. This is because in the non-cooperative game model, the electricity quantity traded with the grid is also taken as a decision variable, so any VPP will trade with the grid in each trading period; trading with the grid will lead to lower benefits. In Scenario 2, the overall benefits of the virtual power plant group are greater than that of Scenario 3 by 20,665 CNY. This is because the goal of the cooperative game is to maximize the overall benefits. However, the benefits of some VPPs are much lower than Scenario 3, so the benefits of each VPP are not guaranteed. It can be seen that the transaction matching mechanism proposed in this paper can improve the benefits of each VPP while ensuring that the overall benefits of the system are not affected, reflecting the economic advantage of this method.

2.

Efficient analysis

The difference between Scenario 3 and Scenario 4 is whether to use the alliance blockchain. As can be seen from

Table 5. Multi-VPPs system trading benefits and solving time.

Scenario	Trading Benefits (CNY)	Solving Time (s)
Scenario 3	900,548	31.8
Scenario 4	853,287	65.2

, the overall benefits increase 47,261 CNY with the use of the alliance blockchain because, for the previous conventional centralized algorithm, each VPP needs to pay an additional fee to the centralized operator, thus ensuring the operator’s benefits. Although a certain record fee is also required to be paid to the multi-VPPs management organization with the blockchain technology, this is very small compared with the former. The blockchain technology can decompose the problems that need to be handled in a centralized way into several subproblems for distributed computing, so it can greatly speed up the solving time, which is more than twice as fast, as shown in the table below. This shows that the distributed model can greatly improve the computing efficiency.

6. Conclusions

In this paper, we first construct a two-stage trading model for multi-VPPs based on the transaction matching mechanism. The first stage is a cooperative game model for each unit within the VPP, with the objective of maximizing the overall benefit of the VPP to determine the respective power output so as to derive the external trading power of the VPP. In the second stage, each VPP sets the initial quotation according to its own market behavior and gradually updates the quotation according to the transaction matching mechanism until the end of the trading. Through simulation analysis, the following conclusions are obtained:

• Compared with other traditional gaming methods, the transaction matching strategy proposed in this paper can ensure that the overall benefits of the multi-VPPs group are maximized while ensuring that the benefits of each VPP are not compromised. The reason is that the weight of direct transactions among multi-VPPs is increased. Moreover, it can flexibly set the price and select the trading partners to improve the flexibility of trading.
• The comparison of the solution speed shows that the proposed method in this paper can greatly improve the efficiency of the system. Using the blockchain technology, the original centralized problem can be decomposed into several problems, and each VPP can conduct distributed computing to improve the system solving speed and ensure the normal operation of the system.
• In this paper, multi-VPPs can participate in the day-ahead trading market and the intraday trading market. The simulation example proves that this method can be applied to the short time scale of intraday trading and compensate for the day-ahead trading to improve the system accuracy.

With the national emphasis on the low-carbon operation of power systems to reduce pollutant emissions, the subsequent research work in this paper will focus on the low-carbon coordinated operation of multi-VPPs. The strategy proposed in this paper does not take the network constraints into account in the energy trading process. These limitations will be further investigated in our future work.