Eco-Efficiency and Its Evolutionary Change under Regulatory Constraints: A Case Study of Chinese Transportation Industry
Abstract
1. Introduction
2. Literature Review
2.1. Performance Evaluation of the Transportation Industry
2.2. Eco-Efficiency Evaluation Based on DEA
3. Methodology
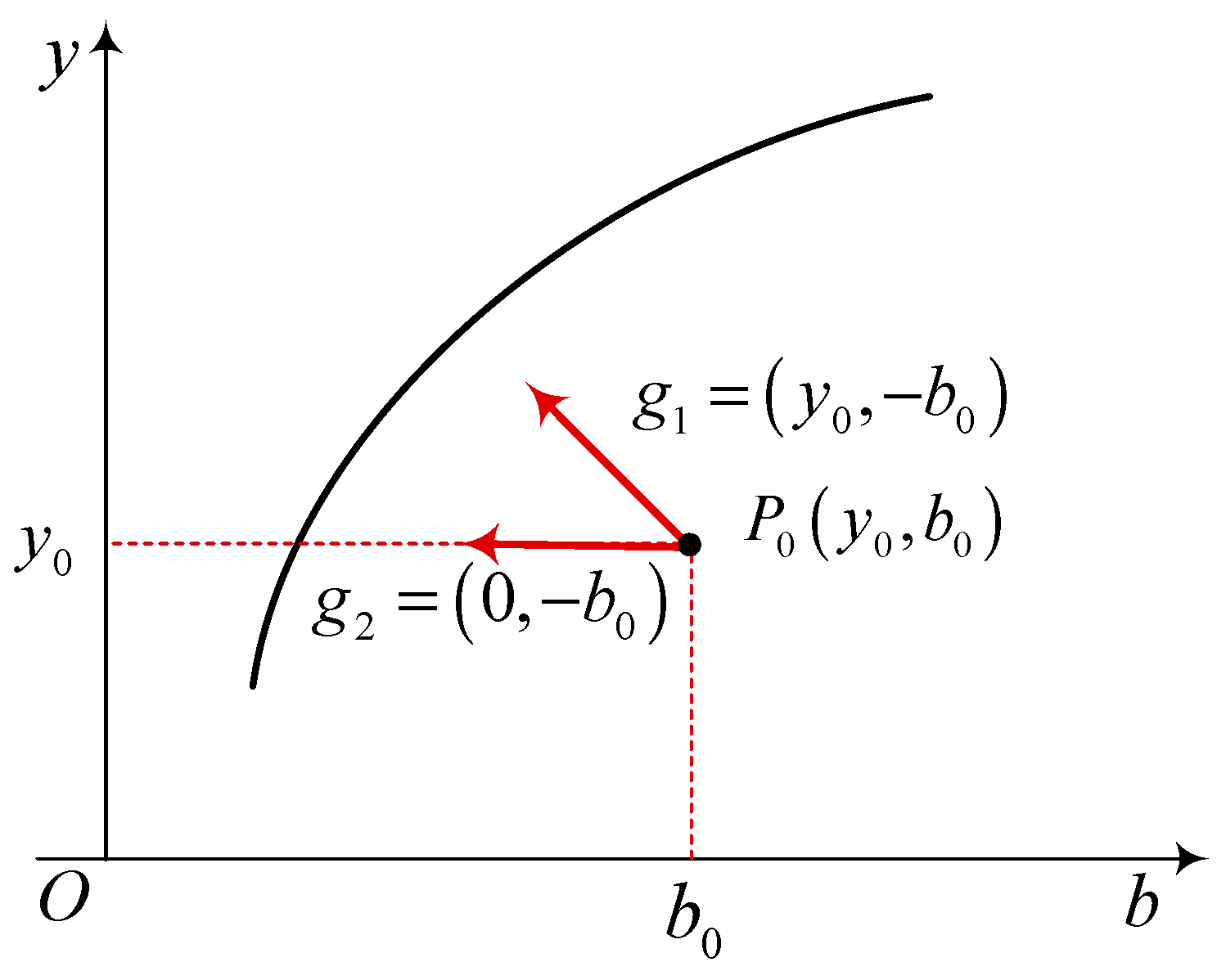
3.1. Eco-Efficiency under Regulatory Constraints
3.2. Global Malmquist–Luenberger Productivity Index
4. Empirical Study
4.1. Data Description
4.2. Empirical Results
4.2.1. Analysis of Eco-Efficiency Results
4.2.2. Analysis of GMLPI Results
4.3. A Summary of the Main Findings
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gohari, A.; Ahmad, A.B.; Balasbaneh, A.T.; Gohari, A.; Hasan, R.; Sholagberu, A.T. Significance of intermodal freight modal choice criteria: MCDM-based decision support models and SP-based modal shift policies. Transp. Policy 2022, 121, 46–60. [Google Scholar] [CrossRef]
- Sheu, J.B. A hybrid fuzzy-based approach for identifying global logistics strategies. Transp. Res. Part E Logist. Transp. Rev. 2004, 40, 39–61. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Zhou, L. Zero-carbon measure prioritization for sustainable freight transport using interval 2 tuple linguistic decision approaches. Appl. Soft Comput. 2023, 132, 109864. [Google Scholar] [CrossRef]
- Garg, C.P.; Kashav, V. Assessment of sustainable initiatives in the containerized freight railways of India using fuzzy AHP framework. Transp. Res. Procedia 2020, 48, 522–539. [Google Scholar] [CrossRef]
- Wanke, P.; Chen, Z.; Zheng, X.; Antunes, J. Sustainability efficiency and carbon inequality of the Chinese transportation system: A Robust Bayesian Stochastic Frontier Analysis. J. Environ. Manag. 2020, 260, 110163. [Google Scholar] [CrossRef]
- Liu, H.; Yang, R.; Wu, J.; Chu, J. Total-factor energy efficiency change of the road transportation industry in China: A stochastic frontier approach. Energy 2021, 219, 119612. [Google Scholar] [CrossRef]
- Hampf, B.; Rødseth, K.L. Carbon dioxide emission standards for US power plants: An efficiency analysis perspective. Energy Econ. 2015, 50, 140–153. [Google Scholar] [CrossRef]
- Xia, Y.S.; Sun, L.X.; Feng, C. What causes spatial inequalities of low-carbon development in China’s transport sector? A newly proposed meta-frontier DEA-based decomposition approach. Socio-Econ. Plan. Sci. 2022, 80, 101151. [Google Scholar] [CrossRef]
- Song, Y.; Ren, X.; Yang, G. Capacity utilization change over time. J. Product. Anal. 2023, 59, 61–78. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Xie, H.; Liu, G.; Liu, Q.; Wang, P. Analysis of spatial disparities and driving factors of energy consumption change in China based on spatial statistics. Sustainability 2014, 6, 2264–2280. [Google Scholar] [CrossRef]
- Lior, N. Sustainable energy development: The present (2009) situation and possible paths to the future. Energy 2010, 10, 3976–3994. [Google Scholar] [CrossRef]
- Beltrán-Esteve, M.; Picazo-Tadeo, A.J. Assessing environmental performance trends in the transport industry: Eco-innovation or catching-up? Energy Econ. 2015, 51, 570–580. [Google Scholar] [CrossRef]
- Cui, Q.; Li, Y. An empirical study on the influencing factors of transportation carbon efficiency: Evidences from fifteen countries. Appl. Energy 2015, 141, 209–217. [Google Scholar] [CrossRef]
- Choi, Y.; Wang, H.; Yang, F.; Lee, H. Sustainable governance of the Korean freight transportation industry from an environmental perspective. Sustainability 2021, 13, 6429. [Google Scholar] [CrossRef]
- Yang, F.; Choi, Y.; Lee, H. Life-cycle data envelopment analysis to measure efficiency and cost-effectiveness of environmental regulation in China’s transport sector. Ecol. Indic. 2021, 126, 107717. [Google Scholar] [CrossRef]
- Egilmez, G.; Park, Y.S. Transportation related carbon, energy and water footprint analysis of US manufacturing: An eco-efficiency assessment. Transp. Res. Part D Transp. Environ. 2014, 32, 143–159. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Aggarwal, U.; Charles, V.J.R.P. An integrated AHP-DEA multi-objective optimization model for sustainable transportation in mining industry. Resour. Policy 2021, 74, 101180. [Google Scholar] [CrossRef]
- Du, Q.; Lu, C.; Zou, P.X.W.; Li, Y.; Li, J.; Cui, X. Estimating transportation carbon efficiency (TCE) across the belt and road initiative countries: An integrated approach of modified three-stage epsilon-based measurement model. Environ. Impact Assess. Rev. 2021, 90, 106634. [Google Scholar] [CrossRef]
- Bai, C.; Chen, Z.; Wang, D. Transportation carbon emission reduction potential and mitigation strategy in China. Sci. Total Environ. 2023, 873, 162074. [Google Scholar] [CrossRef]
- Martín, J.C.; Román, C.; Voltes-Dorta, A. A stochastic frontier analysis to estimate the relative efficiency of Spanish airports. J. Product. Anal. 2009, 31, 163–176. [Google Scholar]
- Cullinane, K.; Wang, T.F.; Song, D.W.; Ji, P. The technical efficiency of container ports: Comparing data envelopment analysis and stochastic frontier analysis. Transp. Res. Part A Policy Pract. 2006, 40, 354–374. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Sengupta, J.K. Data envelopment analysis for efficiency measurement in the stochastic case. Comput. Oper. Res. 1987, 14, 117–129. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Network DEA. Socio-Econ. Plan. Sci. 2000, 34, 35–49. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar]
- Hailu, A.; Veeman, T.S. Alternative methods for environmentally adjusted productivity analysis. Agric. Econ. 2001, 25, 211–218. [Google Scholar] [CrossRef]
- Pishgar-Komleh, S.H.; Zylowski, T.; Rozakis, S.; Kozyra, J. Efficiency under different methods for incorporating undesirable outputs in an LCA + DEA framework: A case study of winter wheat production in Poland. J. Environ. Manag. 2020, 260, 110138. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. A comment on weak disposability in nonparametric production analysis. Am. J. Agric. Econ. 2009, 91, 535–538. [Google Scholar] [CrossRef]
- Wu, C.; Li, Y.; Liu, Q.; Wang, K. A stochastic DEA model considering undesirable outputs with weak disposability. Math. Comput. Model. 2013, 58, 980–989. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.M.; Huang, Z. Environmental efficiency and abatement efficiency measurements of China’s thermal power industry: A data envelopment analysis based materials balance approach. Eur. J. Oper. Res. 2018, 269, 35–50. [Google Scholar] [CrossRef]
- Murty, S. On the theory of a firm: The case of by-production of emissions. Econ. Res. Pap. 2010, 60, 1–40. [Google Scholar]
- Sueyoshi, T.; Goto, M.; Ueno, T. Performance analysis of US coal-fired power plants by measuring three DEA efficiencies. Energy Policy 2010, 38, 1675–1688. [Google Scholar] [CrossRef]
- Nodin, M.N.; Mustafa, Z.; Hussain, S.I. Eco-efficiency assessment of Malaysian rice self-sufficiency approach. Socio-Econ. Plan. Sci. 2023, 85, 101436. [Google Scholar] [CrossRef]
- Wang, X.; Ding, H.; Liu, L. Eco-efficiency measurement of industrial sectors in China: A hybrid super-efficiency DEA analysis. J. Clean. Prod. 2019, 229, 53–64. [Google Scholar] [CrossRef]
- Zuo, Z.; Guo, H.; Li, Y.; Cheng, J. A two-stage DEA evaluation of Chinese mining industry technological innovation efficiency and eco-efficiency. Environ. Impact Assess. Rev. 2022, 94, 106762. [Google Scholar] [CrossRef]
- Zhang, L.; Du, X.; Chiu, Y.; Pang, Q.; Yu, Q. Measuring industrial operational efficiency and factor analysis: A dynamic series-parallel recycling DEA model. Sci. Total Environ. 2022, 851, 158084. [Google Scholar] [CrossRef]
- Liang, X.; Li, J.; Guo, G.; Li, S.; Gong, Q. Evaluation for water resource system efficiency and influencing factors in western China: A two-stage network DEA-Tobit model. J. Clean. Prod. 2021, 328, 129674. [Google Scholar] [CrossRef]
- Kutty, A.A.; Kucukvar, M.; Abdella, G.M.; Bulak, M.E.; Onat, N.C. Sustainability performance of European smart cities: A novel DEA approach with double frontiers. Sustain. Cities Soc. 2022, 81, 103777. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Modeling undesirable factors in efficiency evaluation. Eur. J. Oper. Res. 2002, 142, 16–20. [Google Scholar] [CrossRef]
- Dakpo, K.H.; Jeanneaux, P.; Latruffe, L. Modelling pollution-generating technologies in performance benchmarking: Recent developments, limits and future prospects in the nonparametric framework. Eur. J. Oper. Res. 2016, 250, 347–359. [Google Scholar] [CrossRef]
- Song, Y.; Li, J.; Wang, J.; Yang, G.; Chen, Z. Eco-efficiency of Chinese transportation industry: A DEA approach with non-discretionary input. Socio-Econ. Plan. Sci. 2022, 84, 101383. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, C.; Pasurka, C. Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Productivity and intermediate products: A frontier approach. Econ. Lett. 1996, 50, 65–70. [Google Scholar] [CrossRef]
- Oh, D.; Heshmati, A. A sequential Malmquist-Luenberger productivity index: Environmentally sensitive productivity growth considering the progressive nature of technology. Energy Econ. 2010, 32, 1345–1355. [Google Scholar] [CrossRef]
- Zhang, H.; You, J.X.; Haiyirete, X.; Zhang, T.Y. Measuring logistics efficiency in China considering technology heterogeneity and carbon emission through a meta-frontier model. Sustainability 2020, 12, 8157. [Google Scholar] [CrossRef]
- Cui, Q.; Li, Y. The evaluation of transportation energy efficiency: An application of three-stage virtual frontier DEA. Transp. Res. Part D-Transp. Environ. 2014, 29, 1–11. [Google Scholar] [CrossRef]
- Mavi, R.K.; Fathi, A.; Saen, R.F.; Mavi, N.K. Eco-innovation in transportation industry: A double frontier common weights analysis with ideal point method for Malmquist productivity index. Resour. Conserv. Recycl. 2019, 147, 39–48. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Jiang, L.; Shi, W. Exploring the growth-adjusted energy-emission efficiency of transportation industry in China. Energy Econ. 2020, 90, 104873. [Google Scholar] [CrossRef]

| Variables | Types | Units | Data Sources |
|---|---|---|---|
| Fixed asset investment | Input | Million RMB | China Transportation Statistical Yearbook 2016–2021 |
| Employees | Input | Thousand person | China Transportation Statistical Yearbook 2016–2021 |
| Energy consumption | Input | Thousand tonne | China Energy Statistical Yearbook 2016–2021 |
| Passenger turnover volume | Desirable output | Million person kilometer | China Transportation Statistical Yearbook 2016–2021 |
| Freight turnover volume | Desirable output | Million tonne kilometer | China Transportation Statistical Yearbook 2016–2021 |
| CO2 emission | Undesirable output | Thousand tonne | Calculated referencing the methods provided by Intergovernmental Panel on Climate Change Guidelines |
| Years | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| CPI | 100.00 | 102.00 | 103.63 | 105.78 | 108.84 | 111.48 |
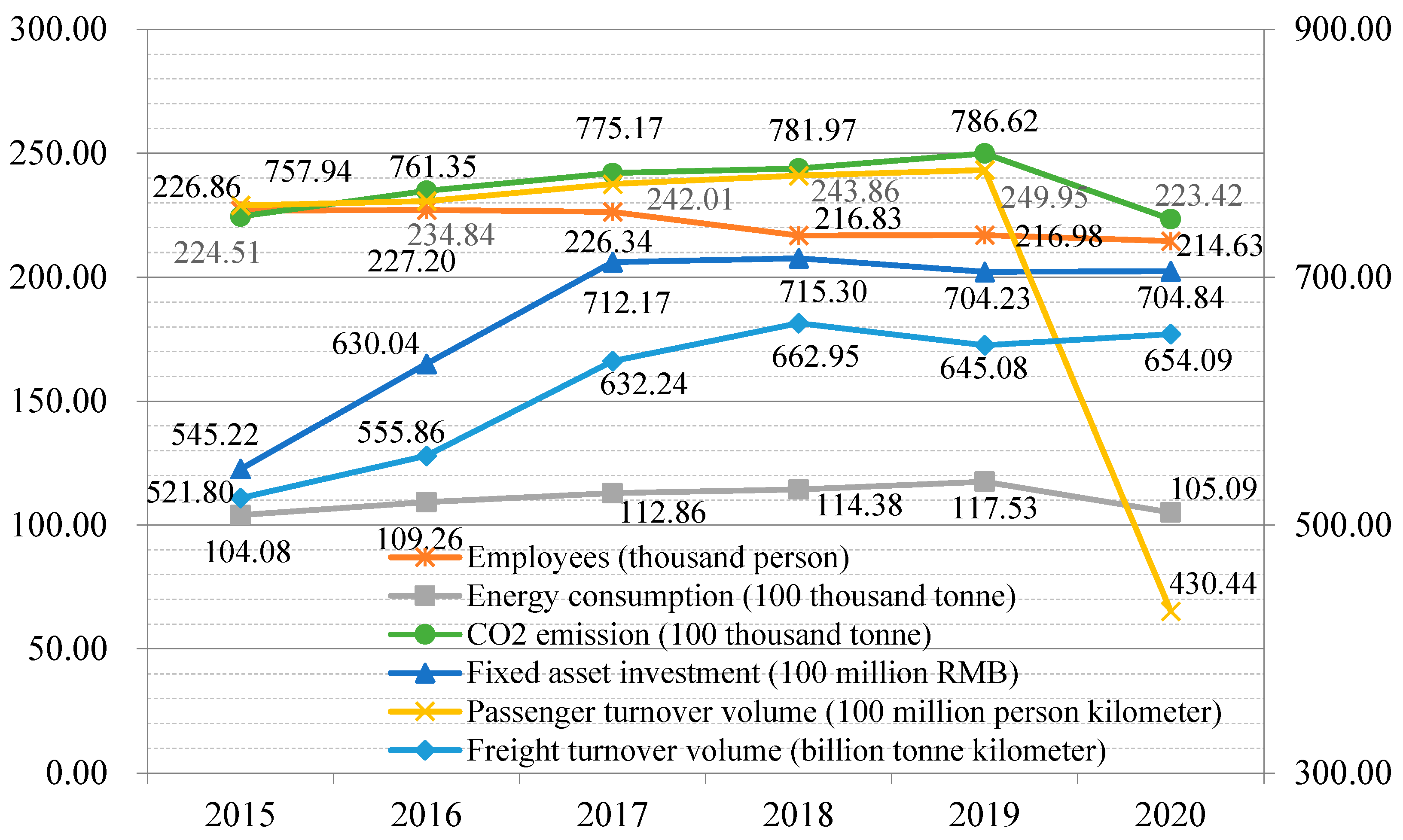
| Year | Statistics | Fixed Asset Investment (Million RMB) | Employees (Thousand Person) | Energy Consumption (Thousand Tonne) | Passenger Turnover Volume (Million Person Kilometer) | Freight Turnover Volume (Million Tonne Kilometer) | CO2 Emission (Thousand Tonne) |
|---|---|---|---|---|---|---|---|
| 2015 | Max | 115,833.11 | 613.16 | 28,160.34 | 179,651.76 | 1,949,588.47 | 60,217.39 |
| Min | 1499.84 | 32.31 | 1462.46 | 11,292.78 | 44,557.70 | 3043.52 | |
| Mean | 54,522.35 | 226.86 | 10,407.94 | 75,793.54 | 521,803.20 | 22,451.39 | |
| Median | 57,710.67 | 202.55 | 9471.79 | 63,894.44 | 359,601.30 | 20,008.64 | |
| Standard deviation | 31,504.31 | 130.66 | 5740.58 | 47,264.96 | 464,050.98 | 12,287.61 | |
| 2016 | Max | 147,058.82 | 635.53 | 31,536.66 | 188,744.51 | 2,180,164.99 | 67,454.11 |
| Min | 12,320.96 | 31.76 | 1682.63 | 10,971.96 | 47,579.99 | 3496.86 | |
| Mean | 63,004.11 | 227.20 | 10,925.54 | 76,135.17 | 555,858.42 | 23,484.26 | |
| Median | 57,303.29 | 201.31 | 9633.08 | 64,412.46 | 373,160.37 | 20,279.49 | |
| Standard deviation | 38,654.86 | 132.44 | 6379.10 | 48,423.73 | 526,776.80 | 13,598.60 | |
| 2017 | Max | 180,704.43 | 641.73 | 31,973.98 | 201,247.23 | 2,791,979.08 | 68,388.00 |
| Min | 5311.43 | 32.28 | 1729.14 | 9919.00 | 51,946.25 | 3637.30 | |
| Mean | 71,217.41 | 226.34 | 11,285.63 | 77,516.68 | 632,243.72 | 24,200.59 | |
| Median | 65,212.94 | 199.44 | 9901.98 | 66,988.95 | 420,118.40 | 21,510.37 | |
| Standard deviation | 47,516.35 | 132.42 | 6720.49 | 50,591.52 | 651,675.57 | 14,324.26 | |
| 2018 | Max | 177,941.24 | 631.96 | 32,583.71 | 208,558.68 | 2,833,832.92 | 69,696.31 |
| Min | 8236.09 | 34.04 | 1515.78 | 8830.62 | 55,135.92 | 3131.92 | |
| Mean | 71,530.10 | 216.83 | 11,437.93 | 78,196.70 | 662,951.29 | 24,385.66 | |
| Median | 62,501.30 | 188.01 | 10,037.10 | 71,633.86 | 443,800.07 | 21,010.05 | |
| Standard deviation | 48,063.55 | 127.35 | 6858.28 | 51,513.08 | 687,040.45 | 14,666.19 | |
| 2019 | Max | 215,077.86 | 630.23 | 32,924.97 | 212,572.02 | 3,032,490.16 | 70,535.38 |
| Min | 7508.23 | 33.82 | 1684.82 | 8703.60 | 39,842.89 | 3441.57 | |
| Mean | 70,423.05 | 216.98 | 11,753.12 | 78,662.11 | 645,077.81 | 24,994.64 | |
| Median | 61,295.74 | 187.90 | 9800.51 | 72,544.81 | 373,721.31 | 20,497.62 | |
| Standard deviation | 53,287.94 | 124.66 | 7057.53 | 52,189.18 | 702,288.86 | 15,108.38 | |
| 2020 | Max | 237,061.92 | 616.67 | 29,002.17 | 119,090.73 | 3,279,499.58 | 62,128.00 |
| Min | 8770.15 | 34.28 | 1600.01 | 5251.05 | 41,573.93 | 3263.76 | |
| Mean | 70,483.57 | 214.63 | 10,508.83 | 43,044.09 | 654,087.99 | 22,342.16 | |
| Median | 57,493.80 | 195.51 | 8323.82 | 40,526.86 | 385,406.46 | 17,540.49 | |
| Standard deviation | 54,761.39 | 122.25 | 6335.88 | 29,196.03 | 728,058.87 | 13,563.25 |
| Provinces | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Average |
|---|---|---|---|---|---|---|---|
| Beijing | 1.0000 | 1.0000 | 0.2462 | 0.2686 | 0.4127 | 0.5027 | 0.5717 |
| Tianjin | 0.7527 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9588 |
| Hebei | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Shanxi | 0.5965 | 0.6970 | 0.5149 | 0.4705 | 0.5909 | 0.4984 | 0.5614 |
| Inner Mongolia | 0.3491 | 0.5491 | 0.5365 | 0.5849 | 0.5549 | 0.4348 | 0.5015 |
| Liaoning | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Jilin | 0.5596 | 0.6278 | 0.7036 | 0.8247 | 0.7914 | 0.8739 | 0.7302 |
| Heilongjiang | 1.0000 | 0.8695 | 0.5166 | 0.6790 | 0.6370 | 0.4901 | 0.6987 |
| Shanghai | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Jiangsu | 0.9304 | 1.0000 | 1.0000 | 0.8440 | 0.9731 | 1.0000 | 0.9579 |
| Zhejiang | 0.8567 | 0.8109 | 0.7385 | 0.7574 | 0.8732 | 0.8773 | 0.8190 |
| Anhui | 1.0000 | 1.0000 | 0.9449 | 1.0000 | 1.0000 | 1.0000 | 0.9908 |
| Fujian | 0.5466 | 0.6062 | 0.5514 | 0.5757 | 0.6987 | 0.6799 | 0.6097 |
| Jiangxi | 1.0000 | 1.0000 | 1.0000 | 0.9517 | 1.0000 | 1.0000 | 0.9919 |
| Shandong | 0.7593 | 0.7274 | 0.6831 | 0.7242 | 0.7450 | 0.7027 | 0.7236 |
| Henan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Hubei | 0.8008 | 0.7653 | 0.7536 | 0.7301 | 0.7554 | 0.5916 | 0.7328 |
| Hunan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Guangdong | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Guangxi | 0.7706 | 0.7766 | 0.7569 | 0.8059 | 0.8230 | 0.9886 | 0.8203 |
| Hainan | 1.0000 | 0.8368 | 0.7747 | 0.6410 | 0.8615 | 1.0000 | 0.8523 |
| Chongqing | 0.6076 | 0.5741 | 0.4999 | 0.5487 | 0.5468 | 0.4742 | 0.5419 |
| Sichuan | 0.8010 | 0.6792 | 0.5711 | 0.5919 | 0.5900 | 0.6982 | 0.6552 |
| Guizhou | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Yunnan | 0.4759 | 0.4642 | 0.4342 | 0.3890 | 0.3777 | 0.3718 | 0.4188 |
| Shaanxi | 0.7869 | 0.9262 | 0.8745 | 0.8638 | 0.8981 | 0.9799 | 0.8882 |
| Gansu | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Qinghai | 1.0000 | 1.0000 | 1.0000 | 0.9144 | 0.8361 | 0.9375 | 0.9480 |
| Ningxia | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Xinjiang | 0.6706 | 0.5653 | 0.4260 | 0.4194 | 0.4433 | 0.3555 | 0.4800 |
| Average | 0.8421 | 0.8492 | 0.7842 | 0.7862 | 0.8136 | 0.8152 | 0.8151 |
| Provinces | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Average |
|---|---|---|---|---|---|---|---|
| Beijing | 1.0000 | 1.0000 | 0.1373 | 0.1321 | 0.2081 | 0.3223 | 0.4666 |
| Tianjin | 0.4049 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9008 |
| Hebei | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Shanxi | 0.2734 | 0.4741 | 0.2711 | 0.3076 | 0.4193 | 0.3319 | 0.3462 |
| Inner Mongolia | 0.2115 | 0.3784 | 0.3666 | 0.4133 | 0.3692 | 0.2346 | 0.3290 |
| Liaoning | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Jilin | 0.3181 | 0.3707 | 0.3948 | 0.6446 | 0.6124 | 0.7372 | 0.5130 |
| Heilongjiang | 0.4317 | 0.4261 | 0.2963 | 0.4514 | 0.3925 | 0.2292 | 0.3712 |
| Shanghai | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Jiangsu | 0.5772 | 0.5718 | 0.5150 | 0.5478 | 0.5312 | 1.0000 | 0.6238 |
| Zhejiang | 0.4998 | 0.5650 | 0.4819 | 0.5115 | 0.6247 | 0.5605 | 0.5406 |
| Anhui | 1.0000 | 1.0000 | 0.7159 | 0.7197 | 1.0000 | 1.0000 | 0.9059 |
| Fujian | 0.3760 | 0.4349 | 0.3807 | 0.4042 | 0.4429 | 0.3221 | 0.3935 |
| Jiangxi | 1.0000 | 1.0000 | 1.0000 | 0.8119 | 1.0000 | 1.0000 | 0.9687 |
| Shandong | 0.4321 | 0.4646 | 0.3835 | 0.4167 | 0.4530 | 0.3413 | 0.4152 |
| Henan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Hubei | 0.5384 | 0.5171 | 0.4611 | 0.4627 | 0.4162 | 0.2902 | 0.4476 |
| Hunan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Guangdong | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Guangxi | 0.5455 | 0.5925 | 0.5167 | 0.5444 | 0.5826 | 0.9683 | 0.6250 |
| Hainan | 1.0000 | 0.7033 | 0.5975 | 0.3844 | 0.7060 | 1.0000 | 0.7319 |
| Chongqing | 0.3994 | 0.3957 | 0.3332 | 0.3781 | 0.3746 | 0.3042 | 0.3642 |
| Sichuan | 0.6680 | 0.4867 | 0.3996 | 0.4204 | 0.4139 | 0.3774 | 0.4610 |
| Guizhou | 0.8601 | 0.8443 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9507 |
| Yunnan | 0.2970 | 0.3023 | 0.2773 | 0.2415 | 0.2316 | 0.1997 | 0.2582 |
| Shaanxi | 0.6486 | 0.8461 | 0.7769 | 0.7602 | 0.8122 | 0.9373 | 0.7969 |
| Gansu | 1.0000 | 1.0000 | 0.9592 | 1.0000 | 1.0000 | 1.0000 | 0.9932 |
| Qinghai | 1.0000 | 1.0000 | 1.0000 | 0.8169 | 0.6533 | 0.8587 | 0.8882 |
| Ningxia | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Xinjiang | 0.4024 | 0.3398 | 0.2706 | 0.2654 | 0.2818 | 0.2162 | 0.2960 |
| Average | 0.6961 | 0.7238 | 0.6512 | 0.6545 | 0.6842 | 0.7077 | 0.6862 |
| Regions | Average Eco-Efficiency in the First Scenario | Ranks | Average Eco-Efficiency in the Second Scenario | Ranks |
|---|---|---|---|---|
| North coast area | 0.8135 | 5 | 0.6957 | 5 |
| Middle Yellow River area | 0.7378 | 7 | 0.6180 | 7 |
| Northeast area | 0.8096 | 6 | 0.6281 | 6 |
| East coast area | 0.9256 | 2 | 0.7215 | 3 |
| South coast area | 0.8207 | 4 | 0.7084 | 4 |
| Middle Yangtze River area | 0.9289 | 1 | 0.8305 | 1 |
| Southwest area | 0.6872 | 8 | 0.5318 | 8 |
| Northwest area | 0.8570 | 3 | 0.7944 | 2 |
| Provinces | 2015–2016 | 2016–2017 | 2017–2018 | 2018–2019 | 2019–2020 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | |
| Beijing | 0.6058 | 1.0000 | 0.6058 | 0.9385 | 0.5702 | 1.6460 | 0.9953 | 1.0129 | 0.9826 | 1.0228 | 1.0908 | 0.9377 | 0.9562 | 1.0602 | 0.9020 |
| Tianjin | 1.1415 | 1.2473 | 0.9152 | 1.1584 | 1.0000 | 1.1584 | 0.9832 | 1.0000 | 0.9832 | 0.9583 | 1.0000 | 0.9583 | 0.9271 | 1.0000 | 0.9271 |
| Hebei | 0.9399 | 1.0000 | 0.9399 | 1.0640 | 1.0000 | 1.0640 | 1.0000 | 1.0000 | 1.0000 | 0.9908 | 1.0000 | 0.9908 | 1.0093 | 1.0000 | 1.0093 |
| Shanxi | 1.0237 | 1.0772 | 0.9503 | 0.9706 | 0.8774 | 1.1062 | 0.9773 | 0.9710 | 1.0066 | 1.0269 | 1.0854 | 0.9461 | 1.0040 | 0.9384 | 1.0699 |
| Inner Mongolia | 1.0846 | 1.1378 | 0.9532 | 1.0105 | 0.9914 | 1.0192 | 1.0092 | 1.0341 | 0.9759 | 0.9817 | 0.9792 | 1.0025 | 0.9723 | 0.9233 | 1.0531 |
| Liaoning | 1.0681 | 1.0000 | 1.0681 | 1.0360 | 1.0000 | 1.0360 | 1.1188 | 1.0000 | 1.1188 | 1.0000 | 1.0000 | 1.0000 | 0.7309 | 1.0000 | 0.7309 |
| Jilin | 1.0051 | 1.0497 | 0.9575 | 1.0617 | 1.0585 | 1.0031 | 1.1330 | 1.1030 | 1.0272 | 0.9438 | 0.9725 | 0.9705 | 0.8217 | 1.0733 | 0.7656 |
| Heilongjiang | 0.9316 | 0.8845 | 1.0532 | 0.9872 | 0.7621 | 1.2953 | 1.0797 | 1.1230 | 0.9614 | 0.9277 | 0.9692 | 0.9572 | 0.8481 | 0.9027 | 0.9395 |
| Shanghai | 0.9590 | 1.0000 | 0.9590 | 1.0722 | 1.0000 | 1.0722 | 1.0780 | 1.0000 | 1.0780 | 1.1284 | 1.0000 | 1.1284 | 1.0000 | 1.0000 | 1.0000 |
| Jiangsu | 1.0012 | 1.0696 | 0.9361 | 1.0221 | 1.0000 | 1.0221 | 1.0270 | 0.8650 | 1.1872 | 1.0031 | 1.1258 | 0.8911 | 0.7859 | 1.0269 | 0.7653 |
| Zhejiang | 0.9898 | 0.9615 | 1.0294 | 1.0097 | 0.9426 | 1.0712 | 1.0359 | 1.0152 | 1.0204 | 1.0320 | 1.1028 | 0.9358 | 0.9034 | 1.0037 | 0.9001 |
| Anhui | 0.9571 | 1.0000 | 0.9571 | 0.9225 | 0.9478 | 0.9733 | 1.1326 | 1.0551 | 1.0734 | 0.9046 | 1.0000 | 0.9046 | 0.9220 | 1.0000 | 0.9220 |
| Fujian | 0.9920 | 1.0428 | 0.9513 | 0.9993 | 0.9622 | 1.0386 | 0.9966 | 1.0170 | 0.9800 | 1.0267 | 1.0945 | 0.9380 | 1.0362 | 0.9858 | 1.0511 |
| Jiangxi | 1.0019 | 1.0000 | 1.0019 | 1.0349 | 1.0000 | 1.0349 | 0.9353 | 0.9539 | 0.9805 | 0.9964 | 1.0483 | 0.9505 | 0.7874 | 1.0000 | 0.7874 |
| Shandong | 1.0132 | 0.9749 | 1.0393 | 1.0123 | 0.9664 | 1.0475 | 1.0243 | 1.0322 | 0.9924 | 1.0209 | 1.0166 | 1.0043 | 0.8482 | 0.9674 | 0.8767 |
| Henan | 1.0219 | 1.0000 | 1.0219 | 1.0089 | 1.0000 | 1.0089 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7145 | 1.0000 | 0.7145 |
| Hubei | 0.9630 | 0.9713 | 0.9915 | 1.0147 | 0.9906 | 1.0243 | 0.9952 | 0.9815 | 1.0139 | 0.9568 | 1.0203 | 0.9377 | 0.8019 | 0.8837 | 0.9075 |
| Hunan | 0.9923 | 1.0000 | 0.9923 | 1.0078 | 1.0000 | 1.0078 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.6757 | 1.0000 | 0.6757 |
| Guangdong | 0.9476 | 1.0000 | 0.9476 | 1.0553 | 1.0000 | 1.0553 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9250 | 1.0000 | 0.9250 |
| Guangxi | 1.0021 | 1.0049 | 0.9972 | 1.0239 | 0.9841 | 1.0404 | 1.0332 | 1.0411 | 0.9924 | 1.0009 | 1.0145 | 0.9866 | 0.8932 | 1.1637 | 0.7676 |
| Hainan | 0.6871 | 0.8597 | 0.7992 | 1.0314 | 0.9493 | 1.0866 | 0.9448 | 0.9016 | 1.0478 | 1.1914 | 1.1937 | 0.9980 | 1.2536 | 1.1385 | 1.1011 |
| Chongqing | 0.9629 | 0.9765 | 0.9861 | 0.9823 | 0.9505 | 1.0334 | 1.0253 | 1.0337 | 0.9919 | 0.9884 | 0.9987 | 0.9897 | 0.9113 | 0.9524 | 0.9568 |
| Sichuan | 0.8700 | 0.9078 | 0.9583 | 0.9641 | 0.9243 | 1.0431 | 1.0058 | 1.0148 | 0.9911 | 0.9861 | 0.9986 | 0.9875 | 0.9075 | 1.0831 | 0.8379 |
| Guizhou | 0.9692 | 1.0000 | 0.9692 | 1.0812 | 1.0000 | 1.0812 | 1.0336 | 1.0000 | 1.0336 | 1.0000 | 1.0000 | 1.0000 | 0.7649 | 1.0000 | 0.7649 |
| Yunnan | 0.9847 | 0.9924 | 0.9922 | 0.9989 | 0.9808 | 1.0185 | 0.9666 | 0.9719 | 0.9945 | 0.9887 | 0.9930 | 0.9956 | 0.9324 | 0.9964 | 0.9358 |
| Shaanxi | 1.0754 | 1.1298 | 0.9518 | 1.0003 | 0.9540 | 1.0485 | 0.9781 | 0.9906 | 0.9874 | 1.0122 | 1.0311 | 0.9817 | 0.8575 | 1.0802 | 0.7938 |
| Gansu | 0.9833 | 1.0000 | 0.9833 | 0.9874 | 1.0000 | 0.9874 | 1.0481 | 1.0000 | 1.0481 | 1.0000 | 1.0000 | 1.0000 | 0.7843 | 1.0000 | 0.7843 |
| Qinghai | 0.9608 | 1.0000 | 0.9608 | 0.9353 | 1.0000 | 0.9353 | 0.9816 | 0.9212 | 1.0657 | 0.9168 | 0.9327 | 0.9829 | 0.8685 | 1.0954 | 0.7929 |
| Ningxia | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Xinjiang | 0.9178 | 0.9266 | 0.9905 | 0.9600 | 0.9115 | 1.0532 | 0.9898 | 0.9959 | 0.9939 | 1.0075 | 1.0154 | 0.9922 | 0.9074 | 0.9466 | 0.9586 |
| Average | 0.9684 | 1.0071 | 0.9620 | 1.0117 | 0.9575 | 1.0671 | 1.0176 | 1.0012 | 1.0176 | 1.0004 | 1.0228 | 0.9789 | 0.8917 | 1.0074 | 0.8872 |
| Provinces | 2015–2016 | 2016–2017 | 2017–2018 | 2018–2019 | 2019–2020 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | GMLPI | EC | BPC | |
| Beijing | 0.5444 | 1.0000 | 0.5444 | 0.9859 | 0.5368 | 1.8364 | 0.9952 | 0.9972 | 0.9979 | 1.0034 | 1.0424 | 0.9625 | 0.9753 | 1.0681 | 0.9131 |
| Tianjin | 1.1684 | 1.5951 | 0.7325 | 1.3681 | 1.0000 | 1.3681 | 0.9575 | 1.0000 | 0.9575 | 0.9189 | 1.0000 | 0.9189 | 0.8704 | 1.0000 | 0.8704 |
| Hebei | 0.8780 | 1.0000 | 0.8780 | 1.1389 | 1.0000 | 1.1389 | 1.0000 | 1.0000 | 1.0000 | 0.9601 | 1.0000 | 0.9601 | 1.0416 | 1.0000 | 1.0416 |
| Shanxi | 0.9881 | 1.1315 | 0.8733 | 1.0040 | 0.8826 | 1.1376 | 1.0188 | 1.0216 | 0.9973 | 1.0208 | 1.0707 | 0.9534 | 1.0032 | 0.9476 | 1.0586 |
| Inner Mongolia | 1.0591 | 1.1029 | 0.9602 | 1.0080 | 0.9928 | 1.0153 | 1.0072 | 1.0294 | 0.9784 | 0.9750 | 0.9730 | 1.0021 | 0.9769 | 0.9238 | 1.0575 |
| Liaoning | 1.0772 | 1.0000 | 1.0772 | 1.0701 | 1.0000 | 1.0701 | 1.2715 | 1.0000 | 1.2715 | 1.0000 | 1.0000 | 1.0000 | 0.6222 | 1.0000 | 0.6222 |
| Jilin | 1.0100 | 1.0323 | 0.9784 | 1.0087 | 1.0150 | 0.9938 | 1.1236 | 1.1843 | 0.9487 | 0.9909 | 0.9767 | 1.0145 | 0.8470 | 1.0989 | 0.7708 |
| Heilongjiang | 0.9649 | 0.9964 | 0.9684 | 1.0035 | 0.9238 | 1.0863 | 1.0346 | 1.1002 | 0.9404 | 0.9817 | 0.9633 | 1.0191 | 0.9043 | 0.9078 | 0.9961 |
| Shanghai | 0.9539 | 1.0000 | 0.9539 | 1.0634 | 1.0000 | 1.0634 | 1.0853 | 1.0000 | 1.0853 | 1.0481 | 1.0000 | 1.0481 | 1.2248 | 1.0000 | 1.2248 |
| Jiangsu | 1.0009 | 0.9962 | 1.0047 | 0.9937 | 0.9617 | 1.0332 | 0.9878 | 1.0226 | 0.9660 | 0.9885 | 0.9887 | 0.9998 | 0.8807 | 1.4688 | 0.5996 |
| Zhejiang | 0.9936 | 1.0454 | 0.9504 | 0.9932 | 0.9453 | 1.0507 | 1.0114 | 1.0199 | 0.9917 | 1.0410 | 1.0823 | 0.9618 | 0.9036 | 0.9554 | 0.9457 |
| Anhui | 0.8270 | 1.0000 | 0.8270 | 0.9408 | 0.7787 | 1.2081 | 0.9874 | 1.0030 | 0.9844 | 1.0217 | 1.2803 | 0.7980 | 0.8592 | 1.0000 | 0.8592 |
| Fujian | 0.9933 | 1.0376 | 0.9572 | 0.9994 | 0.9665 | 1.0341 | 0.9970 | 1.0147 | 0.9825 | 0.9894 | 1.0249 | 0.9653 | 0.9884 | 0.9280 | 1.0652 |
| Jiangxi | 1.0023 | 1.0000 | 1.0023 | 1.0802 | 1.0000 | 1.0802 | 0.8210 | 0.8417 | 0.9754 | 0.9874 | 1.1881 | 0.8311 | 0.8044 | 1.0000 | 0.8044 |
| Shandong | 0.9975 | 1.0211 | 0.9769 | 0.9866 | 0.9498 | 1.0387 | 1.0143 | 1.0210 | 0.9935 | 1.0106 | 1.0235 | 0.9874 | 0.9257 | 0.9327 | 0.9925 |
| Henan | 1.0669 | 1.0000 | 1.0669 | 1.0347 | 1.0000 | 1.0347 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.6185 | 1.0000 | 0.6185 |
| Hubei | 0.9444 | 0.9857 | 0.9581 | 1.0072 | 0.9635 | 1.0453 | 0.9919 | 1.0010 | 0.9909 | 0.9605 | 0.9707 | 0.9896 | 0.8973 | 0.9263 | 0.9687 |
| Hunan | 0.9371 | 1.0000 | 0.9371 | 0.9912 | 1.0000 | 0.9912 | 1.0766 | 1.0000 | 1.0766 | 0.7809 | 1.0000 | 0.7809 | 0.7676 | 1.0000 | 0.7676 |
| Guangdong | 1.1126 | 1.0000 | 1.1126 | 1.2240 | 1.0000 | 1.2240 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8328 | 1.0000 | 0.8328 |
| Guangxi | 0.9918 | 1.0334 | 0.9598 | 0.9879 | 0.9489 | 1.0411 | 1.0084 | 1.0191 | 0.9895 | 1.0133 | 1.0269 | 0.9868 | 0.9468 | 1.3740 | 0.6891 |
| Hainan | 0.5827 | 0.7712 | 0.7557 | 1.0026 | 0.9246 | 1.0844 | 1.0066 | 0.8681 | 1.1595 | 1.0957 | 1.2486 | 0.8775 | 1.5520 | 1.2940 | 1.1994 |
| Chongqing | 0.9734 | 0.9977 | 0.9756 | 0.9857 | 0.9625 | 1.0241 | 1.0206 | 1.0277 | 0.9931 | 0.9904 | 0.9978 | 0.9925 | 0.9324 | 0.9585 | 0.9727 |
| Sichuan | 0.8574 | 0.8802 | 0.9741 | 0.9697 | 0.9456 | 1.0254 | 1.0052 | 1.0131 | 0.9922 | 0.9878 | 0.9959 | 0.9918 | 0.9270 | 0.9775 | 0.9483 |
| Guizhou | 0.9524 | 0.9864 | 0.9656 | 1.1709 | 1.1557 | 1.0131 | 1.0876 | 1.0000 | 1.0876 | 1.0000 | 1.0000 | 1.0000 | 0.6342 | 1.0000 | 0.6342 |
| Yunnan | 0.9885 | 1.0031 | 0.9855 | 0.9993 | 0.9855 | 1.0140 | 0.9758 | 0.9796 | 0.9961 | 0.9921 | 0.9944 | 0.9976 | 0.9560 | 0.9823 | 0.9733 |
| Shaanxi | 1.0999 | 1.1711 | 0.9391 | 1.0017 | 0.9434 | 1.0618 | 0.9693 | 0.9865 | 0.9825 | 1.0170 | 1.0438 | 0.9744 | 0.8326 | 1.1177 | 0.7449 |
| Gansu | 0.9526 | 1.0000 | 0.9526 | 0.9755 | 0.9608 | 1.0153 | 1.1352 | 1.0408 | 1.0907 | 1.0000 | 1.0000 | 1.0000 | 0.6986 | 1.0000 | 0.6986 |
| Qinghai | 0.9182 | 1.0000 | 0.9182 | 0.8765 | 1.0000 | 0.8765 | 0.9740 | 0.8453 | 1.1523 | 0.8633 | 0.8785 | 0.9827 | 0.8680 | 1.1799 | 0.7356 |
| Ningxia | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Xinjiang | 0.9644 | 0.9623 | 1.0021 | 0.9792 | 0.9600 | 1.0201 | 0.9925 | 0.9970 | 0.9956 | 1.0054 | 1.0096 | 0.9959 | 0.9367 | 0.9632 | 0.9725 |
| Average | 0.9600 | 1.0250 | 0.9396 | 1.0284 | 0.9568 | 1.0875 | 1.0185 | 1.0011 | 1.0192 | 0.9881 | 1.0260 | 0.9664 | 0.9076 | 1.0335 | 0.8859 |
| Scenarios | Indices | 2015–2016 | 2016–2017 | 2017–2018 | 2018–2019 | 2019–2020 |
|---|---|---|---|---|---|---|
| The win-win orientation scenario | GMLPI | 0.9684 | 1.0117 | 1.0176 | 1.0004 | 0.8917 |
| EC | 1.0071 | 0.9575 | 1.0012 | 1.0228 | 1.0074 | |
| BPC | 0.9620 | 1.0671 | 1.0176 | 0.9789 | 0.8872 | |
| The win-win orientation scenario | GMLPI | 0.9600 | 1.0284 | 1.0185 | 0.9881 | 0.9076 |
| EC | 1.0250 | 0.9568 | 1.0011 | 1.0260 | 1.0335 | |
| BPC | 0.9396 | 1.0875 | 1.0192 | 0.9664 | 0.8859 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhang, X.; Xue, M.; Song, Y. Eco-Efficiency and Its Evolutionary Change under Regulatory Constraints: A Case Study of Chinese Transportation Industry. Sustainability 2023, 15, 7381. https://doi.org/10.3390/su15097381
Zhu Z, Zhang X, Xue M, Song Y. Eco-Efficiency and Its Evolutionary Change under Regulatory Constraints: A Case Study of Chinese Transportation Industry. Sustainability. 2023; 15(9):7381. https://doi.org/10.3390/su15097381
Chicago/Turabian StyleZhu, Zhiqiang, Xuechi Zhang, Mengqing Xue, and Yaoyao Song. 2023. "Eco-Efficiency and Its Evolutionary Change under Regulatory Constraints: A Case Study of Chinese Transportation Industry" Sustainability 15, no. 9: 7381. https://doi.org/10.3390/su15097381
APA StyleZhu, Z., Zhang, X., Xue, M., & Song, Y. (2023). Eco-Efficiency and Its Evolutionary Change under Regulatory Constraints: A Case Study of Chinese Transportation Industry. Sustainability, 15(9), 7381. https://doi.org/10.3390/su15097381






