Estimation of Crash Modification Factors (CMFs) in Mountain Freeways: Considering Temporal Instability in Crash Data
Abstract
:1. Introduction
2. Literature Review
2.1. Impacts of Risk Factors on Traffic Safety
2.2. Temporal Correlations in Crash Data
2.3. Gaps in the Literature
- (1)
- The pavement performance and meteorological condition indicators of five mountainous freeways in China were investigated using multifunctional inspection vehicles and meteorological observation equipment, and combined with traffic conditions and crash data from different environments to establish a standard crash dataset representative of Chinese freeway conditions;
- (2)
- Autocorrelation priors were embedded into the traditional SPF structure to characterize temporal instability in the modeled data and CMFs were estimated for pavement performance, traffic conditions, and weather conditions to quantify the safety effects of each significant risk factor.
3. Data Collection and Description
3.1. Research Objects
3.2. Sample Division Methods
3.3. Statistical Description of Accident Modeling Data Sets
- ➢
- The acquisition of pavement performance indexes in Table 2 involves two steps: (1) the Pavement Distress Ratio (DR), International Roughness Index (IRI), and Sideway Force Coefficient (SFC) were obtained using a Multifunctional Road Condition Rapid Test Vehicle (SCANNER CiCS II). (2) According to the pavement performance evaluation indexes and calculation methods stipulated in the Highway Technical Condition Evaluation Standard (JTG 5210-2018) [38], the Pavement Condition Index (PCI), Riding Quality Index (RQI), Rutting Depth Index (RDI), and Skidding Resistance Index (SRI) were subsequently obtained (as shown in Table 3). The PCI represents the degree of surface damage, such as pavement cracking, potholes, and collapse, with higher PCI values indicating less surface damage. The RQI evaluates the driving quality of pavements by considering the impact of road surface roughness on driving comfort, with higher RQI values signifying better pavement leveling and driving comfort. The SRI represents the skid resistance of the pavement, derived by converting the lateral force coefficient of the pavement, where higher SRI values indicate better skid resistance;
- ➢
- The Guangdong Freeway Network Toll System (GFNTS) classifies vehicles into five types according to vehicle height, number of axles, number of wheels, and wheelbase (as shown in Table 4). Based on the clues provided by Wen et al. [28], the calculation of the Quarterly Average Daily Traffic Volume (QADT) and traffic compositions, whose formulas are shown in Equations (1)–(5), requires the conversion of Class 1 to Class 5 vehicles into standard traffic volumes by a coefficient of 1:1.5:2:3:3.5, respectively. According to the clues provided by Tang et al. [2], the proportion of Class 1–5 vehicles in a quarter (denoted by the symbols IVE, IIVE, IIIVE, IVVE, and VVE) is strongly associated with crash risks, forming the basis for its inclusion in the risk factors of this study. It should be noted that the proportion of Class 3 vehicles is collinear with other variables, so this variable is excluded;
- ➢
- The weather data, recorded on a county (district) basis, come from the Guangdong Meteorological Data Center. The freeways studied in this paper cover 41 meteorological stations, with an average distance of 36 km between them. The shortest and longest distances between meteorological stations and freeways are 18 km and 34 km, respectively. For counties (districts) containing multiple meteorological observation stations, data were averaged. The weather condition variables selected in this paper include the percentage of small/moderate rain days in a quarter (SMR), the percentage of torrential rain days in a quarter (TR), the percentage of days with no sustained wind in a quarter (WD), and the percentage of days with wind power ≥ 4 in a quarter (WP);
- ➢
- The crash data come from the record ledger of each freeway management center, which documents the geographical location of crashes, the cause of crashes, the related vehicle information, the severity, and the casualty situation. In the initial screening of crash data, we removed crashes caused by parking violations, spilled vehicle contents, and crashes with missing dates or locations, resulting in 1633 crashes for this study.
4. Methodology
4.1. Model Description
4.2. Parameter Estimation Method and Goodness-of-Fit Measures
5. Results and Analysis
5.1. Explanatory of Temporal Instability
5.2. Analysis of Parameter Estimation Results for SPFs
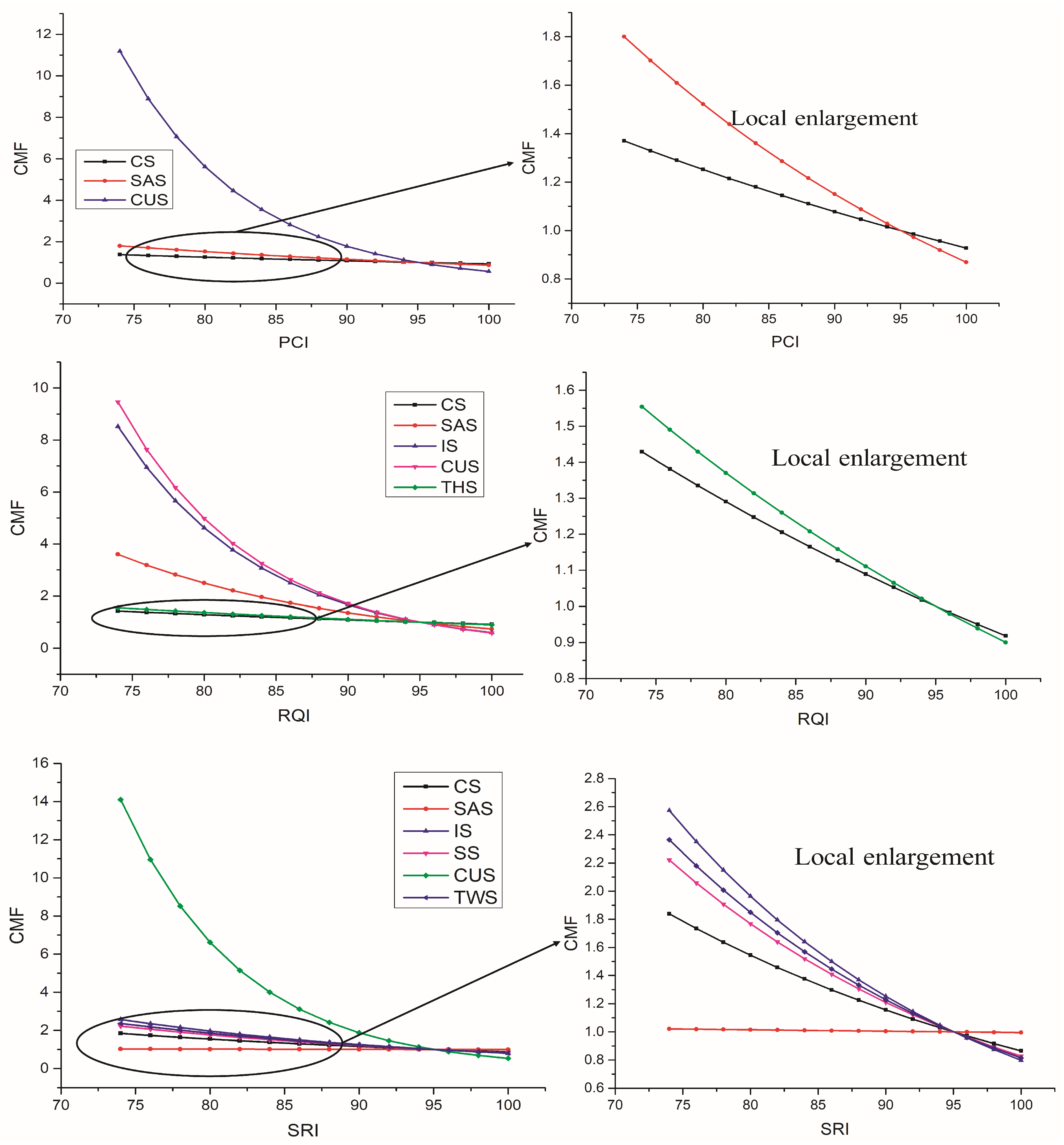
5.3. Analysis of CMFs
5.3.1. Pavement Performance
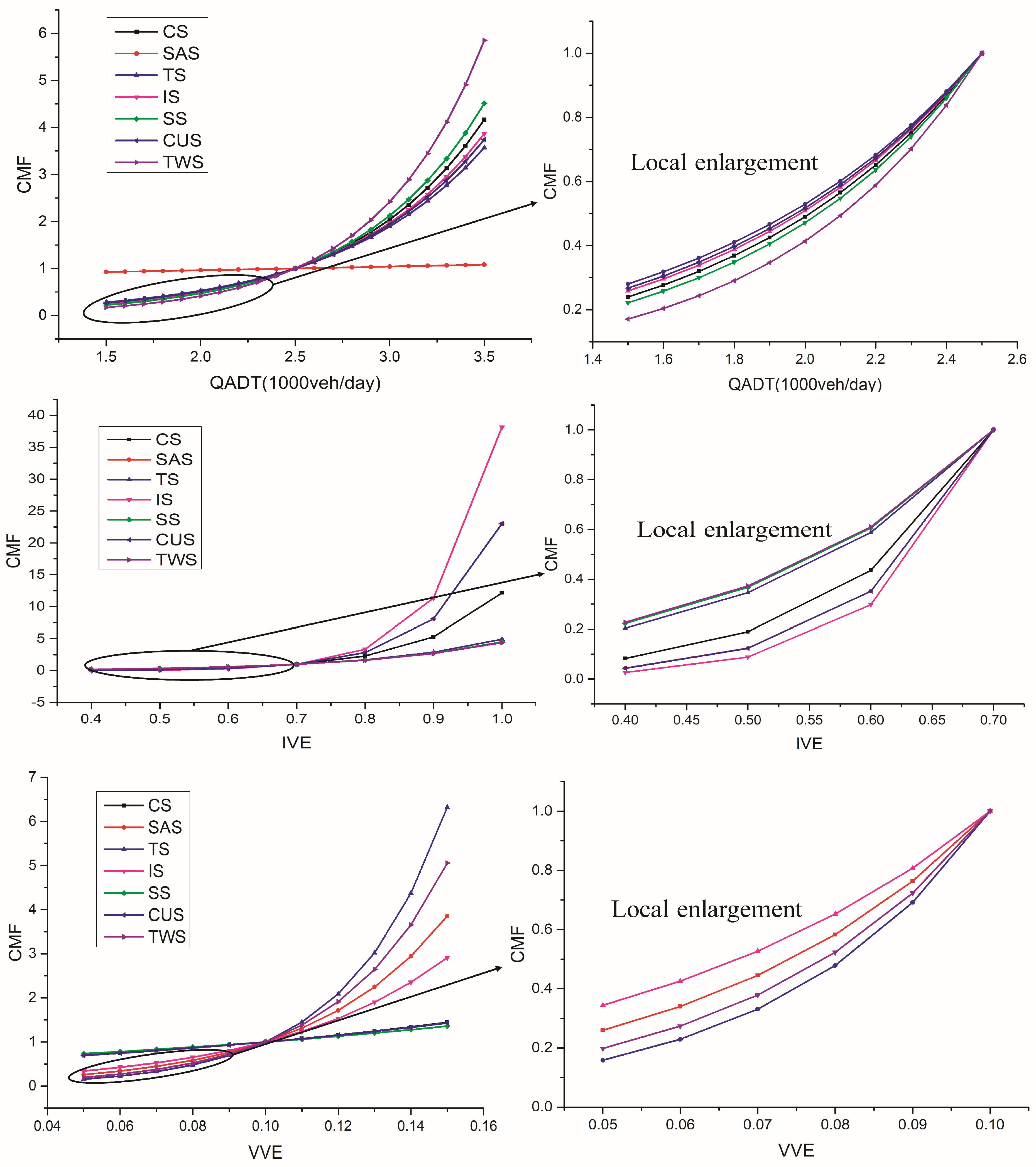
5.3.2. Traffic Conditions
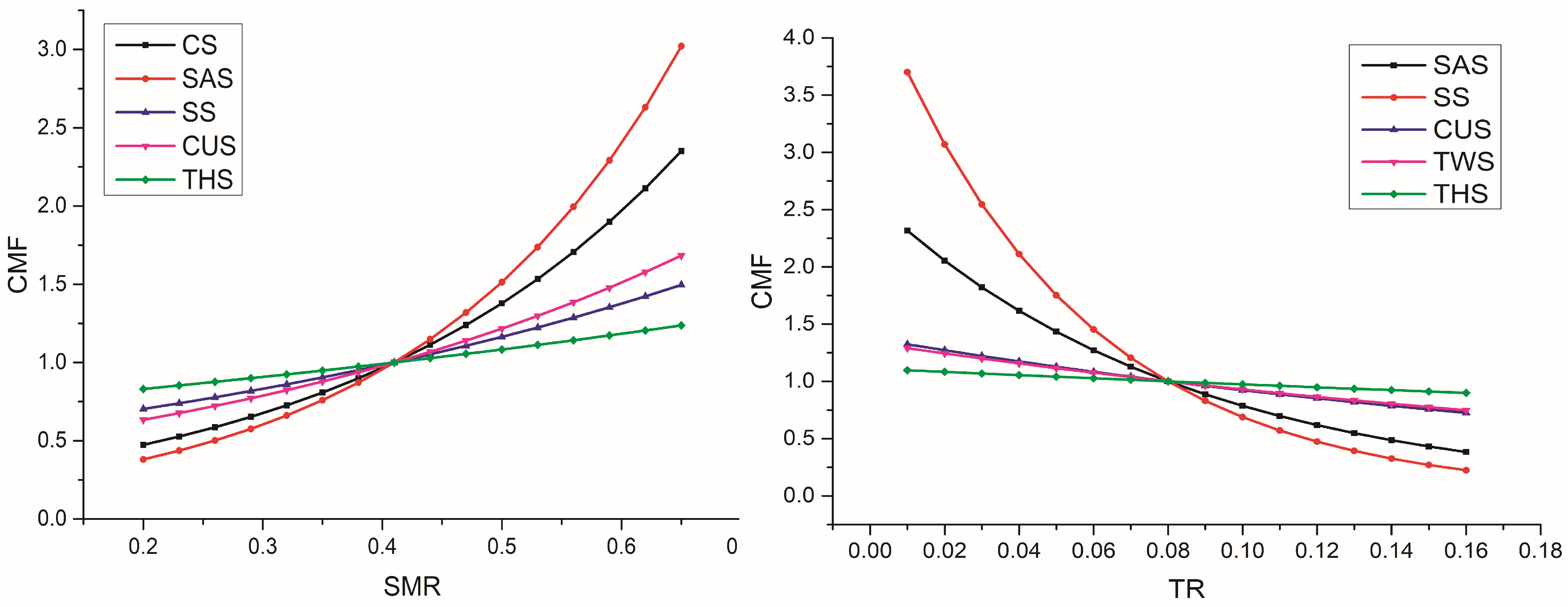
5.3.3. Weather Conditions
6. Discussing
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cafiso, S.; Montella, A.; D’Agostino, C.; Mauriello, F.; Galante, F. Crash modification functions for pavement surface condition and geometric design indicators. Accid. Anal. Prev. 2021, 149, 105887. [Google Scholar] [CrossRef]
- Tang, F.; Fu, X.; Cai, M.; Lu, Y.; Zhong, S. Investigation of the Factors Influencing the Crash Frequency in Expressway Tunnels: Considering Excess Zero Observations and Unobserved Heterogeneity. IEEE Access 2021, 9, 2169–3536. [Google Scholar] [CrossRef]
- Al-Marafi, M.N.; Somasundaraswaran, K. A review of the state-of-the-art methods in estimating crash modification factor (CMF). Transp. Res. Interdiscip. Perspect. 2023, 20, 100839. [Google Scholar] [CrossRef]
- AASHTO. Highway Safety Manual. 2010, p. 20. Available online: https://www.highwaysafetymanual.org/Pages/support_answers.aspx (accessed on 15 January 2024).
- Davis, G.A. Mechanisms, mediators, and surrogate estimation of crash modification factors. Accid. Anal. Prev. 2021, 151, 105978. [Google Scholar] [CrossRef]
- Mbatta, G. Developing Crash Modification Factors for Urban Highway with Substandard Wide Curb Lane; Florida State University: Tallahassee, FL, USA, 2017. [Google Scholar]
- Vinayaraj, V.S.; Perumal, V. Developing Safety Performance Functions and Crash Modification Factors for Urban Roundabouts in Heterogeneous Non-Lane-Based Traffic Conditions. Transp. Res. Rec. 2023, 8, 644–661. [Google Scholar] [CrossRef]
- Gayah, V.V.; Donnell, E.T.; Zhang, P. Crash modification factors for high friction surface treatment on horizontal curves of two-lane highways: A combined propensity scores matching and empirical Bayes before-after approach. Accid. Anal. Prev. 2024, 199, 107536. [Google Scholar] [CrossRef]
- Park, J.; Abdel-Aty, M.; Wang, J.; Lee, C. Assessment of safety effects for widening urban roadways in developing crash modification functions using nonlinearizing link functions. Accid. Anal. Prev. 2015, 79, 80–87. [Google Scholar] [CrossRef]
- Galgamuwa, U.; Vahl, C.I.; Dissanayake, S. Role of driver behaviors and environmental characteristics in evaluating safety effectiveness of roadway countermeasures: A novel approach of estimating crash modification factors. J. Transp. Saf. Secur. 2020, 12, 764–781. [Google Scholar] [CrossRef]
- Park, J.; Abdel-Aty, M.; Lee, J. Developing crash modification functions to assess safety effects of adding bike lanes for urban arterials with different roadway and socio-economic characteristics. Accid. Anal. Prev. 2015, 74, 179–191. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Kargel, A.; McDaniel-Wilson, C.; Kolody, K.; Zhou, H. Evaluating Safety Treatments with Crash Modification Function: Case Study on Combined Safety Treatments for Rural Two-Lane Highways. J. Transp. Eng. Part A Syst. 2023, 149, 04023021. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, L.; Huang, Z. Assessing quality of crash modification factors estimated by empirical Bayes before-after methods. J. Cent. South Univ. 2020, 27, 2259–2268. [Google Scholar] [CrossRef]
- Yan, X.; He, J.; Zhang, C.; Wang, C.; Ye, Y.; Qin, P. Temporal instability and age differences of determinants affecting injury severities in nighttime crashes. Anal. Methods Accid. Res. 2023, 38, 100268. [Google Scholar] [CrossRef]
- Alnawmasi, N.; Ali, Y.; Yasmin, S. Exploring temporal instability effects on bicyclist injury severities determinants for intersection and non-intersection-related crashes. Accid. Anal. Prev. 2024, 194, 107339. [Google Scholar] [CrossRef]
- Cafiso, S.; D’Agostino, C.; Delfino, E. From manual to automatic pavement distress detection and classification. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Naples, Italy, 26–28 June 2017; pp. 433–438. [Google Scholar]
- Roy, U.; Farid, A.; Ksaibati, K. Effects of Pavement Friction and Geometry on Traffic Crash Frequencies: A Case Study in Wyoming. Int. J. Pavement Res. Technol. 2023, 16, 1468–1481. [Google Scholar] [CrossRef]
- Montella, A.; Chiaradonna, S.; Criscuolo, G.; De Martino, S. Development and evaluation of a web-based software for crash data collection, processing and analysis. Accid. Anal. Prev. 2019, 130, 108–116. [Google Scholar] [CrossRef]
- Angelo, A.A.; Sasai, K.; Kaito, K. Assessing Critical Road Sections: A Decision Matrix Approach Considering Safety and Pavement Condition. Sustainability 2023, 15, 7244. [Google Scholar] [CrossRef]
- Chen, S.; Saeed, T.U.; Labi, S. Impact of road-surface condition on rural highway safety: A multivariate random parameters negative binomial approach. Anal. Methods Accid. Res. 2017, 16, 75–89. [Google Scholar] [CrossRef]
- Khayesi, M. The Handbook of Road Safety Measures. Inj. Prev. 2006, 12, 63–64. [Google Scholar]
- Chan, C.; Huang, B.; Yan, X.; Richards, S. Investigating effects of asphalt pavement conditions on traffic accidents in Tennessee based on the pavement management system (PMS). J. Adv. Transport. 2010, 44, 150–161. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Y.; Xing, Y. Comparison and analysis of crash frequency and rate in cross-river tunnels using random-parameter models. J. Transp. Saf. Secur. 2022, 14, 280–304. [Google Scholar] [CrossRef]
- Cheng, W.; Gill, G.S.; Zhou, J.; Ensch, J.L.; Kwong, J.; Jia, X. Alternative multivariate multimodal crash frequency models. J. Transp. Saf. Secur. 2019, 12, 628–652. [Google Scholar] [CrossRef]
- Aguilar, C.; Russo, B.J.; Mohebbi, A.; Akbariyeh, S. Analysis of factors affecting the frequency of crashes on interstate freeways by vehicle type considering multiple weather variables. J. Transp. Saf. Secur. 2022, 14, 973–1001. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M. Utilizing support vector machine in real-time crash risk evaluation. Accid. Anal. Prev. 2013, 51, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Cai, M.; Tang, F.; Fu, X. A Bayesian Bivariate Random Parameters and Spatial-Temporal Negative Binomial Lindley Model for Jointly Modeling Crash Frequency by Severity: Investigation for Chinese Freeway Tunnel Safety. IEEE Access 2022, 10, 38045–38064. [Google Scholar] [CrossRef]
- Wen, H.E.A.; Zhang, X.; Zeng, Q.; Sze, N.N. Bayesian spatial-temporal model for the main and interaction effects of roadway and weather characteristics on freeway crash incidence. Accid. Anal Prev. 2019, 132, 105249. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; He, S.; Zhai, X.; Wang, Z.; Fu, X. Estimating mountainous freeway crash rate: Application of a spatial model with three-dimensional (3D) alignment parameters. Accid. Anal. Prev. 2022, 170, 106634. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Tarko, A.; Meng, X. Investigating factors of crash frequency with random effects and random parameters models: New insights from Chinese freeway study. Accid. Anal. Prev. 2018, 120, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Alnawmasi, N.; Mannering, F. Unobserved heterogeneity and temporal instability in the analysis of work-zone crash-injury severities. Anal. Methods Accid. Res. 2020, 28, 100130. [Google Scholar] [CrossRef]
- Mannering, F.L.; Shankar, V.; Bhat, C.R. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Xu, C.; Li, Z.; Yang, Z. A Markov switching regression analysis of freeway crash risks considering spatial effect. Transport 2020, 173, 159–170. [Google Scholar] [CrossRef]
- Hussain, F.; Ali, Y.; Li, Y.; Haque, M.M. Real-time crash risk forecasting using Artificial-Intelligence based video analytics: A unified framework of generalised extreme value theory and autoregressive integrated moving average model. Anal. Methods Accid. Res. 2023, 40, 100302. [Google Scholar] [CrossRef]
- Chang, F.; Huang, H.; Chan, A.H.; Man, S.S.; Gong, Y.; Zhou, H. Capturing long-memory properties in road fatality rate series by an autoregressive fractionally integrated moving average model with generalized autoregressive conditional heteroscedasticity: A case study of Florida, the United States, 1975–2018. J. Saf. Res. 2022, 81, 216–224. [Google Scholar] [CrossRef]
- Wang, Y.; Kockelman, K.M. A Poisson-lognormal conditional-autoregressive model for multivariate spatial analysis of pedestrian crash counts across neighborhoods. Accid. Anal. Prev. 2013, 60, 71–84. [Google Scholar] [CrossRef]
- Hou, Q.; Huo, X.; Leng, J. A correlated random parameters tobit model to analyze the safety effects and temporal instability of factors affecting crash rates. Accid. Anal. Prev. 2020, 134, 105326. [Google Scholar] [CrossRef]
- Highway Technical Condition Evaluation Standard. In Institute of Highway Science, Ministry of Transportation and Communications. 2018.
- Zhao, L.; Li, F.; Sun, D.; Dai, F. Highway Traffic Crash Risk Prediction Method considering Temporal Correlation Characteristics. J. Adv. Transport. 2023, 2023, 9695433. [Google Scholar] [CrossRef]
- Zheng, L.; Hou, Q.; Meng, X. Comparison of modelling methods accounting for temporal correlation in crash counts. J. Transp. Saf. Secur. 2020, 12, 245–262. [Google Scholar] [CrossRef]
- Lan, B.; Srinivasan, R. Comparison of Crash Modification Factors for Engineering Treatments Estimated by Before–After Empirical Bayes and Propensity Score Matching Methods. Transp. Res. Rec. 2021, 2675, 148–160. [Google Scholar] [CrossRef]
- Wang, K.; Shirani-Bidabadi, N.; Shaon MR, R.; Zhao, S.; Jackson, E. Correlated mixed logit modeling with heterogeneity in means for crash severity and surrogate measure with temporal instability. Accid. Anal. Prev. 2021, 160, 106332. [Google Scholar] [CrossRef]
- Hussein, N.A.; Hassan, R.; Fahey, M.T. Effect of pavement condition and geometrics at signalised intersections on casualty crashes. J. Saf. Res. 2021, 76, 276–288. [Google Scholar] [CrossRef]
- Sawtelle, A.; Shirazi, M.; Garder, P.E.; Rubin, J. Driver, roadway, and weather factors on severity of lane departure crashes in Maine. J. Saf. Res. 2023, 84, 306–315. [Google Scholar] [CrossRef]
- Wu, L.; Meng, Y.; Kong, X.; Zou, Y. Incorporating survival analysis into the safety effectiveness evaluation of treatments: Jointly modeling crash counts and time intervals between crashes. J. Transp. Saf. Secur. 2022, 14, 338–358. [Google Scholar] [CrossRef]
- Assemi, B.; Hickman, M. Relationship between heavy vehicle periodic inspections, crash contributing factors and crash severity. Transp. Res. Part A Policy Pract. 2018, 113, 441–459. [Google Scholar] [CrossRef]
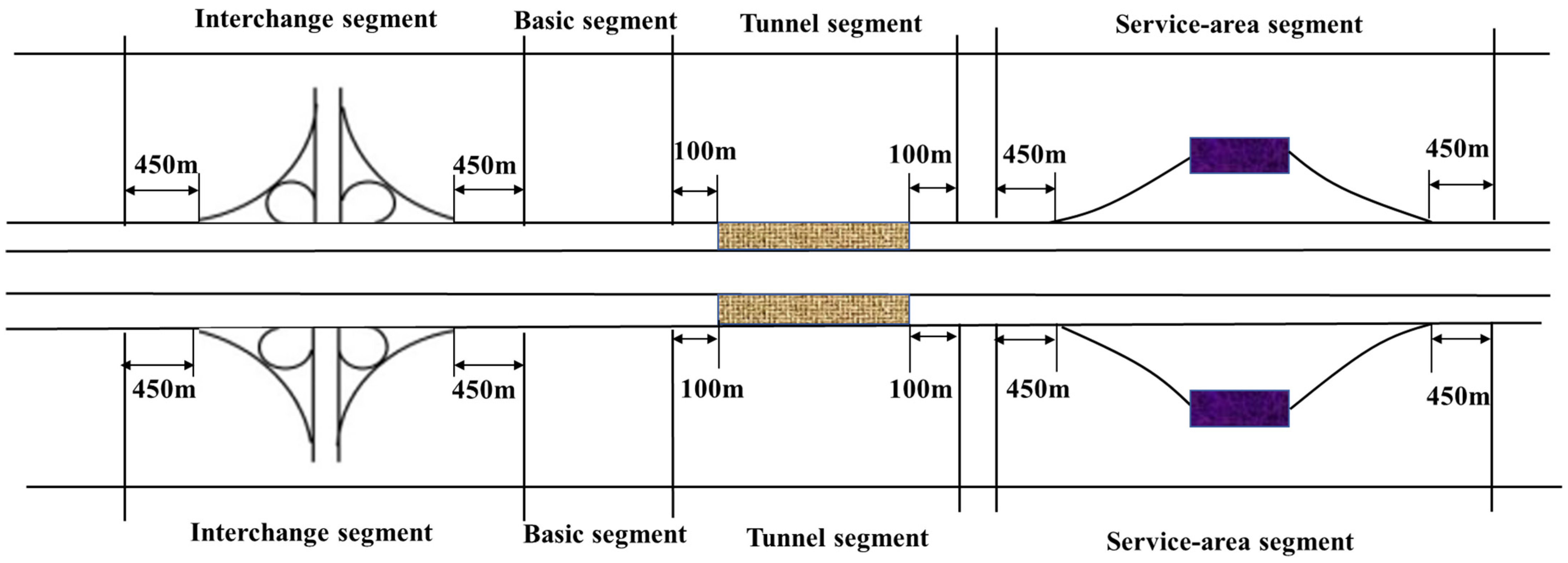
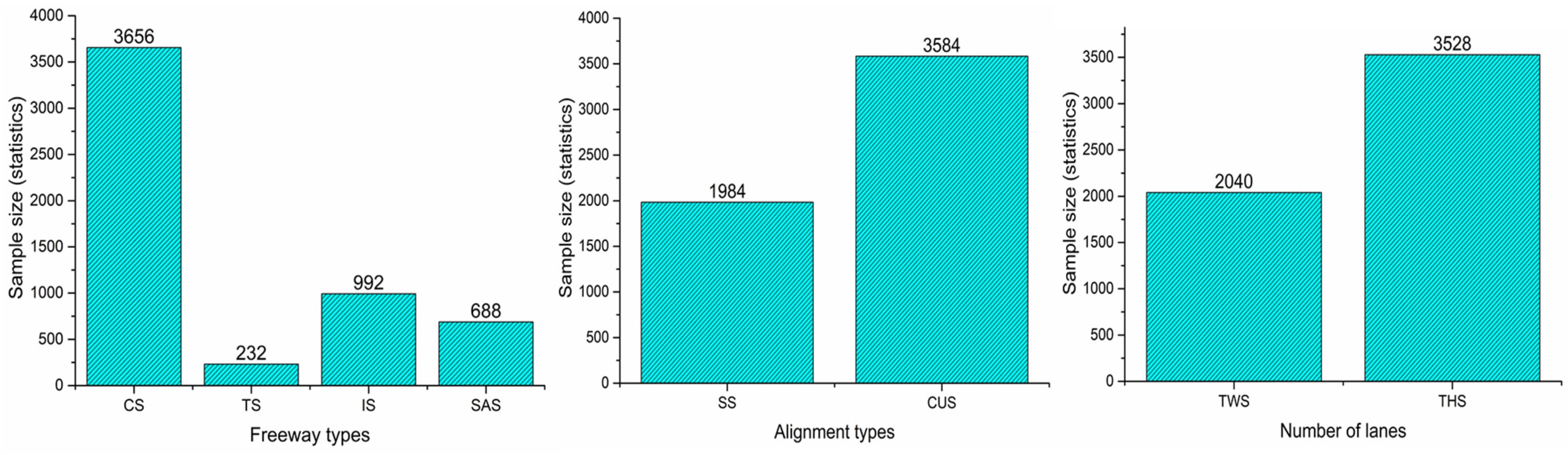
| Freeways | Length (km) | Design Speed (km/h) | Number of Interchanges | Number of Service Areas | Number of Tunnels |
|---|---|---|---|---|---|
| Kaiyang | 125 | 100 | 12 | 2 | 0 |
| Yangmao | 79 | 100 | 16 | 1 | 0 |
| Maozhan | 102 | 120 | 8 | 1 | 0 |
| Lianhuai | 186 | 100 | 14 | 2 | 20 |
| Huaisan | 116 | 120 | 8 | 3 | 30 |
| Total | 611 | -- | 50 | 8 | 50 |
| Indicators | CS | TS | IS | SAS | SS | CUS | TWS | THS |
|---|---|---|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | |
| PCI | 97.151 | 97.342 | 95.404 | 95.816 | 96.935 | 96.694 | 97.769 | 96.208 |
| RQI | 94.452 | 89.241 | 93.506 | 93.483 | 93.898 | 94.077 | 94.638 | 93.652 |
| SRI | 92.412 | 87.832 | 90.313 | 91.325 | 92.191 | 91.565 | 90.441 | 92.567 |
| QADT (1000 veh/d) | 21.869 | 7.336 | 23.724 | 20.906 | 23.123 | 20.654 | 7.323 | 29.753 |
| IVE (%) | 0.742 | 0.752 | 0.736 | 0.736 | 0.74 | 0.741 | 0.755 | 0.733 |
| IIVE(%) | 0.029 | 0.011 | 0.025 | 0.02 | 0.031 | 0.026 | 0.011 | 0.037 |
| IVVE(%) | 0.025 | 0.009 | 0.022 | 0.018 | 0.027 | 0.022 | 0.009 | 0.032 |
| VVE(%) | 0.114 | 0.16 | 0.128 | 0.011 | 0.111 | 0.124 | 0.158 | 0.098 |
| SMR(%) | 0.417 | 0.404 | 0.414 | 0.409 | 0.418 | 0.414 | 0.401 | 0.424 |
| TR(%) | 0.066 | 0.062 | 0.067 | 0.068 | 0.066 | 0.066 | 0.118 | 0.067 |
| WD(%) | 0.841 | 0.902 | 0.847 | 0.858 | 0.837 | 0.851 | 0.904 | 0.812 |
| WP(%) | 0.169 | 0.181 | 0.184 | 0.188 | 0.17 | 0.175 | 0.176 | 0.172 |
| Crashes | 0.259 | 0.263 | 0.445 | 0.406 | 0.298 | 0.291 | 0.094 | 0.409 |
| Indicators | Calculation Methods | Parameter Analysis |
|---|---|---|
| PCI |
| |
| RQI |
| |
| SRI |
|
| Vehicle Types | Classification Standard | Typical Vehicles | |||
|---|---|---|---|---|---|
| Height of Head/m | Number of Axles | Number of Tires | Wheel Base/m | ||
| 1 | <1.3 | 2 | 2–4 | <3.2 | Motorcycles, Cars, Pickup trucks |
| 2 | ≥1.3 | 2 | 4 | ≥3.2 | Minivans, Light trucks, Minibus |
| 3 | ≥1.3 | 2 | 6 | ≥3.2 | Medium buses, Medium trucks, Large ordinary buses |
| 4 | ≥1.3 | 3 | 6–10 | ≥3.2 | Large luxury buses, Large trucks, Large trailers, 20-foot container vehicles |
| 5 | ≥1.3 | >3 | >10 | ≥3.2 | Heavy trucks, Heavy trailers, 40-foot container vehicles |
| CS | TS | IS | SAS | |||||
|---|---|---|---|---|---|---|---|---|
| Indicators | NB | TC-NB | NB | TC-NB | NB | TC-NB | NB | TC-NB |
| DIC | 4966 | 4540 | 2504 | 2319 | 1597 | 1304 | 1724 | 1618 |
| MAD | 2.297 | 2.008 | 2.079 | 1.828 | 2.674 | 2.286 | 2.497 | 2.403 |
| RMSE | 2.401 | 2.167 | 2.205 | 1.982 | 2.791 | 2.548 | 2.619 | 2.741 |
| 0.594 ** | 0.711 ** | 0.417 ** | 0.659 * | |||||
| 0.371 ** | 0.489 ** | 0.268 ** | 0.396 * | |||||
| SS | CUS | TWS | THS | |||||
| Indicators | NB | TC-NB | NB | TC-NB | NB | TC-NB | NB | TC-NB |
| DIC | 2397 | 2353 | 4177 | 4068 | 4755 | 4253 | 5427 | 5162 |
| MAD | 2.093 | 2.055 | 2.374 | 2.09 | 3.014 | 2.752 | 2.177 | 1.742 |
| RMSE | 2.288 | 2.276 | 2.459 | 2.258 | 3.162 | 2.861 | 2.401 | 1.974 |
| 0.462 * | 0.538 ** | 0.253 ** | 0.976 * | |||||
| 0.379 * | 0.201 ** | 0.129 ** | 0.715 * | |||||
| Variables | CS | SAS | TS | IS | SS | CUS | TWS | THS |
|---|---|---|---|---|---|---|---|---|
| Sample length (SL) | 0.638 | 0.397 | −0.009 | 0.804 | 0.700 | 0.660 | 0.003 | 0.712 |
| PCI | −0.015 | −0.028 | −0.115 | |||||
| RQI | −0.017 | −0.061 | −0.102 | −0.287 | −0.021 | |||
| SRI | −0.015 | −0.001 | −0.045 | −0.038 | −0.126 | −0.041 | ||
| QADT | 1.427 | 0.078 | 1.273 | 1.353 | 1.507 | 1.320 | 1.767 | 0.976 |
| IVE | 8.323 | 18.452 | 5.309 | 12.138 | 5.014 | 10.457 | 4.940 | 6.940 |
| IIVE | −4.975 | −1.245 | −8.117 | −2.110 | −4.435 | −4.261 | −3.461 | |
| IVVE | −12.731 | −58.232 | −30.818 | −19.103 | −14.343 | −18.359 | −2.643 | −5.731 |
| VVE | 7.334 | 26.989 | 36.880 | 21.368 | 6.151 | 7.160 | 32.406 | 9.872 |
| SMR | 3.536 | 4.606 | 1.678 | 2.171 | 0.883 | |||
| TR | −12.007 | −18.693 | −4.077 | −3.629 | −1.325 | |||
| _cons | −28.081 | −17.802 | 135.042 | −20.040 | −25.397 | −22.032 | 14.887 |
| Variables | CS | |||||
|---|---|---|---|---|---|---|
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| PCI | −0.015 | 95 | 74 | 100 | 1.370 | 0.928 |
| RQI | −0.017 | 93 | 78 | 99 | 1.290 | 0.903 |
| SRI | −0.029 | 91 | 64 | 99 | 2.188 | 0.793 |
| Variables | SAS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| PCI | −0.028 | 95 | 74 | 100 | 1.800 | 0.869 |
| RQI | −0.061 | 93 | 78 | 99 | 2.497 | 0.694 |
| SRI | −0.001 | 91 | 64 | 99 | 1.027 | 0.992 |
| Variables | IS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| RQI | −0.102 | 93 | 78 | 99 | 4.618 | 0.542 |
| SRI | −0.045 | 91 | 64 | 99 | 3.370 | 0.698 |
| Variables | SS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SRI | −0.038 | 91 | 64 | 99 | 2.790 | 0.738 |
| Variables | CUS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| PCI | −0.115 | 95 | 74 | 100 | 11.190 | 0.563 |
| RQI | −0.107 | 93 | 78 | 99 | 4.978 | 0.526 |
| SRI | −0.126 | 91 | 64 | 99 | 30.024 | 0.365 |
| Variables | TWS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| RQI | −0.021 | 93 | 78 | 99 | 1.370 | 0.882 |
| SRI | −0.041 | 91 | 64 | 99 | 3.025 | 0.720 |
| Variables | CS | |||||
|---|---|---|---|---|---|---|
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.427 | 2.5 | 1.5 | 3.5 | 0.240 | 4.166 |
| IVE | 8.323 | 0.7 | 0.5 | 0.9 | 0.189 | 5.284 |
| VVE | 7.334 | 0.1 | 0.05 | 0.15 | 0.693 | 1.443 |
| Variables | SAS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 0.078 | 2.5 | 1.5 | 3.5 | 0.925 | 1.081 |
| IVE | 10.452 | 0.7 | 0.5 | 0.9 | 0.124 | 8.088 |
| VVE | 26.989 | 0.1 | 0.05 | 0.15 | 0.259 | 3.855 |
| Variables | TS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.273 | 2.5 | 1.5 | 3.5 | 0.280 | 3.572 |
| IVE | 5.309 | 0.7 | 0.5 | 0.9 | 0.346 | 2.892 |
| VVE | 36.88 | 0.1 | 0.05 | 0.15 | 0.158 | 6.322 |
| Variables | IS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.353 | 2.5 | 1.5 | 3.5 | 0.258 | 3.869 |
| IVE | 12.138 | 0.7 | 0.5 | 0.9 | 0.088 | 11.332 |
| VVE | 21.368 | 0.1 | 0.05 | 0.15 | 0.344 | 2.911 |
| Variables | SS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.507 | 2.5 | 1.5 | 3.5 | 0.222 | 4.513 |
| IVE | 5.014 | 0.7 | 0.5 | 0.9 | 0.367 | 2.726 |
| VVE | 6.151 | 0.1 | 0.05 | 0.15 | 0.735 | 1.360 |
| Variables | CUS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.32 | 2.5 | 1.5 | 3.5 | 0.267 | 3.743 |
| IVE | 10.457 | 0.7 | 0.5 | 0.9 | 0.124 | 8.096 |
| VVE | 7.16 | 0.1 | 0.05 | 0.15 | 0.699 | 1.430 |
| Variables | TWS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 1.767 | 2.996 | 1.5 | 3.5 | 0.071 | 2.437 |
| IVE | 4.94 | 0.7 | 0.5 | 0.9 | 0.372 | 2.686 |
| VVE | 32.406 | 0.1 | 0.05 | 0.15 | 0.198 | 5.055 |
| Variables | THS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| QADT | 0.976 | 2.996 | 1.5 | 3.5 | 0.232 | 1.635 |
| IVE | 6.94 | 0.7 | 0.5 | 0.9 | 0.250 | 4.007 |
| VVE | 9.872 | 0.1 | 0.05 | 0.15 | 0.610 | 1.638 |
| Variables | CS | |||||
|---|---|---|---|---|---|---|
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SMR | 3.536 | 0.4 | 0.145 | 0.662 | 0.406 | 2.525 |
| Variables | SAS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SMR | 4.606 | 0.4 | 0.135 | 0.663 | 0.295 | 3.358 |
| TR | −12.007 | 0.07 | 0 | 0.187 | 2.318 | 0.245 |
| Variables | TS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| TR | −18.693 | 0.07 | 0 | 0.187 | 3.701 | 0.112 |
| Variables | SS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SMR | 1.678 | 0.4 | 0 | 0.187 | 0.511 | 0.699 |
| Variables | CUS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SMR | 2.171 | 0.4 | 0.135 | 0.663 | 0.563 | 1.770 |
| TR | −4.007 | 0.07 | 0 | 0.187 | 1.324 | 0.626 |
| Variables | TWS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| TR | −3.629 | 0.07 | 0 | 0.187 | 1.289 | 0.654 |
| Variables | THS | |||||
| Coefficients | Xbase | Xmin | Xmax | CMF(Xmin) | CMF(Xmax) | |
| SMR | 0.883 | 0.4 | 0.135 | 0.663 | 0.791 | 1.261 |
| TR | −1.325 | 0.07 | 0 | 0.187 | 1.097 | 0.856 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Huang, Z.; Kuang, A.; Yu, J.; Cai, M. Estimation of Crash Modification Factors (CMFs) in Mountain Freeways: Considering Temporal Instability in Crash Data. Sustainability 2024, 16, 5068. https://doi.org/10.3390/su16125068
Zhang L, Huang Z, Kuang A, Yu J, Cai M. Estimation of Crash Modification Factors (CMFs) in Mountain Freeways: Considering Temporal Instability in Crash Data. Sustainability. 2024; 16(12):5068. https://doi.org/10.3390/su16125068
Chicago/Turabian StyleZhang, Liang, Zhongxiang Huang, Aiwu Kuang, Jie Yu, and Mingmao Cai. 2024. "Estimation of Crash Modification Factors (CMFs) in Mountain Freeways: Considering Temporal Instability in Crash Data" Sustainability 16, no. 12: 5068. https://doi.org/10.3390/su16125068
APA StyleZhang, L., Huang, Z., Kuang, A., Yu, J., & Cai, M. (2024). Estimation of Crash Modification Factors (CMFs) in Mountain Freeways: Considering Temporal Instability in Crash Data. Sustainability, 16(12), 5068. https://doi.org/10.3390/su16125068






