Study on the Particle Strength and Crushing Patterns of Coal Gangue Coarse-Grained Subgrade Fillers
Abstract
:1. Introduction
2. Particle Crushing Test
2.1. Test Materials and Equipment
2.2. Experimental Programme
3. Particle Strength
3.1. Relationship between Load and Displacement of Particle Crushing
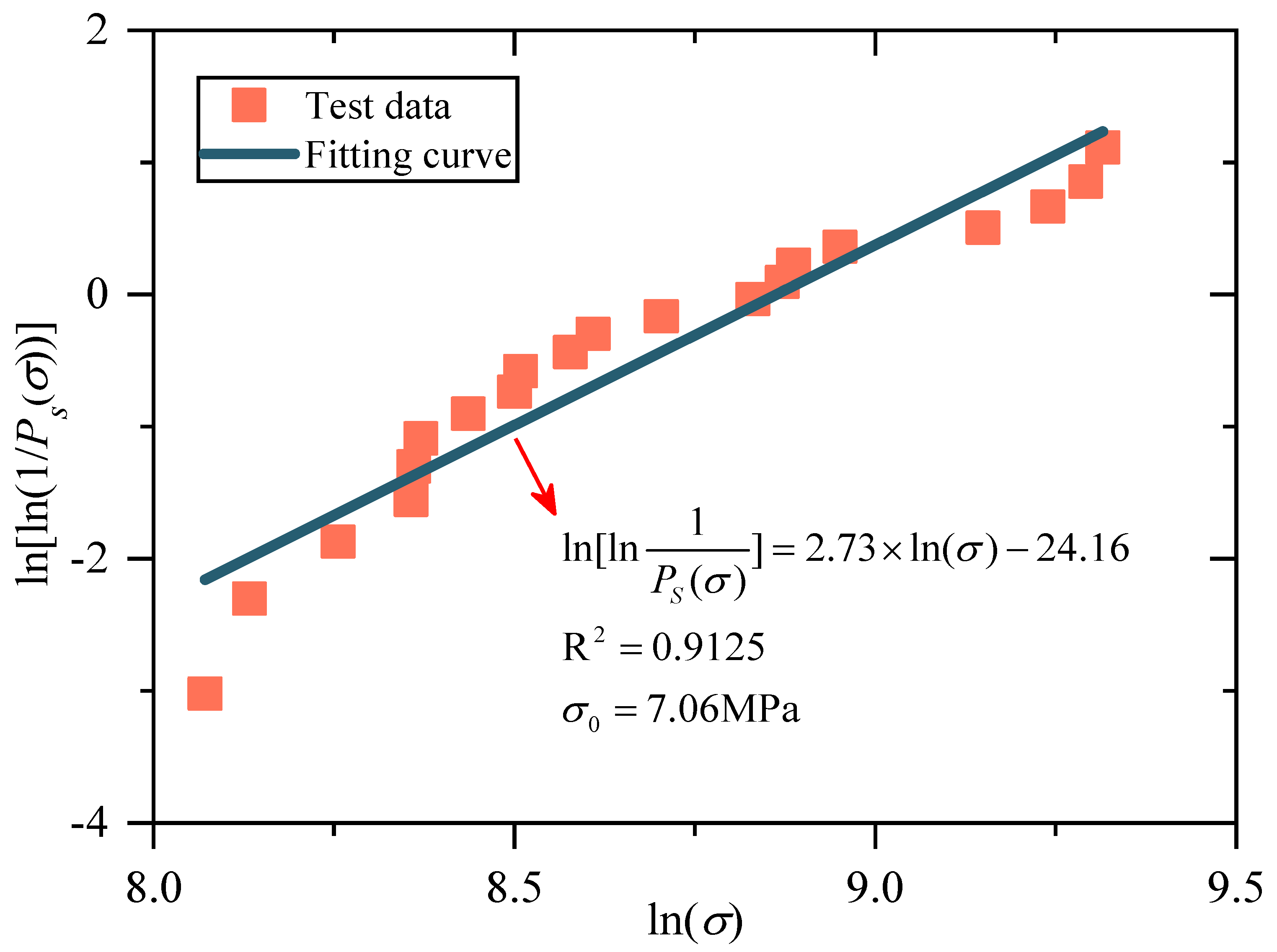
3.2. Particle Crushing Strength
4. Particle Crushing Properties
4.1. Particle Crushing Patterns
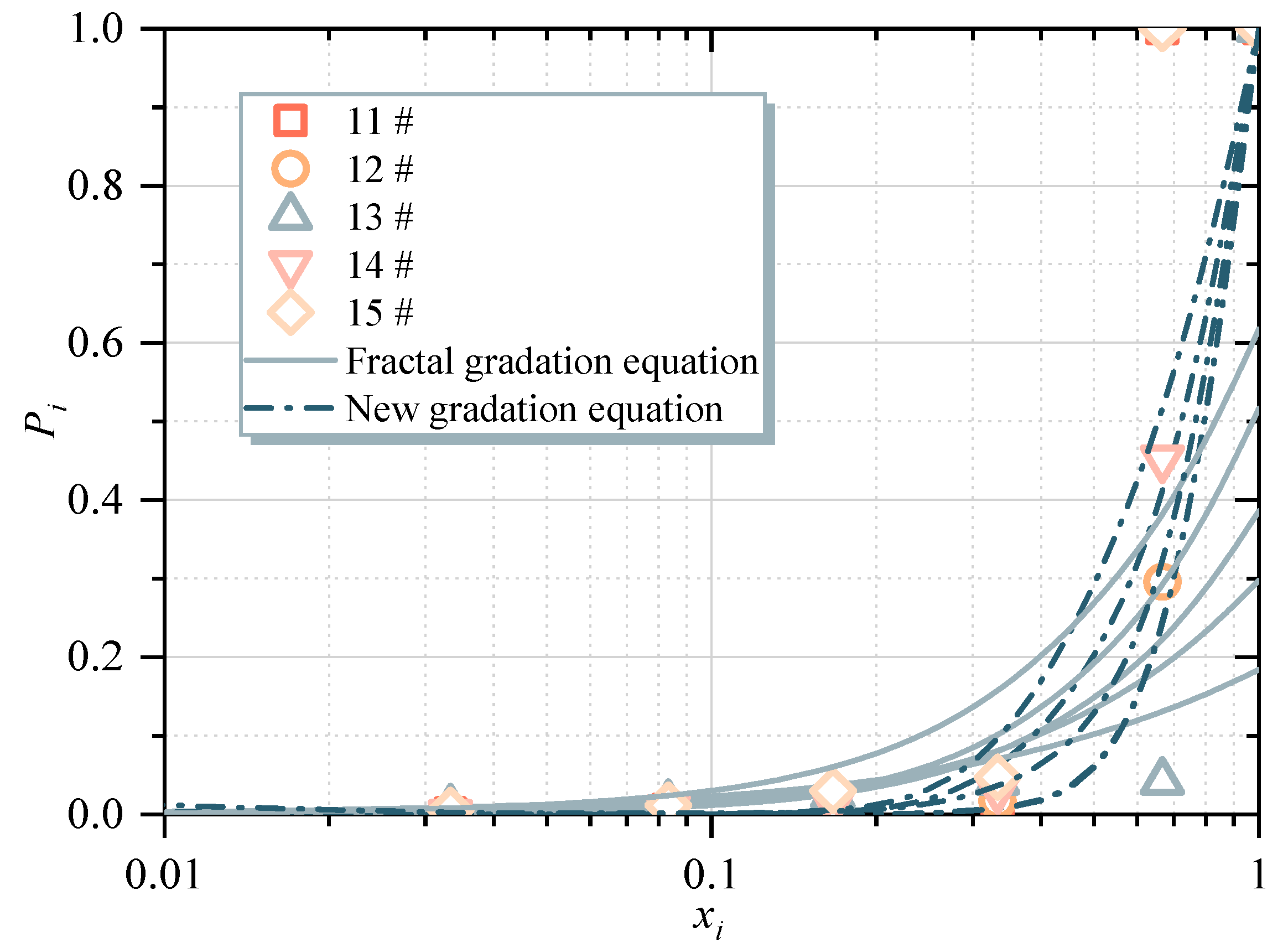
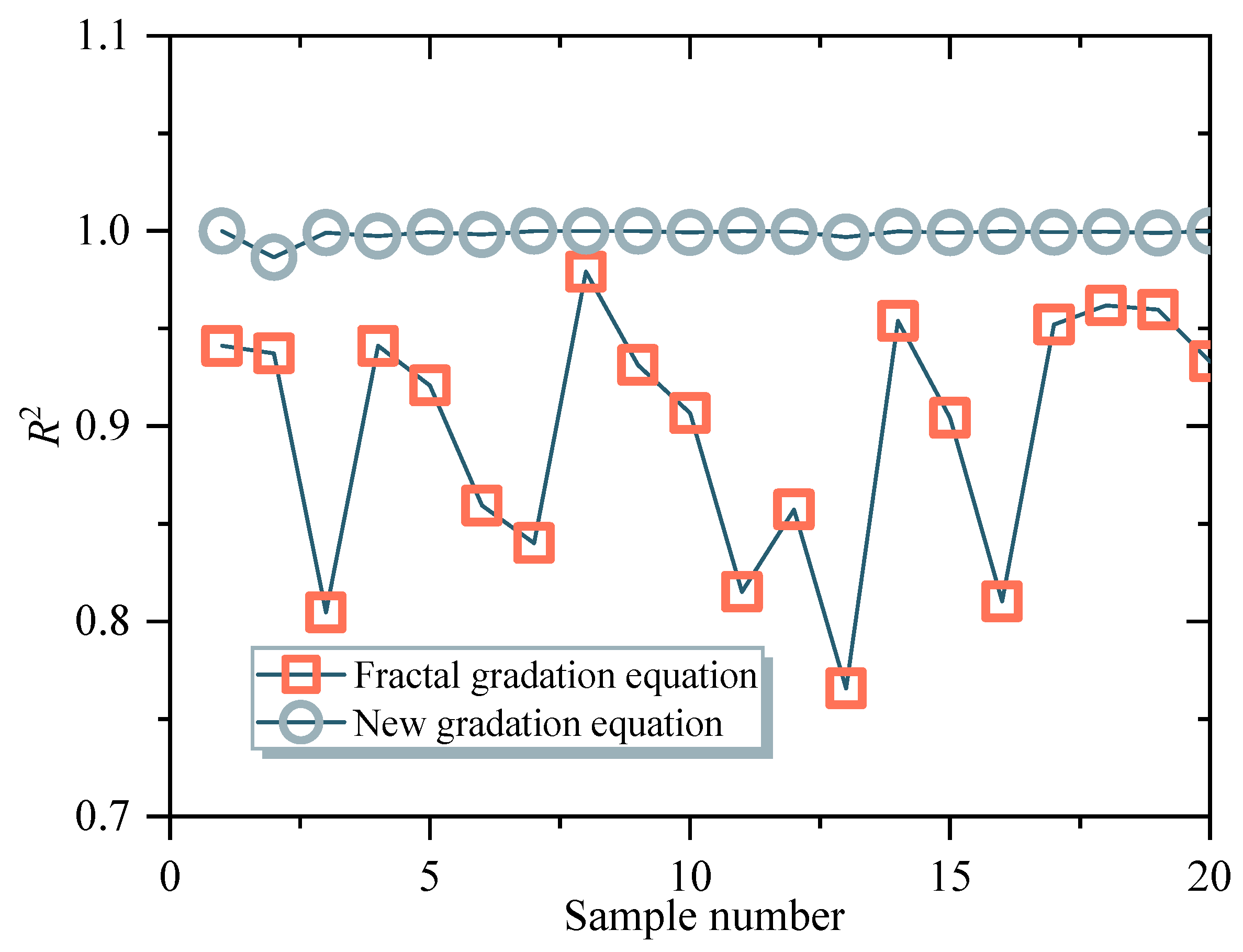
4.2. Particle Gradation after Crushing
5. Conclusions
- (1)
- With the increase in displacement, the relationship curves between load and displacement for CGSF particle crushing can be divided into three types. ① The sharp corners of the particles come into contact with two loading surfaces. During the compression process, each sharp corner is gradually crushed, causing the curve to fluctuate and grow, and multiple extreme values appear. ② The sharp corners where the particles come into contact with the loading surface break and fall off, causing the load to suddenly change to zero. A curve, similar to the first type, with some troughs reaching zero appears. ③ The curve shows approximately linear growth, and failure occurs at small displacements, exhibiting the characteristics of brittle rock failure.
- (2)
- The distribution of particle crushing strength is between 3.02 and 11.11 MPa, and the dispersion of particle strength is relatively large. However, the crushing probability of coal gangue particles and the applied load well satisfy the Weibull distribution function.
- (3)
- A new visual analysis method for the crushing patterns of particles is provided through image analysis. After crushing coal gangue particles, the larger particles mainly present a block shape, the smaller particles are mainly in the form of powder, and the middle-sized particles are mainly flaky and acicular. Particles with a size greater than 5 mm are mainly flaky; acicular particles are the least common.
- (4)
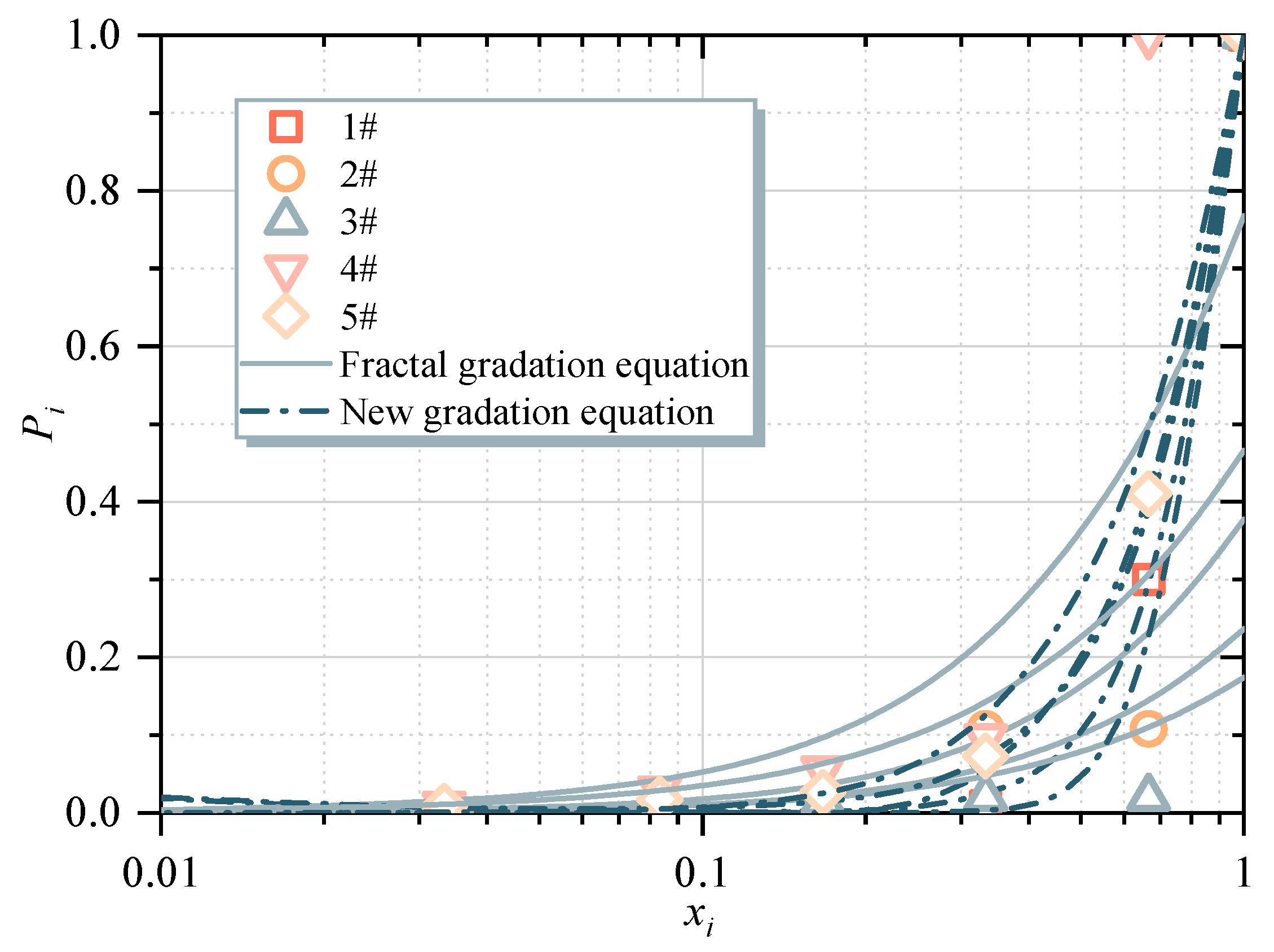
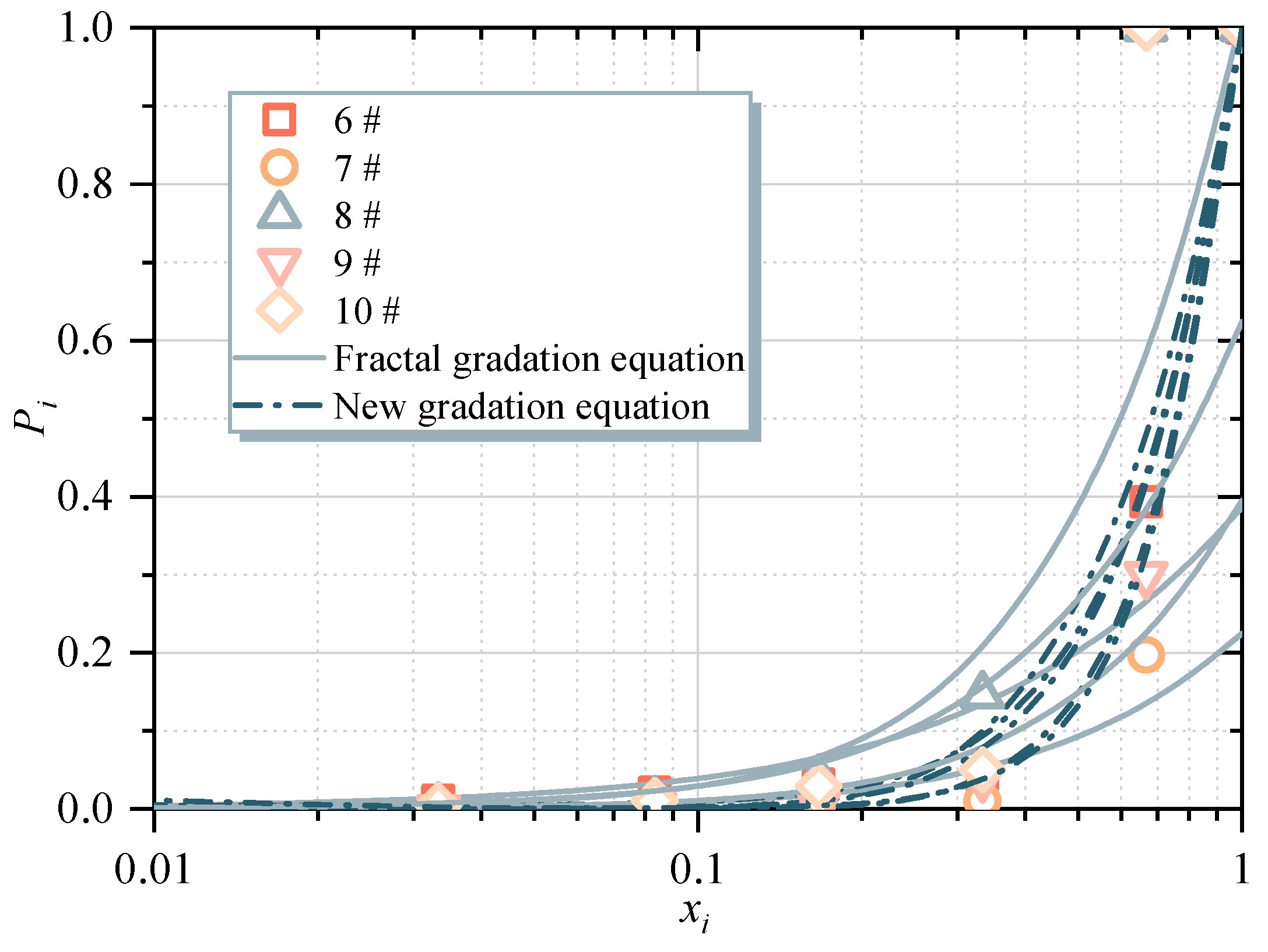
- The particle size distribution of coal gangue fragments after crushing was analyzed, and a new gradation equation based on the traditional fractal model was proposed to describe the crushed particles. Comparative analysis shows that the new model has better descriptive ability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Li, J.; Zhang, D.; Fan, G.; Zhang, W.; Guo, Y. Microscopic fabric evolution and macroscopic deformation response of gangue solid waste filler considering block shape under different confining pressures. Sci. Rep. 2022, 12, 7388. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Yan, H.; Zhang, J.; Zhou, N. Compaction property prediction of mixed gangue backfill materials using hybrid intelligence models: A new approach. Constr. Build. Mater. 2020, 247, 118633. [Google Scholar] [CrossRef]
- Tang, X.; Wan, W.; Zhang, Z.; Gao, W.; Wang, Y. Residual deformation of coal gangue subgrade filler under multi-vibration cyclic loading. Sci. Rep. 2023, 13, 8203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, H.; Wang, J.; Lei, M.; Chen, Z. Stress–strain characteristics of FRP–PVC confined spontaneous combustion gangue concrete columns. Sci. Rep. 2024, 14, 1482. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Long, G.; Ma, K.; Ma, H.; Wang, W.; Zhang, C.; Xie, Y. Preparation of Green Low Strength Mixture for Foundation Reinforcement Treatment by Using Fly Ash and Waste Coal Gangue. Materials 2020, 13, 664. [Google Scholar] [CrossRef]
- Long, G.; Li, L.; Li, W.; Ma, K.; Dong, W.; Bai, C.; Zhou, J.L. Enhanced mechanical properties and durability of coal gangue reinforced cement-soil mixture for foundation treatments. J. Clean. Prod. 2019, 231, 468–482. [Google Scholar] [CrossRef]
- Li, J.; Wang, J. Comprehensive utilization and environmental risks of coal gangue: A review. J. Clean. Prod. 2019, 239, 117946. [Google Scholar] [CrossRef]
- Wang, J.; Qin, Q.; Hu, S.; Wu, K. A concrete material with waste coal gangue and fly ash used for farmland drainage in high groundwater level areas. J. Clean. Prod. 2016, 112, 631–638. [Google Scholar] [CrossRef]
- Ma, S.; Lu, P.; Li, C.; Guo, Z.; Nie, X. Effect of Soil Amendments on Growth of Soybean in Coal Gangue Contaminated Soil. Ecol. Rural Environ. 2011, 27, 101–103. [Google Scholar]
- Zhang, X.; Lin, J.; Liu, J.; Li, F.; Pang, Z. Investigation of Hydraulic-Mechanical Properties of Paste Backfill Containing Coal Gangue-Fly Ash and Its Application in an Underground Coal Mine. Energies 2017, 10, 1309. [Google Scholar] [CrossRef]
- Li, M.; Li, A.; Zhang, J.; Huang, Y.; Li, J. Effects of particle sizes on compressive deformation and particle breakage of gangue used for coal mine goaf backfill. Powder Technol. 2020, 360, 493–502. [Google Scholar] [CrossRef]
- Li, L.H.; Long, G.C.; Bai, C.N.; Ma, K.L.; Wang, M.; Zhang, S. Utilization of Coal Gangue Aggregate for Railway Roadbed Construction in Practice. Sustainability 2020, 12, 4583. [Google Scholar] [CrossRef]
- Liu, B.K.; Fan, J.S.; Hu, H.M.; Fu, L.H. Recycled Technology of Urban Road Construction Waste and Miscellaneous Fill Used as Subgrade Fillings. In Proceedings of 1st International Conference on Civil Engineering, Architecture and Building Materials (CEABM 2011), Haikou, China, 18–20 June 2011; pp. 3460–3464. [Google Scholar]
- Wang, H.Y.; She, H.; Xu, J.; Liang, L.H. A Three-Point Hyperbolic Combination Model for the Settlement Prediction of Subgrade Filled with Construction and Demolition Waste. Materials 2020, 13, 1959. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.T.; Wang, Y.H.; Gao, W.H.; Hu, W.; Liu, S.K. Permanent Deformation and Its Unified Model of Coal Gangue Subgrade Filler under Traffic Cyclic Loading. Appl. Sci. 2023, 13, 4128. [Google Scholar] [CrossRef]
- Jiao, S.J.; Wang, S.; Luo, F.Z. Effects of Coastal Coal Gangue Highway on Groundwater. In Proceedings of 2nd Global Conference on Civil, Structural and Environmental Engineering (GCCSEE 2013), Shenzhen, China, 28–29 September 2013; pp. 2518–2521. [Google Scholar]
- Song, G.Y.; Hui, B.; Cui, Y.J.; Ran, D.Q.; Li, Y.P.; Zhang, W.J.; Song, H.M.; Fan, X.X.; Meng, L.X. Analysis of pH and Conductivity Variation Characteristics of Coal Gangue Used inFreeway Subgrade and Its Correlation. In Proceedings of Asia Conference on Geological Research and Environmental Technology (GRET), Electrical Network, Kamakura City, Japan, 10–11 October 2020. [Google Scholar]
- Koohmishi, M.; Palassi, M. Evaluation of the Strength of Railway Ballast Using Point Load Test for Various Size Fractions and Particle Shapes. Rock Mech. Rock Eng. 2016, 49, 2655–2664. [Google Scholar] [CrossRef]
- Wang, B.; Martin, U.; Rapp, S. Discrete element modeling of the single-particle crushing test for ballast stones. Comput. Geotech. 2017, 88, 61–73. [Google Scholar] [CrossRef]
- Cavarretta, I.; O’Sullivan, C. The mechanics of rigid irregular particles subject to uniaxial compression. Géotechnique 2012, 62, 681–692. [Google Scholar] [CrossRef]
- Hiramatsu, Y.; Oka, Y. Determination of the tensile strength of rock by a compression test of an irregular test piece. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1966, 3, 89–90. [Google Scholar] [CrossRef]
- Jaeger, J.C. Failure of rocks under tensile conditions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1967, 4, 219–227. [Google Scholar] [CrossRef]
- Nakata, Y.; Hyodo, M.; Hyde, A.F.L.; Kato, Y.; Murata, H. Microscopic particle crushing of sand subjected to high pressure one-dimensional compression. Soils Found 2001, 41, 69–82. [Google Scholar] [CrossRef]
- Nakata, Y.; Kato, Y.; Hyodo, M.; Hyde, A.F.L.; Murata, H. One-dimensional compression behaviour of uniformly graded sand related to single particle crushing strength. Soils Found 2001, 41, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Coop, M.R. An investigation of breakage behaviour of single sand particles using a high-speed microscope camera. Géotechnique 2016, 66, 984–998. [Google Scholar] [CrossRef]
- Zhou, B.; Wei, D.; Ku, Q.; Wang, J.; Zhang, A. Study on the effect of particle morphology on single particle breakage using a combined finite-discrete element method. Comput. Geotech. 2020, 122, 103532. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Sullivan, J.D.; Lauzon, P.H. Experimental probability estimators for Weibull plots. J. Mater. Sci. Lett. 1986, 5, 1245–1247. [Google Scholar] [CrossRef]
- Davidge, R.W. Mechanical Behavior of Ceramics; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Al-Saoudi, N.K.S.; Hassan, K.H. Evaluation of Indirect Tensile Strength of Track Ballast Using Weibull Statistics. Geotech. Geol. Eng. 2012, 30, 1097–1102. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, C.; Deng, L.; Liu, G. Impacts of simulated acid solution on the disintegration and cation release of purple rock (mudstone) in Southwest China. Geomorphology 2018, 316, 35–43. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Gao, W.H.; Zeng, C.F.; Tang, X.Y.; Wu, J. Evolution of the disintegration breakage of red-bed soft rock using a logistic regression model. Transp. Geotech. 2020, 24, 100382. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Gao, W.H. Effect of different test methods on the disintegration behaviour of soft rock and the evolution model of disintegration breakage under cyclic wetting and drying. Eng. Geol. 2020, 279, 105888. [Google Scholar] [CrossRef]


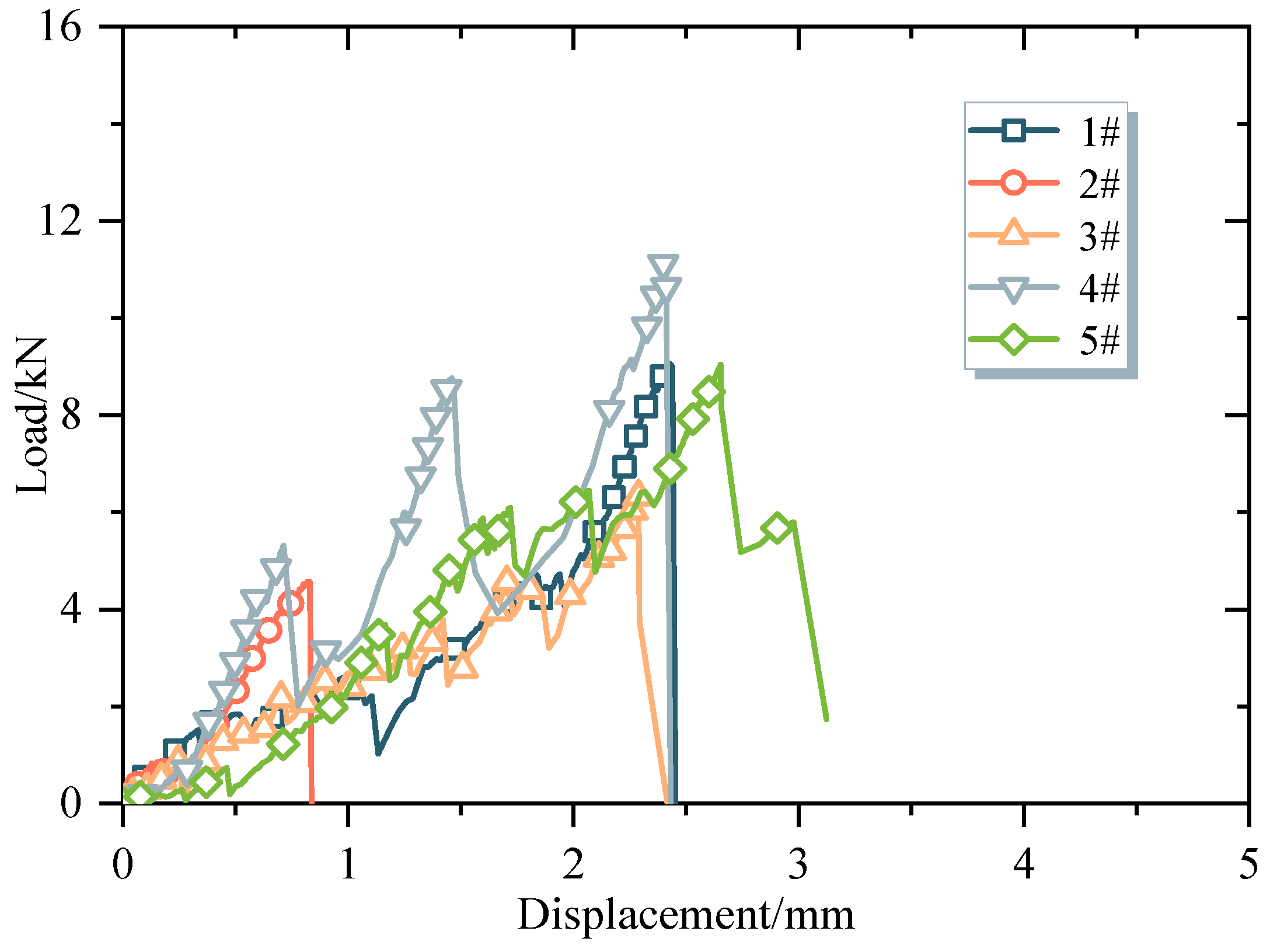

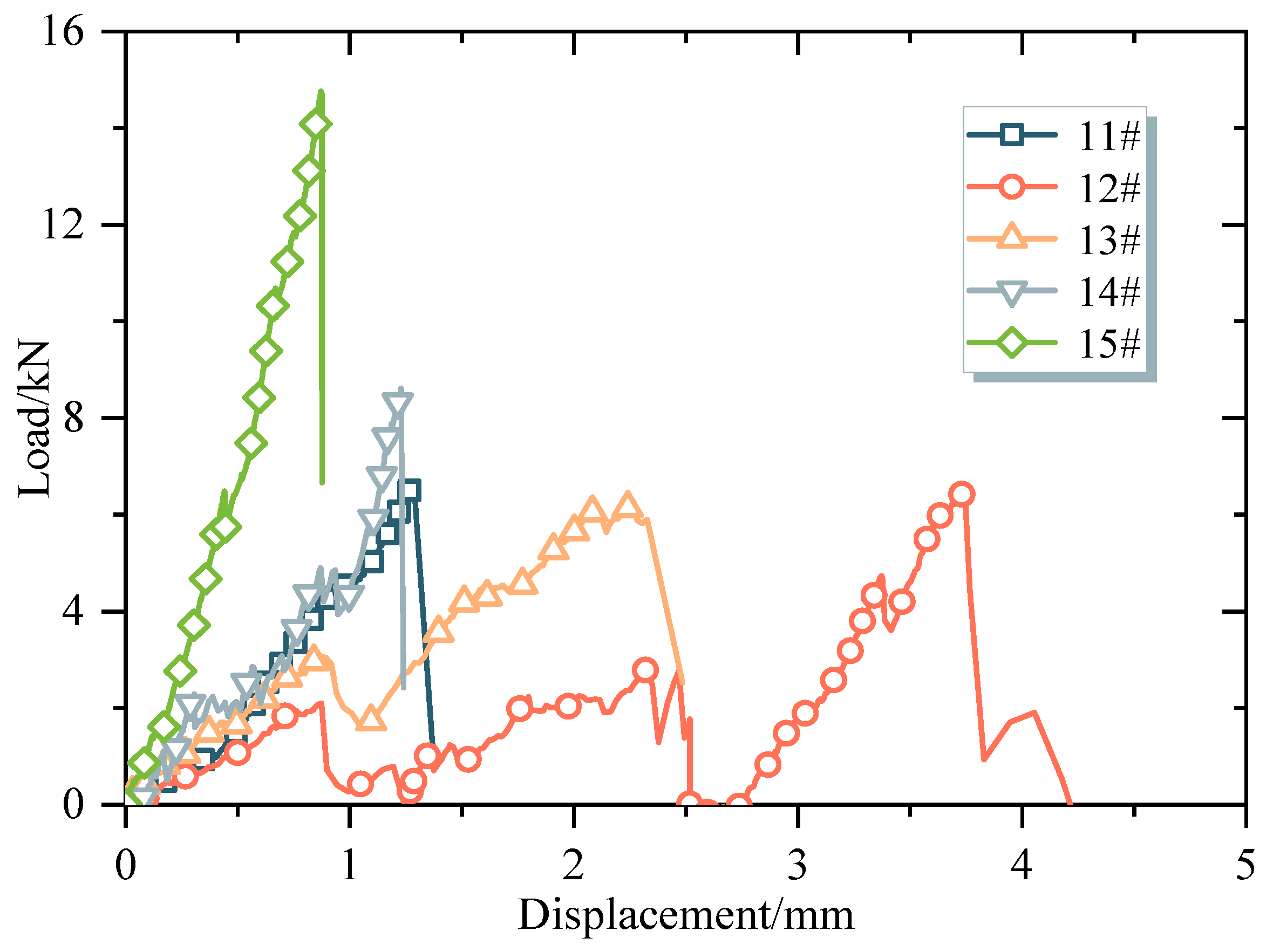
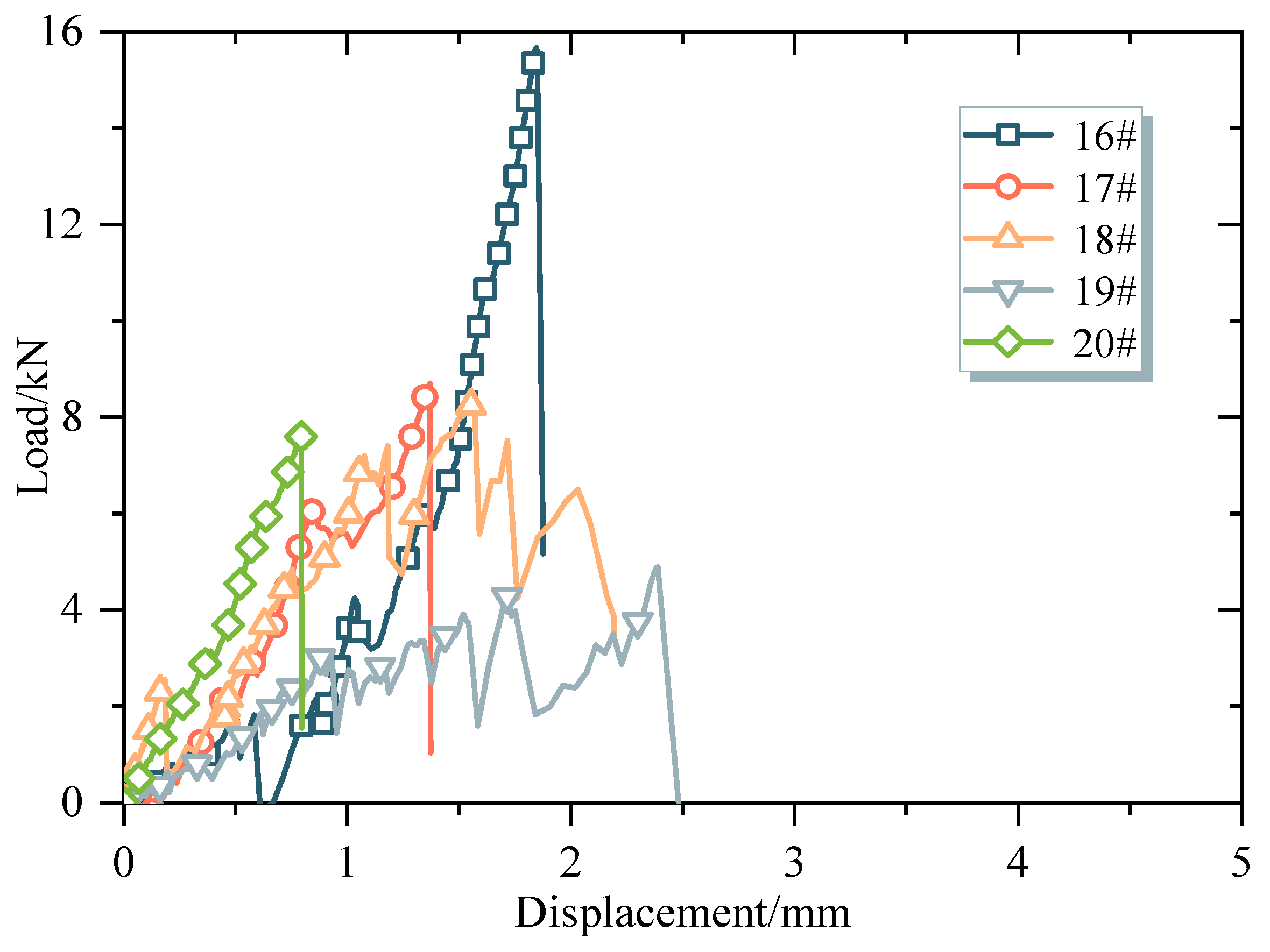
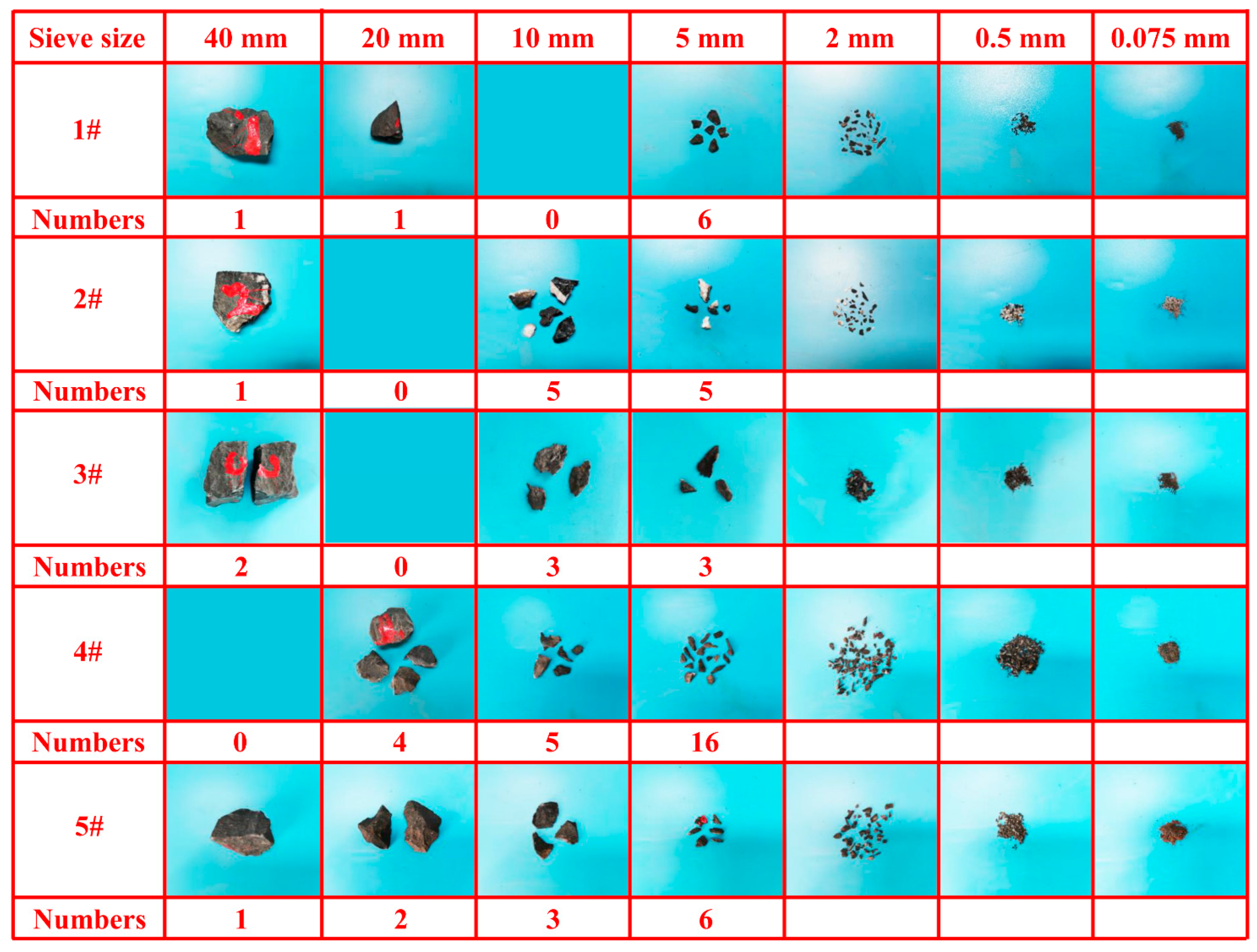


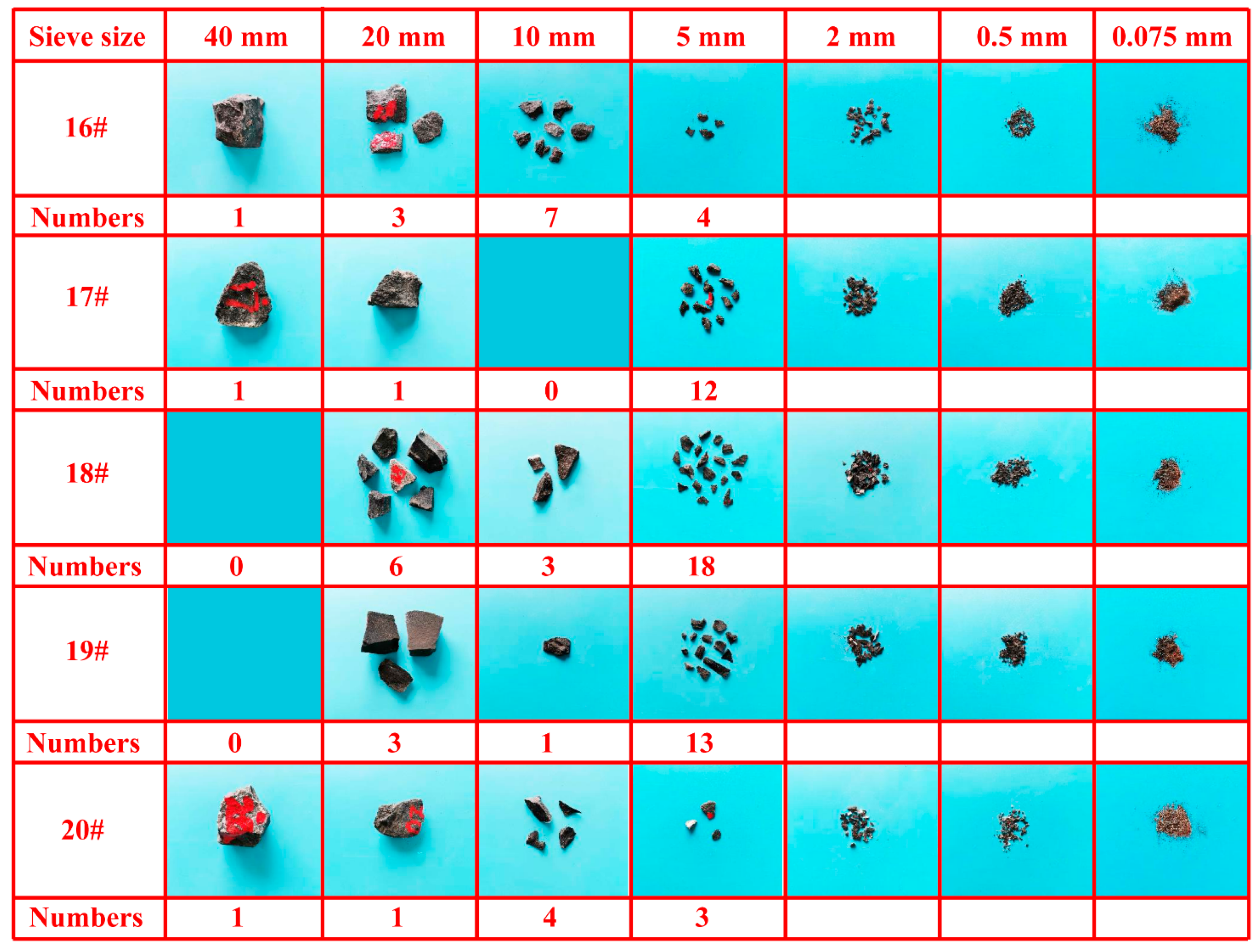

| Number | Strength (MPa) | Number | Strength (MPa) | Number | Strength (MPa) | Number | Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 1# | 6.02 | 6# | 5.31 | 11# | 3.85 | 16# | 7.13 |
| 2# | 3.20 | 7# | 5.48 | 12# | 4.26 | 17# | 4.32 |
| 3# | 4.61 | 8# | 9.41 | 13# | 3.40 | 18# | 4.96 |
| 4# | 11.11 | 9# | 10.85 | 14# | 7.24 | 19# | 4.92 |
| 5# | 6.84 | 10# | 7.72 | 15# | 10.29 | 20# | 4.27 |
| Number | Number | ||||
|---|---|---|---|---|---|
| 1# | 1.5836 | 0.9412 | 11# | 1.3757 | 0.8152 |
| 2# | 1.6014 | 0.9373 | 12# | 1.6915 | 0.8573 |
| 3# | 1.6969 | 0.8046 | 13# | 2.0620 | 0.7657 |
| 4# | 1.7780 | 0.9412 | 14# | 1.3104 | 0.9539 |
| 5# | 1.8247 | 0.9209 | 15# | 1.6188 | 0.9043 |
| 6# | 1.9636 | 0.8593 | 16# | 1.8235 | 0.8102 |
| 7# | 1.5200 | 0.8401 | 17# | 1.4717 | 0.9521 |
| 8# | 1.3642 | 0.9791 | 18# | 1.3472 | 0.9619 |
| 9# | 1.3350 | 0.9313 | 19# | 1.3388 | 0.9597 |
| 10# | 1.5981 | 0.9067 | 20# | 1.2053 | 0.9332 |
| Number | Number | ||||||
|---|---|---|---|---|---|---|---|
| 1# | −1.8680 | 2.2140 | 0.9999 | 11# | 1.4650 | 8.1300 | 0.9999 |
| 2# | 0.9980 | 5.5820 | 0.9865 | 12# | −0.9040 | 2.6390 | 0.9996 |
| 3# | 1.8310 | 10.3960 | 0.9991 | 13# | 1.4960 | 8.3420 | 0.9969 |
| 4# | 0.5800 | 3.5710 | 0.9974 | 14# | −1.6860 | 1.2720 | 0.9997 |
| 5# | −0.0690 | 2.1870 | 0.9994 | 15# | 0.8190 | 4.8240 | 0.9991 |
| 6# | −0.5970 | 2.0680 | 0.9982 | 16# | −0.9030 | 2.4700 | 0.9997 |
| 7# | 0.0470 | 4.0240 | 0.9999 | 17# | 0.5340 | 3.6710 | 0.9993 |
| 8# | 0.4030 | 3.0330 | 0.9999 | 18# | 0.6740 | 4.2100 | 0.9996 |
| 9# | 0.0650 | 3.0040 | 0.9999 | 19# | 0.8080 | 4.8100 | 0.9989 |
| 10# | 0.7990 | 4.7360 | 0.9992 | 20# | −0.6510 | 2.2820 | 0.9999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-T.; Xu, Y.-X.; Liao, J.-B.; Liu, S.-K.; Liu, Z.; Gao, W.-H.; Yi, L.-W. Study on the Particle Strength and Crushing Patterns of Coal Gangue Coarse-Grained Subgrade Fillers. Sustainability 2024, 16, 5155. https://doi.org/10.3390/su16125155
Zhang Z-T, Xu Y-X, Liao J-B, Liu S-K, Liu Z, Gao W-H, Yi L-W. Study on the Particle Strength and Crushing Patterns of Coal Gangue Coarse-Grained Subgrade Fillers. Sustainability. 2024; 16(12):5155. https://doi.org/10.3390/su16125155
Chicago/Turabian StyleZhang, Zong-Tang, Yang-Xun Xu, Ji-Biao Liao, Shun-Kai Liu, Ze Liu, Wen-Hua Gao, and Li-Wei Yi. 2024. "Study on the Particle Strength and Crushing Patterns of Coal Gangue Coarse-Grained Subgrade Fillers" Sustainability 16, no. 12: 5155. https://doi.org/10.3390/su16125155
APA StyleZhang, Z.-T., Xu, Y.-X., Liao, J.-B., Liu, S.-K., Liu, Z., Gao, W.-H., & Yi, L.-W. (2024). Study on the Particle Strength and Crushing Patterns of Coal Gangue Coarse-Grained Subgrade Fillers. Sustainability, 16(12), 5155. https://doi.org/10.3390/su16125155






