Augmented Two-Stage Hierarchical Controller for Distributed Power Generation System Powered by Renewable Energy: Development and Performance Analysis
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
- Proposes the modelling and simulation of a wind energy conversion system to achieve a continuous power supply.
- Design a two-stage hierarchical controller for enhancing frequency response in several operating modes.
- A MATLAB/Simulink model and simulation of a microgrid based on a wind energy conversion system are evaluated for multiple case studies.
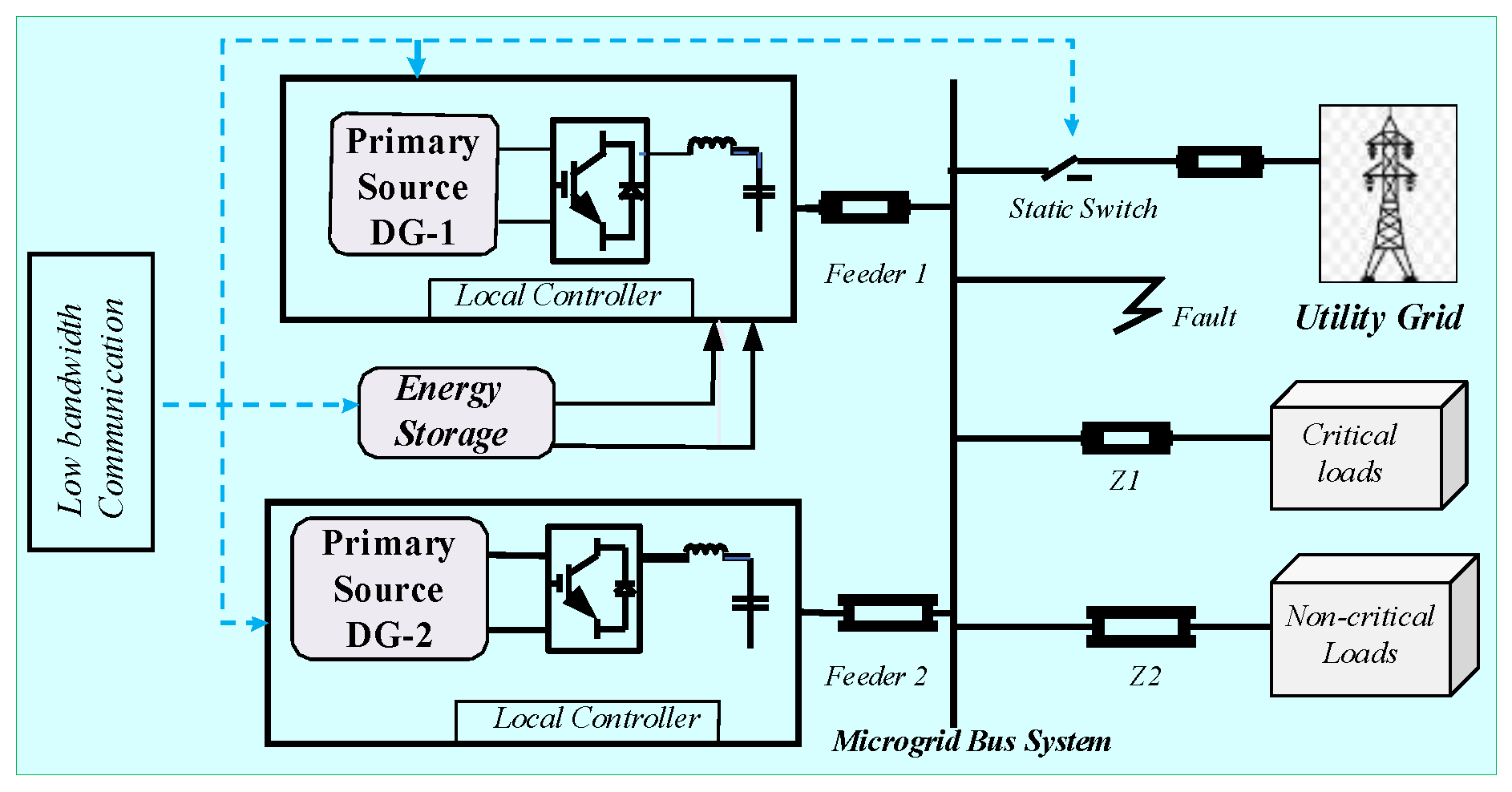
2. WECS-Based Microgrid Model
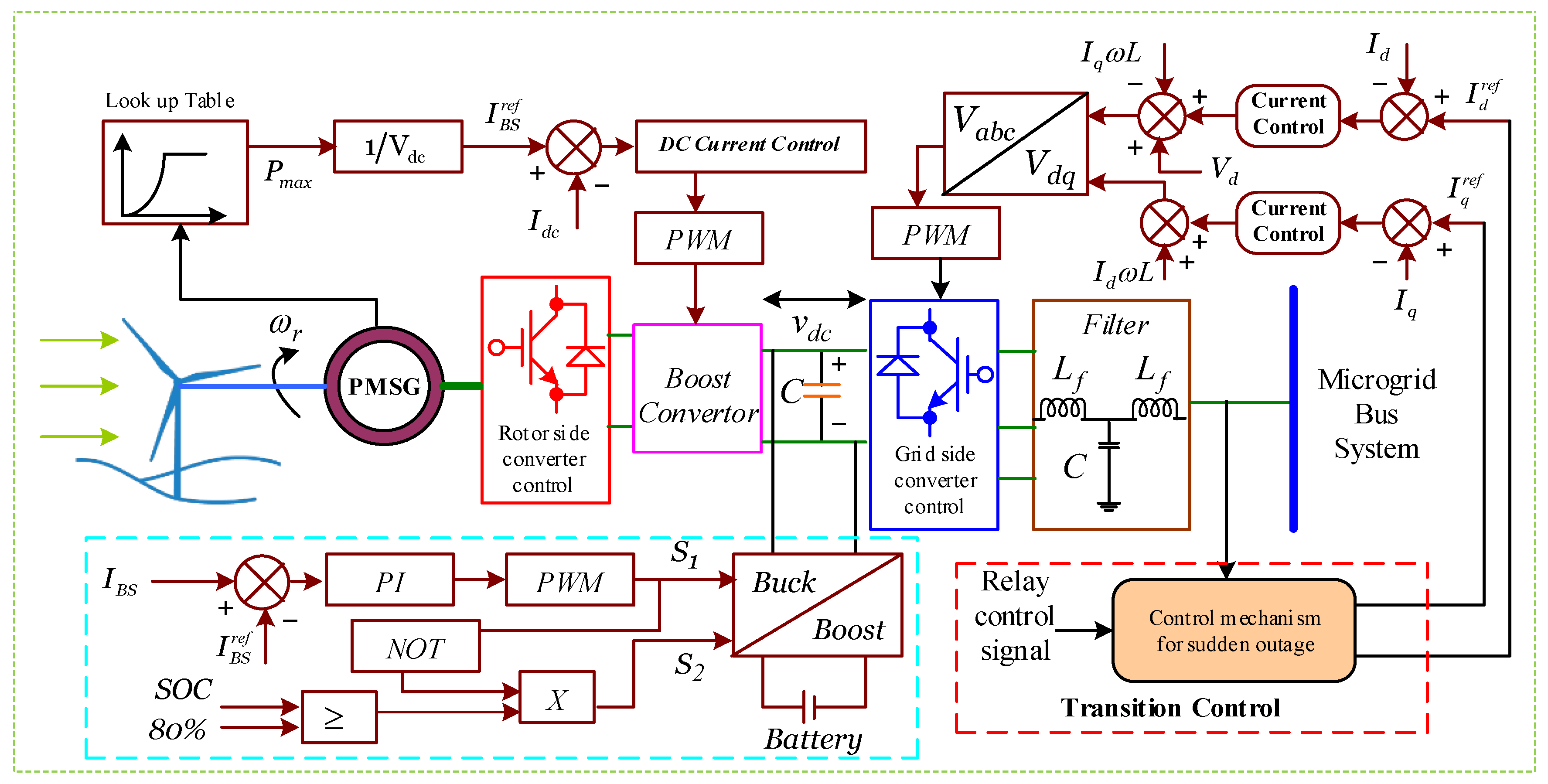
2.1. Modelling of ESSs-Backed DG1
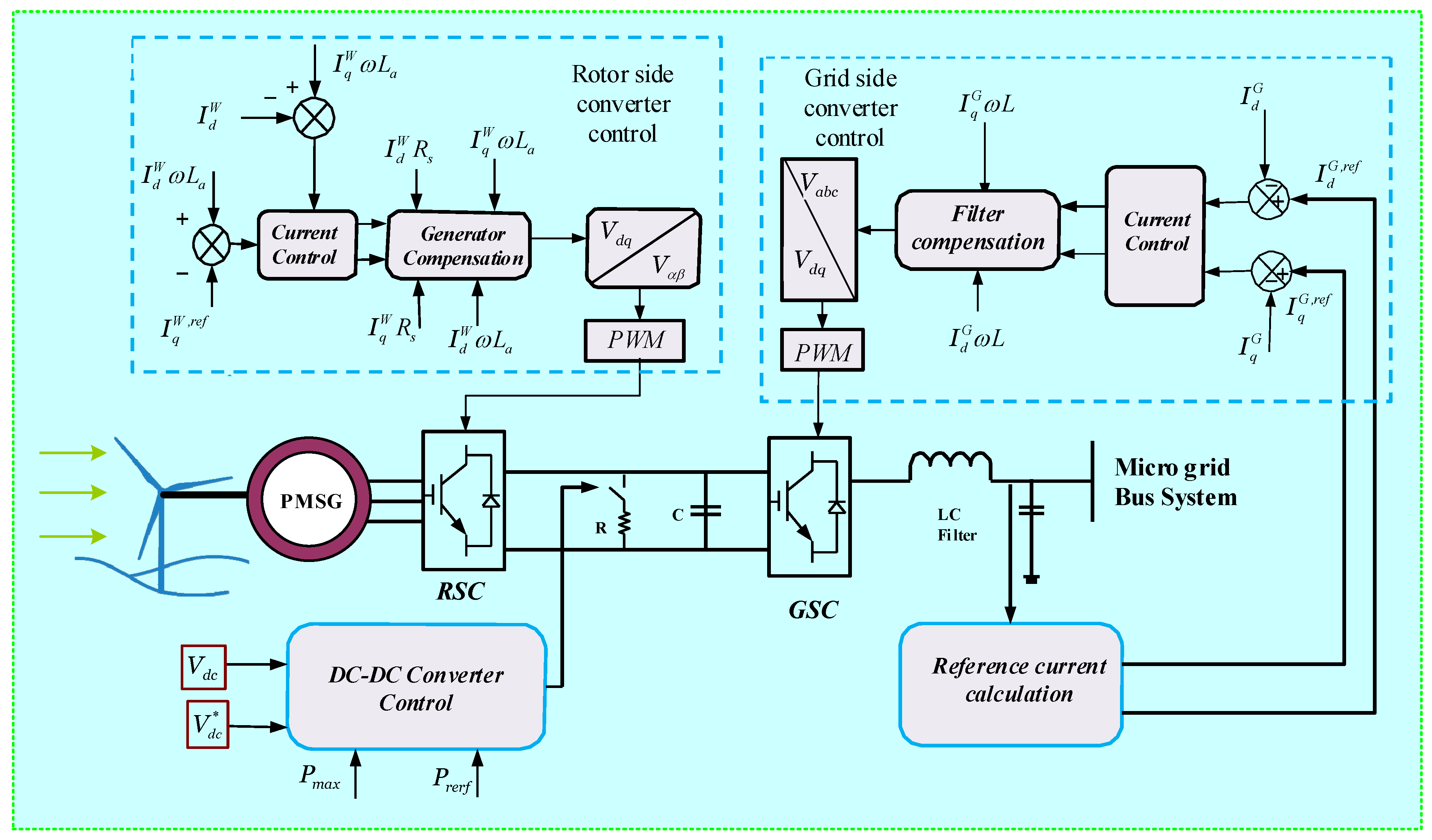
2.2. Control Scheme for PMSG Based DG2
2.3. Battery Energy Storage System
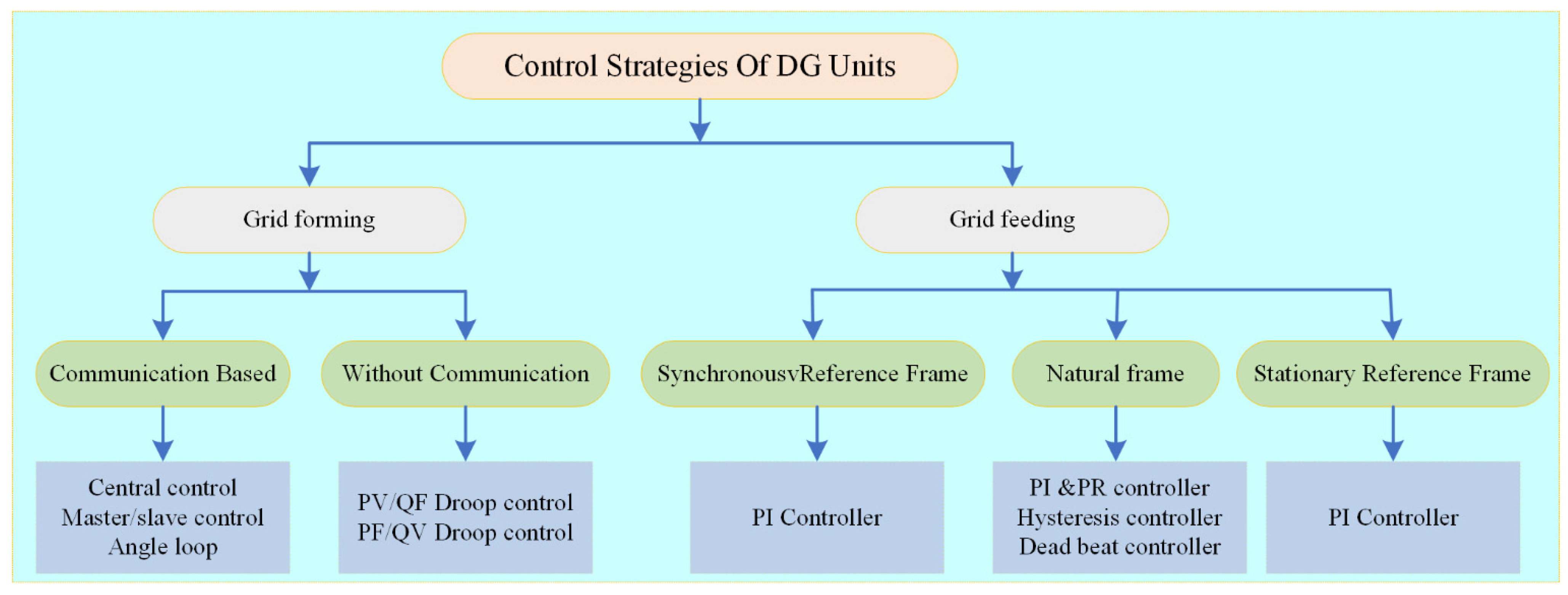
3. Control Strategies for Parallel Operating DGs
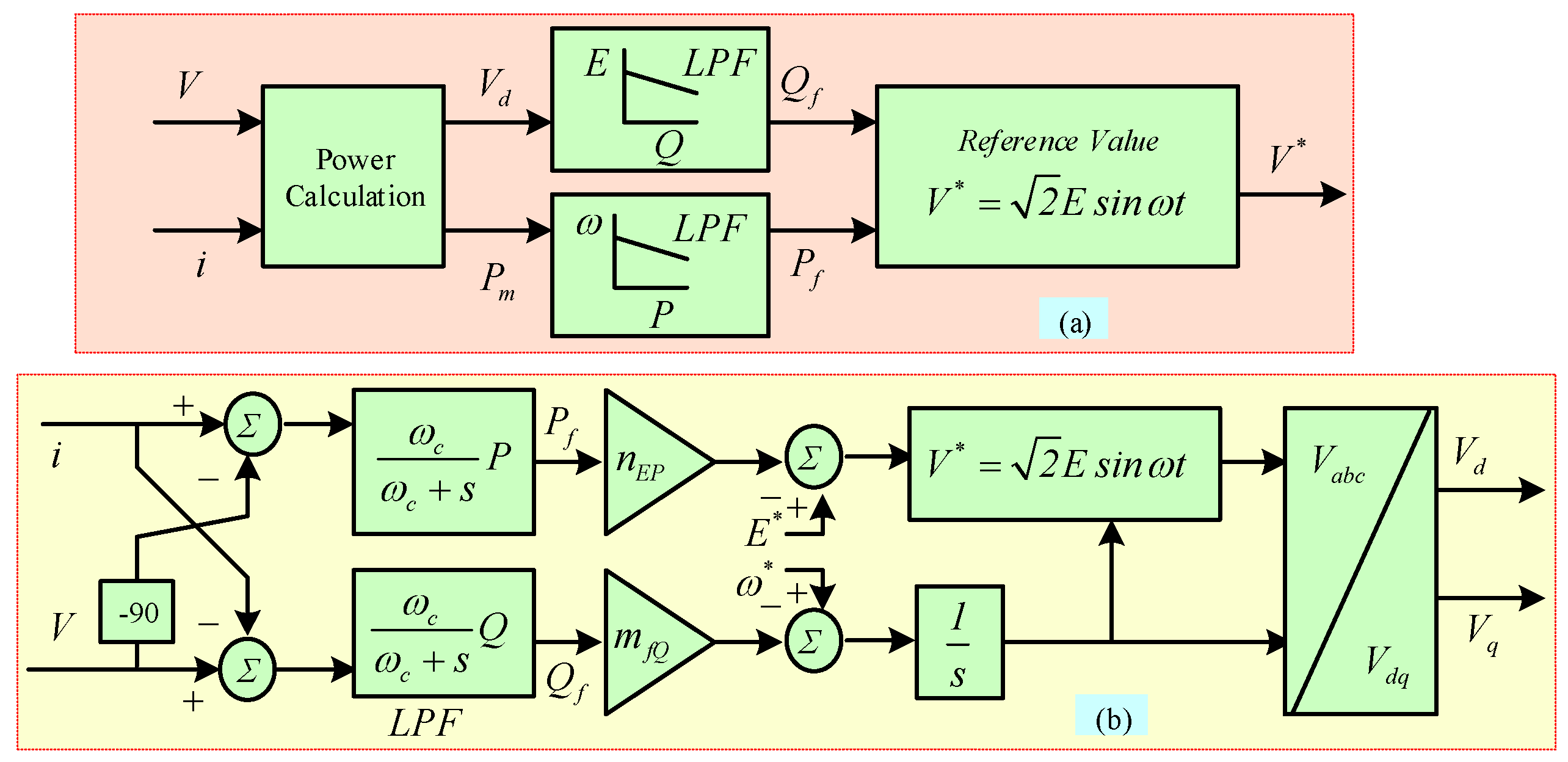
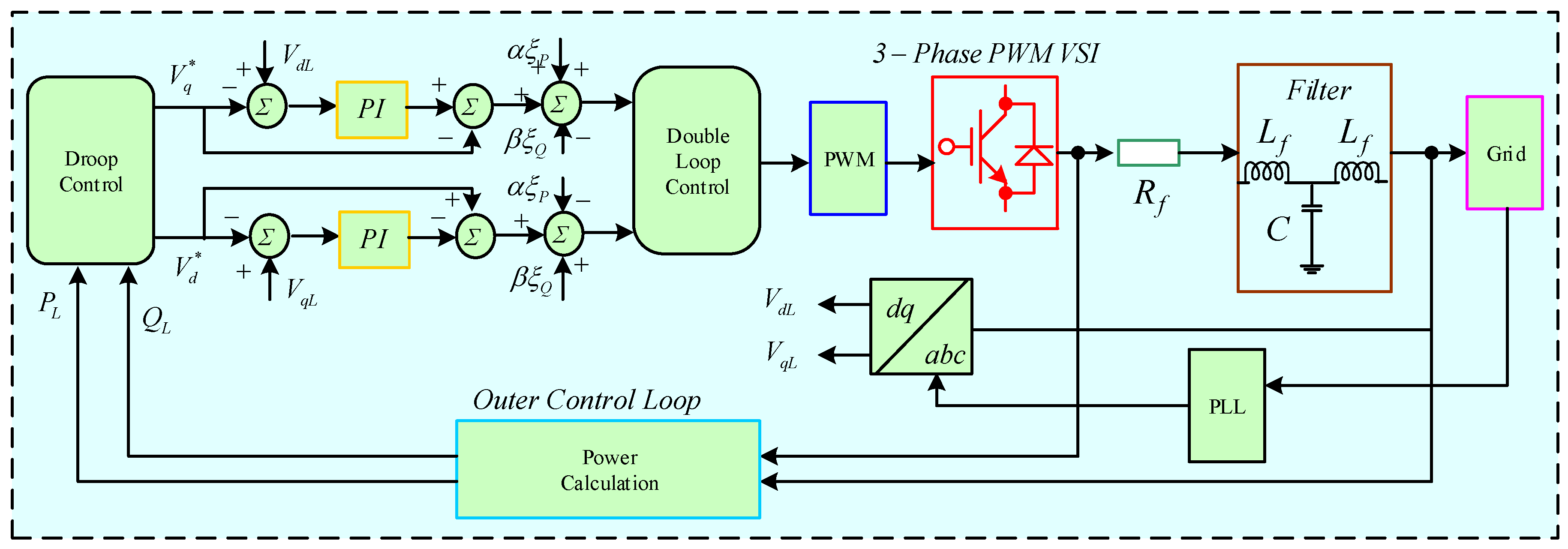
3.1. Droop Control
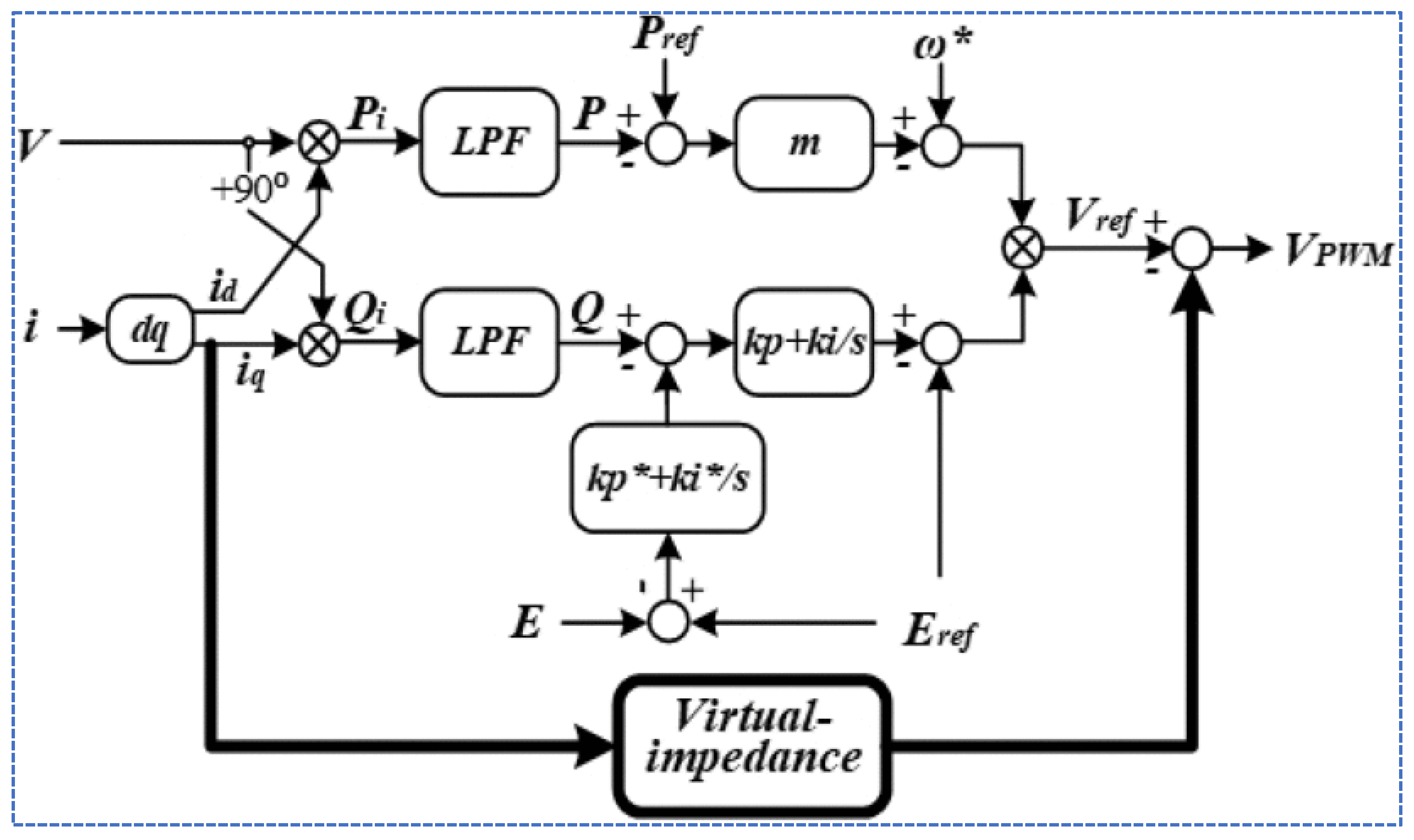
3.2. Virtual Impedance Control
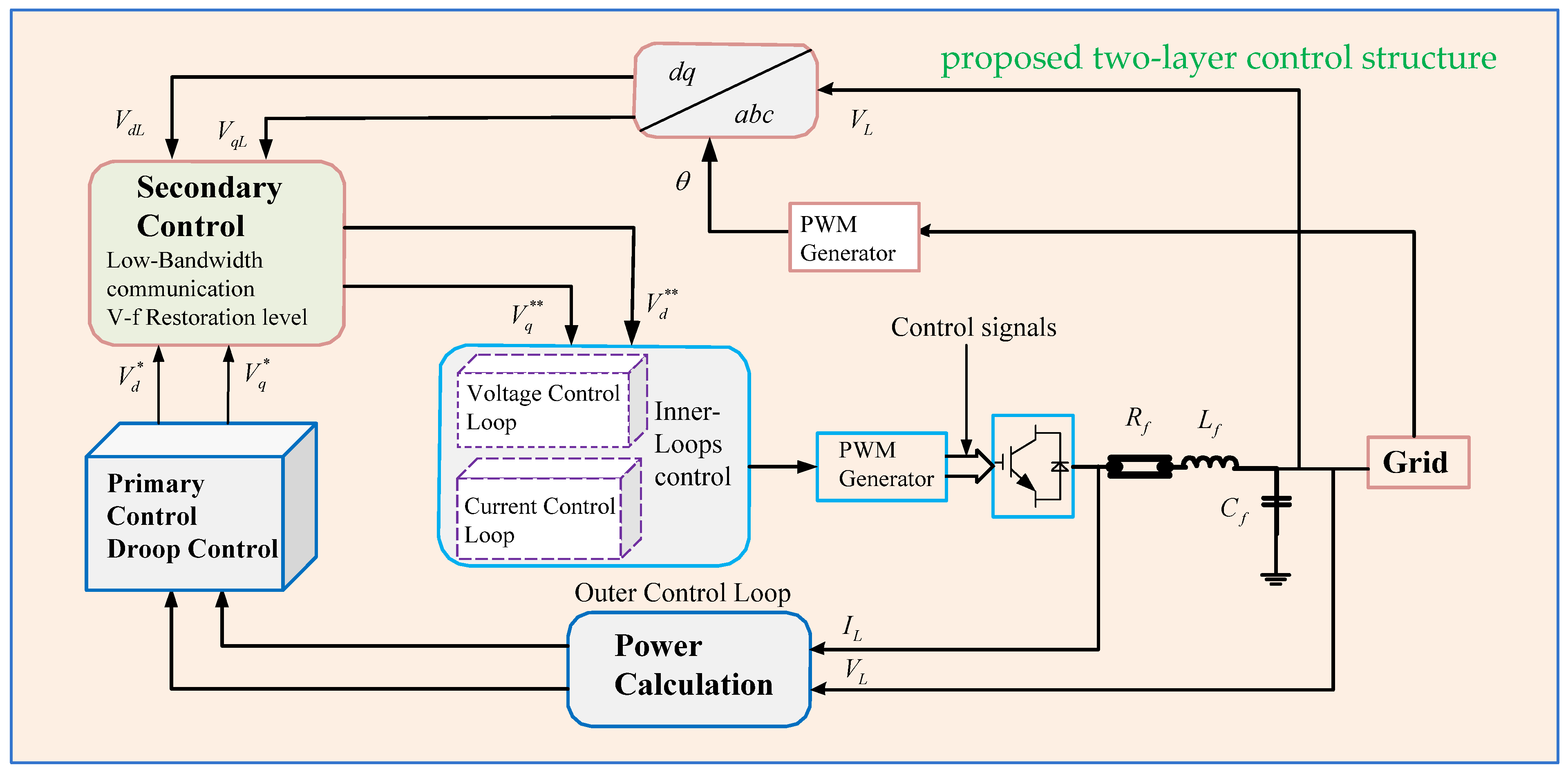
3.3. Hierarchical Control of Microgrid
3.3.1. Proposed Hierarchical Control Mechanism
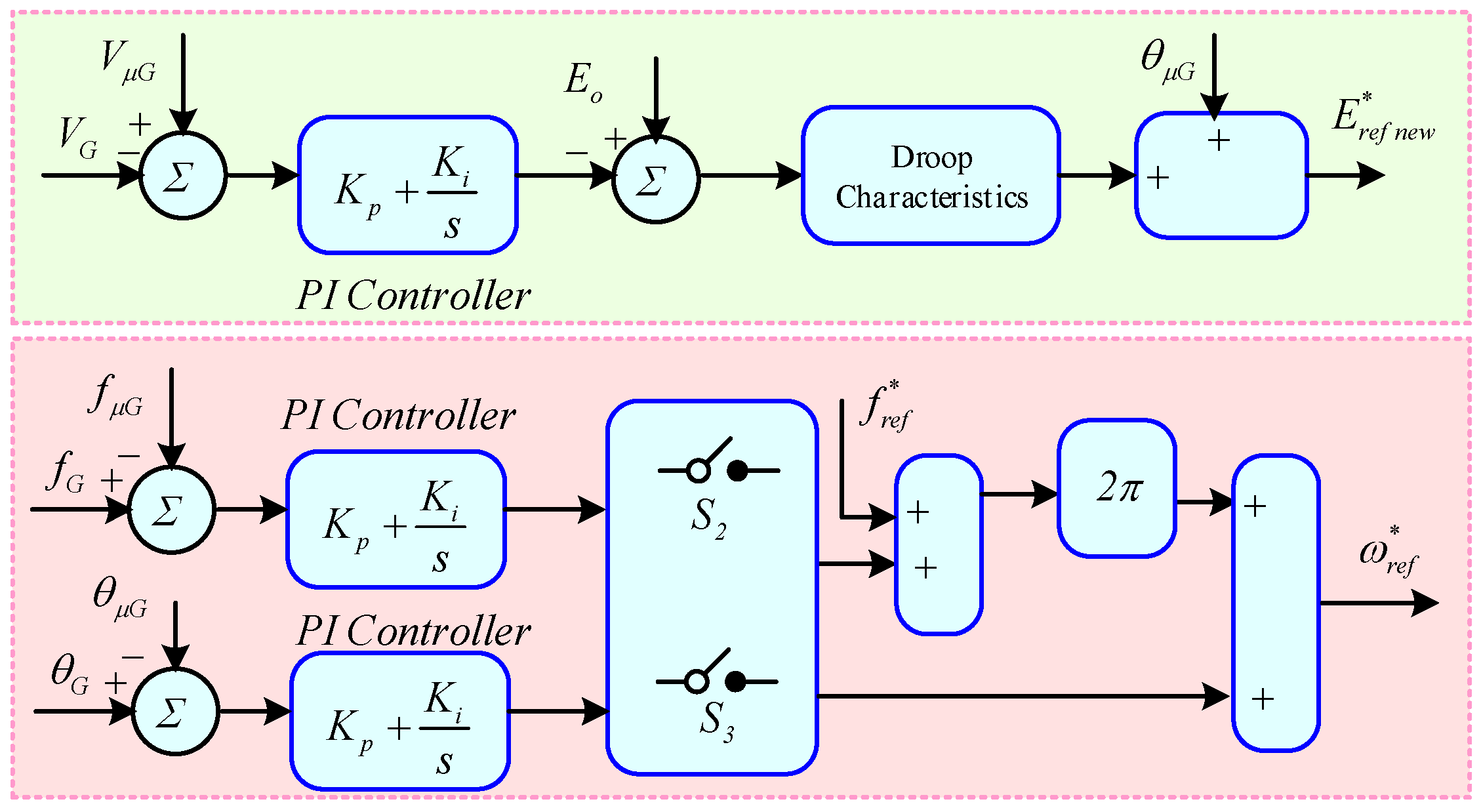
3.3.2. Primary Controller
3.3.3. Secondary Controller
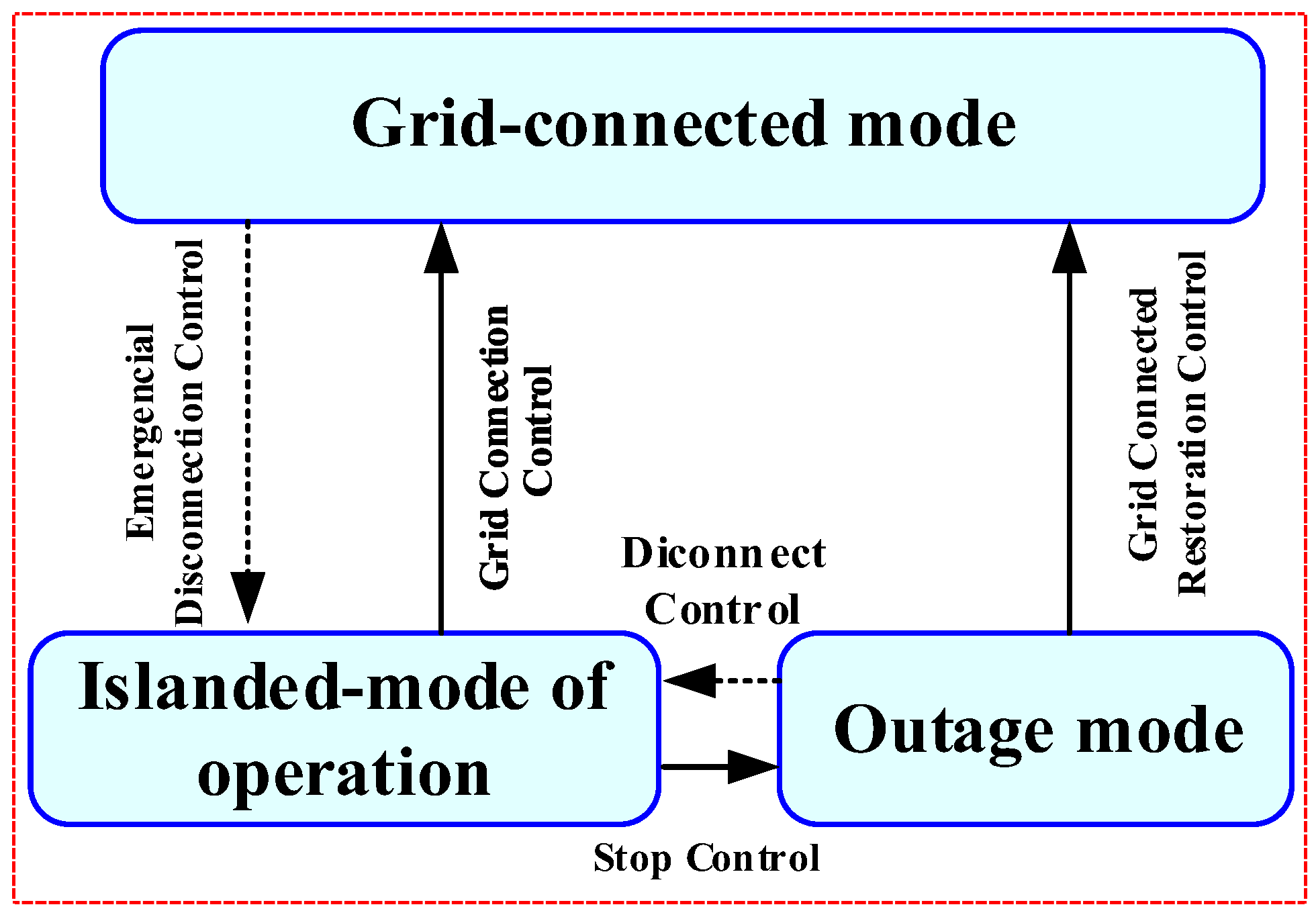
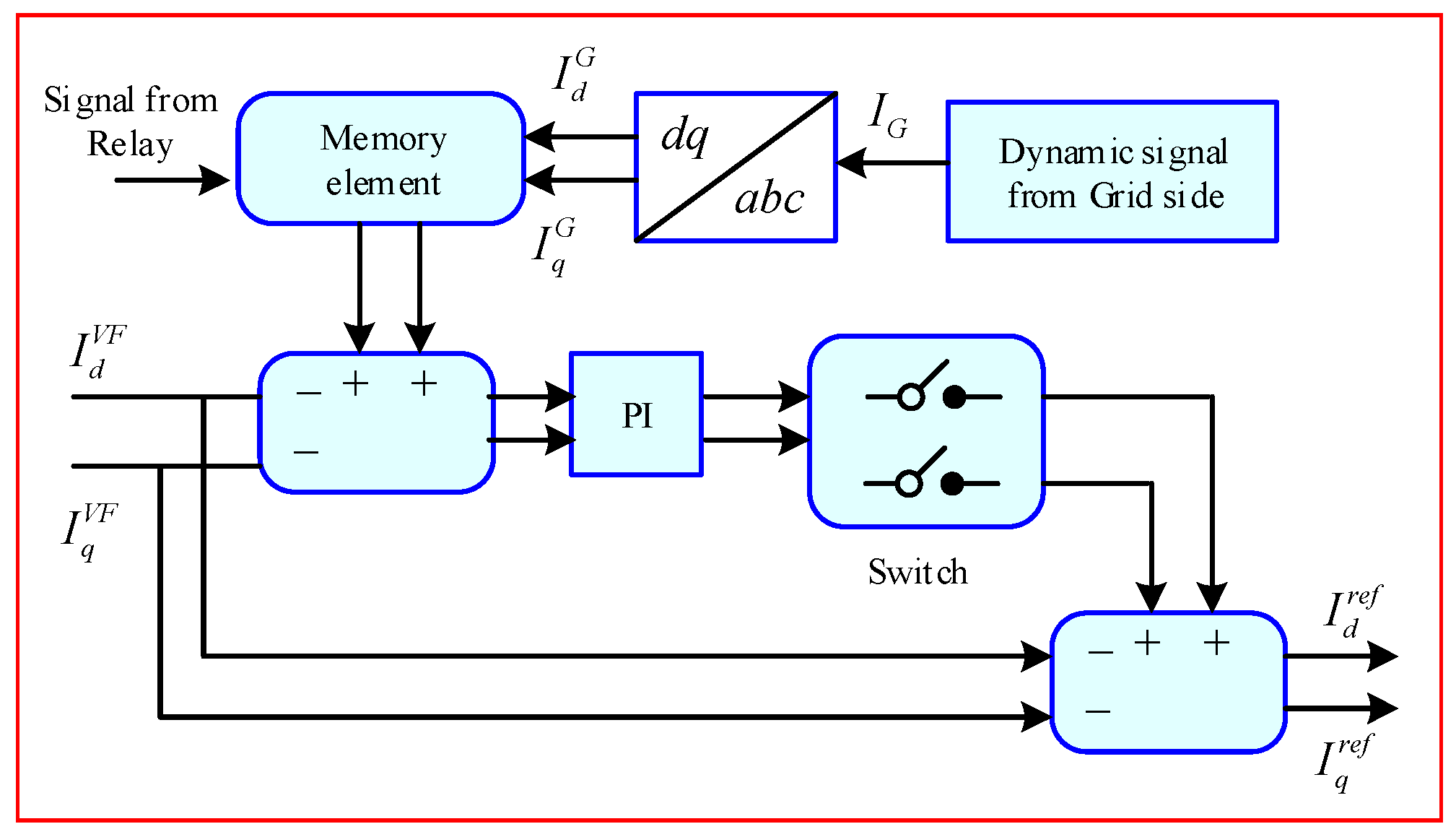
3.3.4. Seamless Mode Transition
3.3.5. Grid-Connected to the Islanded Operating Paradigm
3.3.6. Islanded Mode to Grid-Tied
4. Simulation Results and Discussions
4.1. Proposed Cases
- Case 1: Smooth mode transition
- Case 2: Sudden load variation
- Case 3: Fault analysis
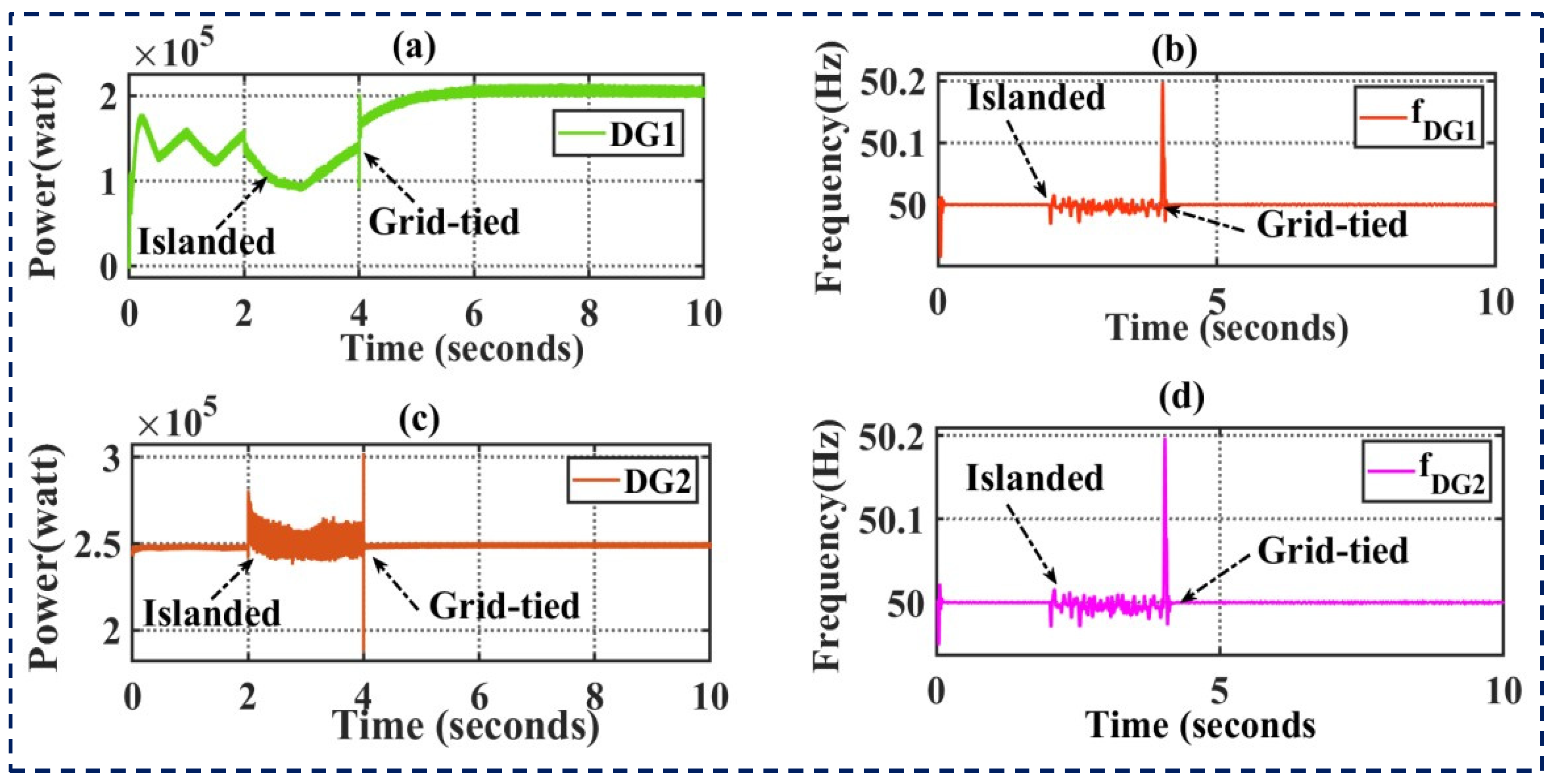
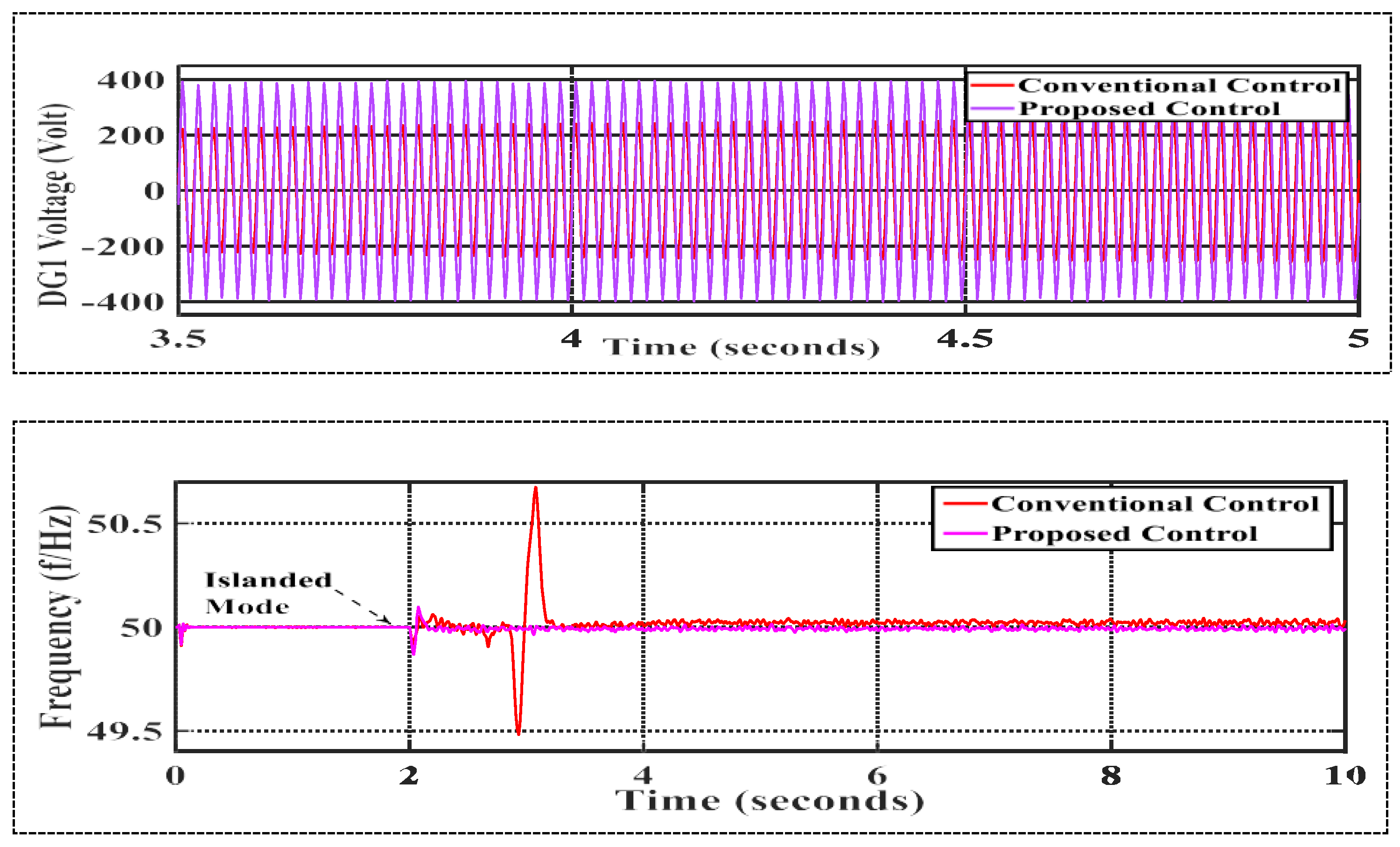
4.2. Seamless Mode Transition
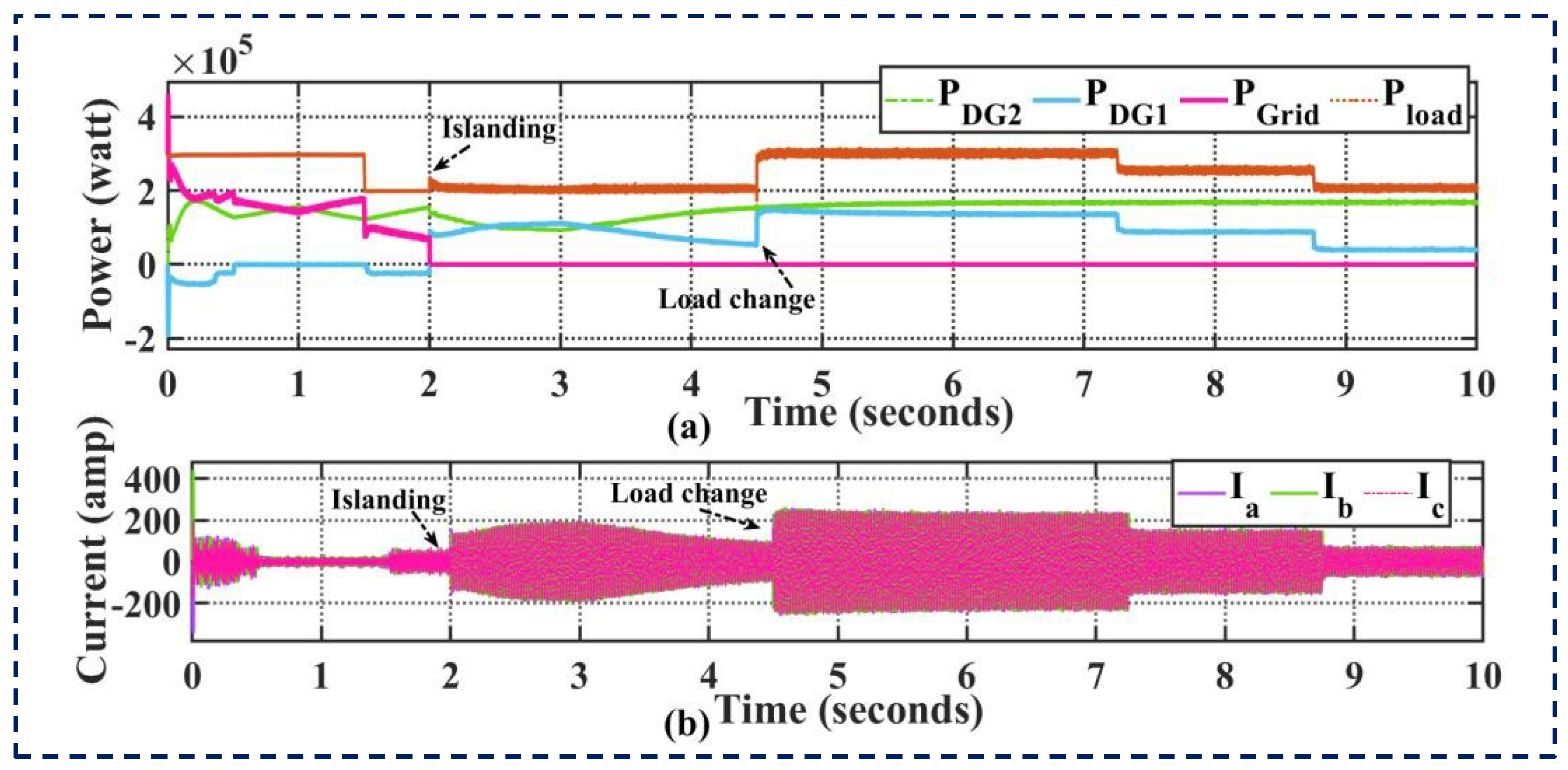
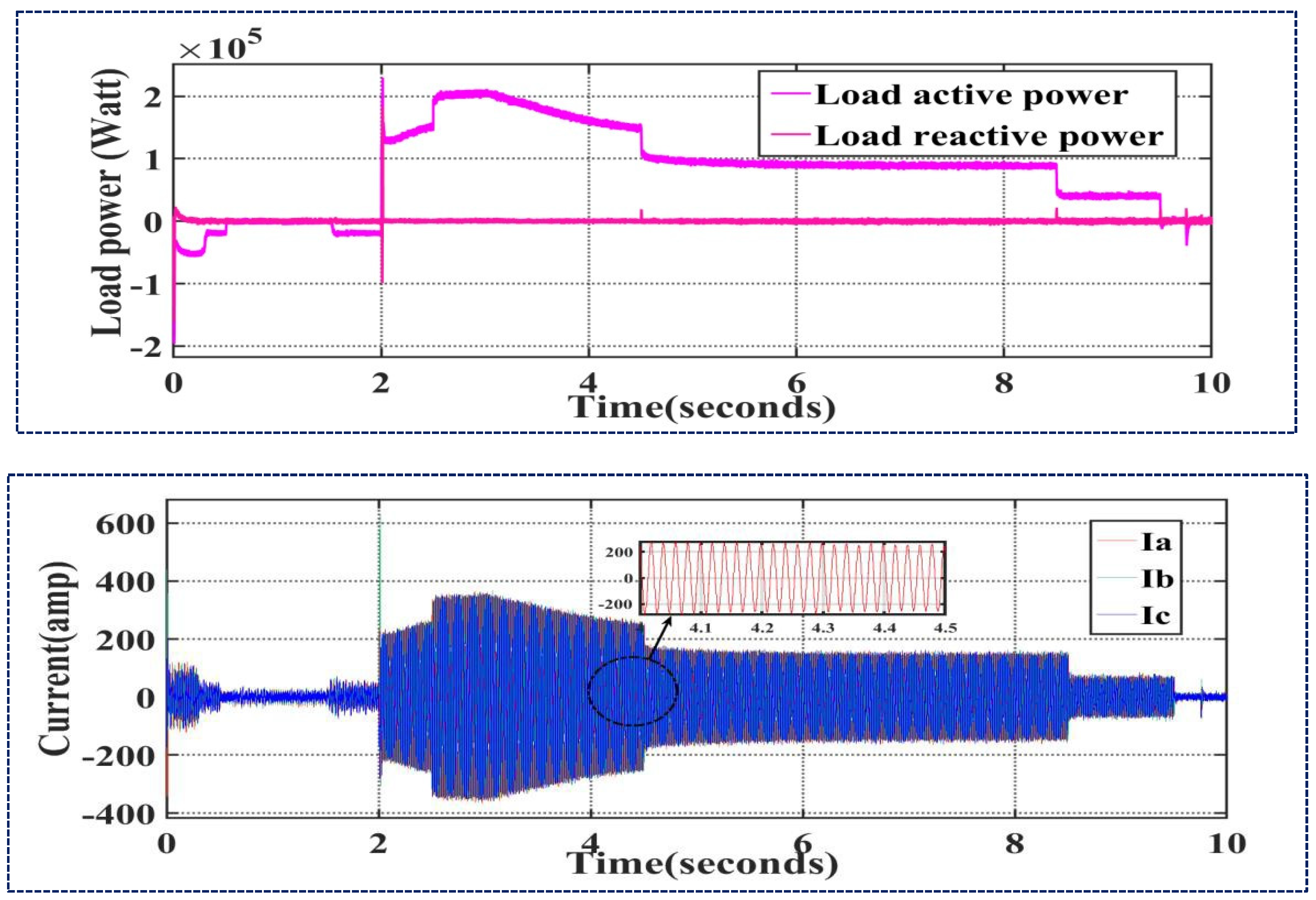
4.3. Effects of Large Changes in Load
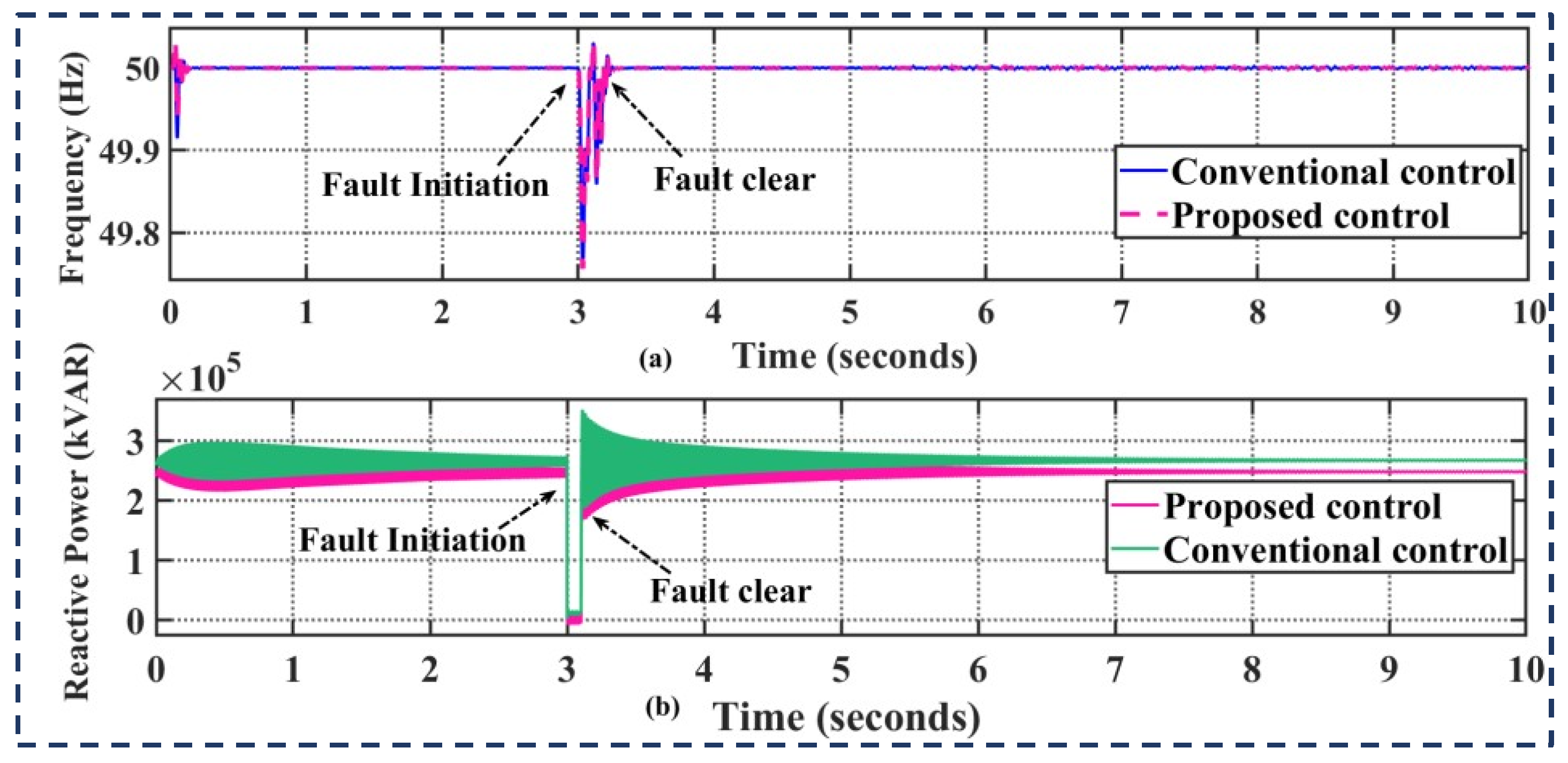
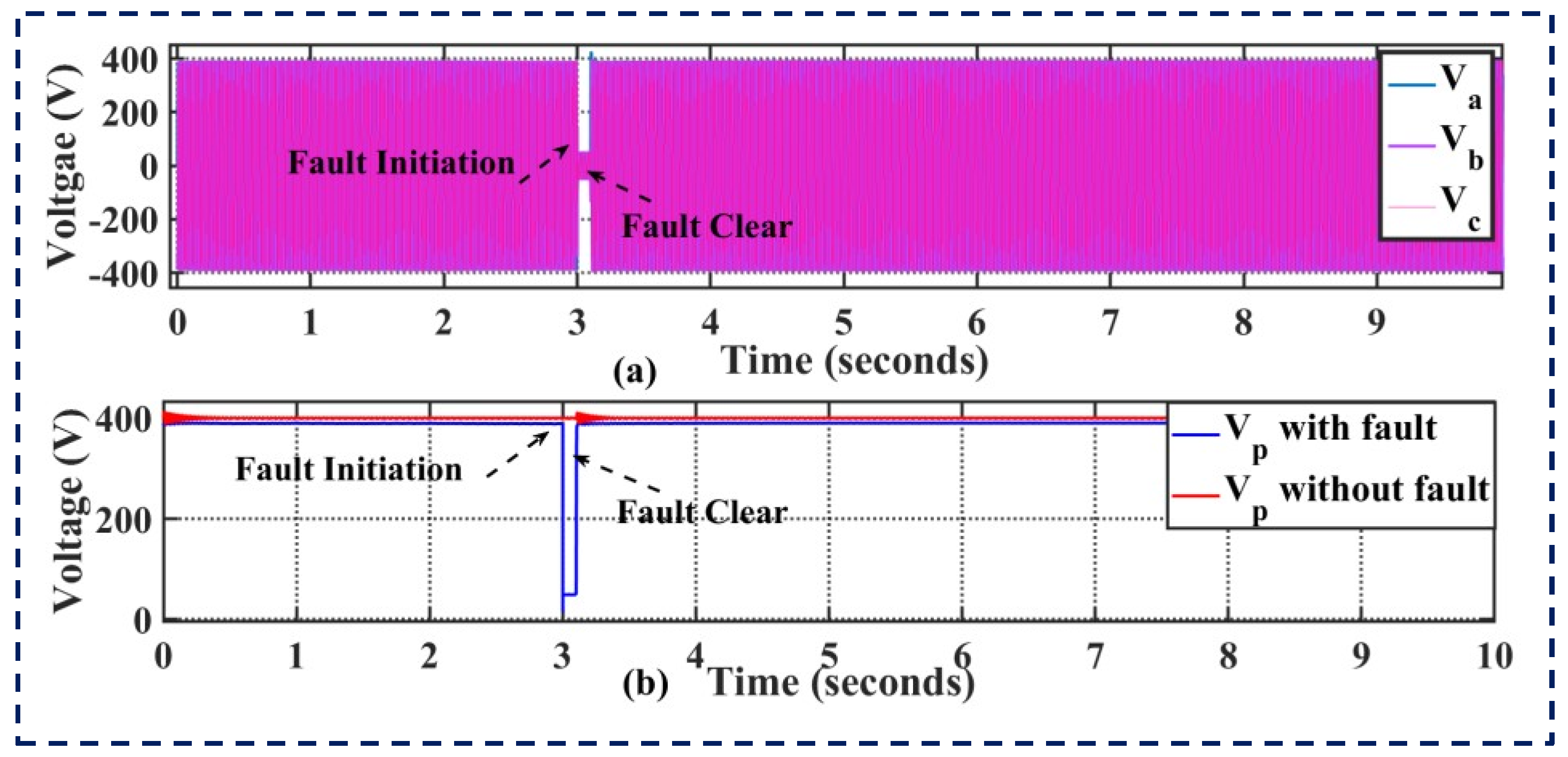
4.4. Performance Analysis during a Three-Phase Fault (Short-Circuit Fault)
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guerrero, J.M.; Kandari, R. Microgrids Modeling, Control, and Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 2021; p. 268. ISBN 9780323854634. [Google Scholar]
- Farhangi, H.; Joos, G. Microgrid Planning and Design: A Concise Guide; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; p. 256. ISBN 9781119453505. [Google Scholar]
- Ren, L.; Zhang, P. Generalized Microgrid Power Flow. IEEE Trans. Smart Grid 2018, 9, 3911–3913. [Google Scholar] [CrossRef]
- Agundis-Tinajero, G.; Segundo-Ramírez, J.; Visairo-Cruz, N.; Savaghebi, M.; Guerrero, J.M.; Barocio, E. Power flow modeling of islanded AC microgrids with hierarchical control. Int. J. Electr. Power Energy Syst. 2019, 105, 28–36. [Google Scholar] [CrossRef]
- Keerthana, M.; Manoharan, P.S.; Ravi, A. Design of Control Strategy for Battery-Supercapacitor Hybrid Storage System. In Proceedings of the 2022 7th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 22–24 June 2022; pp. 798–803. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. Variable structure control for dynamic powersharing and voltage regulation of DC microgrid with a hybrid energy storage system. Int. Trans. Electr. Energy Syst. 2020, 30, e12510. [Google Scholar] [CrossRef]
- Hoang, K.D.; Lee, H.-H. Accurate Power Sharing with Balanced Battery State of Charge in Distributed DC Microgrid. IEEE Trans. Ind. Electron. 2019, 66, 1883–1893. [Google Scholar] [CrossRef]
- Kamal, T.; Hassan, S.Z.; Espinosa-Trujillo, M.J.; Li, H.; Flota, V. An optimal power sharing and power control strategy of photovoltaic/fuel cell/ultra-capacitor hybrid power system. J. Renew. Sustain. Energy 2016, 8, 035301. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, L.; Zhao, H.; Huang, H.; Hu, R. Research on power sharing strategy of hybrid energy storage system in photovoltaic power station based on multi-objective optimization. IET Renew. Power Gener. 2016, 10, 575–583. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Hossain, M.J.; Pota, H.R.; Oo, A.M.T. Robust Nonlinear Distributed Controller Design for Active and Reactive Power Sharing in Islanded Microgrids. IEEE Trans. Energy Convers. 2014, 29, 893–903. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed Secondary Control for Islanded Microgrids—A Novel Approach. IEEE Trans. Power Electron. 2014, 29, 1018–1031. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C.; Teodorescu, R.; Huang, L. Hierarchical Control of Parallel AC-DC Converter Interfaces for Hybrid Microgrids. IEEE Trans. Smart Grid 2014, 5, 683–692. [Google Scholar] [CrossRef]
- Kumar, A.; Bhadu, M. Wide-area damping control system for large wind generation with multiple operational uncertainty. Electr. Power Syst. Res. 2022, 213, 108755. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Power Calculation Using RBF Neural Networks to Improve Power Sharing of Hierarchical Control Scheme in Multi-DER Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1217–1225. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Autonomous Active Power Control for Islanded AC Microgrids with Photovoltaic Generation and Energy Storage System. IEEE Trans. Energy Convers. 2014, 29, 882–892. [Google Scholar] [CrossRef]
- Han, H.; Liu, Y.; Sun, Y.; Su, M.; Guerrero, J.M. An Improved Droop Control Strategy for Reactive Power Sharing in Islanded Microgrid. IEEE Trans. Power Electron. 2015, 30, 3133–3141. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Guerrero, J.M.; Xu, Z.; Green, T.C. Multiple-Time-Scales Hierarchical Frequency Stability Control Strategy of Medium-Voltage Isolated Microgrid. IEEE Trans. Power Electron. 2016, 31, 5974–5991. [Google Scholar] [CrossRef]
- Kumar, A.; Bhadu, M.; Arabi, A.I.A.; Kamangar, S.; Bhutto, J.K.; Ali, M.A.; Kumar, S. Optimized robust control for improving frequency response of delay dependent AC microgrid with uncertainties. Electr. Power Syst. Res. 2024, 229, 110138. [Google Scholar] [CrossRef]
- Han, Y.; Shen, P.; Zhao, X.; Guerrero, J.M. Control Strategies for Islanded Microgrid Using Enhanced Hierarchical Control Structure with Multiple Current-Loop Damping Schemes. IEEE Trans. Smart Grid 2017, 8, 1139–1153. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Matas, J.; de Vicuna, L.G.; Castilla, M.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance. IEEE Trans. Ind. Electron. 2007, 54, 994–1004. [Google Scholar] [CrossRef]
- Ding, B.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Sun, H. A CCP-based distributed cooperative operation strategy for multi-agent energy systems integrated with wind, solar, and buildings. Appl. Energy 2024, 365, 123275. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and Distributed Optimal Energy Management of Active Distribution Networks within Integrated Office Buildings. CSEE J. Power Energy Syst. 2024, 10, 504–517. [Google Scholar] [CrossRef]
- Taher, A.M.; Hasanien, H.M.; Ginidi, A.R.; Taha, A.T.M. Hierarchical Model Predictive Control for Performance Enhancement of Autonomous Microgrids. Ain Shams Eng. J. 2021, 12, 1867–1881. [Google Scholar] [CrossRef]
- IEEE 2030.7-2017; IEEE Standard for the Specification of Microgrid Controllers. IEEE: Piscataway, NJ, USA, 2018; pp. 1–43. [CrossRef]
- La Bella, A.; Cominesi, S.R.; Sandroni, C.; Scattolini, R. Hierarchical Predictive Control of Microgrids in Islanded Operation. IEEE Trans. Autom. Sci. Eng. 2017, 14, 536–546. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.M.; Miret, J.; Castilla, M.; de Vicuña, L.G. Hierarchical Control of Intelligent Microgrids. IEEE Ind. Electron. Mag. 2010, 4, 23–29. [Google Scholar] [CrossRef]
- Li, Y.W.; Kao, C.-N. An Accurate Power Control Strategy for Power-Electronics-Interfaced Distributed Generation Units Operating in a Low-Voltage Multibus Microgrid. IEEE Trans. Power Electron. 2009, 24, 2977–2988. [Google Scholar] [CrossRef]
- Micallef, A.; Apap, M.; Staines, C.S.; Zapata, J.M.G. Secondary control for reactive power sharing and voltage amplitude restoration in droop-controlled islanded microgrids. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 492–498. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Jahanpour-Dehkordi, M.; Vaez-Zadeh, S.; Mohammadi, J. Development of a Combined Control System to Improve the Performance of a PMSG-Based Wind Energy Conversion System Under Normal and Grid Fault Conditions. IEEE Trans. Energy Convers. 2019, 34, 1287–1295. [Google Scholar] [CrossRef]
- Liao, K.; Pang, B.; Yang, J.; He, Z. Output Current Quality Improvement for VSC with Capability of Compensating Voltage Harmonics. IEEE Trans. Ind. Electron. 2024, 71, 9087–9097. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Swatloski, R.P.; Gathings, W. Optimal and Direct-Current Vector Control of Direct-Driven PMSG Wind Turbines. IEEE Trans. Ind. Electron. 2012, 27, 2325–2337. [Google Scholar] [CrossRef]
- Engler, A.; Soultanis, N. Droop control in LV-grids. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Wang, W.; Yao, G.; Ma, H.; Zeng, X.-J.; Guerrero, J.M. A Novel Droop Control Strategy of Reactive Power Sharing Based on Adaptive Virtual Impedance in Microgrids. IEEE Trans. Ind. Electron. 2022, 69, 11335–11347. [Google Scholar] [CrossRef]
- Ling, Y.; Li, Y.; Yang, Z.; Xiang, J. A Dispatchable Droop Control Method for Distributed Generators in Islanded AC Microgrids. IEEE Trans. Ind. Electron. 2021, 68, 8356–8366. [Google Scholar] [CrossRef]
- Sevostyanov, N.A.; Gorbunov, R.L. Control Strategy to Mitigate Voltage Ripples in Droop-Controlled DC Microgrids. IEEE Trans. Ind. Electron. 2023, 38, 15377–15389. [Google Scholar] [CrossRef]
- Alghamdi, B.; Cañizares, C.A. Frequency Regulation in Isolated Microgrids through Optimal Droop Gain and Voltage Control. IEEE Trans. Smart Grid 2021, 12, 988–998. [Google Scholar] [CrossRef]
- Keyvani-Boroujeni, B.; Fani, B.; Shahgholian, G.; Alhelou, H.H. Virtual Impedance-Based Droop Control Scheme to Avoid Power Quality and Stability Problems in VSI-Dominated Microgrids. IEEE Access 2021, 9, 144999–145011. [Google Scholar] [CrossRef]
- Sharma, S.; Iyer, V.M.; Bhattacharya, S. An Optimized Nonlinear Droop Control Method Using Load Profile for DC Microgrids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 3–13. [Google Scholar] [CrossRef]
- Perez, F.; Damm, G.; Verrelli, C.M.; Ribeiro, P.F. Adaptive Virtual Inertia Control for Stable Microgrid Operation Including Ancillary Services Support. IEEE Trans. Control Syst. Technol. 2023, 31, 1552–1564. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, X. Stability Analysis of the Virtual Inductance for LCL Filtered Droop-Controlled Grid-Connected Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2685–2698. [Google Scholar] [CrossRef]
- Cao, W.; Han, M.; Zhang, X.; Guan, Y.; Guerrero, J.M.; Vasquez, J.C. An Integrated Synchronization and Control Strategy for Parallel-Operated Inverters Based on V–I Droop Characteristics. IEEE Trans. Ind. Electron. 2022, 37, 5373–5384. [Google Scholar] [CrossRef]
- Imran, R.M.; Wang, S. Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid. Energies 2018, 11, 1270. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Adaptive Virtual Impedance Controller for Parallel and Radial Microgrids with Varying X/R Ratios. IEEE Trans. Sustain. Energy 2022, 13, 830–843. [Google Scholar] [CrossRef]
- Fan, L. Control and Dynamics in Power Systems and Microgrids; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Li, X.; Wen, C.; Chen, C.; Xu, Q. Adaptive Resilient Secondary Control for Microgrids with Communication Faults. IEEE Trans. Cybern. 2022, 52, 8493–8503. [Google Scholar] [CrossRef] [PubMed]
- Adibi, M.; van der Woude, J. Secondary Frequency Control of Microgrids: An Online Reinforcement Learning Approach. IEEE Trans. Autom. Control 2022, 67, 4824–4831. [Google Scholar] [CrossRef]
- Habibi, S.I.; Sheikhi, M.A.; Khalili, T.; Abadi, S.A.G.K.; Bidram, A.; Guerrero, J.M. Multiagent-Based Nonlinear Generalized Minimum Variance Control for Islanded AC Microgrids. IEEE Trans. Power Syst. 2024, 39, 316–328. [Google Scholar] [CrossRef]
- Talapur, G.G.; Suryawanshi, H.M.; Xu, L.; Shitole, A.B. A Reliable Microgrid with Seamless Transition Between Grid Connected and Islanded Mode for Residential Community with Enhanced Power Quality. IEEE Trans. Ind. Appl. 2018, 54, 5246–5255. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Nutakor, C. Feasibility study and economic analysis of standalone hybrid energy system for southern Ghana. Sustain. Energy Technol. Assess. 2020, 39, 100695. [Google Scholar]
- D’silva, S.; Shadmand, M.; Bayhan, S.; Abu-Rub, H. Towards Grid of Microgrids: Seamless Transition between Grid-Connected and Islanded Modes of Operation. IEEE Open J. Ind. Electron. Soc. 2020, 1, 66–81. [Google Scholar] [CrossRef]
- Das, S.; Singh, B. Self-Synchronizing Control Enabling Disruption-Free Operation and Seamless Mode Transitions in Wind–Solar Based Hybrid AC/DC Microgrid. IEEE Trans. Ind. Appl. 2023, 59, 4797–4807. [Google Scholar] [CrossRef]
- Gao, M.; Chen, M.; Zhao, B.; Li, B.; Qian, Z. Design of Control System for Smooth Mode-Transfer of Grid-Tied Mode and Islanding Mode in Microgrid. IEEE Trans. Ind. Electron. 2020, 35, 6419–6435. [Google Scholar] [CrossRef]
- de Araujo Ribeiro, R.L.; de Oliveira Alves Rocha, T.; de Sousa, R.M.; dos Santos, E.C.; Lima, A.M.N. A Robust DC-Link Voltage Control Strategy to Enhance the Performance of Shunt Active Power Filters without Harmonic Detection Schemes. IEEE Trans. Ind. Electron. 2015, 62, 803–813. [Google Scholar] [CrossRef]


| Symbol | Value |
|---|---|
| 12 rad/s | |
| 0.0007 V/W | |
| 0.0006 rad/s/VAR | |
| 2.4 | |
| 10 | |
| 1.8 | |
| 390 V |
| System Sizing | |
|---|---|
| Equipment | Values |
| DG1 | 260 kVA |
| DG2 | 200 kVA |
| Battery | 350 kWh |
| System Parameter | |
| Grid voltage (L-L) | 480 V |
| Grid frequency | 50 Hz |
| DG1 LC filter | 4 mH, 55 F |
| DG2 LC filter | 4 mH, 55 F |
| Parameters | Kp | Ki | |
|---|---|---|---|
| DG1 | RSC-Current controller -d axis | 3.25 | 39 |
| RSC-Current controller -q axis | 1.7 | 0.66 | |
| RSC-Voltage controller -d axis | 0.84 | 48 | |
| RSC-Voltage controller -q axis | 0.67 | 74.4 | |
| Boost DC current controller | 0.57 | 13.7 | |
| Buck/Boost DC current controller | 4.6 | 61 | |
| DG2 | DG2-GSC-Current controller -q axis | 5.1 | 82 |
| DG2-GSC-DC voltage controller | 10.6 | 62 | |
| DG2-Chopper voltage controller | 21 | 75 | |
| DG2-MSC-Current controller -d axis | 0.3 | 5.9 | |
| DG2-MSC-Current controller -q axis | 3.8 | 11 | |
| DG2-GSC-Current controller -d axis | 3.8 | 11 | |
| Pre synchronization | control-Voltage component | 0.21 | 3.9 |
| control-Frequency component | 4 | 2.3 | |
| control-Phase angle component | 11 | 8.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhutto, J.K. Augmented Two-Stage Hierarchical Controller for Distributed Power Generation System Powered by Renewable Energy: Development and Performance Analysis. Sustainability 2024, 16, 5872. https://doi.org/10.3390/su16145872
Bhutto JK. Augmented Two-Stage Hierarchical Controller for Distributed Power Generation System Powered by Renewable Energy: Development and Performance Analysis. Sustainability. 2024; 16(14):5872. https://doi.org/10.3390/su16145872
Chicago/Turabian StyleBhutto, Javed Khan. 2024. "Augmented Two-Stage Hierarchical Controller for Distributed Power Generation System Powered by Renewable Energy: Development and Performance Analysis" Sustainability 16, no. 14: 5872. https://doi.org/10.3390/su16145872
APA StyleBhutto, J. K. (2024). Augmented Two-Stage Hierarchical Controller for Distributed Power Generation System Powered by Renewable Energy: Development and Performance Analysis. Sustainability, 16(14), 5872. https://doi.org/10.3390/su16145872






