Landslide Susceptibility Assessment Method during the Construction of Highways Based on the Index Complexity Algorithm
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area
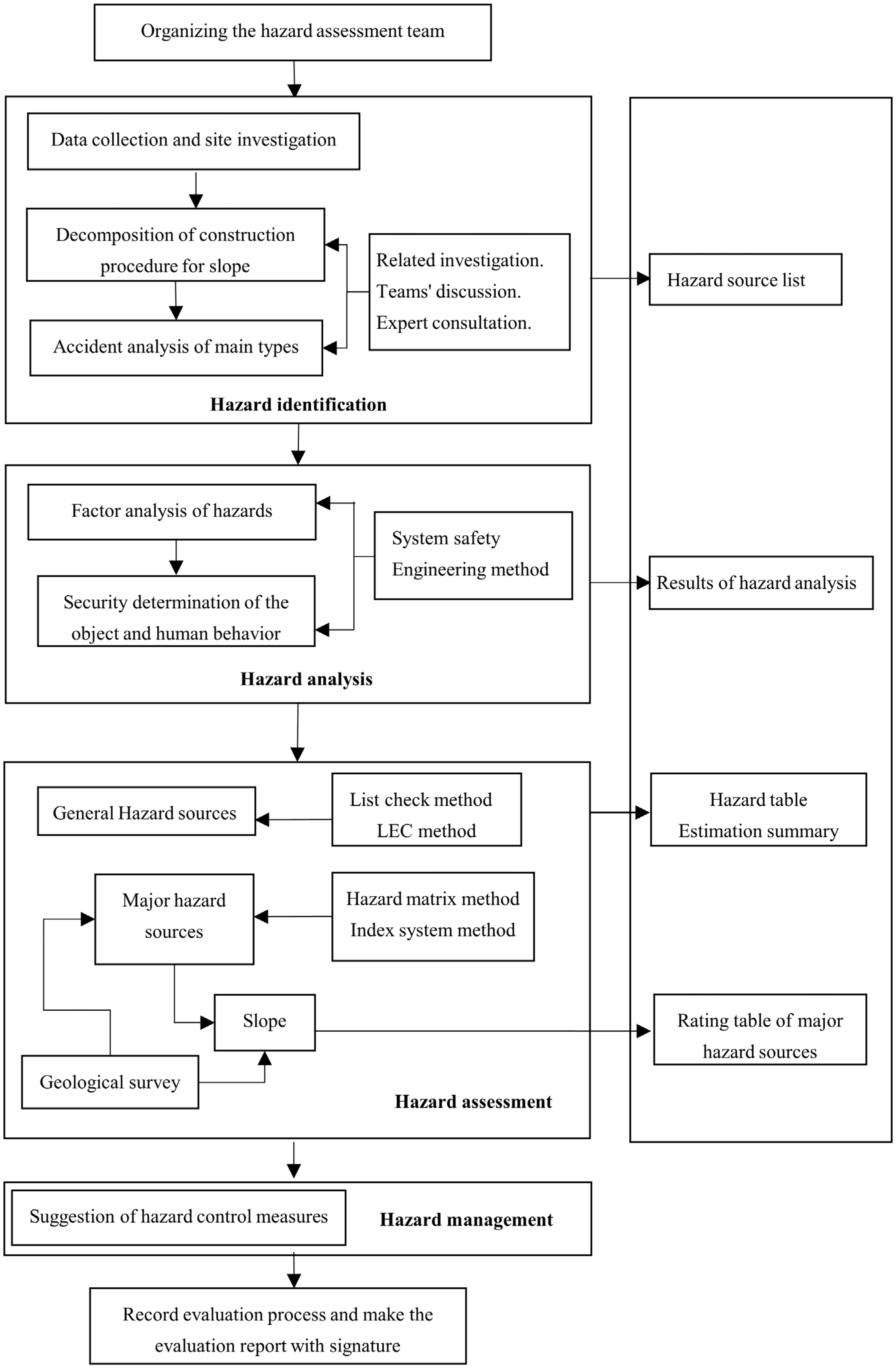
2.2. Hazard Features of Highway-Slope
2.3. Assessment Methodology Based on ICA
2.3.1. Index Establishment of the Assessment Method
2.3.2. Proportional Distribution Based on the ICA for the Method
3. Results
3.1. Hazard Analysis and Evaluation
- (1)
- Construction scale (A1): slope height (a11), slope angle (a12), and slope length (a13)
- (2)
- Geological conditions (A2) hazard analysis: soil structure (a21), engineering surrounding structure (a22), groundwater effect (a23), and unconfined compressive strength of soil Qu (kpa) (a24)
- (3)
- Design and construction scheme (A3) hazard analysis: hazard degree of construction activity (a31), coefficient of slope stability evaluation (a32), design rationality (a33)
3.2. Semiquantitative Procedure for Slope Hazard Assessment
4. Discussion
5. Conclusions
- (1)
- This paper fully considers both subjective and objective factors affecting landslide occurrence and establishes an evaluation method for highway construction slopes, which includes 10 parameters related to construction scale, geological factors, and engineering design.
- (2)
- The newly proposed Index Complexity Algorithm (ICA) overcomes the shortcomings of traditional evaluation methods where subjective judgments affect the weight of factors. The new method can profoundly reflect the differentiation of factors, objectively determine the weights of evaluation factors, and is simple and fast to operate.
- (3)
- The evaluation method proposed in this paper still has certain limitations, such as the inability to evaluate stability under dynamic conditions that change over time (e.g., rainfall). It is more suitable for the evaluation of landslide stability under current conditions. Future surveys and research should refine this method to better apply it to the stability evaluation of landslides under various working conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pal, S.C.; Chakrabortty, R.; Saha, A.; Bozchaloei, S.K.; Pham, Q.B.; Linh, N.T.T.; Anh, D.T.; Janizadeh, S.; Ahmadi, K. Evaluation of debris flow and landslide hazards using ensemble framework of Bayesian- and tree-based models. Bull. Eng. Geol. Environ. 2022, 81, 55. [Google Scholar] [CrossRef]
- Zolkepli, M.F.; Ishak, M.F.; Wahap, M.S. The Application of Unmanned Aerial Vehicles (UAV) for Slope Mapping with the Determination of Potential Slope Hazards; Springer: Cham, Switzerland, 2022; pp. 45–67. [Google Scholar] [CrossRef]
- Samiul, H.; Greg, F. Modeling infrastructure system inter-dependencies and socioeconomic impacts of failure in extreme events: Emerging R&D challenges. Nat. Hazards 2015, 78, 2143–2216. [Google Scholar] [CrossRef]
- Ettinger, S.; Mounaud, L.; Magill, C.; Yao-Lafourcade, A.F.; Thouret, J.C.; Manville, V.; Negulescu, C.; Zuccaro, G.; De Gregorio, D.; Nardone, S.; et al. Building vulnerability to hydro-geomorphic hazards: Estimating damage probability from qualitative vulnerability assessment using logistic regression. J. Hydrol. 2016, 541, 563–581. [Google Scholar] [CrossRef]
- Scott, K. Estimating economic loss from cascading infrastructure failure: A perspective on modelling interdependency. Infrastruct. Complex. 2015, 2, 7. [Google Scholar] [CrossRef]
- Ramli, Z.; Ahmad, F. Slope Hazard and Risk Mapping Project (PBRC)—An Overview of Disaster Risk Reduction Initiative; Springer: Cham, Switzerland, 2021; pp. 385–392. [Google Scholar] [CrossRef]
- Hearn, G.J.; Shakya, N.M. Engineering challenges for sustainable road access in the Himalayas. Eng. Geol. Hydrogeol. 2017, 50, 69–80. [Google Scholar] [CrossRef]
- Sangchini, E.K.; Emami, S.N.; Tahmasebipour, N.; Pourghasemi, H.R.; Naghibi, S.A.; Arami, S.A.; Pradhan, B. Assessment and comparison of combined bivariate and AHP models with logistic regression for landslide susceptibility mapping in the Chaharmahal-e-Bakhtiari Province, Iran. Arab. J. Geosci. 2016, 9, 201–210. [Google Scholar] [CrossRef]
- Ma, K.; Tang, C.A.; Xu, N.W.; Liu, F.; Xu, J.W. Failure precursor of surrounding rock mass around cross tunnel in high-steep rock slope. J. Cent. South Univ. 2013, 20, 207–217. [Google Scholar] [CrossRef]
- Simpson, M.; James, R.; Hall, J.W.; Borgomeo, E.; Ives, M.C.; Almeida, S.; Wagener, T. Decision Analysis for Management of Natural Hazards. Annu. Rev. Environ. Resour. 2016, 41, 489–516. [Google Scholar] [CrossRef]
- Ramanathan, R.; Aydilek, A.H.; Tanyu, B.F. Development of a GIS-based failure investigation system for highway soil slopes. Front. Earth Sci. 2015, 9, 165. [Google Scholar] [CrossRef]
- Khalaj, S.; BahooToroody, F.; Abaei, M.M.; BahooToroody, A.; De Carlo, F.; Abbassi, R. A methodology for uncertainty analysis of landslides triggered by an earthquake. Comput. Geotech. 2020, 117, 32–62. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F.; Frattini, P.; Lari, S. Key Issues in Rock Fall Modeling, Hazard and Risk Assessment for Rock Fall Protection. In Engineering Geology for Society and Territory-Volume 2; Springer: Cham, Switzerland, 2015; pp. 43–58. [Google Scholar] [CrossRef]
- Fattahi, H. Risk assessment and prediction of safety factor for circular failure slope using rock engineering systems. Environ. Earth Sci. 2017, 76, 224. [Google Scholar] [CrossRef]
- Ma, K.; Liu, G.; Xu, N.; Zhang, Z.; Feng, B. Motion characteristics of rockfall by combining field experiments and 3D discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 2021, 138, 140591. [Google Scholar] [CrossRef]
- Leonardi, G.; Palamara, R.; Manti, F.; Tufano, A. GIS-Multicriteria Analysis Using AHP to Evaluate the Landslide Risk in Road Lifelines. Appl. Sci. 2022, 12, 4707. [Google Scholar] [CrossRef]
- Yang, X.; Hao, Z.; Liu, K.; Tao, Z.; Shi, G. An Improved Unascertained Measure-Set Pair Analysis Model Based on Fuzzy AHP and Entropy for Landslide Susceptibility Zonation Mapping. Sustainability 2023, 15, 6205. [Google Scholar] [CrossRef]
- Ganga, A.; Elia, M.; D’Ambrosio, E.; Tripaldi, S.; Capra, G.F.; Gentile, F.; Sanesi, G. Assessing Landslide Susceptibility by Coupling Spatial Data Analysis and Logistic Model. Sustainability 2022, 14, 8426. [Google Scholar] [CrossRef]
- Duan, G.; Hu, J.; Deng, L.; Fu, J. Landslide susceptibility prediction by gray wolf optimized support vector machine model under different factor states. J. Appl. Remote Sens. 2023, 17, 044510. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, W.; Qin, Y.; Lin, Z.; Zhang, G.; Chen, R.; Song, Y.; Lang, T.; Zhou, X.; Huangfu, W.; et al. Mapping Landslide Hazard Risk Using Random Forest Algorithm in Guixi, Jiangxi, China. ISPRS Int. J. Geo-Inf. 2020, 9, 695. [Google Scholar] [CrossRef]
- Deng, H.; Wu, X.; Zhang, W.; Liu, Y.; Li, W.; Li, X.; Zhou, P.; Zhuo, W. Slope-Unit Scale Landslide Susceptibility Mapping Based on the Random Forest Model in Deep Valley Areas. Remote Sens. 2022, 14, 4245. [Google Scholar] [CrossRef]
- Zedek, L.; Šembera, J.; Kurka, J. Inclusion of Nature-Based Solution in the Evaluation of Slope Stability in Large Areas. Land 2024, 13, 372. [Google Scholar] [CrossRef]
- Amarasinghe, M.P.; Kulathilaka, S.A.S.; Robert, D.J.; Zhou, A.; Jayathissa, H.A.G. Risk assessment and management of rainfall-induced landslides in tropical regions: A review. Nat. Hazards 2024, 120, 2179–2231. [Google Scholar] [CrossRef]
- Kieu, L.Q.; Ngo, G.V. Landslide susceptibility assessment for warning of dangerous areas in Tan Uyen district, Lai Chau province, Vietnam. Geogr. Ann. Ser. A Phys. Geogr. 2022, 104, 183–200. [Google Scholar] [CrossRef]
- Ericson, C.A. Hazard Analysis Techniques for System Safety; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 35–44. [Google Scholar]
- Chen, H.X.; Zhang, S.; Peng, M.; Zhang, L.M. A physically-based multi-hazard risk assessment platform for regional rainfall-induced slope failures and debris flows. Eng. Geol. 2015, 203, 15–29. [Google Scholar] [CrossRef]
- Macciotta, R.; Martin, C.D.; Morgenstern, N.R.; Cruden, D.M. Quantitative risk assessment of slope hazards along a section of railway in the Canadian Cordillera—A methodology considering the uncertainty in the results. Landslides 2016, 13, 115–127. [Google Scholar] [CrossRef]
- Lin, D.; Chen, P.; Ma, J.; Zhao, Y.; Xie, T.; Yuan, R.; Li, L. Assessment of slope construction risk uncertainty based on index importance ranking. Bull. Eng. Geol. Environ. 2019, 78, 4217–4228. [Google Scholar] [CrossRef]
- Feng, Z.; Zhu, Y.; Gao, X.; Long, H.; Wang, F.; Zhao, R.; Wen, J.; Wang, G.; Wang, Z. Safety evaluation model of excavating rock slope based on entropy-grey correlation method. J. Traffic Transp. Eng. 2020, 20, 55–65. [Google Scholar] [CrossRef]
- Du, Y.; Bai, Y.; Zhang, X.; Xie, M.; Ma, G. Risk assessment of coal gangue slope considering multiple risk factors. Eng. Mech. 2022, 39, 249–256. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Zhang, H.; Zhang, L.; Zhang, J. Influences of Internal Erosion on Infiltration and Slope Stability. Bull. Eng. Geol. Environ. 2019, 78, 1815–1827. [Google Scholar] [CrossRef]
- Leitner, B. A general model for railway systems risk assessment with the use of railway accident scenarios analysis. Procedia Eng. 2017, 187, 150–159. [Google Scholar] [CrossRef]


| First-Grade Index | Second-Grade Index and Grading Standard | Score | Illustration | |
|---|---|---|---|---|
| Construction scale (A1, ω1) | Slope height (m) (a11, ω11) | ≥45 | 75–100 | These 3 parameters can be calculated based on linear interpolation to obtain the specific values. |
| 35–45 | 50–74 | |||
| 25–35 | 25–49 | |||
| 15–25 | 0–24 | |||
| Slope angle (°) (a12, ω12) | >50 | 75–100 | ||
| 35–50 | 50–74 | |||
| 25–35 | 25–49 | |||
| 15–25 | 0–24 | |||
| Slope length (m) (a13, ω13) | ≥300 | 75–100 | ||
| 200–300 | 50–74 | |||
| 100–200 | 25–49 | |||
| <100 | 0–24 | |||
| Geological factor (A2, ω2) | Structure of soil layers (a21, ω21) | Loose quaternary alluvial soil | 75–100 | |
| Sandstone, mudstone, limestone, shale, and other weathered layers | 50–74 | |||
| Sandstone, mudstone, limestone and shale, such as full weathered, strongly weathered soil | 25–49 | |||
| Cataclastic structure, soil–rock mixture | 0–24 | |||
| Environmental conditions (a22, ω22) | Surrounded by key faults or valleys and rivers | 75–100 | Field investigation needed, focusing on pipelines, mined out spaces, high-voltage tower, water, etc. | |
| Close to normal structures | 50–74 | |||
| No large structure | 25–49 | |||
| Well geological conditions | 0–24 | |||
| Groundwater effect (a23, ω23) | Groundwater is exposed at the lower part of slope (<0.25 H), and well water-bearing capability | 75–100 | ||
| Groundwater is exposed at the lower part of slope (0.25–0.5 H), and well water-bearing capability | 50–74 | |||
| Groundwater is exposed at the lower part of slope (0.5–0.75 H), and general the water-bearing capability | 25–49 | |||
| Groundwater is exposed at the lower part of slope (0.75–1.0 H) and the water-bearing is poor | 0–24 | |||
| Unconfined compressive strength of soil Qu (kpa) (a24, ω24) | 0–60 | 75–100 | From the survey design report. | |
| 60–120 | 50–74 | |||
| 120–240 | 25–49 | |||
| ≥240 | 0–24 | |||
| V Design and construction scheme (A3, ω3) | Hazard degree during construction (a31, ω31) | Grouting, slope protection and inclined drainage hole are the main measures, and most of excavation, support and drainage uses labor | 75–100 | Hazard is judged by the specific engineering measures. |
| Anchor, slope protection and inclined drainage hole are the main measures, and some of excavation, support and drainage use labor | 50–74 | |||
| Retaining wall, drainage channel and slope protection are the main measures, and mechanization is used | 25–49 | |||
| The slope brushing and slope protection are the main measures, and all work is machine operation | 0–24 | |||
| Stability coefficient of slope (a32, ω32) | <1.15 | 75–100 | From the survey design report. | |
| 1.15–1.30 | 50–74 | |||
| 1.30–1.50 | 25–49 | |||
| ≥1.5 | 0–24 | |||
| Design rationality (a33, ω33) | Design data is insufficient; the slope analysis method or parameter calculation is false; the design of water drainage, support system and earthwork is not comprehensive; the construction is not timely | 75–100 | Design factors affect the construction safety, which should be comprehensively evaluated by experts. | |
| Design data is insufficient; selected parameters and conditions for construction are insufficient | 50–74 | |||
| Design qualification is Grade A; employees with experience of 5–10 years can comprehensive understand the design of slope drainage, support and earth excavation | 25–49 | |||
| Design qualification is Grade A; employees with over 10-years’ experience; timely design and construction | 0–24 | |||
| Hazard Level | Result |
|---|---|
| Grade IV (Very high) | R > 60 |
| Grade III (High) | 40 < R ≤ 60 |
| Grade II (Moderate) | 20 < R ≤ 40 |
| Grade I (Low) | R ≤ 20 |
| No | Second-Grade Index | Gjm1 | Gjm2 | Gj1 | Gj2 |
|---|---|---|---|---|---|
| a11 | Slope height | 0 | 100 | 50 | 74 |
| a12 | Slope angle | 0 | 100 | 50 | 74 |
| a13 | Slope length | 0 | 100 | 25 | 49 |
| No | Second-Grade Index | Gjm1 | Gjm2 | Gj1 | Gj2 |
|---|---|---|---|---|---|
| a21 | Structure of soil layer | 0 | 100 | 75 | 80 |
| a22 | Environmental conditions | 0 | 100 | 80 | 95 |
| a23 | Groundwater effect | 0 | 100 | 0 | 24 |
| a24 | Unconfined compressive strength | 0 | 100 | 40 | 55 |
| No | Second-Grade Index | Gjm1 | Gjm2 | Gj1 | Gj2 |
|---|---|---|---|---|---|
| a31 | Hazard degree during construction | 0 | 100 | 75 | 90 |
| a32 | Stability coefficient of slope | 0 | 100 | 75 | 85 |
| a33 | Design rationality | 0 | 100 | 65 | 75 |
| Serial Number | First-Grade Index | Gjm1 | Gjm2 | Gj1 | Gj2 |
|---|---|---|---|---|---|
| 1 | Construction scale | 0 | 100 | 50 | 90 |
| 2 | Geological factors | 0 | 100 | 25 | 40 |
| 3 | Construction organization | 0 | 100 | 65 | 90 |
| Slope | Result |
|---|---|
| Risk assessment score | 43 |
| Risk level | Grade III (High) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Zhang, Y.; Qiu, S.; Bai, M.; Xia, H.; Qiao, W.; Tang, Z. Landslide Susceptibility Assessment Method during the Construction of Highways Based on the Index Complexity Algorithm. Sustainability 2024, 16, 6147. https://doi.org/10.3390/su16146147
Lin D, Zhang Y, Qiu S, Bai M, Xia H, Qiao W, Tang Z. Landslide Susceptibility Assessment Method during the Construction of Highways Based on the Index Complexity Algorithm. Sustainability. 2024; 16(14):6147. https://doi.org/10.3390/su16146147
Chicago/Turabian StyleLin, Daming, Yufang Zhang, Shumao Qiu, Mingzhou Bai, Haoying Xia, Wei Qiao, and Zhenyu Tang. 2024. "Landslide Susceptibility Assessment Method during the Construction of Highways Based on the Index Complexity Algorithm" Sustainability 16, no. 14: 6147. https://doi.org/10.3390/su16146147
APA StyleLin, D., Zhang, Y., Qiu, S., Bai, M., Xia, H., Qiao, W., & Tang, Z. (2024). Landslide Susceptibility Assessment Method during the Construction of Highways Based on the Index Complexity Algorithm. Sustainability, 16(14), 6147. https://doi.org/10.3390/su16146147






