Enhancing Sustainability of Building Foundations with Efficient Open-End Pile Optimization
Abstract
1. Introduction
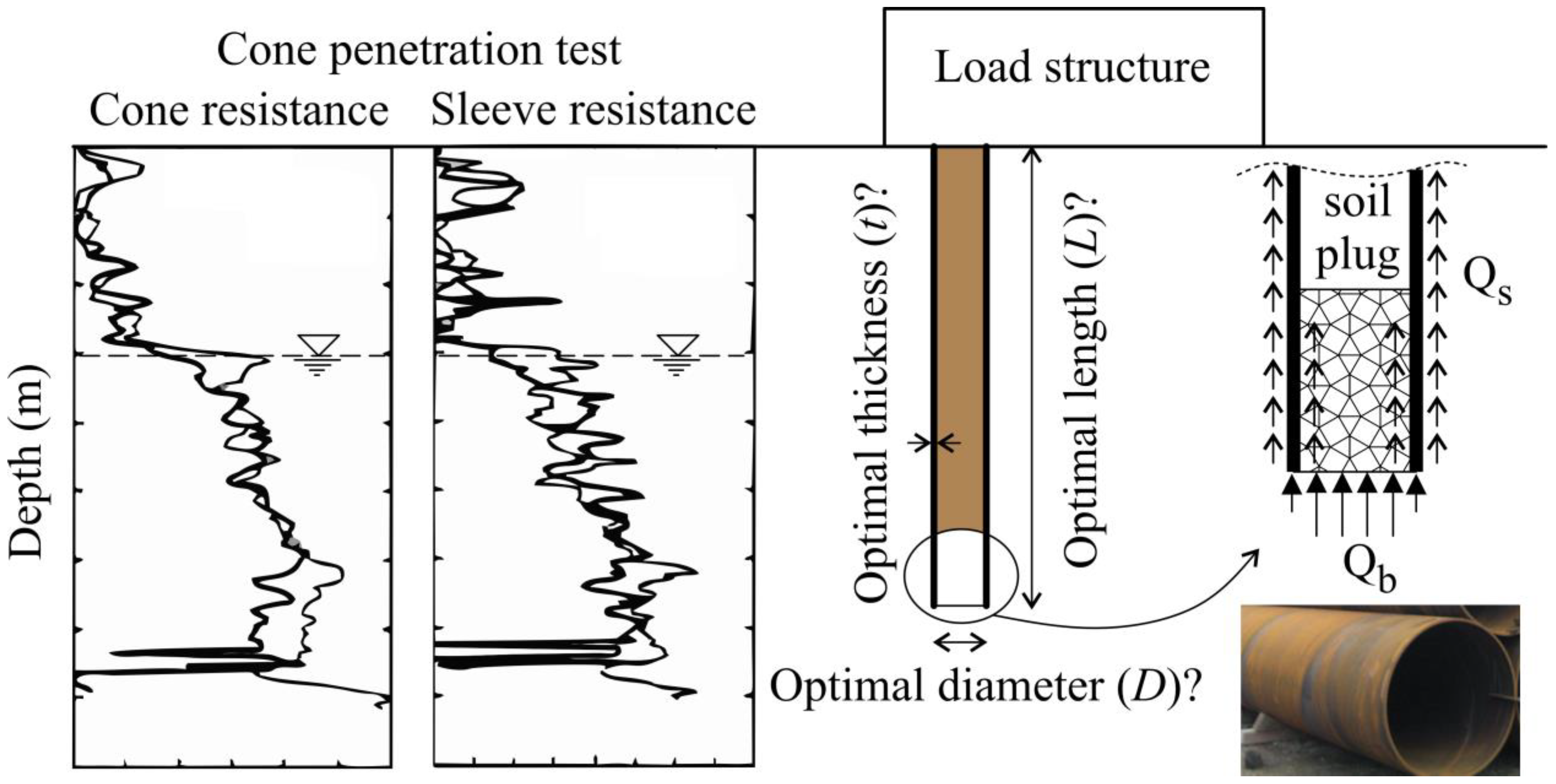
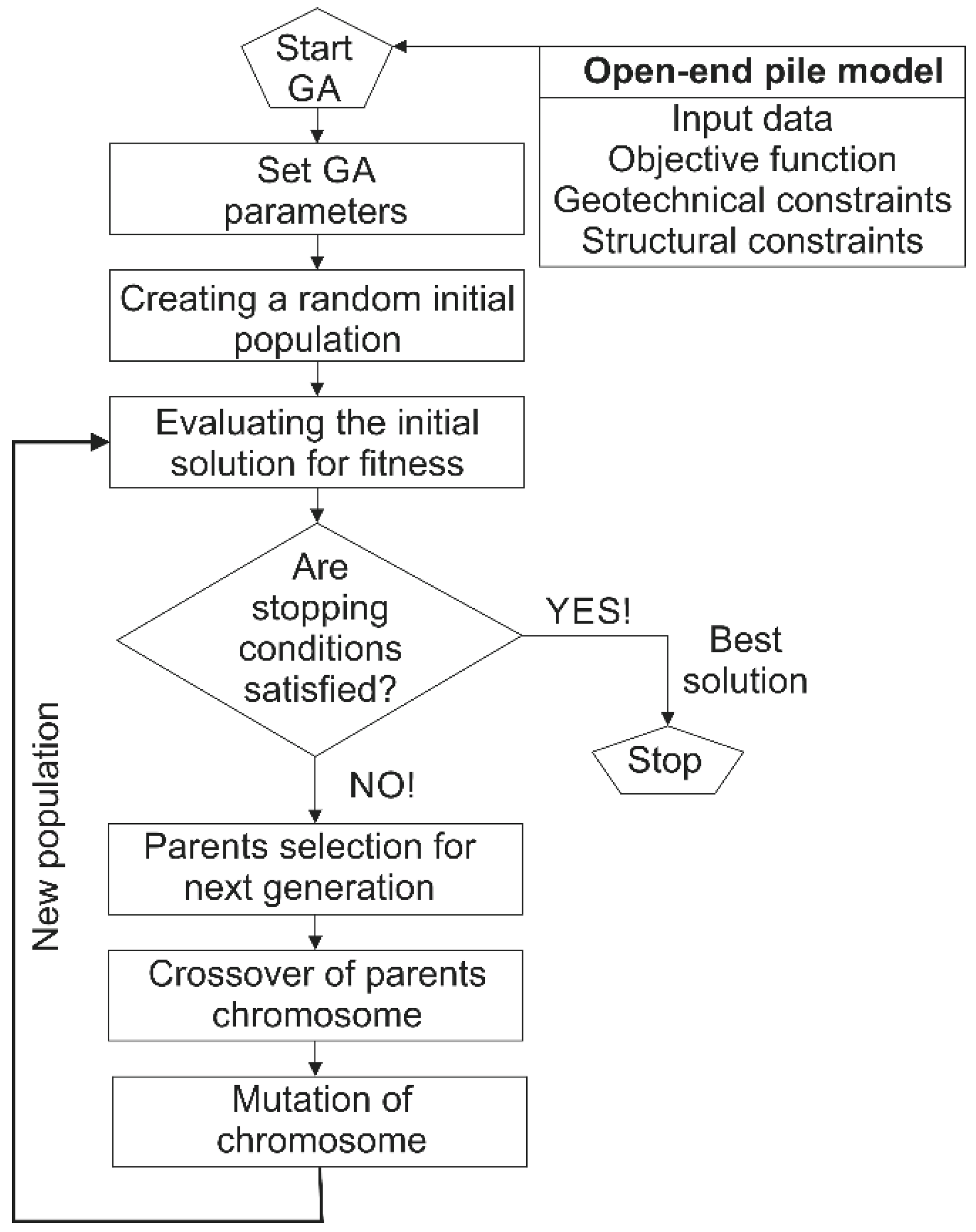
2. Genetic Algorithm and Open-End Pile Optimization Problem
3. Optimization Model for Open-End Piles
- Condition 1: Bearing capacity failure of the pile;
- Condition 2: Ratio of pile length to pile diameter;
- Condition 3: Ratio of pile diameter to pile wall thickness;
- Condition 4: Steel cross-section compression resistance.
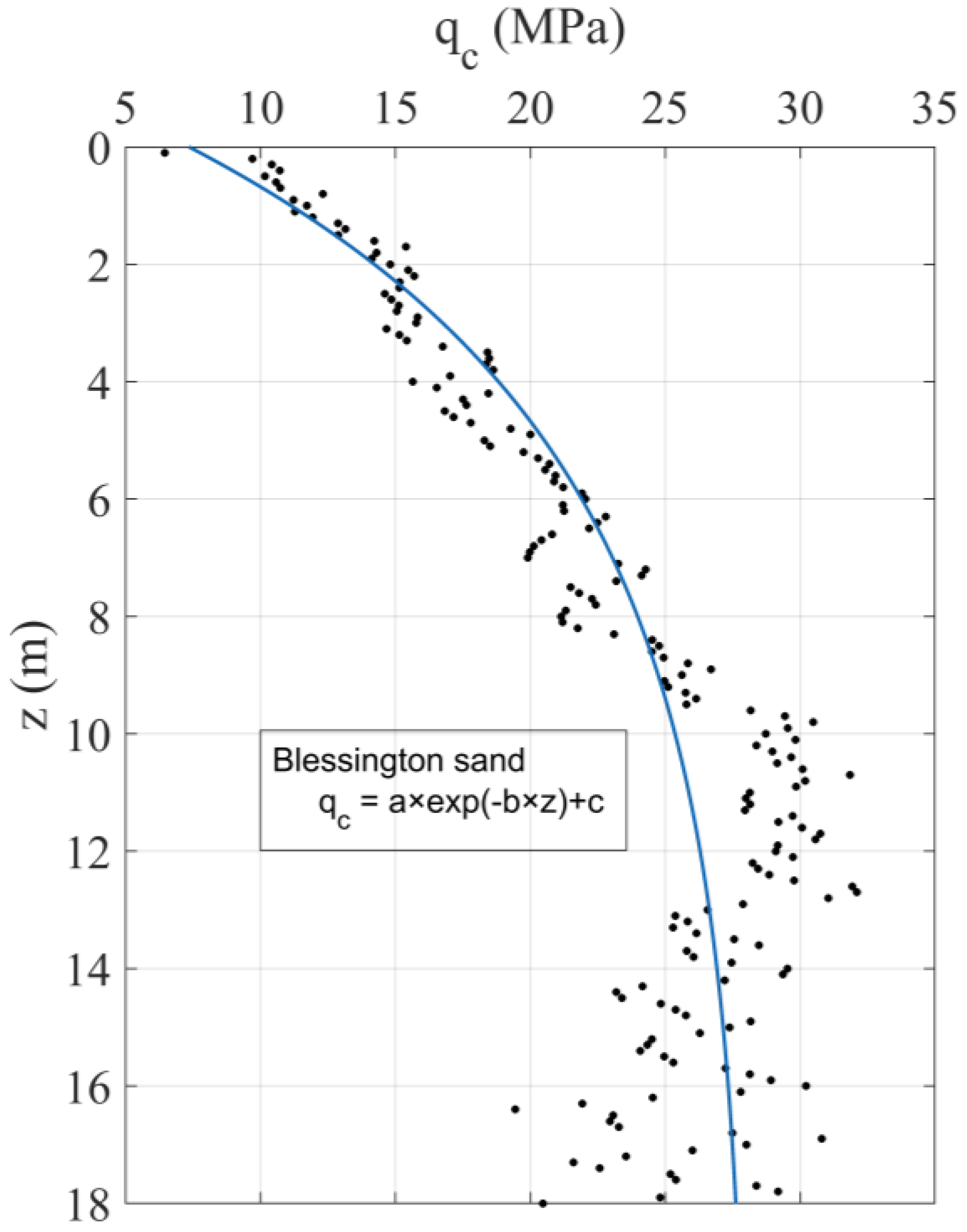
4. Case Study I: Blessington Sand, Ireland
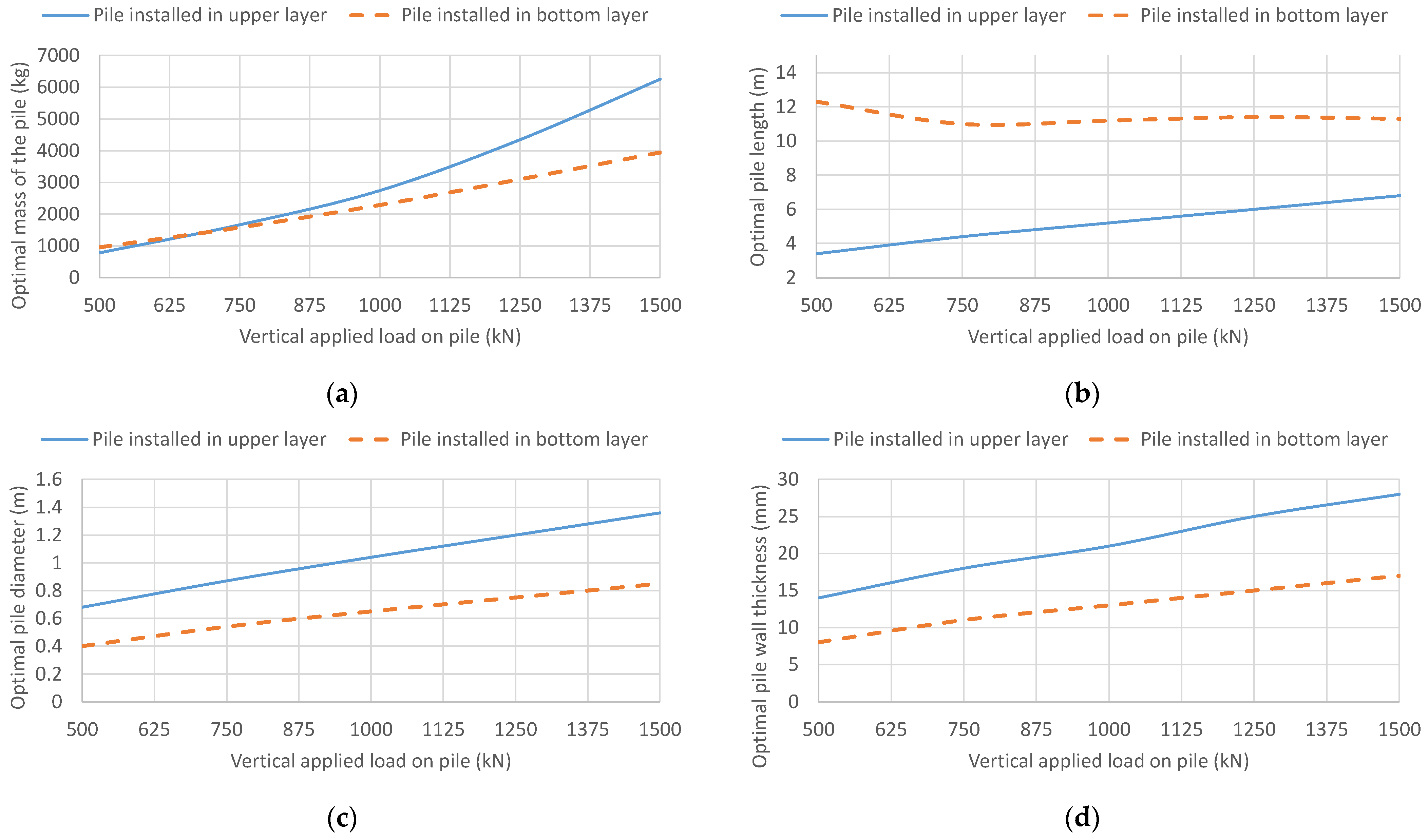
5. Case Study II: Layered Soil Profile
6. Conclusions
- -
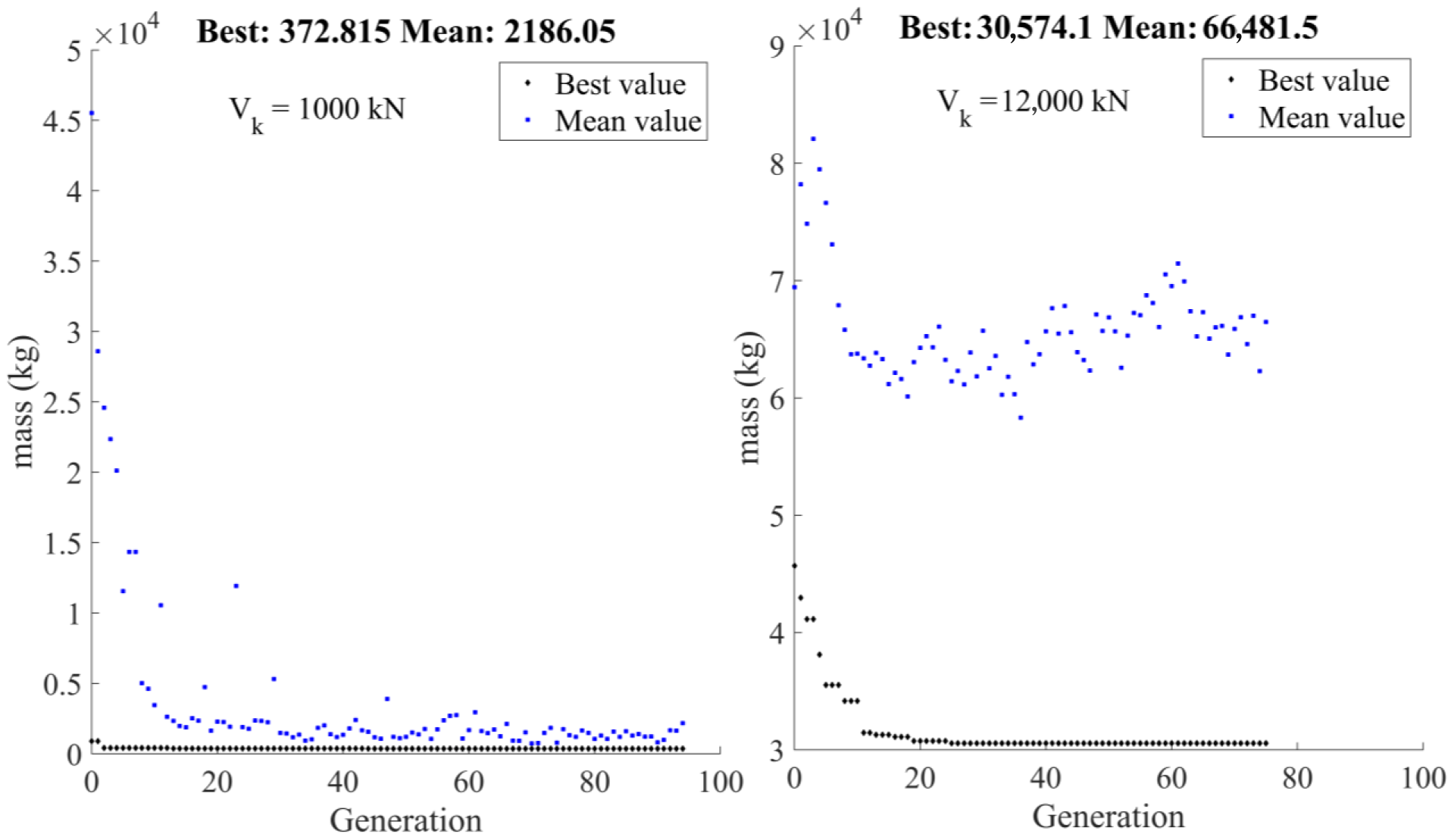
- The linear increase in vertical load leads to an exponential increase in the mass of the pile. A 13-fold increase in the vertical load (from 1000 kN to 13,000 kN) increases the mass of the pile by a factor of 130.4 (from 373 kg to 49,348 kg).
- -
- The optimum ratios of pile length to diameter, diameter to wall thickness and length to wall thickness are 5, 50 and 250, respectively.
- -
- With a vertical load of 9000 kN, the optimum pile diameter reached its maximum value of 1.5 m.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Ab | Area of the pile base |
| Ars | Effective area ratio of the pile shaft |
| Cb | Constant for pipe piles |
| CO2 | Embodied CO2 emissions from pipe pile |
| D | Outside diameter of pile |
| L | Length of the pile |
| Luneff | Depth below the ground level where any shaft friction is ignored |
| MASS | Mass of the pile |
| Nc,Rd | Design axial force resistance |
| Qb | Pile base capacity |
| QRd | Design bearing capacity of the pile |
| Qs | Pile shaft capacity |
| Qult | Total bearing capacity of the pile |
| VEd | Design vertical load |
| VGk | Vertical dead load |
| VQk | Vertical live load |
| a | First best fit coefficient |
| b | Second best fit coefficient |
| c | Third best fit coefficient |
| ciCO2 | Carbon index of steel |
| fs,ave | Average value of cone sleeve resistance |
| fy | Yield strength of steel |
| qc,ave | Average cone tip resistance over a distance 1.5D above and below the pile base |
| t | Thickness of the pile wall |
| z | Depth |
| γG | Partial safety factor for dead load |
| γM0 | Material partial safety factor |
| γQ | Partial safety factor for live load |
| γR | Partial safety factor for bearing capacity |
| γs | Unit weight of the steel |
| δcv | Soil–pile interface friction angle |
| ε | Adjustment by the factor |
| ρs | Density of the steel |
References
- Kolk, H.J.; Baaijens, A.E.; Senders, M. Design criteria for pipe piles in silica sands. In Proceedings of the International Symposium on Frontiers in Offshore Geotechnics, Perth, Australia, 19–21 September 2005. [Google Scholar]
- Jardine, F.M.; Chow, F.C.; Overy, R.F.; Standing, J.R. ICP Design Methods for Driven Piles in Sands and Clays; Thomas Telford Ltd.: London, UK, 2005; ISBN 978-0-7277-3272-9. [Google Scholar]
- Xu, X.; Lehane, B.M. Evaluation of end-bearing capacity of closed-ended pile in sand from cone penetration data. In Proceedings of the International Symposium on Frontiers in Offshore Geotechnics ISFOG 2005, Perth, Australia, 19–21 September 2005. [Google Scholar]
- Xu, X.; Schneider, J.A.; Lehane, B.M. Cone penetration test (CPT) methods for end-bearing assessment of open- and closed-ended driven piles in siliceous sand. Can. Geotech. J. 2008, 45, 1130–1141. [Google Scholar] [CrossRef]
- Gavin, K.G.; Lehane, B.M. The shaft capacity of pipe piles in sand. Can. Geotech. J. 2003, 40, 36–45. [Google Scholar] [CrossRef]
- Igoe, D.; Doherty, P.; Gavin, K. The Development and Testing of an Instrumented Open-Ended Model Pile. Geotech. Test. J. 2010, 33, 72–82. [Google Scholar] [CrossRef]
- Gavin, K.G.; O’Kelly, B.C. Effect of Friction Fatigue on Pile Capacity in Dense Sand. J. Geotech. Geoenviron. Eng. 2007, 133, 63–71. [Google Scholar] [CrossRef]
- Kodsy, A.; Iskander, M. Insights into Plugging of Pipe Piles Based on Pile Dimensions. Appl. Sci. 2022, 12, 2711. [Google Scholar] [CrossRef]
- Lehane, B.M.; Schneider, J.; Xu, X. The UWA-05 method for prediction of axial capacity of driven piles in sand. In Proceedings of the International Symposium on Frontiers in Offshore Geotechnics (IS-FOG 2005), Perth, Australia, 19–21 September 2005. [Google Scholar]
- Bui-Ngoc, T.; Nguyen, T.; Nguyen-Quang, M.-T.; Shiau, J. Predicting load–displacement of driven PHC pipe piles using stacking ensemble with Pareto optimization. Eng. Struct. 2024, 316, 118574. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J.; Du, K.; Khandelwal, M. Enhanced multi-task learning models for pile drivability prediction: Leveraging metaheuristic algorithms and statistical evaluation. Transp. Geotech. 2024, 47, 101288. [Google Scholar] [CrossRef]
- Xi, L.; Jin, L.; Ji, Y.; Liu, P.; Wei, J. Prediction of Ultimate Bearing Capacity of Soil–Cement Mixed Pile Composite Foundation Using SA-IRMO-BPNN Model. Mathematics 2024, 12, 1701. [Google Scholar] [CrossRef]
- Fattahi, H.; Ghaedi, H.; Malekmahmoodi, F.; Armaghani, D.J. Optimizing pile bearing capacity prediction: Insights from dynamic testing and smart algorithms in geotechnical engineering. Measurement 2024, 230, 114563. [Google Scholar] [CrossRef]
- Leung, Y.F.; Klar, A.; Soga, K. Theoretical Study on Pile Length Optimization of Pile Groups and Piled Rafts. J. Geotech. Geoenviron. Eng. 2010, 136, 319–330. [Google Scholar] [CrossRef]
- Xue, J.; Gavin, K.; Murphy, G.; Doherty, P.; Igoe, D. Optimization Technique to Determine the p-y Curves of Laterally Loaded Stiff Piles in Dense Sand. Geotech. Test. J. 2016, 39, 842–854. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal design of piled embankments with basal reinforcement. Geosynth. Int. 2018, 25, 150–163. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Determining optimal designs for conventional and geothermal energy piles. Renew. Energy 2020, 147, 2633–2642. [Google Scholar] [CrossRef]
- Charles, J.A.; Gourvenec, S.M.; Vardy, M.E. Coupling site wide CPT profiles and genetic algorithms for whole-site offshore windfarm layout optimization. In Cone Penetration Testing 2022; CRC Press: London, UK, 2022; pp. 870–875. [Google Scholar]
- Abushama, K.; Hawkins, W.; Pelecanos, L.; Ibell, T. Minimising the embodied carbon of reinforced concrete piles using a multi-level modelling tool with a case study. Structures 2023, 58, 105476. [Google Scholar] [CrossRef]
- Abushama, K.; Hawkins, W.; Pelecanos, L.; Ibell, T. Embodied carbon optimisation of concrete pile foundations and comparison of the performance of different pile geometries. Eng. Struct. 2024, 310, 118109. [Google Scholar] [CrossRef]
- Lyu, F.; Shao, H.; Zhang, W. Comparative analysis about carbon emission of precast pile and cast-in-situ pile. Energy Rep. 2022, 8, 514–525. [Google Scholar] [CrossRef]
- Pop, I.; Wan-Wendner, L.; Vits, W. Optimized Structural Design of Concrete Pile Plug in Steel Pipe Piles. ACI Struct. J. 2022, 119, 153–163. [Google Scholar] [CrossRef]
- Inazumi, S.; Shakya, S. A Comprehensive Review of Sustainable Assessment and Innovation in Jet Grouting Technologies. Sustainability 2024, 16, 4113. [Google Scholar] [CrossRef]
- Lee, J.-H.; Tran, N.X.; Kim, S.-R. Development and field application of GFRP suction pile. Ocean Eng. 2019, 173, 308–318. [Google Scholar] [CrossRef]
- Almallah, A.; El Naggar, H.; Sadeghian, P. Axial Behavior of Innovative Sand-Coated GFRP Piles in Cohesionless Soil. Int. J. Geomech. 2020, 20, 04020179. [Google Scholar] [CrossRef]
- Lowry, K.; Rayhani, M.T. Factors affecting axial and lateral load transfer of hollow fibre-reinforced polymer piles in soft clay. Int. J. Geotech. Eng. 2023, 17, 644–653. [Google Scholar] [CrossRef]
- Farhangi, V.; Karakouzian, M. Effect of Fiber Reinforced Polymer Tubes Filled with Recycled Materials and Concrete on Structural Capacity of Pile Foundations. Appl. Sci. 2020, 10, 1554. [Google Scholar] [CrossRef]
- Rens, K.L.; Liu, R.; Foltz, S.D. Sustainable Approach for Optimal Steel Sheet Pile Structure Assessment, Maintenance, and Rehabilitation. J. Perform. Constr. Facil. 2013, 27, 181–190. [Google Scholar] [CrossRef]
- Das, B.M. Principles of Foundation Engineering, 7th ed.; CL-Engineering: Chonburi, Thailand, 2010; ISBN 0495668109. [Google Scholar]
- Suzuki, Y.; Akash, Y.; Sawaizumi, S.; Hirakaw, T.; Kameyama, A.; Taenaka, S. Nippon Steel Corporation’ s Construction Products and Technologies for Carbon Neutral Buildings and Infrastructures; Nippon Steel Technical Report; Nippon Steel Corporation: Tokyo, Japan, 2024; pp. 10–16. [Google Scholar]
- The Model of the Eco-costs/Value Ratio (EVR). Available online: www.ecocostsvalue.com/eco-costs/eco-costs-emissions/ (accessed on 7 June 2024).
- Poulos, H.G. Pile behaviour—Theory and application. Géotechnique 1989, 39, 365–415. [Google Scholar] [CrossRef]
- Quevedo-Reina, R.; Álamo, G.M.; François, S.; Lombaert, G.; Aznárez, J.J. Importance of the soil–structure interaction in the optimisation of the jacket designs of offshore wind turbines. Ocean Eng. 2024, 303, 117802. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, Z.; Chen, P.; Luo, H.; Zhang, R.; Yu, C.; Zhan, C. Experimental and Numerical Analysis of Pile–Rock Interaction Characteristics of Steel Pipe Piles Penetrating into Coral Reef Limestone. Sustainability 2022, 14, 13761. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J. Study on the structure parameters and design method optimization of blade-type screw steel pipe pile. Heliyon 2024, 10, e35046. [Google Scholar] [CrossRef]
- Forcellini, D. Analytical fragility curves of pile foundations with soil-structure interaction (SSI). Geosciences 2021, 11, 66. [Google Scholar] [CrossRef]
- Mina, D.; Forcellini, D.; Karampour, H. Analytical fragility curves for assessment of the seismic vulnerability of HP/HT unburied subsea pipelines. Soil Dyn. Earthq. Eng. 2020, 137, 106308. [Google Scholar] [CrossRef]
- Tomlinson, M.; Woodward, J. Pile Design and Construction Practice; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9780429224461. [Google Scholar]
- Bowles, J.E. Foundation Analysis and Design; Civil Engineering Series; McGraw-Hill: New York, NY, USA, 1997; ISBN 9780071188449. [Google Scholar]
- Abouzaid, A.; El Naggar, M.H.; Drbe, O. Comprehensive Evaluation of Lateral Performance of Innovative Post in Sand. Appl. Sci. 2024, 14, 2442. [Google Scholar] [CrossRef]
- Bao, H.; Peng, J.; Cheng, Z.; Hong, J.; Gao, Y. Experimental Study on Inner Interface Mechanical Properties of the ESDCM Pile with Steel Core. Buildings 2023, 13, 486. [Google Scholar] [CrossRef]
- Aleem, M.; Bhattacharya, S.; Cui, L.; Amani, S.; Salem, A.R.; Jalbi, S. Load utilisation (LU) ratio of monopiles supporting offshore wind turbines: Formulation and examples from European Wind Farms. Ocean Eng. 2022, 248, 110798. [Google Scholar] [CrossRef]
- Deep, K.; Singh, K.P.; Kansal, M.L.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]
- Venkataraman, P. Applied Optimization with Matlab Programming; Wiley: Hoboken, NJ, USA, 2009; ISBN 047008488X. [Google Scholar]
- The MathWorks, Inc., R. How the Genetic Algorithm Works. 2021. Available online: https://se.mathworks.com/help/gads/how-the-genetic-algorithmworks.html (accessed on 8 June 2024).
- Lehane, B.M.; Randolph, M.F. Evaluation of a Minimum Base Resistance for Driven Pipe Piles in Siliceous Sand. J. Geotech. Geoenviron Eng. 2002, 128, 198–205. [Google Scholar] [CrossRef]
- EN 1993-1-1 Eurocode 3; Design of Steel Structures. General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2005.
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- De Nicola, A.; Randolph, M.F. The plugging behaviour of driven and jacked piles in sand. Géotechnique 1997, 47, 841–856. [Google Scholar] [CrossRef]

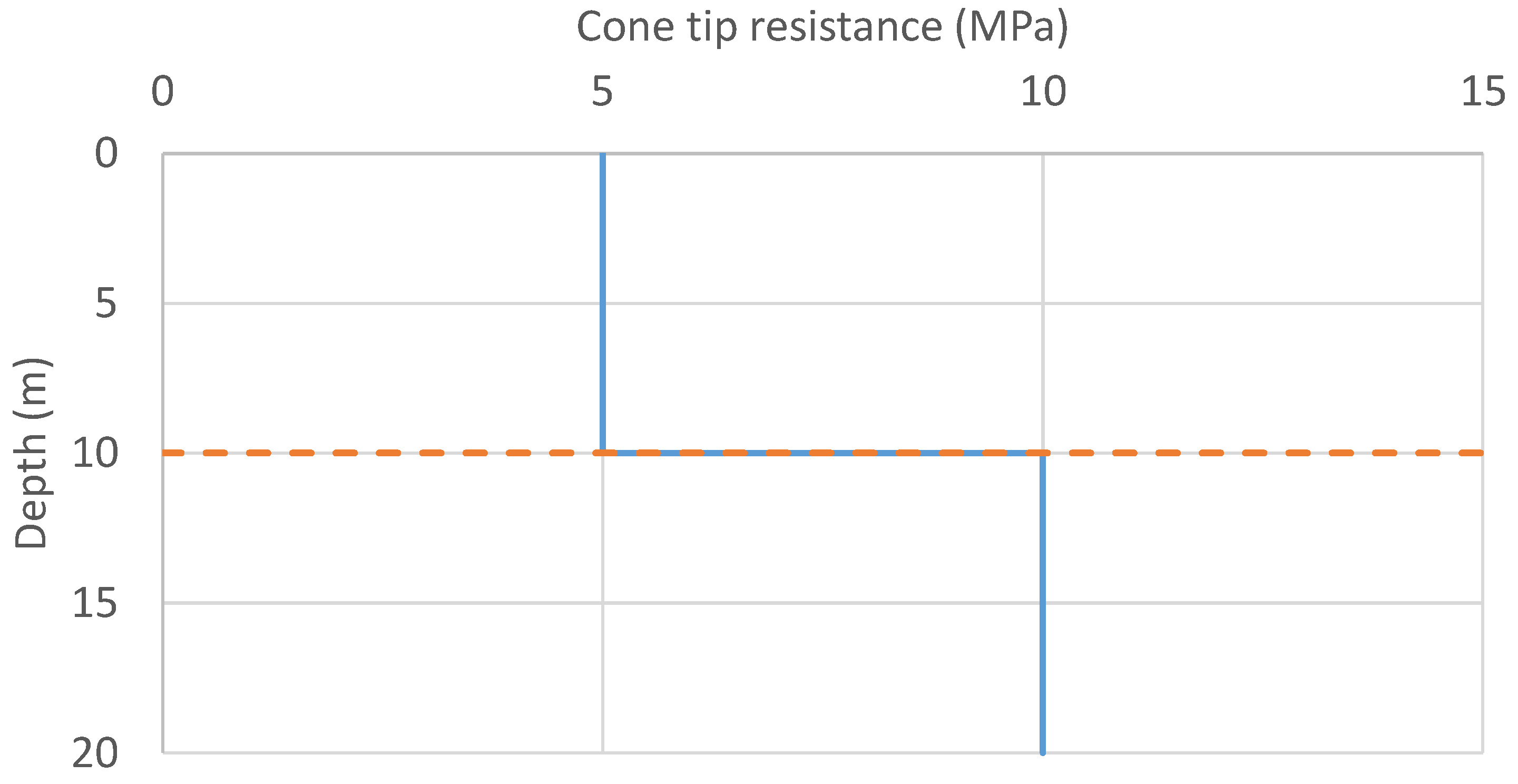
| Variable | Minimum | Increment (Step) | Maximum | Number of Discrete Alternatives |
|---|---|---|---|---|
| D (m) | 0.30 | 0.1 | 1.50 | 121 |
| L (m) | 2.0 | 0.1 | 50.0 | 481 |
| t (m) | 0.005 | 0.001 | 0.050 | 46 |
| Blessington Sand (a = −28.83, b = 0.1999, c = 28.18) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Load VGk (kN) | 1000 | 2000 | 3000 | 4000 | 5000 | 7000 | 9000 | 11,000 | 12,000 | 13,000 |
| D (m) | 0.52 | 0.73 | 0.88 | 1.02 | 1.15 | 1.37 | 1.5 | 1.5 | 1.5 | 1.5 |
| L (m) | 2.7 | 3.7 | 4.5 | 5.2 | 5.8 | 6.9 | 10.1 | 11.9 | 17.1 | 27.6 |
| t (mm) | 11 | 15 | 18 | 21 | 23 | 28 | 30 | 50 | 50 | 50 |
| MASS (kg) | 373 | 979 | 1722 | 2690 | 3708 | 6394 | 10,984 | 21,277 | 30,574 | 49,348 |
| CO2 (kgCO2) | 324.3 | 851.4 | 1498.1 | 2340.6 | 3225.7 | 5562.9 | 9556.5 | 18,510.7 | 26,599.5 | 42,932.5 |
| Utilization rate of geotechnical and structural conditions | ||||||||||
| VEd/QRd (%) | 100 | 98 | 100 | 99 | 99 | 100 | 100 | 100 | 100 | 100 |
| L/Lmin (%) | 96 | 99 | 98 | 98 | 99 | 99 | 74 | 63 | 44 | 27 |
| (L/D)/50 (%) | 10 | 10 | 10 | 10 | 10 | 10 | 13 | 16 | 23 | 37 |
| (D/t)/50 (%) | 95 | 97 | 98 | 97 | 100 | 98 | 100 | 60 | 60 | 60 |
| VEd/Ncrd (%) | 24 | 25 | 26 | 26 | 26 | 25 | 28 | 21 | 23 | 25 |
| Ratios of pipe pile dimensions | ||||||||||
| L/D | 5.2 | 5.1 | 5.1 | 5.1 | 5.0 | 5.0 | 6.7 | 7.9 | 11.4 | 18.4 |
| D/t | 47.3 | 48.7 | 48.9 | 48.6 | 50.0 | 48.9 | 50.0 | 30.0 | 30.0 | 30.0 |
| L/t | 245.5 | 246.7 | 250.0 | 247.6 | 252.2 | 246.4 | 336.7 | 238.0 | 342.0 | 552.0 |
| Pile Base Installed in Upper Layer | |||||
|---|---|---|---|---|---|
| Load VGk (kN) | 500 | 750 | 1000 | 1250 | 1500 |
| L/D | 5.0 | 5.1 | 5.0 | 5.0 | 5.0 |
| D/t | 48.6 | 48.3 | 49.5 | 48.0 | 48.6 |
| L/t | 243 | 244 | 248 | 240 | 243 |
| Pile Base Installed in Bottom Layer | |||||
| L/D | 30.8 | 20.4 | 17.2 | 15.2 | 13.3 |
| D/t | 50.0 | 49.1 | 50.0 | 50.0 | 50.0 |
| L/t | 1538 | 1000 | 862 | 760 | 665 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jelušič, P. Enhancing Sustainability of Building Foundations with Efficient Open-End Pile Optimization. Sustainability 2024, 16, 6880. https://doi.org/10.3390/su16166880
Jelušič P. Enhancing Sustainability of Building Foundations with Efficient Open-End Pile Optimization. Sustainability. 2024; 16(16):6880. https://doi.org/10.3390/su16166880
Chicago/Turabian StyleJelušič, Primož. 2024. "Enhancing Sustainability of Building Foundations with Efficient Open-End Pile Optimization" Sustainability 16, no. 16: 6880. https://doi.org/10.3390/su16166880
APA StyleJelušič, P. (2024). Enhancing Sustainability of Building Foundations with Efficient Open-End Pile Optimization. Sustainability, 16(16), 6880. https://doi.org/10.3390/su16166880








