An Enhanced Continuation Power Flow Method Using Hybrid Parameterization
Abstract
:1. Introduction
- A simple modification to the basic parameterization method allows convenient adaptation to CPF applications.
- The proposed method reduces the processing time by 32.76% from the well-known arc-length parameterization method while maintaining accuracy.
- The paper proposes a quantitative evaluation method for the accuracy of load margin assessment, which has not previously existed for CPF studies.
- The enhanced computational efficiency of the proposed method enables fast assessment of numerous scenarios to ensure power system stability under a complex and uncertain renewable-integrated grid.
2. Proposed Method
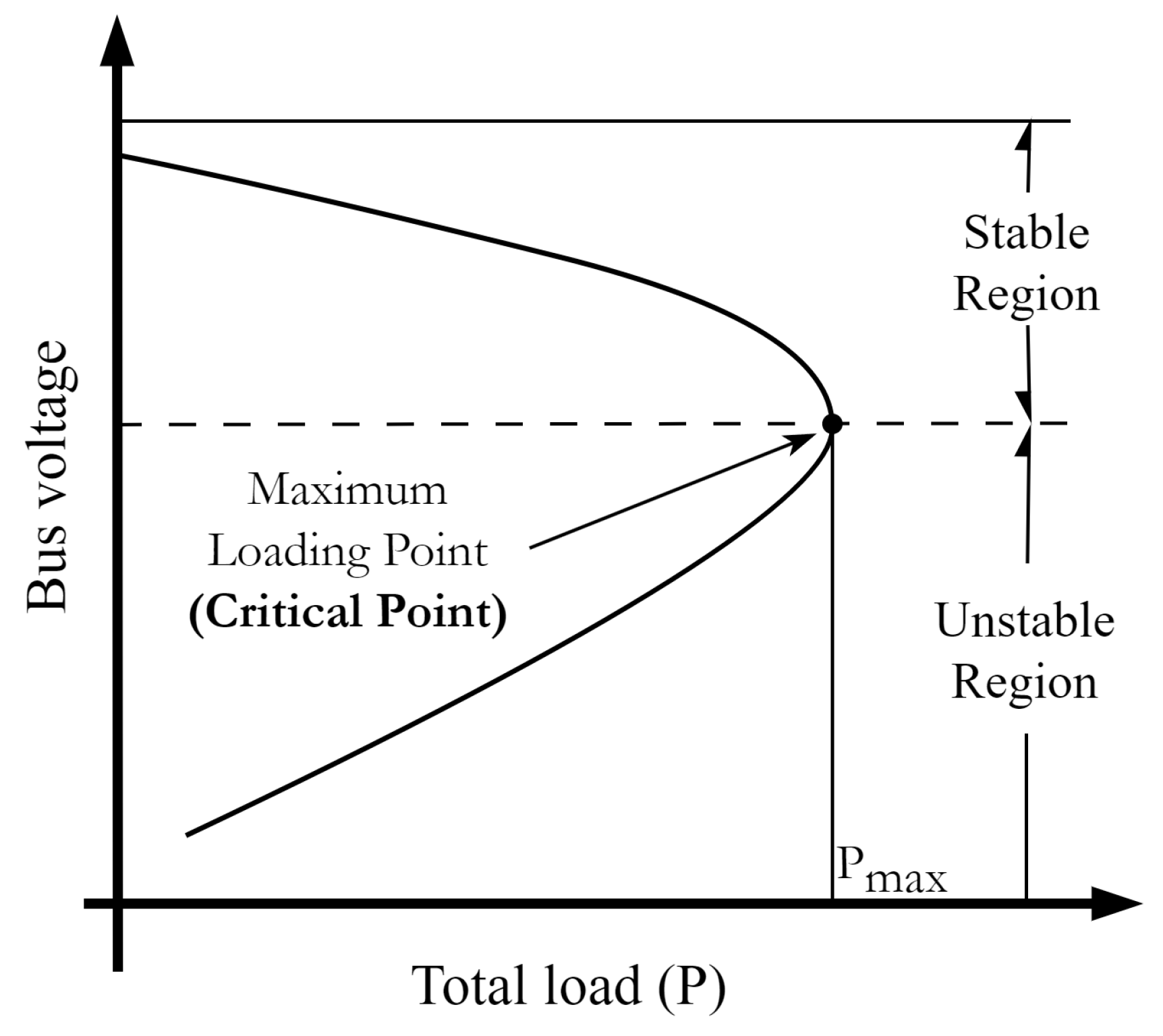
2.1. P-V Curve and Loadability Factor
2.2. Process of Continuation Power Flow
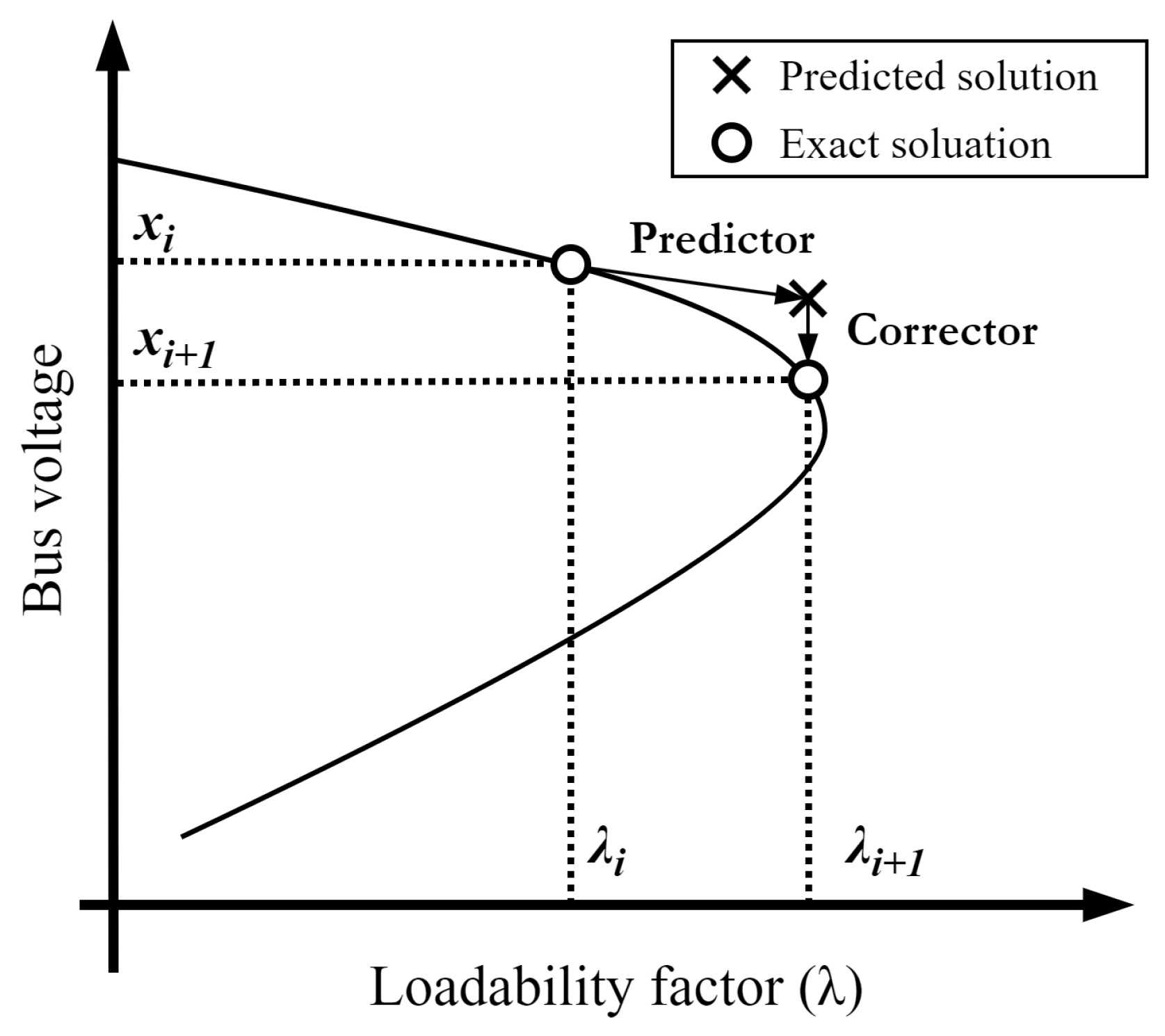
2.2.1. Predictor
2.2.2. Corrector
2.2.3. Parameterization
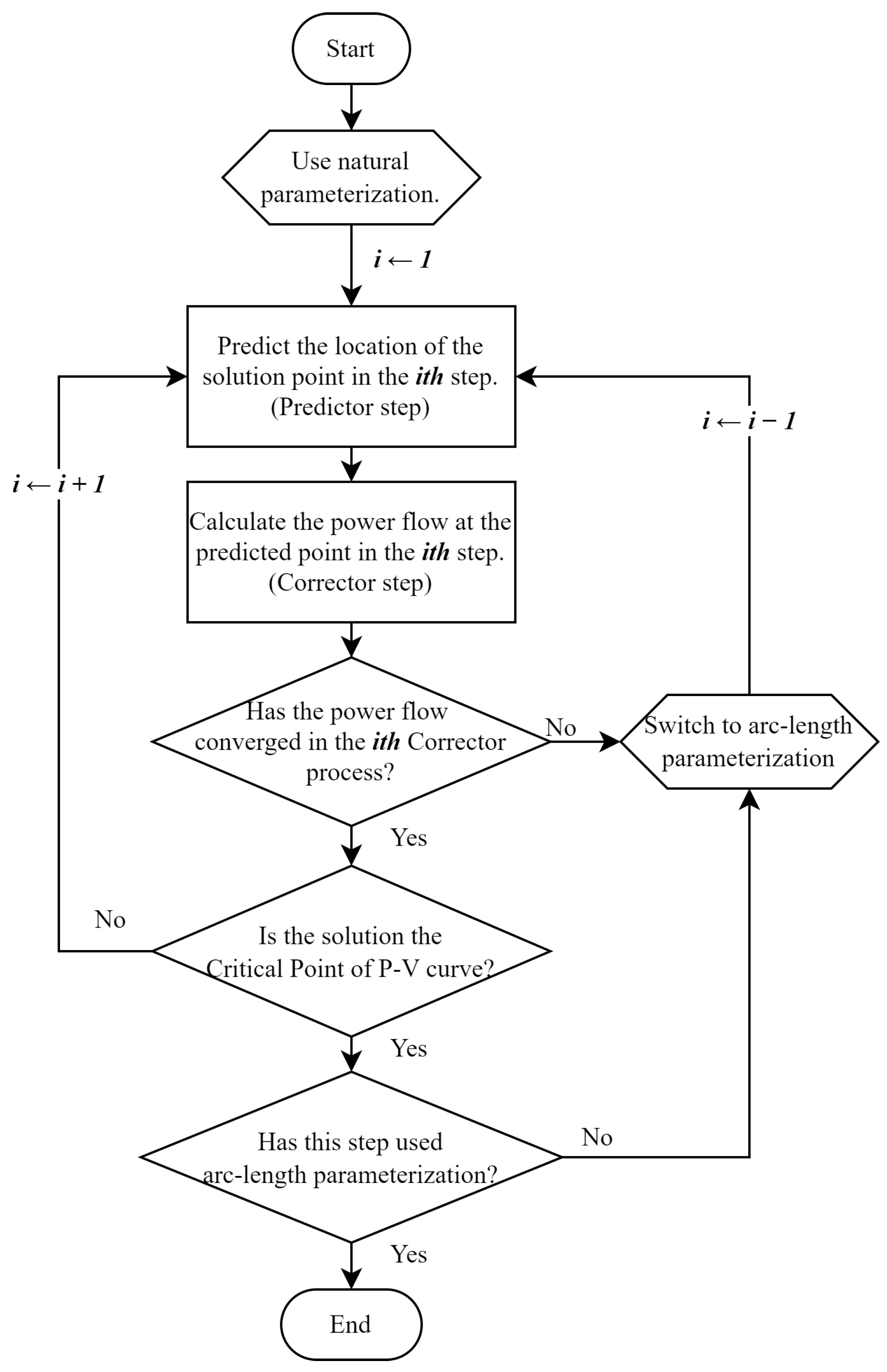
2.3. Hybrid Parameterization
3. Case Study
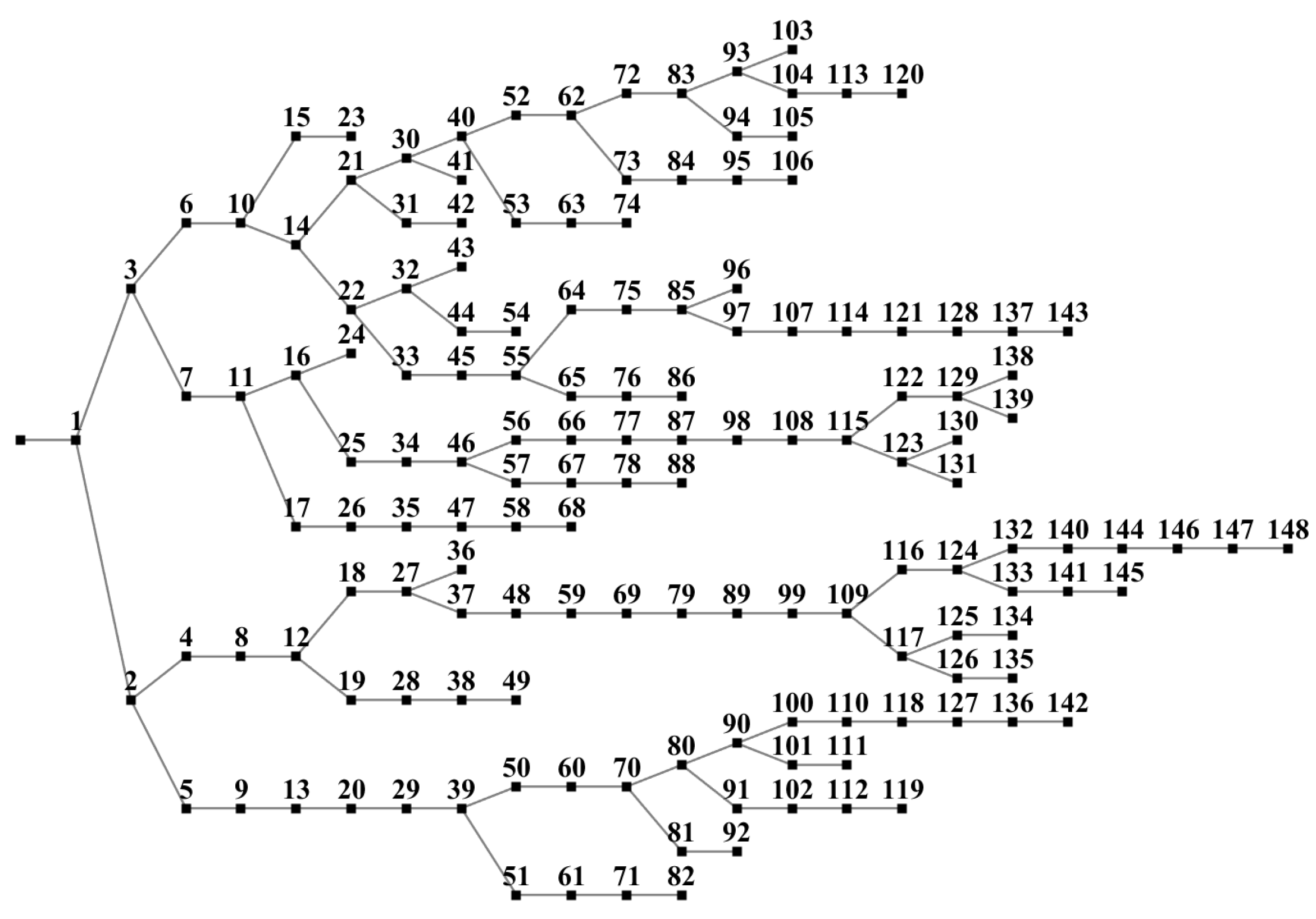
3.1. Power Grid Test Case
3.2. DG Scenarios
3.3. Parameterization Comparison
3.3.1. Metrics
3.3.2. Performance
3.4. Performance over Different Step Sizes
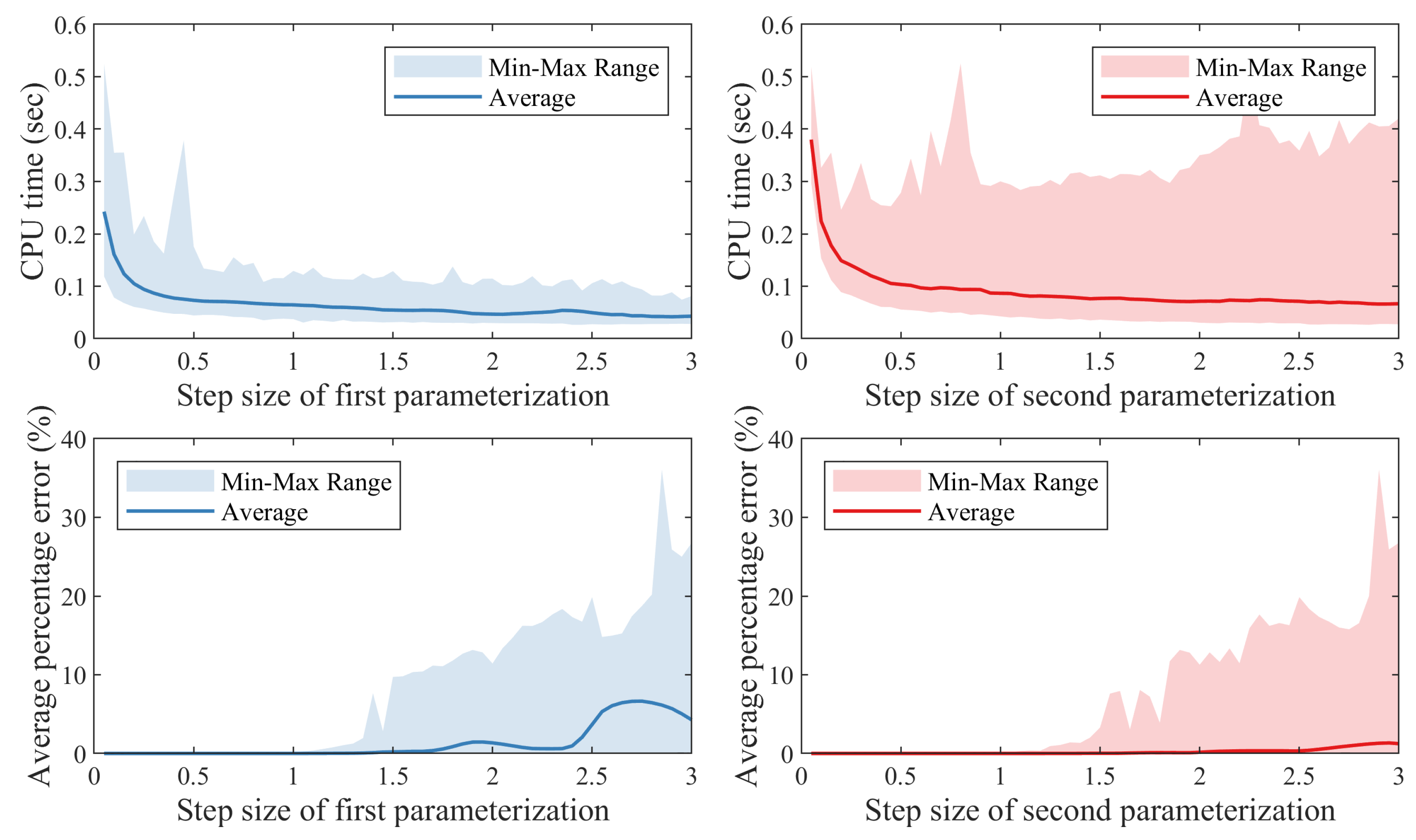
3.5. Other Parameterization Combinations for the Hybrid Method
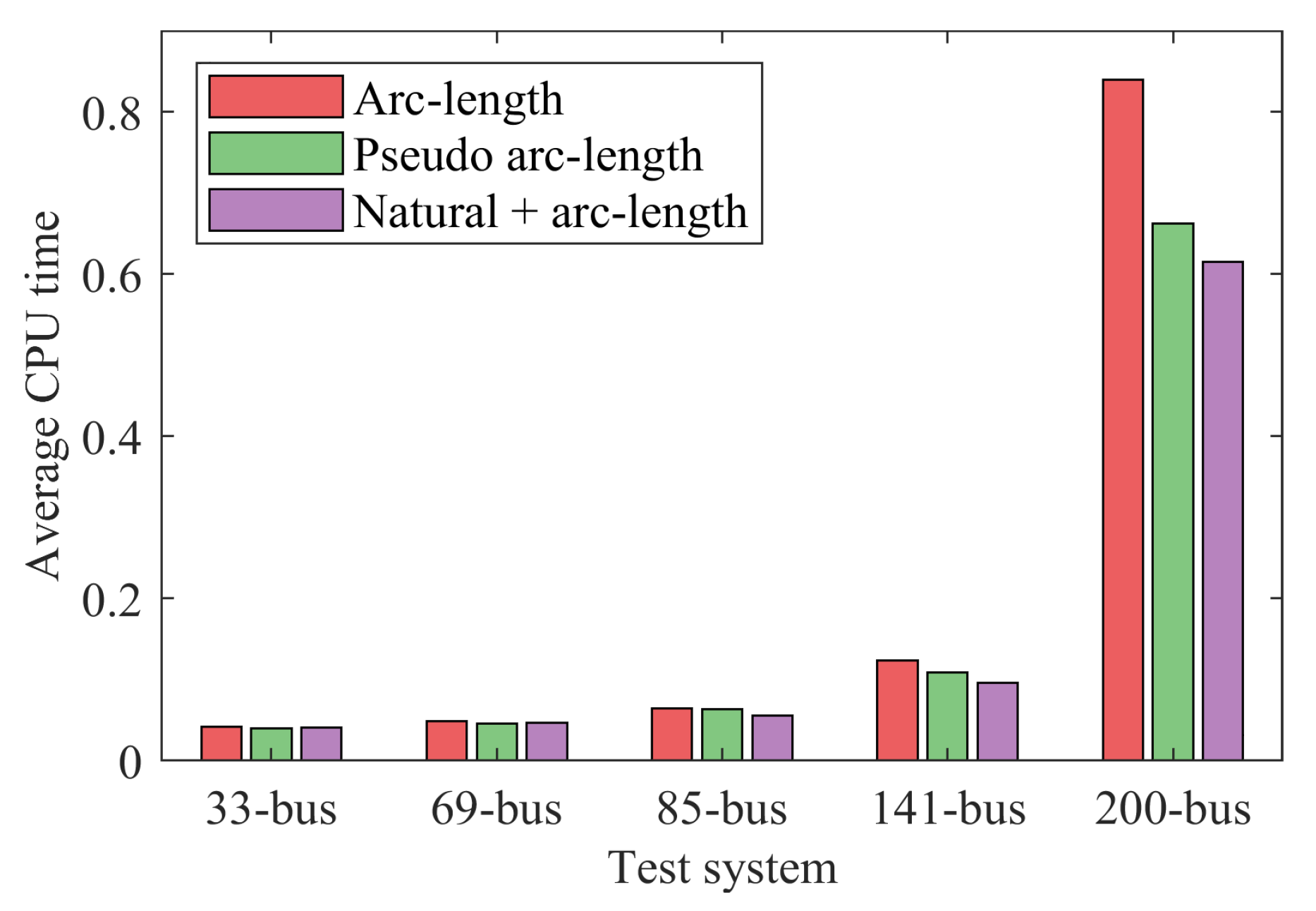
3.6. Performace Comparation on Different Grid Scales
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Canizares, C.; Alvarado, F. Point of collapse and continuation methods for large AC/DC systems. IEEE Trans. Power Syst. 1993, 8, 1–8. [Google Scholar] [CrossRef]
- Woo, H.; Son, Y.; Cho, J.; Choi, S. Stochastic Second-Order Conic Programming for Optimal Sizing of Distributed Generator Units and Electric Vehicle Charging Stations. Sustainability 2022, 14, 4964. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, C.; Li, J.; Zhu, L.; Zhou, B.; Zhou, Q.; Cheng, L.; Shuai, Z. A Novel Interval Power Flow Method Based on Hybrid Box-Ellipsoid Uncertain Sets. IEEE Trans. Power Syst. 2024, 39, 6111–6114. [Google Scholar] [CrossRef]
- Lee, M.; Yoon, M.; Cho, J.; Choi, S. Probabilistic Stability Evaluation Based on Confidence Interval in Distribution Systems with Inverter-Based Distributed Generations. Sustainability 2022, 14, 3806. [Google Scholar] [CrossRef]
- Jaramillo, M.D.; Carrión, D.F.; Muñoz, J.P. A Novel Methodology for Strengthening Stability in Electrical Power Systems by Considering Fast Voltage Stability Index under N − 1 Scenarios. Energies 2023, 16, 3396. [Google Scholar] [CrossRef]
- Jaramillo, M.; Carrión, D.; Muñoz, J. A Deep Neural Network as a Strategy for Optimal Sizing and Location of Reactive Compensation Considering Power Consumption Uncertainties. Energies 2022, 15, 9367. [Google Scholar] [CrossRef]
- Iba, K.; Suzuki, H.; Egawa, M.; Watanabe, T. Calculation of critical loading condition with nose curve using homotopy continuation method. IEEE Trans. Power Syst. 1991, 6, 584–593. [Google Scholar] [CrossRef]
- Ajjarapu, V.; Christy, C. The continuation power flow: A tool for steady state voltage stability analysis. IEEE Trans. Power Syst. 1992, 7, 416–423. [Google Scholar] [CrossRef]
- Farid, K.; Shahriar, A.; Reza Shabani, H. The Continuation Power Flow (CPF) Methods. In Voltage Stability in Electrical Power Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2022; Chapter 5; pp. 97–118. [Google Scholar] [CrossRef]
- Chiang, H.D.; Flueck, A.J.; Shah, K.S.; Balu, N. CPFLOW: A practical tool for tracing power system steady-state stationary behavior due to load and generation variations. IEEE Trans. Power Syst. 1995, 10, 623–634. [Google Scholar] [CrossRef]
- Flueck, A.; Dondeti, J. A new continuation power flow tool for investigating the nonlinear effects of transmission branch parameter variations. IEEE Trans. Power Syst. 2000, 15, 223–227. [Google Scholar] [CrossRef]
- Li, S.H.; Chiang, H.D. Nonlinear predictors and hybrid corrector for fast continuation power flow. IET Gener. Transm. Distrib. 2008, 2, 341–354. [Google Scholar] [CrossRef]
- Mori, H.; Yamada, S. Continuation power flow with the nonlinear predictor of the Lagrange’s polynomial interpolation formula. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; Volume 2, pp. 1133–1138. [Google Scholar] [CrossRef]
- Kim, H.T.; Lee, J.; Yoon, M.; Lee, M.J.; Cho, N.; Choi, S. Continuation power flow based distributed energy resource hosting capacity estimation considering renewable energy uncertainty and stability in distribution systems. Energies 2020, 13, 4367. [Google Scholar] [CrossRef]
- Alves, D.; da Silva, L.; Castro, C.; da Costa, V. Continuation fast decoupled power flow with secant predictor. IEEE Trans. Power Syst. 2003, 18, 1078–1085. [Google Scholar] [CrossRef]
- Dong, X.; Wang, C.; Yun, Z.; Han, X.; Liang, J.; Wang, Y.; Zhao, P. Calculation of optimal load margin based on improved continuation power flow model. Int. J. Electr. Power Energy Syst. 2018, 94, 225–233. [Google Scholar] [CrossRef]
- Liang, H.; Zhao, J. A New Method of Continuous Power Flow for Voltage Stability Analysis. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021; pp. 337–340. [Google Scholar] [CrossRef]
- Neto, A.B.; Filho, L.R.A.G.; Alves, D.A. Continuation Power Flow: A Parameterization Technique and Adaptive Step Size Control. In Proceedings of the 2021 IEEE URUCON, Montevideo, Uruguay, 24–26 November 2021; pp. 75–79. [Google Scholar] [CrossRef]
- Pourbagher, R.; Derakhshandeh, S.Y.; Hamedani Golshan, M.E. An adaptive multi-step Levenberg-Marquardt continuation power flow method for voltage stability assessment in the Ill-conditioned power systems. Int. J. Electr. Power Energy Syst. 2022, 134, 107425. [Google Scholar] [CrossRef]
- Alves, D.A.; da Silva, L.C.; Castro, C.A.; da Costa, V.F. Alternative parameters for the continuation power flow method. Electr. Power Syst. Res. 2003, 66, 105–113. [Google Scholar] [CrossRef]
- Ju, Y.; Wu, W.; Zhang, B.; Sun, H. Continuation power flow based on a novel local geometric parameterisation approach. IET Gener. Transm. Distrib. 2014, 8, 811–818. [Google Scholar] [CrossRef]
- Ruan, C.; Wang, X.; Wang, X.; Gao, F.; Li, Y. Improved Continuation Power Flow Calculation Method Based on Coordinated Combination of Parameterization. In Proceedings of the 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–6 November 2018; pp. 207–211. [Google Scholar] [CrossRef]
- Gao, H.; Wang, L.; Yang, D.; Cai, G. Mechanism Enhanced Data-Driven Method for Reliability Improvement of Load Margin Estimation. IEEE Trans. Power Syst. 2024, 39, 3715–3724. [Google Scholar] [CrossRef]
- Bento, M.E.C. Physics-Guided Neural Network for Load Margin Assessment of Power Systems. IEEE Trans. Power Syst. 2024, 39, 564–575. [Google Scholar] [CrossRef]
- Lee, B.; Song, H.; Kwon, S.H.; Jang, G.; Kim, J.H.; Ajjarapu, V. A study on determination of interface flow limits in the KEPCO system using modified continuation power flow (MCPF). IEEE Trans. Power Syst. 2002, 17, 557–564. [Google Scholar] [CrossRef]
- de Araujo, L.R.; Penido, D.R.R.; de Souza, B.C.; de Alcântara Vieira, F. Discontinuities and unstable solutions beyond the maximum load point of nonlinear unbalanced distribution systems. Electr. Power Syst. Res. 2023, 214, 108865. [Google Scholar] [CrossRef]
- Zhang, X.P.; Ju, P.; Handschin, E. Continuation three-phase power flow: A tool for voltage stability analysis of unbalanced three-phase power systems. IEEE Trans. Power Syst. 2005, 20, 1320–1329. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Gao, W. Fast Calculation Method for Continuous Power Flow of Microgrid Based on Levenberg-Marquardt Algorithm. IEEE Access 2023, 11, 49578–49586. [Google Scholar] [CrossRef]
- Colombari, L.F.S.; Kuiava, R.; Peric, V.; Ramos, R.A. Continuation Load Flow Considering Discontinuous Behaviors of Distribution Grids. IEEE Trans. Power Syst. 2019, 34, 3476–3483. [Google Scholar] [CrossRef]
- Nirbhavane, P.S.; Corson, L.; Rizvi, S.M.H.; Srivastava, A.K. TPCPF: Three-Phase Continuation Power Flow Tool for Voltage Stability Assessment of Distribution Networks with Distributed Energy Resources. IEEE Trans. Ind. Appl. 2021, 57, 5425–5436. [Google Scholar] [CrossRef]
- Zeng, L.; Chiang, H.D.; Neves, L.S.; Alberto, L.F.C. On the accuracy of power flow and load margin calculation caused by incorrect logical PV/PQ switching: Analytics and improved methods. Int. J. Electr. Power Energy Syst. 2023, 147, 108905. [Google Scholar] [CrossRef]
- Wang, T.; Wang, S.; Ma, S.; Guo, J.; Zhou, X. An Extended Continuation Power Flow Method for Static Voltage Stability Assessment of Renewable Power Generation-Penetrated Power Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 71, 1. [Google Scholar] [CrossRef]
- Zhang, X.; Shin, D.; Son, Y.; Woo, H.; Kim, S.Y.; Choi, S. Three-Stage Flexibility Provision Framework for Radial Distribution Systems Considering Uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 948–961. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Q.; Zhou, B.; Chung, C.Y.; Li, J.; Zhu, L.; Shuai, Z. A Central Limit Theorem-Based Method for DC and AC Power Flow Analysis Under Interval Uncertainty of Renewable Power Generation. IEEE Trans. Sustain. Energy 2023, 14, 563–575. [Google Scholar] [CrossRef]
- Yoon, M.; Cho, N.; Choi, S. Analysis of temporary overvoltage due to inverter-based distributed generation in networked distribution systems. Appl. Energy 2023, 341, 121059. [Google Scholar] [CrossRef]
- Cho, J.; Kim, H.; Ryu, H.; Son, Y.; Choi, S. Analysis of distributed power generation forecasting model for power distribution planning. Trans. Korean Inst. Electr. Eng. 2021, 70, 1248–1262. [Google Scholar] [CrossRef]
- Zhang, X.; Woo, H.; Choi, S. An interval power flow method for radial distribution systems based on hybrid second-order cone and linear programming. Sustain. Energy Grids Netw. 2023, 36, 101158. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Liang, H.; Xu, J. Application of an Improved Continuous Power Flow Method in Voltage Stability Analysis. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 244–248. [Google Scholar] [CrossRef]
- Kuroda, E.; Watanabe, M.; Kato, D.; Saito, N.; Yatsu, M. Fast computation method of static voltage stability using geometric parameter adjustment for the continuation power flow. Electr. Eng. Jpn. 2021, 214, e23296. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Das, D. Optimal placement of capacitors in radial distribution system using a Fuzzy-GA method. Int. J. Electr. Power Energy Syst. 2008, 30, 361–367. [Google Scholar] [CrossRef]
- Das, D.; Kothari, D.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
- Khodr, H.; Olsina, F.; Jesus, P.D.O.D.; Yusta, J. Maximum savings approach for location and sizing of capacitors in distribution systems. Electr. Power Syst. Res. 2008, 78, 1192–1203. [Google Scholar] [CrossRef]
- Birchfield, A.B.; Xu, T.; Gegner, K.M.; Shetye, K.S.; Overbye, T.J. Grid Structural Characteristics as Validation Criteria for Synthetic Networks. IEEE Trans. Power Syst. 2017, 32, 3258–3265. [Google Scholar] [CrossRef]
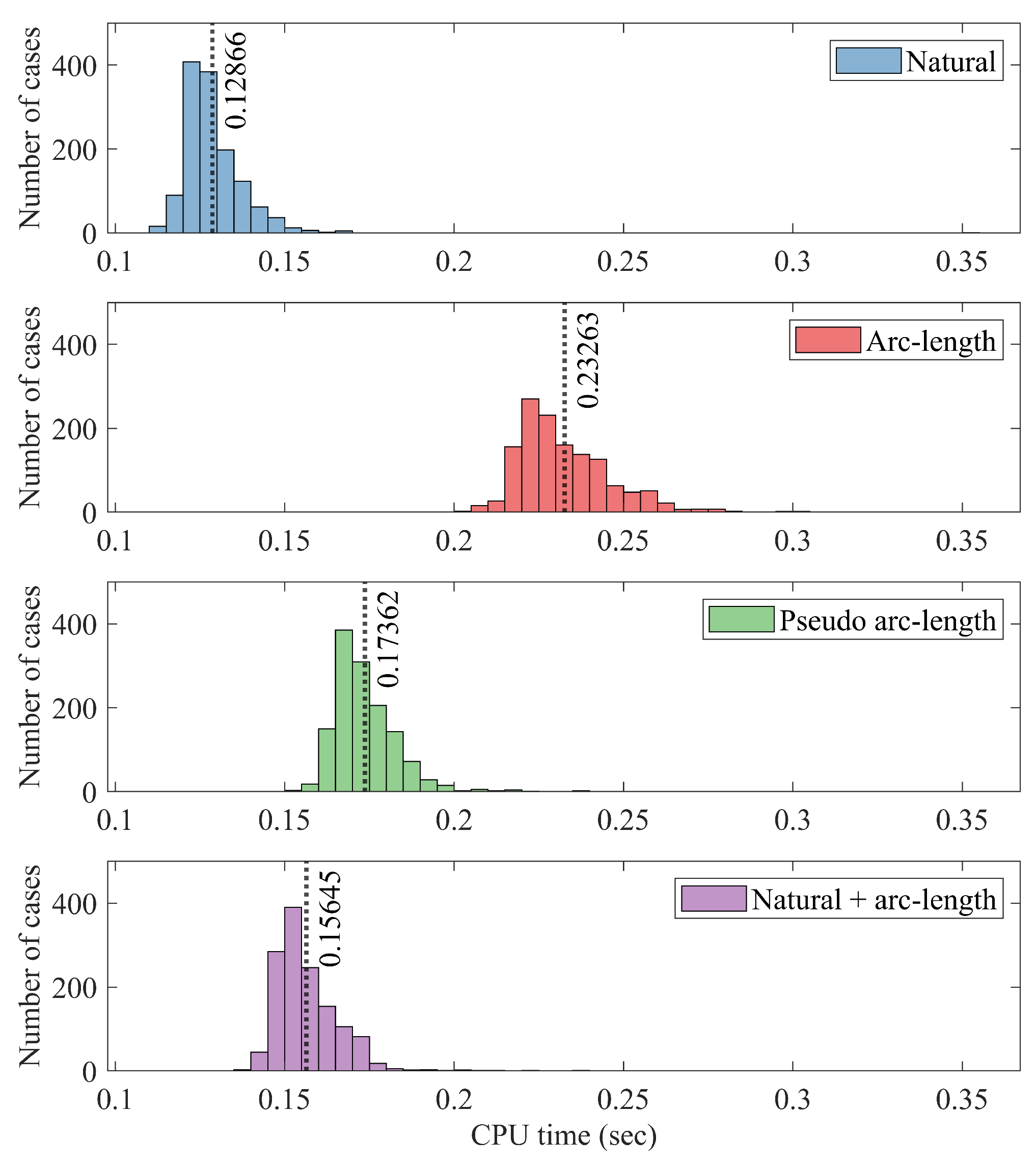
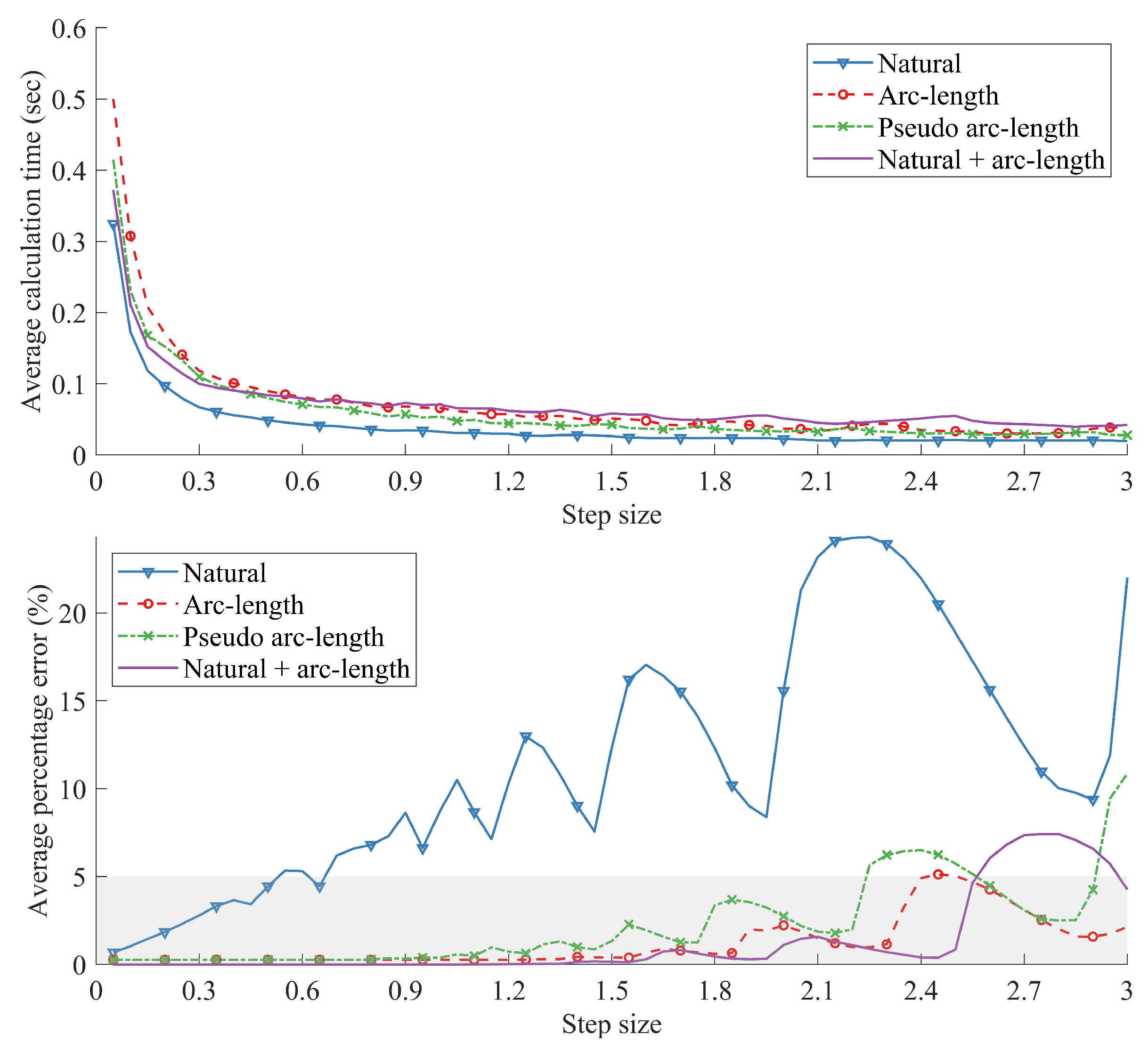
| Parameterization | Percentage Error (%) | CPU Time (s) |
|---|---|---|
| Natural | 0.7822 | 0.12866 |
| Arc-length | 0.23263 | |
| Pseudo arc-length | 0.17362 | |
| Natural + arc-length | 0.15645 |
| First Parameterization | Second Parameterization | Percentage Error (%) | CPU Time (s) |
|---|---|---|---|
| Arc-length | Natural | 0.17964 | |
| Arc-length | Arc-length | 0.17833 | |
| Arc-length | Pseudo arc-length | 0.18789 | |
| Pseudo arc-length | Natural | 0.16849 | |
| Pseudo arc-length | Arc-length | 0.16346 | |
| Pseudo arc-length | Pseudo arc-length | 0.16023 | |
| Natural | Natural | 2.9825 | 0.10397 |
| Natural | Arc-length | 0.13917 | |
| Natural | Pseudo arc-length | 0.14294 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Woo, H.; Yoon, Y.; Kim, H.-T.; Kim, Y.J.; Kang, M.; Zhang, X.; Choi, S. An Enhanced Continuation Power Flow Method Using Hybrid Parameterization. Sustainability 2024, 16, 7595. https://doi.org/10.3390/su16177595
Kim H, Woo H, Yoon Y, Kim H-T, Kim YJ, Kang M, Zhang X, Choi S. An Enhanced Continuation Power Flow Method Using Hybrid Parameterization. Sustainability. 2024; 16(17):7595. https://doi.org/10.3390/su16177595
Chicago/Turabian StyleKim, Haelee, Hyeon Woo, Yeunggurl Yoon, Hyun-Tae Kim, Yong Jung Kim, Moonho Kang, Xuehan Zhang, and Sungyun Choi. 2024. "An Enhanced Continuation Power Flow Method Using Hybrid Parameterization" Sustainability 16, no. 17: 7595. https://doi.org/10.3390/su16177595






