Simulation of a Hazardous Chemical Cascading Accident Using the Graph Neural Network
Abstract
:1. Introduction
1.1. Challenges in Quantitatively Characterizing the Spatial Relationships among Hazardous Chemicals
1.2. Challenges in Information Fusion Mechanisms for Various Relationships
- (1)
- Introducing the definition of cascading accidents and studying the evolution of accidents after the intervention of emergency rescue measures, filling the gap in traditional accident chains (domino effect), which focus on the period from accident occurrence to the beginning of emergency intervention. This provides a new approach to explore complete accident chain simulation.
- (2)
- Proposing a quantitative representation algorithm for the spatial correlation of dangerous chemicals based on the pyramid spatial positioning mechanism, which enriches the understanding of dangerous chemicals’ spatial correlation, better reflecting the mutual influence between dangerous chemicals.
- (3)
- A simulation mechanism based on a graph neural network for hazardous chemical cascade accidents is proposed. By leveraging deep learning models in graph space, it comprehensively considers the cumulative impacts of cascading accidents resulting from standard emergency measures, thereby improving the real-time and scientific aspects of the simulation process. The integration of artificial intelligence technologies like graph neural networks can advance emergency responses to hazardous chemical incidents to a more intelligent and scientific level.
2. Related Works
2.1. Accident Chain
2.2. Simulation of Hazardous Chemical Accidents
2.3. Graph Neural Networks
3. The Spatial Location of Pyramid Approach
3.1. A Dynamic Renewal of the Spread Distance
3.2. Construction of a Model of Hazardous Chemical Accident Scenes Based on Pyramid Coding
| Algorithm 1 Spatial Pyramid Localization |
| Input: ln (n ∊ [1,N]), the shape and area of nodes (hazardous chemical); L, location of the accident scene. Output: pyramid coordinates of nodes. |
| 1 Begin: 2 , , , = Spatial Division(L) //Divide the two-dimensional space into //four quadrants; i represents the level of a multi-level pyramid. The starting value is 1. 3 while ln in { , , , } do // 4 = || //Spatial encoding at i levels by the ratio of hazardous chemical coverage 5 // area within the ; ∊ {, , , }; the ‘||’ operator signifies a vector join. 6 end while 7 if ≤ 0.5 then // Recursive processing: 8 L = 9 i = i + 1 //If the ratio is less than 0.5 increas i by 1, 10 goto setp2; // and return to step 2; otherwise, proceed to next step. 11 = Z-order() // Ultimately, Z-order algorithm is used to reduce the dimension of the 12 //two-dimensional raster space to one-dimensional coding. 13 = paddint(,0) //aligned by padding with zeros in the grid 14 output() 15 End |
3.3. The Advantage of Pyramid Coding
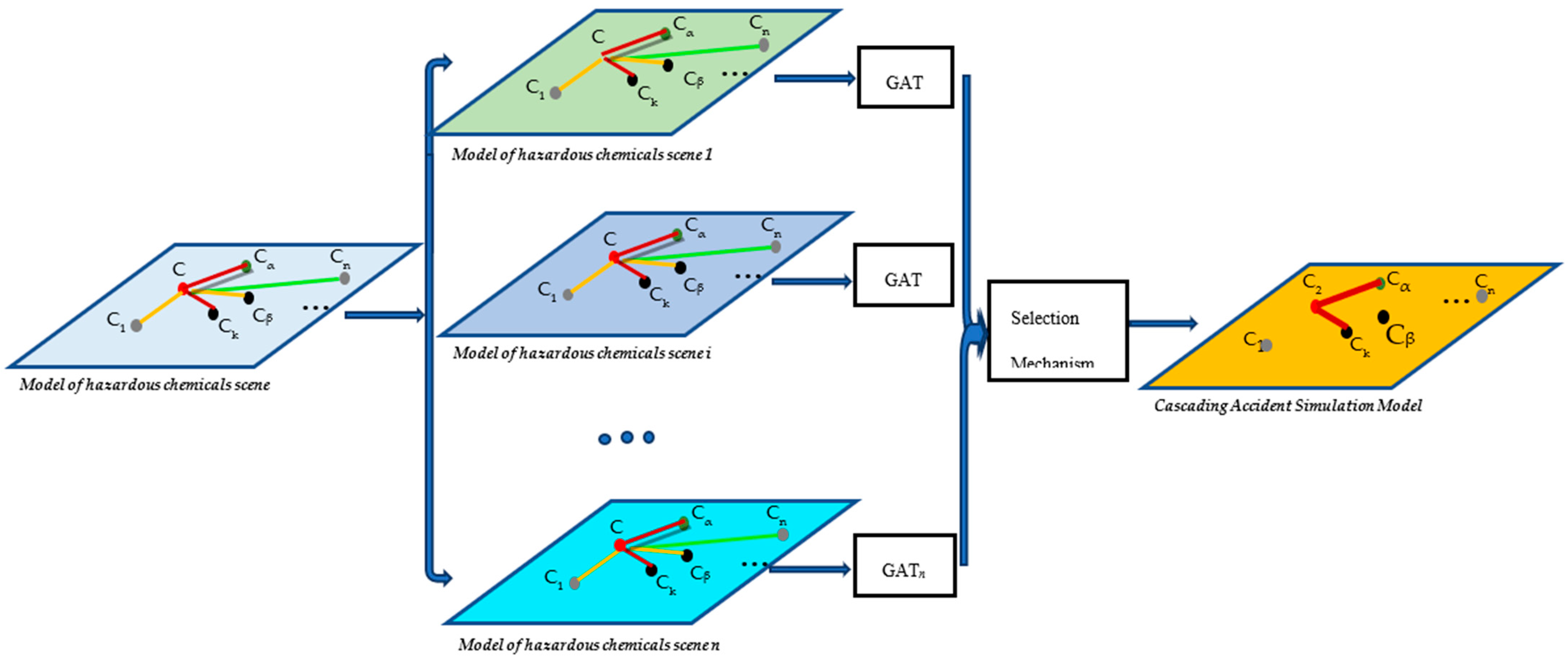
4. Cascading Accident Simulation of Hazardous Chemicals Based on Graph Attention Networks
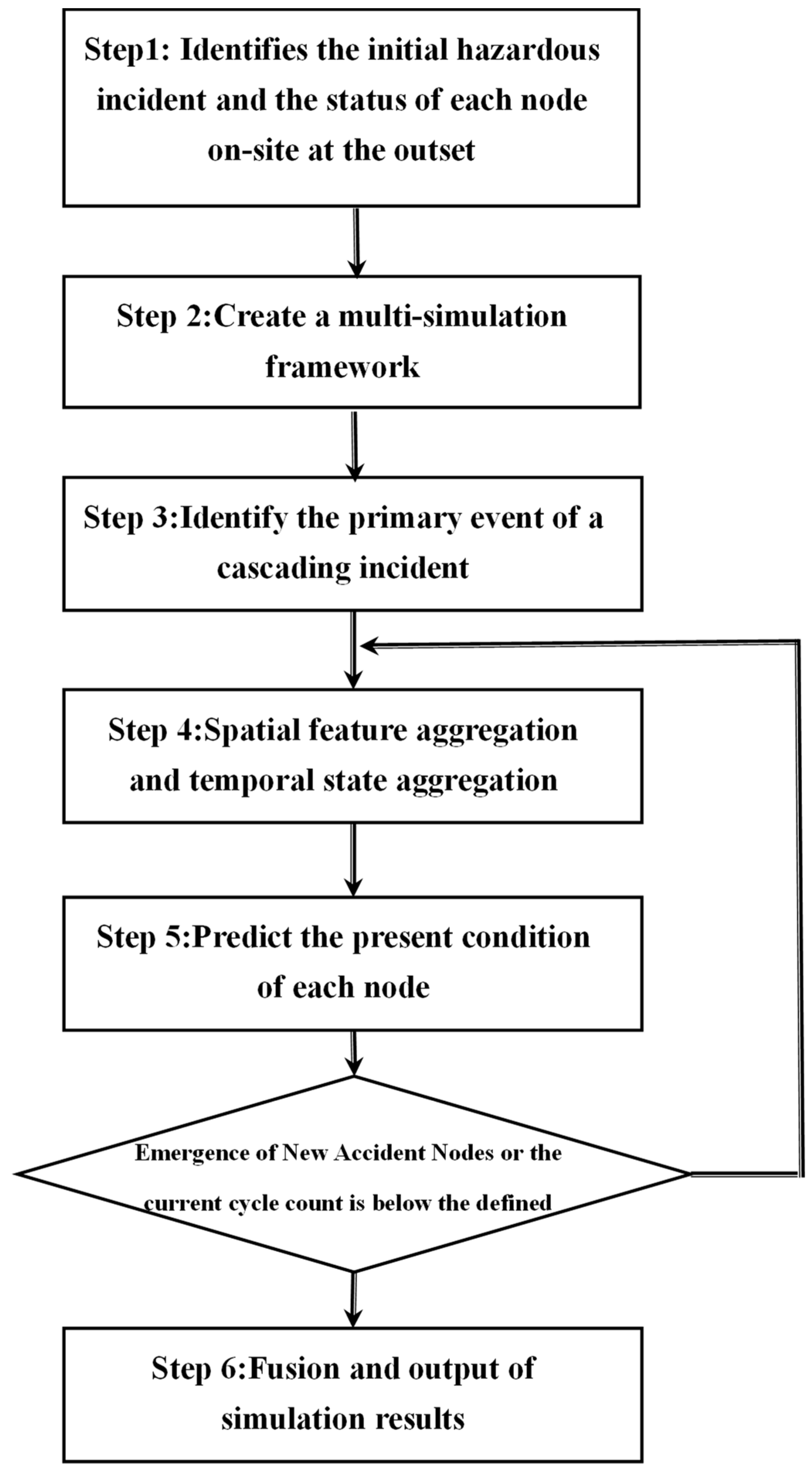
4.1. Parallel and Dynamic Simulation Strategy Design
- Step 1: Initialization: Identify the initial hazardous incident and the status of each node on-site at the outset.
- Step 2: Create a multi-simulation framework.
- Step 3: Identify the primary event of a cascading incident.
- Step 4: Spatial feature aggregation and temporal state aggregation.
- Step 5: Predict the present condition of each node.
- Step 6: Fusion and output of simulation results.
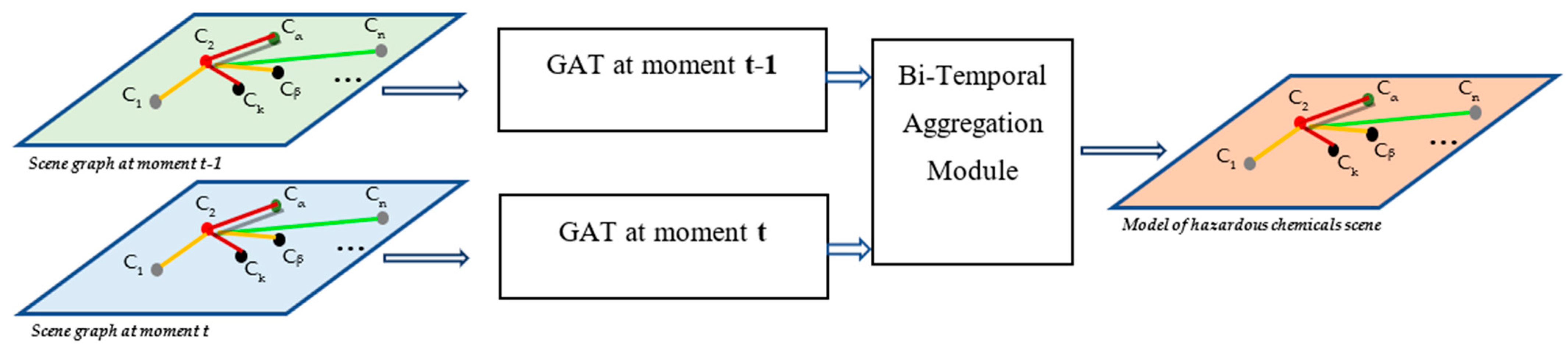
4.2. The Design of Graph Aggregation Function
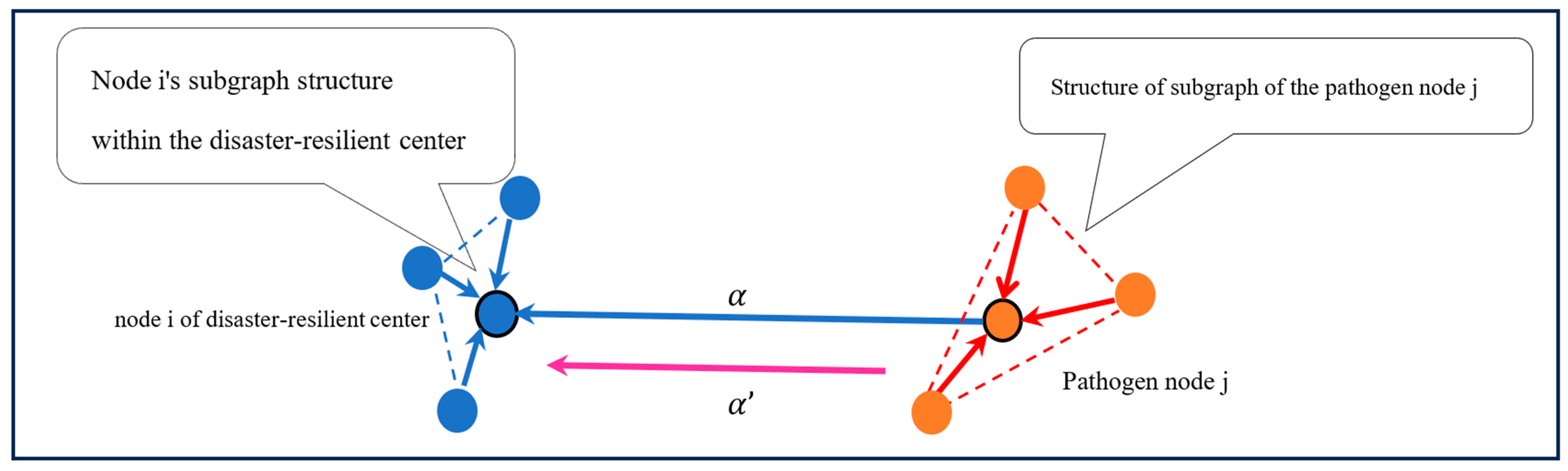
4.2.1. Spatial Information Aggregation
4.2.2. Bi-Temporal Information Aggregation
5. Experiment and Result Analysis
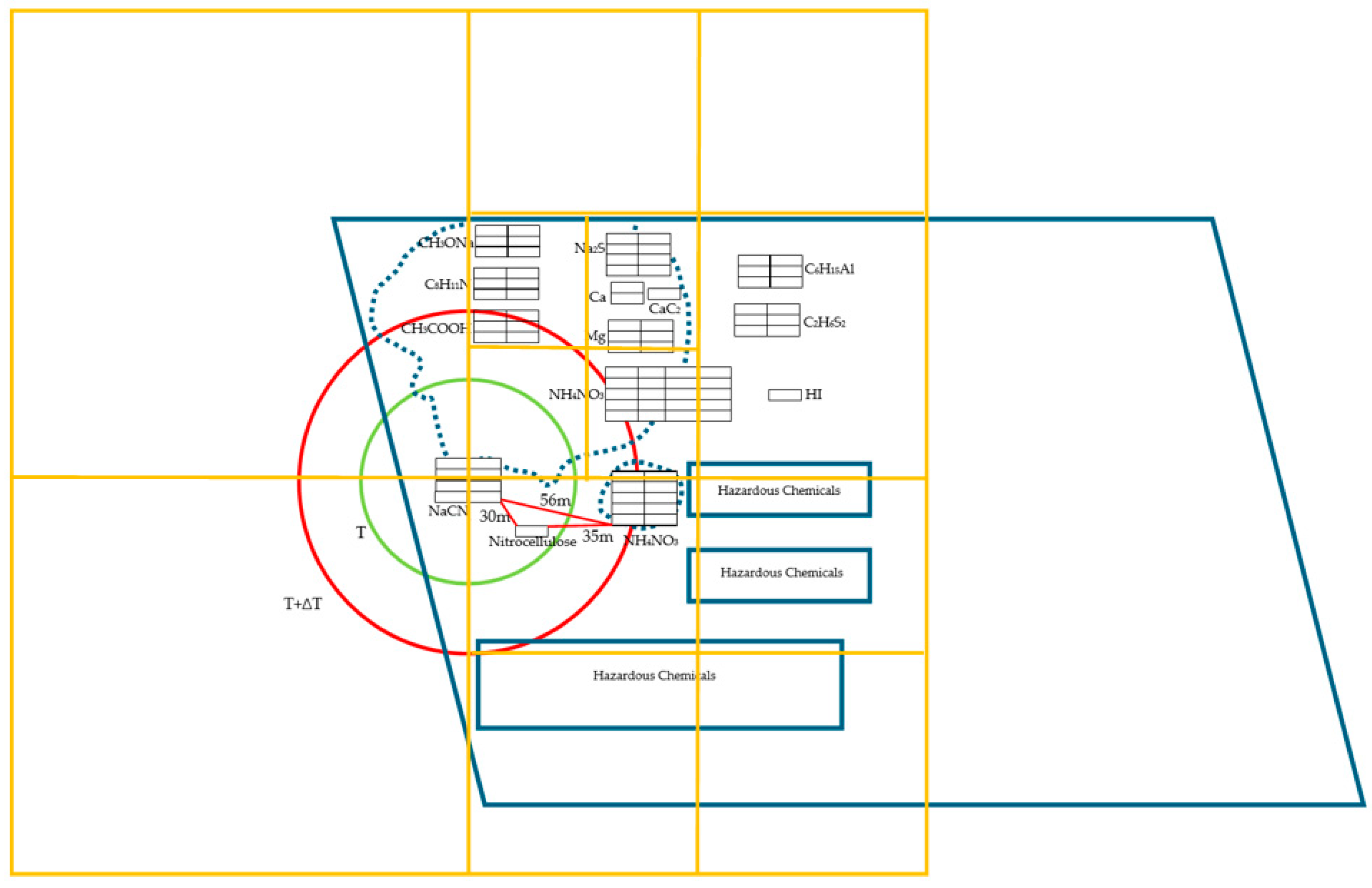
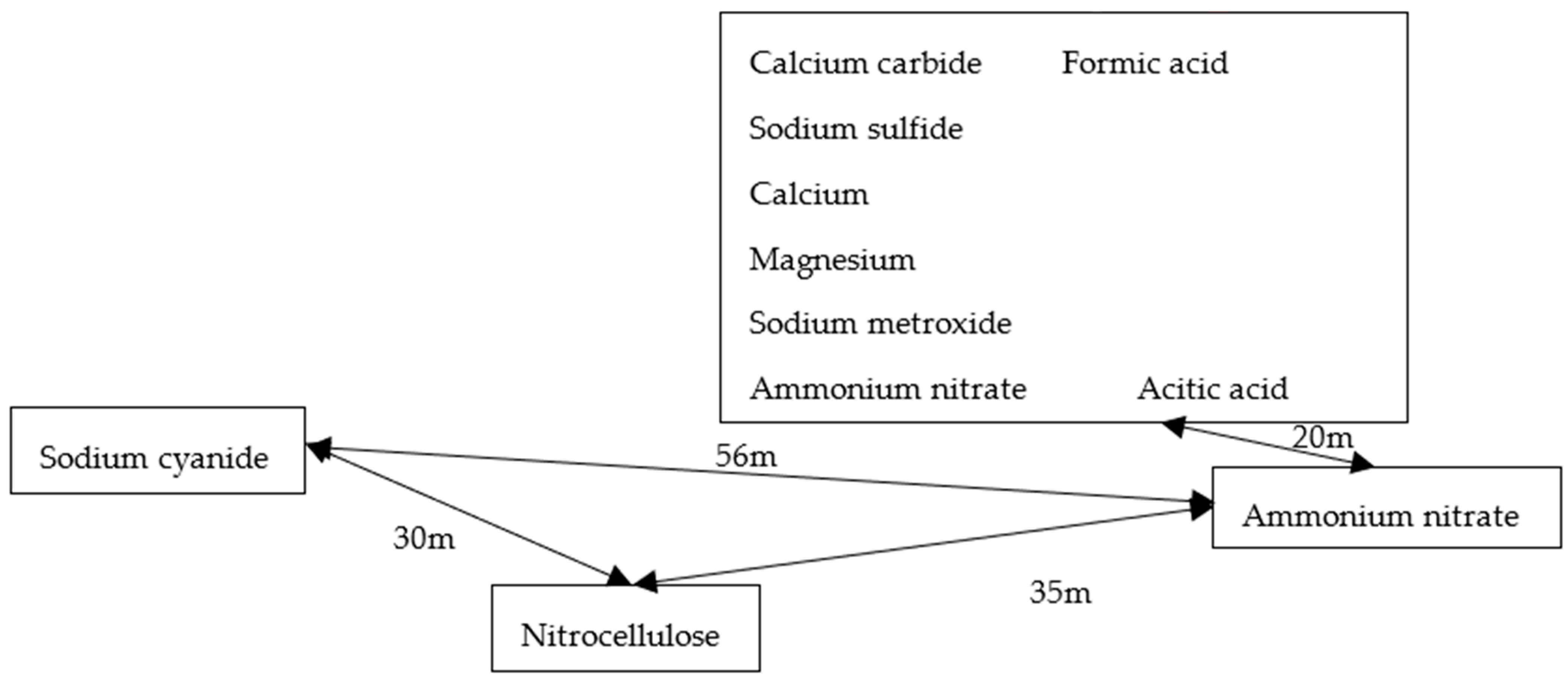
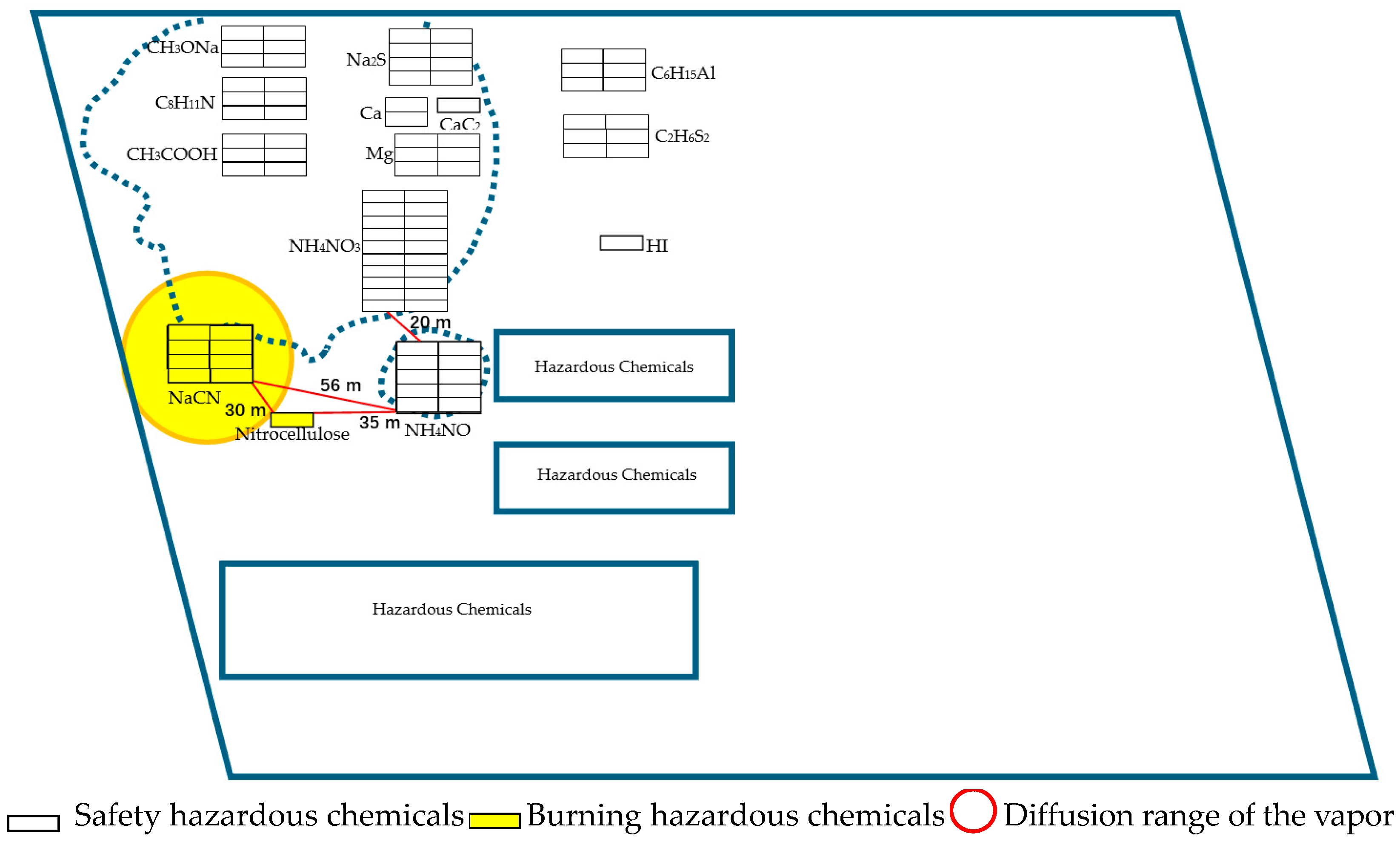
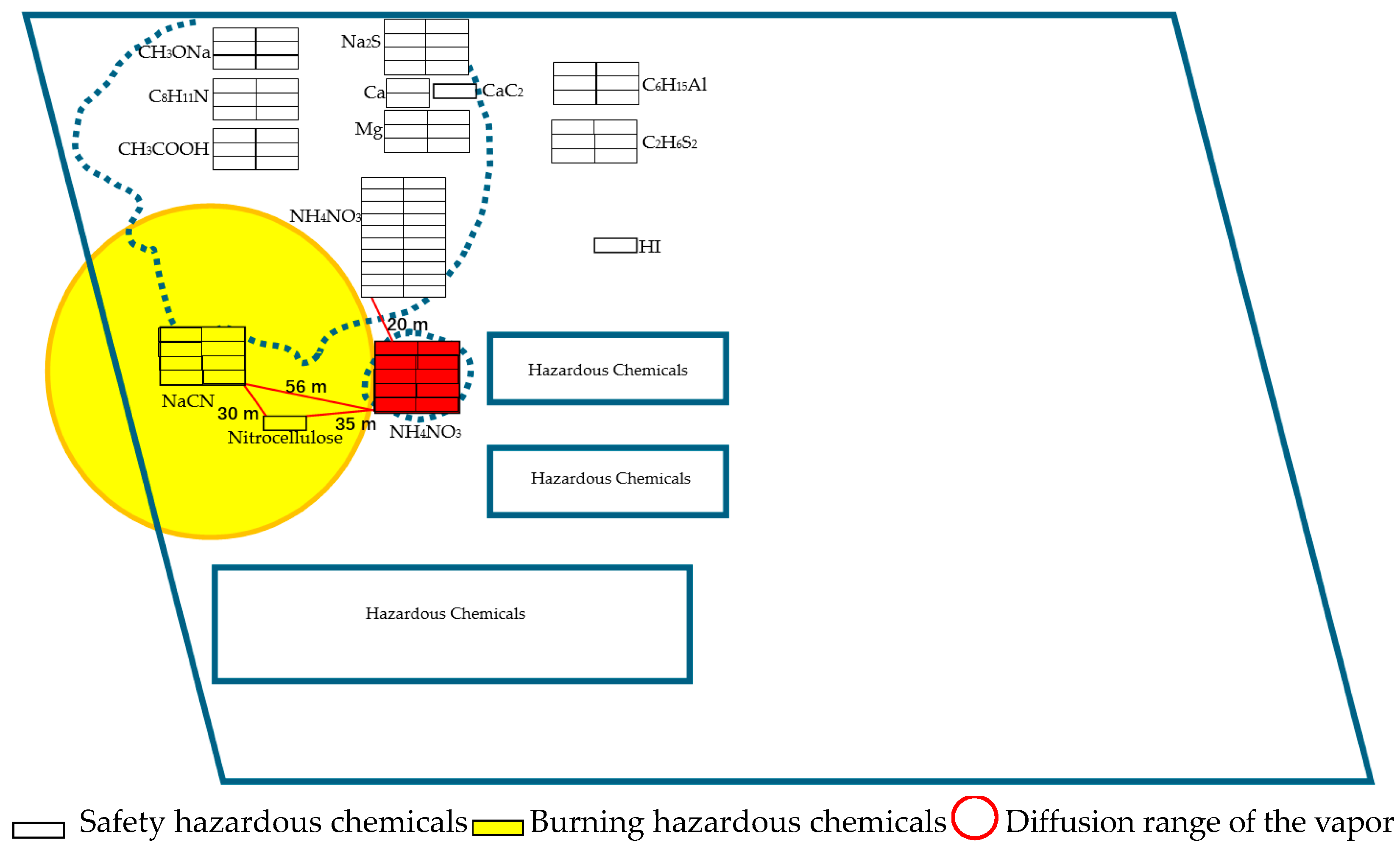
5.1. Accident Background and Scene Diagram
5.2. Node Properties and Model Parameters
5.2.1. Experimental Data—Node Properties
5.2.2. The Graph Neural Network and the Hyperparameters
5.3. Experimental Analysis
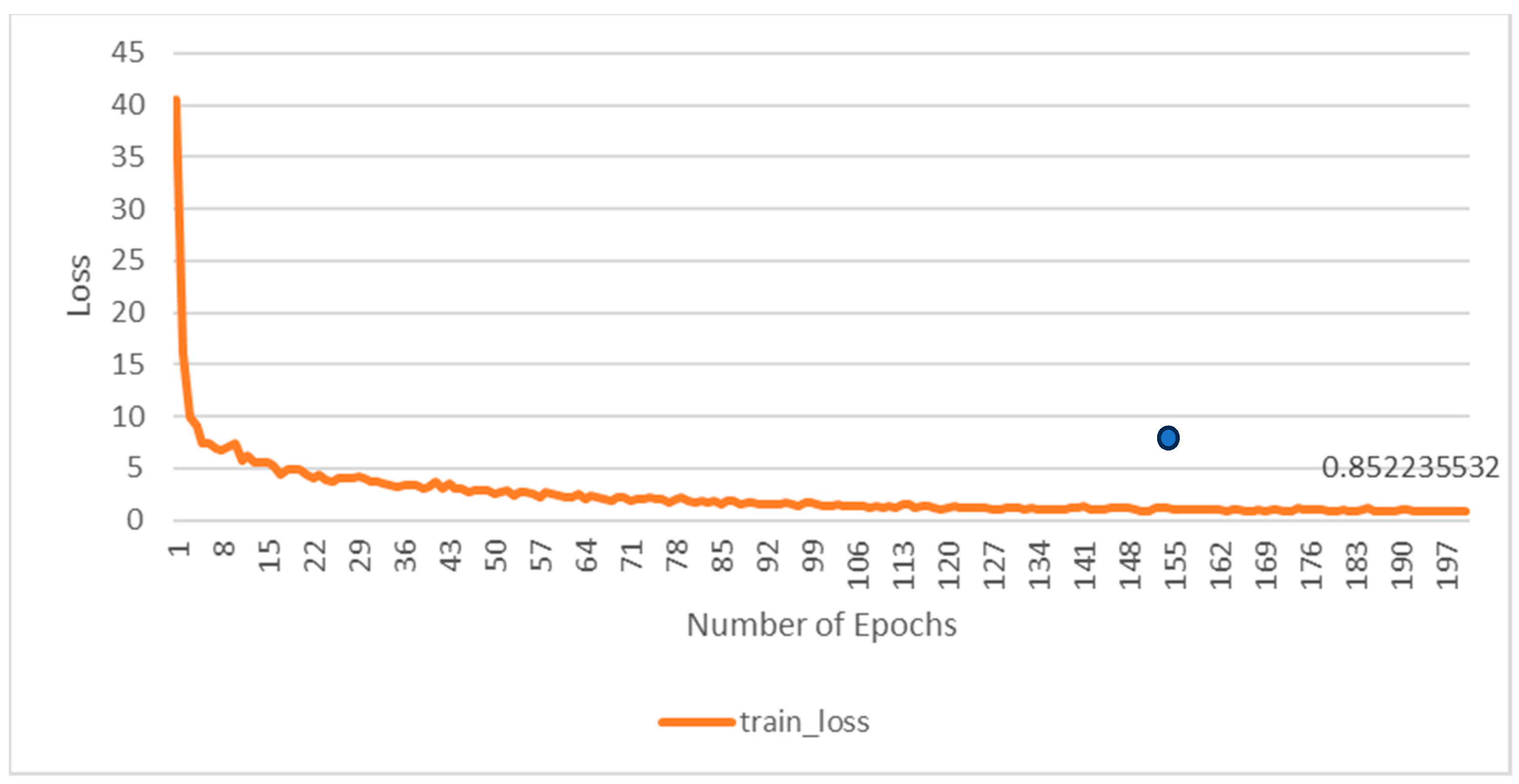
5.3.1. Model Training Procedure
5.3.2. Cascade Accident Simulation
- (1)
- Before 22:52, the initial accident (nitrocellulose combustion) occurred.
- (2)
- At 22:56, the initial state at time zero was (1, 0, 0, 0, 0, 0, 0, 0, 0, 0).
- (3)
- The vapor cloud starts to diffuse into a combustion state.
- (4)
- The primary event that initiated cascading accident 1—first explosion at 23:34:06.
- (5)
- The first explosion triggered cascade accident 2—second explosion at 23:34:37, which occurred 31 s later.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- GB15603-2022; General Rules for the Storage of Hazardous Chemicals. SAMR: Beijing, China, 2023.
- He, Z.; Weng, W. A Dynamic and Simulation-Based Method for Quantitative Risk Assessment of the Domino Accident in Chemical Industry. Process Saf. Environ. Prot. 2020, 144, 79–92. [Google Scholar] [CrossRef]
- Lan, M.; Gardoni, P.; Weng, W.; Shen, K.; He, Z.; Pan, R. Modeling the Evolution of Industrial Accidents Triggered by Natural Disasters Using Dynamic Graphs: A Case Study of Typhoon-Induced Domino Accidents in Storage Tank Areas. Reliab. Eng. Syst. Saf. 2024, 241, 109656. [Google Scholar] [CrossRef]
- Huang, W.; Chen, X.; Qin, Y. A Simulation Method for the Dynamic Evolution of Domino Accidents in Chemical Industrial Parks. Process Saf. Environ. Prot. 2022, 168, 96–113. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Wang, B. Complex chain evolution mechanism and its modeling of major accident based on entropy theory. J. Saf. Sci. Technol. 2016, 12, 10–15. [Google Scholar]
- Wu, C.; Wang, B. Research on Establishment of the Science of Safety Relations. Sci. Technol. Res. 2017, 20, 254–261. [Google Scholar]
- Jia, M.; Chen, G.; Hu, K. Review of risk assessment and pre-control of Domino effect in Chemical Industry Park. Park. Chem. Indus. Eng. Progress 2017, 36, 1534–1543. [Google Scholar]
- Yuan, N. Research on Scenario Construction of Liquid Ammonia Leakage Accident Based on Bayesian Network and Business Community Management; Beijing Jiaotong University: Beijing, China, 2016. [Google Scholar]
- Li, S.; Liang, D.; Wei, Y.; Zhang, X. Quantitative modeling of drought-forest fire disaster chain based on the Bayesian network. J. Nat. Dis. 2023, 1, 38–46. [Google Scholar]
- Kang, J.; Liu, Y. Study on safety assessment of bridge construction based on Bayesian network. China Saf. Sci. J. 2016, 7, 157–162. [Google Scholar]
- Wang, X.; Gui, L. Research on Emergency Disaster Events Evolution Network Based on Hypergraph. Math. Pract. Theo. 2019, 12, 63–71. [Google Scholar]
- Wang, B. Secondary risk and its governance: Study on the structural appearance and evolutionary mechanism of hazardous chemicals. J. ZULI 2023, 24, 60–67. [Google Scholar]
- Wang, S.; Wu, F.; Zhou, P. Measuring Urban Environmental Performance in China: A Euclidean Distance Function Approach. J. Environ. Manag. 2024, 361, 121272. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wu, J.; Shao, S.; Shi, S.; Zhou, R.; Wang, W. Prediction Model for Road Transportation Accidents of Hazardous Chemicals Based on Bayesian Network. China Saf. Sci. J. 2022, 32, 174–181. [Google Scholar]
- Li, X.; Chen, C.; Hong, Y.; Yang, F. Exploring Hazardous Chemical Explosion Accidents with Association Rules and Bayesian Networks. Reliab. Eng. Syst. Saf. 2023, 233, 109099. [Google Scholar] [CrossRef]
- Hanifi, S.; Laal, F.; Ghasghaei, M.; Ahmadi, O.; Mandali, H. Providing a Model to Evaluate the Spread of Fire in a Chemical Warehouse Using Numerical Simulation and Bayesian Network. Process Saf. Environ. Prot. 2024, 183, 124–137. [Google Scholar] [CrossRef]
- Khan, R.; Yin, J.; Mustafa, F.; Wang, S. Analyzing Human Factor Involvement in Sustainable Hazardous Cargo Port Operations. Ocean Eng. 2022, 250, 111028. [Google Scholar] [CrossRef]
- Shan, X.; Wang, F.; Li, X.; Bian, J. Risk Analysis of Hazardous Chemical Road Transportation Accidents Based on Analytic Hierarchy Process. J. Sec. Saf. Technol. 2023, 11, 30–39. [Google Scholar]
- Ayvaz, B.; Tatar, V.; Sagir, Z.; Pamucar, D. An Integrated Fine-Kinney Risk Assessment Model Utilizing Fermatean Fuzzy AHP-WASPAS for Occupational Hazards in the Aquaculture Sector. Process Saf. Environ. Prot. 2024, 186, 232–251. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, Z.; Dang, W.; Yu, A. Acidic gas pipe leakage risk analysis based on CFD. Fire Sci. Technol. 2016, 35, 1481–1485. [Google Scholar]
- Lyu, S.; Zhang, S.; Huang, X.; Peng, S.; Yang, D.; Sun, M.; Qi, Q. CFD Simulations of Instantaneously Released Liquefied Gas in Urban Area: A Case Study of LPG Tank Truck Accident in Wenling, China. Sustain. Cities Soc. 2023, 94, 104550. [Google Scholar] [CrossRef]
- Efthimiou, G.; Andronopoulos, S.; Tavares, R.; Bartzis, J. CFD-RANS Prediction of the Dispersion of a Hazardous Airborne Material Released During a Real Accident in an Industrial Environment. J. Loss Prev. Process Ind. 2017, 46, 23–36. [Google Scholar] [CrossRef]
- Yet-Polo, I.; Chen, T. Application of CFD Model in an LPG Tank Explosion Accident. J. Loss Prev. Process Ind. 2021, 69, 104367. [Google Scholar]
- Kim, H.; Park, M.; Kim, C.; Shin, D. Source Localization for Hazardous Material Release in an Outdoor Chemical Plant via a Combination of LSTM-RNN and CFD Simulation. Comput. Chem. Eng. 2019, 125, 476–489. [Google Scholar] [CrossRef]
- Kang, Y.; Wu, Z.; Ma, S.; Zhao, M.; Li, W. CFD-Based Assessment and Visualization of the Failure Consequences of LPG Tankers. J. Loss Prev. Process Ind. 2023, 82, 105008. [Google Scholar] [CrossRef]
- Huang, W.; Chen, J.; Qin, Q.; Wang, Z.; Song, L. Causation Analysis and Governance Strategy for Hazardous Cargo Accidents at Ports: Case Study of Tianjin Port’s Hazardous Cargo Explosion Accident. Mar. Pollut. Bull. 2021, 173, 113053. [Google Scholar]
- Zhao, S.; Hu, C.; Ma, L. Construction of Scenario Deduction Network for Hazardous Chemical Accidents and Analysis of Key Nodes. J. Saf. Sci. Technol. 2022, 18, 36–42. [Google Scholar]
- Quan, X.; Wang, K.; Wang, B.; Wang, X.; Zhang, X. Research and Design of Gas Diffusion Emergency Analysis Based on 3D GIS. Geomat. Spa. Info. Technol. 2023, 7, 82–84. [Google Scholar]
- Wang, H.; Li, R.; Tu, Y.; Cui, Y. Analysis of the Causes of Road Transportation Accidents for Hazardous Chemicals Based on Grounded Theory and Grey Relation. J. Hunan Univ. Sci. Technol. 2022, 37, 17–23. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Cui, W.; He, X.; Yao, M.; Wang, Z.; Li, J.; Hao, Y.; Wu, W.; Zhao, H.; Chen, X.; Cui, W. Landslide Image Captioning Method Based on Semantic Gate and Bi-Temporal LSTM. ISPRS Int. J. Geo-Inf. 2020, 9, 194. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. 2015, 39, 640–651. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Kriege, M.; Johansson, D.; Morris, C. A survey on graph Neural Networks. Appl. Net. Sci. 2020, 5, 1–42. [Google Scholar]
- Chen, C.; Reniers, G.; Khakzad, N. A Dynamic Multi-Agent Approach for Modeling the Evolution of Multi-Hazard Accident Scenarios in Chemical Plants. Reliab. Eng. Syst. Saf. 2021, 207, 107349. [Google Scholar] [CrossRef]
- Ares de Parga-Regalado, A.M. Analytical Approximation of Optimal Thermoeconomic Efficiencies for a Novikov Engine with a Stefan-Boltzmann Heart Transfer Law. Results Phys. 2023, 54, 107059. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, N. Research on the Emergency Disposal of the Hazardous Chemical Accidents Based on the Dynamic Bayesian Network Scenario Deduction. J. Saf. Environ. 2020, 20, 1420–1426. [Google Scholar]
- Wang, Q.; Wang, H. A Scenario Construction Based Study on Emergency Evacuation in Hazardous Chemicals Accidents. China Saf. Sci. J. 2017, 27, 147–152. [Google Scholar]
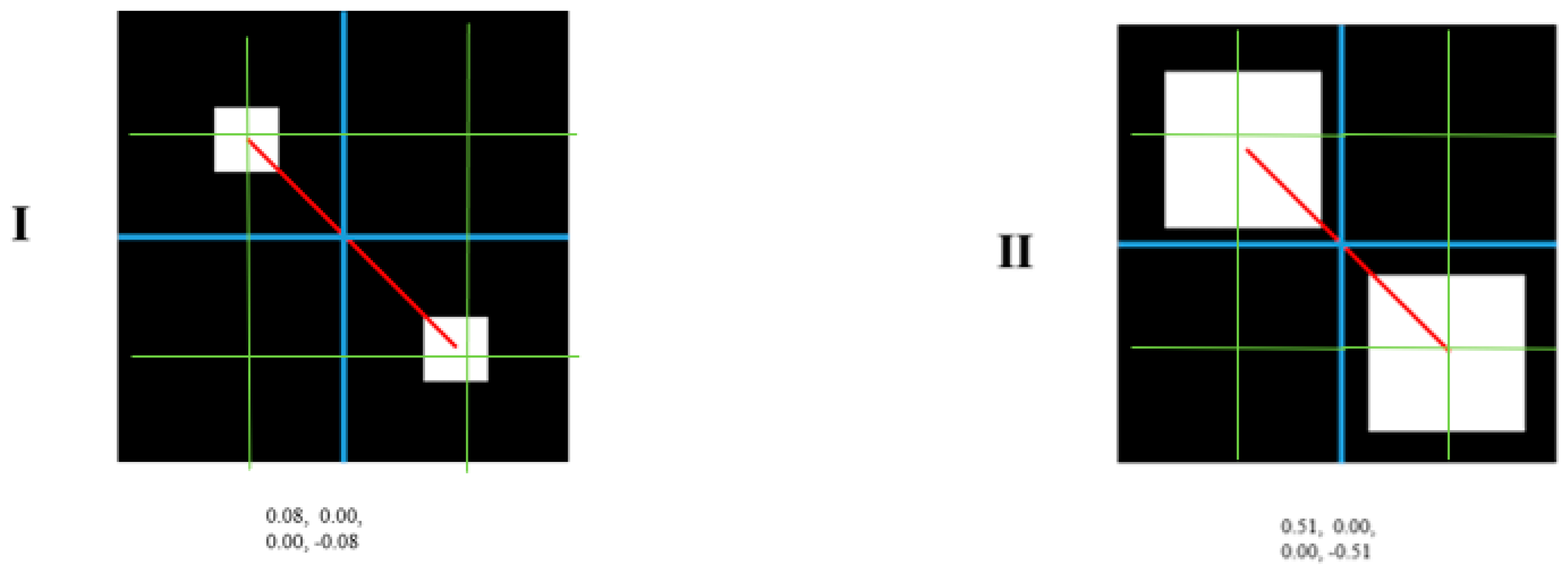


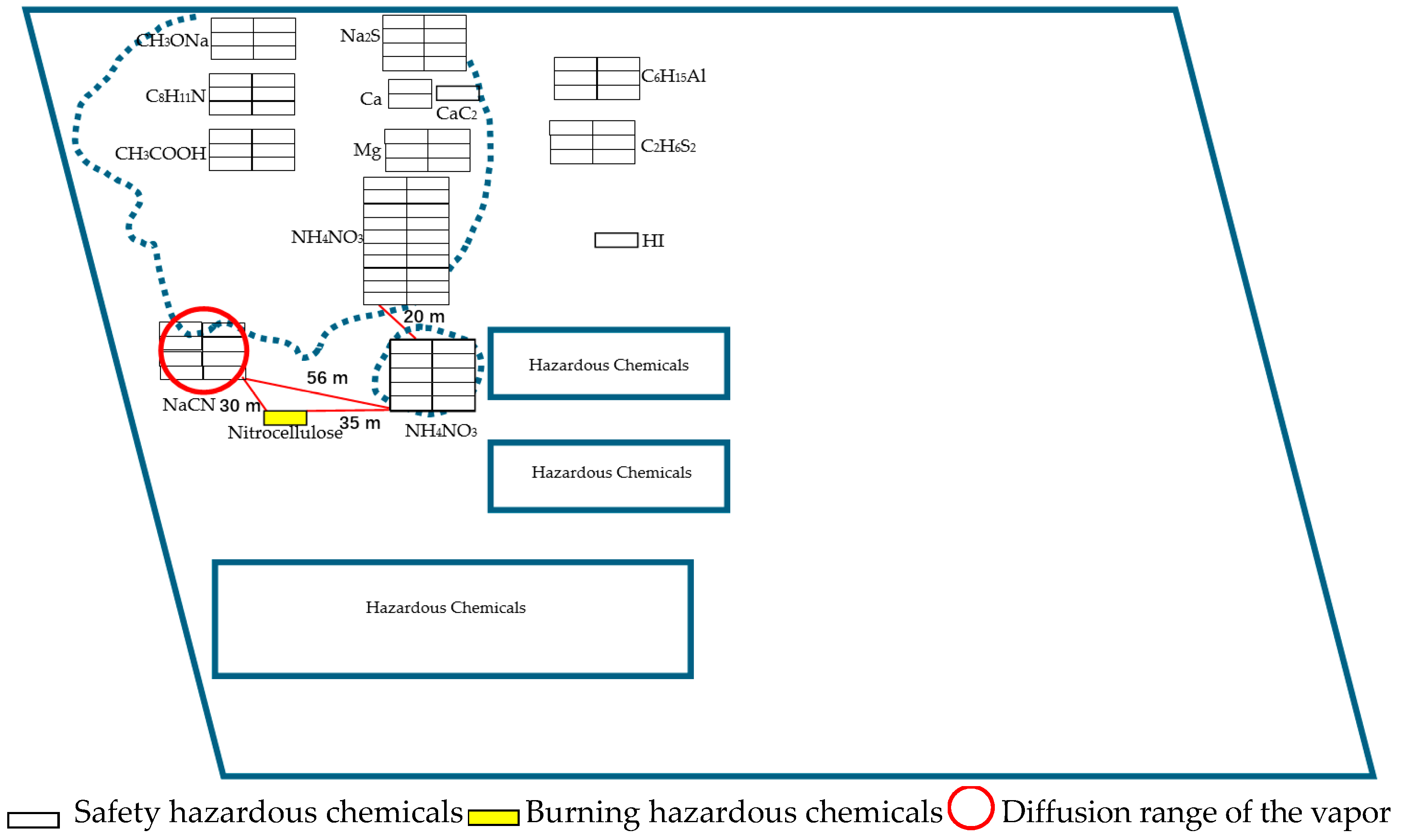

| Centroid Euclidean Distance | Spatial Relationship | |
|---|---|---|
| I | 36.8 | Aparting |
| II | 36.8 | Aparting |
| Vector of Pyramid Spatial Distance | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 0.08 | 0.00 | 0.00 | 0.08 | 0.02 | 0.06 | 0.06 | 0.73 | 0.00 | 0.08 | 0.08 | 0.08 | 0.08 |
| II | 0.51 | 0.00 | 0.00 | 0.51 | 0.33 | 0.49 | 0.49 | 0.18 | 0.00 | 0.51 | 0.51 | 0.51 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Chen, X.; Li, W.; Li, K.; Liu, K.; Feng, Z.; Chen, J.; Tian, Y.; Chen, B.; Chen, X.; et al. Simulation of a Hazardous Chemical Cascading Accident Using the Graph Neural Network. Sustainability 2024, 16, 7880. https://doi.org/10.3390/su16187880
Cui W, Chen X, Li W, Li K, Liu K, Feng Z, Chen J, Tian Y, Chen B, Chen X, et al. Simulation of a Hazardous Chemical Cascading Accident Using the Graph Neural Network. Sustainability. 2024; 16(18):7880. https://doi.org/10.3390/su16187880
Chicago/Turabian StyleCui, Wenqi, Xinwu Chen, Weisong Li, Kunjing Li, Kaiwen Liu, Zhanyun Feng, Jiale Chen, Yueling Tian, Boyu Chen, Xianfeng Chen, and et al. 2024. "Simulation of a Hazardous Chemical Cascading Accident Using the Graph Neural Network" Sustainability 16, no. 18: 7880. https://doi.org/10.3390/su16187880
APA StyleCui, W., Chen, X., Li, W., Li, K., Liu, K., Feng, Z., Chen, J., Tian, Y., Chen, B., Chen, X., & Cui, W. (2024). Simulation of a Hazardous Chemical Cascading Accident Using the Graph Neural Network. Sustainability, 16(18), 7880. https://doi.org/10.3390/su16187880






