Nonlinear Analysis of the Mechanical Response of an Existing Tunnel Induced by Shield Tunneling during the Entire Under-Crossing Process
Abstract
:1. Introduction
2. Mathematical Model
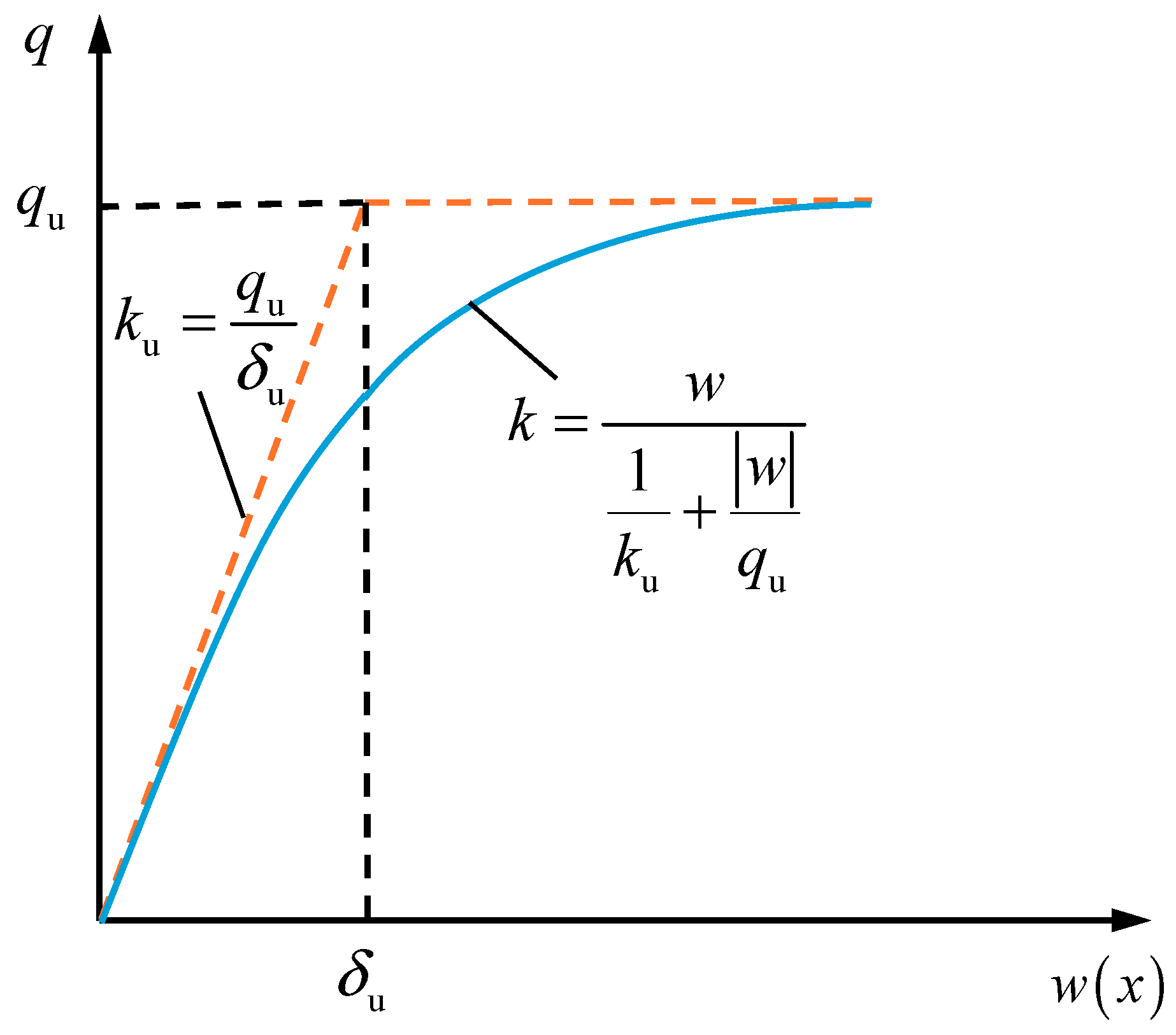
2.1. Nonlinear Pasternak Foundation Model
2.2. Additional Stresses Induced by a New Under-Crossing Shield Tunnel
- (i)
- Stage I, the initiation of the new shield tunnel construction occurs, resulting in the excavation face being positioned at a considerable distance from the existing tunnel. The distance from the excavation face to the intersection point with the existing tunnel is represented as a negative value, i.e., b < 0;
- (ii)
- Stage II, as the new shield tunnel is continued to excavate, its excavation face gradually approaches the intersection point with the existing tunnel, i.e., b = 0;
- (iii)
- Stage III, the new tunnel under-crosses the existing tunnel, and its excavation face gradually advances away from the intersection point with the existing tunnel, i.e., b > 0.
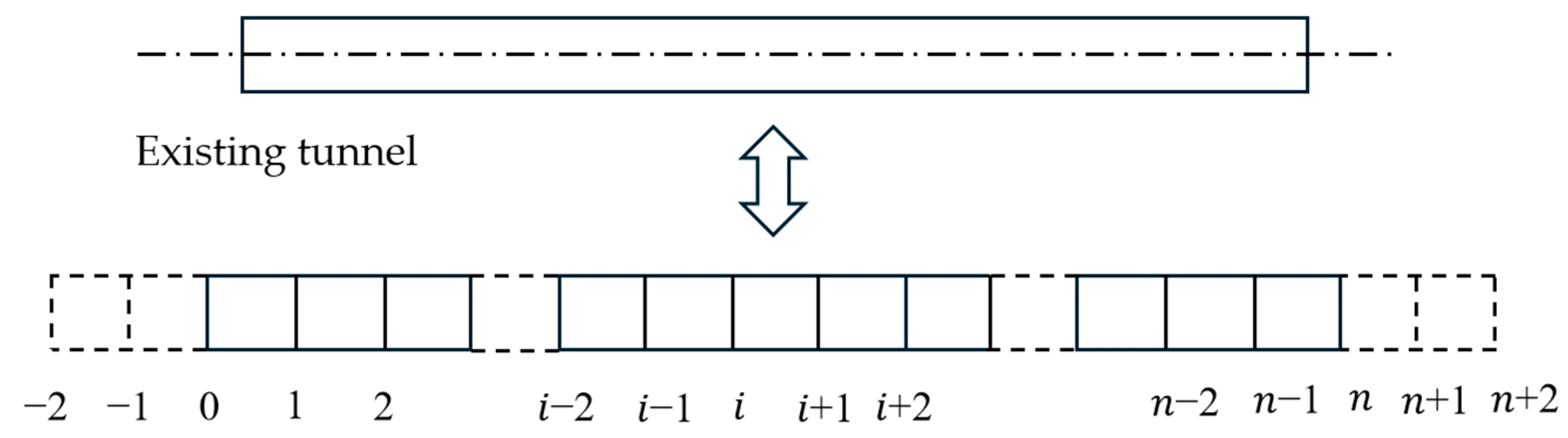
2.3. Governing Differential Equation of Existing Tunnel
3. Theoretical Solution and Calculation Method
4. Case Study and Validation
5. Parameter Studies
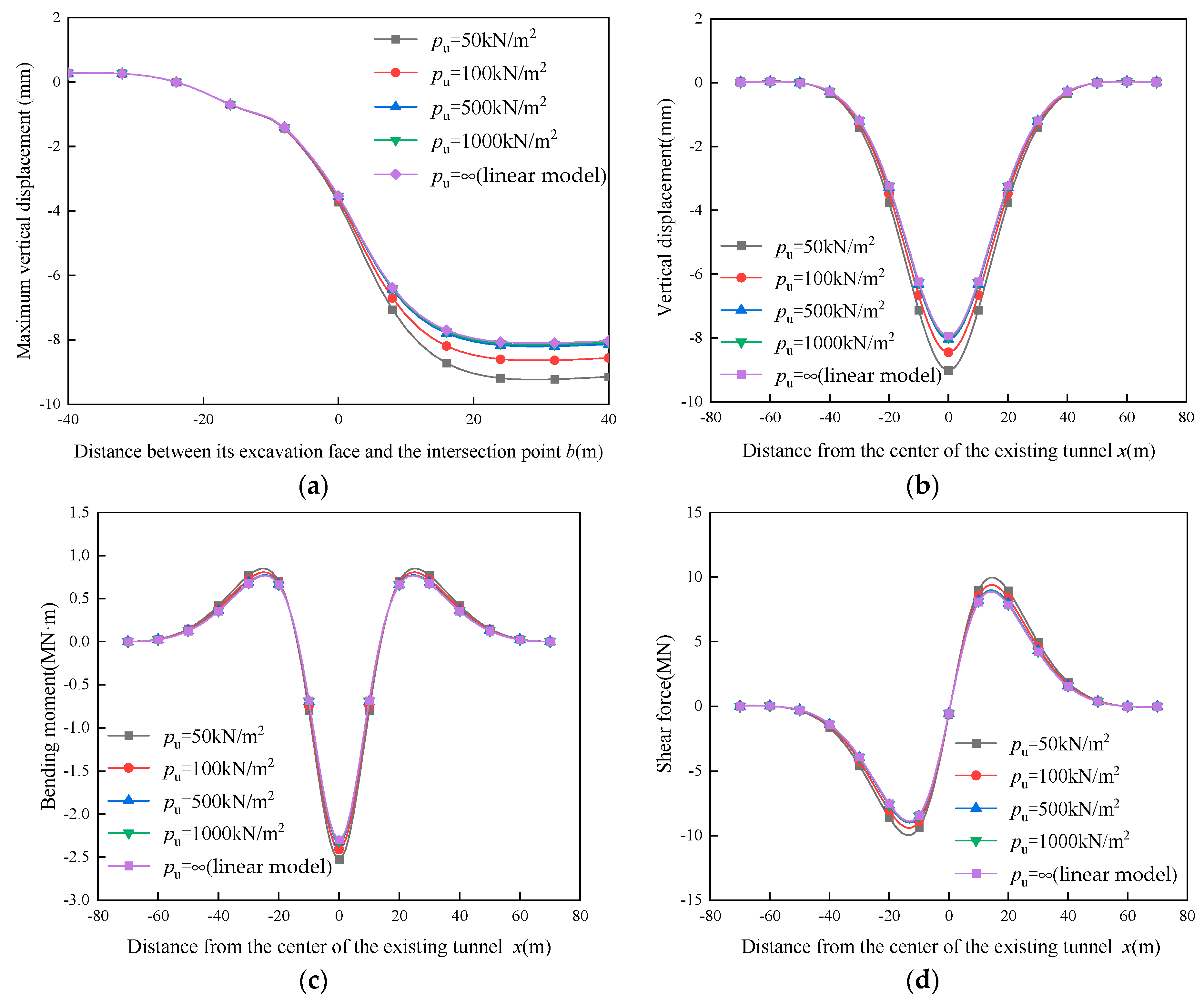
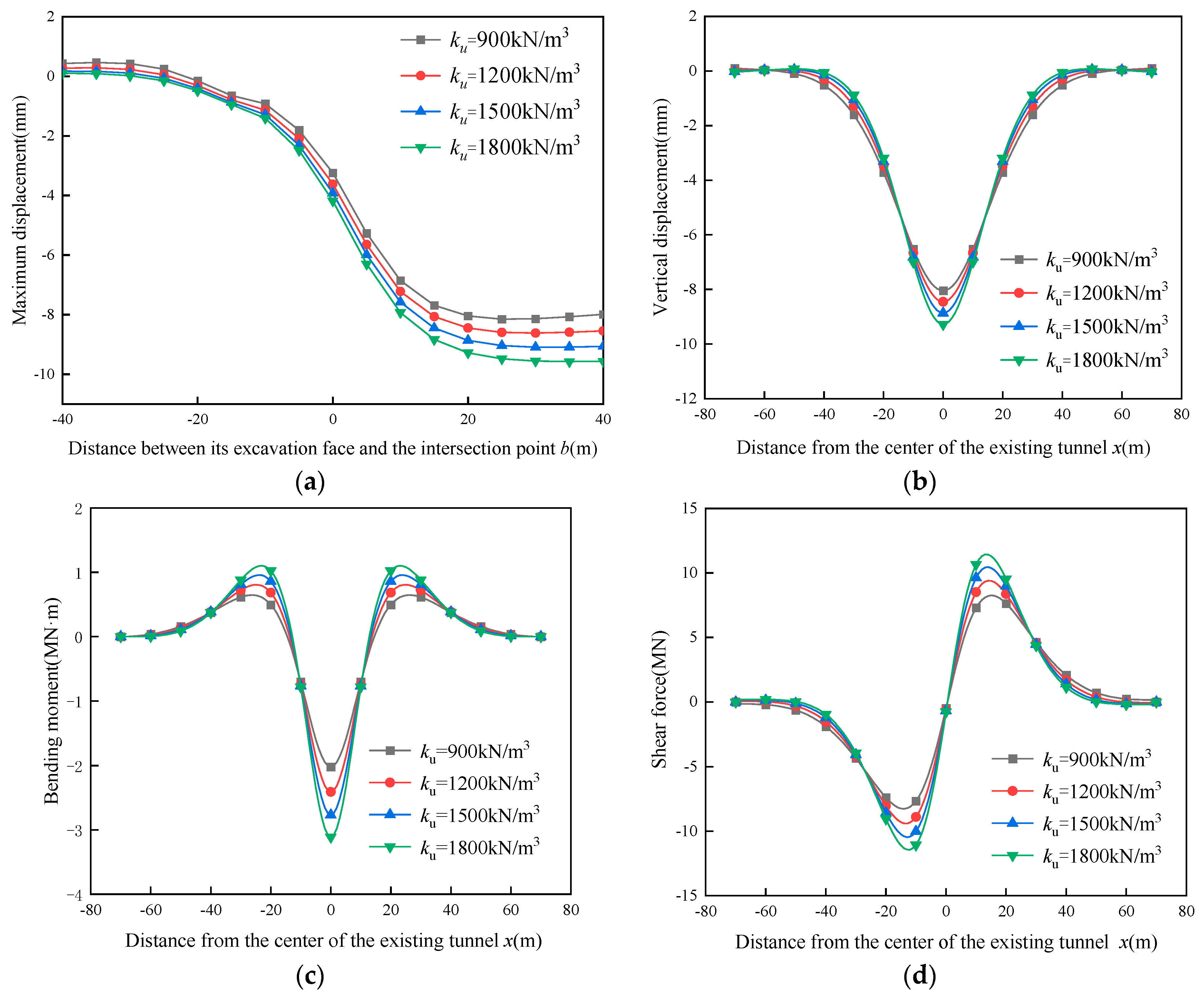
5.1. Influence of the Ultimate Resistance of Surrounding Soils
5.2. Influence of the Reaction Coefficient of Surrounding Soils
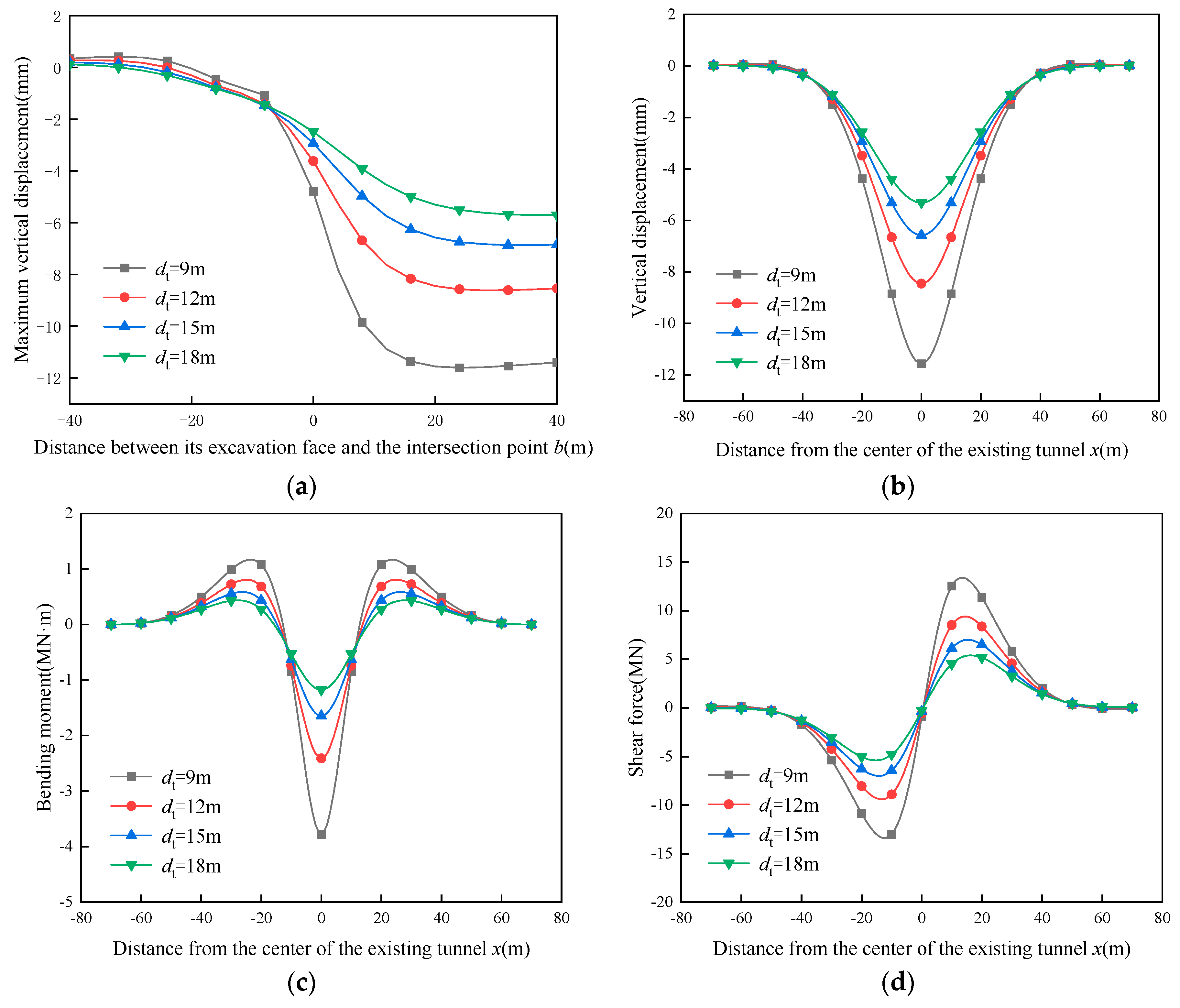
5.3. Influence of the Vertical Distance between Existing and Under-Crossing Tunnels
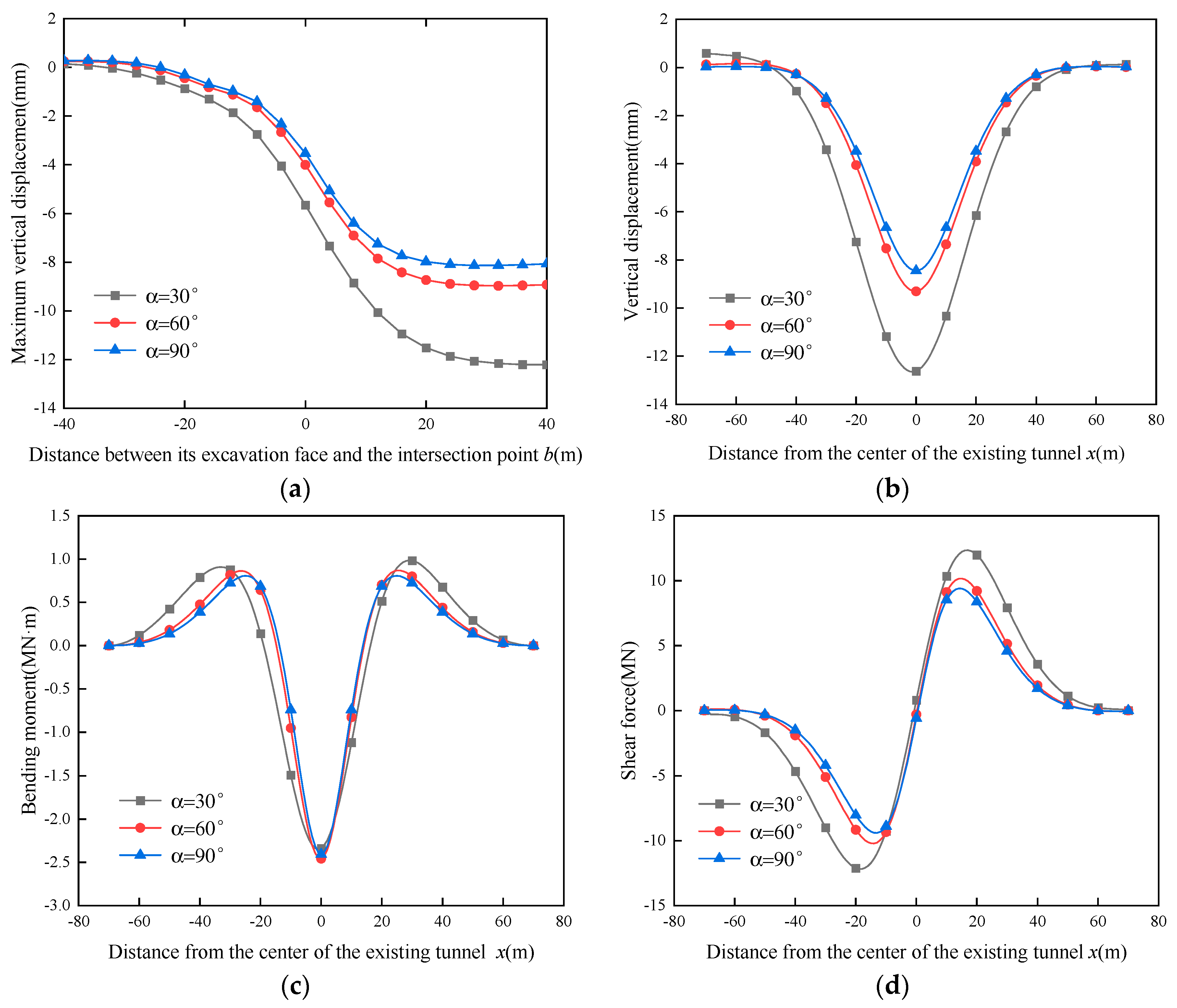
5.4. Influence of the Intersection Angle between Existing and Under-Crossing Tunnels
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Fang, Q.; Zhang, D.; Wang, Z. Behaviour of existing tunnel due to new tunnel construction below. Comput. Geotech. 2019, 110, 71–81. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, D.; Fang, Q.; Cao, L.; Xu, T.; Li, Q. Surface settlement of subway station construction using pile-beam-arch approach. Tunn. Undergr. Space Technol. 2019, 90, 340–356. [Google Scholar] [CrossRef]
- Li, P.; Wei, Y.; Zhang, M.; Huang, Q.; Wang, F. Influence of non-associated flow rule on passive face instability for shallow shield tunnels. Tunn. Undergr. Space Technol. 2022, 119, 104–202. [Google Scholar] [CrossRef]
- Hu, M.; Sun, J.; Wu, B.; Wu, H.; Xu, Z. Shield Tunnel (Segment) Uplift Prediction and Control Based on Interpretable Machine Learning. Sustainability 2024, 16, 910. [Google Scholar] [CrossRef]
- Attewell, P.B.; Yeates, J.; Selby, A.R. Soil Movements Induced by Tunnelling and Their Effects on Pipelines and Structures; Blackie and Son: London, UK, 1986. [Google Scholar]
- Klar, A.; Vorster, T.E.B.; Soga, K.; Mair, R.J. Soil-pipe interaction due to tunnelling: Comparison between Winkler and elastic continuum solutions. Geotechnique 2005, 55, 461–466. [Google Scholar] [CrossRef]
- Klar, A. Elastic continuum solution for tunneling effects on buried pipelines using Fourier expansion. J. Geotech. Geoenviron. 2018, 144, 04018062. [Google Scholar] [CrossRef]
- Huang, M.; Zhou, Z.; Hu, Z.; Wang, K.; Zhou, S. Analysis of the buried pipeline response induced by twin tunneling using the generalized Hermite spectral method. Sustainability 2023, 15, 9949. [Google Scholar] [CrossRef]
- Avgerinos, V.; Potts, D.M.; Standing, J.R. Numerical investigation of the effects of tunnelling on existing tunnels. Géotechnique 2017, 67, 808–822. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Chakeri, H.; Hasanpour, R.; Hindistan, M.A.; Ünver, B. Analysis of interaction between tunnels in soft ground by 3D numerical modeling. Bull. Eng. Geol. Environ. 2011, 70, 439–448. [Google Scholar] [CrossRef]
- Choi, J.I.; Lee, S.W. Influence of existing tunnel on mechanical behavior of new tunnel. KSCE J. Civ. Eng. 2010, 14, 773–783. [Google Scholar] [CrossRef]
- Boonyarak, T.; Ng, C.W. Effects of construction sequence and cover depth on crossing-tunnel interaction. Can. Geotech. J. 2015, 52, 851–867. [Google Scholar] [CrossRef]
- Ng, C.W.; Boonyarak, T.; Mašín, D. Three-dimensional centrifuge and numerical modeling of the interaction between perpendicularly crossing tunnels. Can. Geotech. J. 2013, 50, 935–946. [Google Scholar] [CrossRef]
- Gue, C.Y.; Wilcock, M.J.; Alhaddad, M.M.; Elshafie, M.Z.E.B.; Soga, K.; Mair, R.J. Tunnelling close beneath an existing tunnel in clay–perpendicular undercrossing. Géotechnique 2017, 67, 795–807. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, C.; Wei, G. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula. Rock Soil Mech. 2014, 35, 2212–2218. [Google Scholar]
- Fang, Q.; Du, J.; Li, J.; Zhang, D.; Cao, L.Q. Settlement characteristics of large-diameter shield excavation below existing subway in close vicinity. J. Cent. South Univ. 2021, 28, 882–897. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Yu, L.; Li, Y.; Wang, X.; Zhang, D.; Ye, L.; Yang, S. Mechanical Responses of New Tunnel Down-crossing Existing Tunnel Considering Tunnelling Process. Railw. Stand. Des. 2024, 68, 141–152. [Google Scholar]
- Zhang, Q.; Lin, C.; Ding, Z.; Xia, T.; Shan, H. Theoretical analysis of vertical deformation of existing metro tunnel induced by shield tunneling under-passing in a short distance. Rock Soil Mech. 2015, 36, 568–572. [Google Scholar]
- Wei, G.; Yang, B.; Wu, H.; Zhang, X. Research on Longitudinal Deformation of Existing Shield Tunnel Caused by Shield Tunneling. J. Undergr. Space Eng. 2020, 16, 1754–1762+1808. [Google Scholar]
- Zhou, Z.; Zheng, Y.; Hu, J.; Yang, H.; Gong, C.J. Deformation analysis of shield undercrossing and vertical paralleling excavation with existing tunnel in composite stratum. J. Cent. South Univ. 2023, 30, 3127–3144. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, M.; Zhang, X.; Wei, X.J. Theoretical analysis on the deformation of existing tunnel caused by under-crossing of large-diameter slurry shield considering construction factors. Tunn. Undergr. Space Technol. 2023, 133, 104913. [Google Scholar] [CrossRef]
- Liang, R. Simplified analytical method for evaluating the effects of overcrossing tunnelling on existing shield tunnels using the nonlinear Pasternak foundation model. Soils Found. 2019, 59, 1711–1727. [Google Scholar] [CrossRef]
- Liang, R.; Wang, L.; Li, Z.; Kang, C.; Gao, K.; Ke, Z. Effect of ground surface surcharge on longitudinal deformation of existing shield tunnel. J. Archit. Civ. Eng. 2019, 40, 130–141. [Google Scholar]
- Kang, C.; Ye, C.; Liang, R.; Sun, L.; Fang, Y.; Wu, W. Nonlinear longitudinal deformation of underlying shield tunnels induced by foundation excavation. J. Rock Mech. Geotech. Eng. 2020, 39, 2341–2350. [Google Scholar]
- Zhang, Z.; Liang, R.; Gao, K.; Li, Z.; Xiao, M.; Guo, Y.; Yue, T.; Wu, W. Analysis of longitudinal displacement of existing shield tunnel due to construction of above-crossing new tunnel considering the weakening of circumferential joint. J. Rock Mech. Geotech. Eng. 2022, 41, 2955–2970. [Google Scholar]
- Mindlin, R.D. Force at a point in the interior of a semi-infinite solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Ke, Z.; Liang, R.; Tong, Z.; Yue, T.; Guo, Y. Simplified analytical solution for nonlinear longitudinal deformation of shield tunnels under surface surcharge. J. Rock Mech. Geotech. Eng. 2023, 41, 245–248. [Google Scholar]
- Wang, Y.; Shi, J.; Ng, C.W. Numerical modeling of tunneling effect on buried pipelines. Can. Geotech. J. 2019, 48, 1125–1137. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, Z.; Wu, S.; Li, Z.; Liu, G. Study of ground heave and subsidence induced by shield tunnelling in soft ground. J. Rock Mech. Geotech. Eng. 2011, 30, 2583–2592. [Google Scholar]
- Loganathan, N.; Poulos, H.G. Analytical prediction for tunneling-induced ground movements in clays. J. Geotech. Geoenviron. 1988, 124, 846–856. [Google Scholar] [CrossRef]
- Shiba, Y.; Kawashima, K.; Obinata, N.; Kano, T. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses. Doboku Gakkai Ronbunshu 1988, 398, 319–327. [Google Scholar] [CrossRef]
- Wu, X.; Yang, S.; Tian, J.; Chen, W.; Hu, Y.; Chen, B. Analysis on the Influence of Shield Tunneling Construction on the Proximity of Existing Tunnels and Research on Proximity Zoning. J. Civ. Eng. Manag. 2021, 38, 96–109+114. [Google Scholar]




| Surrounding Soils | γ (kN/m3) | Es(kPa) | v | c (kPa) | φ(°) | Hi (m) |
|---|---|---|---|---|---|---|
| Plain fill | 18.6 | 10.2 | 0.35 | 18 | 16 | 8.2 |
| Silty clay | 20.5 | 12.8 | 0.3 | 0 | 18.4 | 6.8 |
| Medium-coarse sand | 20.2 | 24.5 | 0.32 | 25 | 30.5 | 10.4 |
| Strongly weathered granite | 19.5 | 41 | 0.28 | 32 | 28.4 | 20.5 |
| Medium weathered granite | 25.0 | 48 | 0.3 | 48 | 42.6 | 26.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Wang, K.; Lu, J.; Zhong, Y.; Zhou, S. Nonlinear Analysis of the Mechanical Response of an Existing Tunnel Induced by Shield Tunneling during the Entire Under-Crossing Process. Sustainability 2024, 16, 8224. https://doi.org/10.3390/su16188224
Huang M, Wang K, Lu J, Zhong Y, Zhou S. Nonlinear Analysis of the Mechanical Response of an Existing Tunnel Induced by Shield Tunneling during the Entire Under-Crossing Process. Sustainability. 2024; 16(18):8224. https://doi.org/10.3390/su16188224
Chicago/Turabian StyleHuang, Minghua, Keping Wang, Jinbin Lu, Yuxuan Zhong, and Suhua Zhou. 2024. "Nonlinear Analysis of the Mechanical Response of an Existing Tunnel Induced by Shield Tunneling during the Entire Under-Crossing Process" Sustainability 16, no. 18: 8224. https://doi.org/10.3390/su16188224







