Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges
Abstract
:1. Introduction
2. Lightened Slab Bridge Deck Description
3. Methodology
3.1. Kriging Metamodel
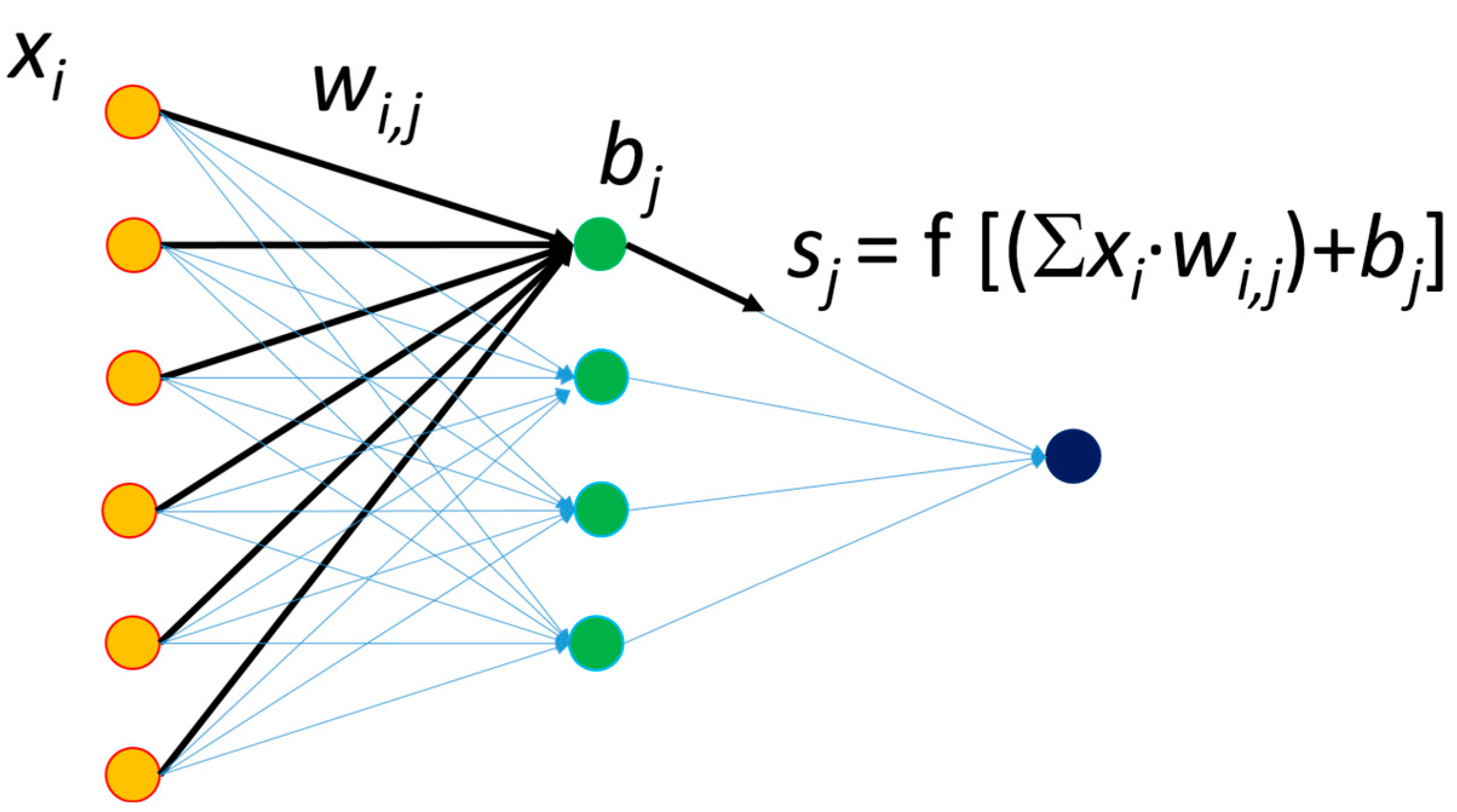
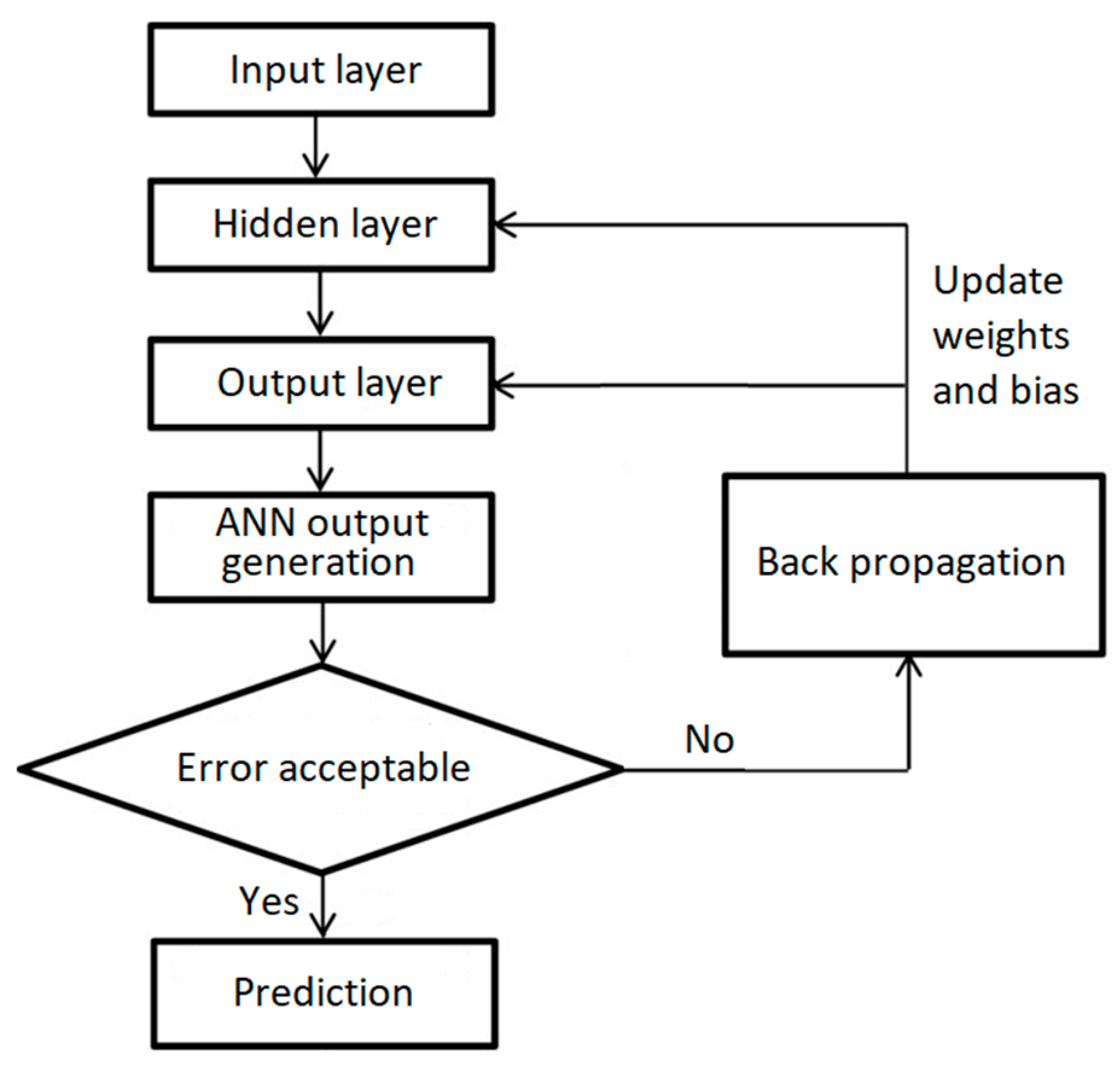
3.2. Artificial Neural Network
4. Results and Discussion
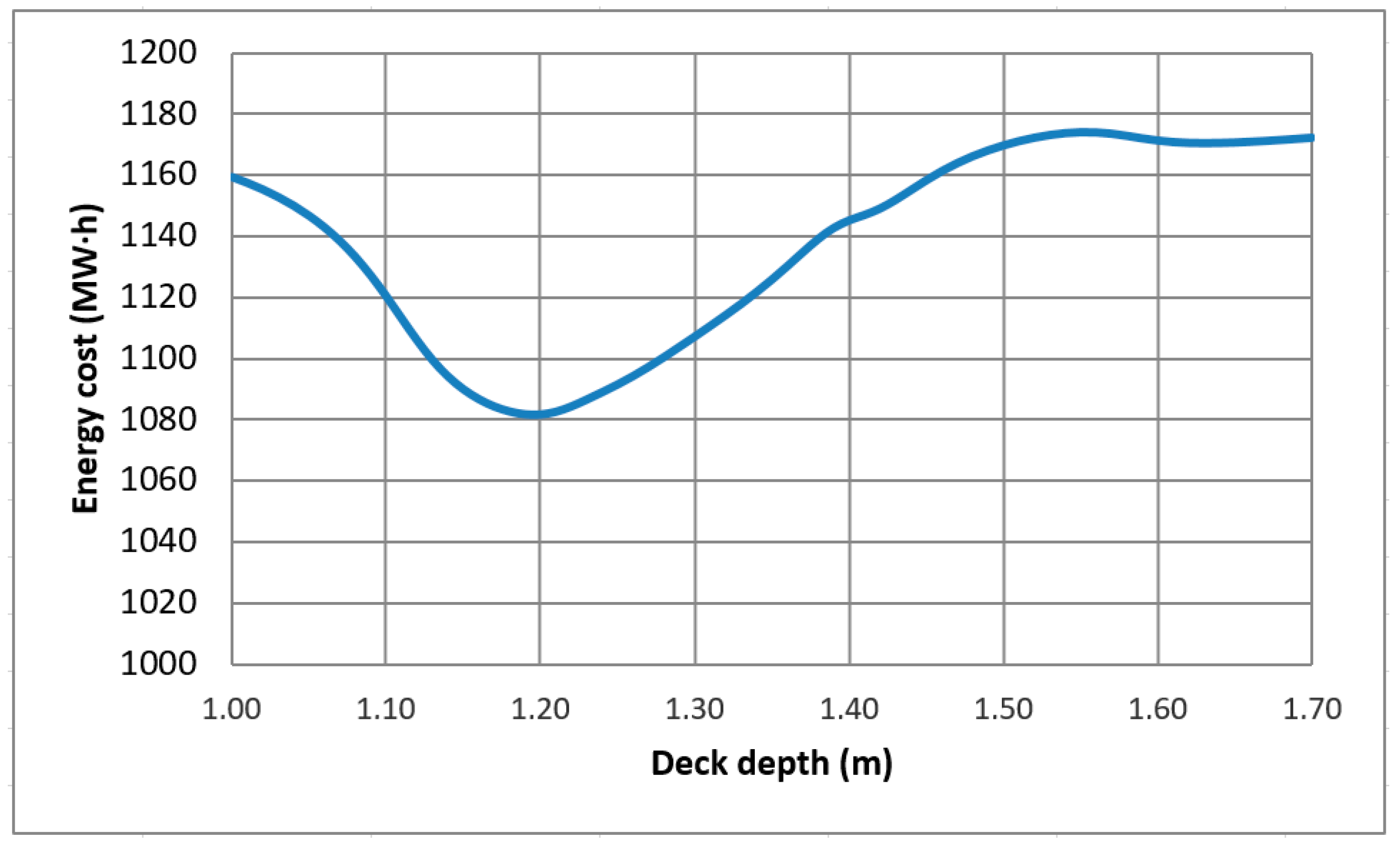
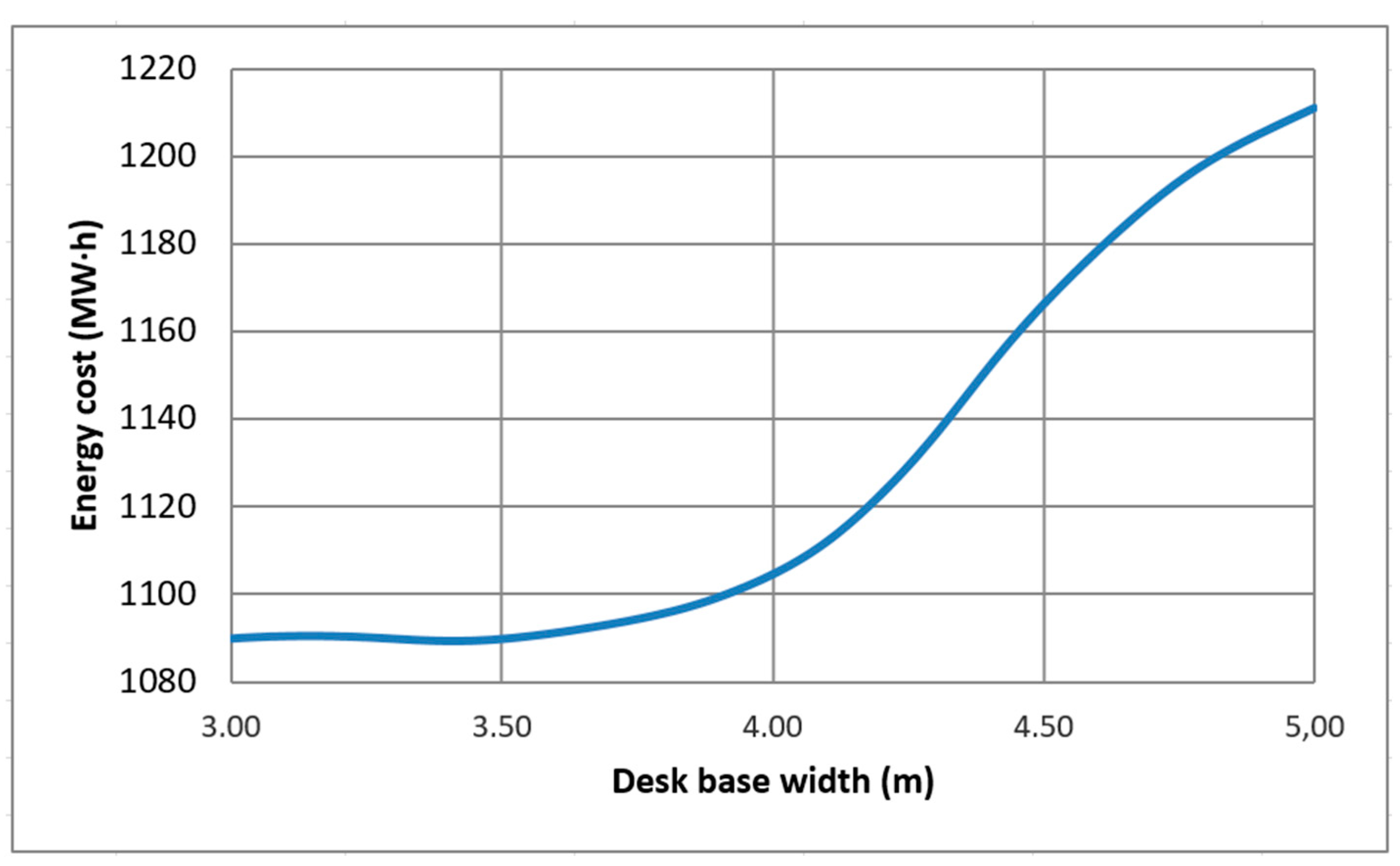
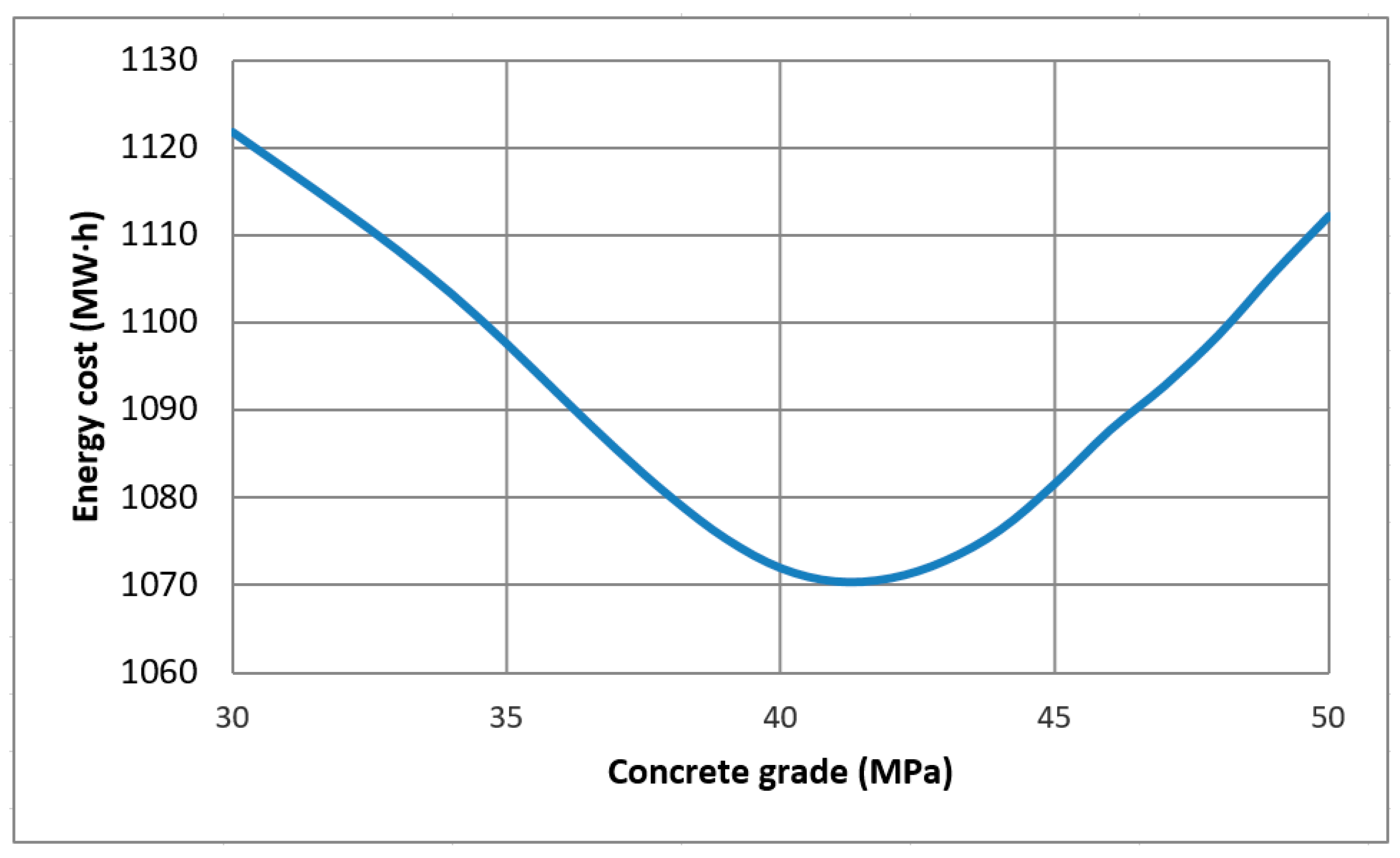
4.1. Visualization of Observed Data
4.2. Comparison of Predictive Models
4.3. Error Analysis
4.4. Practical Recommendations
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA; UNEP. Global Status Report: Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector; International Energy Agency and the United Nations Environment Programme: Paris, France, 2018. [Google Scholar]
- Wang, T.; Lee, I.S.; Kendall, A.; Harvey, J.; Lee, E.B.; Kim, C. Life cycle energy consumption and GHG emission from pavement rehabilitation with different rolling resistance. J. Clean Prod. 2012, 33, 86–96. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z. A hybrid Data Quality Indicator and statistical method for improving uncertainty analysis in LCA of complex system—Application to the whole-building embodied energy analysis. J. Clean Prod. 2013, 43, 166–173. [Google Scholar] [CrossRef]
- Halder, A.; Batra, S. Application of Predictive Analytics in Built Environment Research: A Comprehensive Bibliometric Study to Explore Knowledge Domains and Future Research Agenda. Arch. Computat. Methods Eng. 2023, 30, 4299–4324. [Google Scholar] [CrossRef]
- Opoku, D.G.J.; Agyekum, K.; Ayarkwa, J. Drivers of environmental sustainability of construction projects: A thematic analysis of verbatim comments from built environment consultants. Int. J. Constr. Manag. 2022, 22, 1033–1041. [Google Scholar] [CrossRef]
- Leonhardt, F. Prestressed Concrete: Design and Construction; Ernst & Sohn: Berlin, Germany, 1982. [Google Scholar]
- Warner, R.F.; Rangan, B.V.; Hall, A.S.; Faulkes, K.A. Concrete Structures; Longman: North Lakes, QLD, Australia, 1998. [Google Scholar]
- Yeo, D.; Gabbai, R.D. Sustainable design of reinforced concrete structures through embodied energy optimization. Energ. Buildings 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Quaglia, C.P.; Yu, N.; Thrall, A.P.; Paolucci, S. Balancing energy efficiency and structural performance through multi-objective shape optimization: Case study of a rapidly deployable origami-inspired shelter. Energ. Buildings 2014, 82, 733–745. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Boquera, L.; Chàfer, M.; Vérez, D. Embodied energy and embodied carbon of structural building materials: Worldwide progress and barriers through literature map analysis. Energy Build 2021, 231, 110612. [Google Scholar] [CrossRef]
- Miller, D.; Doh, J.H.; Mulvey, M. Concrete slab comparison and embodied energy optimisation for alternate design and construction techniques. Constr. Build Mater. 2015, 80, 329–338. [Google Scholar] [CrossRef]
- Foraboschi, P.; Mercanzin, M.; Trabucco, D. Sustainable structural design of tall buildings based on embodied energy. Energ. Buildings 2014, 68, 254–269. [Google Scholar] [CrossRef]
- Alcalá, J.; González-Vidosa, F.; Yepes, V.; Martí, J.V. Embodied energy optimization of prestressed concrete slab bridge decks. Technologies 2018, 6, 43. [Google Scholar] [CrossRef]
- Martí, J.V.; García-Segura, T.; Yepes, V. Structural design of prescast-prestressed concrete U-beam road bridges based on embodied energy. J. Clean. Prod. 2016, 120, 231–240. [Google Scholar] [CrossRef]
- Minunno, R.; O’Grady, T.; Morrison, G.M.; Gruner, R.L. Investigating the embodied energy and carbon of buildings: A systematic literature review and meta-analysis of life cycle assessments. Renew. Sustain. Energy Rev. 2021, 143, 110935. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Cressie, N. The origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Martí, P. Diseño óptimo robusto utilizando modelos Kriging: Aplicación al diseño óptimo robusto de estructuras articuladas. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2014, 30, 97–105. [Google Scholar] [CrossRef]
- YiFei, L.; MaoSen, C.; Hoa, T.N.; Khatir, S.; Minh, H.L.; SangTo, T.; Cuong-Le, T.; Wahab, M.A. Metamodel-assisted hybrid optimization strategy for model updating using vibration response data. Adv. Eng. Softw. 2023, 185, 103515. [Google Scholar] [CrossRef]
- Sánchez-Zabala, V.F.; Gómez-Acebo, T. Building energy performance metamodels for district energy management optimisation platforms. Energy Convers. Manag. X 2024, 21, 100512. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. CO2-optimization of post-tensioned concrete slab-bridge decks using surrogate modeling. Materials 2022, 15, 4776. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. Embodied energy optimization of prestressed concrete road flyovers by a two-phase Kriging surrogate model. Materials 2023, 16, 6767. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, G. Seismic vulnerability analysis of RC bridges based on Kriging model. J. Earthq. Eng. 2019, 23, 242–260. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, F.; Zou, C.; Zhang, R.; Li, C.; Huang, S.; Zhou, Y. Swarm intelligent optimization conjunction with Kriging model for bridge structure finite element model updating. Buildings 2022, 12, 504. [Google Scholar] [CrossRef]
- Cheng, A.; Low, Y.M. A new metamodel for predicting the nonlinear time-domain response of offshore structures subjected to stochastic wave current and wind loads. Comput. Struct. 2024, 297, 107340. [Google Scholar] [CrossRef]
- Martí-Vargas, J.R.; Ferri, F.J.; Yepes, V. Prediction of the transfer length of prestressing strands with neural networks. Comput. Concr. 2013, 12, 187–209. [Google Scholar] [CrossRef]
- Hong, W.K.; Nguyen, M.C.; Pham, T.D. Pre-tensioned concrete beams optimized with a unified function of objective (UFO) using ANN-based Hong-Lagrange method. J. Asian Archit. Build Eng. 2023, 23, 1573–1595. [Google Scholar] [CrossRef]
- Lophaven, N.S.; Nielsen, H.B.; Sondergaard, J. MATLAB Kriging Toolbox DACE (Design and Analysis of Computer Experiments) Version 2.0. 2002. Available online: http://www2.imm.dtu.dk/pubdb/p.php?1460 (accessed on 11 July 2024).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximator. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L.; PDP Research Group. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, UK, 1986; Volume 1. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Dirección General de Carreteras. Obras de paso de Nueva Construcción: Conceptos Generales; Ministerio de Fomento, Centro de Publicaciones: Madrid, Spain, 2000. (In Spanish)
- SETRA. Ponts-Dalles. Guide de Conception; Ministère de l’Equipement, du Logement des Transports et de la Mer: Bagneux, France, 1989. (In French)





| Material | kWh/kg | kWh/m3 | kWh/m2 |
|---|---|---|---|
| Y-1860-S7 steel | 5.64 | ||
| B-500-St steel | 3.03 | ||
| Lighting | 604.42 | ||
| Slab formwork | 2.24 | ||
| C-30 concrete | 227.01 | ||
| C-35 concrete | 263.96 | ||
| C-40 concrete | 298.57 | ||
| C-45 concrete | 330.25 | ||
| C-50 concrete | 358.97 | ||
| Lighting | 604.42 | ||
| Slab formwork | 2.24 |
| Deck | Deck Depth (m) | Base Width (m) | Concrete Grade (MPa) | Energy Cost (MW·h) |
|---|---|---|---|---|
| 1 | 1.65 | 3.65 | 35 | 1149.88 |
| 2 | 1.70 | 3.80 | 45 | 1182.89 |
| 3 | 1.20 | 3.85 | 40 | 1065.87 |
| 4 | 1.55 | 3.60 | 45 | 1140.79 |
| 5 | 1.20 | 4.85 | 50 | 1170.72 |
| 6 | 1.15 | 4.50 | 50 | 1199.59 |
| 7 | 1.35 | 3.95 | 30 | 1103.18 |
| 8 | 1.30 | 4.45 | 30 | 1180.31 |
| 9 | 1.35 | 4.25 | 45 | 1132.71 |
| 10 | 1.50 | 4.55 | 30 | 1138.00 |
| 11 | 1.60 | 4.20 | 40 | 1267.85 |
| 12 | 1.25 | 4.70 | 40 | 1191.65 |
| 13 | 1.50 | 4.05 | 45 | 1183.17 |
| 14 | 1.45 | 4.35 | 35 | 1119.17 |
| 15 | 1.65 | 3.45 | 45 | 1145.07 |
| 16 | 1.55 | 4.10 | 35 | 1162.92 |
| 17 | 1.25 | 3.50 | 45 | 1073.75 |
| 18 | 1.40 | 3.30 | 40 | 1152.33 |
| 19 | 1.45 | 3.90 | 45 | 1145.21 |
| 20 | 1.35 | 3.60 | 35 | 1094.86 |
| 21 | 1.50 | 3.35 | 45 | 1134.93 |
| 22 | 1.50 | 4.50 | 45 | 1189.53 |
| 23 | 1.55 | 3.20 | 30 | 1103.41 |
| 24 | 1.25 | 3.00 | 50 | 1101.04 |
| 25 | 1.40 | 3.45 | 45 | 1201.73 |
| 26 | 1.50 | 3.55 | 35 | 1105.44 |
| 27 | 1.70 | 3.85 | 45 | 1165.47 |
| 28 | 1.20 | 3.60 | 40 | 1083.41 |
| 29 | 1.30 | 4.90 | 40 | 1215.82 |
| 30 | 1.45 | 4.75 | 35 | 1163.59 |
| 31 | 1.20 | 3.40 | 40 | 1059.87 |
| 32 | 1.15 | 3.90 | 35 | 1129.22 |
| 33 | 1.05 | 3.50 | 35 | 1237.89 |
| 34 | 1.10 | 3.80 | 45 | 1178.72 |
| 35 | 1.15 | 3.35 | 45 | 1074.77 |
| 36 | 1.25 | 3.60 | 45 | 1078.71 |
| 37 | 1.10 | 3.45 | 40 | 1124.21 |
| 38 | 1.20 | 3.35 | 45 | 1065.44 |
| 39 | 1.25 | 3.40 | 45 | 1084.92 |
| 40 | 1.15 | 3.60 | 45 | 1104.77 |
| 41 | 1.15 | 3.35 | 40 | 1051.00 |
| 42 | 1.15 | 3.70 | 40 | 1038.28 |
| #41 | #42 | Absolute Error #41 | Relative Error #41 | Absolute Error #42 | Relative Error #42 | |
|---|---|---|---|---|---|---|
| Observed | 1051.00 | 1038.28 | 0.00 | 0.00% | 0.00 | 0.00% |
| Kriging 1 | 1130.68 | 1091.95 | 79.68 | 7.58% | 53.67 | 5.17% |
| Kriging 2 | 1073.98 | 1085.84 | 22.98 | 2.19% | 47.56 | 4.58% |
| Kriging 3 | 1060.58 | 1079.81 | 9.58 | 0.91% | 41.53 | 4.00% |
| ANN average | 1073.06 | 1091.85 | 22.06 | 2.10% | 53.57 | 5.16% |
| Predictive Models | MSE | RMSE |
|---|---|---|
| Kriging 1 | 2212.98 | 47.04 |
| Kriging 2 | 3923.49 | 62.64 |
| Kriging 3 | 4976.80 | 70.55 |
| ANN average | 1037.22 | 30.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges. Sustainability 2024, 16, 8450. https://doi.org/10.3390/su16198450
Yepes-Bellver L, Brun-Izquierdo A, Alcalá J, Yepes V. Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges. Sustainability. 2024; 16(19):8450. https://doi.org/10.3390/su16198450
Chicago/Turabian StyleYepes-Bellver, Lorena, Alejandro Brun-Izquierdo, Julián Alcalá, and Víctor Yepes. 2024. "Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges" Sustainability 16, no. 19: 8450. https://doi.org/10.3390/su16198450
APA StyleYepes-Bellver, L., Brun-Izquierdo, A., Alcalá, J., & Yepes, V. (2024). Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges. Sustainability, 16(19), 8450. https://doi.org/10.3390/su16198450











