Energy and Exergy Performance Analysis of Solar-Assisted Thermo-Mechanical Vapor Compression Cooling System
Abstract
1. Introduction
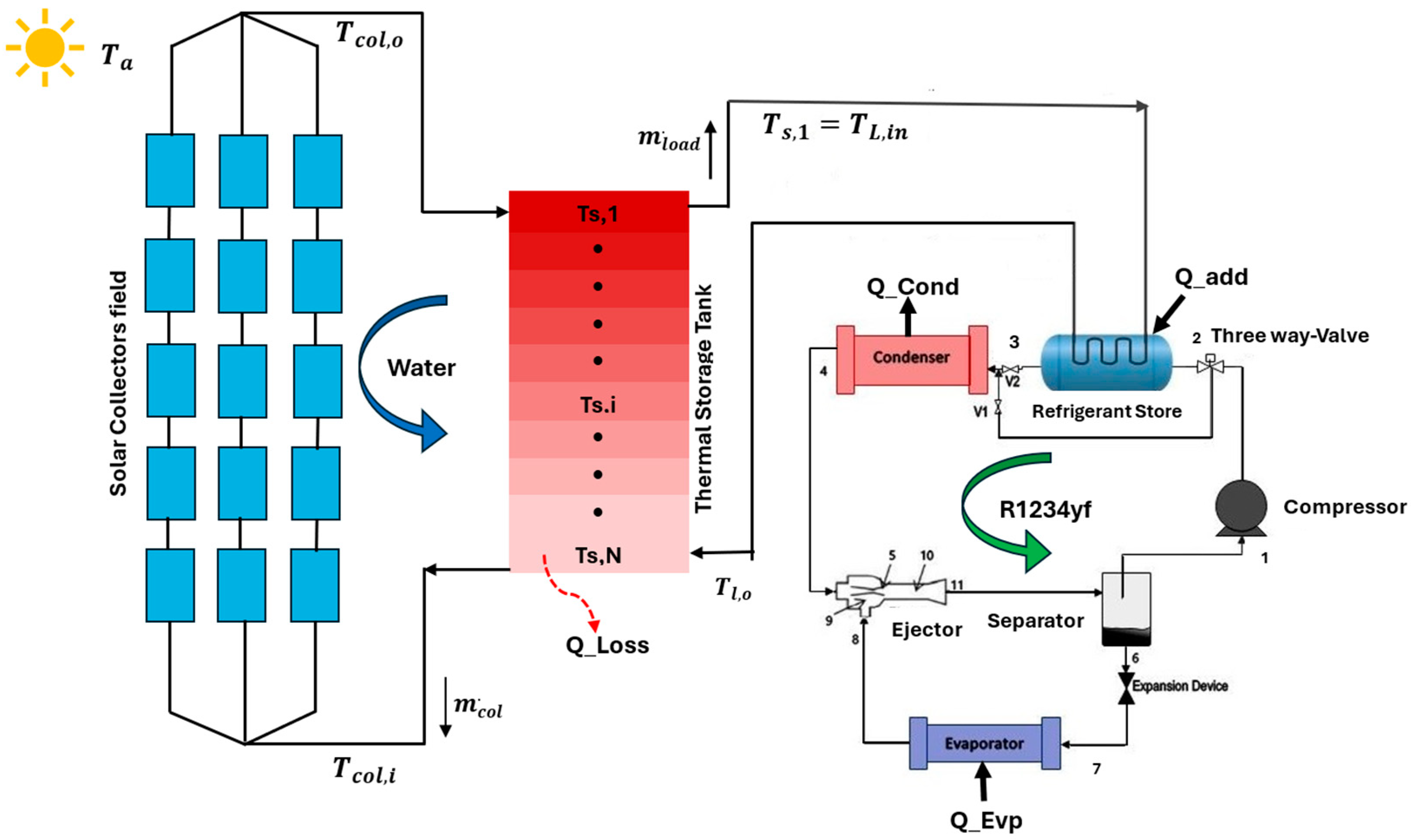
2. Description of the Hybrid Cooling System
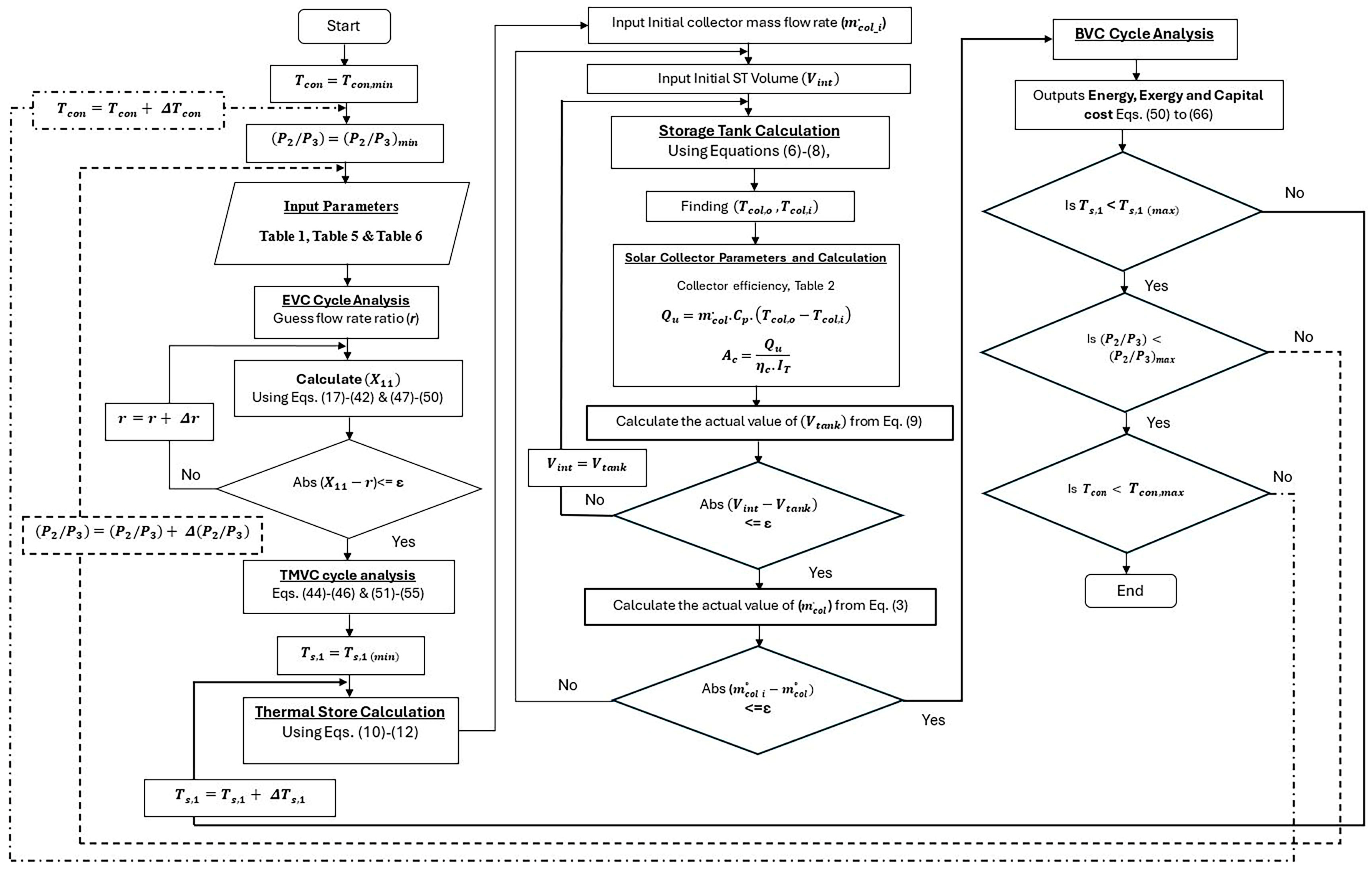
3. Research Method
4. Mathematical Model
4.1. Solar Collector Field Performance
4.2. Thermal Storage Tank
4.3. Refrigerant Vessel
4.4. TMVC System Mathematical Model Formulation
- The system operates under fully established steady-state conditions.
- Heat losses and pressure drops in the system’s components are negligible.
- The refrigerant at the suction line (point 1) and (point 8) is superheated, and in the discharge line (point 4), it is supercooled.
- The refrigerant in the ejector is considered a one-dimensional homogeneous equilibrium flow and undergoes constant-pressure mixing at point (10).
4.5. System Energy Performance Parameters
4.6. Exergy Performance Analysis
5. Simulation Parameters
6. Model Verification
7. Results and Discussion
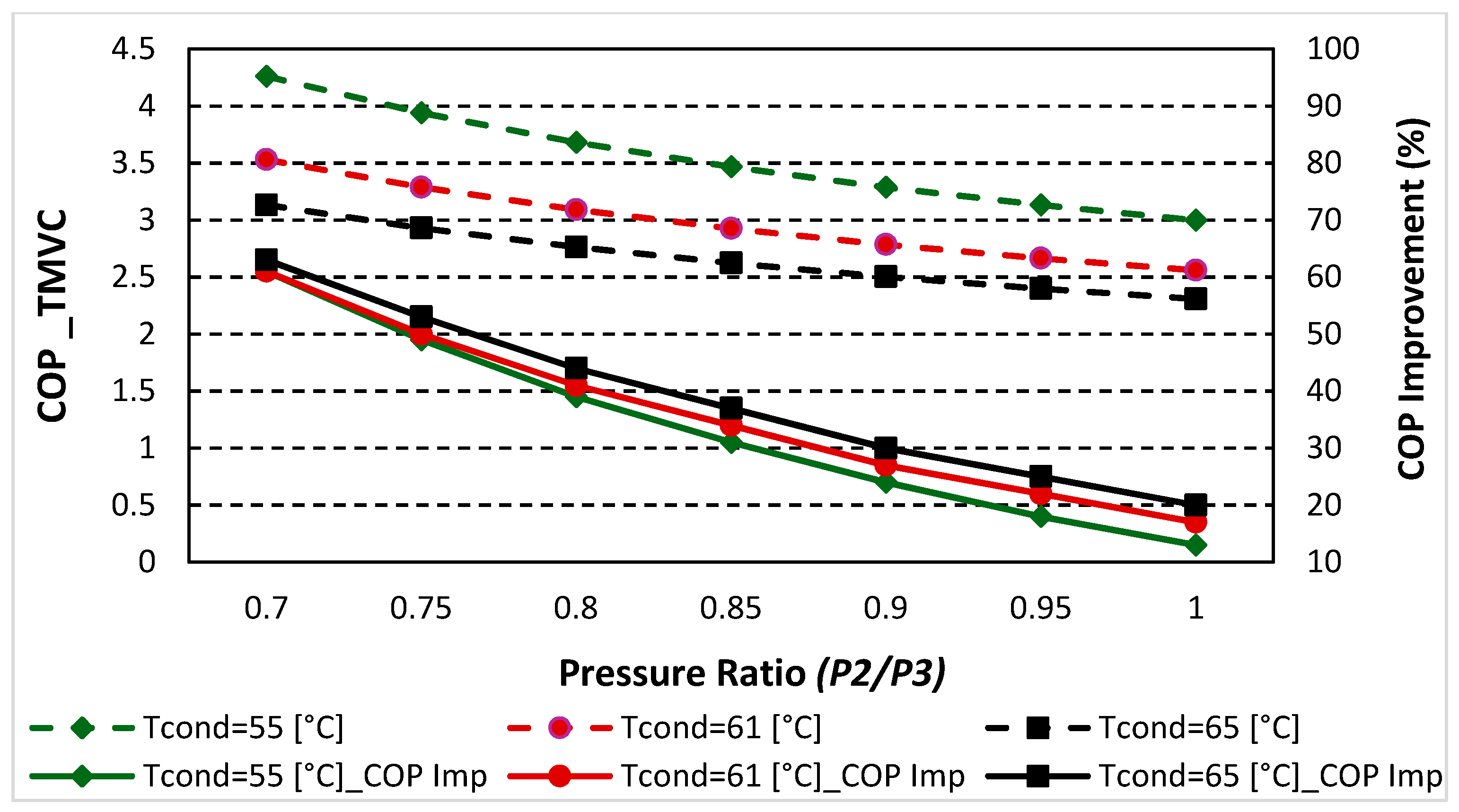
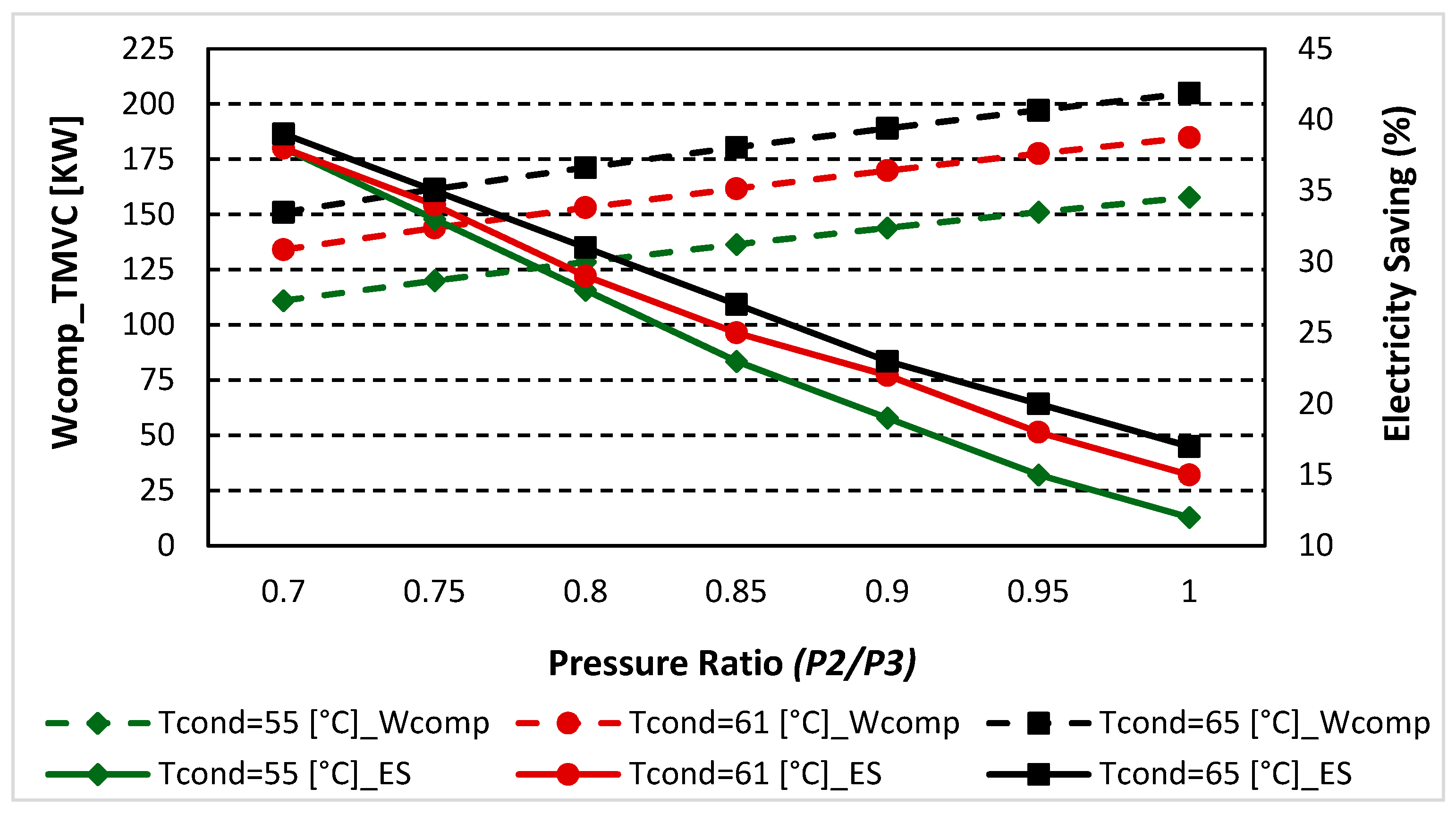
7.1. Effect of Condenser Temperatures and Thermal Pressure Ratio
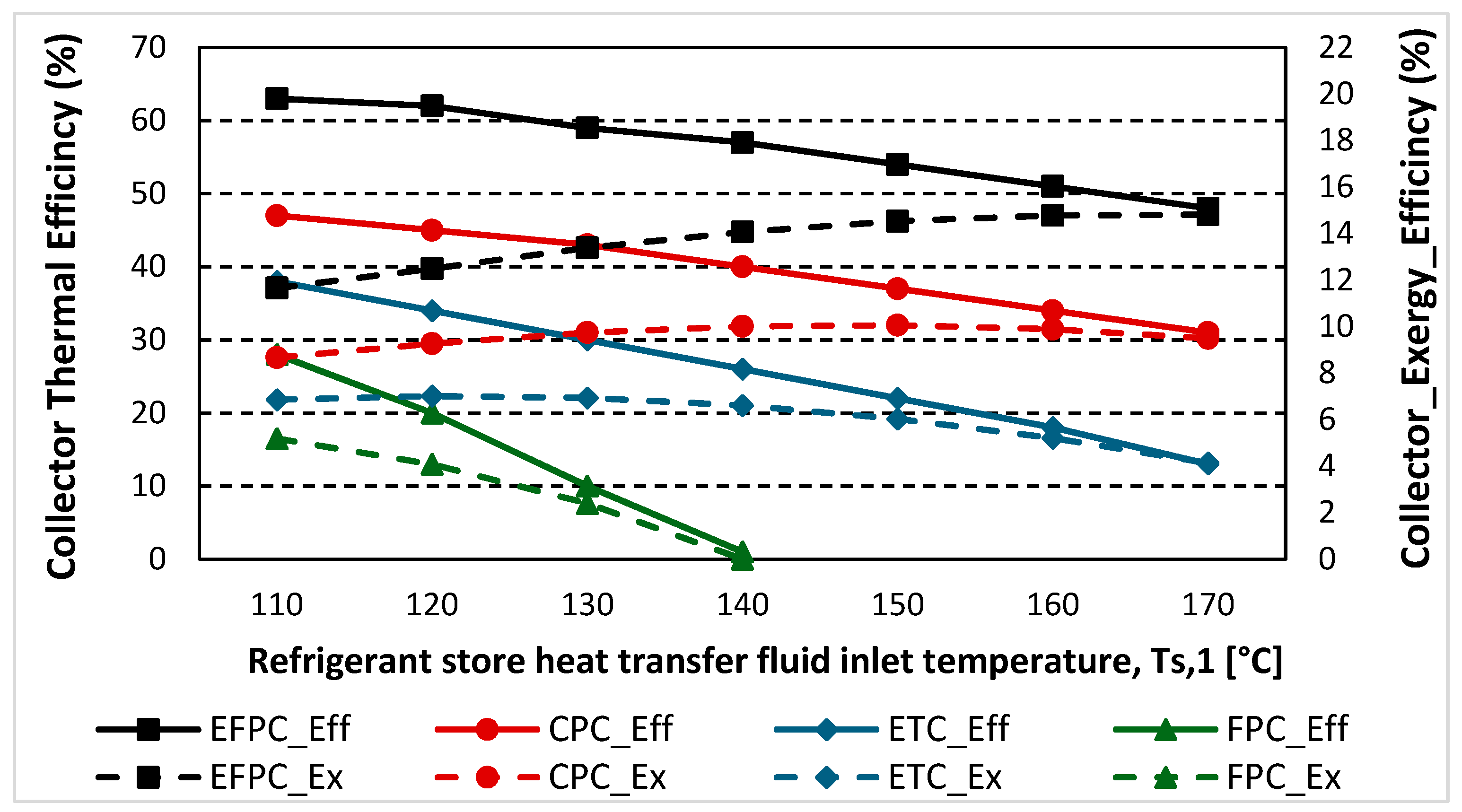
7.2. Effect of the Refrigerant Store Heat Transfer Fluid Inlet Temperature on the Solar Collector Efficiency and Exergy
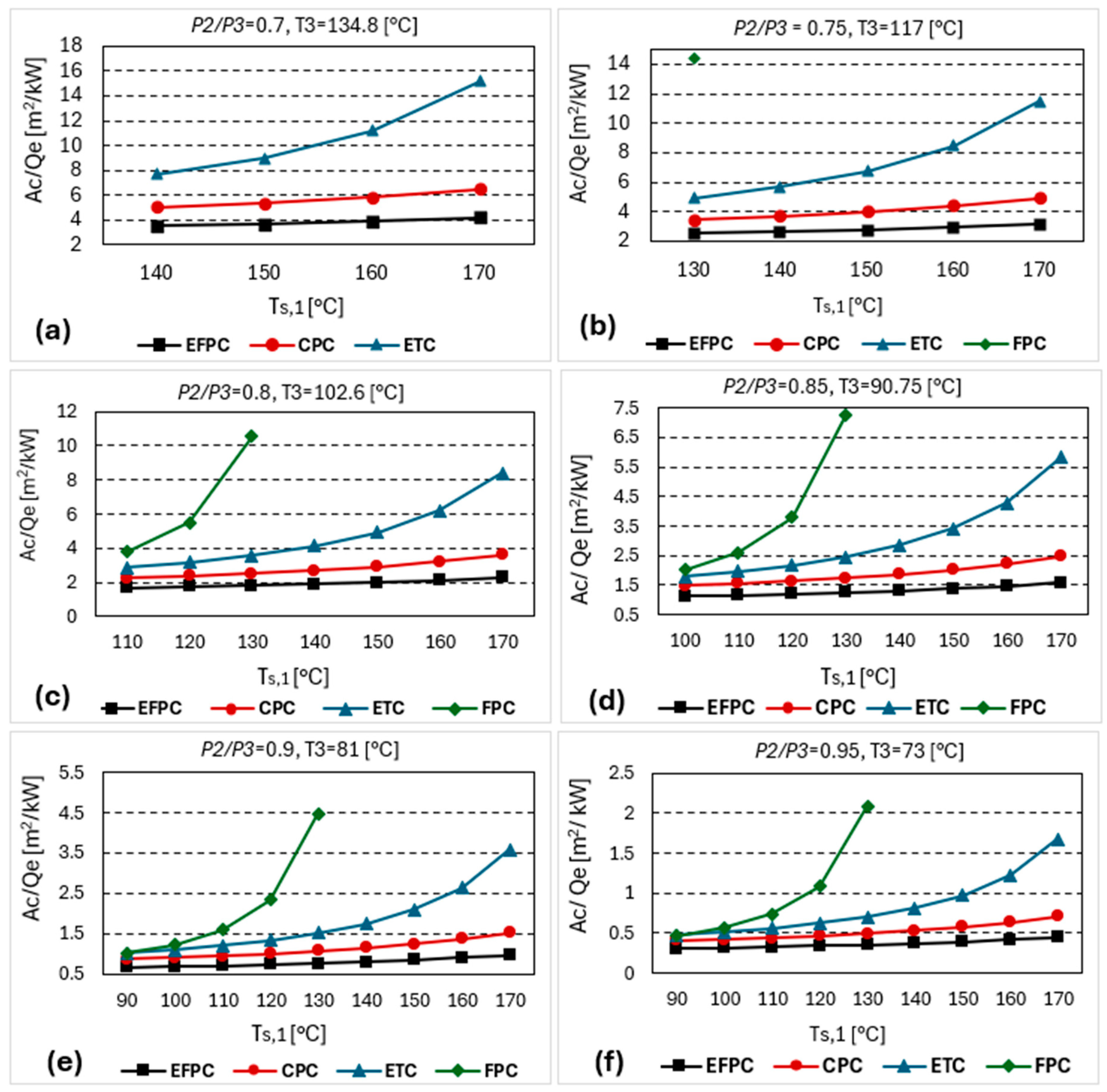
7.3. Effect of Thermal Pressure Ratio and the Refrigerant Store Heat Transfer Fluid Inlet Temperature on the Specific Collector Area
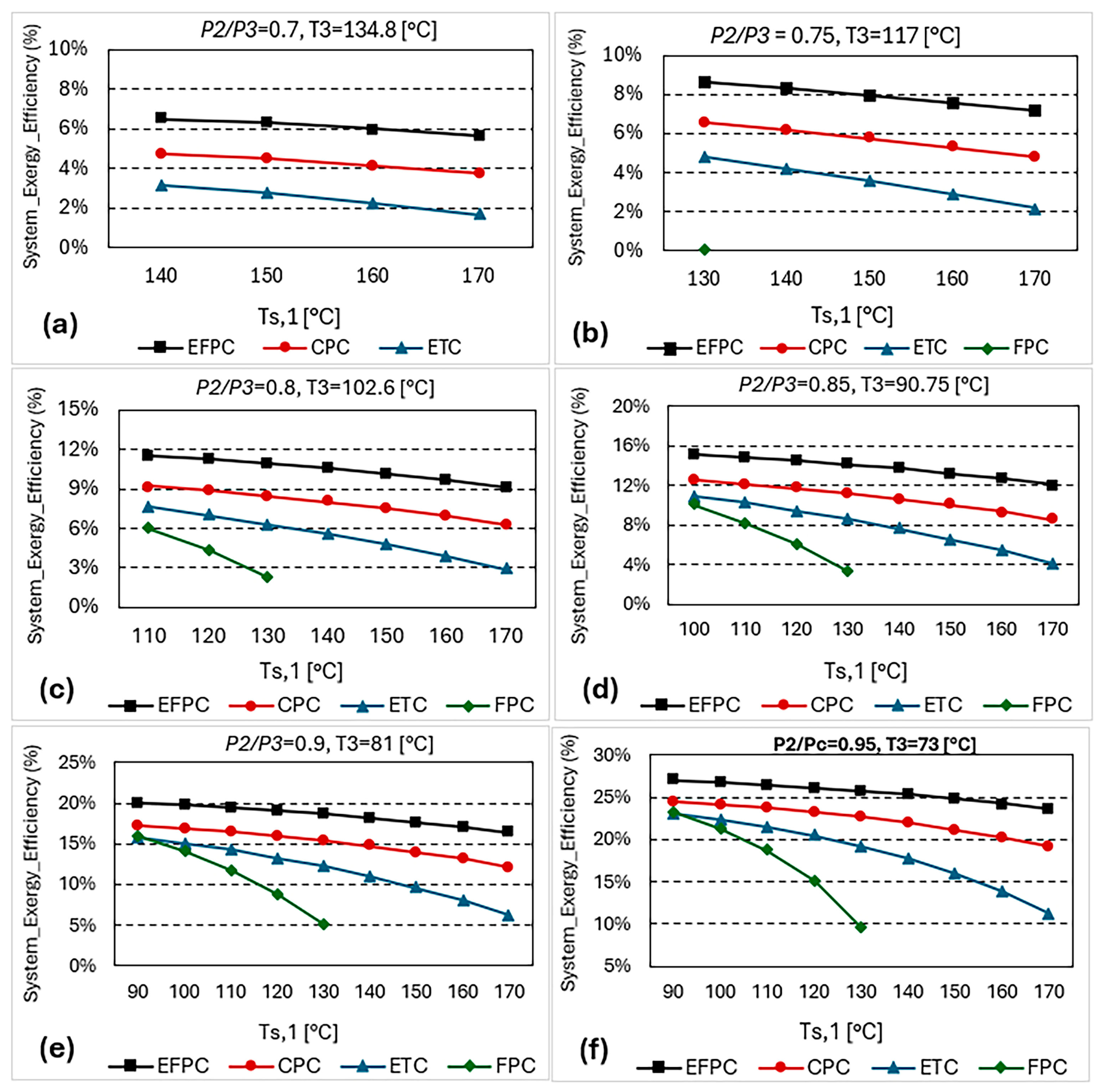
7.4. Effect of Thermal Pressure Ratio and the Refrigerant Store Heat Transfer Fluid Inlet Temperature on the Overall System Exergy Efficiency
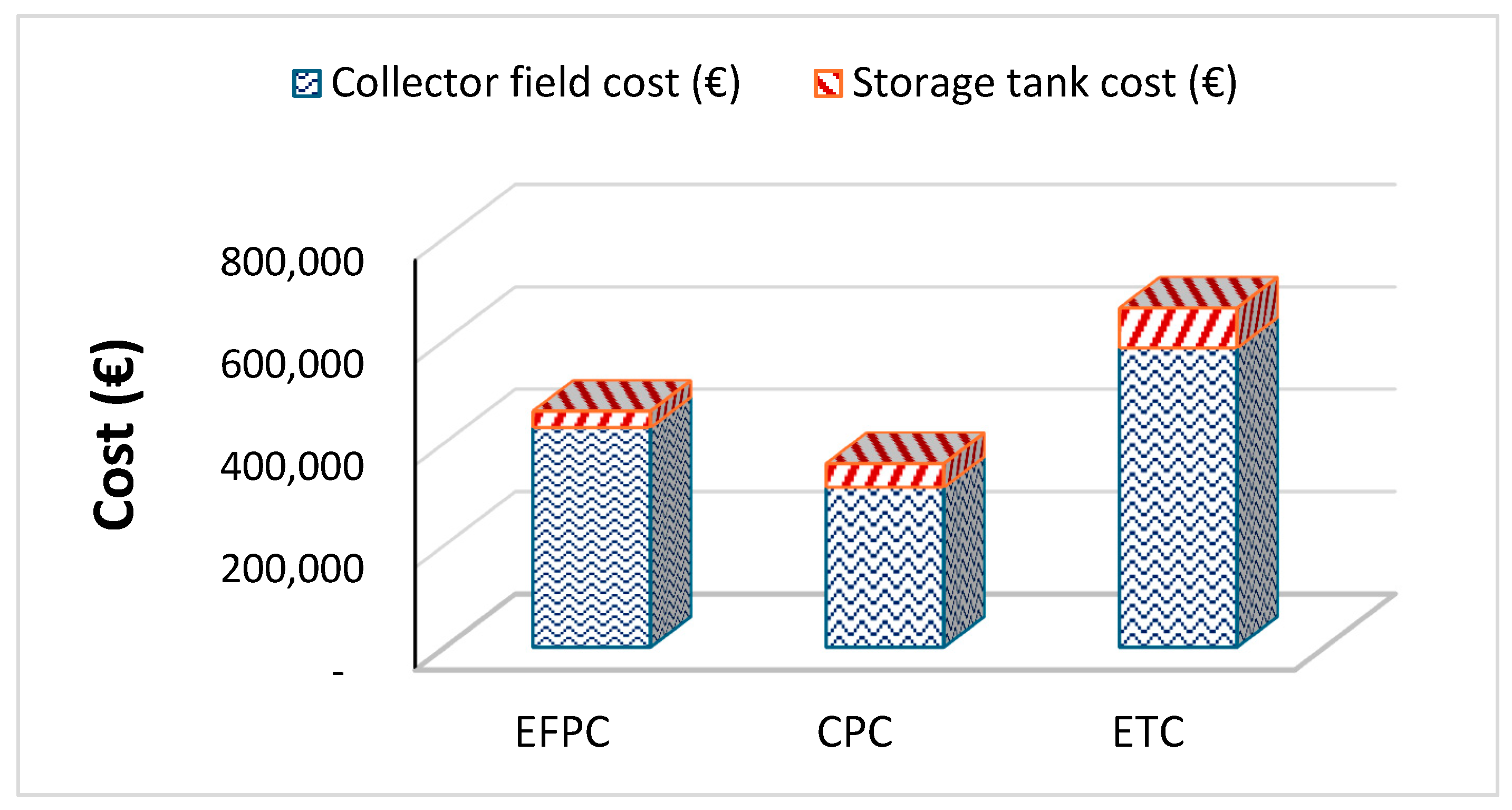
7.5. Cost of Integration of Solar Collectors
- Solar collector thermal and exergy efficiency
- Operating temperature
- Solar collector area
- Capital and maintenance cost
8. Comparison of Solar Cooling Technology
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variable | Description/Unit |
| Coefficient of performance | |
| Refrigerant specific enthalpy (kJ/kg) | |
| Working fluid mass flow rate (kg/s) | |
| Pressure (kPa) | |
| Condenser heat (W) | |
| Cooling capacity (W) | |
| Entropy (kJ/kg.K) | |
| Temperature (°C) | |
| Velocity (m/s) | |
| Compressor work (W) | |
| Vapor quality | |
| Symbols | |
| Efficiency | |
| Entrainment ratio | |
| Specific volume (m3/kg) | |
| Subscripts | |
| Basic vapor compression cycle | |
| Condenser | |
| Diffuser | |
| Discharge | |
| Evaporator | |
| HS | Heat source |
| Intermediate pressure | |
| Isentropic | |
| Mechanical | |
| mn | Motive nozzle |
| Storage tank | |
| Subcooled | |
| Superheated | |
| Suction nozzle | |
| ue | Useful |
| Es | Exergy |
| cs | Cooling system |
| Col | Collector |
| sys | system |
References
- Bandyopadhyay, B.; Banerjee, M. Decarbonization of Cooling of Buildings. Sol. Compass 2022, 2, 100025. [Google Scholar] [CrossRef]
- Parkinson, T.; Schiavon, S.; de Dear, R.; Brager, G. Overcooling of Offices Reveals Gender Inequity in Thermal Comfort. Sci. Rep. 2021, 11, 23684. [Google Scholar] [CrossRef] [PubMed]
- International Energy Agency. The Future of Cooling: Opportunities for Energy-Efficient Air Conditioning. Together Secure Sustainable. 2018. Available online: https://www.iea.org/reports/the-future-of-cooling (accessed on 15 August 2024).
- Mastrucci, A.; van Ruijven, B.; Byers, E.; Poblete-Cazenave, M.; Pachauri, S. Global Scenarios of Residential Heating and Cooling Energy Demand and CO2 Emissions. Clim. Change 2021, 168, 14. [Google Scholar] [CrossRef]
- Mathur, D. A Review on Solar Cooling Technologies. Int. J. Mech. Eng. Technol. 2020, 11, 12–21. Available online: https://iaeme.com/MasterAdmin/Journal_uploads/IJMET/VOLUME_11_ISSUE_5/IJMET_11_05_002.pdf (accessed on 15 August 2024). [CrossRef]
- Bilgili, M. Hourly Simulation and Performance of Solar Electric-Vapor Compression Refrigeration System. Sol. Energy 2011, 85, 2720–2731. [Google Scholar] [CrossRef]
- Kumar Sahu, B. A Study on Global Solar PV Energy Developments and Policies with Special Focus on the Top Ten Solar PV Power Producing Countries. Renew. Sustain. Energy Rev. 2015, 43, 621–634. [Google Scholar] [CrossRef]
- Nikbakhti, R.; Wang, X.; Hussein, A.K.; Iranmanesh, A. Absorption Cooling Systems—Review of Various Techniques for Energy Performance Enhancement. Alex. Eng. J. 2020, 59, 707–738. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M.; Arıcı, M. A Review on Solar-Powered Cooling and Air-Conditioning Systems for Building Applications. Energy Rep. 2022, 8, 2888–2907. [Google Scholar] [CrossRef]
- Hwang, Y.; Radermacher, R.; Alili, A.A.; Kubo, I. Review of Solar Cooling Technologies. HVACR Res. 2008, 14, 507–528. [Google Scholar] [CrossRef]
- Gündüz Altiokka, A.B.; Arslan, O. Design and Optimization of Absorption Cooling System Operating under Low Solar Radiation for Residential Use. J. Build. Eng. 2023, 73, 106697. [Google Scholar] [CrossRef]
- Al-Falahi, A.; Alobaid, F.; Epple, B. A New Design of an Integrated Solar Absorption Cooling System Driven by an Evacuated Tube Collector: A Case Study for Baghdad, Iraq. Appl. Sci. 2020, 10, 3622. [Google Scholar] [CrossRef]
- Sapienza, A.; Santamaria, S.; Frazzica, A.; Freni, A. Influence of the Management Strategy and Operating Conditions on the Performance of an Adsorption Chiller. Energy 2011, 36, 5532–5538. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S. Solar Cooling Technologies: State of Art and Perspectives. Energy Convers. Manag. 2020, 214, 112896. [Google Scholar] [CrossRef]
- Sim, L.F. Numerical Modelling of a Solar Thermal Cooling System under Arid Weather Conditions. Renew. Energy 2014, 67, 186–191. [Google Scholar] [CrossRef]
- Fasfous, A.; Asfar, J.; Al-Salaymeh, A.; Sakhrieh, A.; Al-Hamamre, Z.; Al-Bawwab, A.; Hamdan, M. Potential of Utilizing Solar Cooling in the University of Jordan. Energy Convers. Manag. 2013, 65, 729–735. [Google Scholar] [CrossRef]
- Angrisani, G.; Roselli, C.; Sasso, M.; Tariello, F. Assessment of Energy, Environmental and Economic Performance of a Solar Desiccant Cooling System with Different Collector Types. Energies 2014, 7, 6741–6764. [Google Scholar] [CrossRef]
- Bouzenada, S.; McNevin, C.; Harrison, S.; Kaabi, A. Performance of a Liquid Desiccant Air-Conditioner Driven by Evacuated-Tube, Flat-Plate, or Hybrid Solar Thermal Arrays. Energy Build. 2016, 117, 53–62. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and Numerical Investigation of the Influence of the Two-Phase Ejector Geometry on the Performance of the R744 Heat Pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Vidal, H.; Colle, S.; Pereira, G.D.S. Modelling and Hourly Simulation of a Solar Ejector Cooling System. Appl. Therm. Eng. 2006, 26, 663–672. [Google Scholar] [CrossRef]
- Chen, Q.; Hwang, Y.; Yan, G.; Yu, J. Theoretical Investigation on the Performance of an Ejector Enhanced Refrigeration Cycle Using Hydrocarbon Mixture R290/R600a. Appl. Therm. Eng. 2020, 164, 114456. [Google Scholar] [CrossRef]
- Elakhdar, M.; Tashtoush, B.M.; Nehdi, E.; Kairouani, L. Thermodynamic Analysis of a Novel Ejector Enhanced Vapor Compression Refrigeration (EEVCR) Cycle. Energy 2018, 163, 1217–1230. [Google Scholar] [CrossRef]
- Direk, M.; İşkan, Ü.; Tunçkal, C.; Mert, M.S.; Yüksel, F. An Experimental Investigation of Ejector Employed in a Dual-Evaporator Vapor Compression Refrigeration System under Various Entrainment Ratios Using R134a as the Refrigerant. Sustain. Energy Technol. Assess. 2022, 52, 102293. [Google Scholar] [CrossRef]
- Gullo, P.; Birkelund, M.; Kriezi, E.E.; Kærn, M.R. Comprehensive Experimental Performance Study on a Small-Capacity Transcritical R744 Vapour-Compression Refrigeration Unit Equipped with an Innovative Ejector. Int. J. Refrig. 2023, 152, 192–203. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M.; Szabo, M. Solar Absorption Cooling Systems Versus Traditional Air-Conditioning in Hot Climate. 2016. Available online: https://www.researchgate.net/publication/327781210 (accessed on 30 September 2024).
- Albatayneh, A.; Jaradat, M.; Al-Omary, M.; Zaquot, M. Evaluation of Coupling PV and Air Conditioning vs. Solar Cooling Systems—Case Study from Jordan. Appl. Sci. 2021, 11, 511. [Google Scholar] [CrossRef]
- Palomba, V.; Wittstadt, U.; Bonanno, A.; Tanne, M.; Harborth, N.; Vasta, S. Components and Design Guidelines for Solar Cooling Systems: The Experience of ZEOSOL. Renew. Energy 2019, 141, 678–692. [Google Scholar] [CrossRef]
- Hassan, Q.; Abbas, M.K.; Abdulateef, A.M.; Abulateef, J.; Mohamad, A. Assessment of the Potential Solar Energy with the Models for Optimum Tilt Angles of Maximum Solar Irradiance for Iraq. Case Stud. Chem. Environ. Eng. 2021, 4, 100140. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- The Solar Keymark/CEN Keymark Scheme. Available online: https://solarkeymark.eu/database/ (accessed on 26 August 2024).
- Saloux, E.; Candanedo, J.A. Control-Oriented Modelling of Stratified Storage Tanks: An Enhanced Approach. Energy Procedia 2018, 193, 193–201. [Google Scholar]
- Bellos, E.; Tzivanidis, C.; Symeou, C.; Antonopoulos, K.A. Energetic, Exergetic and Financial Evaluation of a Solar Driven Absorption Chiller—A Dynamic Approach. Energy Convers. Manag. 2017, 137, 34–48. [Google Scholar] [CrossRef]
- Kleinbach, E.M. Performance Study of One-Dimensional Models for Stratified Thermal Storage Tank. Sol. Energy 1990, 50, 155–166. [Google Scholar] [CrossRef]
- Kutlu, C.; Li, J.; Su, Y.; Pei, G.; Riffat, S. Off-Design Performance Modelling of a Solar Organic Rankine Cycle Integrated with Pressurized Hot Water Storage Unit for Community Level Application. Energy Convers. Manag. 2018, 166, 132–145. [Google Scholar] [CrossRef]
- Li, T.; Liu, Y.; Wang, D.; Shang, K.; Liu, J. Optimization Analysis on Storage Tank Volume in Solar Heating System. Procedia Eng. 2015, 121, 1356–1364. [Google Scholar] [CrossRef]
- Kilic, M.; Kaynakli, O. Second Law-Based Thermodynamic Analysis of Water-Lithium Bromide Absorption Refrigeration System. Energy 2007, 32, 1505–1512. [Google Scholar] [CrossRef]
- Özgür, A.E.; Kabul, A.; Kizilkan, Ö. Exergy Analysis of Refrigeration Systems Using an Alternative Refrigerant (HFO-1234yf) to R-134a. Int. J. Low-Carbon Technol. 2014, 9, 56–62. [Google Scholar] [CrossRef]
- Li, H.; Cao, F.; Bu, X.; Wang, L.; Wang, X. Performance Characteristics of R1234yf Ejector-Expansion Refrigeration Cycle. Appl. Energy 2014, 121, 96–103. [Google Scholar] [CrossRef]
- Brunin, O.; Feidt, M.; Hivet, B. Comparison of the Working Domains of Some Compression Heat Pumps and a Compression-Absorption Heat Pump. Int. J. Refrig. 1997, 20, 97. [Google Scholar] [CrossRef]
- Lateef Tarish, A.; Talib Hamzah, M.; Assad Jwad, W. Thermal and Exergy Analysis of Optimal Performance and Refrigerant for an Air Conditioner Split Unit Under Different Iraq Climatic Conditions. Therm. Sci. Eng. Prog. 2020, 19, 100595. [Google Scholar] [CrossRef]
- Bellos, E.; Vrachopoulos, M.G.; Tzivanidis, C. Energetic and Exergetic Investigation of a Novel Solar-Assisted Mechanical Compression Refrigeration System. Energy Convers. Manag. 2017, 147, 1–18. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, H.; Wang, H.; Zhang, S.; Guan, X. Exergy Analysis of Flat Plate Solar Collectors. Entropy 2014, 16, 2549–2567. [Google Scholar] [CrossRef]
- Petela, R. Exergy of Undiluted Thermal Radiation. Sol. Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Thermal Collectors and Applications. Prog. Energy Combust. Sci. 2004, 30, 231–295. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. Exergetic, Energetic and Financial Evaluation of a Solar Driven Absorption Cooling System with Various Collector Types. Appl. Therm. Eng. 2016, 102, 749–759. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. A Detailed Investigation of an Evacuated Flat Plate Solar Collector. Appl. Therm. Eng. 2023, 234, 121334. [Google Scholar] [CrossRef]
- Shirazi, A.; Taylor, R.A.; Morrison, G.L.; White, S.D. Solar-Powered Absorption Chillers: A Comprehensive and Critical Review. Energy Convers. Manag. 2018, 171, 59–81. [Google Scholar] [CrossRef]
- Hasan, A.A.; Juaidi, A.; Abdallah, R.; Salameh, T.; Ayadi, O.; Jaradat, M.; Hammad, R.E.; Campana, P.E.; Aqel, O.A. A Review of Solar Thermal Cooling Technologies in Selected Middle East and North African Countries. Sustain. Energy Technol. Assess. 2022, 54, 102871. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Radiation on the tilted angle (It) | 629 W/m2 |
| Beam radiation component (Ib) | 434.35 W/m2 |
| Diffuse radiation component (Id) | 208.34 W/m2 |
| Ground reflected value (ρ) | 0.2 |
| Ambient temperature | 46 °C |
| Latitude angle Φ | 33° |
| Declination angle | 21.18° |
| Tilt angle | 1.8 |
| (incident angle modifier (IAM)) | 0.98 |
| 1.006 | |
| 1.19 | |
| 0.98 | |
| Storage tank heat transfer coefficient | 0.5 W.m−2. K−1 |
| Number of storage tank nodes | 10 |
| Solar thermal system working fluid | Water |
| Solar Collector | Acronym | ηopt | c1 | c2 | Manufacturer |
|---|---|---|---|---|---|
| Basic flat plate collectors | FPC | 0.725 | 3.33 | 0.015 | Solarbayer GmbH |
| Evacuated flat plate collectors | EFPC | 0.737 | 0.504 | 0.006 | TVP Solar SA |
| Evacuated tube collectors | ETC | 0.466 | 1.41 | 0.006 | ONOSI |
| Compound parabolic collectors | CPC | 0.556 | 0.45 | 0.007 | CMG Solari SRL |
| Key Parameter | Equation | |
|---|---|---|
| Compressor work | (13) | |
| Cooling capacity | (14) | |
| Condenser heat rejection | (15) | |
| COP | (16) |
| Thermodynamic State | Refrigerant Property | Relationship | Equation |
|---|---|---|---|
| Condenser discharge line (point 4) | Pressure Enthalpy Entropy | (17) (18) (19) | |
| Ejector discharge (point 5) | Pressure Enthalpy (iso) Entropy Enthalpy (actual) Refrigerant velocity | (20) (21) (22) (23) (24) | |
| Separator liquid line (point 6) | Enthalpy | (25) | |
| Evaporator inlet (point 7) | Enthalpy | (26) | |
| Ejector suction line (point 8) | Pressure Enthalpy Entropy | (27) (28) (29) | |
| Ejector suction chamber (point 9) | Entropy Enthalpy (iso) Enthalpy (actual) Refrigerant velocity | (30) (31) (32) (33) | |
| Constant area of the ejector (point 10) | Enthalpy Entropy | (34) (35) | |
| Ejector diffuser exit (point 11) | Pressure Enthalpy Enthalpy (iso) Entropy Vapor quality | , ) , | (36) (37) (38) (39) (40) |
| Compressor suction line (point 1) | Enthalpy | (41) | |
| Compressor discharge line (point 2) | Enthalpy | (42) (43) | |
| Thermal store vapor line (point 3) | Specific volume Enthalpy Temperature | , | (44) (45) (46) |
| List of Parameters | Value |
|---|---|
| Pressure ratio | 0.7–0.95 |
| Heat transfer fluid supply temperature | 90 °C–170 °C |
| Condenser temperature | 55 °C–65 °C |
| Superheated temperature | 5 °C |
| Subcooled temperature | 5 °C |
| Evaporator temperature | 5 °C |
| Ambient temperature at 3:00 PM | 46.38 °C |
| Refrigerant store efficiency | 0.8 |
| Compressor mechanical efficiency | 0.8 |
| Ejector suction nozzle pressure drop | 20 Kpa |
| Motive nozzle efficiency | 0.85 |
| Suction nozzle efficiency | 0.85 |
| Diffuser efficiency | 0.85 |
| Cooling load | 473 kW |
| Refrigerant working fluid | R1234yf |
| Collector Type | FPC | CPC | ETC | EFPC | Storage Tank |
|---|---|---|---|---|---|
| Cost (EUR/m2) | 150 | 225 | 250 | 450 | 1000 (EUR/m3) |
| Reference | [45] | [45] | [45] | [46] | [32] |
| Basic Vapor Compression Cycle | Tcon (°C) | 35 | 40 | 45 | 50 | 55 |
| Tev (°C) | 5 | −5 | −10 | −10 | −15 | |
| [41] | 0.3639 | 0.3033 | 0.2567 | 0.2172 | 0.1820 | |
| (Present study) | 0.3652 | 0.3045 | 0.2576 | 0.2177 | 0.182 | |
| Deviation (%) | 0.36 | 0.40 | 0.35 | 0.23 | 0.0 | |
| COP [41] | 4.046 | 2.323 | 1.688 | 1.428 | 1.044 | |
| COP (Present study) | 4.0612 | 2.3317 | 1.6936 | 1.4315 | 1.0437 | |
| Deviation (%) | 0.38 | 0.37 | 0.33 | 0.25 | −0.03 | |
| Basic Vapor Compression with Solar Energy | Tcon (°C) | 35 | 40 | 45 | 50 | 55 |
| Tev (°C) | 5 | 5 | 5 | 5 | 5 | |
| Ac (m2/kW) [41] | 1.177 | 1.278 | 1.394 | 1.532 | 1.704 | |
| Ac (m2/kW) (Present study) | 1.187 | 1.267 | 1.414 | 1.5323 | 1.681 | |
| Deviation (%) | 0.85 | −0.86 | 1.43 | 0.02 | −1.35 |
| Solar Thermal Collector Parameters at Optimum Ts,1 | ||||
| Collector Type | EFPC | CPC | ETC | FPC |
| 150 | 120 | 110 | ||
| 14.8% | 10% | 7% | 5.20% | |
| 48.4% | 37.40% | 34.20% | 28.50% | |
| Collector Operation Parameters P2/P3 = 0.8, Ts,1 = 150 °C and Tcond = 61 °C | ||||
| (m2) | 953.5 | 1387 | 2338 | - |
| (m3) | 31.78 | 46.26 | 77.93 | - |
| (kg/s) | 19 | 27.75 | 46.76 | - |
| (kg/s) | 1.77 | 1.77 | 1.77 | - |
| 54% | 37% | 22% | - | |
| 14.5% | 10% | 6% | - | |
| /Qe (m2/kW) | 2.01 | 2.93 | 4.94 | - |
| Cooling System | Location | Application | Collector Type | Specific Collector Area (m2/kW) | Reference |
|---|---|---|---|---|---|
| TMVC (Present Study) | Baghdad, Iraq | Residential Building | EFPC | 1.7–2.28 | Present Study |
| Absorption, Double-Effect | Delhi India | Swiss Embassy | CPC | 3 | [14] |
| Absorption, Double-Effect | Dammam, Saudi Arabia | Demonstration | EFPC | 2.28 | [47] |
| Absorption, Single-Effect | Dead Sea, Jordan | Hotel | ETC | 9.7 | [47] |
| Absorption, Single-Effect | Firenze, Italy | Health Facility | ETC | 6.3 | [47] |
| Absorption, Single-Effect | Assiut, Egypt | University- German/Egyptian Demonstration | ETC | 5.3 | [48] |
| Absorption, Single-Effect | Casablanca, Morocco | Hospital | FPC | 8.3 | [47] |
| Absorption, Single-Effect | Jordan | University Research Experimental Project | FPC | 7.3 | [48] |
| Adsorption | Freiburg, Germany | Kitchen | FPC | 4 | [14] |
| Adsorption | Perpignan, France | Research Center Office | FPC | 3.33 | [14] |
| Desiccant | Abu Dhabi, UAE | Residential Home | FPC | 2–3.33 | [48] |
| Desiccant, Liquid | Freiburg, Germany | Solar Info Center | FPC | 1.68 | [14] |
| Desiccant, Solid | Gleisdorf, Austria | Office Building | FPC | 8.6 | [14] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Khiro, H.A.; Boukhanouf, R. Energy and Exergy Performance Analysis of Solar-Assisted Thermo-Mechanical Vapor Compression Cooling System. Sustainability 2024, 16, 8625. https://doi.org/10.3390/su16198625
Al Khiro HA, Boukhanouf R. Energy and Exergy Performance Analysis of Solar-Assisted Thermo-Mechanical Vapor Compression Cooling System. Sustainability. 2024; 16(19):8625. https://doi.org/10.3390/su16198625
Chicago/Turabian StyleAl Khiro, Hussein A., and Rabah Boukhanouf. 2024. "Energy and Exergy Performance Analysis of Solar-Assisted Thermo-Mechanical Vapor Compression Cooling System" Sustainability 16, no. 19: 8625. https://doi.org/10.3390/su16198625
APA StyleAl Khiro, H. A., & Boukhanouf, R. (2024). Energy and Exergy Performance Analysis of Solar-Assisted Thermo-Mechanical Vapor Compression Cooling System. Sustainability, 16(19), 8625. https://doi.org/10.3390/su16198625






