An Electrochemical Performance Model Considering of Non-Uniform Gas Distribution Based on Porous Media Method in PEMFC Stack
Abstract
:1. Introduction
1.1. The Importance of the Fuel Cell Electrochemical Performance Model
1.2. The Influence of the Gas Flow Distribution in PEMFC Stack
2. The Combined Model of Electrochemical Performance and Gas Distribution
2.1. The Single-Channel Electrochemical Performance Model
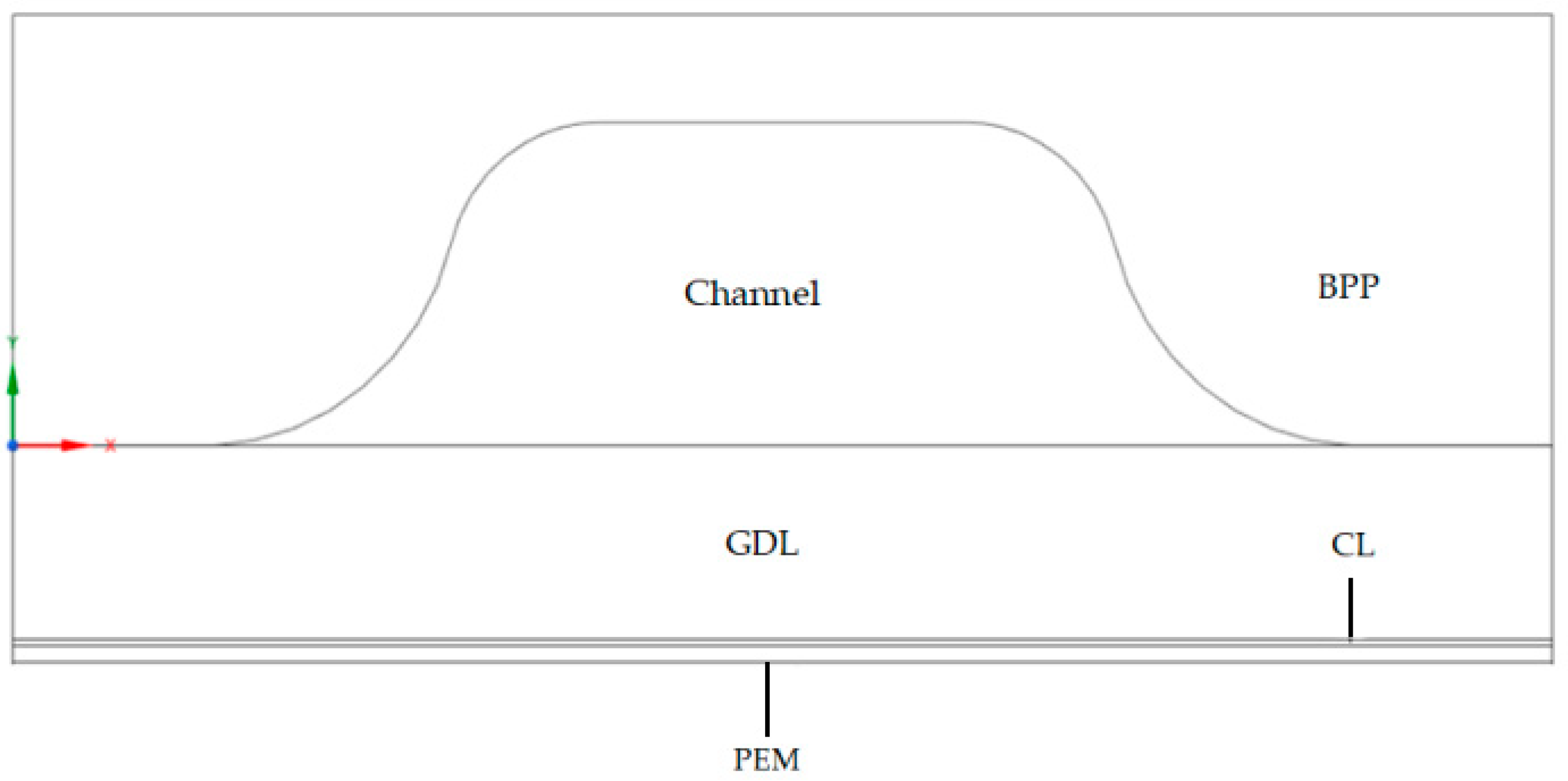
2.1.1. The FEA Model Considering of GDL Compression
2.1.2. The Electrochemical Performance Model of PEMFC
2.2. The Gas Distribution Model Based on Porous Media Theory
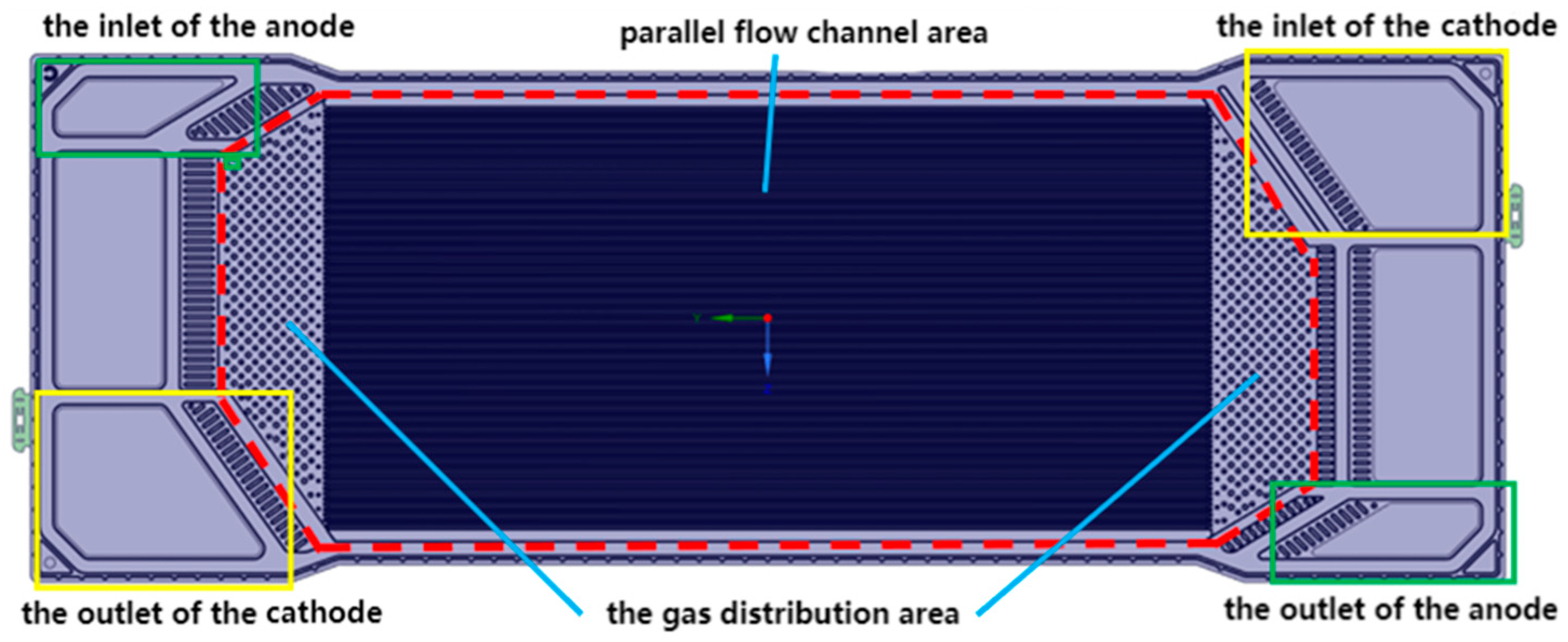
2.2.1. The Gas Distribution Model of Single Fuel Cell
2.2.2. The Gas Distribution Model of Fuel Cell Stack
3. Optimization and Validation of the Electrochemical Performance Model
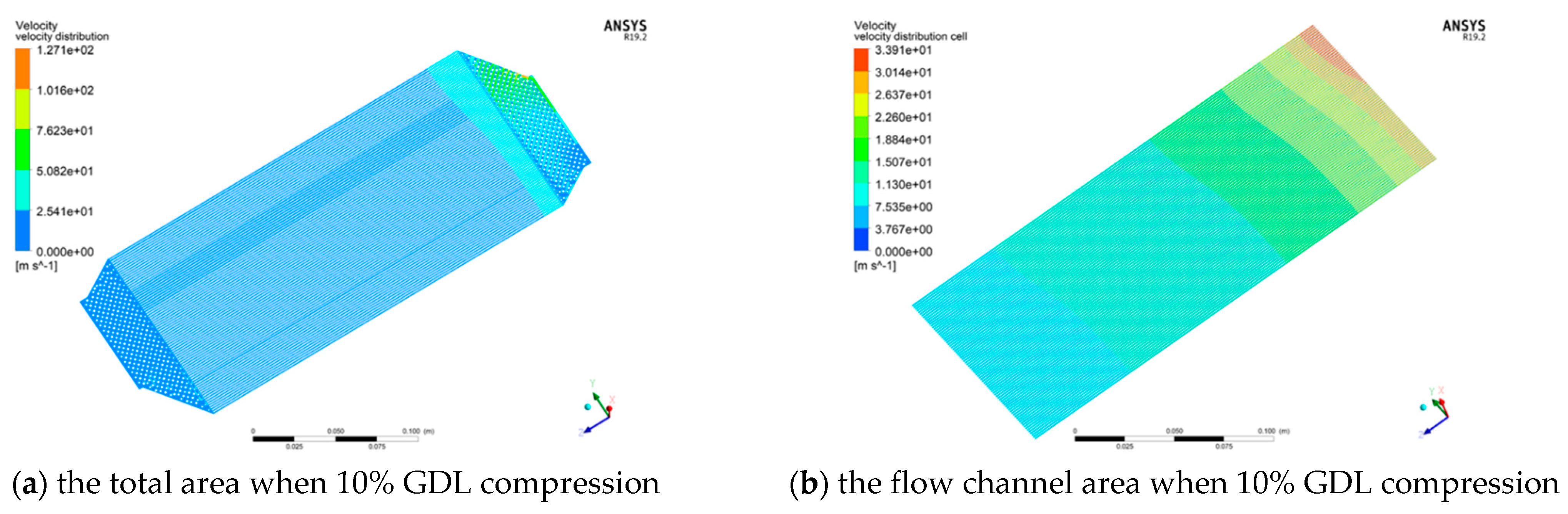
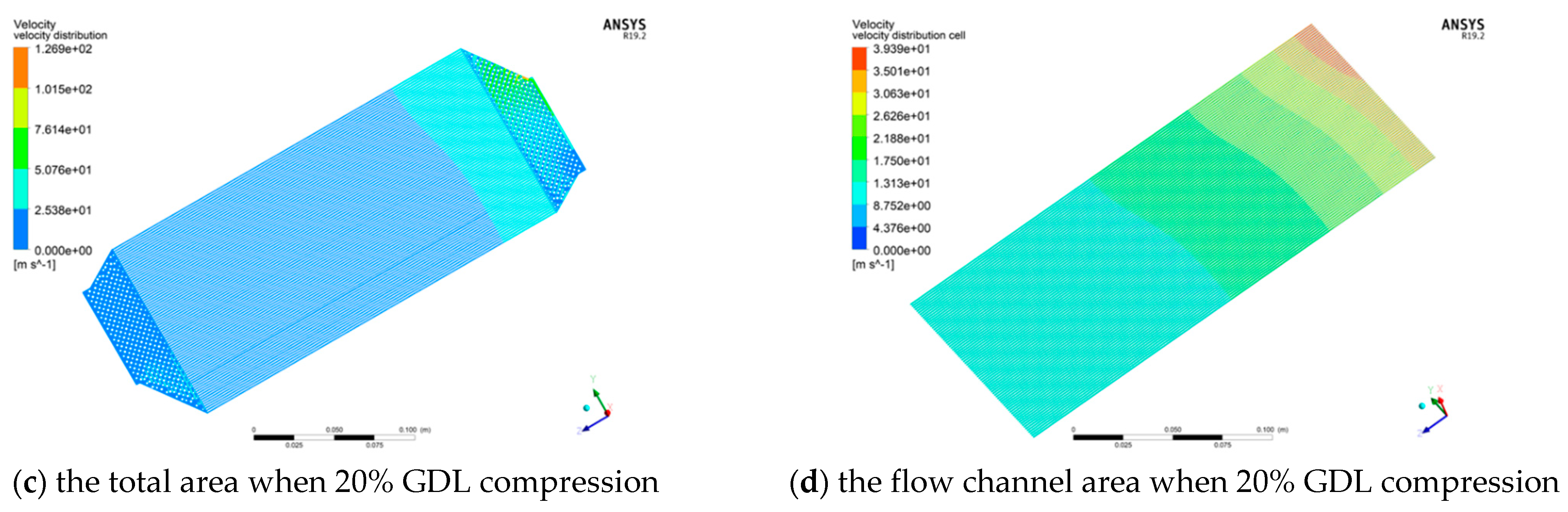
3.1. The Analysis of Gas Distribution in a Single Fuel Cell
3.2. The Gas Distribution of Fuel Cell Stack
3.3. The Optimized Electrochemical Performance Model and Validation
4. Conclusions
- (1)
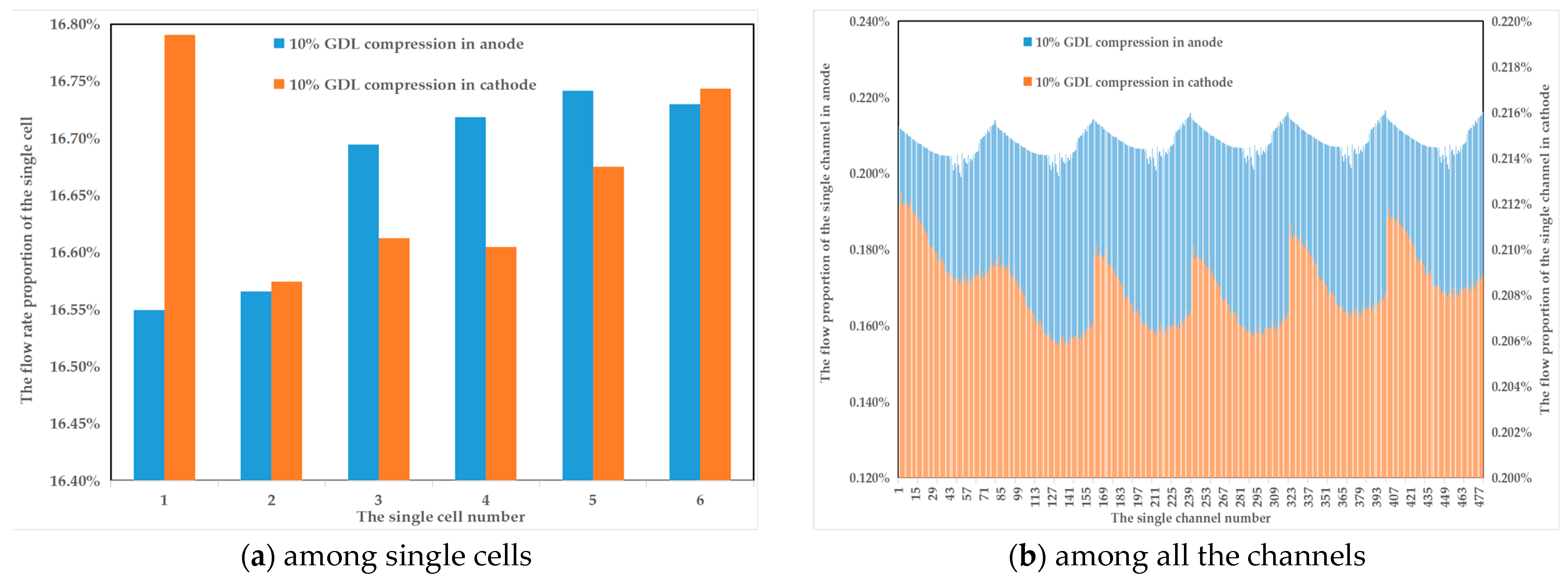
- The gas flow distribution in the single-cell anode flow field exhibits an overall trend where the flow rate is higher near both sides and lower in the middle. On the other hand, in the cathode flow field, the flow rate is higher near the inlet side;
- (2)
- When the clamping force increases, the gas distribution consistency of the anode flow field is slightly improved;
- (3)
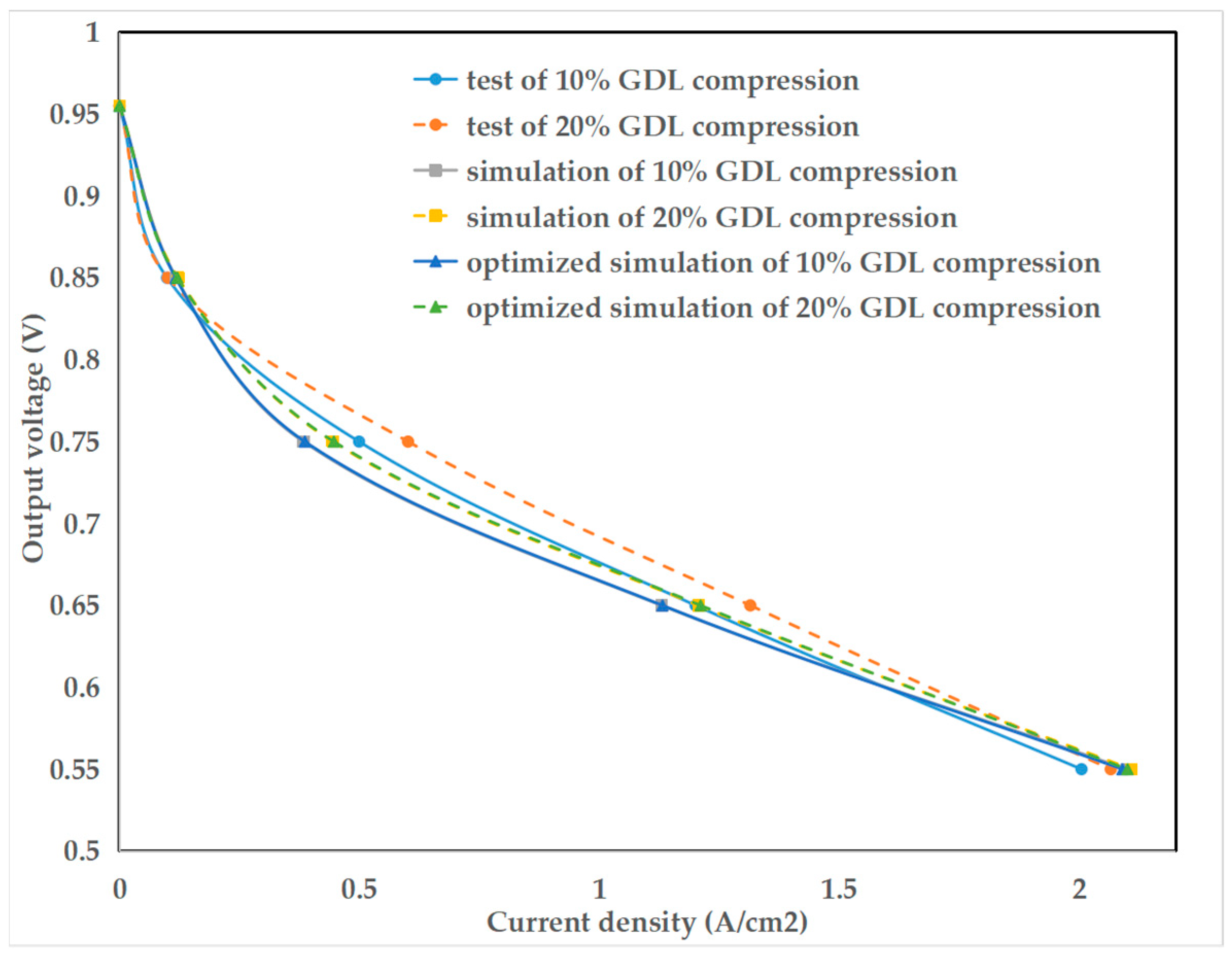
- The results of the stack performance experiment and simulation show that the output performance of PEMFC can be improved by increasing the clamping force appropriately;
- (4)
- Compared to the performance model without considering gas distribution, the simulation results obtained from the performance model considering gas distribution exhibit greater consistency with the test results, resulting in higher accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton Exchange Membrane Fuel Cell |
| GDL | Gas Distribution Layer |
| FEA | Finite Element Analysis |
| CFD | Computational Fluid Dynamics |
| PEM | Proton Exchange Membrane |
| UDF | User Defined Function |
| BPP | Bipolar Plate |
| CL | Catalyst Layer |
References
- Pramuanjaroenkij, A.; Kaka, S. The fuel cell electric vehicles: The highlight review. Int. J. Hydrog. Energy 2023, 48, 9401–9425. [Google Scholar] [CrossRef]
- Mancino, A.; Menale, C.; Vellucci, F. PEM Fuel Cell Applications in Road Transport. Energies 2023, 16, 6129. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. Learning-based model predictive energy management for fuel cell hybrid electric bus with health-aware control. Appl. Energy 2024, 355, 122228. [Google Scholar] [CrossRef]
- Dirkes, S.; Leidig, J.; Fisch, P.; Pischinger, S. Prescriptive Lifetime Management for PEM fuel cell systems in transportation applications, Part I: State of the art and conceptual design. Energy Convers. Manag. 2023, 277, 116598. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. A novel health-aware deep reinforcement learning energy management for fuel cell bus incorporating offline high-quality experience. Energy 2023, 282, 128928. [Google Scholar] [CrossRef]
- Tang, A.; Yang, Y.; Yu, Q.; Zhang, Z.; Yang, L. A Review of Life Prediction Methods for PEMFCs in Electric Vehicles. Sustainability 2022, 14, 9842. [Google Scholar] [CrossRef]
- Carcadea, E.; Ismail, M.S.; Ingham, D.B.; Patularu, L.; Varlam, M. Effects of geometrical dimensions of flow channels of a large-active-area PEM fuel cell: A CFD study. Int. J. Hydrog. Energy 2020, 46, 13572–13582. [Google Scholar] [CrossRef]
- Jia, C.; Li, K.; He, H.; Zhou, J.; Li, J.; Wei, Z. Health-aware energy management strategy for fuel cell hybrid bus considering air-conditioning control based on TD3 algorithm. Energy 2023, 283, 128462. [Google Scholar] [CrossRef]
- Zhang, G.; Qu, Z.; Wang, Y. Full-scale three-dimensional simulation of air-cooled proton exchange membrane fuel cell stack: Temperature spatial variation and comprehensive validation. Energy Convers. Manag. 2022, 270, 116211. [Google Scholar] [CrossRef]
- Atyabi, S.A.; Afshari, E.; Wongwises, S.; Yan, W.-M.; Hadjadj, A.; Shadloo, M.S. Effects of assembly pressure on PEM fuel cell performance by taking into accounts electrical and thermal contact resistances. Energy 2019, 179, 490–501. [Google Scholar] [CrossRef]
- Taş, M.; Elden, G. Three-dimensional and anisotropic numerical analysis of a PEM fuel cell. Int. J. Hydrog. Energy 2022, 47, 19758–19771. [Google Scholar] [CrossRef]
- Chen, B.; Deng, Q.; Yang, G.; Zhou, Y.; Chen, W.; Cai, Y.; Tu, Z. Numerical study on heat transfer characteristics and performance evaluation of PEMFC based on multiphase electrochemical model coupled with cooling channel. Energy 2023, 285, 128933. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Li, K.; Zhang, X.; Zhang, C.; Zhang, T. A Multi-Field Coupled PEMFC Model with Force-Temperature-Humidity and Experimental Validation for High Electrochemical Performance Design. Sustainability 2023, 15, 12436. [Google Scholar] [CrossRef]
- Shi, L.; Xu, S.; Liu, J. Influences of assembly pressure and flow channel size on performances of proton exchange membrane fuel cells based on a multi-model. Int. J. Hydrog. Energy 2022, 47, 7902–7914. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, X. A numerical study of flow crossover between adjacent flow channels in a proton exchange membrane fuel cell with serpentine flow field. J. Power Sources 2008, 185, 985–992. [Google Scholar] [CrossRef]
- Yan, X.; Lin, C.; Zheng, Z.; Chen, J.; Wei, G.; Zhang, J. Effect of clamping pressure on liquid-cooled PEMFC stack performance considering inhomogeneous gas diffusion layer compression. Appl. Energy 2020, 258, 114073. [Google Scholar] [CrossRef]
- Yong, Z.; Shirong, H.; Xiaohui, J.; Yuntao, Y.; Mu, X.; Xi, Y. Performance study on a large-scale proton exchange membrane fuel cell with cooling. Int. J. Hydrog. Energy 2022, 47, 10381–10394. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, X.; Zhang, Y.; Jiao, K.; Du, Q.; Hao, D. Effects of U-type and Z-type configurations on proton exchange membrane fuel cell stack performances considering non-uniform flow distribution phenomena. Int. J. Green Energy 2022, 19, 1160–1169. [Google Scholar] [CrossRef]
- Yong, Z.; Shirong, H.; Xiaohui, J.; Yuntao, Y.; Mu, X.; Xi, Y. Characteristics of proton exchange membrane fuel cell considering ‘dot matrix’ gas distribution zones and waveform staggered flow field with cooling channels. Energy Convers. Manag. 2022, 267, 115881. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Jiang, X.H. Three-dimensional multi-phase simulation of different flow fields with cooling channel in proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2022, 47, 37929–37944. [Google Scholar] [CrossRef]
- Yu, Y.; Zhan, Z.; He, L. Effects of Distribution Zone Design on Flow Uniformity and Pressure Drop in PEMFC. J. Electrochem. Soc. 2021, 9, 168. [Google Scholar] [CrossRef]
- Jeon, D.H.; Greenway, S.; Shimpalee, S.; Zee, J.W.V. The effect of serpentine flow-field designs on PEM fuel cell performance. Int. J. Hydrog. Energy 2008, 33, 1052–1066. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K.; Shi, M. A novel energy management strategy for hybrid electric bus with fuel cell health and battery thermal-and health-constrained awareness. Energy 2023, 271, 127105. [Google Scholar] [CrossRef]
- Son, J.; Um, S.; Kim, Y.-B. Numerical analysis of the effect of anisotropic gas diffusion layer permeability on polymer electrolyte membrane fuel cell performance with various channel types. Fuel 2021, 289, 119888. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, Z. Optimization of serpentine flow field in proton-exchange membrane fuel cell under the effects of external factors—ScienceDirect. Alex. Eng. J. 2020, 60, 421–433. [Google Scholar] [CrossRef]
- Scholta, J.; Escher, G.; Zhang, W. Investigation on the influence of channel geometries on PEMFC performance. J. Power Sources 2006, 155, 66–71. [Google Scholar] [CrossRef]
- Hu, H.; Xu, X.; Mei, N.; Li, C. Multi-angle study of the effects of different wave flow field plates on fuel cell performance. Int. J. Mod. Phys. B Condens. Matter Phys. B Stat. Phys. Appl. Phys. 2021, 35, 2150062. [Google Scholar] [CrossRef]
- Mohammedi, A.; Sahli, Y.; Ben Moussa, H. 3D investigation of the channel cross-section configuration effect on the power delivered by PEMFCs with straight channels. Fuel 2020, 263, 116713. [Google Scholar] [CrossRef]
- Yin, R.-J.; Zeng, W.-C.; Bai, F.; Chen, L.; Tao, W.-Q. Study on the effects of manifold structure on the gas flow distribution uniformity of anode of PEMFC stack with 140-cell. Renew. Energy 2024, 221, 119693. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, X.; Zhang, X. In Non-uniformity Analysis of Parameter Distribution in a 7-channel Serpentine Flow Field Proton Exchange Membrane Fuel Cell. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–5. [Google Scholar]
- Yang, Z.; Jiao, K.; Liu, Z.; Yin, Y.; Du, Q. Investigation of performance heterogeneity of PEMFC stack based on 1+1D and flow distribution models. Energy Convers. Manag. 2020, 207, 112502. [Google Scholar] [CrossRef]
- Molaeimanesh, G.R.; Googarchin, H.S.; Moqaddam, A.Q. Lattice Boltzmann simulation of proton exchange membrane fuel cells—A review on opportunities and challenges. Int. J. Hydrog. Energy 2016, 41, 22221–22245. [Google Scholar] [CrossRef]
- Jiao, K.; Park, J.; Li, X. Experimental investigations on liquid water removal from the gas diffusion layer by reactant flow in a PEM fuel cell. Appl. Energy 2010, 87, 2770–2777. [Google Scholar] [CrossRef]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, Z.; Liu, Z.; Du, W.; Sun, Y.; Deng, C. Parameter analysis of flow distribution characteristics of proton exchange membrane fuel cell stack. Zhongnan Daxue Xuebao (Ziran Kexue Ban) J. Cent. South Univ. (Sci. Technol.) 2022, 53, 4627–4636. [Google Scholar]







| Dimensions | Units | Values |
|---|---|---|
| BPP height | mm | 0.4 |
| BPP width | mm | 1.508 |
| GDL height | mm | 0.18 |
| Anode CL height | mm | 0.006 |
| Cathode CL height | mm | 0.008 |
| PEM height | mm | 0.016 |
| Channel height | mm | 0.3 |
| Channel length | mm | 250 |
| Channel width (top) | mm | 0.359 |
| Channel width (bottom) | mm | 1.149 |
| Channel | mm | 0.15 |
| Material Properties | BPP | GDL | CL | PEM |
|---|---|---|---|---|
| Elastic modulus (103 MPa) | 200 | 8.92 | 164.6 | 0.446 |
| Poisson’s ratio | 0.3 | 0.31 | 0.396 | 0.25 |
| Thermal expansion coefficient (10−6 K−1) | 17.3 | 8 | 8.93 | 20 |
| Thermal conductivity (W m−1 K−1) | 15.1 | 1.869 | 73 | 0.033 |
| Parameters | Value |
|---|---|
| Anode inlet pressure (kPa) | 150 |
| Cathode inlet pressure (kPa) | 170 |
| Anode stoichiometric coefficient | 1.5 |
| Cathode stoichiometric coefficient | 2 |
| Anode inlet humidity (%) | 50 |
| Cathode inlet humidity (%) | 50 |
| Working temperature (°C) | 80 |
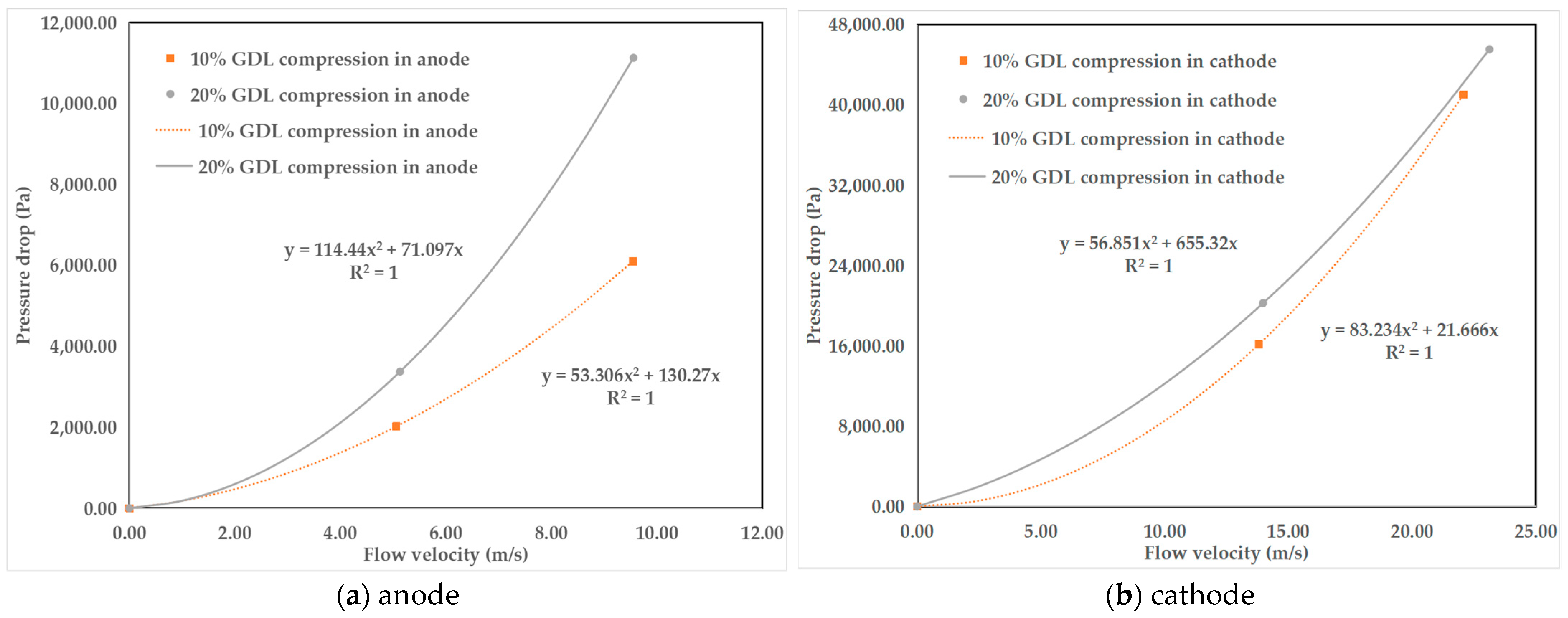
| Flow Field | GDL Compression Rate | Inertial Resistance Coefficient | Viscous Resistance Coefficient |
|---|---|---|---|
| Anode | 10% | 2.37 × 103 | 1.21 × 107 |
| 20% | 3.97 × 103 | 9.48 × 106 | |
| Cathode | 10% | 2.89 × 103 | 2.89 × 106 |
| 20% | 1.97 × 103 | 8.74 × 107 |
| Flow Field | Compression | Inertial Resistance Coefficient | Viscous Resistance Coefficient |
|---|---|---|---|
| Anode | 10% | 1.04 × 104 | 3.09 × 108 |
| 20% | 2.07 × 104 | 2.86 × 108 | |
| Cathode | 10% | 2.98 × 103 | 5.10 × 108 |
| 20% | 9.40 × 102 | 8.01 × 108 |
| The Compression of GDL | Voltage (V) | Current Density (A/cm2) | |
|---|---|---|---|
| Test | 10% | 0.955 | 0 |
| 0.85 | 0.099 | ||
| 0.75 | 0.499 | ||
| 0.65 | 1.200 | ||
| 0.55 | 2.004 | ||
| 20% | 0.955 | 0 | |
| 0.85 | 0.101 | ||
| 0.75 | 0.601 | ||
| 0.65 | 1.314 | ||
| 0.55 | 2.065 | ||
| Simulation | 10% | 0.955 | 0 |
| 0.85 | 0.118 | ||
| 0.75 | 0.383 | ||
| 0.65 | 1.129 | ||
| 0.55 | 2.098 | ||
| 20% | 0.955 | 0 | |
| 0.85 | 0.122 | ||
| 0.75 | 0.444 | ||
| 0.65 | 1.206 | ||
| 0.55 | 2.108 | ||
| Optimized simulation | 10% | 0.955 | 0 |
| 0.85 | 0.117 | ||
| 0.75 | 0.386 | ||
| 0.65 | 1.131 | ||
| 0.55 | 2.090 | ||
| 20% | 0.955 | 0 | |
| 0.85 | 0.121 | ||
| 0.75 | 0.447 | ||
| 0.65 | 1.211 | ||
| 0.55 | 2.100 |
| Compression | Single Fuel Cell Model | Optimized Model |
|---|---|---|
| 10% | 0.9963 | 0.9966 |
| 20% | 0.9946 | 0.9950 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Quan, C.; Wu, S.; Zhang, T.; Zhang, J. An Electrochemical Performance Model Considering of Non-Uniform Gas Distribution Based on Porous Media Method in PEMFC Stack. Sustainability 2024, 16, 587. https://doi.org/10.3390/su16020587
Zhang Z, Quan C, Wu S, Zhang T, Zhang J. An Electrochemical Performance Model Considering of Non-Uniform Gas Distribution Based on Porous Media Method in PEMFC Stack. Sustainability. 2024; 16(2):587. https://doi.org/10.3390/su16020587
Chicago/Turabian StyleZhang, Zhiming, Chenfu Quan, Sai Wu, Tong Zhang, and Jinming Zhang. 2024. "An Electrochemical Performance Model Considering of Non-Uniform Gas Distribution Based on Porous Media Method in PEMFC Stack" Sustainability 16, no. 2: 587. https://doi.org/10.3390/su16020587
APA StyleZhang, Z., Quan, C., Wu, S., Zhang, T., & Zhang, J. (2024). An Electrochemical Performance Model Considering of Non-Uniform Gas Distribution Based on Porous Media Method in PEMFC Stack. Sustainability, 16(2), 587. https://doi.org/10.3390/su16020587






