Assessing Forest Conservation for Finland: An ARDL-Based Evaluation
Abstract
:1. Introduction
- ➢
- RQ1: Is there a correlation between the expansion of the Finnish economy and the growth of forested areas?
- ➢
- RQ2: Does the use of electricity generated from renewable energy sources impact deforestation practices in Finland?
2. Literature Review
2.1. ARDL Technique Application and Studies in Finland
2.2. Impact of Electricity Generation on Forest Cover
2.3. Role of Renewable Energy Consumption in Deforestation
2.4. Economic Growth and Deforestation
2.5. Urbanization, Trade, and Deforestation
2.6. Political, Institutional, and Governance Structures and Deforestation
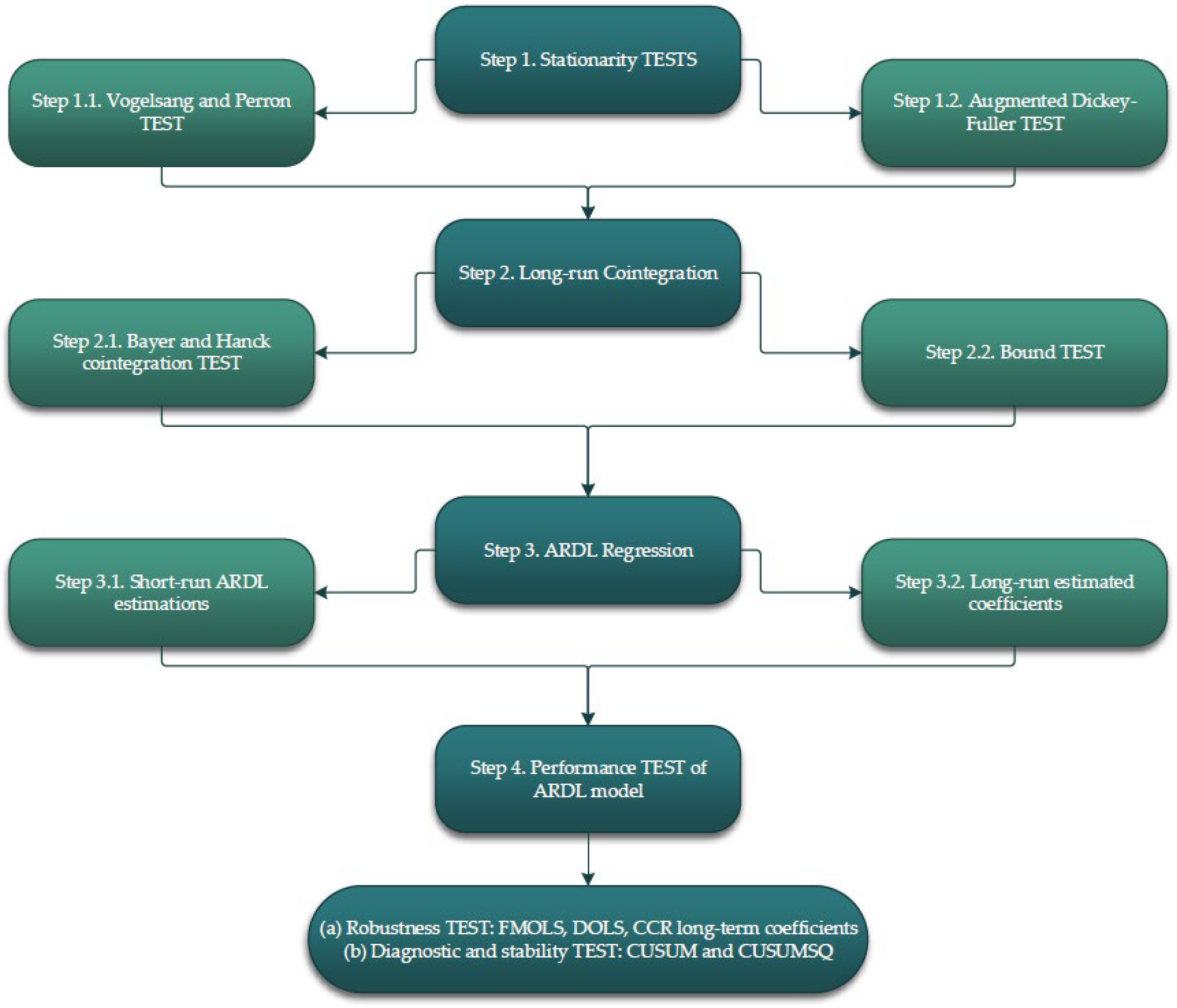
3. Materials and Methods
3.1. ARDL Methodology
3.2. Data Sources
4. Results
4.1. The Overall Trend of FAG and Other Factors in Finland
4.2. Stationarity Analysis and Lag Selection for the VAR Model
4.3. Analysis of Cointegration and Long-Term Effects for the ARDL Model
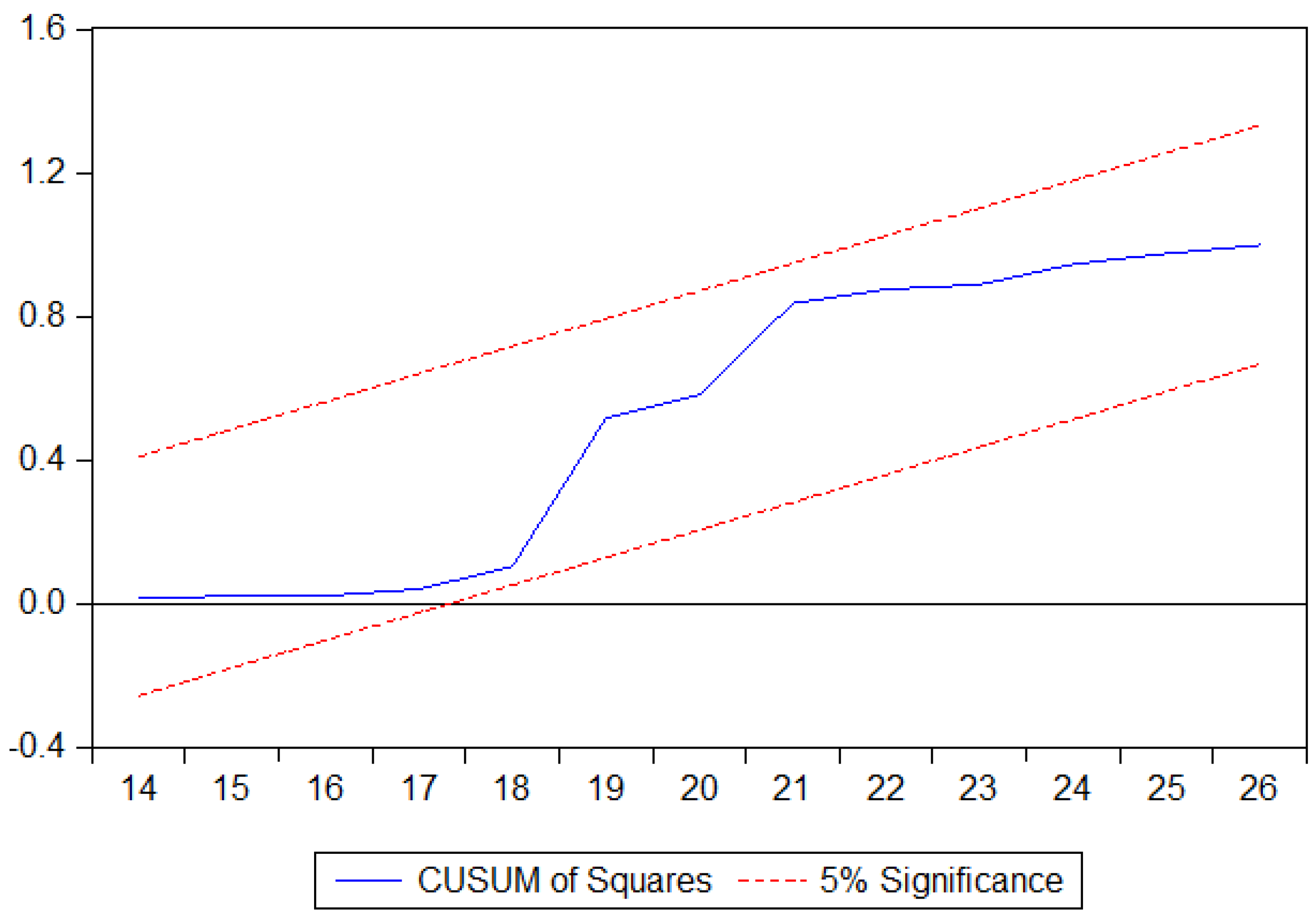
4.4. Evaluation of Model Assumptions and Diagnostic Analysis
5. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARDL | Autoregressive Distributed Lag |
| ECM | Error correction model |
| GDP | Gross domestic product |
| GHG | Greenhouse gas |
| RENP | Renewable energy production |
| URB | Urbanization |
| FA | Forest area |
| FAG | Forest area growth |
| FMOLS | Fully Modified Ordinary Least Squares |
| DOLS | Dynamic Ordinary Least Squares |
| CCR | Canonical Cointegration Regression |
| CUSUM | Cumulative sum |
| CUSUMSQ | Cumulative sum of squares |
References
- Tanner, A.M.; Johnston, A.L. The Impact of Rural Electric Access on Deforestation Rates. World Dev. 2017, 94, 174–185. [Google Scholar] [CrossRef]
- Prochazka, P.; Abrham, J.; Cerveny, J.; Kobera, L.; Sanova, P.; Benes, D.; Fink, J.-M.; Jiraskova, E.; Primasova, S.; Soukupova, J.; et al. Understanding the Socio-Economic Causes of Deforestation: A Global Perspective. Front. For. Glob. Change 2023, 6, 1288365. [Google Scholar] [CrossRef]
- Belušić, D.; Fuentes-Franco, R.; Strandberg, G.; Jukimenko, A. Afforestation Reduces Cyclone Intensity and Precipitation Extremes over Europe. Environ. Res. Lett. 2019, 14, 074009. [Google Scholar] [CrossRef]
- Rădulescu, C.V.; Bran, F.; Ciuvăț, A.L.; Bodislav, D.A.; Buzoianu, O.C.; Ștefănescu, M.; Burlacu, S. Decoupling the Economic Development from Resource Consumption: Implications and Challenges in Assessing the Evolution of Forest Area in Romania. Land 2022, 11, 1097. [Google Scholar] [CrossRef]
- Majava, A.; Vadén, T.; Toivanen, T.; Järvensivu, P.; Lähde, V.; Eronen, J.T. Sectoral Low-Carbon Roadmaps and the Role of Forest Biomass in Finland’s Carbon Neutrality 2035 Target. Energy Strategy Rev. 2022, 41, 100836. [Google Scholar] [CrossRef]
- Triviño, M.; Potterf, M.; Tijerín, J.; Ruiz-Benito, P.; Burgas, D.; Eyvindson, K.; Blattert, C.; Mönkkönen, M.; Duflot, R. Enhancing Resilience of Boreal Forests Through Management Under Global Change: A Review. Curr. Landsc. Ecol. Rep. 2023, 8, 103–118. [Google Scholar] [CrossRef]
- Finnish Forests. Finland Is a Country That Lives off Its Forests—Culturally, Socially, and Economically. Available online: https://toolbox.finland.fi/wp-content/uploads/sites/2/2023/06/suomi-finland-narrative-packages-finnish-forests.pdf (accessed on 12 October 2023).
- European Parliament Sustainable Forestry in Finland. Available online: https://www.europarl.europa.eu/RegData/etudes/STUD/2016/578979/IPOL_STU(2016)578979_EN.pdf (accessed on 12 October 2023).
- Global Forest Watch. Available online: https://www.globalforestwatch.org/dashboards/global/ (accessed on 12 October 2023).
- França, L.C.D.J.; Júnior, F.W.A.; Jarochinski E Silva, C.S.; Monti, C.A.U.; Ferreira, T.C.; Santana, C.J.D.O.; Gomide, L.R. Forest Landscape Planning and Management: A State-of-the-Art Review. Trees For. People 2022, 8, 100275. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Matsumoto, K. The Effect of Forest Certification on Conservation and Sustainable Forest Management. J. Clean. Prod. 2022, 363, 132374. [Google Scholar] [CrossRef]
- Mönkkönen, M.; Aakala, T.; Burgas, D.; Duflot, R.; Eyvindson, K.; Kouki, J.; Laaksonen, T.; Punttila, P. More Wood but Less Biodiversity in Forests in Finland: A Historical Evaluation. Memo. Soc. Fauna Flora Fenn. 2022, 98, 1–11. [Google Scholar]
- Aakala, T.; Kulha, N.; Kuuluvainen, T. Human Impact on Forests in Early Twentieth Century Finland. Landsc. Ecol. 2023, 38, 2417–2431. [Google Scholar] [CrossRef]
- Murshed, M.; Ferdaus, J.; Rashid, S.; Tanha, M.M.; Islam, M.J. The Environmental Kuznets Curve Hypothesis for Deforestation in Bangladesh: An ARDL Analysis with Multiple Structural Breaks. Energ. Ecol. Environ. 2021, 6, 111–132. [Google Scholar] [CrossRef]
- Georgescu, I.; Kinnunen, J. The Role of Foreign Direct Investments, Urbanization, Productivity, and Energy Consumption in Finland’s Carbon Emissions: An ARDL Approach. Environ. Sci. Pollut. Res. 2023, 30, 87685–87694. [Google Scholar] [CrossRef]
- Cozma, A.-C.; Coroș, M.M.; Pop, A.M.; Gavrilescu, I.; Dinucă, N.C. Corruption, Deforestation, and Tourism—Europe Case Study. Heliyon 2023, 9, e19075. [Google Scholar] [CrossRef] [PubMed]
- Ditta, A.; Asim, H.; Rehman, H.U. An Econometric Analysis of Exigent Determinants of Trade Balance in Finland: An Autoregressive Distributed Lag (ARDL) Approach. Rev. Appl. Manag. Soc. Sci. 2020, 3, 347–360. [Google Scholar] [CrossRef]
- Ponce, P.; Del Río-Rama, M.D.L.C.; Álvarez-García, J.; Oliveira, C. Forest Conservation and Renewable Energy Consumption: An ARDL Approach. Forests 2021, 12, 255. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahbaz, M.; Qasim, A.; Long, W. The Linkages between Deforestation, Energy and Growth for Environmental Degradation in Pakistan. Ecol. Indic. 2015, 49, 95–103. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Ohiare, S. The Chinese Electricity Access Model for Rural Electrification: Approach, Experience and Lessons for Others. Energy Policy 2012, 49, 676–687. [Google Scholar] [CrossRef]
- Bakehe, N.P. L’accès à l’électricité: Une Solution Pour Réduire La Déforestation En Afrique? Afr. Dev. Rev. 2020, 32, 338–348. [Google Scholar] [CrossRef]
- Woldemedhin, D.G.; Assefa, E.; Seyoum, A. Forest Covers, Energy Use, and Economic Growth Nexus in the Tropics: A Case of Ethiopia. Trees For. People 2022, 8, 100266. [Google Scholar] [CrossRef]
- Nazir, M.S.; Bilal, M.; Sohail, H.M.; Liu, B.; Chen, W.; Iqbal, H.M.N. Impacts of Renewable Energy Atlas: Reaping the Benefits of Renewables and Biodiversity Threats. Int. J. Hydrog. Energy 2020, 45, 22113–22124. [Google Scholar] [CrossRef]
- Bakehe, N.P.; Hassan, R. The Effects of Access to Clean Fuels and Technologies for Cooking on Deforestation in Developing Countries. J. Knowl. Econ. 2023, 14, 2561–2577. [Google Scholar] [CrossRef]
- Acheampong, A.O.; Opoku, E.E.O. Energy Justice, Democracy and Deforestation. J. Environ. Manag. 2023, 341, 118012. [Google Scholar] [CrossRef]
- Omar Makame, M. Adoption of Improved Stoves and Deforestation in Zanzibar. Manag. Environ. Qual. Int. J. 2007, 18, 353–365. [Google Scholar] [CrossRef]
- Ajanaku, B.A.; Collins, A.R. Economic Growth and Deforestation in African Countries: Is the Environmental Kuznets Curve Hypothesis Applicable? For. Policy Econ. 2021, 129, 102488. [Google Scholar] [CrossRef]
- Caravaggio, N. A Global Empirical Re-Assessment of the Environmental Kuznets Curve for Deforestation. For. Policy Econ. 2020, 119, 102282. [Google Scholar] [CrossRef]
- Zambrano-Monserrate, M.A.; Carvajal-Lara, C.; Urgilés-Sanchez, R.; Ruano, M.A. Deforestation as an Indicator of Environmental Degradation: Analysis of Five European Countries. Ecol. Indic. 2018, 90, 1–8. [Google Scholar] [CrossRef]
- Tsiantikoudis, S.; Zafeiriou, E.; Kyriakopoulos, G.; Arabatzis, G. Revising the Environmental Kuznets Curve for Deforestation: An Empirical Study for Bulgaria. Sustainability 2019, 11, 4364. [Google Scholar] [CrossRef]
- Arcand, J.-L.; Guillaumont, P.; Jeanneney, S.G. Deforestation and the Real Exchange Rate. J. Dev. Econ. 2008, 86, 242–262. [Google Scholar] [CrossRef]
- Faria, W.R.; Almeida, A.N. Relationship between Openness to Trade and Deforestation: Empirical Evidence from the Brazilian Amazon. Ecol. Econ. 2016, 121, 85–97. [Google Scholar] [CrossRef]
- Nathaniel, S.P.; Bekun, F.V. Environmental Management amidst Energy Use, Urbanization, Trade Openness, and Deforestation: The Nigerian Experience. J. Public Aff. 2020, 20, e2037. [Google Scholar] [CrossRef]
- Yameogo, C.E.W. Globalization, Urbanization, and Deforestation Linkage in Burkina Faso. Environ. Sci. Pollut. Res. 2021, 28, 22011–22021. [Google Scholar] [CrossRef] [PubMed]
- Rydning Gaarder, A.; Vadlamannati, K.C. Does Democracy Guarantee (de)Forestation? An Empirical Analysis. Int. Area Stud. Rev. 2017, 20, 97–121. [Google Scholar] [CrossRef]
- Moreira-Dantas, I.R.; Söder, M. Global Deforestation Revisited: The Role of Weak Institutions. Land Use Policy 2022, 122, 106383. [Google Scholar] [CrossRef]
- Russo, E.; Foster-McGregor, N. Characterizing Growth Instability: New Evidence on Unit Roots and Structural Breaks in Countries’ Long Run Trajectories. J. Evol. Econ. 2022, 32, 713–756. [Google Scholar] [CrossRef]
- Lütkepohl, H.; Xu, F. The Role of the Log Transformation in Forecasting Economic Variables. Empir. Econ. 2012, 42, 619–638. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427. [Google Scholar] [CrossRef]
- Bayer, C.; Hanck, C. Combining Non-cointegration Tests. J. Time Ser. Anal. 2013, 34, 83–95. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica 1987, 55, 251. [Google Scholar] [CrossRef]
- Johansen, S. Statistical Analysis of Cointegration Vectors. J. Econ. Dyn. Control. 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Peter Boswijk, H. Testing for an Unstable Root in Conditional and Structural Error Correction Models. J. Econom. 1994, 63, 37–60. [Google Scholar] [CrossRef]
- Banerjee, A.; Dolado, J.; Mestre, R. Error-correction Mechanism Tests for Cointegration in a Single-equation Framework. J. Time Ser. Anal. 1998, 19, 267–283. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds Testing Approaches to the Analysis of Level Relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum Likelihood Estimation and Inference on Cointegration—With Applications to the Demand for Money. Oxf. Bull. Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Samargandi, N.; Fidrmuc, J.; Ghosh, S. Is the Relationship Between Financial Development and Economic Growth Monotonic? Evidence from a Sample of Middle-Income Countries. World Dev. 2015, 68, 66–81. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Hansen, B.E. Statistical Inference in Instrumental Variables Regression with I(1) Processes. Rev. Econ. Stud. 1990, 57, 99. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. A Simple Estimator of Cointegrating Vectors in Higher Order Integrated Systems. Econometrica 1993, 61, 783. [Google Scholar] [CrossRef]
- Park, J.Y. Canonical Cointegrating Regressions. Econometrica 1992, 60, 119. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for Testing the Constancy of Regression Relationships Over Time. J. R. Stat. Soc. Ser. B Methodol. 1975, 37, 149–163. [Google Scholar] [CrossRef]
- Pesaran, M.H. An Autoregressive Distributed-Lag Modelling Approach to Cointegration Analysis. In Econometrics and Economic Theory in the 20th Century: The Ragnar Frisch Centennial Symposium; Strøm, S., Ed.; Cambridge University Press: New York, NY, USA, 1998; pp. 371–413. ISBN 978-0-521-63323-9. [Google Scholar]
- Ceccherini, G.; Duveiller, G.; Grassi, G.; Lemoine, G.; Avitabile, V.; Pilli, R.; Cescatti, A. Abrupt Increase in Harvested Forest Area over Europe after 2015. Nature 2020, 583, 72–77. [Google Scholar] [CrossRef]
- Vogelsang, T.J.; Perron, P. Additional Tests for a Unit Root Allowing for a Break in the Trend Function at an Unknown Time. Int. Econ. Rev. 1998, 39, 1073. [Google Scholar] [CrossRef]
- Dogan, E.; Ozturk, I. The Influence of Renewable and Non-Renewable Energy Consumption and Real Income on CO2 Emissions in the USA: Evidence from Structural Break Tests. Environ. Sci. Pollut. Res. 2017, 24, 10846–10854. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.S.; Law, S.H.; Zannah, T.I. Dynamic Impact of Urbanization, Economic Growth, Energy Consumption, and Trade Openness on CO2 Emissions in Nigeria. Environ. Sci. Pollut. Res. 2016, 23, 12435–12443. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y. Transitioning to Sustainable Energy: Opportunities, Challenges, and the Potential of Blockchain Technology. Front. Energy Res. 2023, 11, 1258044. [Google Scholar] [CrossRef]
- Chipangamate, N.S.; Nwaila, G.T. Assessment of Challenges and Strategies for Driving Energy Transitions in Emerging Markets: A Socio-Technological Systems Perspective. Energy Geosci. 2024, 5, 100257. [Google Scholar] [CrossRef]
- Farghali, M.; Osman, A.I.; Chen, Z.; Abdelhaleem, A.; Ihara, I.; Mohamed, I.M.A.; Yap, P.-S.; Rooney, D.W. Social, Environmental, and Economic Consequences of Integrating Renewable Energies in the Electricity Sector: A Review. Environ. Chem. Lett. 2023, 21, 1381–1418. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]



| Factor | Abbreviation | Measurement Unit | Data Origin |
|---|---|---|---|
| Forest area | FA | % of land area | World Bank |
| Electricity production from renewable sources, excluding hydroelectric | RENB | % of total | World Bank |
| Gross domestic product | GDP | Constant 2015 USD | World Bank |
| Urbanization | URB | % | World Bank |
| FAG | GDP | RENB | URB | |
|---|---|---|---|---|
| Mean | −2.23 | 10.57 | 2.59 | 4.41 |
| Median | −1.92 | 10.65 | 2.55 | 4.41 |
| Maximum | 4.60 | 10.75 | 2.99 | 4.45 |
| Minimum | −5.97 | 10.23 | 2.14 | 4.38 |
| Std. Dev. | 1.92 | 0.17 | 0.26 | 0.02 |
| Skewness | 0.71 | −0.82 | −0.01 | −0.10 |
| Kurtosis | 7.34 | 2.20 | 1.95 | 1.85 |
| Jarque–Bera | 26.17 | 4.17 | 1.36 | 1.68 |
| Probability | 0.00 | 0.12 | 0.50 | 0.42 |
| Variable | Level | First Difference | Order of Integration |
|---|---|---|---|
| t-Statistics | t-Statistics | ||
| FAG | −2.30 (0.02) | −1.93 (0.05) | I(0) |
| GDP | 2.15 (0.99) | −3.49 (0.00) | I(1) |
| RENP | 1.35 (0.95) | −5.71 (0.00) | I(1) |
| URB | 1.70 (0.97) | −1.88 (0.05) | I(1) |
| Variable | t-Statistics | Break Year | Order of Integration | ||
|---|---|---|---|---|---|
| Level | First Difference | Level | First Difference | ||
| FAG | −4.96 (0.00) | −7.02 (0.00) | 2000 | 2021 | I(0) |
| GDP | −3.72 (0.26) | −6.98 (0.00) | 1996 | 2008 | I(1) |
| RENP | −1.99 (0.98) | −6.86 (0.00) | 2010 | 1998 | I(1) |
| URB | −8.73 (0.00) | −4.87 (0.01) | 2009 | 2013 | I(1) |
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 104.56 | NA | 1.25 × | −5.14 | −8.94 | −9.09 |
| 1 | 195.41 | 140.39 | 1.44 × | −15.94 | −14.95 | −15.71 |
| 2 | 217.13 | 25.66 | 1.02 × | −16.46 | −14.68 | −16.04 |
| 3 | 255.75 | 31.60 * | 2.15 × * | −18.52 * | −15.94 * | −17.91 * |
| Test Statistic | Value | K (Number of Regressors) |
|---|---|---|
| F-statistic | 6.29 | 3 |
| Critical value bounds | ||
| Significance | I(0) | I(1) |
| 10% | 2.67 | 3.58 |
| 5% | 3.27 | 4.30 |
| 1% | 4.61 | 5.96 |
| Fisher Statistics EG-JOH-BO-BDM | Fisher Statistics EG-JOH | EG-JOH-BO-BDM Fisher Critical Value at 5% Level | EG-JOH Fisher Critical Value at 5% Level | Inference |
|---|---|---|---|---|
| 111.63 | 56.35 | 20.48 | 10.63 | Cointegration |
| Variable | Coefficient | t-Statistics | Prob. |
|---|---|---|---|
| GDP | −4.94 | −7.81 | 0.00 |
| URB | 8.68 | 0.69 | 0.49 |
| RENP | 1.70 | 2.23 | 0.04 |
| C | 7.17 | 0.14 | 0.84 |
| Variable | Coefficient | t-Statistics | Prob. |
|---|---|---|---|
| D(GDP) | 0.60 | 0.31 | 0.754 |
| D(GDP(−1)) | 1.01 | 0.55 | 0.587 |
| D(GDP(−2)) | 3.14 | 1.91 | 0.076 |
| D(URB) | 141.18 | 5.57 | 0.001 |
| D(RENP) | 1.02 | 1.89 | 0.081 |
| CointEq(−1) | −1.46 | −6.41 | 0.000 |
| R-squared | 0.76 | ||
| Adjusted R-squared | 0.69 |
| Variable | FMOLS | DOLS | CCR |
|---|---|---|---|
| GDP | −4.80 *** (−5.93) | −2.95 *** (−4.29) | −4.72 *** (−0.24) |
| URB | 6.54 (0.49) | −28.11 * (−2.21) | 3.48 (0.28) |
| RENP | 1.38 * (1.70) | 4.04 *** (3.17) | 1.58 * (1.71) |
| C | 16.29 (0.32) | 142.21 ** (2.72) | 28.37 (0.58) |
| Test | Decision Statistics (p-Value) | |
|---|---|---|
| Serial correlation | There is no serial correlation in the residuals | 1.59 (0.25) |
| Heteroscedasticity | There is no autoregressive conditional heteroscedasticity | 0.07 (0.78) |
| Normal distribution | Normal distribution | 0.01 (0.99) |
| Ramset RESET | The absence of model misspecification | 3.54 (0.06) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgescu, I.; Kinnunen, J.; Nica, I. Assessing Forest Conservation for Finland: An ARDL-Based Evaluation. Sustainability 2024, 16, 612. https://doi.org/10.3390/su16020612
Georgescu I, Kinnunen J, Nica I. Assessing Forest Conservation for Finland: An ARDL-Based Evaluation. Sustainability. 2024; 16(2):612. https://doi.org/10.3390/su16020612
Chicago/Turabian StyleGeorgescu, Irina, Jani Kinnunen, and Ionuț Nica. 2024. "Assessing Forest Conservation for Finland: An ARDL-Based Evaluation" Sustainability 16, no. 2: 612. https://doi.org/10.3390/su16020612
APA StyleGeorgescu, I., Kinnunen, J., & Nica, I. (2024). Assessing Forest Conservation for Finland: An ARDL-Based Evaluation. Sustainability, 16(2), 612. https://doi.org/10.3390/su16020612








