Greenhouse Gas Emissions Performance of Electric, Hydrogen and Fossil-Fuelled Freight Trucks with Uncertainty Estimates Using a Probabilistic Life-Cycle Assessment (pLCA)
Abstract
:1. Introduction
1.1. Life-Cycle Analysis
1.2. Background and Purpose of This Study
2. Materials and Methods
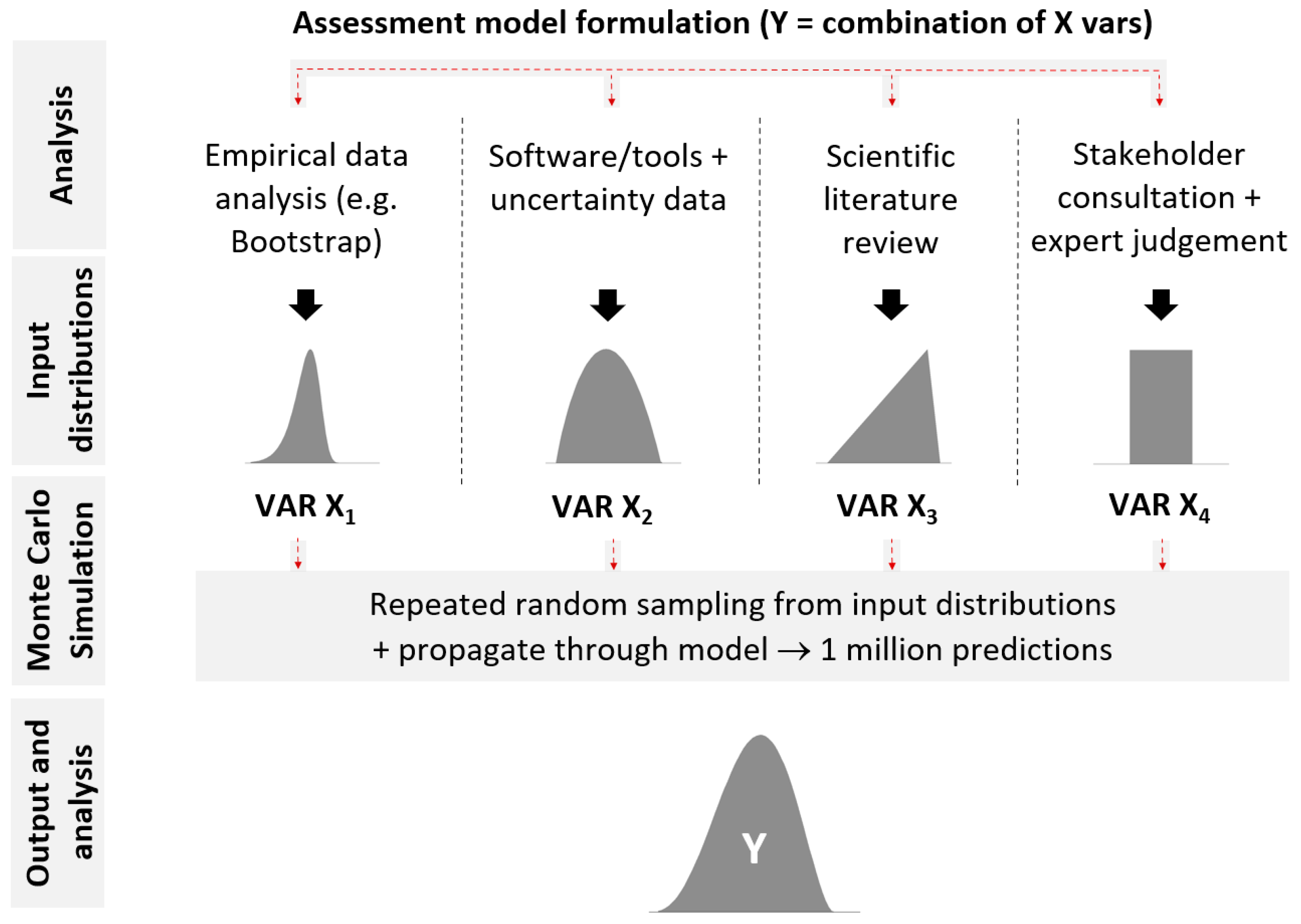
2.1. Probabilistic LCA (pLCA)
2.2. Model Definition
2.3. Developing Input Distributions
| eICEV = evehicle,ICEV + einfra,ICEV + efuel,ICEV + eroad,ICEV + edisposal,ICEV | (1) |
| evehicle,ICEV = wICEV φv,ICEV/MICEV | |
| eBEV = evehicle,BEV + einfra,BEV + efuel,BEV + eroad,BEV + edisposal,BEV | (2) |
| evehicle,BEV = ((MBEV − MBAT) φv,BEV + (ΓBAT φBAT θBAT))/MBEV | |
| einfra,BEV = ε σelec/(ηg ηb) | |
| efuel,BEV = ε ϕelec/ηb | |
| eroad,BEV = ε ωelec/(ηg ηb) | |
| eFCEV = evehicle,FCEV + einfra, FCEV + efuel,FCEV + eroad,FCEV + edisposal, FCEV | (3) |
| evehicle,FCEV = ((MFCEV − MBAT − MFCL) φv,FCEV + (ΓBAT φBAT θBAT) + (ΓFCL φFCL ρFCL))/MFCEV | |
| einfra,FCEV = H σH2,p/ηh | |
| efuel,FCEV = H ϕH2,p/ηh | |
| eroad,FCEV = H ωH2,p/ηr |
2.4. Scenario Definitions and Heavy-Duty Vehicle Classification
- Medium commercial (rigid) vehicles (MCV); GVM 3.5–12.0 t;
- Heavy commercial (rigid) vehicles (HCV); GVM 12.0–25.0 t;
- Articulated trucks (AT), gross vehicle mass; GVM > 25.0 t.
- The Recent Past Scenario (2019) reflects the Australian electricity mix and hydrogen production pathways in 2019. A mix of two hydrogen production pathways were considered: steam–methane reforming and green hydrogen production with electrolysis (Table 3).
- The Future Scenario (~2050) is a more decarbonised Australian scenario, loosely allocated to the year 2050, which assumes the Australian electricity generation mix and hydrogen-production pathways shown in Table 3. This assumption is in line and consistent with a similar pLCA study for passenger vehicles [17]. It is noted, however, that this scenario is not necessarily restricted to 2050. It would apply to any current situation where renewable low-carbon energy is used for the different life-cycle aspects. Examples are the use of solar panels to charge batteries or the use of grid electricity that is currently generated in Tasmania with almost 95% renewables [17].
3. Input Distributions
3.1. Lifetime Mileage and System Durability
- Alternative usage of the ageing truck (e.g., shifting to shorter-distance transport missions) may allow for a lower SOC and, therefore, longer battery durability. This may include the use of ageing trucks along freight corridors with a high density of fast-charging stations and therefore more regular (fast) charging opportunities, or different types of and shorter distance missions, both making a lower SOC acceptable.
- The use of shared and externally charged batteries (battery swapping) in either OEM or retrofitted long-distance truck operations may increase the battery durability (slow charging) and may also allow for a lower SOC, although a larger number of batteries (spare for charging) would be required in this setup, impacting life-cycle emissions.
- The secondary use of truck batteries in non-transport applications, in which the GHG emission impacts of battery production should at least partly be passed on to the non-transport application. In this case, one to two battery replacements should likely sufficiently account for the GHG emission impacts of battery production on transport emissions.
- BEV: 1.5 for MCV/HCV in 2019 and 1.0 in 2050;
- BEV: 4.0 for AT in 2019 and 2.5 in 2050;
- FCEV: 2.2 for MCV/HCV in 2019 and 1.2 in 2050;
- FCEV: 4.0 for AT in 2019 and 2.2 in 2050.
3.2. Mass of Vehicle, Battery and the Fuel-Cell System
3.3. Electricity Production, Distribution and Recharging Losses
3.4. Hydrogen Production, Distribution and Refuelling Losses
3.5. Future Improvements in LCA Input Variables
3.6. Truck Manufacturing
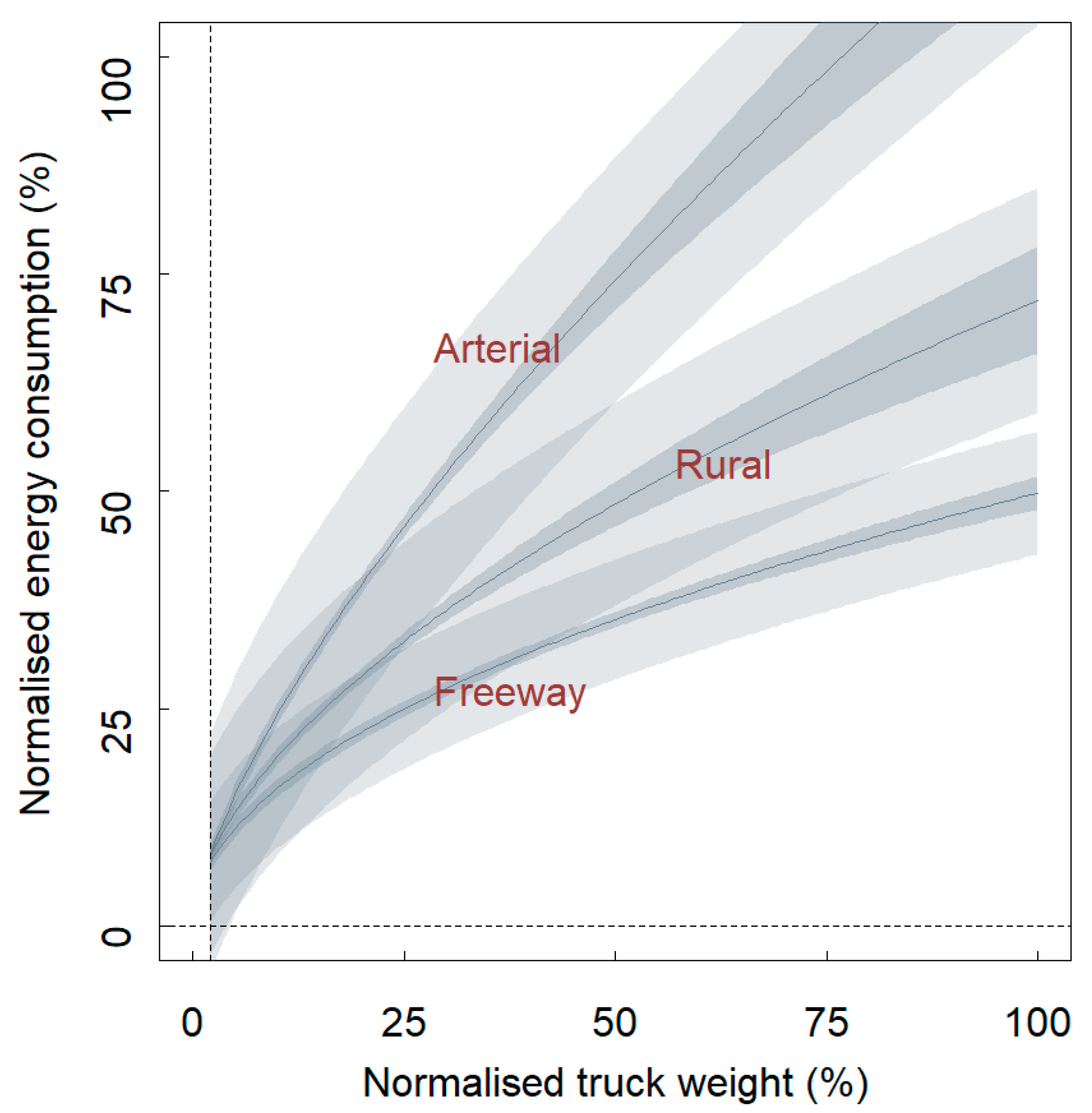
3.7. Operational Electricity Use, Fuel Consumption and Emissions (On-Road Driving)
- 70% and 15% VKT share of urban driving (30 km/h);
- 5% and 10% VKT share of rural driving (75 km/h);
- 25% and 75% VKT share of highway driving (100 km/h).
- Specifically, for compression-ignition (diesel) ICEVs, further technological “system approach” engine improvements are expected to lead to an overall 10–20% fuel efficiency improvement in 2050 (U: 0.80, 0.90). Measures to achieve this may include, but are not limited to, advanced systems for valve-train control, use of low-viscosity lubricants, variable compression ratios, re-use of waste heat and engine downsizing [49,77,78].
- BEV energy improvement is expected to be larger and is expected to occur sooner than that for FCEVs. One of these expected improvements is a significant increase in battery energy density, as was discussed in Section 3.2. It has been assumed in this study that this will largely translate into a range and power increase without affecting battery mass significantly. There are several potential improvements that will lead to significant efficiency improvements for BEVs, for instance, purpose design, in-wheel or wheel-hub electric motors rather than central engines, improved energy recuperation, decreased coasting resistance and the application of lightweight chassis components [50]. The expected improvement in energy efficiency for BEVs is assumed to be in the order of 20–30% in 2050 (U: 0.70, 0.80).
- Although some studies assume zero improvement for FCEVs [76], further improvement in the fuel-cell energy efficiency is expected from the current 50–60% to 65% in the near term and up to 70% in the long term [49,54,55]. This leads to an estimated improvement in energy efficiency for FCEVs of 15–25% in 2050 (U: 0.75, 0.85). It has been assumed in this study that this will largely translate into a range and power increase.
3.8. Truck Maintenance
3.9. Energy Infrastructure
3.10. Upstream Emissions (Fuel/Energy)
3.11. Vehicle Disposal and Recycling
4. Results and Discussion
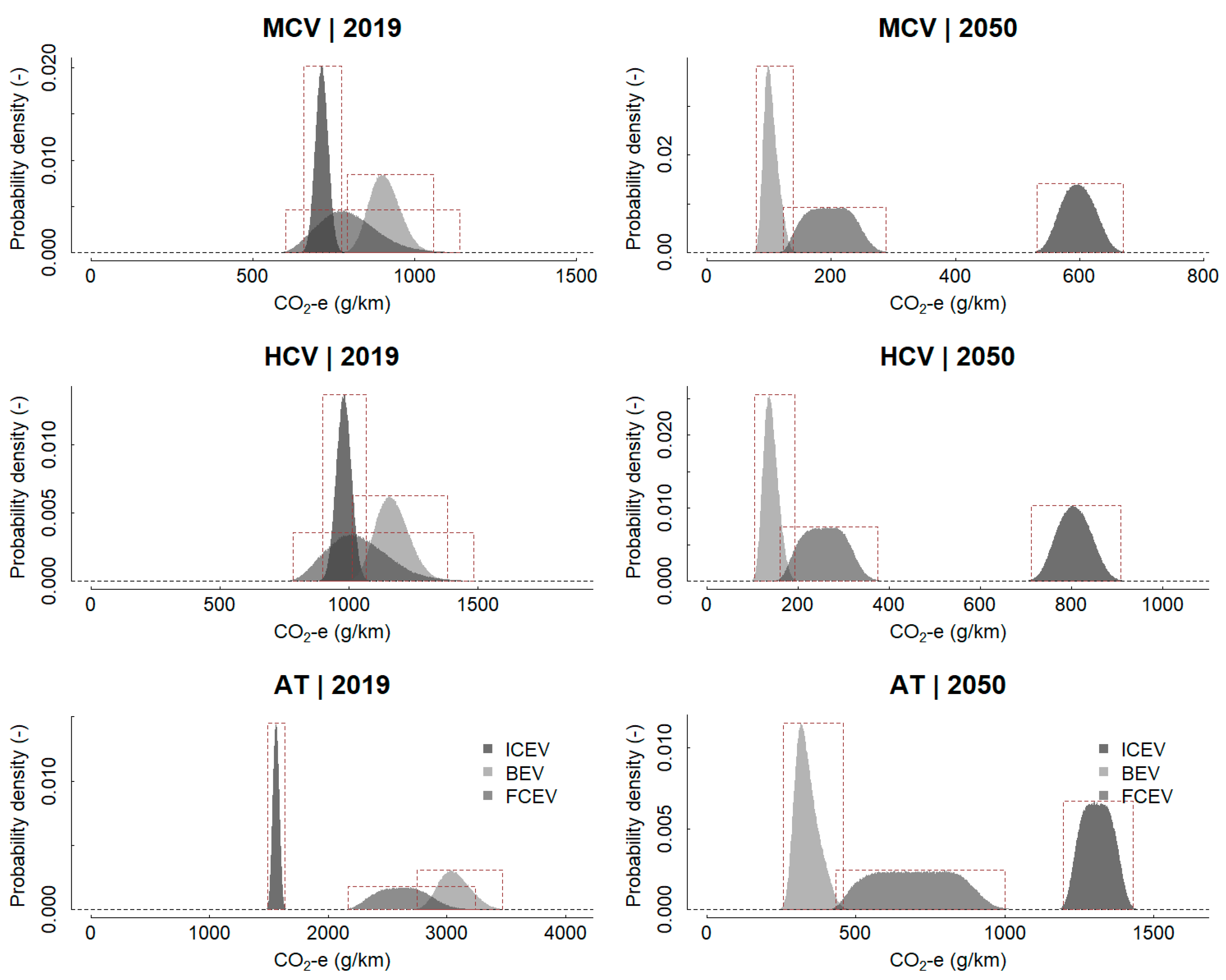
4.1. Average Life-Cycle GHG Emission Factors for Trucks
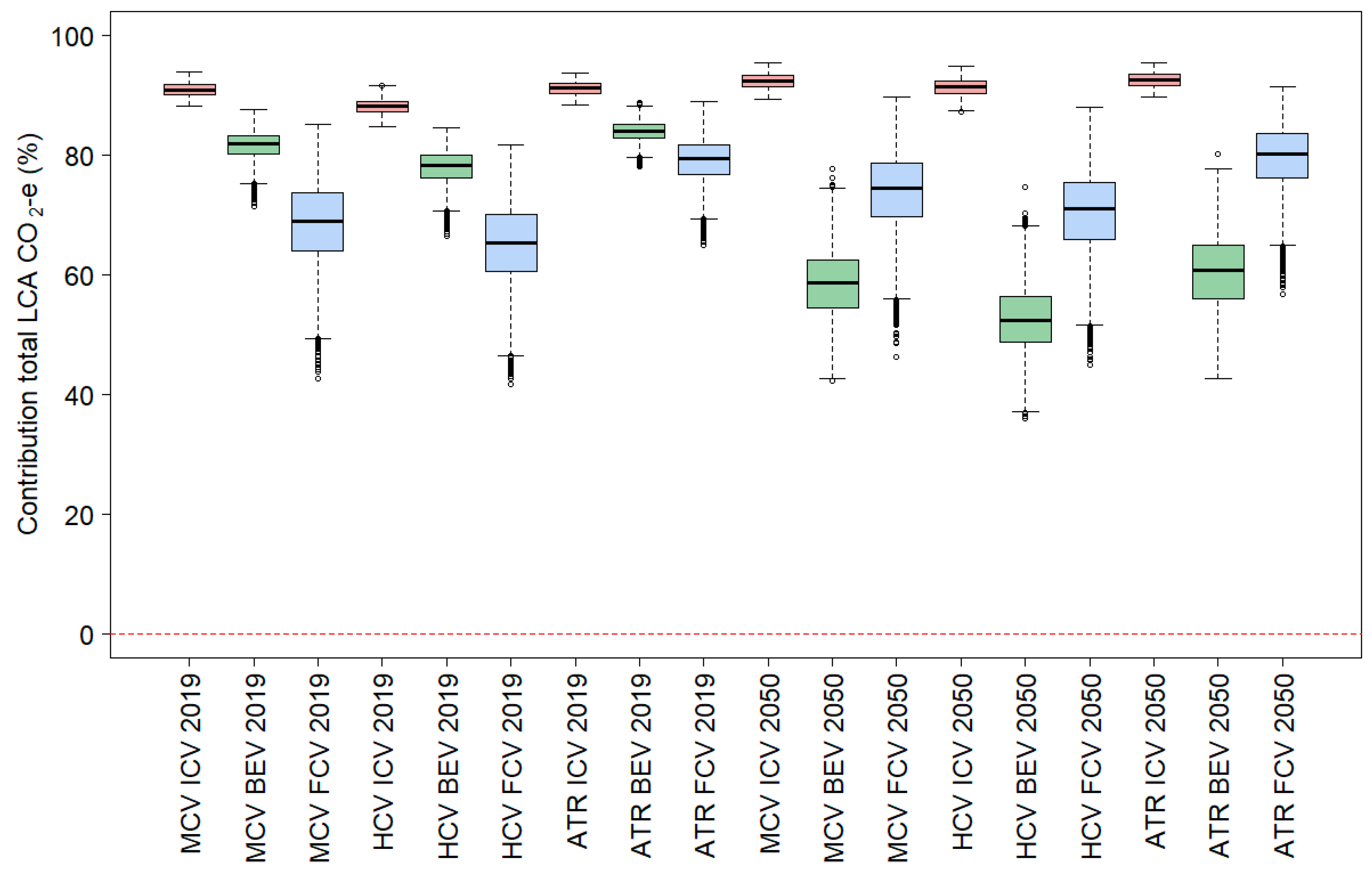
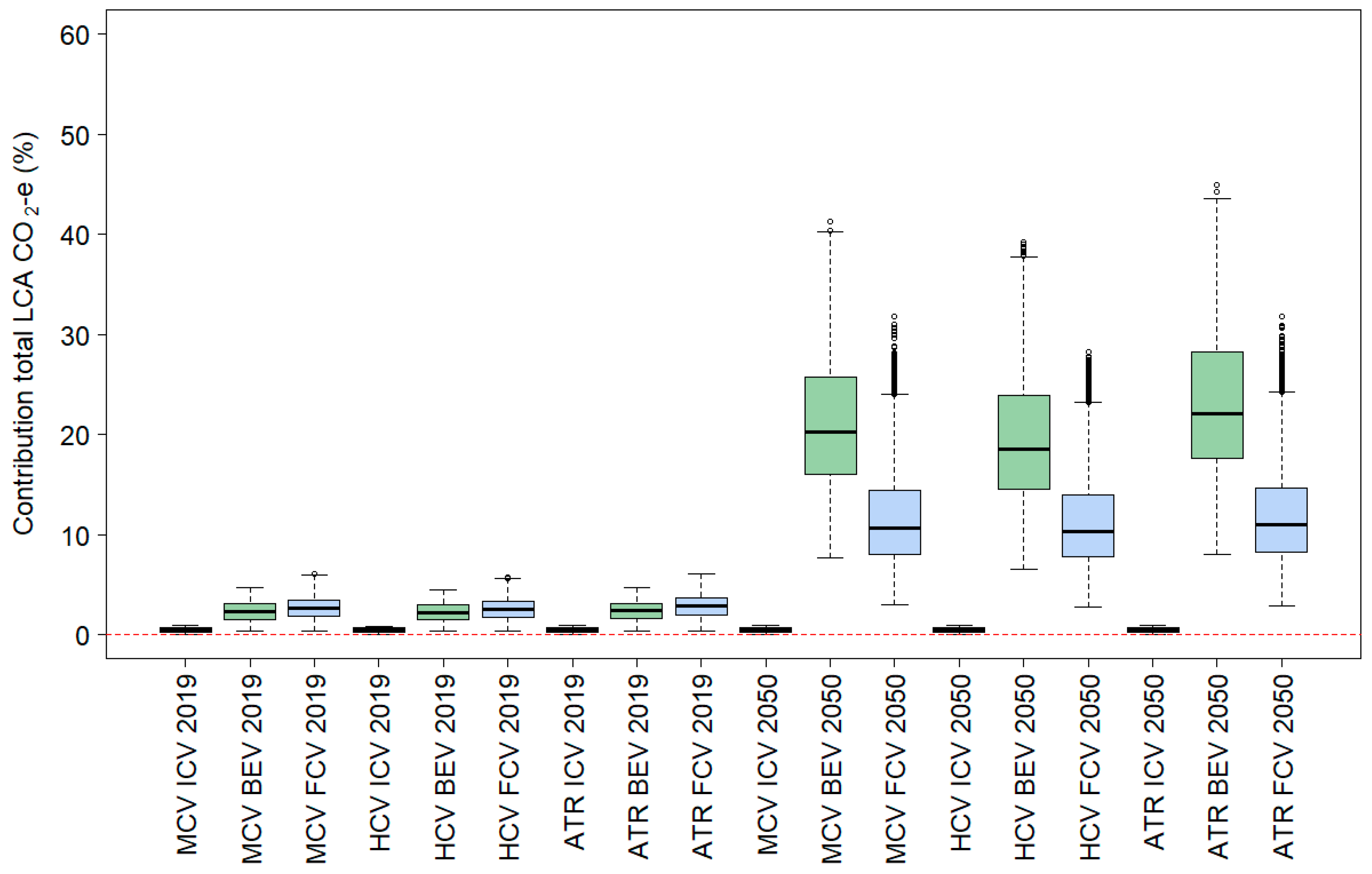
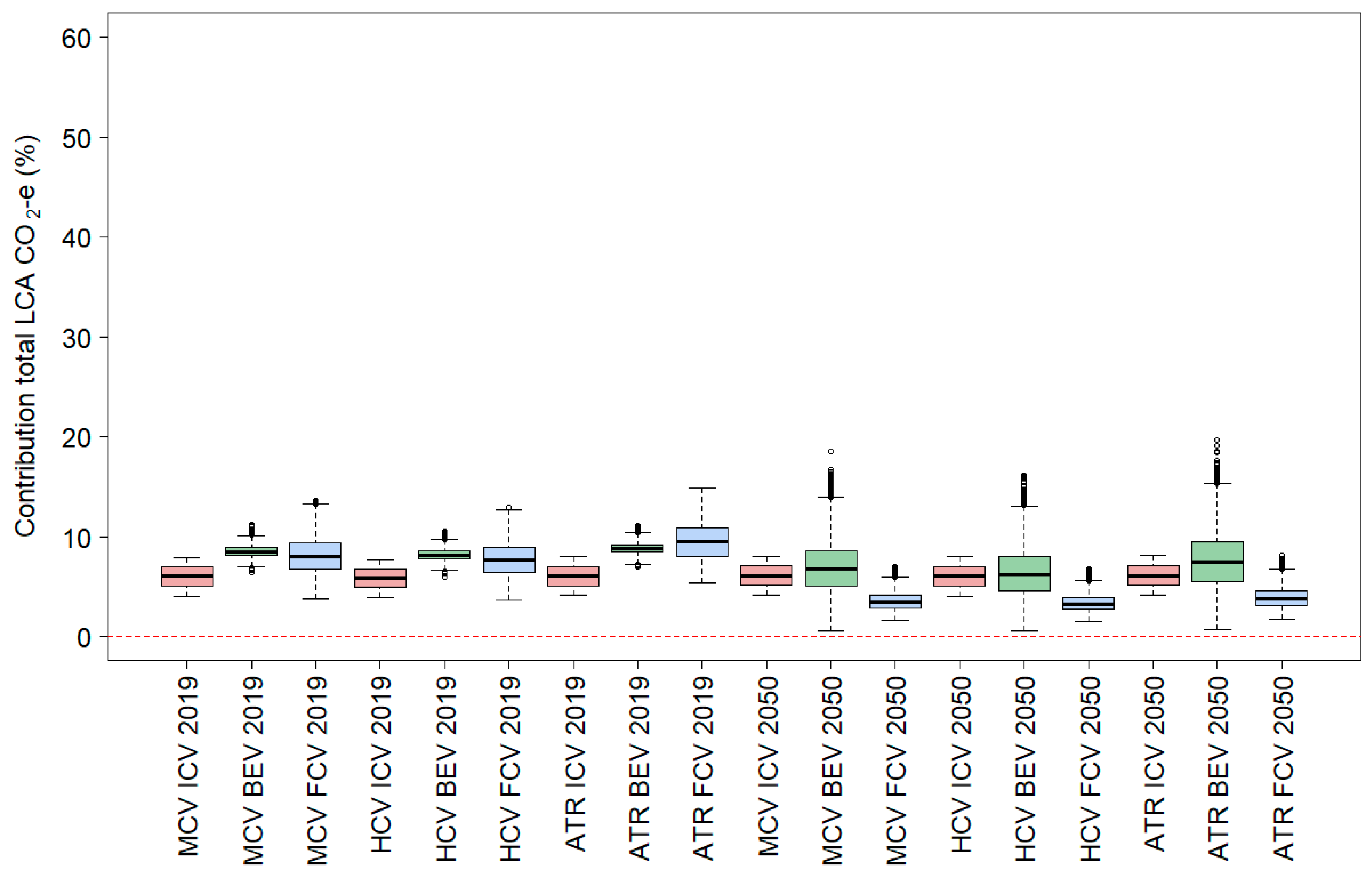
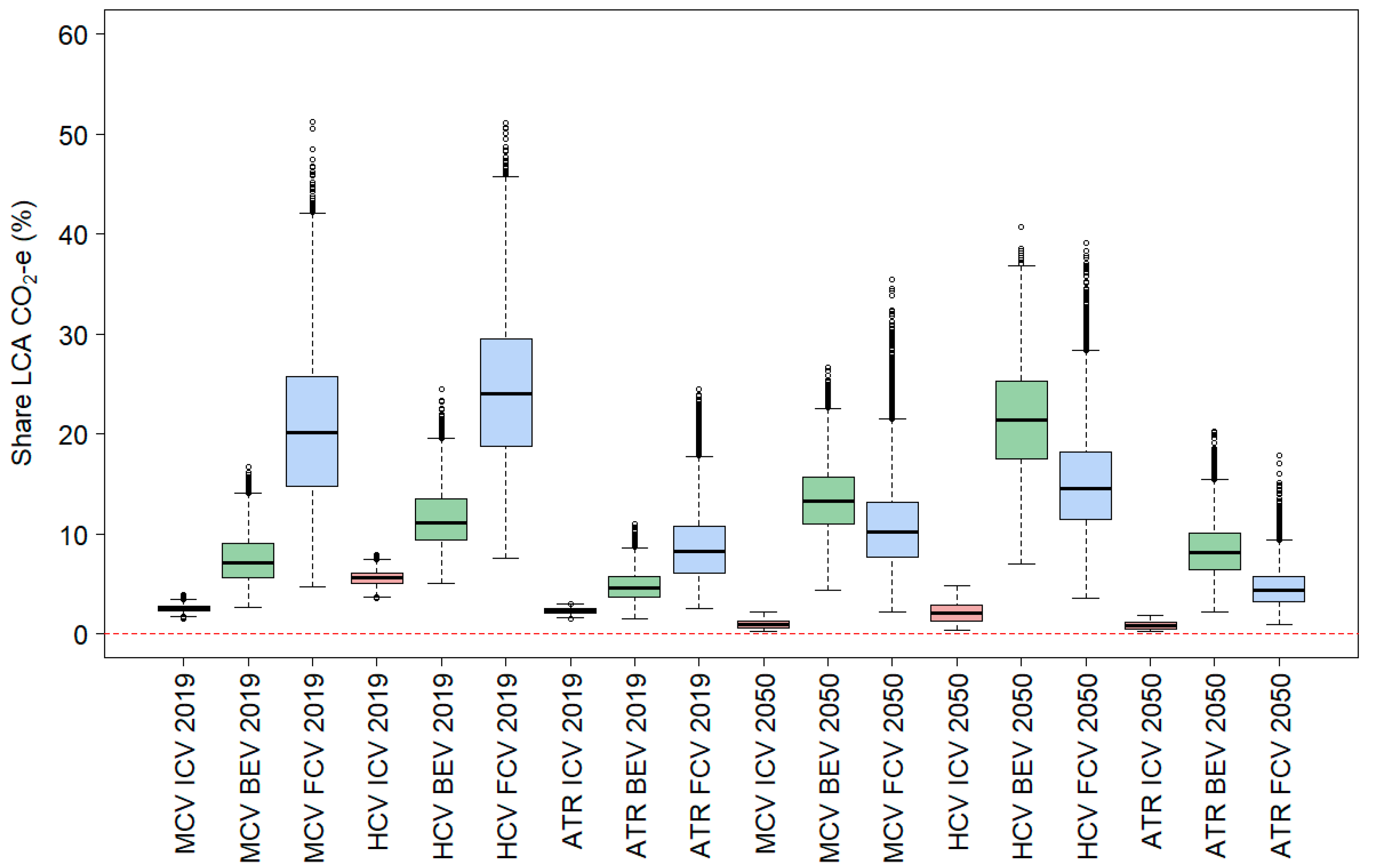
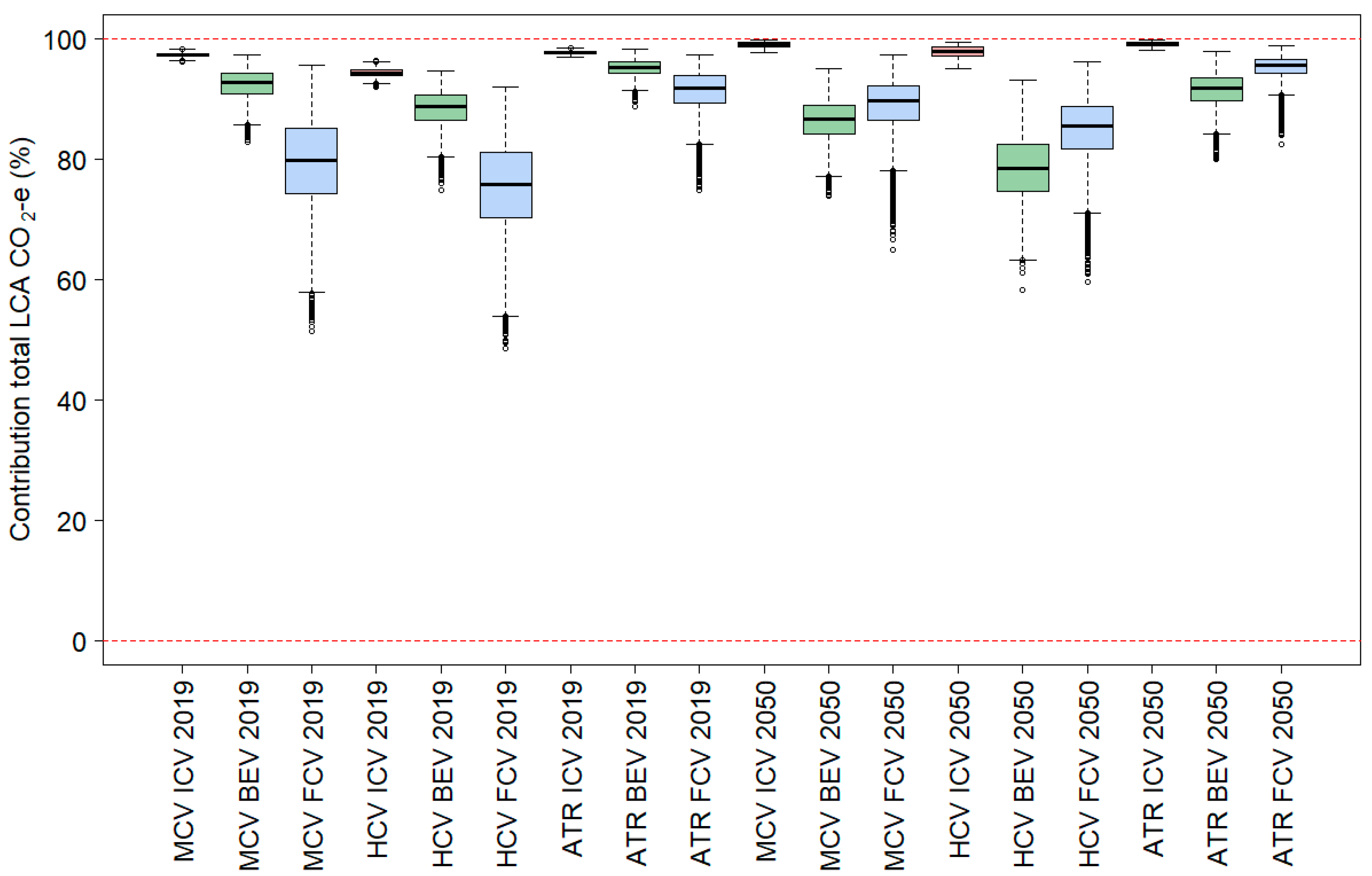
4.2. The Relevance of Different Life-Cycle Aspects
- First, it is clear that life-cycle emission factor distributions for trucks vary widely in magnitude, range and shape. They all depend on the year of assessment, truck vehicle class and powertrain technology.
- Second, any cost-effective emission reduction policies would naturally favour truck types that have narrow life-cycle GHG emissions distributions, which are as close to zero emissions as possible. They represent the maximum potential for emissions reduction and are the most robust and least uncertain technology choice. Whereas diesel trucks appear to have had the best life-cycle emissions performance in 2019, the situation is the inverse in 2050 (or in a more decarbonised situation). The simulation suggests that battery electric trucks are expected to achieve the greatest and most reliable and robust reductions in life-cycle GHG emissions.
- Third, the contribution of different life-cycle aspects is quite different, and this is particularly clear when diesel trucks are compared with electric trucks.
4.3. Comparison to Other Studies
- First, this study estimates low emission intensities (per tonne km) for heavy articulated trucks (AT), but it is unclear if these heavy vehicles were included in the IPCC data. Medium-duty trucks (MDT, Figure 9) in IPCC [20] refer to the US American classification for trucks with gross vehicle masses between 7 tonnes and 13 tonnes, while heavy-duty trucks (HDT) refer to trucks with vehicle masses > 16.5 tonnes [86]. In this study, articulated trucks are defined as trucks > 25 tonnes, and the AT modelled in this study has a gross vehicle mass of 90 tonnes (Table 2).
- Second, this study estimates a significantly wider plausible range in the life-cycle emissions performance of hydrogen trucks (FCEV), whereas the IPCC estimates quite a narrow range. This is an interesting result. Our study suggests that the elevated uncertainty in several life-cycle aspects for FCEVs can produce the highest emission intensities for all technology classes.
5. Conclusions
6. Recommendations for Future Work and Refinement
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary of Terms
| ABS | Australian Bureau of Statistics |
| AFM | Australian Fleet Model |
| AT | Articulated truck |
| B | Non-standard beta distribution |
| BE(V) | Battery electric (vehicle) |
| CDF | Cumulative distribution function |
| CI | Confidence interval |
| D | Dirac Delta function |
| eICEV, eBEV, and eFCEV | Life-cycle GHG emission factor |
| E | Exponential distribution |
| EV | Electric vehicle |
| G | Gamma distribution |
| GHG | Greenhouse gas |
| GWP | Global-warming potential |
| GVM | Gross vehicle mass |
| FC | Fuel consumption |
| FCE(V) | Fuel-cell electric (vehicle) |
| HCV | Heavy commercial (rigid) vehicle |
| HDT | Heavy-duty truck |
| HDV | Heavy-duty vehicle |
| HEV | Hybrid electric vehicle |
| ICE(V) | Internal combustion engine (vehicle) |
| IPCC | Intergovernmental Panel on Climate Change |
| L | Lognormal distribution |
| LCA | Life-cycle assessment |
| MCV | Medium commercial (rigid) vehicle |
| MDT | Medium-duty truck |
| N | Normal distribution |
| NGA | National greenhouse accounts (factors) |
| PHEV | Plug-in hybrid electric vehicle |
| pLCA | Probabilistic LCA |
| Probability density function | |
| PV | Passenger vehicle |
| Quantile–quantile (plot) | |
| RSE | Relative standard error |
| SOC | State of charge |
| SCR | Selective catalytic reduction |
| SMR | Steam–methane reforming |
| SMVU | Survey of Motor Vehicle Use |
| T | Triangular distribution |
| U | Uniform distribution |
| VKT | Vehicle kilometres travelled |
| W | Weibull distribution |
Appendix A
| Name | Range | Parameters | Probability Density Function (PDF) |
|---|---|---|---|
| Uniform—U(x:a,b) | a ≤ x ≤ b | : Minimum, : Maximum, | |
| Triangular—T(x:a,b,c) | a ≤ x ≤ b | : Minimum, : Maximum, : Mode, | |
| Normal—N(x:m,s) | −∞ ≤ x ≤ +∞ | : Mean, : Standard deviation, | |
| Lognormal—L(x:m,s) | 0 ≤ x ≤ +∞ | : Log-mean, : Scale, | |
| Weibull—W(x:s,k) | 0 ≤ x ≤ +∞ | : Scale, : Shape, | |
| Gamma—G(x:s,k) | 0 ≤ x ≤ +∞ | : Scale, : Rate, | |
| Exponential—E(x:s) | 0 ≤ x ≤ +∞ | : Scale, | |
| Non-Standard Beta—B(x:s,k,a,b) | a ≤ x ≤ b | : Scale, : Shape, : Minimum, : Maximum, | |
| Skew t—S(x:m,s,a,d) | -∞ ≤ x ≤ +∞ | : Mean, : Scale, : Skew, : Degrees of freedom, | where and is the cumulative distribution function. |
| Dirac Delta—D(x:m) | -∞ ≤ x ≤ +∞ Practically x = m | : Location, |
Appendix B

References
- Smit, R. An independent and detailed assessment of greenhouse gas emissions, fuel use, electricity and energy consumption from Australian road transport in 2019 and 2050. Air Qual. Clim. Chang. 2023, 57, 30–41. Available online: https://www.transport-e-research.com/publications (accessed on 27 November 2023).
- O’Connell, A.; Pavlenko, N.; Bieker, G.; Searle, S. A Comparison of the Life-Cycle Greenhouse Gas Emissions of European Heavy-Duty Vehicles and Fuels, February 2023; 1500 K Street NW, Suite 650; International Council on Clean Transportation (ICCT): Washington, DC, USA, 2005. [Google Scholar]
- European Parliament. CO2 Emissions from Cars: Facts and Figures (Infographics). European Parliament, News. 2023. Available online: https://www.europarl.europa.eu/news/en/headlines/society/20190313STO31218/co2-emissions-from-cars-facts-and-figures-infographics (accessed on 10 October 2023).
- Cullen, D.A.; Neyerlin, K.C.; Ahluwalia, R.K.; Mukundan, R.; More, K.L.; Borup, R.L.; Weber, A.Z.; Myers, D.J.; Kusoglu, A. New roads and challenges for fuel cells in heavy-duty transportation. Nat. Energy 2021, 6, 462–474. [Google Scholar] [CrossRef]
- Australian Government. Australia’s National Greenhouse Accounts; Australian Government (AG): Canberra, Australia, 2023. Available online: https://ageis.climatechange.gov.au/ (accessed on 27 November 2023).
- Nordelöf, A.; Messagie, M.; Tillman, A.M.; Söderman, M.L.; Van Mierlo, J. Environmental impacts of hybrid, plug-in hybrid, and battery electric vehicles—What can we learn from life-cycle assessment? Int. J. Life Cycle Assess. 2014, 19, 1866–1890. [Google Scholar] [CrossRef]
- Helmers, E.; Dietz, J.; Weiss, M. Sensitivity analysis in the life-cycle assessment of electric vs. combustion engine cars under approximate real-world conditions. Sustainability 2020, 12, 1241. [Google Scholar] [CrossRef]
- Samaras, C.; Meisterling, K. Life-cycle assessment of greenhouse gas emissions from plug-in hybrid vehicles: Implications for policy. Environ. Sci. Technol. 2008, 42, 3170–3176. [Google Scholar] [CrossRef]
- ISO 14040:2006; Environmental Management—Life-Cycle Assessment—Principles and Framework. International Organization for Standardization: Geneva, Switzerland, 2006.
- ISO 14044:2006; Environmental Management—Life-Cycle Assessment—Requirements and Guidelines. International Organization for Standardization: Geneva, Switzerland, 2006.
- ISO 14067:2018; Greenhouse Gases—Carbon Footprint of Products—Requirements and Guidelines for Quantification. International Organization for Standardization: Geneva, Switzerland, 2006.
- Noshadravan, A.; Cheah, L.; Roth, R.; Freire, F.; Dias, L.; Gregory, J. Stochastic comparative assessment of life-cycle greenhouse gas emissions from conventional and electric vehicles. Int. J. Life Cycle Assess. 2015, 20, 854–864. [Google Scholar] [CrossRef]
- Wang, Z.; Karki, R. Exploiting PHEV to augment power system reliability. IEEE Trans. Smart Grid 2016, 8, 2100–2108. [Google Scholar] [CrossRef]
- Karaaslan, E.; Zhao, Y.; Tatari, O. Comparative life-cycle assessment of sport utility vehicles with different fuel options. Int. J. Life Cycle Assess. 2018, 23, 333–347. [Google Scholar] [CrossRef]
- Helmers, E.; Chang, C.C.; Dauwels, J. Carbon Footprinting of Universities Worldwide Part II: First quantification of complete embodied impacts of two campuses in Germany and Singapore. Sustainability 2022, 14, 3865. [Google Scholar] [CrossRef]
- Bastani, P.; Heywood, J.B.; Hope, C. Fuel use and CO2 emissions under uncertainty from light-duty vehicles in the U.S. to 2050. J. Energy Resour. Technol. 2012, 134, 42202. [Google Scholar] [CrossRef]
- Smit, R.; Kennedy, D.W. Greenhouse gas emissions performance of electric and fossil-fueled passenger vehicles with uncertainty estimates using a probabilistic life-cycle assessment. Sustainability 2022, 14, 3444. [Google Scholar] [CrossRef]
- Breuer, J.L.; Samsun, R.C.; Stolten, D.; Peters, R. How to reduce the greenhouse gas emissions and air pollution caused by light and heavy duty vehicles with battery-electric, fuel cell-electric and catenary trucks. Environ. Int. 2021, 152, 106474. [Google Scholar] [CrossRef] [PubMed]
- Lajevardi, S.M.; Axsen, J.; Crawford, C. Examining the role of natural gas and advanced vehicle technologies in mitigating CO2 emissions of heavy-duty trucks: Modeling prototypical British Columbia routes with road grades. Transp. Res. Part D Transp. Environ. 2018, 62, 186–211. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2022—Mitigation of Climate Change. Working Group III Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Chapter 10: Transport; IPCC: Geneva, Switzerland, 2022; p. 1083. Available online: https://www.ipcc.ch/report/ar6/wg3/downloads/report/IPCC_AR6_WGIII_FullReport.pdf (accessed on 20 October 2023).
- Cullen, A.C.; Frey, H.C. Probabilistic Techniques in Exposure Assessment; Society of Risk Analysis: McLean, VA, USA, 1999; ISBN 0 306 45956 6. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jacknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ripley, B. Package ‘Boot’. R Package Version 1.3-28. 2021. Available online: https://cran.r-project.org/web/packages/boot/boot.pdf (accessed on 6 January 2022).
- Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1993; ISBN 0 471 55951 2. [Google Scholar]
- Wolodzko, T. ExtraDistr: Additional Univariate and Multivariate Distributions. R Package Version 1.9.1. 2020. Available online: https://CRAN.R-project.org/package=extraDistr (accessed on 6 January 2022).
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B Stat. Methodol. 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Novomestky, F.; Nadarajah, S. Truncdist: Truncated Random Variables, R Package Version 1.0-2. 2016. Available online: https://CRAN.R-project.org/package=truncdist (accessed on 6 January 2022).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Azzalini, A. The R Package ‘sn’: The Skew-Normal and Related Distributions Such as the Skew-T and the SUN (Version 2.0.0). 2021. Available online: https://cran.r-project.org/web/packages/sn/sn.pdf (accessed on 6 January 2022).
- Cramer, H. On the composition of elementary errors. Scand. Actuar. J. 1928, 1, 13–74. [Google Scholar] [CrossRef]
- Valenzuela, M.M.; Espinosa, M.; Virguez, E.A.; Behrentz, E. Uncertainty of greenhouse gas emission models: A case in Columbia’s transport sector. Transp. Res. Procedia 2017, 25, 4606–4622. [Google Scholar] [CrossRef]
- Chart-Asa, C.; Gibson, J.M. Health impact assessment of traffic-related air pollution at the urban project scale: Influence of variability and uncertainty. Sci. Total. Environ. 2015, 506–507, 409–421. [Google Scholar] [CrossRef]
- Madachy, R.J. Introduction to Statistics of Simulation, Software Process Dynamics; The Institute of Electrical and Electronics Engineers, Inc.: Piscataway, NJ, USA, 2008; Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/9780470192719.app1 (accessed on 27 November 2023).
- Australian Bureau of Statistics. Survey of Motor Vehicle Use, 9210.0.55.001 and 9208.0.DO.001; Australian Bureau of Statistics: Canberra, Australian, 2019. Available online: www.abs.gov.au (accessed on 1 September 2023).
- Rahimzei, E.; Sann, K.; Vogel, M. Kompendium: Li-Ionen-Batterien, Grundlagen, Bewertungskriterien, Gesetzte und Normen; VDE Verband der Elektrotechnik: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Simons, A.; Bauer, C. A life-cycle perspective on automotive fuel cells. Appl. Energy 2015, 157, 884–896. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Wei, X.; Wang, R.-Z.; Zhao, W.; Chen, G.; Chai, M.-R.; Zhang, L.; Zhang, J. Recent research progress in PEM fuel cell electrocatalyst degradation and mitigation strategies. EnergyChem 2021, 3, 100061. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.; Zeng, C.; Chen, Y.; Guo, Z.; Li, D.; Ye, H.; Shao, R.; Shu, H.; Yu, T. Recent advances and summarization of fault diagnosis techniques for proton exchange membrane fuel cell systems: A critical overview. J. Power Sources 2021, 500, 229932. [Google Scholar] [CrossRef]
- Verbruggen, F.J.R.; Hoekstra, A.; Hofman, T. Evaluation of the state-of-the-art of full-electric medium and heavy-duty trucks. In Proceedings of the 31st International Electric Vehicle Symposium and Exhibition, EVS 2018 and International Electric Vehicle Technology Conference 2018, EVTeC 2018, Kobe, Japan, 30 September–3 October 2018; pp. 1–8. [Google Scholar]
- Tsakiris, A. Analysis of hydrogen fuel cell and battery efficiency. In Proceedings of the World Sustainable Energy Days 2019, Wels, Austria, 27 February–1 March 2019. [Google Scholar]
- MacDonnell, O.; Wang, X.; Qiu, Y.; Song, S. Zero-Emission Truck and Bus Market Update, Calstart. 2023. Available online: https://globaldrivetozero.org/publication/global-zero-emission-truck-and-bus-market-update-2023/ (accessed on 3 October 2023).
- Helmers, E.; Marx, P. Electric cars: Technical characteristics and environmental impacts. Environ. Sci. Eur. 2012, 24, 14. [Google Scholar] [CrossRef]
- Chatzikomis, C.I.; Spentzas, K.N.; Mamalis, A.G. Environmental and economic effects of widespread introduction of electric vehicles in Greece. Eur. Transp. Res. Rev. 2014, 6, 365–376. [Google Scholar] [CrossRef]
- Mayyas, A.; Omar, M.; Hayajneh, M.; Mayyas, A.R. Vehicle’s lightweight design vs. electrification from life-cycle assessment perspective. J. Clean. Prod. 2017, 167, 687–701. [Google Scholar] [CrossRef]
- FVV. Zukünftige Kraftstoffe: FVV-Kraftstoffstudie IV, Project 1378, Forschungsvereinigung Verbrennungskraftmaschinen e.V., Research Association for Combustion Engines, 2021. Final report No 1269, Frankfurt (Germany). Forschungsvereinigung Verbrennungskraftmaschinen e.V (FVV). Available online: https://www.fvv-net.de/fileadmin/Storys/020.50_Sechs_Thesen_zur_Klimaneutralitaet_des_europaeischen_Verkehrssektors/FVV__Future_Fuels__StudyIV_The_Transformation_of_Mobility__H1269_2021-10__EN.pdf (accessed on 7 January 2024).
- Rexeis, M.; Present, S.; Opetnik, M.; Schwinghackl, M.; Weller, K.; Silberholz, G.; Grabner, P.; Hausberger, S. Comparison of propulsion technologies for heavy-duty vehicles based on EU Legislation (VECTO) and an LCA assessment. In Proceedings of the Wiener Motorensymposium 2023, Vienna, Austria, 26–28 April 2023. [Google Scholar]
- EC. Determining the Environmental Impacts of Conventional and Alternatively Fuelled Vehicles through LCA. European Commission, DG Climate Action, Prepared by Ricardo Energy & Environment, Ref ED11344 (3), 13 July 2020, 34027703/2018/782375/ETU/CLIMA.C.4. Available online: https://op.europa.eu/en/publication-detail/-/publication/1f494180-bc0e-11ea-811c-01aa75ed71a1 (accessed on 7 January 2024).
- Weiss, M.; Cloos, K.C.; Helmers, E. Energy efficiency trade-offs in small to large electric vehicles. Environ. Sci. Eur. 2020, 32, 46. [Google Scholar] [CrossRef]
- Aminudin, M.A.; Kamarudin, S.K.; Lim, B.H.; Majilan, E.H.; Masdar, M.S.; Shaari, N. An overview: Current progress on hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Wang, G.; Yu, Y.; Liu, H.; Gong, C.; Wen, S.; Wang, X.; Tu, Z. Progress on design and development of polymer electrolyte membrane fuel cell systems for vehicle applications: A review. Fuel Process. Technol. 2018, 179, 203–228. [Google Scholar] [CrossRef]
- US Department of Energy. DOE Hydrogen and Fuel Cells Program Record; Record 20005; US Department of Energy: Washington, DC, USA, 2020. [Google Scholar]
- Kumar, A.; Sehgal, M. Hydrogen Fuel Cell Technology for a Sustainable Future: A Review; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2018; pp. 1–11. [Google Scholar] [CrossRef]
- Smit, R.; Whitehead, J.; Washington, S. Where are we heading with electric vehicles? Air Qual. Clim. Chang. 2018, 52, 18–27. [Google Scholar]
- Bossel, U. Does a hydrogen economy make sense? Proc. IEEE 2006, 94, 1826–1837. [Google Scholar] [CrossRef]
- Argonne National Laboratory. Well-To-Wheels Analysis of Energy Use and Greenhouse Gas Emissions of Plug-in Hybrid Electric Vehicles; Argonne National Laboratory (ANL): Lemont, IL, USA, 2010. [Google Scholar]
- Kim, H.C.; Wallington, T.J. Life-cycle assessment of vehicle light weighting: A physics-based model to estimate use-phase fuel consumption of electrified vehicles. Environ. Sci. Technol. 2016, 50, 11226–11233. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, Y.; Zhou, B.; Wang, R.; Ke, W.; Zhang, S.; Hao, J. Real-world performance of battery electric buses and their life-cycle benefits with respect to energy consumption and carbon dioxide emissions. Energy 2016, 96, 603–613. [Google Scholar] [CrossRef]
- Williams, B.; Martin, E.; Lipman, T.; Kammen, D. Plug-in-hybrid vehicle use, energy consumption, and greenhouse emissions: An analysis of household vehicle placements in Northern California. Energies 2011, 4, 435–457. [Google Scholar] [CrossRef]
- Apostolaki-Iosifidou, E.; Codani, P.; Kempton, W. Measurement of power loss during electric vehicle charging and discharging. Energy 2017, 127, 730–742. [Google Scholar] [CrossRef]
- Frank, E.D.; Elgowainy, A.; Reddi, K.; Bafana, A. Life-cycle analysis of greenhouse gas emissions from hydrogen delivery: A cost-guided analysis. Int. J. Hydrogen Energy 2021, 46, 22670–22683. [Google Scholar] [CrossRef]
- Fernández, R.A.; Pérez-Dávila, O. Fuel cell hybrid vehicles and their role in the decarbonisation of road transport. J. Clean. Prod. 2022, 342, 130902. [Google Scholar] [CrossRef]
- Bieker, G. A Global Comparison of the Life-Cycle Greenhouse Gas Emissions of Combustion Engine and Electric Passenger Cars; International Council on Clean Transportation (ICCT): Berlin, Germany, 2021; Available online: https://theicct.org/publication/a-global-comparison-of-the-life-cycle-greenhouse-gas-emissions-of-combustion-engine-and-electric-passenger-cars/ (accessed on 5 July 2023).
- Jacobson, M.Z.; Colella, W.G.; Golden, D.M. Atmospheric science: Cleaning the air and improving health with hydrogen fuel-cell vehicles. Science 2005, 308, 1901–1905. [Google Scholar] [CrossRef]
- Weger, L.B.; Leitão, J.; Lawrence, M.G. Expected impacts on greenhouse gas and air pollutant emissions due to a possible transition towards a hydrogen economy in German road transport. Int. J. Hydrogen Energy 2021, 46, 5875–5890. [Google Scholar] [CrossRef]
- Hawkins, T.; Gausen, O.; Strømman, A. Environmental impacts of hybrid and electric vehicles—A review. Int. J. Life Cycle Assess. 2012, 17, 997–1014. [Google Scholar] [CrossRef]
- David, F.; Holger, H.; Stefan, L. Die Ökobilanz Von Schweren Nutzfahrzeugen und Bussen; Report REP-0801; Umweltbundesamt: Vienna, Austria, 2022. [Google Scholar]
- Burul, D.; Algenste, D. Life-Cycle Assessment of Distribution Vehicles, Battery Electric vs. Diesel Driven, Scania. 2023. Available online: https://www.scania.com/content/dam/group/press-and-media/press-releases/documents/Scania-Life-cycle-assessment-of-distribution-vehicles.pdf (accessed on 10 January 2024).
- La Picirelli de Souza, L.; Lora, E.E.S.; Palacio, J.C.E.; Rocha, M.H.; Reno, M.L.G.; Venturini, O.J. Comparative environmental life-cycle assessment of conventional vehicles with different fuel options, plug-in hybrid and electric vehicles for a sustainable transportation system in Brazil. J. Clean. Prod. 2018, 203, 444–468. [Google Scholar] [CrossRef]
- Hausfather, Z. Factcheck: How Electric Vehicles Help to Tackle Climate Change. Carbon Brief. 2020. Available online: https://www.carbonbrief.org/factcheck-how-electric-vehicles-help-to-tackle-climate-change (accessed on 7 February 2020).
- Smit, R.; Kingston, P.; Wainwright, D.; Tooker, R. A tunnel study to validate motor vehicle emission prediction software in Australia. Atmos. Environ. 2017, 151, 188–199. [Google Scholar] [CrossRef]
- Smit, R.; Kingston, P.; Neale, D.W.; Brown, M.K.; Verran, B.; Nolan, T. Monitoring on-road air quality and measuring vehicle emissions with remote sensing in an urban area. Atmos. Environ. 2019, 218, 116978. [Google Scholar] [CrossRef]
- Smit, R.; Awadallah, M.; Bagheri, S.; Surawski, N.C. Real-world emission factors for SUVs using on-board emission testing and geo-computation. Transp. Res. Part D Transp. Environ. 2022, 107, 103286. [Google Scholar] [CrossRef]
- Smit. Australian Motor Vehicle Emission Inventory for the National Pollutant Inventory (NPI), Prepared for the Department of Environment, UniQuest Project No. C01772. 2014. Available online: https://www.dcceew.gov.au/environment/protection/npi/publications/australian-motor-vehicle-emission-inventory-national-pollutant-inventory-npi (accessed on 2 August 2014).
- Oshiro, K.; Masui, T. Diffusion of low emission vehicles and their impact on CO2 emission reduction in Japan. Energy Policy 2015, 81, 215–225. [Google Scholar] [CrossRef]
- ERTRAC. Future Light and Heavy Duty ICE Powertrain Technologies; Version: 1.0, 9 June 2016; ERTRAC Working Group Energy and Environment: Brussels, Belgium, 2016; pp. 1–75. [Google Scholar]
- Craglia, M.; Cullen, J. Modelling transport emissions in an uncertain future: What actions make a difference? Transp. Res. Part D Transp. Environ. 2020, 89, 102614. [Google Scholar] [CrossRef]
- Elgowainy, A.; Rousseau, A.; Wang, M.; Ruth, M.; Andress, D.; Ward, J.; Joseck, F.; Nguyen, T.; Das, S. Cost of ownership and well-to-wheels carbon emissions/oil use of alternative fuels and advanced light-duty vehicle technologies. Energy Sustain. Dev. 2013, 17, 626–641. [Google Scholar] [CrossRef]
- González Palencia, J.C.; Sakamaki, T.; Araki, M.; Shiga, S. Impact of powertrain electrification, vehicle size reduction and lightweight materials substitution on energy use, CO2 emissions and cost of a passenger light-duty vehicle fleet. Energy 2015, 93, 1489–1504. [Google Scholar] [CrossRef]
- Transport & Environment (T&E). How to Decarbonise European Transport by 2050; Transport & Environment: Brussels, Belgium, 2018. [Google Scholar]
- Turconi, R.; Boldrin, A.; Astrup, T. Life-cycle assessment (LCA) of electricity generation technologies: Overview, comparability and limitations. Renew. Sustain. Energy Rev. 2013, 28, 555–565. [Google Scholar] [CrossRef]
- Bruckner, T.; Bashmakov, I.A.; Mulugetta, Y.; Chum, H.; De la Vega Navarro, A.; Edmonds, J.; Faaij, A.; Fungtammasan, B.; Garg, A.; Hertwich, E.; et al. Energy Systems. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the 5th Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Tessum, C.W.; Hill, J.D.; Marshall, D. Life-cycle air quality impacts of conventional and alternative light-duty transportation in the United States. Proc. Natl. Acad. Sci. USA 2014, 111, 18490–18495. [Google Scholar] [CrossRef]
- Luk, J.M.; Saville, B.A.; MacLean, H.L. Life-cycle air emissions impacts and ownership costs of light-duty vehicles using natural gas as a primary energy source. Environ. Sci. Technol. 2015, 49, 5151–5160. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Vehicle Weight Classes & Categories. 2023. Available online: https://afdc.energy.gov/data/10380 (accessed on 21 October 2023).




| Notation | Description and Units | Time Variable |
|---|---|---|
| Mx | lifetime mileage for technology x (x = ICEV, BEV, FCEV) (km) | No (S.3.1) |
| ΓBAT | battery replacement factor (−) | Yes (S.3.1) |
| ΓFCL | fuel-cell replacement factor (−) | Yes (S.3.1) |
| Mx | vehicle tare mass for technology x (x = ICEV, BEV, FCEV) (kg) | No (S.3.2) |
| MBAT | battery mass for BEV or FCEV (kg) | No (S.3.2) |
| MFCL | fuel-cell mass (kg) | No (S.3.2) |
| θBAT | battery capacity (kWh) | Yes (S.3.2) |
| ρFCL | fuel-cell rated power (kW) | Yes (S.3.2) |
| ωelec (1) | GHG emission-intensity electricity generation (g CO2-e/kWh generated) | Yes (S.3.3) |
| ηb | battery recharging efficiency (−) | Yes (S.3.3) |
| ηg | grid transmission efficiency (−) | Yes (S.3.3) |
| ωH2,P | GHG emission-intensity hydrogen production (g CO2-e/g fuel) for production pathway P | Yes (S.3.4) |
| σelec | GHG emission-intensity electricity infrastructure (g CO2-e/kWh generated) | Yes (S.3.5) |
| ηh | hydrogen distribution efficiency (−) | Yes (S.3.4) |
| ηr | hydrogen refuelling efficiency (−) | Yes (S.3.4) |
| σH2,P | GHG emission-intensity H2 production infrastructure (g CO2-e/g fuel) production pathway P | Yes (S.3.5) |
| ϕelec (2) | GHG emission-intensity upstream fuels for electricity generation (g CO2-e/kWh consumed) | Yes (S.3.5) |
| ϕH2,p (2) | GHG emission-intensity upstream H2 production (g CO2-e/g fuel) for production pathway P | Yes (S.3.5) |
| φv,ICEV | GHG emission-intensity ICEV production (kg CO2-e/kg vehicle) | Yes (S.3.6) |
| φv,BEV | GHG emission-intensity BEV production without battery (kg CO2-e/kg vehicle) | Yes (S.3.6) |
| φv,FCEV | GHG emission-intensity FCEV production without battery/fuel cell (kg CO2-e/kg vehicle) | Yes (S.3.6) |
| φBAT | GHG emission-intensity battery production (kg CO2-e/kWh battery capacity) | Yes (S.3.6) |
| φFCL | GHG emission-intensity fuel-cell production (kg CO2-e/kW fuel-cell-rated power) | Yes (S.3.6) |
| ε | real-world electricity consumption BEV (kWh/km) | Yes (S.3.7) |
| H | real-world hydrogen consumption FCEV (g/km) | Yes (S.3.7) |
| Vehicle Class | Powertrain | GVM * (t) | Tare Mass ** (t) | Payload *** (t) | Typical Rated Power (kW) | Typical Battery Capacity (kWh) |
|---|---|---|---|---|---|---|
| MCV | ICEV | 7.5 | 3.1 | 2.2 | 125 | - |
| BEV | 7.5 | Variable | 2.2 | 115 | 200 | |
| FCEV | 7.5 | Variable | 2.2 | 140 | 60 (40 ****) | |
| HCV | ICEV | 17.2 | 9.2 | 4.0 | 247 | - |
| BEV | 17.2 | Variable | 4.0 | 220 | 340 | |
| FCEV | 17.2 | Variable | 4.0 | 200 | 80 (40 ****) | |
| AT | ICEV | 90.0 | 24.3 | 32.9 | 510 | - |
| BEV | 90.0 | Variable | 32.9 | 394 | 600 | |
| FCEV | 90.0 | Variable | 32.9 | 400 | 150 (80 ****) |
| Scenario, Jurisdictions | Coal | Gas | Oil | Nuclear | Hydro | Wind | Biomass | Solar |
|---|---|---|---|---|---|---|---|---|
| Electricity, Australia, Past (2019) | 58.4% | 20.0% | 1.9% | 0.0% | 6.0% | 6.7% | 1.3% | 5.6% |
| Electricity, Australia, Future (2050) | 5.0% | 5.0% | 0.0% | 0.0% | 30.0% | 25.0% | 5.0% | 30.0% |
| Hydrogen, Australia, Past (2019) | - | 75.0% * | - | - | - | 25.0% ** | - | - |
| Hydrogen, Australia, Future (2050) | - | 10.0% * | - | - | - | 90.0% ** | - | - |
| Year | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value (kg) | Plausible Min–Max Value (kg) |
|---|---|---|---|---|---|
| 2019 | MC-BEV | MBAT,BEV,MCV | Weibull, W (6.22, 1161.68) | 1080 | 868–1283 |
| 2019 | HC-BEV | MBAT,BEV,HCV | Weibull, W (6.07, 1891.85) | 1755 | 1384–2101 |
| 2019 | AT-BEV | MBAT,BEV,AT | Non-standard beta, B (2.91, 3.21) | 3454 | 2352–4541 |
| 2050 | MC-BEV | MBAT,BEV,MCV | Normal, N (719, 136) | 719 | 578–854 |
| 2050 | HC-BEV | MBAT,BEV,HCV | Weibull, W (5.69, 1258.83) | 1165 | 915–1395 |
| 2050 | AT-BEV | MBAT,BEV,AT | Weibull, W (3.54, 2547.64) | 2292 | 1533–3027 |
| 2019 | MC-FCEV | MBAT,FCEV,MCV | Non-standard beta, B (3.51, 6.28) | 394 | 315–477 |
| 2019 | HC-FCEV | MBAT,FCEV,HCV | Non-standard beta, B (3.17, 5.98) | 551 | 422–690 |
| 2019 | AT-FCEV | MFCL,FCEV,AT | Non-standard beta, B (3.68, 4.72) | 888 | 748–1027 |
| 2050 | MC-FCEV | MBAT,FCEV,MCV | Non-standard beta, B (3.31, 8.19) | 261 | 206–317 |
| 2050 | HC-FCEV | MBAT,FCEV,HCV | Non-standard beta, B (3.16, 7.83) | 367 | 278–460 |
| 2050 | AT-FCEV | MBAT,FCEV,HCV | Non-standard beta, B (5.32, 9.75) | 589 | 492–684 |
| 2019 + 2050 | MC-FCEV | MFCL,FCEV,MCV | Non-standard beta, B (4.82, 10.14) | 223 | 181–265 |
| 2019 + 2050 | HC-FCEV | MFCL,FCEV,HCV | Non-standard beta, B (4.79, 7.61) | 305 | 255–356 |
| 2019 + 2050 | AT-FCEV | MFCL,FCEV,AT | Non-standard beta, B (4.76, 9.04) | 608 | 459–756 |
| Year | Input Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|
| 2019 | Normal, N (760, 11.4) | 760 | 725–794 |
| 2050 | Skewed t, S (78.66, 4.52, 2.87, 27.08) | 82 | 74–96 |
| Year | Input Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|
| 2019 | Uniform, U (9.3, 13.2) | 11.2 | 9.3–13.2 |
| 2050 | Uniform, U (2.3, 5.4) | 3.8 | 2.3–5.4 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| M 2019 | MC-ICEV | evehicle,ICEV,MCV | Non-standard beta, B (8.82, 10.47) | 18 | 12–25 |
| M 2019 | HC-ICEV | evehicle,ICEV,HCV | Non-standard beta, B (9.66, 11.63) | 52 | 34–72 |
| M 2019 | AT-ICEV | evehicle,ICEV,AT | Non-standard beta, B (5.15, 4.170) | 35 | 24–44 |
| M 2050 | MC-ICEV | evehicle,ICEV,MCV | Non-standard beta, B (2.66, 3.56) | 6 | 1–12 |
| M 2050 | HC-ICEV | evehicle,ICEV,HCV | Weibull, W (2.25, 18.54) | 16 | 4–35 |
| M 2050 | AT-ICEV | evehicle,ICEV,AT | Weibull, W (2.28, 12.20) | 11 | 3–22 |
| M 2019 | MC-BEV | evehicle,BEV,MCV | Non-standard beta, B (3.15, 39.66) | 68 | 28–150 |
| M 2019 | HC-BEV | evehicle,BEV,HCV | Lognormal, L (4.86, 0.29) | 134 | 63–277 |
| M 2019 | AT-BEV | evehicle,BEV,AT | Gamma, G (10.37, 0.07) | 145 | 57–300 |
| M 2050 | MC-BEV | evehicle,BEV,MCV | Non-standard beta, B (4.94, 10.40) | 14 | 5–25 |
| M 2050 | HC-BEV | evehicle,BEV,HCV | Non-standard beta, B (4.02, 7.08) | 30 | 11–56 |
| M 2050 | AT-BEV | evehicle,BEV,AT | Non-standard beta, B (5.56, 22.64) | 28 | 8–62 |
| M 2019 | MC-FCEV | evehicle,FCEV,MCV | Non-standard beta, B (2.42, 13.12) | 169 | 43–474 |
| M 2019 | HC-FCEV | evehicle,FCEV,HCV | Non-standard beta, B (2.76, 11.81) | 260 | 84–658 |
| M 2019 | AT-FCEV | evehicle,FCEV,AT | Lognormal, L (5.34, 0.44) | 228 | 73–657 |
| M 2050 | MC-FCEV | evehicle,FCEV,MCV | Lognormal, L (2.97, 0.41) | 21 | 6–64 |
| M 2050 | HC-FCEV | evehicle,FCEV,HCV | Gamma, G (7.50, 0.20) | 38 | 11–96 |
| M 2050 | AT-FCEV | evehicle,FCEV,AT | Lognormal, L (3.37, 0.38) | 31 | 9–84 |
| Life-Cycle Aspect | Vehicle Technology | LCA model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| O 2019 | MC-ICEV | eroad,ICEV,MCV | Normal, N (644, 13) | 644 | 605–682 |
| O 2019 | HC-ICEV | eroad,ICEV,HCV | Normal, N (860, 17) | 860 | 808–911 |
| O 2019 | AT-ICEV | eroad,ICEV,AT | Normal, N (1420, 14) | 1420 | 1377–1462 |
| O 2050 | MC-ICEV | eroad,ICEV,MCV | Non-standard beta, B (3.57, 3.91) | 547 | 496–603 |
| O 2050 | HC-ICEV | eroad,ICEV,HCV | Non-standard beta, B (3.52, 3.77) | 731 | 663–804 |
| O 2050 | AT-ICEV | eroad,ICEV,AT | Triangular, T (1111, 1309, 1198) | 1207 | 1111–1309 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| O 2019 | MC-BEV | εMCV | Non-standard beta, B (5.77, 11.49) | 908 | 821–1021 |
| O 2019 | HC-BEV | εHCV | Non-standard beta, B (5.53, 11.05) | 1229 | 1113–1384 |
| O 2019 | AT-BEV | εAT | Non-standard beta, B (3.81, 7.65) | 3343 | 3080–3695 |
| O 2050 | MC-BEV | εMCV | Non-standard beta, B (4.14, 4.58) | 646 | 574–720 |
| O 2050 | HC-BEV | εHCV | Non-standard beta, B (4.17, 4.68) | 875 | 778–979 |
| O 2050 | AT-BEV | εAT | Non-standard beta, B (2.92, 3.17) | 2380 | 2163–2622 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| O 2019 | MC-FCEV | HMCV | Non-standard beta, B (11.42, 11.82) | 45 | 43–48 |
| O 2019 | HC-FCEV | HHCV | Non-standard beta, B (71.83, 62.17) | 61 | 58–64 |
| O 2019 | AT-FCEV | HAT | Gamma, G (8168.15, 45.95) | 178 | 173–183 |
| O 2050 | MC-FCEV | HMCV | Gamma, G (564.18, 15.63) | 36 | 33–40 |
| O 2050 | HC-FCEV | HHCV | Non-standard beta, B (3.07, 3.35) | 49 | 45–54 |
| O 2050 | AT-FCEV | HAT | Triangular, T (130, 155, 140) | 142 | 131–154 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| O 2019 | MC-BEV | eroad,BEV,MCV | Non-standard beta, B (6.47, 12.41) | 690 | 618–780 |
| O 2019 | HC-BEV | eroad,BEV,HCV | Non-standard beta, B (6.64, 13.03) | 934 | 837–1059 |
| O 2019 | AT-BEV | eroad,BEV,AT | Non-standard beta, B (5.01, 9.58) | 2541 | 2305–2837 |
| O 2050 | MC-BEV | eroad,BEV,MCV | Non-standard beta, B (9.71, 23.05) | 53 | 46–64 |
| O 2050 | HC-BEV | eroad,BEV,HCV | Lognormal, L (4.27, 0.06) | 72 | 62–86 |
| O 2050 | AT-BEV | eroad,BEV,AT | Non-standard beta, B (8.24, 19.56) | 195 | 170–232 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| O 2019 | MC-FCEV | eroad,FCEV,MCV | Non-standard beta, B (2.51, 2.60) | 529 | 446–623 |
| O 2019 | HC-FCEV | eroad,FCEV,HCV | Gamma, G (157.57, 0.22) | 718 | 611–834 |
| O 2019 | AT-FCEV | eroad,FCEV,AT | Non-standard beta, B (1.57, 1.71) | 2083 | 1795–2398 |
| O 2050 | MC-FCEV | eroad,FCEV,MCV | Location-scale t, O (2,289,788, 142, 32) | 142 | 83–209 |
| O 2050 | HC-FCEV | eroad,FCEV,HCV | Non-standard beta, B (1.53, 1.81) | 193 | 113–821 |
| O 2050 | AT-FCEV | eroad,FCEV,AT | Non-standard beta, B (1.67, 1.78) | 560 | 331–814 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| I 2019 | MC-ICEV | einfra,ICEV,MCV | Uniform, U (0.4, 6.2) | 3 | 0–6 |
| I 2019 | HC-ICEV | einfra,ICEV,HCV | Uniform, U (0.6, 8.3) | 4 | 1–8 |
| I 2019 | AT-ICEV | einfra,ICEV,AT | Uniform, U (0.9, 13.5) | 7 | 1–14 |
| I 2050 | MC-ICEV | einfra,ICEV,MCV | Uniform, U (0.4, 5.7) | 3 | 0–6 |
| I 2050 | HC-ICEV | einfra,ICEV,HCV | Uniform, U (0.5, 7.6) | 4 | 1–8 |
| I 2050 | AT-ICEV | einfra,ICEV,AT | Uniform, U (0.8, 12.3) | 6 | 1–12 |
| Fuel Type | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|
| Biomass | Uniform, U (0.04, 2.00) | 0.45 | 0.04–2.00 |
| Coal | Uniform, U (0.8, 46.0) | 8.00 | 0.80–46.00 |
| Gas | Triangular, T (0.60, 1.85, 3.10) | 1.85 | 0.60–3.10 |
| Hydro | Uniform, U (3.10, 20.00) | 7.40 | 3.10–20.00 |
| Oil | Triangular, T (1.00, 2.20, 3.00) | 2.20 | 1.00–3.00 |
| Solar | Exponential, E (0.015) | 67.94 | 20.00–190.00 |
| Wind | Uniform, U (3.00, 41.00) | 18.93 | 3.00–41.00 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| I 2019 | MC-BEV | einfra,BEV,MCV | Non-standard beta, B (2.25, 2.82) | 19 | 4–37 |
| I 2019 | HC-BEV | einfra,BEV,HCV | Non-standard beta, B (2.18, 2.61) | 26 | 5–51 |
| I 2019 | AT-BEV | einfra,BEV,AT | Non-standard beta, B (2.19, 2.59) | 71 | 15–137 |
| I 2050 | MC-BEV | einfra,BEV,MCV | Gamma, G (6.38, 0.29) | 22 | 7–49 |
| I 2050 | HC-BEV | einfra,BEV,HCV | Lognormal, L (3.31, 0.40) | 30 | 10–67 |
| I 2050 | AT-BEV | einfra,BEV,AT | Non-standard beta, B (2.11, 4.82) | 81 | 28–183 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| F 2019 | MC-ICEV | efuel,ICEV,MCV | Location-scale t, O (2,180,536, 43, 8) | 43 | 28–59 |
| F 2019 | HC-ICEV | efuel,ICEV,HCV | Uniform, U (37, 79) | 57 | 37–79 |
| F 2019 | AT-ICEV | efuel,ICEV,AT | Uniform, U (63, 127) | 94 | 63–127 |
| F 2050 | MC-ICEV | efuel,ICEV,MCV | Location-scale t, O (1,556,144, 36, 7) | 36 | 23–51 |
| F 2050 | HC-ICEV | efuel,ICEV,HCV | Normal, N (48, 10) | 49 | 31–68 |
| F 2050 | AT-ICEV | efuel,ICEV,AT | Non-standard beta, B (1.54, 1.79) | 80 | 51–112 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| F 2019 | MC-BEV | efuel,BEV,MCV | Lognormal, L (4.26, 0.07) | 71 | 58–88 |
| F 2019 | HC-BEV | efuel,BEV,HCV | Lognormal, L (4.56, 0.07) | 96 | 78–121 |
| F 2019 | AT-BEV | efuel,BEV,AT | Lognormal, L (5.57, 0.07) | 263 | 214–328 |
| F 2050 | MC-BEV | efuel,BEV,MCV | Weibull, W (2.67, 7.85) | 7 | 1–16 |
| F 2050 | HC-BEV | efuel,BEV,HCV | Non-standard beta, B (4.39, 11.13) | 10 | 1–22 |
| F 2050 | AT-BEV | efuel,BEV,AT | Non-standard beta, B (4.38, 11.32) | 26 | 4–61 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| U 2019 | MC-FCEV | eupstream,FCEV,MCV | Normal, N (64, 13) | 64 | 40–91 |
| U 2019 | HC-FCEV | eupstream,FCEV,HCV | Location-scale t, O (2,191,700, 86, 17) | 86 | 54–122 |
| U 2019 | AT-FCEV | eupstream,FCEV,AT | Non-standard beta, B (2.01, 2.16) | 249 | 157–355 |
| U 2050 | MC-FCEV | eupstream,FCEV,MCV | Triangular, T (3.8, 10.3, 5.8) | 7 | 4–10 |
| U 2050 | HC-FCEV | eupstream,FCEV,HCV | Triangular, T (5.4, 13.9, 7.9) | 9 | 6–14 |
| U 2050 | AT-FCEV | eupstream,FCEV,AT | Non-standard beta, B (1.91, 2.59) | 27 | 16–40 |
| Life-Cycle Aspect | Vehicle Technology | LCA Model Input Variable | Distribution | Typical Value | Plausible Min–Max Value |
|---|---|---|---|---|---|
| D | MC-ICEV | edisposal,ICEV,MCV | Uniform, U (0.1, 1.4) | 1 | 0–1 |
| D | HC-ICEV | edisposal,ICEV,HCV | Uniform, U (0.2, 4.1) | 2 | 0–4 |
| D | AT-ICEV | edisposal,ICEV,AT | Uniform, U (0.1, 2.7) | 1 | 0–3 |
| D | MC-EV | edisposal,EV,MCV | Uniform, U (0.1, 1.7) | 1 | 0–2 |
| D | HC-EV | edisposal,EV,HCV | Uniform, U (0.3, 5.6) | 3 | 0–6 |
| D | AT-EV | edisposal,EV,AT | Uniform, U (0.2, 3.3) | 2 | 0–3 |
| Vehicle Class | Powertrain Technology | Year of Assessment | Mean | Median | Lower 99.7% Confidence Limit (mean) | Upper 99.7% Confidence Limit (mean) |
|---|---|---|---|---|---|---|
| MCV | ICEV | 2019 | 714 | 714 | 658 | 773 |
| MCV | BEV | 2019 | 909 | 907 | 792 | 1059 |
| MCV | FCEV | 2019 | 799 | 790 | 603 | 1139 |
| HCV | ICEV | 2019 | 981 | 981 | 899 | 1067 |
| HCV | BEV | 2019 | 1171 | 1167 | 1011 | 1380 |
| HCV | FCEV | 2019 | 1041 | 1030 | 784 | 1483 |
| AT | ICEV | 2019 | 1563 | 1563 | 1491 | 1636 |
| AT | BEV | 2019 | 3070 | 3062 | 2750 | 3471 |
| AT | FCEV | 2019 | 2627 | 2623 | 2166 | 3239 |
| MCV | ICEV | 2050 | 598 | 597 | 531 | 670 |
| MCV | BEV | 2050 | 104 | 102 | 79 | 140 |
| MCV | FCEV | 2050 | 198 | 198 | 123 | 288 |
| HCV | ICEV | 2050 | 806 | 805 | 711 | 908 |
| HCV | BEV | 2050 | 141 | 140 | 104 | 192 |
| HCV | FCEV | 2050 | 258 | 258 | 160 | 375 |
| AT | ICEV | 2050 | 1310 | 1310 | 1195 | 1430 |
| AT | BEV | 2050 | 337 | 331 | 257 | 458 |
| AT | FCEV | 2050 | 697 | 697 | 432 | 1001 |
| Vehicle Class | Powertrain Technology | Year of Assessment | Vehicle Manufacturing | Upstream Infrastructure | Upstream Fuel and Energy | Operational (on-Road + Maintenance) | Disposal and Recycling |
|---|---|---|---|---|---|---|---|
| MCV | ICEV | 2019 | 2.5 (1.7–3.4) | 0.5 (0.1–0.9) | 6.0 (4.1–7.9) | 91.0 (88.6–93.5) | 0.1 (0.0–0.2) |
| MCV | BEV | 2019 | 7.4 (3.1–15.6) | 2.3 (0.5–4.4) | 8.5 (6.9–10.4) | 81.6 (74.0–86.8) | 0.1 (0.0–0.2) |
| MCV | FCEV | 2019 | 20.5 (6.1–44.3) | 2.7 (0.5–5.6) | 8.1 (4.3–13.0) | 68.6 (47.7–83.3) | 0.1 (0.0–0.3) |
| HCV | ICEV | 2019 | 5.3 (3.6–7.3) | 0.4 (0.1–0.8) | 5.8 (3.9–7.7) | 88.2 (85.2–91.2) | 0.2 (0.0–0.4) |
| HCV | BEV | 2019 | 11.4 (5.7–21.2) | 2.2 (0.4–4.2) | 8.2 (6.5–10.1) | 78.0 (69.1–84.0) | 0.3 (0.0–0.5) |
| HCV | FCEV | 2019 | 24.3 (9.4–47.1) | 2.5 (0.5–5.3) | 7.8 (4.1–12.4) | 65.2 (45.1–80.0) | 0.3 (0.0–0.7) |
| AT | ICEV | 2019 | 2.2 (1.6–2.8) | 0.5 (0.1–0.9) | 6.0 (4.1–7.9) | 91.2 (88.9–93.7) | 0.1 (0.0–0.2) |
| AT | BEV | 2019 | 4.7 (1.8–9.5) | 2.4 (0.5–4.5) | 8.8 (7.3–10.7) | 84.0 (79.1–88.0) | 0.1 (0.0–0.1) |
| AT | FCEV | 2019 | 8.6 (2.8–21.9) | 2.8 (0.6–5.7) | 9.5 (5.6–14.2) | 79.1 (66.4–87.7) | 0.1 (0.0–0.1) |
| MCV | ICEV | 2050 | 0.9 (0.2–2.0) | 0.5 (0.1–0.9) | 6.1 (4.1–8.0) | 92.5 (89.9–95.2) | 0.0 (0.0–0.1) |
| MCV | BEV | 2050 | 13.1 (5.1–23.7) | 21.3 (8.4–39.3) | 6.9 (1.1–15.6) | 58.4 (43.6–73.3) | 0.3 (0.0–0.9) |
| MCV | FCEV | 2050 | 10.8 (3.0–30.1) | 11.6 (3.6–27.6) | 3.5 (1.7–6.6) | 74.0 (52.5–87.6) | 0.1 (0.0–0.5) |
| HCV | ICEV | 2050 | 2.0 (0.4–4.4) | 0.5 (0.1–0.9) | 6.0 (4.1–8.0) | 91.4 (87.9–94.8) | 0.1 (0.0–0.2) |
| HCV | BEV | 2050 | 20.8 (8.1–35.4) | 19.6 (7.5–37.6) | 6.4 (1.0–14.5) | 52.6 (38.5–68.7) | 0.6 (0.0–2.1) |
| HCV | FCEV | 2050 | 14.8 (4.3–34.9) | 11.1 (3.5–26.5) | 3.4 (1.7–6.3) | 70.4 (48.9–85.7) | 0.4 (0.0–1.3) |
| AT | ICEV | 2050 | 0.8 (0.2–1.7) | 0.5 (0.1–0.9) | 6.1 (4.2–8.0) | 92.6 (90.0–95.2) | 0.0 (0.0–0.1) |
| AT | BEV | 2050 | 8.3 (2.4–17.7) | 23.5 (9.5–42.4) | 7.7 (1.2–17.1) | 60.4 (44.4–76.1) | 0.2 (0.0–0.5) |
| AT | FCEV | 2050 | 4.6 (1.2–13.1) | 11.9 (3.7–28.5) | 3.9 (1.9–7.4) | 79.6 (61–90.5) | 0.1 (0.0–0.3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smit, R.; Helmers, E.; Schwingshackl, M.; Opetnik, M.; Kennedy, D. Greenhouse Gas Emissions Performance of Electric, Hydrogen and Fossil-Fuelled Freight Trucks with Uncertainty Estimates Using a Probabilistic Life-Cycle Assessment (pLCA). Sustainability 2024, 16, 762. https://doi.org/10.3390/su16020762
Smit R, Helmers E, Schwingshackl M, Opetnik M, Kennedy D. Greenhouse Gas Emissions Performance of Electric, Hydrogen and Fossil-Fuelled Freight Trucks with Uncertainty Estimates Using a Probabilistic Life-Cycle Assessment (pLCA). Sustainability. 2024; 16(2):762. https://doi.org/10.3390/su16020762
Chicago/Turabian StyleSmit, Robin, Eckard Helmers, Michael Schwingshackl, Martin Opetnik, and Daniel Kennedy. 2024. "Greenhouse Gas Emissions Performance of Electric, Hydrogen and Fossil-Fuelled Freight Trucks with Uncertainty Estimates Using a Probabilistic Life-Cycle Assessment (pLCA)" Sustainability 16, no. 2: 762. https://doi.org/10.3390/su16020762
APA StyleSmit, R., Helmers, E., Schwingshackl, M., Opetnik, M., & Kennedy, D. (2024). Greenhouse Gas Emissions Performance of Electric, Hydrogen and Fossil-Fuelled Freight Trucks with Uncertainty Estimates Using a Probabilistic Life-Cycle Assessment (pLCA). Sustainability, 16(2), 762. https://doi.org/10.3390/su16020762






