Study on the Mechanism of Safety Risk Propagation in Subway Construction Projects
Abstract
:1. Introduction
1.1. Background
1.2. Point of Departure
2. Literature Review
2.1. Construction Safety in Sustainability
2.2. Metro Construction Safety Risks
2.3. Risk Propagation Models
3. Generation and Attributes Analysis of the Subway Construction Safety Risk Network (SCSRN)
3.1. Identification of Safety Risks in Subway Construction
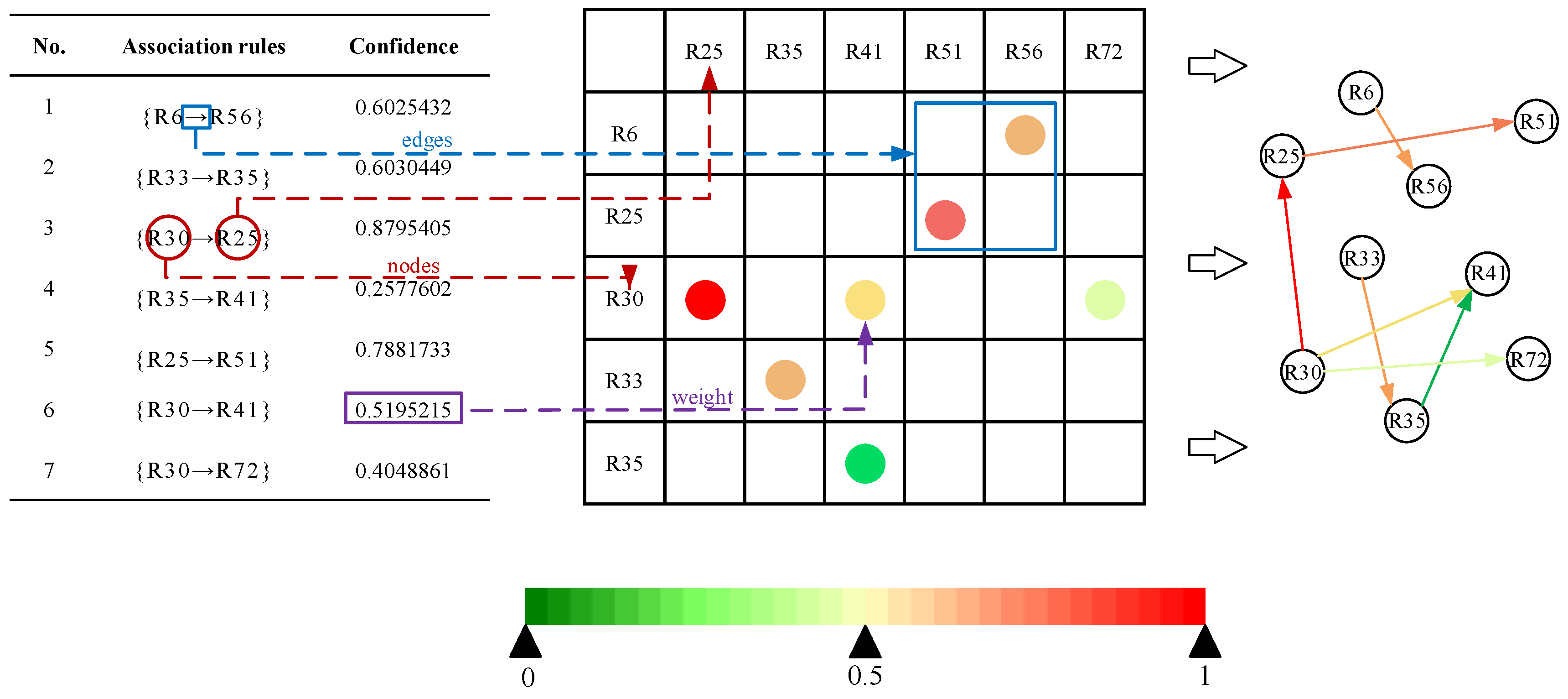
3.2. Identification of Relationships among Safety Risks in Subway Construction
3.3. Visualization of the SCSRN
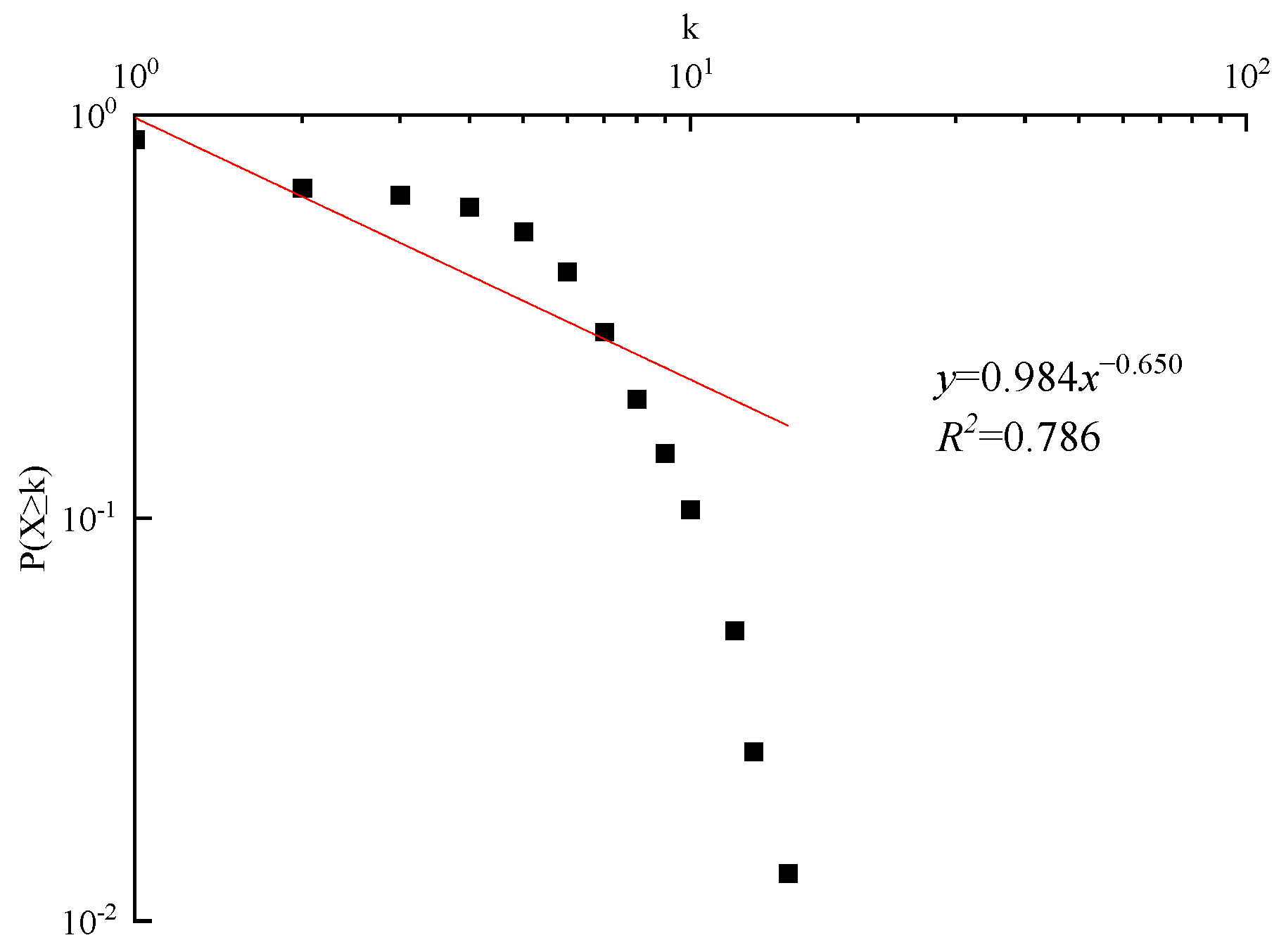
3.4. Attributes Analysis of the SCSRN
4. Modeling the Subway Construction Safety Risk Propagation
4.1. Model Assumptions
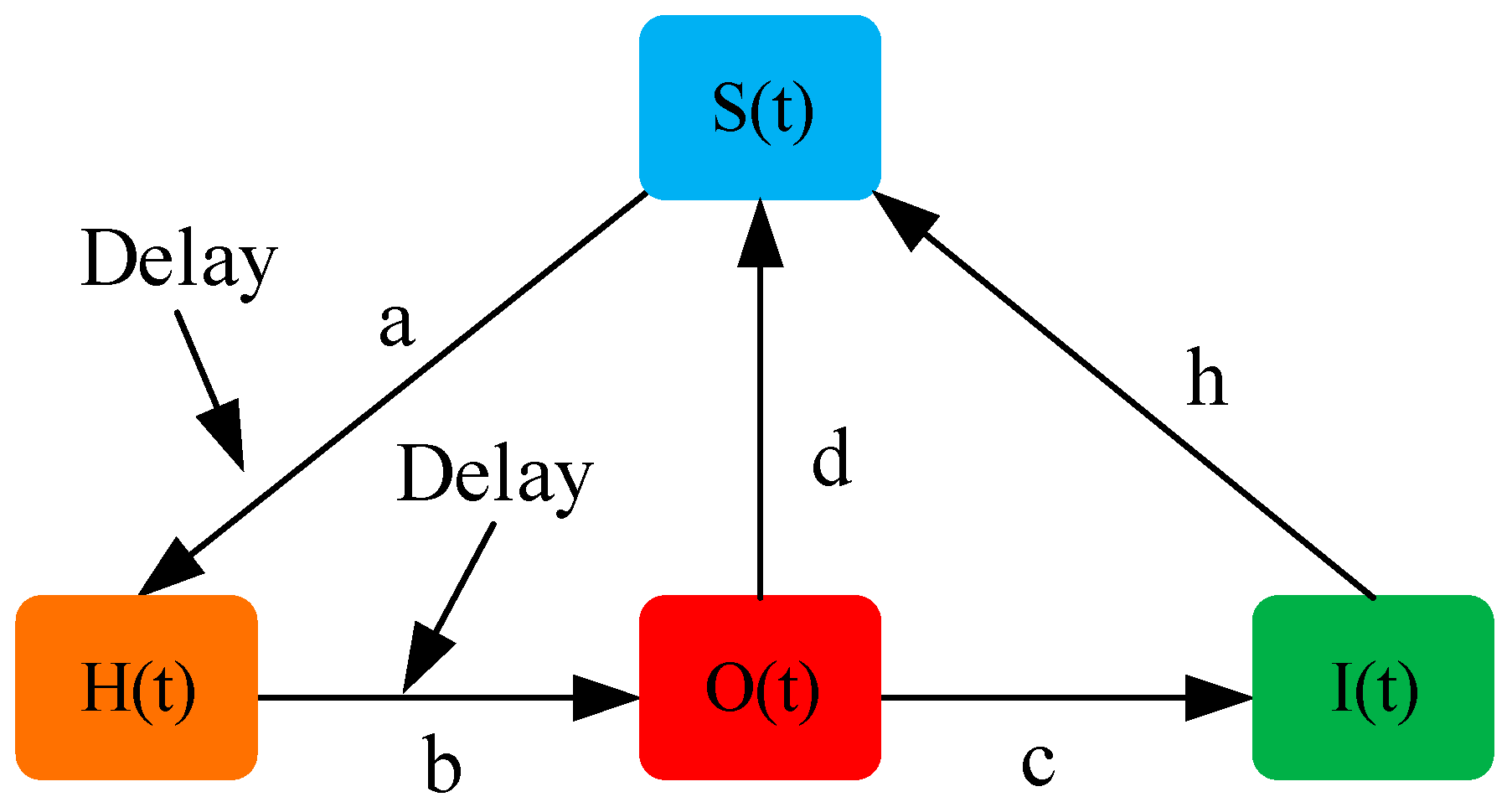
4.2. Construction of the SHOIS Model
4.3. Equilibrium and Stability Analysis
4.3.1. Risk Aversion Equilibrium and Stability Analysis
4.3.2. Risk Outbreak Equilibrium and Stability Analysis
4.4. Propagation Threshold Analysis
4.5. Steady-State Density Analysis
5. Simulation Analysis of Subway Construction Safety Risk Propagation Model
5.1. Parameter Setting
5.2. Simulation Results Discussion and Analysis
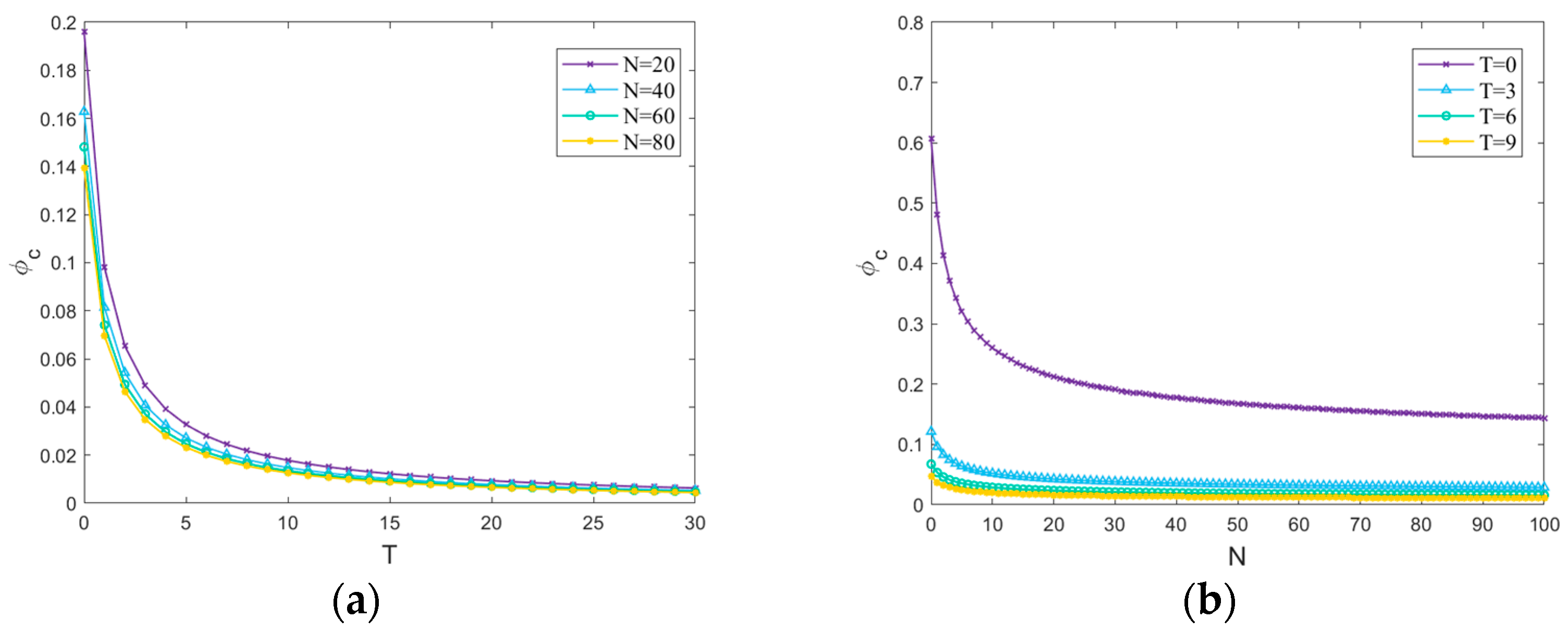
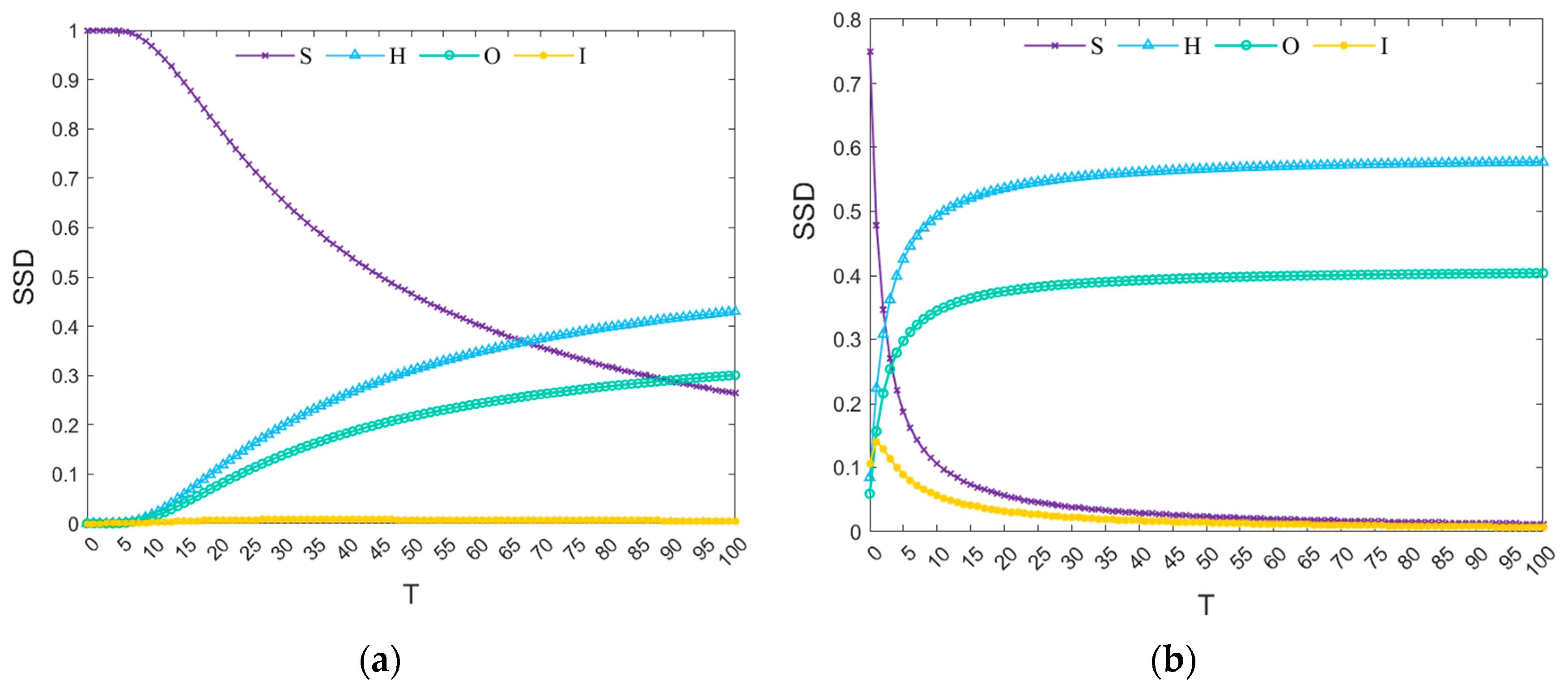
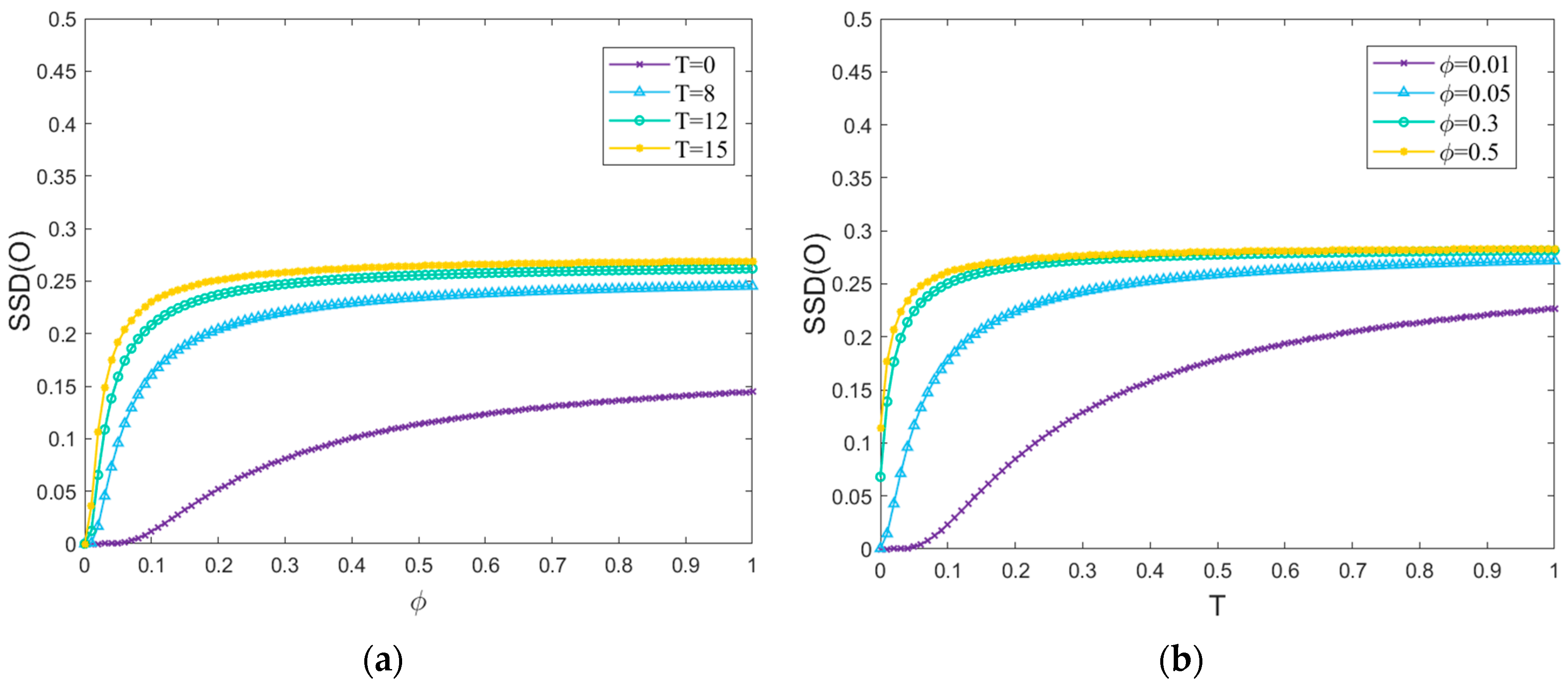
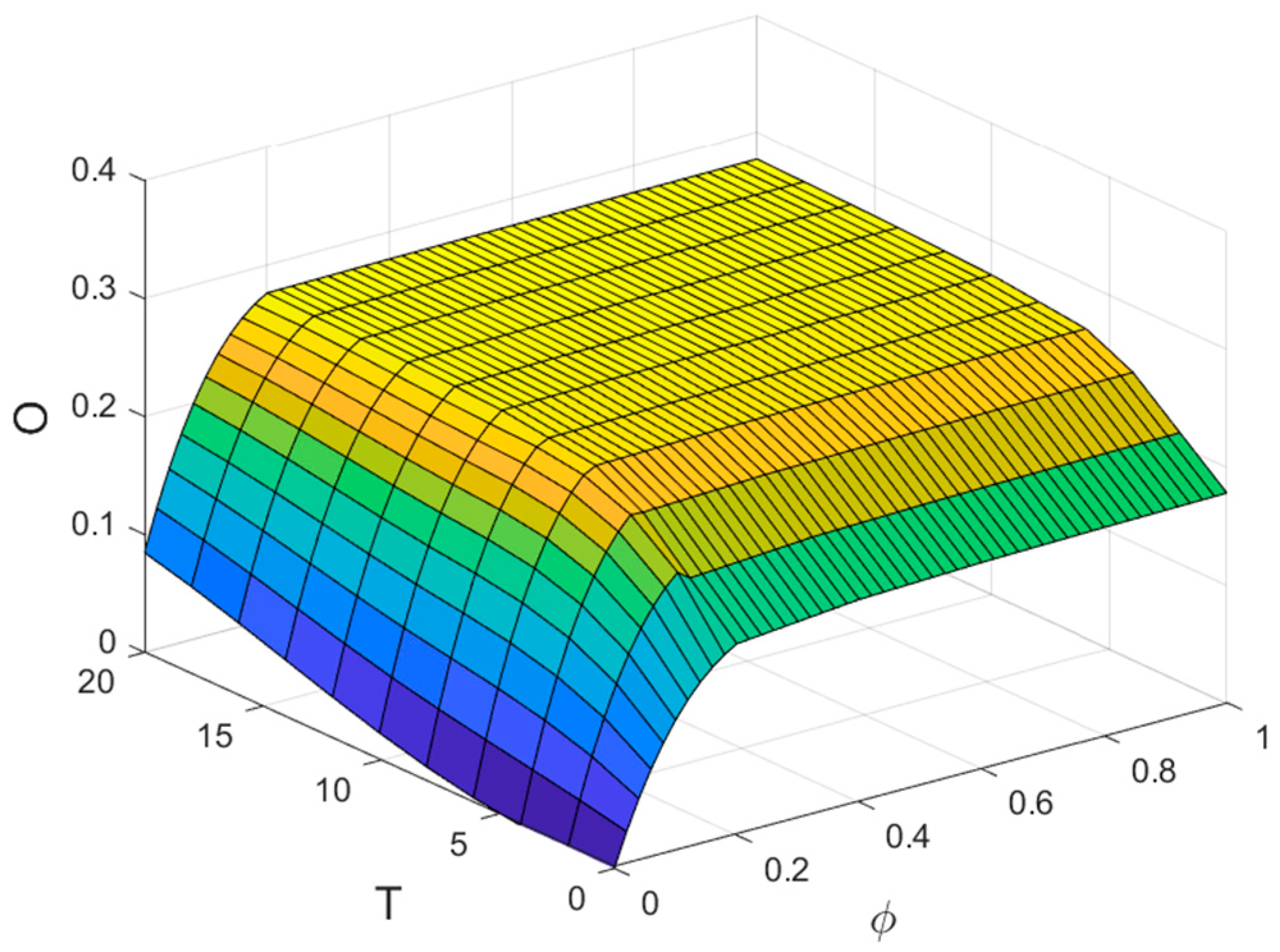
5.2.1. Influence of T on Propagation Thresholds
5.2.2. Influence of T on Steady-State Density
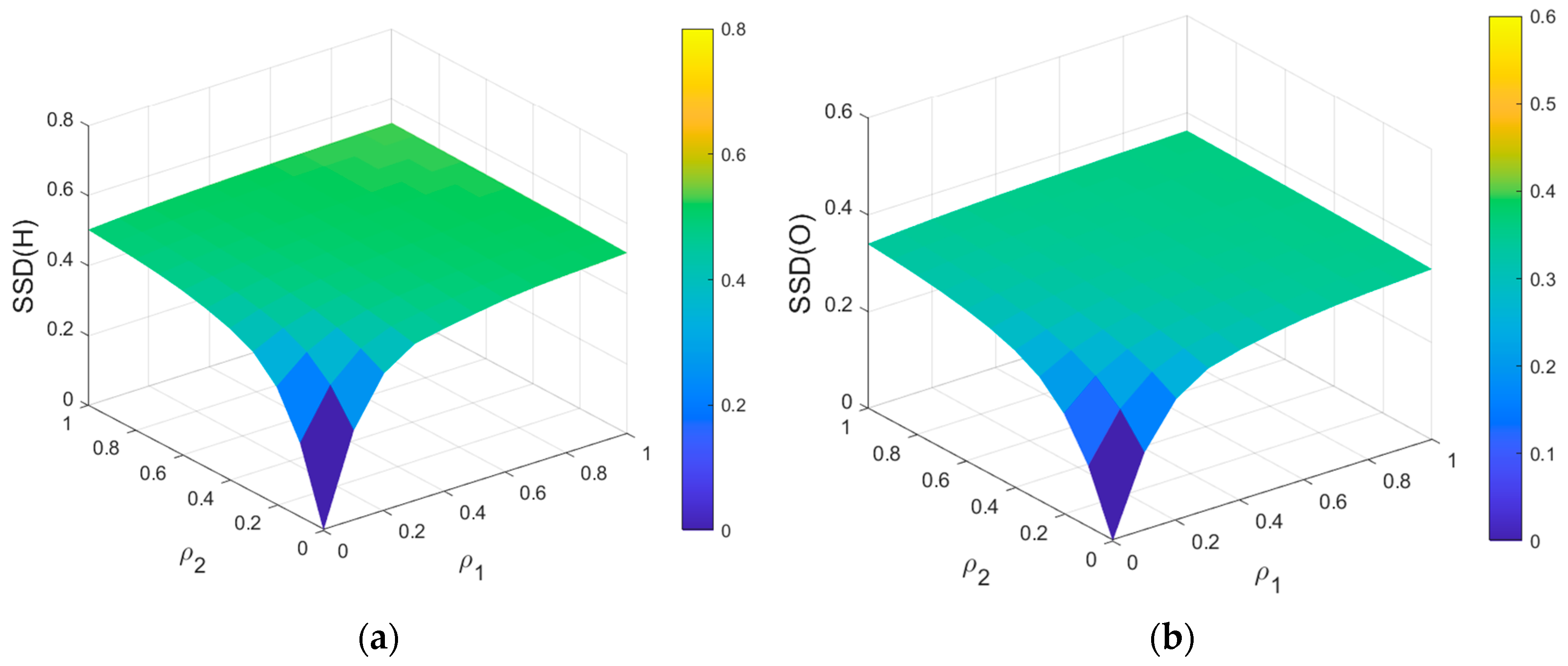
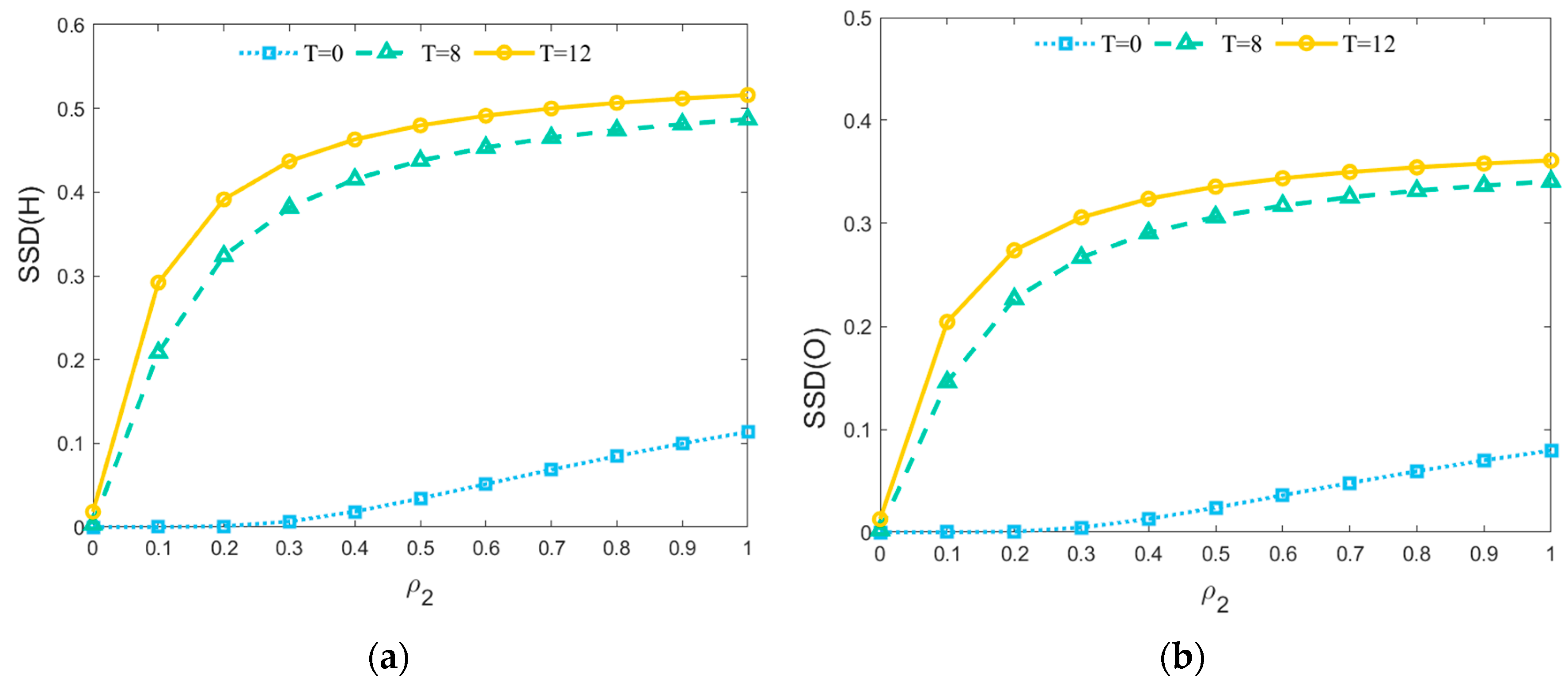
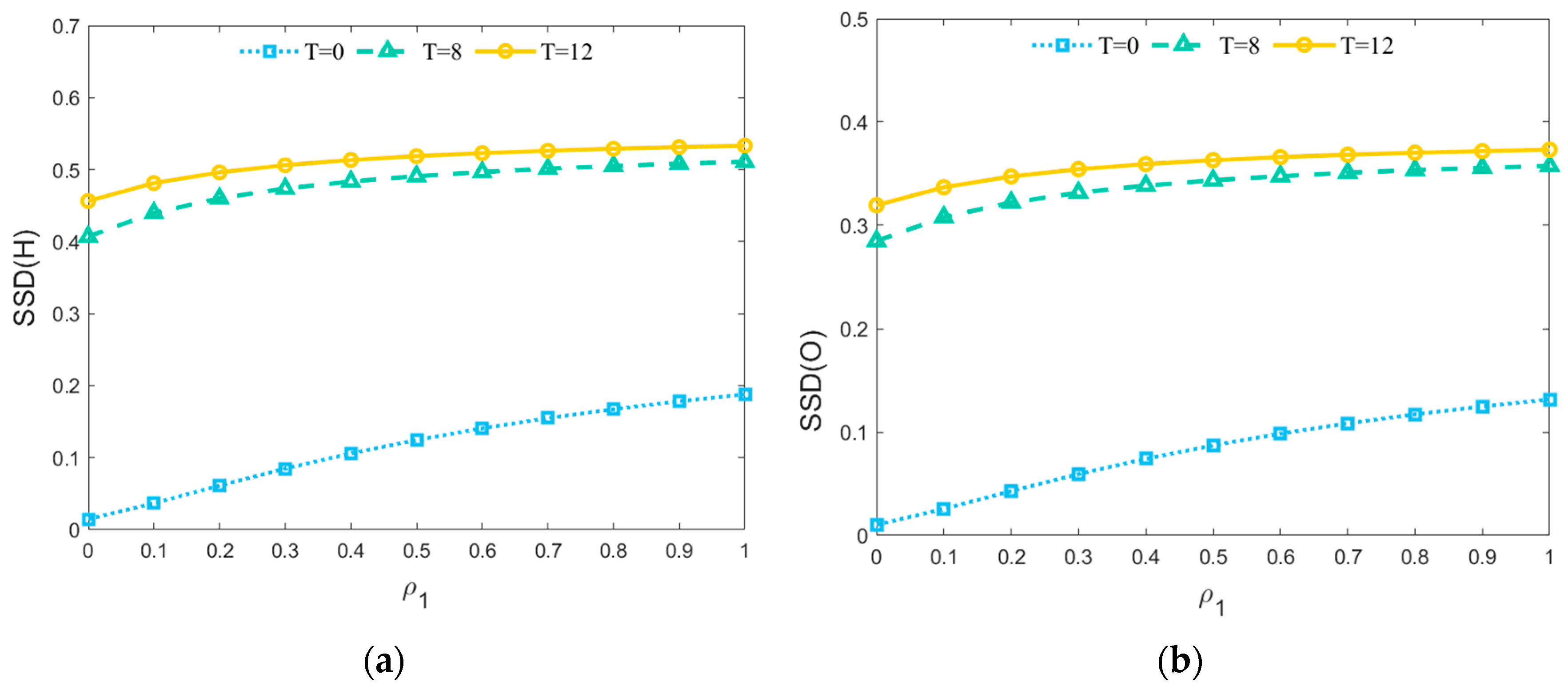
5.2.3. Influence of ρ1, ρ2 on Steady-State Density
5.2.4. Impact of φ on the Proportion of Risk Outbreak
5.3. Impact of Relevant Parameters on the Proportion of Risk Outbreaks
6. Conclusions
- (1)
- The subway construction safety risk network has the dual characteristics of scale-free and small world. This means that safety accidents in the subway construction industry are not random events but rather the result of a strong correlation between different safety risk factors.
- (2)
- The delay time T significantly affects the propagation behavior of risk and the achievement of the equilibrium state in the network. For the case of φ < φc (max), a longer T is required to transition the steady-state density of various nodes from the risk-averse state to the risk-bursting state. While in the case of φ > φc (max), only a shorter T is needed to reach the equilibrium state, and T speeds up the equilibrium state achievement.
- (3)
- In the process of risk propagation, the time element is more decisive than the network size. The transmissibility of risk factors in the hidden state plays a critical role in the whole process of risk diffusion, and the delay effect of propagation accelerates the diffusion of risk in the network. When the parameters are certain, the steady-state densities of all risk nodes within the network are related to the contagion rates ρ1 and ρ2 and the delay time T. However, the different values of ρ1 and ρ2 have almost no effect on the values of steady-state densities that eventually reach the equilibrium state.
- (4)
- Construction enterprises need to focus on the propagation of hidden state risk nodes and the delay of risk contagion when developing subway construction safety risk control programs. The safety state nodes and hidden state nodes should be monitored and warned to block the spread of risk in the network promptly and to control the delay time of risk in the network to reduce the probability of risk occurrence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, H.A.; Zhou, Z.P.; Yuan, J.F.; Li, N.; Zhou, J.L. Accident pattern recognition in subway construction for the provision of customized safety measures. Tunn. Undergr. Space Technol. 2023, 137, 105157. [Google Scholar] [CrossRef]
- Zhou, Z.; Goh, Y.M.; Shi, Q.; Qi, H.; Liu, S. Data-driven determination of collapse accident patterns for the mitigation of safety risks at metro construction sites. Tunn. Undergr. Space Technol. 2022, 127, 104616. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Song, L.; Ni, G.; Xu, N. Exploring the metro construction accidents and causations for improving safety management based on data mining and network theory. Eng. Constr. Arch. Manag. 2023, 1–25. [Google Scholar] [CrossRef]
- Zhou, Z.P.; Irizarry, J.; Guo, W.Y. A network-based approach to modeling safety accidents and causations within the context of subway construction project management. Saf. Sci. 2021, 139, 105261. [Google Scholar] [CrossRef]
- Xu, N.; Ma, L.; Liu, Q.; Wang, L.; Deng, Y. An improved text mining approach to extract safety risk factors from construction accident reports. Saf. Sci. 2021, 138, 105216. [Google Scholar] [CrossRef]
- Chen, F.Y.; Wang, H.W.; Xu, G.Y.; Ji, H.C.; Ding, S.L.; Wei, Y.C. Data-driven safety enhancing strategies for risk networks in construction engineering. Reliab. Eng. Syst. Saf. 2020, 197, 106806. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, L.P.; Hu, Z.G.; Chen, S.; Zheng, X.Z. Risk Propagation in Multilayer Heterogeneous Network of Coupled System of Large Engineering Project. J. Manage. Eng. 2022, 38, 13. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, Y.; Zhang, Y. Exploring the risk propagation mechanisms of supply chain for prefabricated building projects. J. Build. Eng. 2023, 74, 106771. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Z.; Liu, Q.; Zhao, M. Risk Propagation of Delayed Payment in Stakeholder Network of Large Hydropower Project Construction considering Risk Resistance and Mitigation. Math. Probl. Eng. 2018, 2018, 8013207. [Google Scholar] [CrossRef]
- Halabi, Y.; Xu, H.; Long, D.; Chen, Y.; Yu, Z.; Alhaek, F.; Alhaddad, W. Causal Factors and Risk Assessment of Fall Accidents in the U.S. Construction Industry: A Comprehensive Data Analysis (2000–2020). Saf. Sci. 2022, 146, 105537. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X. Developing a Holistic Occupational Health and Safety Risk Assessment Model: An Application to a case of Sustainable Construction Project. J. Clean. Prod. 2021, 291, 125934. [Google Scholar] [CrossRef]
- Zuo, J.; Rameezdeen, R.; Hagger, M.; Zhou, Z.; Ding, Z. Dust Pollution Control on Construction Sites: Awareness and self-responsibility of Managers. J. Clean. Prod. 2017, 166, 312–320. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, D.S.; Kim, J.D.; Kim, G.H. Priority of Accident Cause Based on Tower Crane Type for the Realization of Sustainable Management at Korean Construction Sites. Sustainability 2020, 13, 242. [Google Scholar] [CrossRef]
- Dong, N.; Fu, Y.; Xiong, F.; Li, L.; Ao, Y.; Martek, I. Sustainable Construction Project Management (SCPM) Evaluation—A Case Study of the Guangzhou Metro Line-7, PR China. Sustainability 2019, 11, 5731. [Google Scholar] [CrossRef]
- Xing, X.; Zhong, B.; Luo, H.; Li, H.; Wu, H. Ontology for Safety Risk Identification in Metro Construction. Comput. Ind. 2019, 109, 14–30. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, C. Fuzzy Comprehensive Bayesian Network-Based Safety Risk Assessment for Metro Construction Projects. Tunn. Undergr. Space Technol. 2017, 70, 330–342. [Google Scholar] [CrossRef]
- Yan, H.; Gao, C.; Elzarka, H.; Mostafa, K.; Tang, W. Risk Assessment for Construction of Urban Rail Transit Projects. Saf. Sci. 2019, 118, 583–594. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Wu, X.; Skibniewski, M.J.; Qunzhou, Y. Safety Management in Tunnel Construction: Case Study of Wuhan metro Construction in China. Saf. Sci. 2014, 62, 8–15. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, Y.; Luo, H.; Wu, X. Using nD Technology to Develop an Integrated Construction Management System for City rail Transit Construction. Autom. Constr. 2012, 21, 64–73. [Google Scholar] [CrossRef]
- Li, Y.; Xiang, P.; You, K.; Guo, J. Dynamic Network Analysis of the Risks of Mega Infrastructure Projects from a Sustainable Development Perspective. Buildings 2022, 12, 434. [Google Scholar] [CrossRef]
- Fang, M.; Zhang, Y.; Zhu, M.; Chen, S. Cause Mechanism of Metro Collapse Accident Based on Risk Coupling. Int. J. Environ. Res. Public Health 2022, 19, 2102. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Wang, X.; Zhao, H.; Li, M. Interactions among Safety Risks in Metro Deep Foundation Pit Projects: An Association Rule Mining-Based Modeling Framework. Reliab. Eng. Syst. Saf. 2022, 221, 108381. [Google Scholar] [CrossRef]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Jung, H.; Phoa, F.K.H. On the effects of capability and popularity on network dynamics with applications to YouTube and Twitch networks. Physica A 2020, 571, 125663. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Z.; Liu, Q. Exploring the properties of cost overrun risk propagation network (corpn) for promoting cost management. J. Civ. Eng. Manag. 2019, 25, 1–18. [Google Scholar] [CrossRef]
- Marinovg, T.T.; Marinovag, R.S. Inverse problem for adaptive SIR model: Application to COVID-19 in Latin America. Infect. Dis. Model. 2021, 7, 134–148. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Y.; Ma, Y. Modeling the competitive diffusions of rumor and knowledge and the impacts on epidemic spreading. Appl. Math. Comput. 2020, 388, 125536. [Google Scholar] [CrossRef]
- Wang, Y.C.; Sun, R.; Ren, L.Y.; Geng, X.X.; Wang, X.M.; Lv, L. Risk Propagation Model and Simulation of an Assembled Building Supply Chain Network. Buildings 2023, 13, 981. [Google Scholar] [CrossRef]
- Kang, H.; Sun, M.; Yu, Y.; Fu, X.; Bao, B. Spreading Dynamics of an SEIR Model with Delay on Scale-Free Networks. IEEE Trans. Netw. Sci. Eng. 2018, 7, 489–496. [Google Scholar] [CrossRef]
- Kiselev, I.N.; Akberdin, I.R.; Kolpakov, F.A. Delay-Differential SEIR Modeling for Improved Modelling of Infection Dynamics. Sci. Rep. 2023, 13, 1–15. [Google Scholar] [CrossRef]
- GB6441-1986; Classification for Casualty Accidents of Enterprise Staff and Workers. Standardization Administration of the P.R.C.: Beijing, China, 1986.
- Suh, Y. Sectoral Patterns of Accident Process for Occupational Safety Using Narrative Texts of OSHA Database. Saf. Sci. 2021, 142, 105363. [Google Scholar] [CrossRef]
- Grant, A.; Hinze, J. Construction worker fatalities related to trusses: An analysis of the OSHA fatality and catastrophic incident database. Saf. Sci. 2014, 65, 54–62. [Google Scholar] [CrossRef]
- GB/T15236-2008; General Administration of Quality Supervision, Inspection and Quarantine and Standardization Administration. Occupational Safety and Health Glossary: Beijing, China, 2008.
- Telikani, A.; Gandomi, A.H.; Shahbahrami, A. A survey of evolutionary computation for association rule mining. Inf. Sci. 2020, 524, 318–352. [Google Scholar] [CrossRef]
- Czibula, G.; Czibula, I.G.; Miholca, D.L.; Crivei, L.M. A novel concurrent relational association rule mining approach. Expert Syst. Appl. 2019, 125, 142–156. [Google Scholar] [CrossRef]
- Han, Y.; Bao, X. Topological mapping of complex networks from high slope deformation time series for landslide risk assessment. Expert Syst. Appl. 2022, 206, 117816. [Google Scholar] [CrossRef]
- Fang, C.; Marle, F.; Zio, E.; Bocquet, J.-C. Network theory-based analysis of risk interactions in large engineering projects. Reliab. Eng. Syst. Saf. 2012, 106, 1–10. [Google Scholar] [CrossRef]
- Fang, X.; Yang, Q.; Yan, W. Topological characterization and modeling of dynamic evolving power distribution networks. Simul. Model. Pract. Theory 2012, 31, 186–196. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, S.; Zhu, X. Information Diffusion under Public Crisis in BA Scale-Free Network Based on SEIR Model—Taking COVID-19 as an Example. Phys. A Stat. Mech. Its Appl. 2021, 571, 125848. [Google Scholar] [CrossRef]
- Li, R.; Wang, W.; Shu, P.; Yang, H.; Pan, L.; Cui, A.; Tang, M. Review of Threshold Theoretical Analysis About Epidemic Spreading Dynamics on Complex Networks. Complex Syst. Complex. Sci. 2016, 13, 1–39. [Google Scholar] [CrossRef]




| Expert | Position | Experience (Year) | Role | Educational Background | Professional |
|---|---|---|---|---|---|
| 1 | Project manager | 15–20 | Owner | MEM | Civil Engineering |
| 2 | Project manager | 15–20 | Contractor | MEM | Project Management |
| 3 | Safety officer | 10–15 | Contractor | Master’s degree | Safety management |
| 4 | Safety officer | >15 | Contractor | Master’s degree | Safety management |
| 5 | Project manager | 15–20 | Contractor | PHD | Civil Engineering |
| 6 | Engineer | 10–15 | Supervisory unit | PHD | Urban railway transportation |
| 7 | Safety officer | >20 | Subcontractor | Undergraduate | Safety management |
| 8 | Safety officer | 15–20 | Contractor | Undergraduate | Safety management |
| 9 | Safety officer | 10–15 | Contractor | Master’s degree | Safety management |
| 10 | Safety officer | 10 | Contractor | Master’s degree | Safety management |
| Risk Factors (Code) | Description |
|---|---|
| Human and organizational factors | |
| Owner | |
| High pressure on schedule (R1) | Inadequate owner preparation leads to schedule pressure, e.g., financing and land acquisition. |
| Supervision unit | |
| Unqualified supervisory qualifications, skills, and experience (R2) | The supervision agency lacks professional certificates, professional skills, and work experience. |
| Oversight programs and responsibilities not implemented (R3) | The supervisory personnel did not execute the supervision plan or fulfill their obligations. |
| Inadequate supervisory safety education and training (R4) | Supervisors did not receive appropriate education and training to improve their work abilities. |
| Weak supervisory safety awareness and responsibility (R5) | Supervisors lack safety awareness and a sense of responsibility. |
| Inadequate supervisory oversight, inspection, and documentation (R6) | The supervisory personnel did not conduct necessary supervision, review, and recording by the work requirements. |
| Survey unit | |
| Unsatisfactory survey qualifications, skills, and experience (R7) | Survey agencies lack professional certificates, professional skills, and work experience. |
| Inadequate surveys or remedial surveys (R8) | Insufficiently detailed investigation of hydrological, geological, environmental, and other factors |
| Weak awareness and responsibility for survey safety (R9) | Survey personnel lack safety awareness and a sense of responsibility. |
| Measuring specifications not implemented (R10) | Failure to operate by regulatory requirements during the survey process. |
| Insufficient survey accuracy (R11) | The survey accuracy of crucial information such as geology, hydrology, and environment makes it challenging to meet construction requirements. |
| Survey security plan not engaged (R12) | The survey personnel did not fully participate in the design and implementation of the safety plan. |
| Monitoring unit | |
| Unqualified monitoring qualifications, skills, and experience (R13) | Monitoring institutions lack professional certificates, professional skills, and work experience. |
| Inadequate monitoring programs and their implementation (R14) | Monitoring personnel did not implement the monitoring plan. |
| Weak awareness and responsibility for monitoring security (R15) | Monitoring personnel lack safety awareness and a sense of responsibility. |
| Monitoring equipment inspection and maintenance (R16) | Regular calibration, cleaning, sensor replacement, and maintenance. |
| Inaccurate monitoring (R17) | Inaccurate monitoring data on surface subsidence, deformation of surrounding buildings and structures, and pipeline subsidence. |
| Monitoring and early warning processing and reporting (R18) | Inadequate detection, reporting, and emergency response measures for abnormal monitoring data. |
| Designer | |
| Unqualified design qualifications, skills, and experience (R19) | The design unit lacks a professional certificate, professional skills, and work experience. |
| Flawed design solutions (R20) | The design scheme does not meet the expected construction standards. |
| Weak design security awareness and responsibility (R21) | Designers lack safety awareness and a sense of responsibility. |
| Design Changes (R22) | Changes in engineering content due to design errors, omissions, and modifications in process technology |
| Design specifications not implemented (R23) | Failure to design by regulatory requirements during the design process. |
| Design of security plans without participation (R24) | Designers did not fully participate in the design and implementation of the safety plan. |
| Contractor | |
| Unauthorized work by construction workers (R25) | Improper use of personal protective equipment, non-compliance with workplace safety operating procedures, and failure to comply with safety production instructions. |
| Improper handling by construction personnel (R26) | Poor behavior or incorrect operation of workers. |
| Construction workers without a license (R27) | Workers participate in construction without obtaining relevant operation or professional qualification certificates for their respective occupations. |
| Insufficient specialized skills and experience of construction personnel (R28) | Insufficient professional knowledge, experience, and skills of workers. |
| Directing against the rules (R29) | Improper or non-compliant direction of construction operations by personnel in violation of relevant statutes, rules, and regulations or safety operating procedures. |
| Poor security awareness among contractors (R30) | Neglect of safety equipment and facilities by contractors, failure to implement safety standards and procedures, and pursuit of speed at the expense of safety. |
| Inadequate or unfulfilled safety management system (R31) | Incomplete safety system procedures or failure to strictly follow safety regulations. |
| Failure to implement the primary responsibility for production safety (R32) | The management has not fully assumed the primary responsibility for safety production. |
| Failure to implement safety specifications (R33) | Failure to follow safety regulations during the construction process. |
| Inadequate contractor safety education and training (R34) | The contractor did not provide sufficient safety training to the workers. |
| Incomplete technical disclosure (R35) | The construction party’s disclosure of engineering technical details, operating methods, and safety regulations is insufficient or comprehensive. |
| Unreasonable construction plan (R36) | Unreasonable construction schedule, irrational resource allocation, and construction plan not meeting construction requirements. |
| Inadequate safety supervision of on-site workers by management personnel (R37) | Insufficient supervision and guidance of workers by construction site management personnel. |
| Inadequate safety management organization (R38) | Chaotic organizational structure in security management. |
| Improper management of subcontractors and suppliers (R39) | The contractor failed to effectively supervise and control the work and behavior of subcontractors and suppliers. |
| Insufficient emergency plans and drills (R40) | Inadequate emergency response plans, measures, and drills. |
| Inadequate identification of hidden dangers (R41) | Failure to fully identify, identify, and resolve potential safety hazards. |
| Chaotic construction site management (R42) | Including unclear construction processes and chaotic division of labor among personnel. |
| Poor construction organization and coordination (R43) | Lack of effective communication and coordination in terms of resources, progress, and safety plans, and inadequate communication and coordination in terms of safety plans. |
| Improper use of mechanical equipment (R44) | Continue using a specific device when it is not suitable for use. |
| Worker fatigue work (R45) | The workers were in a high-intensity working state for several consecutive hours. |
| Insufficient investment in funds, materials, and personnel (R46) | The acquisition of funds, materials, and personnel cannot meet the safety requirements of subway construction. |
| Safety culture and atmosphere (R47) | The company lacks an atmosphere emphasizing a safety culture, and staff are indifferent to safety issues. |
| Improper remedial measures (R48) | After problems or dangerous situations arise, the measures taken are not effective, inappropriate, or appropriate enough to solve the problem or prevent risks effectively. |
| Safety protection measures not implemented (R49) | Although there are prescribed safety measures, in reality, these measures have not been effectively implemented. |
| Lack of safety signs (R50) | Dangerous areas not indicated. |
| Not following the construction plan for construction (R51) | The construction process was not carried out according to the established construction plan or plan. |
| Failure to construct according to design requirements (R52) | The construction process was not carried out according to the design requirements. |
| Inaccurate hydrogeological survey (R53) | There are errors or deficiencies in the hydrogeological survey conducted before construction. |
| Insufficient exploration and maintenance of surrounding buildings (structures) (R54) | Insufficient exploration or protection of adjacent or crossing existing or protective buildings (structures) may cause settlement, cracks, deformation, and other impacts. |
| Improper construction reinforcement measures (R55) | The structure of tunnels, stations, and track systems has not been strengthened using high-strength concrete, fiber-reinforced materials, rock anchor support, and other methods. |
| Improper construction of deep foundation pits (R56) | Failure to take adequate support measures, failure to control the groundwater level during excavation, and failure to effectively protect the surrounding buildings and underground pipelines. |
| Improper construction of manually excavated and poured piles (R57) | Significant deviation in aperture, uneven quality of pile concrete pouring, steel reinforcement not meeting design requirements, and unqualified verticality of pile body. |
| Improper construction of steel reinforcement engineering (R58) | Wrong binding of steel bars, misalignment, weak connection of steel bars, insufficient concrete cover layer. |
| Improper construction of bridge high piers (R59) | Uneven concrete pouring and improper foundation treatment. |
| Improper construction of bridge superstructure (R60) | Uneven pouring of the beam body, improper control of prestressed tension, improper setting of expansion joints, and unstable connection of the beam body. |
| Improper installation and removal of templates, brackets, and arches (R61) | The unstable support structure, incorrect template positioning, inconsistent support height, and insufficient overall stability of the arch. |
| Improper installation and removal of temporary facilities (R62) | Installation and removal of tower cranes, gantry cranes, dormitories, office areas. |
| Improper construction of tunnel entrance slope engineering (R63) | Poor stability of the entrance slope. |
| Improper excavation and construction of tunnel body (R64) | Unreasonable excavation methods. |
| Improper construction of support lining system (R65) | Lining void, lining cracking, leakage, cracks. |
| Structural construction quality defects (R66) | Insufficient strength of engineering structure and improper construction technology. |
| Machine and material | |
| Unreasonable stacking of materials and equipment (R67) | The stacking method of materials and equipment does not comply with the principles of safety, order, and efficiency |
| Mechanical equipment failure (R68) | Machine equipment fails or encounters problems during operation due to various reasons. |
| Insufficient inspection and maintenance of machines and materials (R69) | The machinery, equipment, and materials used were not inspected and maintained in a timely and appropriate manner |
| Overload operation of machines and equipment (R70) | Equipment operates beyond its design load and capacity |
| Improper selection of materials and equipment (R71) | Incorrect choice of materials that do not meet engineering requirements or pieces of equipment with inappropriate specifications and performance mismatch |
| Improper operation of machinery and equipment (R72) | Not following the operating manual or manufacturer’s instructions for mechanical equipment |
| Environment | |
| Bad weather (R73) | Persistent gale and rainstorms |
| Unknown underground hydrological conditions (R74) | Unknown water level and unclear water quality characteristics |
| Complex geological conditions (R75) | Underground cavities, complex strata, soil conditions, different types, hardness, and stability of rocks |
| Narrow, messy, and overlapping work environment (R76) | The construction site is limited, chaotic, and overlapping, which affects construction efficiency and safety |
| Accident name | “2.20” Qingdao Metro Line 5 Shilaoren Bathing Station Choking Accident |
| Accident time | 20 February 2023 |
| Analysis of causes | Direct cause: ➀ Maintenance personnel have a weak sense of safety and discipline when repairing rotary drilling rigs, do not comply with the company’s safety management rules and regulations, disobey the company’s maintenance instructions. ➁ Workers do not identify the safety risks, risk entering the rotary drilling rig drill pipe inside (narrow, limited space) work. ➂ The operator did not implement safety specifications, used a hand-held electric angle grinder in violation of the law, and improperly operated the equipment. ➃ Sparks generated during the operation of an angle grinder ignited combustible materials. They produced a large amount of smoke, which caused the safety rope to break and trap the person, resulting in death by asphyxiation. ➄ Management personnel did not supervise the safety of the construction site, hidden dangers were not investigated, and combustible materials were piled up randomly, posing a potential safety hazard. Indirect causes: ➀ Inadequate control of the construction site by managers. ➁ The operator did not identify the risk in place. It did not recognize that after the rotary drilling rig malfunctioned, the lifting device fell off, forming a narrow space inside the drill pipe. ➂ Work safety education and training are not in place. Practitioners fail to truly grasp the knowledge and skills of production safety, resulting in a weak sense of production safety, compliance with rules and regulations, the complexity of limited space operations, and an insufficient understanding of the dangers and risky operations. |
| Accident data sets | {R25, R26, R30, R33, R34, R37, R41, R42, R68, R72, R76} |
| Network | Nodes | Edges | Density | Diameter | L | C | k |
|---|---|---|---|---|---|---|---|
| SCSRN | 76 | 330 | 0.058 | 5.62 | 1.997 | 0.114 | 4.342 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Shen, J.; Zhu, X.; An, B.; Liu, F.; Bao, X. Study on the Mechanism of Safety Risk Propagation in Subway Construction Projects. Sustainability 2024, 16, 796. https://doi.org/10.3390/su16020796
Han Y, Shen J, Zhu X, An B, Liu F, Bao X. Study on the Mechanism of Safety Risk Propagation in Subway Construction Projects. Sustainability. 2024; 16(2):796. https://doi.org/10.3390/su16020796
Chicago/Turabian StyleHan, Yuanwen, Jiang Shen, Xuwei Zhu, Bang An, Fusheng Liu, and Xueying Bao. 2024. "Study on the Mechanism of Safety Risk Propagation in Subway Construction Projects" Sustainability 16, no. 2: 796. https://doi.org/10.3390/su16020796
APA StyleHan, Y., Shen, J., Zhu, X., An, B., Liu, F., & Bao, X. (2024). Study on the Mechanism of Safety Risk Propagation in Subway Construction Projects. Sustainability, 16(2), 796. https://doi.org/10.3390/su16020796






