A State-of-the-Art Review of Hydraulic Fracturing in Geothermal Systems
Abstract
:1. Introduction
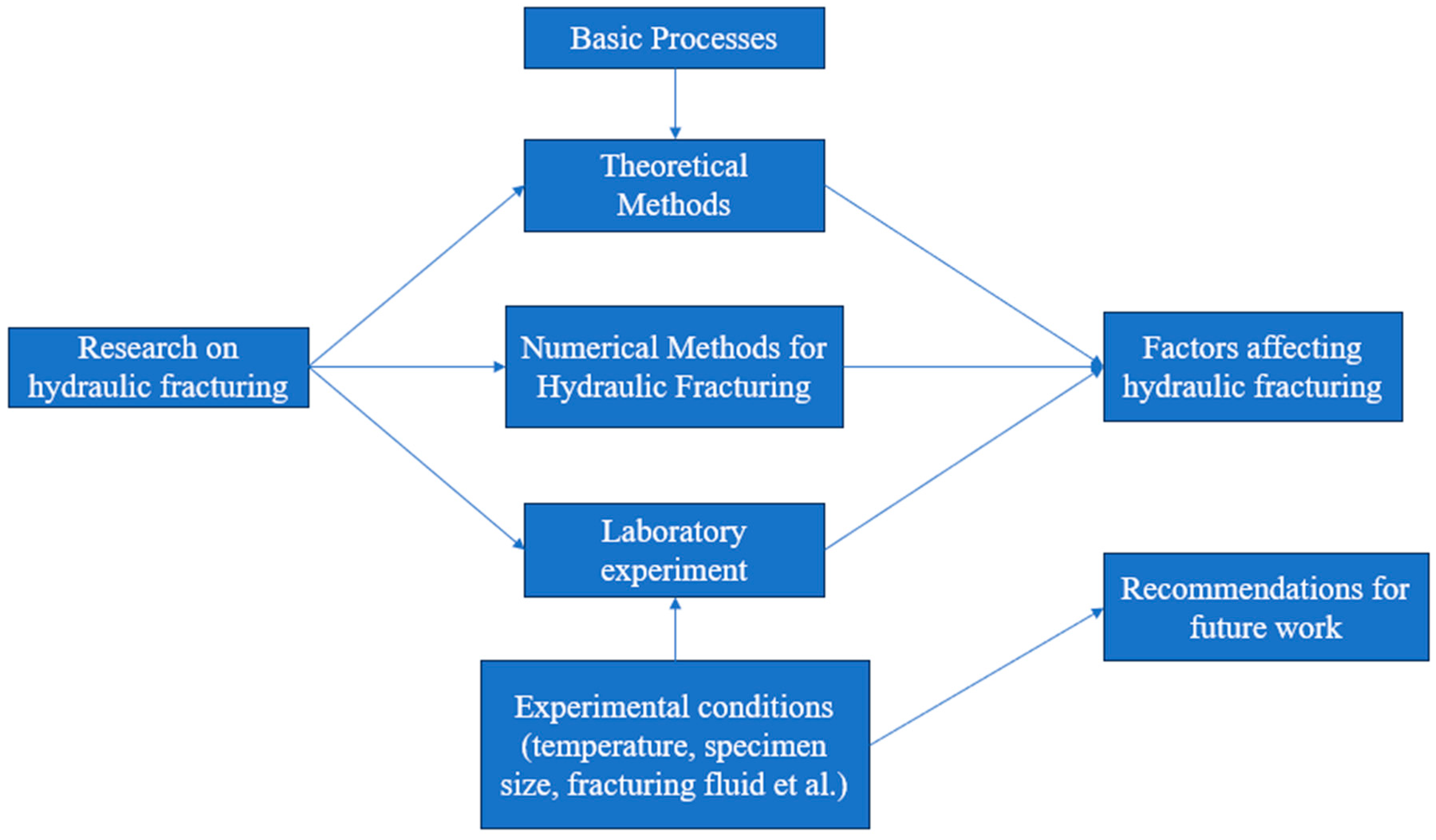
2. Laboratory Methods for Hydraulic Fracturing
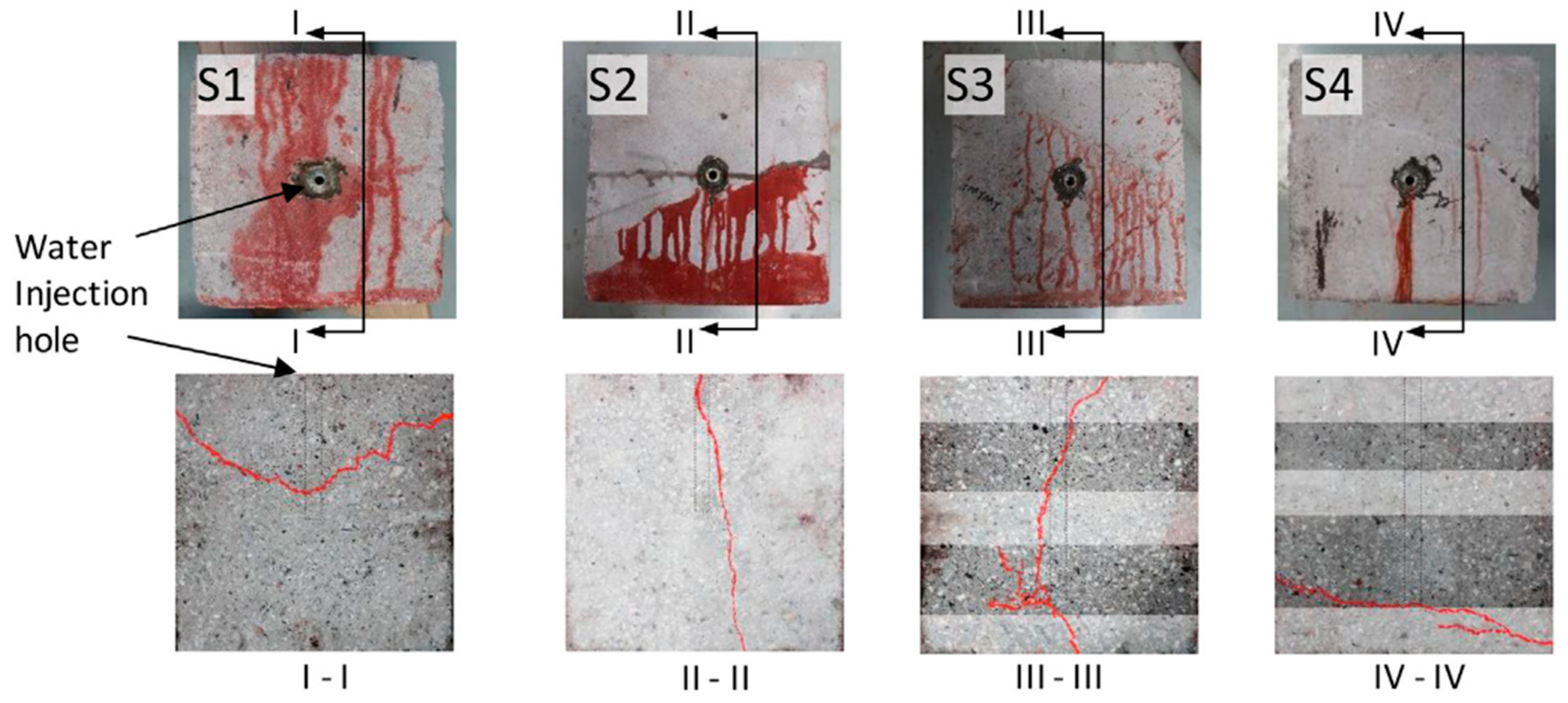
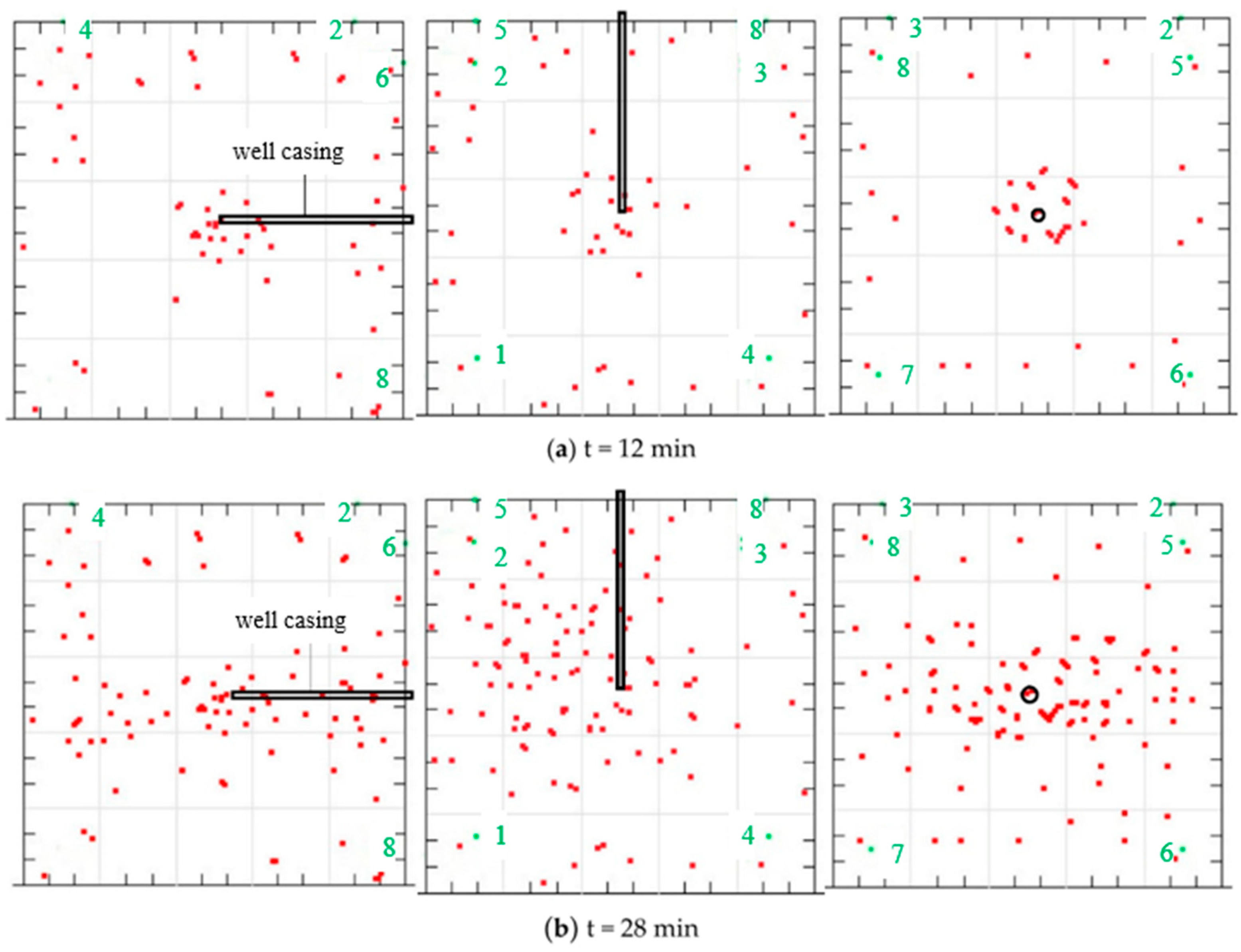
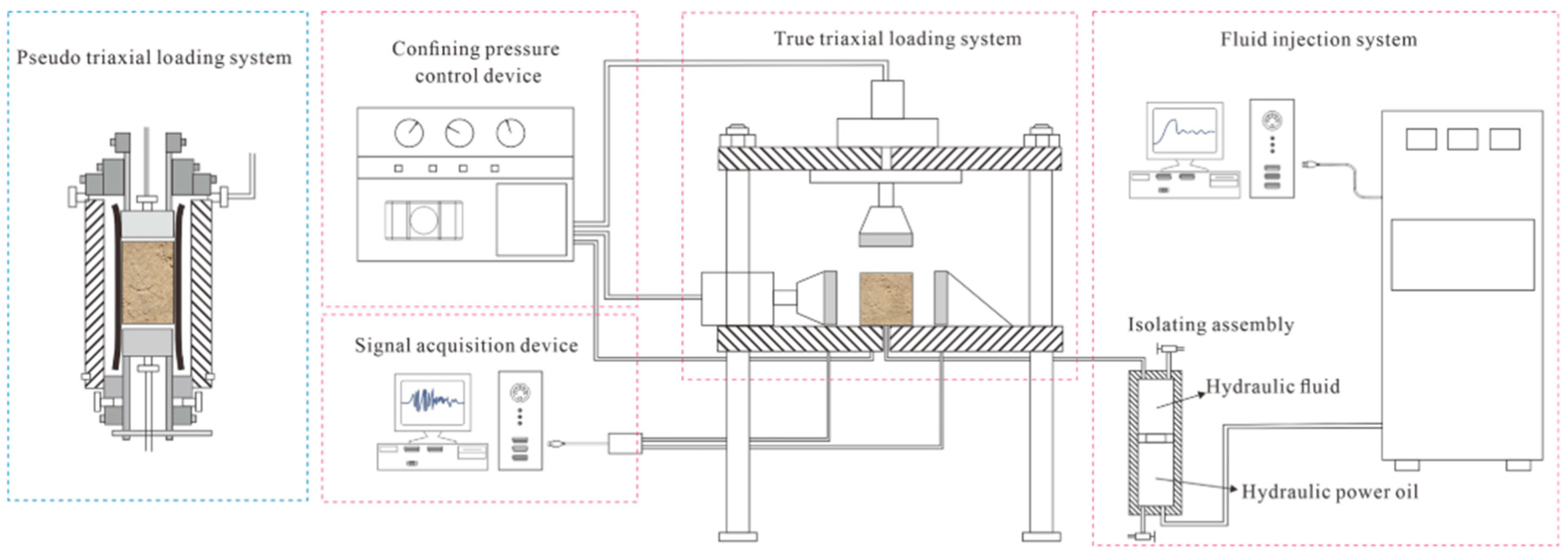
2.1. Specimens and Experimental Setup
| Specimen Type | Rock Type | Specimen Dimensions (mm) | Borehole Dimension (mm) | Applied Stress (MPa) | Injection Fluid Type (MPa.s) | Injection Rate (mm3/s) | References |
|---|---|---|---|---|---|---|---|
| Cylinder | Westerly granite | D 50, H 125 | 6.35 | σ1 = 30, σ2 = 10 | water | 0.016 | Goodfellow et al., 2015 [52] |
| granite | D 50, H 100 | 10 | σ1 = 15, σ2 = 5, 10, 15, 20 | water | 0.2 | Ma et al., 2019 [44] | |
| pyroxene andesite | D 35, H 70 | 3.5 | σ1 = 5, σ2 = 6, 8, 10, 12, 14, 16, 18, 20 | saturated brine | 1.75 | Sawayama et al., 2021 [53] | |
| Inada granite | D 30, H 25 | 1.5 | σ1 = 90, σ2 = 40 | water | 0.05 | Goto et al., 2021 [47] | |
| sandstone from Ordos Basin | D 50, H 125 | 5 | σ1 = 83, σ2 = 35.5 | water | 5 | Qin et al., 2021 [54] | |
| concrete | D 53, H 105 | 10 | σ1 = 1 σ2 = 0.6, 0.8, 1, 1.4, 2 | oil | 0.05 | Rodríguez et al., 2021 [55] | |
| granite | D 50, H 100 | 2 | σ1 = 10, σ2 = 10 | water | 0.004 | Zhang et al., 2022 [56] | |
| mixture of gypsum and cement | D 43, H 6.6 | 16 | σ1 = 6.6, σ2 = 1 | mineral oil 0.12 | 0.17 0.2 | Novikova et al., 2023 [36] | |
| Cubic | concrete blocks | 300 × 300 × 300 | 10 | σ1 = 10, σ2 = 6, σ3 = 4 | water | 0.058 | Yan et al., 2011 [37] |
| shale outcrops | 300 × 300 × 300 | 10 | σ1 = 20, σ2 = 10, σ3 = 8 | guanidine gum 2, 6.5, 15, 20 | 0.326 | Hou et al., 2014 [38] | |
| Longmaxi shale | 400 × 400 × 400 | 16 | σ1 = 22.1, σ2 = 26.3, σ3 = 19.1 | water | 0.163~0.652 | Cheng et al., 2015 [57] | |
| concrete block | 300 × 300 × 300 | 30 | σ1 = 6.5, σ2 = 12, σ3 = 11.5 | water and guar gum, 1.35 | 0.2, 0.4 | Deng et al., 2016 [58] | |
| granite from Shandong | 300 × 300 × 300 | 25 | σ1 = σ2 = σ3 = 0.1; σ1 = 30, σ2 = 25, σ3 = 10 | CaCl2 solution, 1 | 0.033 | Xing et al., 2019 [48] | |
| artificial carbonate blocks | 300 × 300 × 300 | 20 | σ1 = 16, σ2 = 14, σ3 = 7 | water-based guanidine gum solution, 10 | 0.333 | Liu et al., 2019 [59] | |
| granite and gabbro | 330 × 330 × 330 | 20.1 | σ1 = 3.45, σ2 = 10.34, σ3 = 6.89 | NaCl solution, 0.002 mol/L | 0.417 | Hu et al., 2020 [60] | |
| concrete block | 300 × 300 × 300 | 10 | σ1 = 20, σ2 = 10, σ3 = 5; σ1 = 27.7, σ2 = 13.8, σ3 = 6.9 | gel solution, 16.5 | 0.326 | Zeng et al., 2020 [32] | |
| concrete blocks | 300 × 300 × 300 | 25 | σ1 = 20, σ2 = 10, σ3 = 5; σ1 = 28, σ2 = 17, σ3 = 7 | Glycerin, 5.5 | 0.5 | Ali 2020 [61] | |
| Inada granite | 100 × 100 × 100 | 10 | σ1 = 40, σ2 = 15, σ3 = 5 | water | 0.15 | Goto et al., 2021 [47] | |
| granite outcrops in the Gonghe Basin | 200 × 200 × 200 | 20 | σ1 = 18, σ2 = 12, σ3 = 6; σ1 = 24, σ2 = 15, σ3 = 6 | water | 0.083~0.333 | Liu et al., 2022 [62] | |
| granite | 150 × 75 × 20 | 10 | σ1 = 20, σ2 = σ3 = 0 | water | 0.326 | Zhu et al., 2024 [63] | |
| granite outcrop in Gonghe Basin | 300 × 300 × 300 | 22 | σ1 = 11.81, σ2 = 7.87, σ3 = 5.51 | water | 0.5 | Tan et al., 2024 [46] | |
| granite from Luya Mountain | 200 × 200 × 200 | 15 | σ1 = σ2 = σ3 = 25 | water | 1 | Yin et al., 2024 [64] |
2.2. Loading Scheme
3. Theoretical Methods for Hydraulic Fracturing
3.1. Basic Processes
3.1.1. Rock Deformation
3.1.2. Fluid Flow in Fracture
3.1.3. Fracture Propagation
3.2. Theoretical Methods
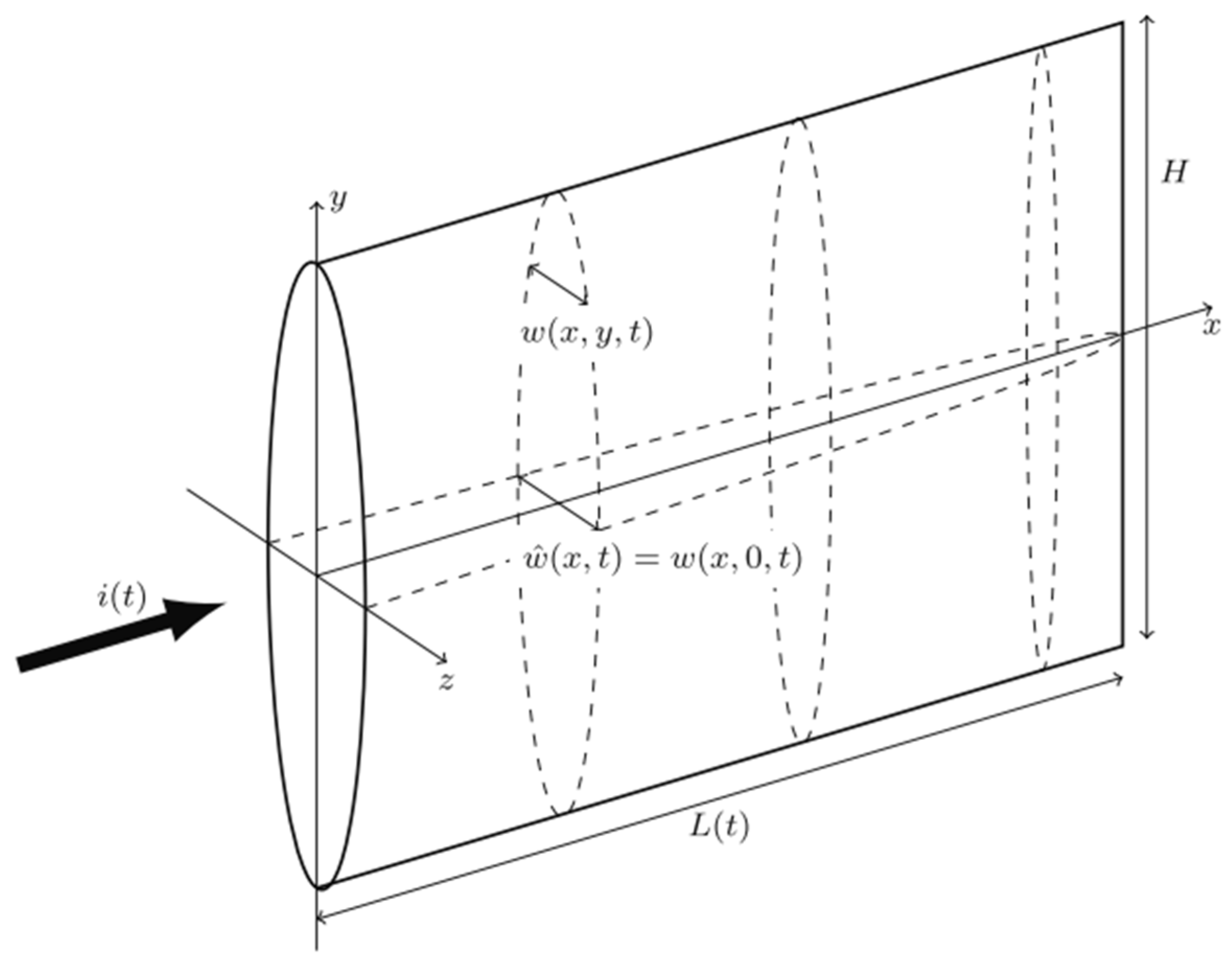
3.2.1. PKN Model
3.2.2. KGD Model
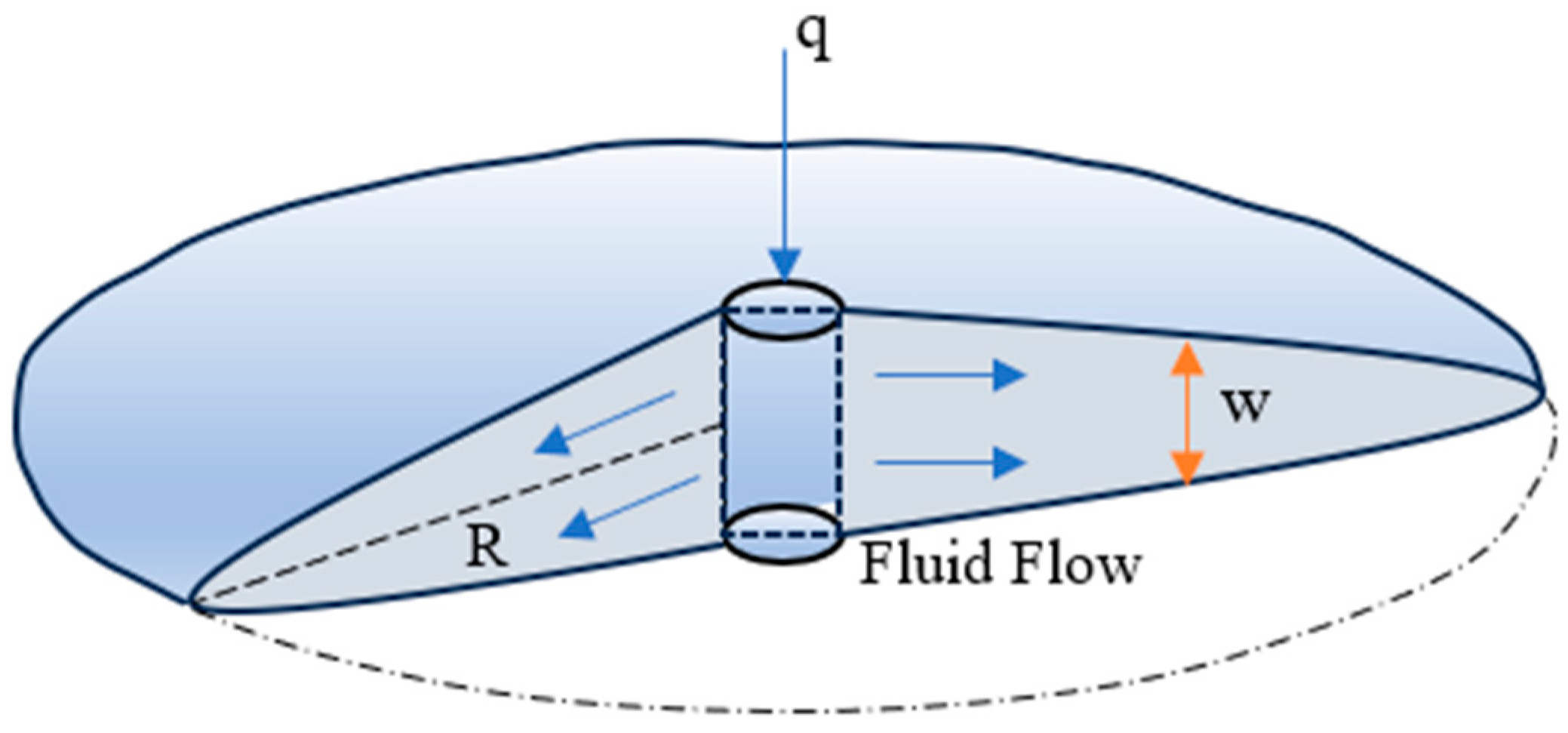
3.2.3. Radial Model
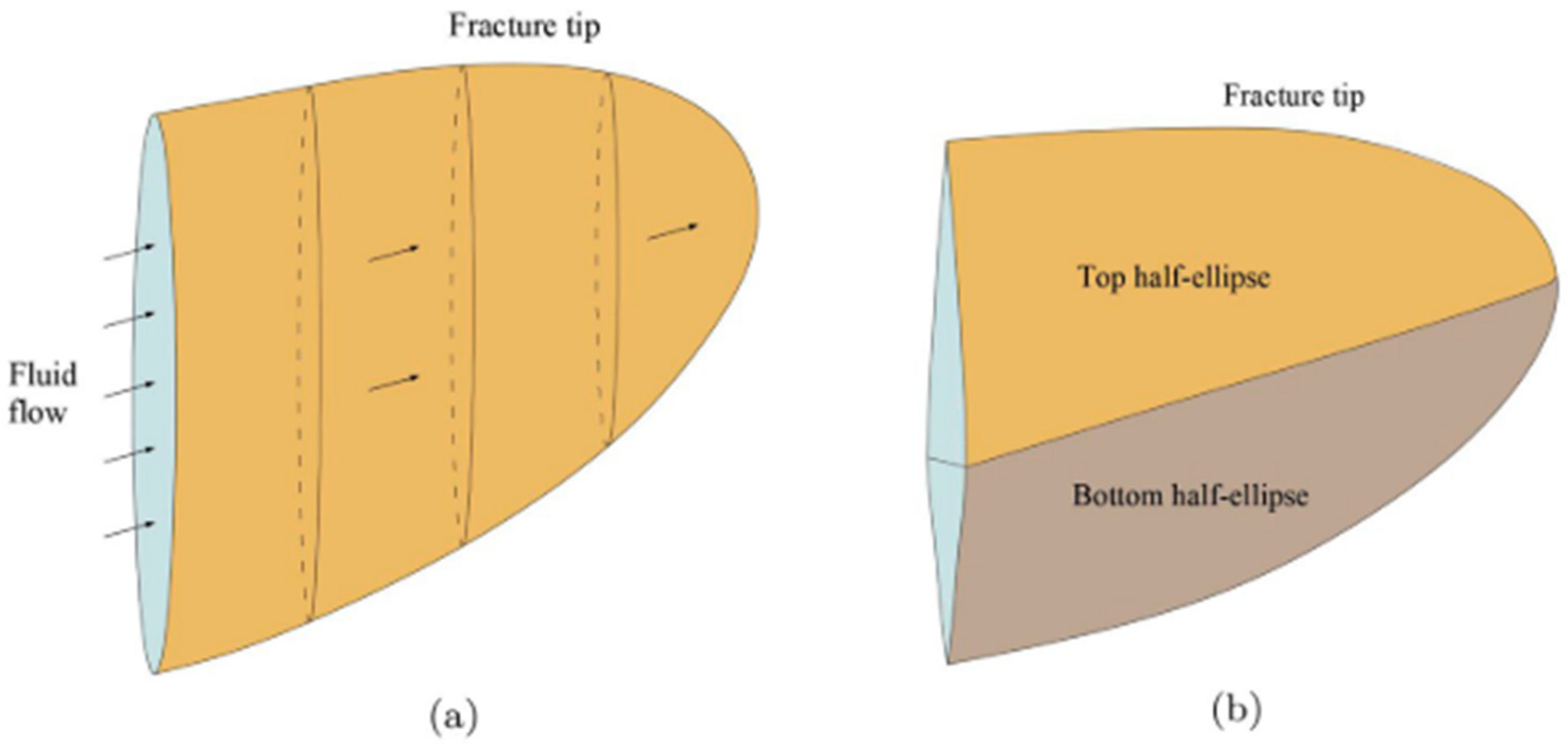
3.2.4. Pseudo 3D (P3D) Model and Planar 3D (PL3D) Model
| Model | Assumptions | Characteristic | References |
|---|---|---|---|
| PKN | Fracture height remains constant, surrounding solid deformation remains small, with the material being linearly elastic and isotropic. Beyond a certain fracture distance, energy dissipation due to rock material toughness is negligible compared to that caused by fluid flow, making fracture propagation driven mainly by fluid velocity. | 3D fracture geometry, elliptical vertical cross-section. | [73,82,83] |
| KGD | The formation is homogeneous and isotropic, fracture deformation is linearly elastic, the fracturing fluid is purely viscous, without considering the influence of proppant, and fluid flow within the fracture is laminar. | 2D fracture geometry, rectangular cross-section. | [84,85,86] |
| Radial Model | The wellbore radius is much smaller than the fracture radius, fluid reaches the fracture tip, the fracture expansion is in a translational state, and lubrication theory is applicable. | Hydraulic fracture in the shape of a penny. | [73,75] |
| P3D Model | All sections perpendicular to the expansion direction of the main fracture maintain plane strain state. | The P3D model provides a more realistic description of hydraulic fracture growth in three dimensions accounting for fracture height variations. | [97,98] |
| PL3D Model | PL3D eliminates the elastic response assumption of the PKN model. | PL3D models can be implemented using either fixed or moving grid methods | [99] |
4. Numerical Methods for Hydraulic Fracturing
4.1. Finite Element Method (FEM)
4.2. Discrete Element Method (DEM)
4.3. Finite–Discrete Element Method (FDEM)
4.4. Boundary Element Method (BEM)
5. Factors Affecting Hydraulic Fracturing
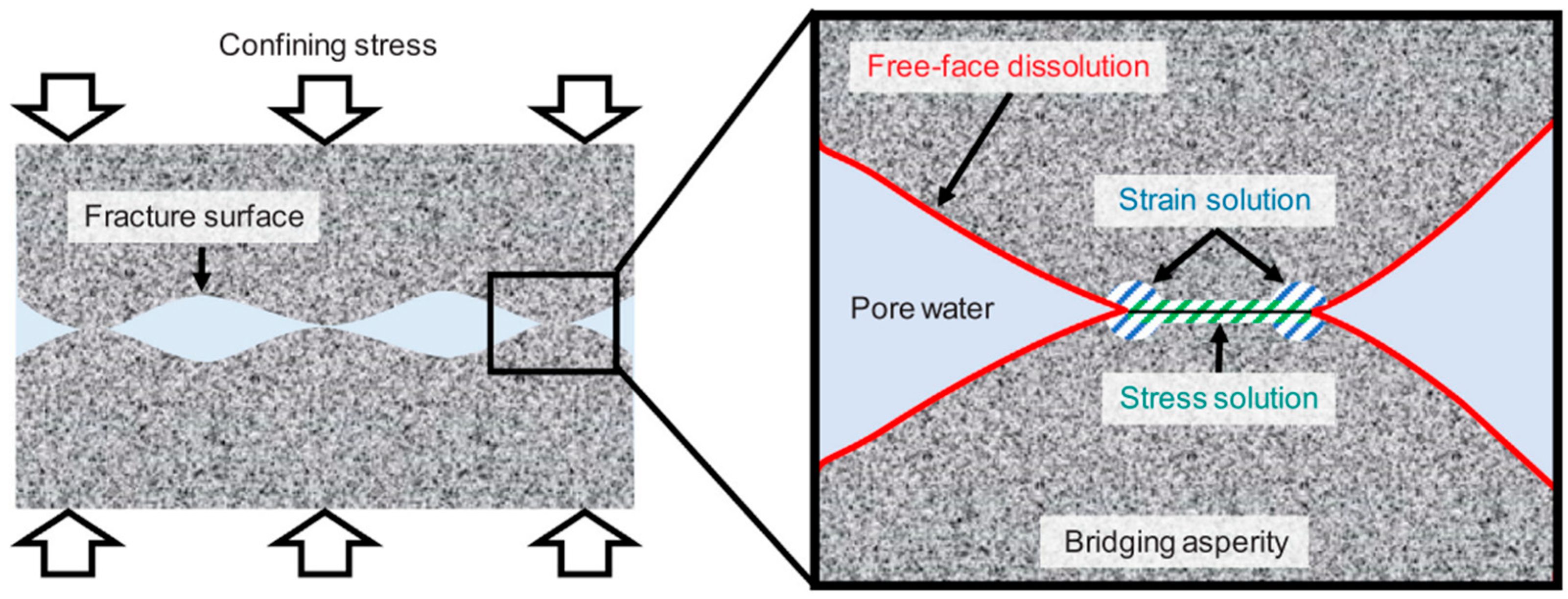
5.1. HDR Matrix
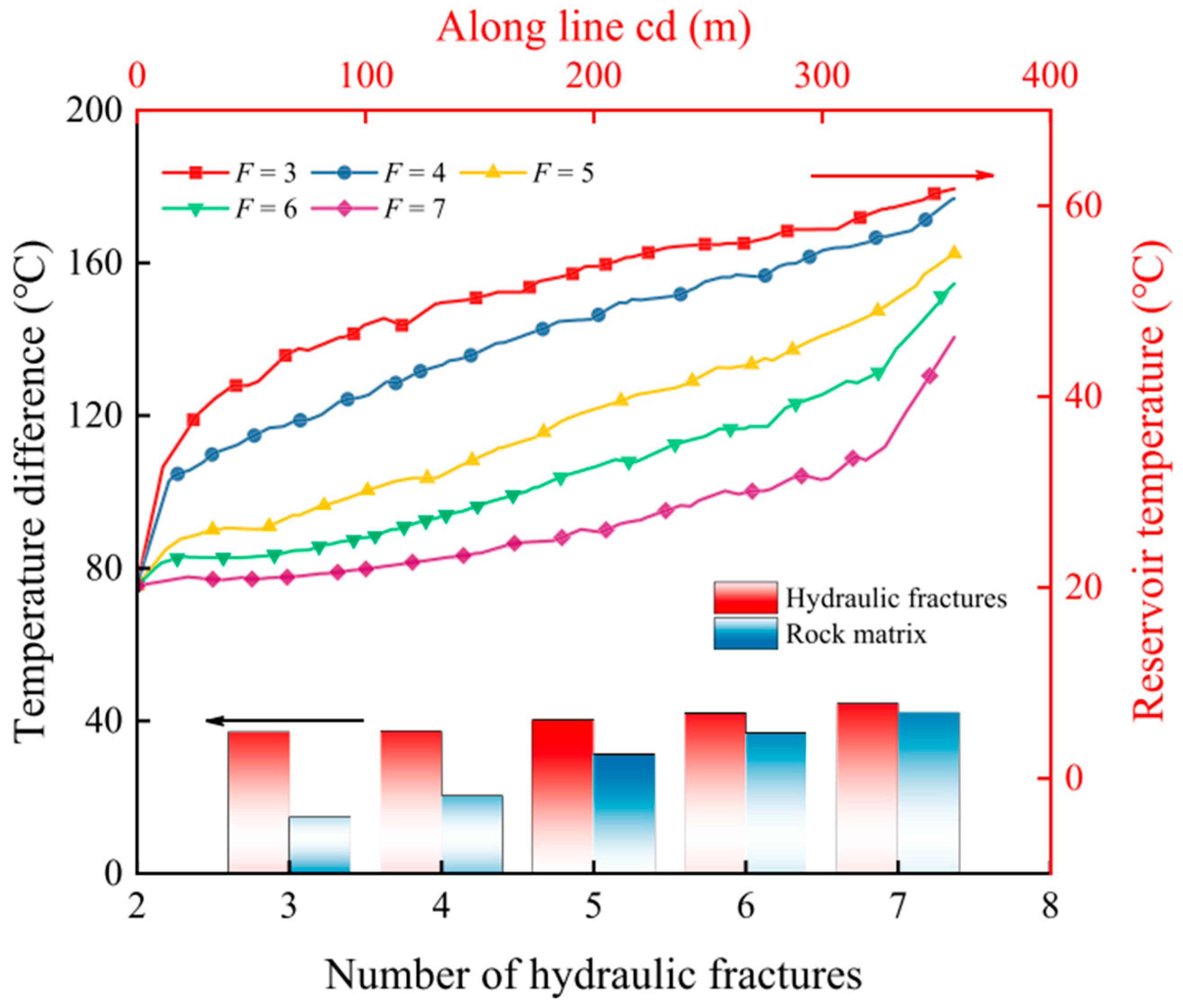
5.2. Temperature
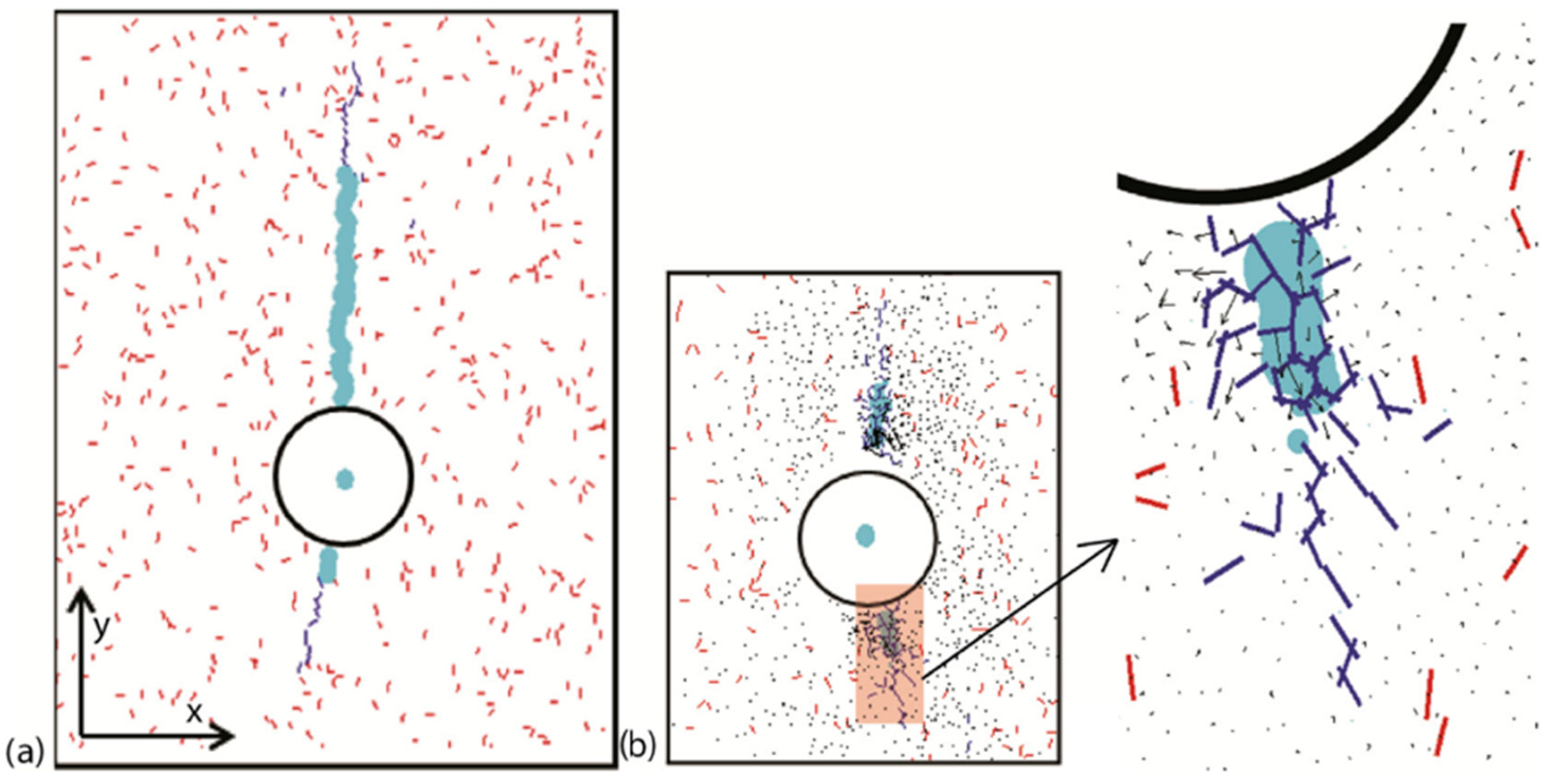
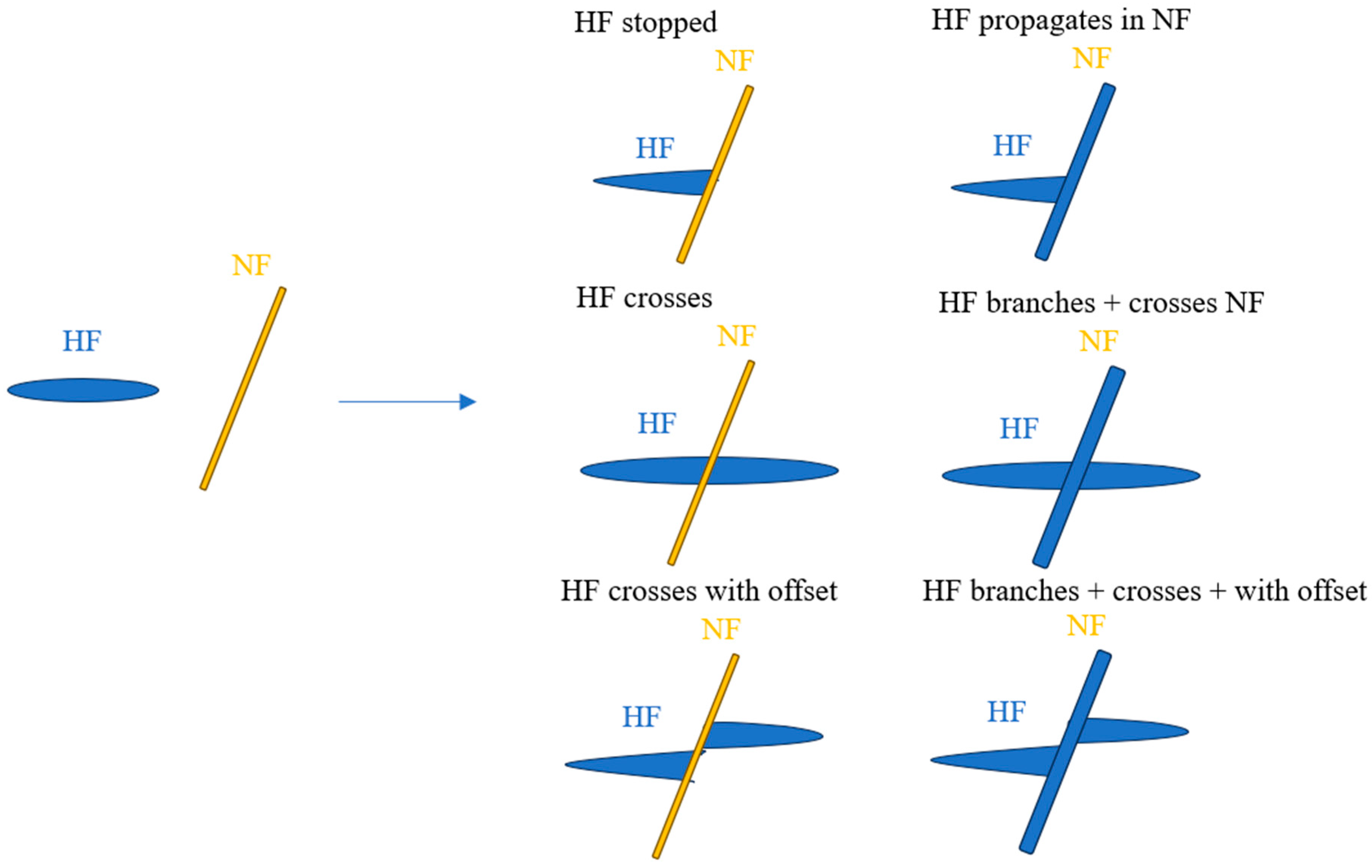
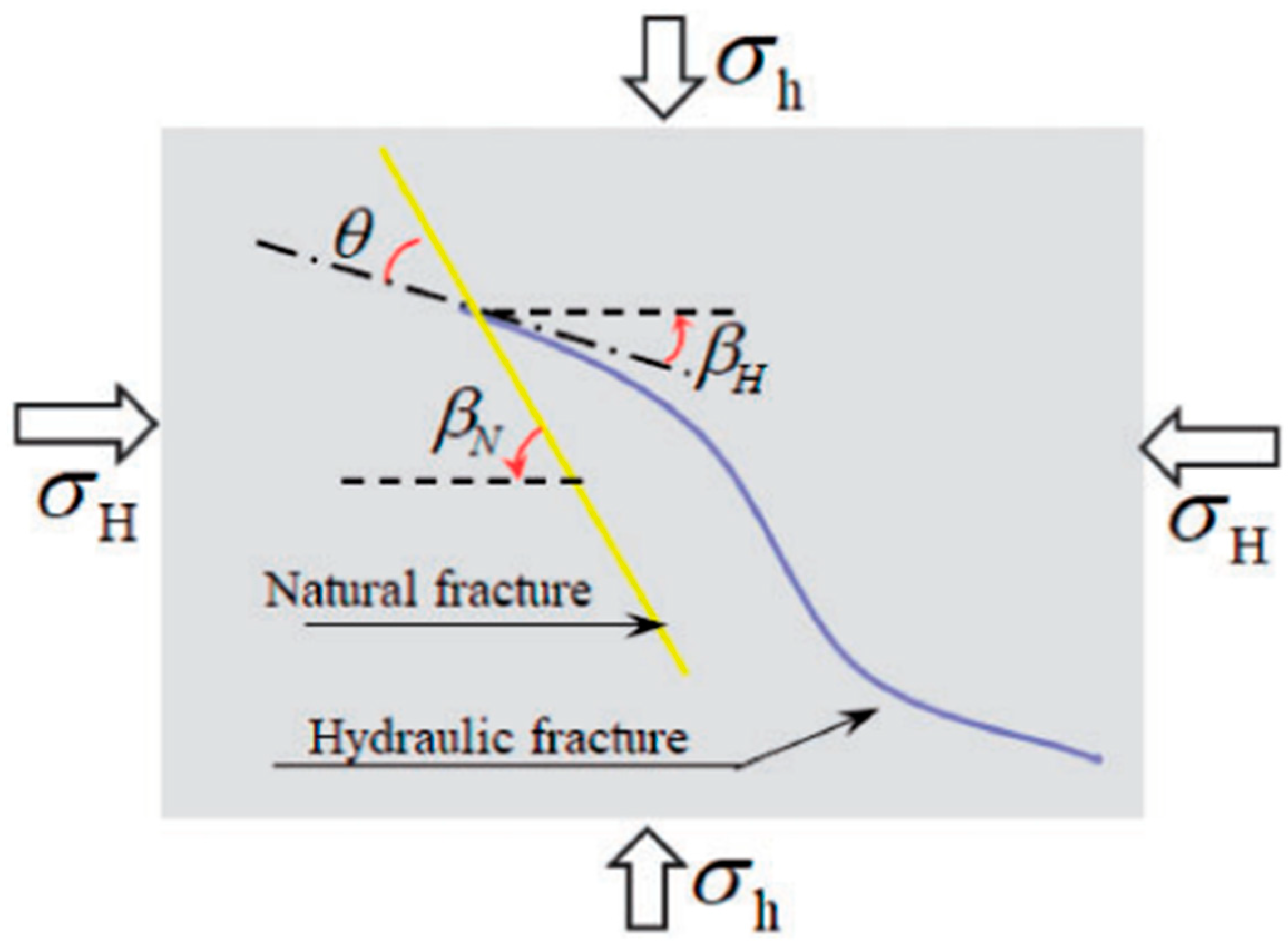
5.3. Natural Fracture
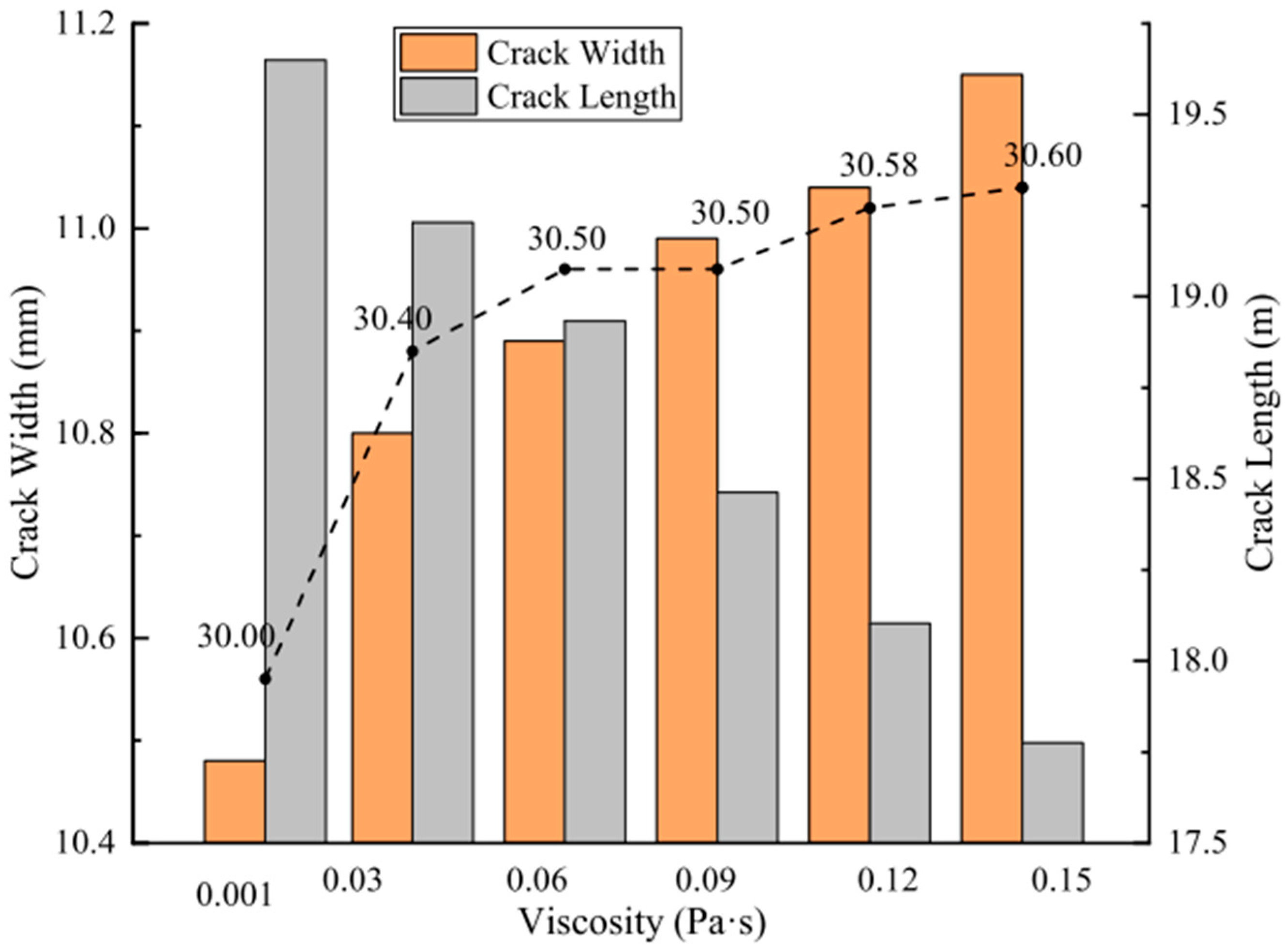
5.4. Fracturing Fluid
5.5. Stress State
6. Conclusions
- (1)
- Influence of experimental conditions: Fracturing outcomes are influenced by sample size, natural fracture distribution, joint characteristics, temperature, and fracturing fluid properties. Different experimental geometries, such as cylindrical or cubic blocks, simulate distinct stress conditions. High temperature induces thermal stress in the rock matrix, causing cracking and damage. As injection pressure increases, cracks connect to form a fracture network. Injection rates play a critical role in fracture propagation, with higher rates promoting lateral fracture propagation, while lower rates may fail to sustain hydraulic fracture growth.
- (2)
- Hydraulic fracture modeling: Classical models like the PKN and the KGD are limited to planar fracture propagation. By contrast, numerical models better capture complex fracture growth, especially in naturally fractured reservoirs. The finite element method offers a detailed fluid–structure coupling but has high computational costs. The discrete element method simulates fluid–rock interactions but cannot represent fracture networks. The finite–discrete element method is well-suited for modeling complex hydraulic fractures in reservoirs but remains computationally intensive.
- (3)
- Rock properties and fracture formation: Variations in the mineral composition and fracture toughness of rocks impact fracture behavior. High rock elasticity and temperature contribute to more complex fracture networks, while high initial rock temperatures facilitate thermal stress-induced fractures. The greater the fracture toughness of the rock matrix, the faster the formation of hydraulic fracture.
- (4)
- Fracture network complexity: Natural fractures significantly alter hydraulic fracture propagation, leading to more complex fracture systems, but also causing fluid leakage and energy dissipation. Fracture network complexity is influenced by stress conditions, rock temperature, and fluid injection rates. Four interaction modes between hydraulic and natural fractures have been identified: (a) crossover, (b) opening, (c) combined opening, and (d) opening crossover.
- (5)
- Proppant and fluid dynamics: Proppant use ensures fractures remain open after pumping pressure is reduced, affecting fracture shape and conductivity. Low injection rates hinder fracture propagation, while high injection rates enhance fracture width and area but can induce fluid-cooling effects.
- (6)
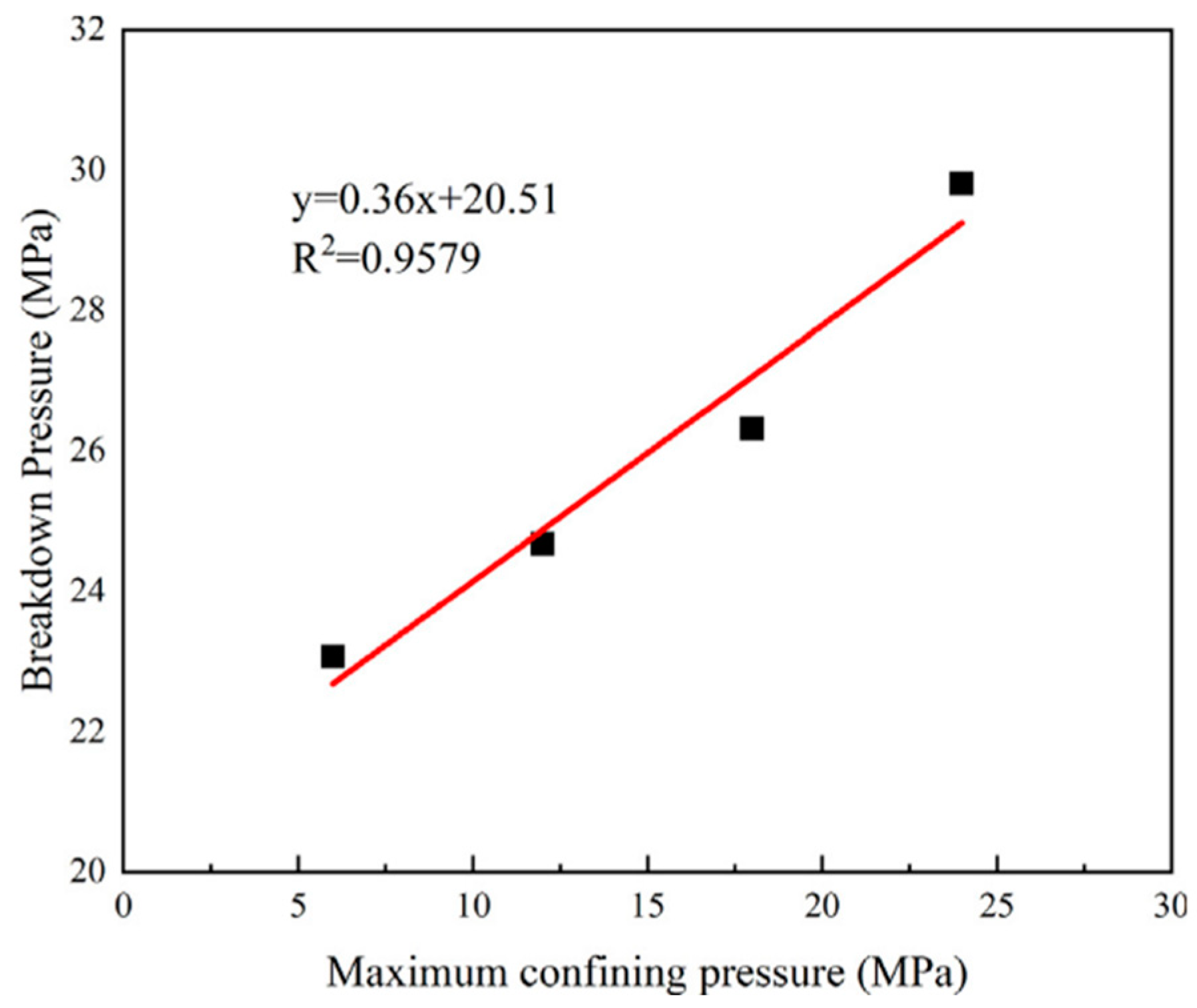
- Stress conditions: Horizontal and vertical stress differences dictate the propagation direction and complexity of hydraulic fractures. Under low confining pressure, more vertical fractures form, while higher confining pressure results in fewer, simpler fractures. The smaller the horizontal stress difference, the larger the deflection in the propagation direction of hydraulic fracture.
7. Recommendations for Future Work
- (1)
- Ultra-high temperature experiments: Most studies have been limited to temperatures up to 200 °C [216]. There is a need for research on hydraulic fracturing under ultra-high temperature conditions, particularly near the supercritical temperature of water, where complex “cloud fracture networks” form. Investigating whether this phenomenon is driven by thermal or fluid viscosity changes could provide valuable insights. Develop materials like polyether ether ketone (PEEK), with a melting point of 343 °C, and customize fluorine rubber for high-temperature wellbore sealing. These materials can simulate borehole conditions more effectively.
- (2)
- Large-scale experiments: Future studies should explore larger rock samples to minimize boundary effects and better simulate real-world conditions. Enhancing the load capacity and high-temperature resistance of triaxial testing devices will allow for more accurate replication of field stress and temperature conditions. Utilize advanced triaxial testing systems, such as the YJW-20000S [217], which can accommodate samples larger than 1000 mm, to minimize boundary effects and replicate field conditions more accurately.
- (3)
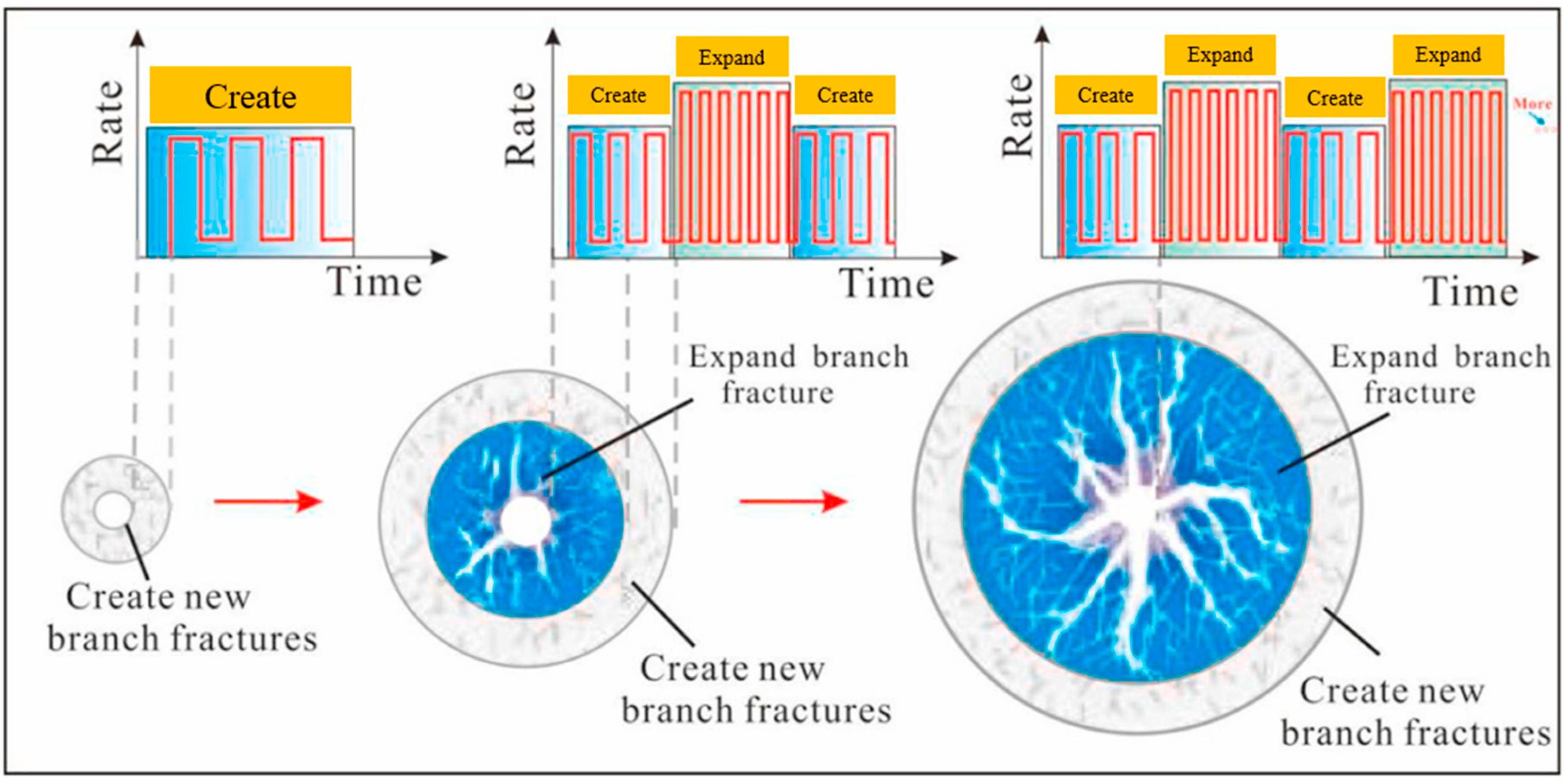
- New fracturing techniques: To improve fracture network complexity, especially in HDR with limited natural fractures, new methods such as cyclic hydraulic fracturing and temporary plug fracturing should be explored. Cyclic hydraulic fracturing has shown the potential to create more complex fracture systems by reducing the plastic deformation effect with each cycle. Compared with conventional hydraulic fracturing, cyclic injection hydraulic fracturing can significantly increase fracture permeability under the same confining pressure, and cyclic hydraulic fracturing can produce more complex fracture networks and reduce the possibility of induced earthquakes.
- (4)
- Stress condition studies: Further research is needed on the impact of varying vertical and horizontal stress differences on fracture network formation. This includes understanding how these stresses influence fracture propagation direction and the development of complex fracture networks, especially under high-stress environments. To conduct hydraulic fracturing experiments under in situ stress conditions, true triaxial stress loading and permeability testing systems could provide potential applications [218].
- (5)
- Improving rock and fracture property assessment: Evaluating the physical and mechanical properties of rocks remains a challenge in hydraulic fracturing. Improved characterization techniques are needed to better predict fracture behavior in both intact and fractured reservoirs, ultimately optimizing fracturing strategies for complex geological formations. Some advanced techniques such as CT can be applied to obtain the internal structures of rocks and observe the direction of fracture expansion [219].
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | cross-sectional area of fracture | Young’s modulus | |
| elasticity tensor | stress tensor | ||
| D | diameter of cylindrical specimen | product of rock density | |
| plane strain modulus | time | ||
| H | height of specimen | gravitational acceleration | |
| σ1 | vertical stress | p | fluid pressure, |
| σ2 | maximum horizontal stress | q | flow rate |
| σ3 | minimum horizontal stress | fracture height | |
| μ | viscosity of the fracturing fluid | s | local coordinate along the fracture |
| leak-off flow rate | fracture width | ||
| bottom hole pressure | maximum aperture | ||
| fracture length at the center | Mode I stress intensity factor | ||
| average fracture width | internal fluid pressure | ||
| maximum radius radial fracture |
References
- Jia, Y.; Tsang, C.F.; Hammar, A.; Niemi, A. Hydraulic stimulation strategies in enhanced geothermal systems (EGS): A review. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 211. [Google Scholar] [CrossRef]
- Allahvirdizadeh, P. A review on geothermal wells: Well integrity issues. J. Clean. Prod. 2020, 275, 124009. [Google Scholar] [CrossRef]
- Sircar, A.; Solanki, K.; Bist, N.; Yadav, K. Enhanced geothermal systems—Promises and challenges. Int. J. Renew. Energy Dev. 2022, 11, 333–346. [Google Scholar] [CrossRef]
- Hamm, S.G.; Anderson, A.; Blankenship, D.; Boyd, L.W.; Brown, E.A.; Frone, Z.; Hamos, I.; Hughes, H.J.; Kalmuk, M. Geothermal energy R&D: An overview of the U.S. department of energy’s geothermal technologies office. J. Energy Resour. Technol. Trans. ASME 2021, 143, 1–34. [Google Scholar]
- Zhuang, L.; Zang, A. Laboratory hydraulic fracturing experiments on crystalline rock for geothermal purposes. Earth-Sci. Rev. 2021, 216, 103580. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, S.; Ranjith, P.G.; Tian, W.; Tian, H.; Zheng, J.; Jiang, G.; Dou, B. A comprehensive review on mechanical responses of granite in enhanced geothermal systems (EGSs). J. Clean. Prod. 2023, 383, 135378. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.; Zhu, X.; Li, T. Occurrence of geothermal resources and prospects for exploration and development in China. Energy Explor. Exploit. 2021, 39, 536–552. [Google Scholar] [CrossRef]
- Acar, H.I. A review of geothermal energy in Turkey. Energy Sources 2003, 25, 1083–1088. [Google Scholar] [CrossRef]
- Tomac, I.; Sauter, M. A review on challenges in the assessment of geomechanical rock performance for deep geothermal reservoir development. Renew. Sustain. Energy Rev. 2018, 82, 3972–3980. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, Y.; Guo, Q.; Tan, L.; Zhuang, Y.; Liu, M.; Zhang, C.; Zhu, M.; Xiang, W. Chemical stimulation on the hydraulic properties of artificially fractured granite for enhanced geothermal system. Energy 2018, 142, 754–764. [Google Scholar] [CrossRef]
- Moska, R.; Labus, K.; Kasza, P. Hydraulic fracturing in enhanced geothermal systems—Field, tectonic and rock mechanics conditions—A review. Energies 2021, 14, 5725. [Google Scholar] [CrossRef]
- Kim, K.I.L.; Min, K.B.; Kim, K.Y.; Choi, J.W.; Yoon, K.S.; Yoon, W.S.; Yoon, B.; Lee, T.J.; Song, Y. Protocol for induced microseismicity in the first enhanced geothermal systems project in Pohang, Korea. Renew. Sustain. Energy Rev. 2018, 91, 1182–1191. [Google Scholar] [CrossRef]
- Alcolea, A.; Meier, P.; Vilarrasa, V.; Olivella, S.; Carrera, J. Hydromechanical modeling of the hydraulic stimulations in borehole PX2 (Pohang, South Korea). Geothermics 2024, 120, 103009. [Google Scholar] [CrossRef]
- Song, G.; Song, X.; Gensheng, L.I.; Ruina, X.U.; Cao, W.; Zhao, C. Multi-objective optimization of geothermal extraction from the enhanced geothermal system in Qiabuqia geothermal field, Gonghe basin. Acta Geol. Sin. 2021, 95, 1844–1856. [Google Scholar] [CrossRef]
- Yue, G.; Li, X.; Zhang, W. Risk assessment of earthquakes induced during HDR development: A case study in the Gonghe Basin, Qinghai Province, China. Geothermics 2023, 111, 102721. [Google Scholar] [CrossRef]
- Fang, Y.; den Hartog, S.A.M.; Elsworth, D.; Marone, C.; Cladouhos, T. Anomalous distribution of microearthquakes in the Newberry Geothermal Reservoir: Mechanisms and implications. Geothermics 2016, 63, 62–73. [Google Scholar] [CrossRef]
- Rutqvist, J.; Dobson, P.F.; Garcia, J.; Hartline, C.; Jeanne, P.; Oldenburg, C.M.; Vasco, D.W.; Walters, M. The Northwest Geysers EGS demonstration project, California: Pre-stimulation modeling and interpretation of the stimulation. Math. Geosci. 2015, 47, 3–29. [Google Scholar] [CrossRef]
- Feng, H.; Wang, E.; Zhao, A.; Wei, H.; Liu, Y.; Lu, J. Study on the law of true triaxial hydraulic fracturing by acoustic emission monitoring. ACS Omega 2024, 9, 24624–24632. [Google Scholar]
- Chen, Y.; Meng, Q.; Zhang, J. Effects of the notch angle, notch length and injection rate on hydraulic fracturing under true triaxial stress: An experimental study. Water 2018, 10, 801. [Google Scholar] [CrossRef]
- Hu, Y.; Su, B.; Mao, G. An experimental approach for determining unsaturated hydraulic properties of rock fractures. Nord. Hydrol. 2004, 35, 251–260. [Google Scholar]
- Zhuang, L.; Zang, A.; Jung, S. Grain-scale analysis of fracture paths from high-cycle hydraulic fatigue experiments in granites and sandstone. Int. J. Rock Mech. Min. Sci. 2022, 157, 105177. [Google Scholar] [CrossRef]
- Kusmierczyk, P.; Mishuris, G.; Wrobel, M. Remarks on application of different variables for the PKN model of hydrofracturing: Various fluid-flow regimes. Int. J. Fract. 2013, 184, 185–213. [Google Scholar] [CrossRef]
- Garikapati, H.; Verhoosel, C.V.; van Brummelen, E.H.; Zlotnik, S.; Díez, P. Sampling-based stochastic analysis of the PKN model for hydraulic fracturing. Comput. Geosci. 2019, 23, 81–105. [Google Scholar] [CrossRef]
- Peck, D.; Wrobel, M.; Perkowska, M.; Mishuris, G. Fluid velocity based simulation of hydraulic fracture: A penny shaped model—Part I: The numerical algorithm. Meccanica 2018, 53, 3615–3635. [Google Scholar] [CrossRef]
- Esfandiari, M.; Pak, A. XFEM modeling of the effect of in-situ stresses on hydraulic fracture characteristics and comparison with KGD and PKN models. J. Pet. Explor. Prod. Technol. 2023, 13, 185–201. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, T.; Qu, Z.; Wang, J.; Chen, M.; Liu, X. Numerical simulation of fracture propagation and production performance in a fractured geothermal reservoir using a 2D FEM-based THMD coupling model. Energy 2023, 273, 127175. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Stolle, D.F.E.; Liang, L.; Shi, Y. Modeling hydraulic fracture in heterogeneous rock materials using permeability-based hydraulic fracture model. Undergr. Space 2020, 5, 167–183. [Google Scholar] [CrossRef]
- Qian, Y.; Guo, P.; Wang, Y.; Zhao, Y.; Lin, H.; Liu, Y. Advances in laboratory-scale hydraulic fracturing experiments. Adv. Civ. Eng. 2020, 2020, 1386581. [Google Scholar] [CrossRef]
- Fu, H.; Huang, L.; Hou, B.; Weng, D.; Guan, B.; Zhong, T.; Zhao, Y. Experimental and numerical investigation on interaction mechanism between hydraulic fracture and natural fracture. Rock Mech. Rock Eng. 2024, 57, 10571–10582. [Google Scholar] [CrossRef]
- He, Y.; Bai, B.; Li, X. Investigation on heat transfer properties of supercritical water in a rock fracture for enhanced geothermal systems. Int. J. Thermophys. 2018, 39, 136. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, Y.; Hu, Z.; Lei, H.; Bai, L.; Lei, Z.; Zhang, Q. An experimental investigation into the characteristics of hydraulic fracturing and fracture permeability after hydraulic fracturing in granite. Renew. Energy 2019, 140, 615–624. [Google Scholar] [CrossRef]
- Zeng, Y.; Cheng, W.; Zhang, X.; Xiao, B. A criterion for identifying a mixed-mode I/II hydraulic fracture crossing a natural fracture in the subsurface. Energy Explor. Exploit. 2020, 38, 2507–2520. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Yu, Z.; Ma, Y.; Zhang, C. Experimental investigation of seepage and heat transfer in rough fractures for enhanced geothermal systems. Renew. Energy 2019, 135, 846–855. [Google Scholar] [CrossRef]
- Hyman, J.D.; Jiménez-Martínez, J.; Viswanathan, H.S.; Carey, J.W.; Porter, M.L.; Rougier, E.; Karra, S.; Kang, Q.; Frash, L.; Chen, L.; et al. Understanding hydraulic fracturing: A multi-scale problem. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150426. [Google Scholar] [CrossRef]
- El-MShokir, E.M.; Al-Quraishi, A.A. Experimental and numerical investigation of proppant placement in hydraulic fractures. Pet. Sci. Technol. 2009, 27, 1690–1703. [Google Scholar] [CrossRef]
- Novikova, E.V.; Trimonova, M.A.; Turuntaev, S.B.; Zenchenko, E.V.; Zenchenko, P.E. Backstress Influence on the Formation Stress Field in Hydraulic Fracturing Experiments. Geosciences 2023, 13, 153. [Google Scholar] [CrossRef]
- Yan, T.; Li, W.; Bi, X. An experimental study of fracture initiation mechanisms during hydraulic fracturing. Pet. Sci. 2011, 8, 87–92. [Google Scholar] [CrossRef]
- Hou, B.; Chen, M.; Li, Z.; Wang, Y.; Diao, C. Propagation area evaluation of hydraulic fracture networks in shale gas reservoirs. Pet. Explor. Dev. 2014, 41, 833–838. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Q.; Hu, Q.; Liang, Y.; Xu, Y.; Liu, L.; Wu, X.; Li, X.; Wang, X.; Hu, L.; et al. Acoustic emission characteristics in hydraulic fracturing of stratified rocks: A laboratory study. Powder Technol. 2020, 371, 267–276. [Google Scholar] [CrossRef]
- Tan, P.; Chen, Z.; Fu, S.; Zhao, Q. Experimental investigation on fracture growth for integrated hydraulic fracturing in multiple gas bearing formations. Geoenergy Sci. Eng. 2023, 231, 212316. [Google Scholar] [CrossRef]
- Hadei, M.R.; Veiskarami, A. An experimental investigation of hydraulic fracturing of stratified rocks. Bull. Eng. Geol. Environ. 2021, 80, 491–506. [Google Scholar] [CrossRef]
- Zhuang, D.; Yin, T.; Li, Q.; Wu, Y.; Tan, X. Effect of injection flow rate on fracture toughness during hydraulic fracturing of hot dry rock (HDR). Eng. Fract. Mech. 2022, 260, 108207. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Dong, Y.; Sun, D.; Yu, B. Experimental investigation of thermal effect on fracability index of geothermal reservoirs. Nat. Resour. Res. 2021, 30, 273–288. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Huang, Y.; Zhang, Y.; Hu, Z. Experimental study on flow and heat transfer characteristics of water flowing through a rock fracture induced by hydraulic fracturing for an enhanced geothermal system. Appl. Therm. Eng. 2019, 154, 433–441. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, W.; Lei, Y.; Wu, P.; Qin, G.; Ba, R. Experimental study of heat transfer by water flowing through smooth and rough rock fractures. Energy Rep. 2019, 5, 1025–1029. [Google Scholar] [CrossRef]
- Tan, P.; Pang, H.; Jin, Y.; Zhou, Z. Experiments and analysis of hydraulic fracturing in hot dry rock geothermal reservoirs using an improved large-size high-temperature true triaxial apparatus. Nat. Gas. Ind. B. 2024, 11, 83–94. [Google Scholar] [CrossRef]
- Goto, R.; Watanabe, N.; Sakaguchi, K.; Miura, T.; Chen, Y.; Ishibashi, T.; Pramudyo, E.; Parisio, F.; Yoshioka, K.; Nakamura, K.; et al. Creating cloud-fracture network by flow-induced microfracturing in superhot geothermal environments. Rock Mech. Rock Eng. 2021, 54, 2959–2974. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, G.; Luo, T.; Jiang, Y.; Ning, S. Hydraulic fracturing in high-temperature granite characterized by acoustic emission. J. Pet. Sci. Eng. 2019, 178, 475–484. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Z.; Zhang, Y.; Wang, Z.; Jiang, H. Experimental and numerical evaluation of hydraulic fracturing under high temperature and embedded fractures in large concrete samples. Water 2020, 12, 3171. [Google Scholar] [CrossRef]
- Wang, D.; Bian, X.; Qin, H.; Sun, D.; Yu, B. Experimental investigation of mechanical properties and failure behavior of fluid-saturated hot dry rocks. Nat. Resour. Res. 2021, 30, 289–305. [Google Scholar] [CrossRef]
- Zenchenko, E.V.; Turuntaev, S.B.; Nachev, V.A.; Chumakov, T.K.; Zenchenko, P.E. Study of the interaction of a hydraulic fracture with a natural fracture in a laboratory experiment based on ultrasonic transmission monitoring. Energies 2024, 17, 277. [Google Scholar] [CrossRef]
- Goodfellow, S.D.; Nasseri, M.H.B.; Maxwell, S.C.; Young, R.P. Hydraulic fracture energy budget: Insights from the laboratory. Geophys. Res. Lett. 2015, 42, 3179–3187. [Google Scholar] [CrossRef]
- Sawayama, K.; Ishibashi, T.; Jiang, F.; Tsuji, T.; Nishizawa, O.; Fujimitsu, Y. Scale-independent relationship between permeability and resistivity in mated fractures with natural rough surfaces. Geothermics 2021, 94, 102065. [Google Scholar] [CrossRef]
- Qin, Q.; Xue, Q.; Ma, Z.; Zheng, Y.; Zhai, H. Hydraulic fracturing simulations with real-time evolution of physical parameters. Energies 2021, 14, 1678. [Google Scholar] [CrossRef]
- Rodríguez Villarreal, O.; Varela Valdez, A.; La Borderie, C.; Pijaudier-Cabot, G.; Hinojosa Rivera, M. Estimation of Fracture Energy from Hydraulic Fracture Tests on Mortar and Rocks at Geothermal Reservoir Temperatures. Rock Mech. Rock Eng. 2021, 54, 4111–4119. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Huang, Y.; Xia, Y. Experimental study of fracture evolution in enhanced geothermal systems based on fractal theory. Geothermics 2022, 102, 102406. [Google Scholar] [CrossRef]
- Cheng, W.; Jin, Y.; Chen, M. Reactivation mechanism of natural fractures by hydraulic fracturing in naturally fractured shale reservoirs. J. Nat. Gas. Sci. Eng. 2015, 27, 1357–1365. [Google Scholar] [CrossRef]
- Deng, J.Q.; Lin, C.; Yang, Q.; Liu, Y.R.; Tao, Z.F.; Duan, H.F. Investigation of directional hydraulic fracturing based on true tri-axial experiment and finite element modeling. Comput. Geotech. 2016, 75, 28–47. [Google Scholar] [CrossRef]
- Liu, B.; Jin, Y.; Chen, M. Influence of vugs in fractured-vuggy carbonate reservoirs on hydraulic fracture propagation based on laboratory experiments. J. Struct. Geol. 2019, 124, 143–150. [Google Scholar] [CrossRef]
- Hu, L.; Ghassemi, A. Heat production from lab-scale enhanced geothermal systems in granite and gabbro. Int. J. Rock Mech. Min. Sci. 2020, 126, 104205. [Google Scholar] [CrossRef]
- Dehghan, A.N. An experimental investigation into the influence of pre-existing natural fracture on the behavior and length of propagating hydraulic fracture. Eng. Fract. Mech. 2020, 240, 107330. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, T.; Yuan, Y.; Feng, B.; Tang, X.; Liu, X.; Cui, Z. A laboratory study on fracture initiation and propagation of granite under cyclic-injection hydraulic fracturing. J. Pet. Sci. Eng. 2022, 212, 110278. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, C.; Zhang, H.; Wang, B.; Mao, M.; Geng, H.; Zhao, C. Micro mechanism investigation of hydraulic fracturing process based a fluid-solid coupling discrete element model. Comput. Geotech. 2024, 174, 106640. [Google Scholar] [CrossRef]
- Yin, W.; Feng, Z.; Zhao, Y. Investigation on the characteristics of hydraulic fracturing in fractured-subsequently-filled hot dry rock geothermal formation. Renew. Energy 2024, 223, 120061. [Google Scholar] [CrossRef]
- Huang, B.; Li, P.; Ma, J.; Chen, S. Experimental investigation on the basic law of hydraulic fracturing after water pressure control blasting. Rock Mech. Rock Eng. 2014, 47, 1321–1334. [Google Scholar] [CrossRef]
- Yu, J.; Li, N.; Hui, B.; Zhao, W.; Li, Y.; Kang, J.; Hu, P.; Chen, Y. Experimental simulation of fracture propagation and extension in hydraulic fracturing: A state-of-the-art review. Fuel 2024, 363, 131021. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Yu, Z.; Hu, Z.; Yang, Y. An investigation on hydraulic fracturing characteristics in granite geothermal reservoir. Eng. Fract. Mech. 2020, 237, 107252. [Google Scholar] [CrossRef]
- Li, N.; Xie, H.; Hu, J.; Li, C. A critical review of the experimental and theoretical research on cyclic hydraulic fracturing for geothermal reservoir stimulation. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 7. [Google Scholar] [CrossRef]
- Zhong, C.; Xu, T.; Yuan, Y.; Cui, G.; Gherardi, F.; Li, X. Coupled effects of elastic and plastic deformation on hydraulic properties of the geothermal fracture induced by cyclic loading-unloading processes. Eng. Geol. 2023, 313, 106929. [Google Scholar] [CrossRef]
- Kc, B.; Ghazanfari, E.; McLennan, J.; Frash, L.P.; Meng, M. Evaluation of sintered bauxite proppant for binary enhanced geothermal systems. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 21. [Google Scholar] [CrossRef]
- Wu, X.; Guo, Y.; Chang, X.; Bi, Z.; Zhao, G.; Yang, H.; Guo, W. Experimental study on cyclic hydraulic fracturing of tight sandstone under In-Situ stress. Processes 2023, 11, 875. [Google Scholar] [CrossRef]
- Feng, G.; Wang, X.; Kang, Y.; Zhang, Z. Effect of thermal cycling-dependent cracks on physical and mechanical properties of granite for enhanced geothermal system. Int. J. Rock Mech. Min. Sci. 2020, 134, 104476. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Chen, B.; Barboza1, B.R.; Sun, Y.; Bai, J.; Thomas1, H.R.; Dutko, M.; Cottrel, M.; Li, C. A Review of Hydraulic Fracturing Simulation. Arch. Comput. Methods Eng. 2022, 29, 1–58. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S. A comprehensive review of numerical simulation methods for hydraulic fracturing. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 1433–1459. [Google Scholar] [CrossRef]
- Aliyu, M.D.; Chen, H.P. Enhanced geothermal system modelling with multiple pore media: Thermo-hydraulic coupled processes. Energy 2018, 165, 931–948. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Lee, J.H.; Elraies, K.A. A review of PKN-type modeling of hydraulic fractures. J. Pet. Sci. Eng. 2020, 195, 107607. [Google Scholar] [CrossRef]
- Dalla Barba, F.; Picano, F. A novel approach for direct numerical simulation of hydraulic fracture problems. Flow Turbul. Combust. 2020, 105, 335–357. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Lee, J.H.; Elraies, K.A. Pseudo-three-dimensional simulations of a vertical hydraulic fracture with time-dependent injection rates. Pet. Sci. Technol. 2022, 40, 1349–1368. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. The influence of the cohesive process zone in hydraulic fracturing modelling. Int. J. Fract. 2011, 167, 33–45. [Google Scholar] [CrossRef]
- Meng, Q.; Xue, H.; Zhuang, X.; Zhang, Q.; Zhu, C.; He, B.; Feng, G.; Rabczuk, T. An IFS-based fractal discrete fracture network for hydraulic fracture behavior of rock mass. Eng. Geol. 2023, 324, 107247. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Khristianovich, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous liquid. World Pet. Congr. 2015, 141, 226–235. [Google Scholar]
- Detournay, E.; Hakobyan, Y. Hydraulic fracturing of weak rock during waterflooding. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 416–435. [Google Scholar] [CrossRef]
- Wrobel, M.; Papanastasiou, P.; Peck, D. A simplified modelling of hydraulic fractures in elasto-plastic materials. Int. J. Fract. 2022, 233, 153–178. [Google Scholar] [CrossRef]
- Carbonell, R.; Desroches, J.; Detournay, E. A comparison between a semi-analytical and a numerical solution of a two-dimensional hydraulic fracture. Int. J. Solids Struct. 1999, 36, 4869–4888. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Peirce, A.P. Proppant transport in hydraulic fracturing: Crack tip screen-out in KGD and P3D models. Int. J. Solids Struct. 2015, 63, 206–218. [Google Scholar] [CrossRef]
- Jin, T. A consistent linearization scheme for KGD problems using fracture tip asymptotic solutions. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2899–2924. [Google Scholar] [CrossRef]
- Jin, J.; Wang, X.; Liu, X.; Xu, Y.; Lu, D. A novel hydraulic fracturing model for the fluid-driven fracture propagation in poroelastic media containing the natural cave. Phys. Fluids 2023, 35, 096602. [Google Scholar] [CrossRef]
- Gee, B.; Gracie, R. Inertial and turbulent flow in hydro-mechanically coupled KGD-like fractures. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2925–2950. [Google Scholar] [CrossRef]
- Green, A.E.; Sneddon, I.N. The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid. Math. Proc. Camb. Philos. Soc. 1950, 46, 159–163. [Google Scholar] [CrossRef]
- Savitski, A.; Detournay, E. Propagation of a penny-shape hydraulic fracture in an impermeable rock. In Proceedings of the Vail Rocks 1999—37th US Symposium on Rock Mechanics (USRMS), Vail, Colorado, 7–9 June 1999; Volume 39, pp. 851–858. [Google Scholar]
- Mašín, D.; Tamagnini, C.; Viggiani, G.; Costanzo, D. Directional response of a reconstituted fine-grained soil—Part II: Performance of different constitutive models. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1303–1336. [Google Scholar] [CrossRef]
- Zolfaghari, N.; Dontsov, E.; Bunger, A.P. Solution for a plane strain rough-walled hydraulic fracture driven by turbulent fluid through impermeable rock. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 587–617. [Google Scholar] [CrossRef]
- Linkov, A.M.; Markov, N.S. Improved pseudo three-dimensional model for hydraulic fractures under stress contrast. Int. J. Rock Mech. Min. Sci. 2020, 130, 104316. [Google Scholar] [CrossRef]
- Adachi, J.I.; Detournay, E.; Peirce, A.P. Analysis of the classical pseudo-3D model for hydraulic fracture with equilibrium height growth across stress barriers. Int. J. Rock Mech. Min. Sci. 2010, 47, 625–639. [Google Scholar] [CrossRef]
- Simonson, E.R.; Abou-Sayed, A.S.; Clifton, R.J. Containment of massive hydraulic fractures. Soc. Pet. Eng. J. 1978, 18, 27–32. [Google Scholar] [CrossRef]
- Fomin, S.; Hashida, T.; Shimizu, A.; Matsuki, K.; Sakaguchi, K. Fractal concept in numerical simulation of hydraulic fracturing of the hot dry rock geothermal reservoir. Hydrol. Process. 2003, 17, 2975–2989. [Google Scholar] [CrossRef]
- Chen, M.; Guo, T.; Zou, Y.; Zhang, S.; Qu, Z. Numerical simulation of proppant transport coupled with Multi-Planar-3D hydraulic fracture propagation for Multi-Cluster fracturing. Rock Mech. Rock Eng. 2022, 55, 565–590. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H. Three-Dimensional hydromechanical model of hydraulic fracturing with arbitrarily discrete fracture networks using finite-discrete element method. Int. J. Geomech. 2017, 17, 6. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Chen, W. Three-dimensional hydraulic fracturing modeling based on peridynamics. Eng. Anal. Bound. Elem. 2022, 141, 153–166. [Google Scholar] [CrossRef]
- Zia, H.; Lecampion, B.; Zhang, W. Impact of the anisotropy of fracture toughness on the propagation of planar 3D hydraulic fracture. Int. J. Fract. 2018, 211, 103–123. [Google Scholar] [CrossRef]
- Li, F.; Xu, T.; Li, S.; Feng, B.; Jia, X.; Feng, G.; Zhu, H.; Jiang, Z. Assessment of energy production in the deep carbonate geothermal reservoir by wellbore-reservoir integrated fluid and heat transport modeling. Geofluids 2019, 2019, 8573182. [Google Scholar] [CrossRef]
- Salimzadeh, S.; Nick, H.M.; Zimmerman, R.W. Thermoporoelastic effects during heat extraction from low-permeability reservoirs. Energy 2018, 142, 546–558. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Q.; Liu, B.; Kang, Y.; He, J. Numerical manifold method for thermal–hydraulic coupling in fractured enhance geothermal system. Eng. Anal. Bound. Elem. 2019, 101, 67–75. [Google Scholar] [CrossRef]
- Gao, X.; Li, T.; Zhang, Y.; Kong, X.; Meng, N. A review of simulation models of heat extraction for a geothermal reservoir in an enhanced geothermal system. Energies 2022, 15, 7148. [Google Scholar] [CrossRef]
- Rawal, C.; Ghassemi, A. A reactive thermo-poroelastic analysis of water injection into an enhanced geothermal reservoir. Geothermics 2014, 50, 10–23. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique. Eng. Fract. Mech. 2014, 131, 269–281. [Google Scholar] [CrossRef]
- Shauer, N.; Duarte, C.A. Improved algorithms for generalized finite element simulations of three-dimensional hydraulic fracture propagation. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2707–2742. [Google Scholar] [CrossRef]
- Ma, G.; Wang, Y.; Li, T.; Chen, Y. A mesh mapping method for simulating stress-dependent permeability of three-dimensional discrete fracture networks in rocks. Comput. Geotech. 2019, 108, 95–106. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H.; Li, T.; Wang, Y.; Ren, F.; Ma, G. Evaluation of geothermal development considering proppant embedment in hydraulic fractures. Renew. Energy 2020, 153, 985–997. [Google Scholar] [CrossRef]
- Profit, M.; Dutko, M.; Yu, J.; Cole, S.; Angus, D.; Baird, A. Complementary hydro-mechanical coupled finite/discrete element and microseismic modelling to predict hydraulic fracture propagation in tight shale reservoirs. Comput. Part. Mech. 2016, 3, 229–248. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, X.; Ghassemi, A. Numerical simulation of reservoir stimulation with reference to the Newberry EGS. Geothermics 2019, 77, 327–343. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Z.; Feng, Z.; Yang, D.; Liang, W. THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573K and buried depth 6000–7000M. Energy 2015, 82, 193–205. [Google Scholar] [CrossRef]
- Bakhshi, E.; Golsanami, N.; Chen, L. Numerical modeling and lattice method for characterizing hydraulic fracture propagation: A review of the numerical, experimental, and field studies. Arch. Comput. Methods Eng. 2021, 28, 3329–3360. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Maulianda, B.; Savitri, C.D.; Prakasan, A.; Atdayev, E.; Yan, T.W.; Yong, Y.K.; Elrais, K.A.; Barati, R. Recent comprehensive review for extended finite element method (XFEM) based on hydraulic fracturing models for unconventional hydrocarbon reservoirs. J. Pet. Explor. Prod. Technol. 2020, 10, 3319–3331. [Google Scholar] [CrossRef]
- Ren, Q.; Dong, Y.; Yu, T. Numerical modeling of concrete hydraulic fracturing with extended finite element method. Sci. China Ser. E Technol. Sci. 2009, 52, 559–565. [Google Scholar] [CrossRef]
- Zheng, A.X.; Luo, X.Q. Hydro-mechanical modeling of impermeable discontinuity in rock by extended finite element method. J. Cent. South Univ. 2015, 22, 4337–4346. [Google Scholar] [CrossRef]
- Zheng, A.; Luo, X. A mathematical programming approach for frictional contact problems with the extended finite element method. Arch. Appl. Mech. 2016, 86, 599–616. [Google Scholar] [CrossRef]
- Xu, D.D.; Liu, Z.L.; Zhuang, Z.; Zeng, Q.L.; Wang, T. Study on interaction between induced and natural fractures by extended finite element method. Sci. China Phys. Mech. Astron. 2017, 60, 024611. [Google Scholar] [CrossRef]
- Zhou, Z.; Mikada, H.; Takekawa, J.; Xu, S. Numerical simulation of hydraulic fracturing in enhanced geothermal systems considering thermal stress cracks. Pure Appl. Geophys. 2022, 179, 1775–1804. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhao, B.; Zhang, Z. Numerical simulation of particle plugging in hydraulic fracture by element partition method. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1857–1879. [Google Scholar] [CrossRef]
- Torres, S.A.G.; Castaño, J.D.M. Simulation of the hydraulic fracture process in two dimensions using a discrete element method. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2007, 75, 066109. [Google Scholar] [CrossRef]
- Leonardi, C.R.; McCullough, J.W.S.; Jones, B.D.; Williams, J.R. Electromagnetic excitation of particle suspensions in hydraulic fractures using a coupled lattice Boltzmann-discrete element model. Comput. Part. Mech. 2016, 3, 125–140. [Google Scholar] [CrossRef]
- Cao, M.; Sharma, M.M. Effect of fracture geometry, topology and connectivity on energy recovery from enhanced geothermal systems. Energy 2023, 282, 128368. [Google Scholar] [CrossRef]
- Yang, W.; Lv, X.; Wang, L.; Peng, D.; Chen, X. A DEM–CFD coupling method for modelling two-hole synchronous hydraulic fracturing. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 6. [Google Scholar] [CrossRef]
- Yasin, Q.; Majdanski, M.; Awan, R.S.; Golsanami, N. An analytical hierarchy-based method for quantifying hydraulic fracturing stimulation to improve geothermal well productivity. Energies 2022, 15, 7368. [Google Scholar] [CrossRef]
- Ju, Y.; Chen, J.; Wang, Y.; Gao, F.; Xie, H. Numerical analysis of hydrofracturing behaviors and mechanisms of heterogeneous reservoir glutenite, Using the continuum-Based discrete element method while considering hydromechanical coupling and leak-Off effects. J. Geophys. Res. Solid Earth 2018, 123, 3621–3644. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F.; White, J.K. Combined single and smeared crack model in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Qu, T.; Feng, Y.T.; Wang, M.; Jiang, S. Calibration of parallel bond parameters in bonded particle models via physics-informed adaptive moment optimisation. Powder Technol. 2020, 366, 527–536. [Google Scholar] [CrossRef]
- Munjiza, A.; Owen, D.R.J.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H.; Sun, G.; Ge, X. Combined finite-discrete element method for simulation of hydraulic fracturing. Rock Mech. Rock Eng. 2016, 49, 1389–1410. [Google Scholar] [CrossRef]
- Zheng, H.; Pu, C.; Sun, C. Numerical investigation on the hydraulic fracture propagation based on combined finite-discrete element method. J. Struct. Geol. 2020, 130, 103926. [Google Scholar] [CrossRef]
- Wu, M.; Gao, K.; Liu, J.; Song, Z.; Huang, X. Influence of rock heterogeneity on hydraulic fracturing: A parametric study using the combined finite-discrete element method. Int. J. Solids Struct. 2022, 234–235, 111293. [Google Scholar] [CrossRef]
- Yan, C.; Xie, X.; Ren, Y.; Ke, W.; Wang, G. A FDEM-based 2D coupled thermal-hydro-mechanical model for multiphysical simulation of rock fracturing. Int. J. Rock Mech. Min. Sci. 2022, 149, 104964. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.; Ma, J.; Huang, L. A finite-discrete element based appoach for modelling the hydraulic fracturing of rocks with irregular inclusions. Eng. Fract. Mech. 2022, 261, 108209. [Google Scholar] [CrossRef]
- Behnia, M.; Goshtasbi, K.; Marji, M.F.; Golshani, A. Numerical simulation of crack propagation in layered formations. Arab. J. Geosci. 2014, 7, 2729–2737. [Google Scholar] [CrossRef]
- Behnia, M.; Goshtasbi, K.; Marji, M.F.; Golshani, A. Numerical simulation of interaction between hydraulic and natural fractures in discontinuous media. Acta Geotech. 2015, 10, 533–546. [Google Scholar] [CrossRef]
- Shi, J.; Shen, B. A numerical study of effect of cold temperature on growth orientation of horizontal fractures using displacement discontinuity method. Geomech. Energy Environ. 2022, 31, 100319. [Google Scholar] [CrossRef]
- Zhou, X.X.; Ghassemi, A.; Cheng, A.H.-D. A three-dimensional integral equation model for calculating poro- and thermoelastic stresses induced by cold water injection into a geothermal reservoir. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1613–1640. [Google Scholar] [CrossRef]
- Ghassemi, A.; Zhou, X. A three-dimensional thermo-poroelastic model for fracture response to injection/extraction in enhanced geothermal systems. Geothermics 2011, 40, 39–49. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, Q.; Yang, S.; Tan, X. A semi-analytical solution of finite-conductivity multi-wing fractured well in naturally fractured reservoirs by boundary element method. J. Pet. Sci. Eng. 2021, 203, 108584. [Google Scholar] [CrossRef]
- He, Y.; Yang, Z.; Li, X.; Song, R. Numerical simulation study on three-dimensional fracture propagation of synchronous fracturing. Energy Sci. Eng. 2020, 8, 944–958. [Google Scholar] [CrossRef]
- Kebir, H.; Roelandt, J.M.; Foulquier, J. A new singular boundary element for crack problems: Application to bolted joints. Eng. Fract. Mech. 1999, 62, 497–510. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, M.; Zhang, X.; Wu, B.; Chen, Z.; Lei, Z.; Tan, P. Numerical study of hydraulic fracturing near a wellbore using dual boundary element method. Int. J. Solids Struct. 2022, 239–240, 111479. [Google Scholar] [CrossRef]
- Ji, J.; Song, X.; Song, G.; Xu, F.; Shi, Y.; Lv, Z.; Li, S.; Yi, J. Study on fracture evolution model of the enhanced geothermal system under thermal-hydraulic-chemical-deformation coupling. Energy 2023, 269, 126604. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Guo, T.; Wang, Z. Study of the enhanced geothermal system (EGS) heat mining from variably fractured hot dry rock under thermal stress. Renew. Energy 2019, 143, 855–871. [Google Scholar] [CrossRef]
- Ma, W.; Wang, Y.; Wu, X.; Liu, G. Hot dry rock (HDR) hydraulic fracturing propagation and impact factors assessment via sensitivity indicator. Renew. Energy 2020, 146, 2716–2723. [Google Scholar] [CrossRef]
- Guo, L.L.; Zhang, Y.B.; Zhang, Y.J.; Yu, Z.W.; Zhang, J.N. Experimental investigation of granite properties under different temperatures and pressures and numerical analysis of damage effect in enhanced geothermal system. Renew. Energy 2018, 126, 107–125. [Google Scholar] [CrossRef]
- Li, Y.; Long, M.; Tang, J.; Chen, M.; Fu, X. A hydraulic fracture height mathematical model considering the influence of plastic region at fracture tip. Pet. Explor. Dev. 2020, 47, 184–195. [Google Scholar] [CrossRef]
- Yu, L.; Wu, X.; Wang, Y.; Ma, W.; Liu, G. Stratified rock hydraulic fracturing for enhanced geothermal system and fracture geometry evaluation via effective length. Renew. Energy 2020, 152, 713–723. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, S.; Liu, X.; Zhang, W.; Qu, G. Numerical simulation of hydraulic fracturing of hot dry rock under thermal stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Kolawole, O.; Ispas, I.; Kolawole, F.; Germay, C.; McLennan, J.D. Mechanical zonation of rock properties and the development of fluid migration pathways: Implications for enhanced geothermal systems in sedimentary-hosted geothermal reservoirs. Geotherm. Energy 2021, 9, 14. [Google Scholar] [CrossRef]
- Huang, W.; Cao, W.; Jiang, F. Heat extraction performance of EGS with heterogeneous reservoir: A numerical evaluation. Int. J. Heat. Mass. Transf. 2017, 108, 645–657. [Google Scholar] [CrossRef]
- Liu, J.; Xue, Y.; Peng, C.; Wang, H.; Liang, X.; Li, S.T. The role of spatially-autocorrelated heterogeneous and anisotropic fracture roughness on the thermal breakthrough of geothermal doublet systems. Geoenergy Sci. Eng. 2024, 237, 212801. [Google Scholar] [CrossRef]
- Liu, D.D.; Xiang, Y.Y.; Zheng, J.L. Integral equation solution for three-dimensional heat transfer in multiple-fracture enhanced geothermal reservoirs. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1511–1524. [Google Scholar] [CrossRef]
- Han, D.; Zhang, W.; Jiao, K.; Yu, B.; Li, T.; Gong, L.; Wang, S. Thermal−hydraulic−mechanical−chemical coupling analysis of enhanced geothermal systems based on an embedded discrete fracture model. Nat. Gas. Ind. B 2023, 10, 533–546. [Google Scholar] [CrossRef]
- Duan, X.Y.; Huang, D.; Lei, W.X.; Chen, S.C.; Huang, Z.Q.; Zhu, C.Y. Investigation of Heat Extraction in an Enhanced Geothermal System Embedded with Fracture Networks Using the Thermal–Hydraulic–Mechanical Coupling Model. Energies 2023, 16, 3758. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Hu, B. Numerical analysis of the impacts of multiscale fractures on geothermal reservoir capacity. J. Energy Eng. 2023, 149, 1–16. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Wang, H.; Li, T. Evaluation of geothermal development in fractured hot dry rock based on three dimensional unified pipe-network method. Appl. Therm. Eng. 2018, 136, 219–228. [Google Scholar] [CrossRef]
- Yang, S.; Qin, F.; Hu, J.; Wang, H. Thermo-hydro-mechanical optimization of the enhanced geothermal system for commercial utilization. Appl. Therm. Eng. 2022, 213, 118641. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Sun, Y.; Zhu, C.; Xiong, F.; Tang, Q. Numerical simulation on heat transfer characteristics of water flowing through the fracture of high-temperature rock. Geofluids 2020, 2020, 8864028. [Google Scholar] [CrossRef]
- Slatlem Vik, H.; Salimzadeh, S.; Nick, H.M. Heat recovery from multiple-fracture enhanced geothermal systems: The effect of thermoelastic fracture interactions. Renew. Energy 2018, 121, 606–622. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Tang, C. Fracture spacing in horizontal well multi-perforation fracturing optimized by heat extraction. Geothermics 2022, 101, 102376. [Google Scholar] [CrossRef]
- He, R.; Rong, G.; Tan, J.; Phoon, K.K.; Quan, J. Numerical evaluation of heat extraction performance in enhanced geothermal system considering rough-walled fractures. Renew. Energy 2022, 188, 524–544. [Google Scholar] [CrossRef]
- Wang, G.; Ma, X.; Song, X.; Li, G. Modeling flow and heat transfer of fractured reservoir: Implications for a multi-fracture enhanced geothermal system. J. Clean. Prod. 2022, 365, 132708. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, Z.; Guo, T.; Sheng, M.; Chen, M.; Wang, J.; Wang, Y.; Guo, C. Coupled thermal-hydraulic investigation on the heat extraction performance considering a fractal-like tree fracture network in a multilateral well enhanced geothermal system. Appl. Therm. Eng. 2022, 208, 118221. [Google Scholar] [CrossRef]
- Watanabe, N.; Saito, K.; Okamoto, A.; Nakamura, K.; Ishibashi, T.; Saishu, H.; Komai, T.; Tsuchiya, N. Stabilizing and enhancing permeability for sustainable and profitable energy extraction from superhot geothermal environments. Appl. Energy 2020, 260, 114306. [Google Scholar] [CrossRef]
- Shi, Y.; Song, X.; Li, J.; Wang, G.; Zheng, R.; YuLong, F. Numerical investigation on heat extraction performance of a multilateral-well enhanced geothermal system with a discrete fracture network. Fuel 2019, 244, 207–226. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, L.; Li, X.; Chen, J.; Liu, Z. Comprehensive heat extraction performance and fractured reservoir cooling effect analysis of a novel mine enhanced geothermal system. Appl. Therm. Eng. 2024, 245, 122790. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, Z.; Xie, X.; Hu, Y. Coupled thermal–hydraulic–mechanical model for an enhanced geothermal system and numerical analysis of its heat mining performance. Renew. Energy 2022, 181, 1440–1458. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, S.; Chai, J.; Liu, J.; Ranjith, P.G.; Cai, C.; Gao, F.; Bai, X. Effect of water-cooling shock on fracture initiation and morphology of high-temperature granite: Application of hydraulic fracturing to enhanced geothermal systems. Appl. Energy 2023, 337, 120858. [Google Scholar] [CrossRef]
- Li, J.; Ma, W.; Jiang, P.; Xu, R. Heat transfer characterizations of water flow through a single fracture with integrating water dissolution effects for the Enhanced Geothermal Systems. Appl. Therm. Eng. 2024, 239, 122133. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, P.; Wang, Z.; Xu, R. Convective heat transfer of supercritical CO2 in a rock fracture for enhanced geothermal systems. Appl. Therm. Eng. 2017, 115, 923–936. [Google Scholar] [CrossRef]
- Bakhsh, K.J.; Nakagawa, M.; Arshad, M.; Dunnington, L. On heat and mass transfer within thermally shocked region of enhanced geothermal system. Geofluids 2017, 2017, 2759267. [Google Scholar]
- Tomac, I.; Gutierrez, M. Coupled hydro-thermo-mechanical modeling of hydraulic fracturing in quasi-brittle rocks using BPM-DEM. J. Rock Mech. Geotech. Eng. 2017, 9, 92–104. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, T.; Qu, Z.; Wang, Z. Research of fracture initiation and propagation in HDR fracturing under thermal stress from meso-damage perspective. Energy 2019, 178, 508–521. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, Z.; Elsworth, D. Failure behavior of Hot-Dry-Rock (HDR) in enhanced geothermal systems: Macro to micro scale effects. Geofluids 2020, 2020, 8878179. [Google Scholar] [CrossRef]
- Hu, M.; Veveakis, M.; Poulet, T.; Regenauer-Lieb, K. The role of temperature in shear instability and bifurcation of internally pressurized deep boreholes. Rock Mech. Rock Eng. 2017, 50, 3003–3017. [Google Scholar] [CrossRef]
- Zheng, J.; Li, P.; Dou, B.; Fan, T.; Tian, H.; Lai, X. Impact research of well layout schemes and fracture parameters on heat production performance of enhanced geothermal system considering water cooling effect. Energy 2022, 255, 124496. [Google Scholar] [CrossRef]
- Regenauer-Lieb, K.; Bunger, A.; Chua, H.T.; Dyskin, A.; Fusseis, F.; Gaede, O.; Jeffrey, R.; Karrech, A.; Kohl, T.; Liu, J.; et al. Deep geothermal: The ‘Moon Landing’ mission in the unconventional energy and minerals space. J. Earth Sci. 2015, 26, 2–10. [Google Scholar] [CrossRef]
- Dang-trung, H.; Keilegavlen, E. Modelling of mixed- mechanism stimulation for the enhancement of geothermal reservoirs. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2024, 382, 20230420. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Zhang, Y.; Zhang, S.; Shi, Y. Numerical study of hydraulic fracturing treatments and geothermal energy extraction from a naturally fractured granitic formation. Geothermics 2023, 111, 102692. [Google Scholar] [CrossRef]
- Ouyang, P.; Rao, P.; Wu, J.; Cui, J.; Nimbalkar, S.; Chen, Q. Hydromechanical modeling of high-voltage electropulse-assisted fluid injection for rock fracturing. Rock Mech. Rock Eng. 2023, 56, 3861–3886. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.P.; Sun, W. A review of laboratory studies and theoretical analysis for the interaction mode between induced hydraulic fractures and pre-existing fractures. J. Nat. Gas. Sci. Eng. 2021, 86, 103719. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Xu, X.F. Current status and potentials of enhanced geothermal system in China: A review. Renew. Sustain. Energy Rev. 2014, 33, 214–223. [Google Scholar] [CrossRef]
- Lepillier, B.; Yoshioka, K.; Parisio, F.; Bakker, R.; Bruhn, D. Variational phase-field modeling of hydraulic fracture interaction with natural fractures and application to enhanced geothermal systems. J. Geophys. Res. Solid. Earth 2020, 125, e2020JB019856. [Google Scholar] [CrossRef]
- Putra, V.; Furui, K. Phase-field modeling of coupled thermo-hydromechanical. Energies 2023, 16, 7942. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Z.; Peng, H. Convective heat transfer of water flow in intersected rock fractures for enhanced geothermal extraction. J. Rock Mech. Geotech. Eng. 2022, 14, 108–122. [Google Scholar] [CrossRef]
- Haris, M.; Hou, M.Z.; Feng, W.; Mehmood, F.; bin Saleem, A. A regenerative enhanced geothermal system for heat and electricity production as well as energy storage. Renew. Energy 2022, 197, 342–358. [Google Scholar] [CrossRef]
- Liang, X.; Xu, T.; Chen, J.; Jiang, Z. A deep-learning based model for fracture network characterization constrained by induced micro-seismicity and tracer test data in enhanced geothermal system. Renew. Energy 2023, 216, 119046. [Google Scholar] [CrossRef]
- Jiang, H.; Guo, L.; Kang, F.; Wang, F.; Cao, Y.; Sun, Z.; Shi, M. Geothermal Characteristics and Productivity Potential of a Super-Thick Shallow Granite-Type Enhanced Geothermal System: A Case Study in Wendeng Geothermal Field, China. Sustainability 2023, 15, 3551. [Google Scholar] [CrossRef]
- Fan, Z.; Parashar, R. Analytical solutions for a wellbore subjected to a non-isothermal fluid flux: Implications for optimizing injection rates, fracture reactivation, and EGS hydraulic stimulation. Rock Mech. Rock Eng. 2019, 52, 4715–4729. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Z.; Zhang, K.; Jiang, C.; Xin, Y.; Mao, Q. Investigation on heat extraction performance of fractured geothermal reservoir using coupled thermal-hydraulic-mechanical model based on equivalent continuum method. Energies 2019, 12, 127. [Google Scholar] [CrossRef]
- Ma, Y.; Li, S.; Zhang, L.; Li, H.; Liu, Z. Numerical simulation on heat extraction performance of enhanced geothermal system under the different well layout. Energy Explor. Exploit. 2020, 38, 274–297. [Google Scholar] [CrossRef]
- Zuo, L.; Weijermars, R. Longevity of enhanced geothermal systems with brine circulation in hydraulically fractured hydrocarbon wells. Fluids 2019, 4, 63. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, S.; Ma, H.; Luan, H.; Ding, Z. Study of characteristics of fault slip and induced seismicity during hydraulic fracturing in HDR geothermal exploitation in the Yishu fault zone in China. Geofluids 2021, 2021, 5515665. [Google Scholar] [CrossRef]
- Yao, S.; Chang, C.; Hai, K.; Huang, H.; Li, H. A review of experimental studies on the proppant settling in hydraulic fractures. J. Pet. Sci. Eng. 2022, 208, 109211. [Google Scholar] [CrossRef]
- Suri, Y.; Islam, S.Z.; Hossain, M. Numerical modelling of proppant transport in hydraulic fractures. Fluid. Dyn. Mater. Processing. 2020, 16, 297–337. [Google Scholar] [CrossRef]
- Sharma, V.; Sircar, A.; Gupta, A. Hydraulic fracturing design and 3D modeling: A case study from Cambay Shale and Eagleford Shale. Multiscale Multidiscip. Model. Exp. Des. 2019, 2, 1–13. [Google Scholar] [CrossRef]
- Bao, J.; Liu, H.; Zhang, G.; Jin, J.; Cheng, W.; Liu, J. Fracture propagation laws in staged hydraulic fracturing and their effects on fracture conductivities. Pet. Explor. Dev. 2017, 44, 306–314. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, G.; Zhou, J.; Liu, J. Fracture network volume fracturing technology in high-temperature hard formation of hot dry rock. Acta Geol. Sin. 2021, 95, 1828–1834. [Google Scholar] [CrossRef]
- Xu, H.; Peng, N.; Ma, T.; Yang, B. Investigation of thermal stress of cement sheath for geothermal wells during fracturing. Energies 2018, 11, 2581. [Google Scholar] [CrossRef]
- Okoroafor, E.R.; Williams, M.J.; Gossuin, J.; Keshinro, O.; Horne, R.N. Fracture roughness considerations in comparing CO2 and water as enhanced geothermal system working fluids. Geothermics 2022, 106, 102578. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Huang, W.; Zhang, C. Numerical simulation of the thermo-hydro-chemical coupling in enhanced geothermal systems: Impact of SiO2 dissolution/precipitation in matrix and fractures. Energy 2024, 290, 130190. [Google Scholar] [CrossRef]
- Davoodi, S.; Al-Shargabi, M.; Wood, D.A.; Rukavishnikov, V.S. A comprehensive review of beneficial applications of viscoelastic surfactants in wellbore hydraulic fracturing fluids. Fuel 2023, 338, 127228. [Google Scholar] [CrossRef]
- Shibaev, A.V.; Osiptsov, A.A.; Philippova, O.E. Novel trends in the development of surfactant-based hydraulic fracturing fluids: A review. Gels 2021, 7, 258. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Liao, J.; Zhao, P.; Xia, K.; Li, C. Effects of fracture evolution and non-Darcy flow on the thermal performance of enhanced geothermal system in 3D complex fractured rock. Int. J. Min. Sci. Technol. 2024, 34, 443–459. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Gan, Q.; Zhi, S. Influence of fracture pattern between Hot Sedimentary Aquifer (HSA) and Enhanced Geothermal Systems (EGS) on thermal production and permeability evolution. Geothermics 2023, 114, 102804. [Google Scholar] [CrossRef]
- Ucar, E.; Berre, I.; Keilegavlen, E. Postinjection normal closure of fractures as a mechanism for induced seismicity. Geophys. Res. Lett. 2017, 44, 9598–9606. [Google Scholar] [CrossRef]
- Liu, J.; Mei, L.; Ding, W.; Xu, K.; Yang, H.; Liu, Y. Asymmetric propagation mechanism of hydraulic fracture networks in continental reservoirs. Bull. Geol. Soc. Am. 2023, 135, 678–688. [Google Scholar] [CrossRef]
- Watanabe, N.; Egawa, M.; Sakaguchi, K.; Ishibashi, T.; Tsuchiya, N. Hydraulic fracturing and permeability enhancement in granite from subcritical/brittle to supercritical/ductile conditions. Geophys. Res. Lett. 2017, 44, 5468–5475. [Google Scholar] [CrossRef]
- Zhao, Q.X.; Cao, P.; Lu, Z.; Li, H.; Liu, T.; Li, K.; Liu, Z. Development of 20 MN large-scale rock mass three-direction five-surface test system and its application. Chin. J. Rock Mech. Eng. 2023, 42, 1847–1865. [Google Scholar]
- He, P.; Pan, L.; Lu, Z.; Zhou, J.; Meng, C.; Yu, H. Experimental study to quantify fracture propagation in hydraulic fracturing treatment. ACS Omega 2022, 7, 27490–27502. [Google Scholar] [CrossRef]
- Jia, L.; Chen, M.; Sun, L.; Sun, Z.; Zhang, W.; Zhu, Q.; Sun, Z.; Jin, Y. Experimental study on propagation of hydraulic fracture in volcanic rocks using industrial CT technology. Pet. Explor. Dev. 2013, 40, 405–408. [Google Scholar] [CrossRef]




| Approach | Software | Advantages | Disadvantages |
|---|---|---|---|
| FEM/XFEM | ANSYS 15.0, ABAQUS 6.9, COMSOL Multiphysics 6.0 | In FEM analysis, the fracture surface is represented by a grid, which is convenient to calculate the fracture width and can handle the boundary conditions well. The main advantage of XFEM is its ability to simulate fractures that propagate along arbitrary paths, unlike other methods that require predefined trajectories. | In FEM analysis, repartitioning increases computational costs and leads to accuracy issues due to variable mapping between the old and new grids. XFEM has the same limitations as FEM when dealing with complex structures resulting from the intersection of hydraulic and natural fractures. |
| DEM | PFC3D 4.0, 3DEC 5.2.247 | No extra fracture criteria are needed to control fracture propagation. The initiation and propagation of hydraulic fractures can be simulated uniformly, and it is not necessary to update the topology with the expansion of hydraulic fractures. | The calculation cost of DEM is relatively large, and it is not suitable for micro-scale or mesoscale problems. At the same time, it is not as clear as the grid surface representation in the continuum method. |
| FDEM | Y-Code | DEM is used to simulate the relationship between different regions produced by fracturing, and FEM is used to analyze the deformation of each solid region. So FDEM is suitable for problems involving progressive fracturing. | The simulation time is long, and the calculation cost is high. Due to finite stiffness, the material stiffness is reduced. |
| BEM | FRACOD, FRAN3D 6.0 | It only needs to discretize the boundary, rather than the entire region, thus reducing the computational cost. | It is difficult to solve the fracture mechanics problem involving complex 3D fracture intersections. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Han, D.; Li, J.; Li, K. A State-of-the-Art Review of Hydraulic Fracturing in Geothermal Systems. Sustainability 2024, 16, 11087. https://doi.org/10.3390/su162411087
Xie Z, Han D, Li J, Li K. A State-of-the-Art Review of Hydraulic Fracturing in Geothermal Systems. Sustainability. 2024; 16(24):11087. https://doi.org/10.3390/su162411087
Chicago/Turabian StyleXie, Zhiqiang, Dongya Han, Jiangteng Li, and Kaihui Li. 2024. "A State-of-the-Art Review of Hydraulic Fracturing in Geothermal Systems" Sustainability 16, no. 24: 11087. https://doi.org/10.3390/su162411087
APA StyleXie, Z., Han, D., Li, J., & Li, K. (2024). A State-of-the-Art Review of Hydraulic Fracturing in Geothermal Systems. Sustainability, 16(24), 11087. https://doi.org/10.3390/su162411087








