Coordinated Hybrid Approach Based on Firefly Algorithm and Particle Swarm Optimization for Distributed Secondary Control and Stability Analysis of Direct Current Microgrids
Abstract
1. Introduction
- A distributed secondary control strategy for a DC microgrid is proposed, incorporating a new weighting parameter that concurrently ensures fair current distribution and eliminates bus voltage variations across several DERs.
- An innovative FFA-PSO is introduced to aid in the parameter selection for the distributed control approach. This algorithm helps in fulfilling the control objectives of the microgrid.
- A DC microgrid state-space model that incorporates eigenvalue observation analysis is developed to evaluate the impacts of the optimized secondary distributed control on the stability of the microgrid. This analysis helps in understanding the stability of the system.
- A real-time testing setup using MATLAB/Simulink® is built and implemented on a Speedgoat™ real-time machine to verify the practical performance of the proposed approach in real-world applications.
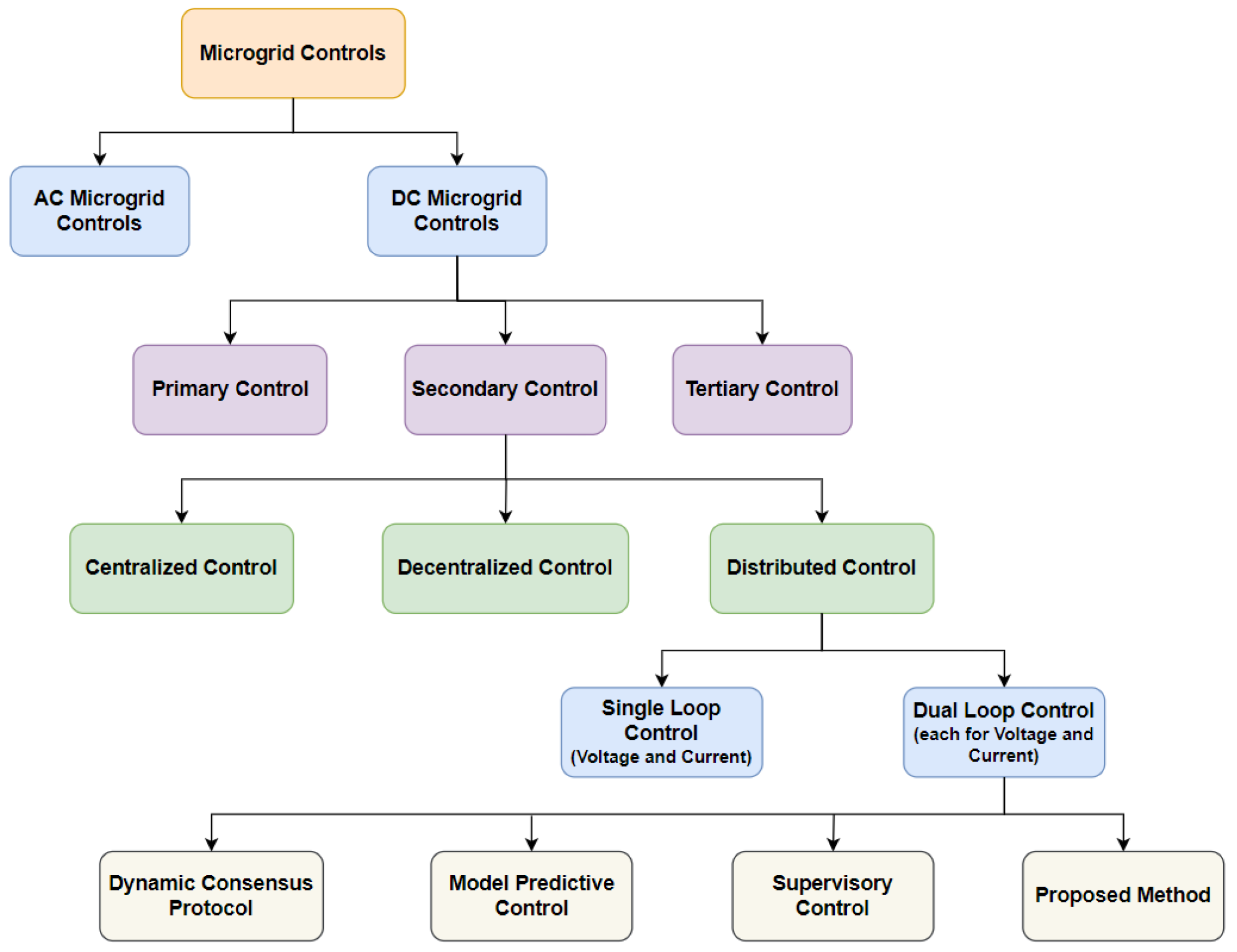
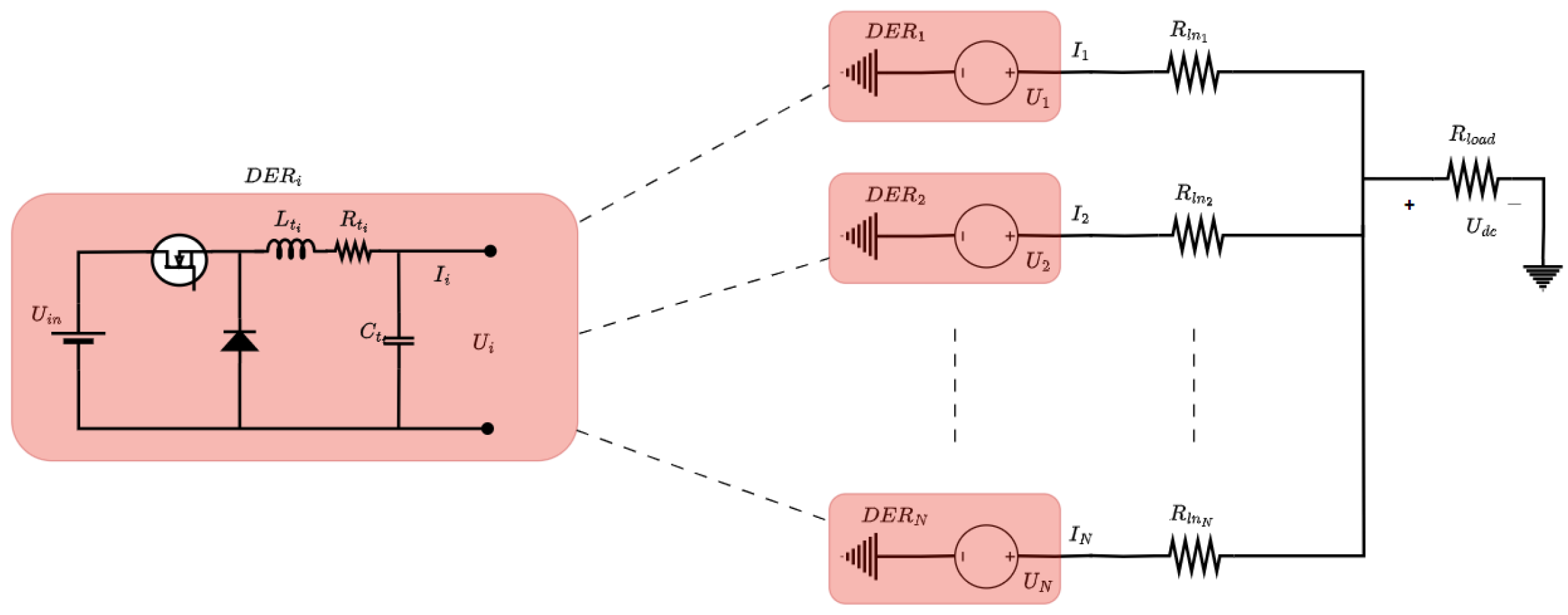
2. DC Microgrid Modelling
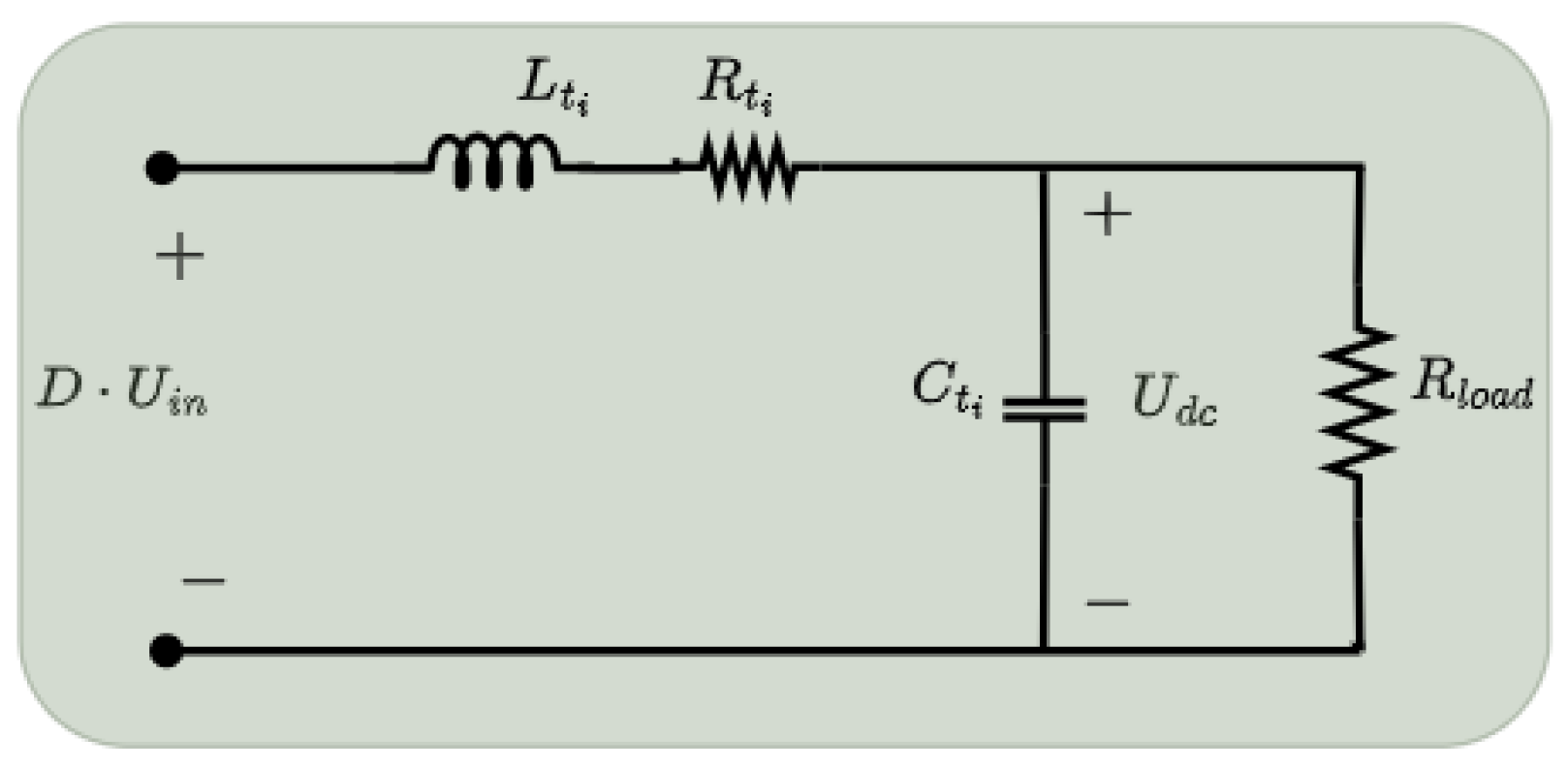
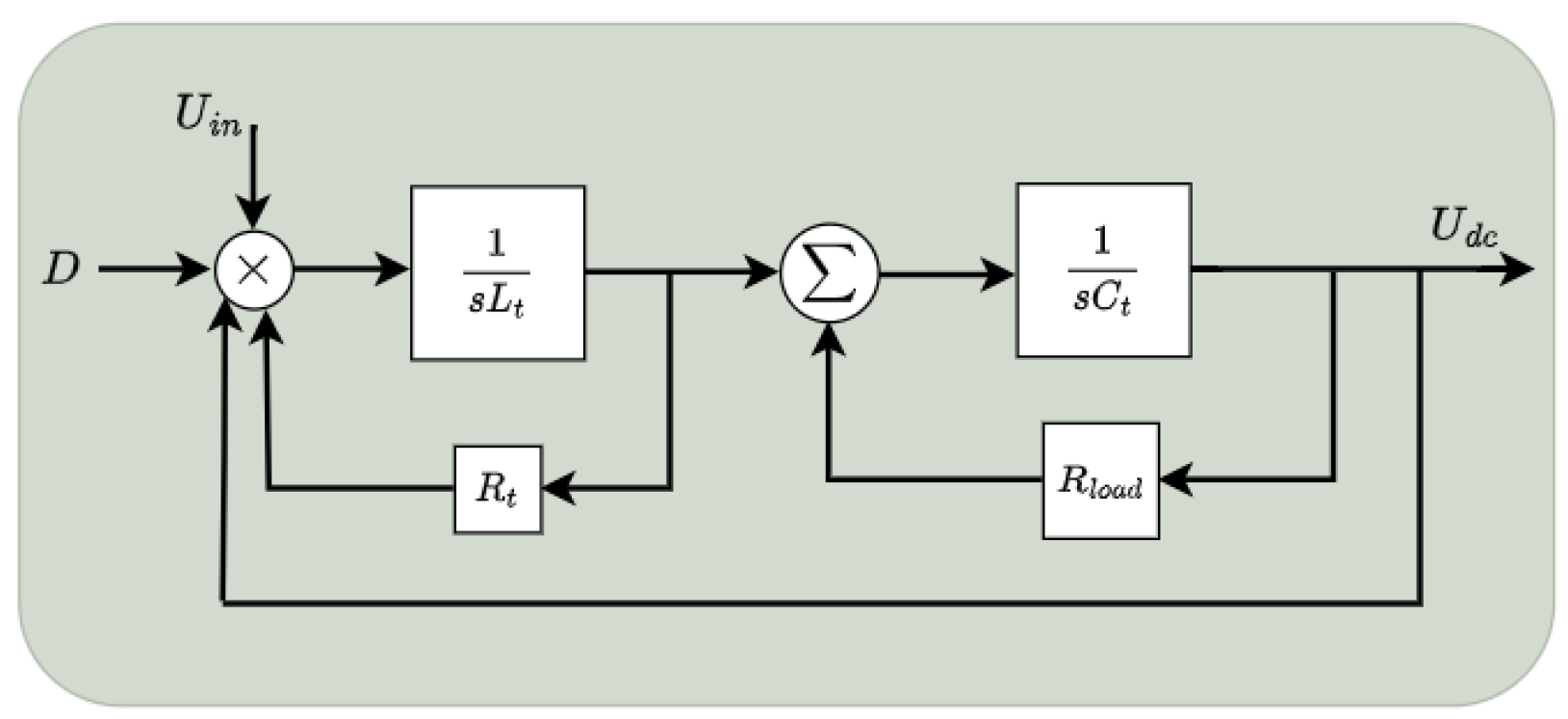
2.1. DC-DC Buck Converter Modelling
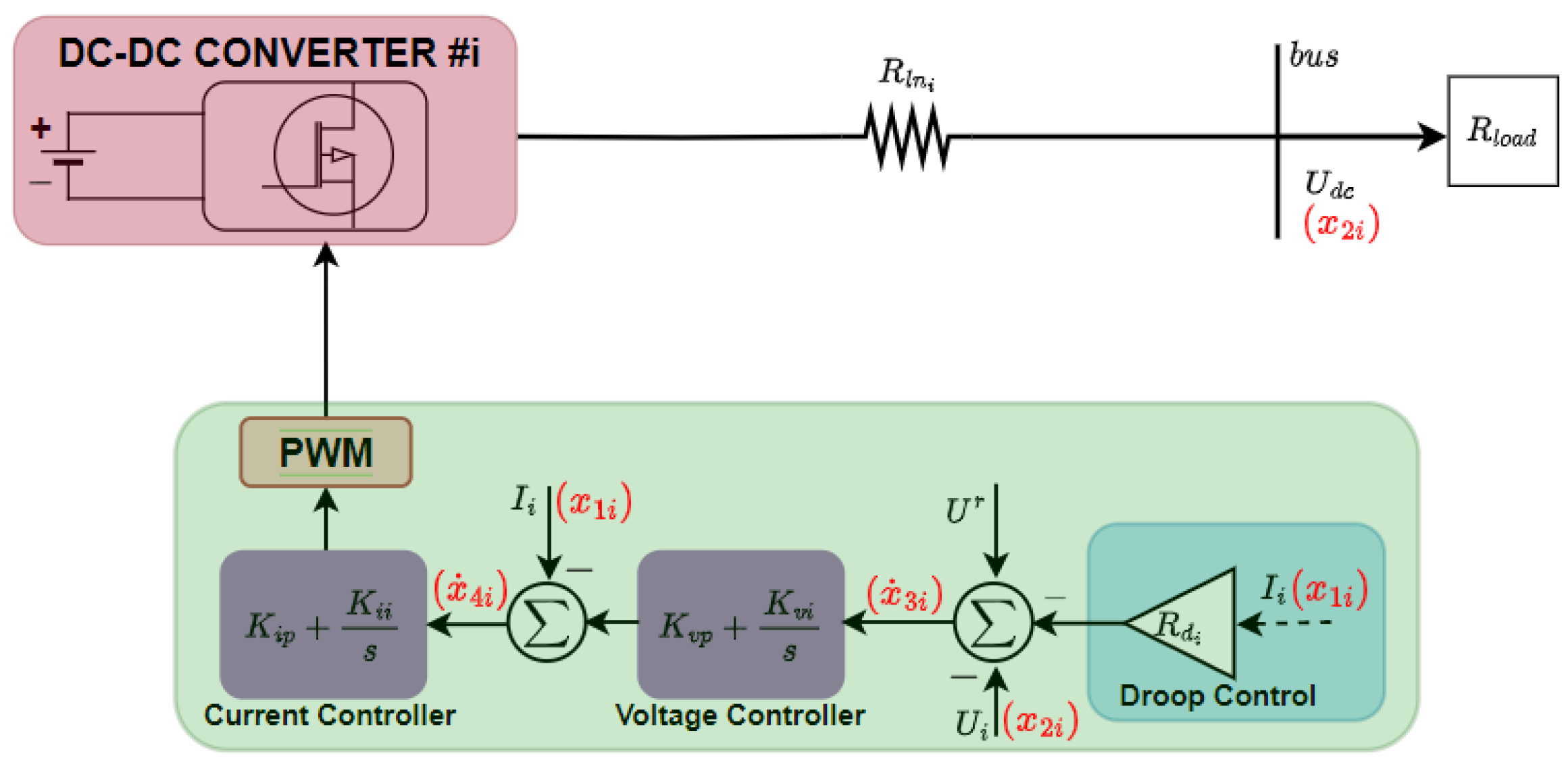
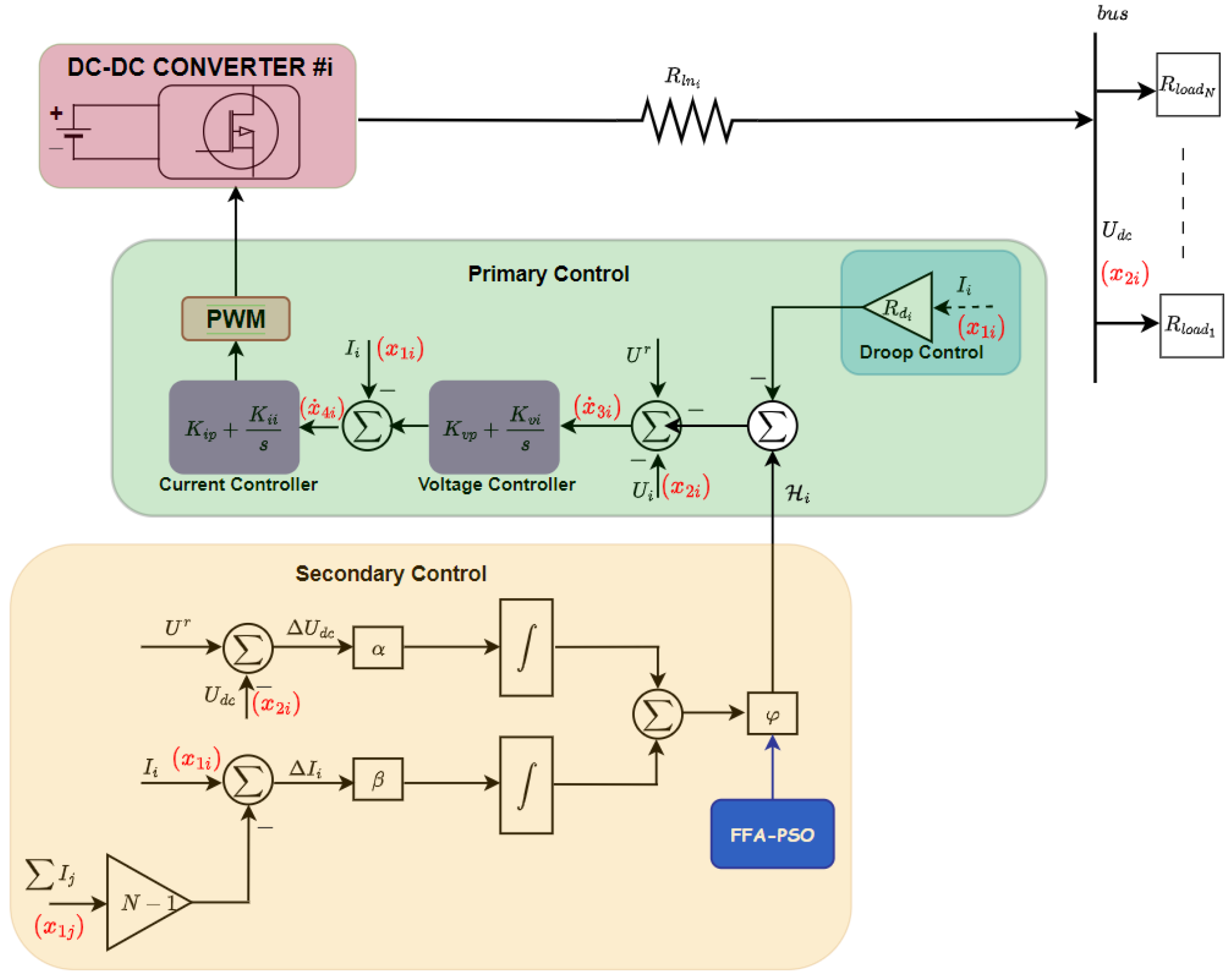
2.2. Primary Control Model
3. Distributed Secondary Control Technique
3.1. Communication Graph
3.2. Control Objectives
3.3. Proposed Control Design
4. Distributed Secondary Control Enhanced Tuning Approach
4.1. Particle Swarm Optimization (PSO)
4.2. Firefly Optimization Algorithm (FFA)
4.3. Proposed Hybrid FFA–PSO for Distributed Secondary Control
| Algorithm 1 Proposed Hybrid FFA–PSO Algorithm Implementation |
Rank and provide the most optimal solution. |
5. Results and Discussion
5.1. Stability Analysis
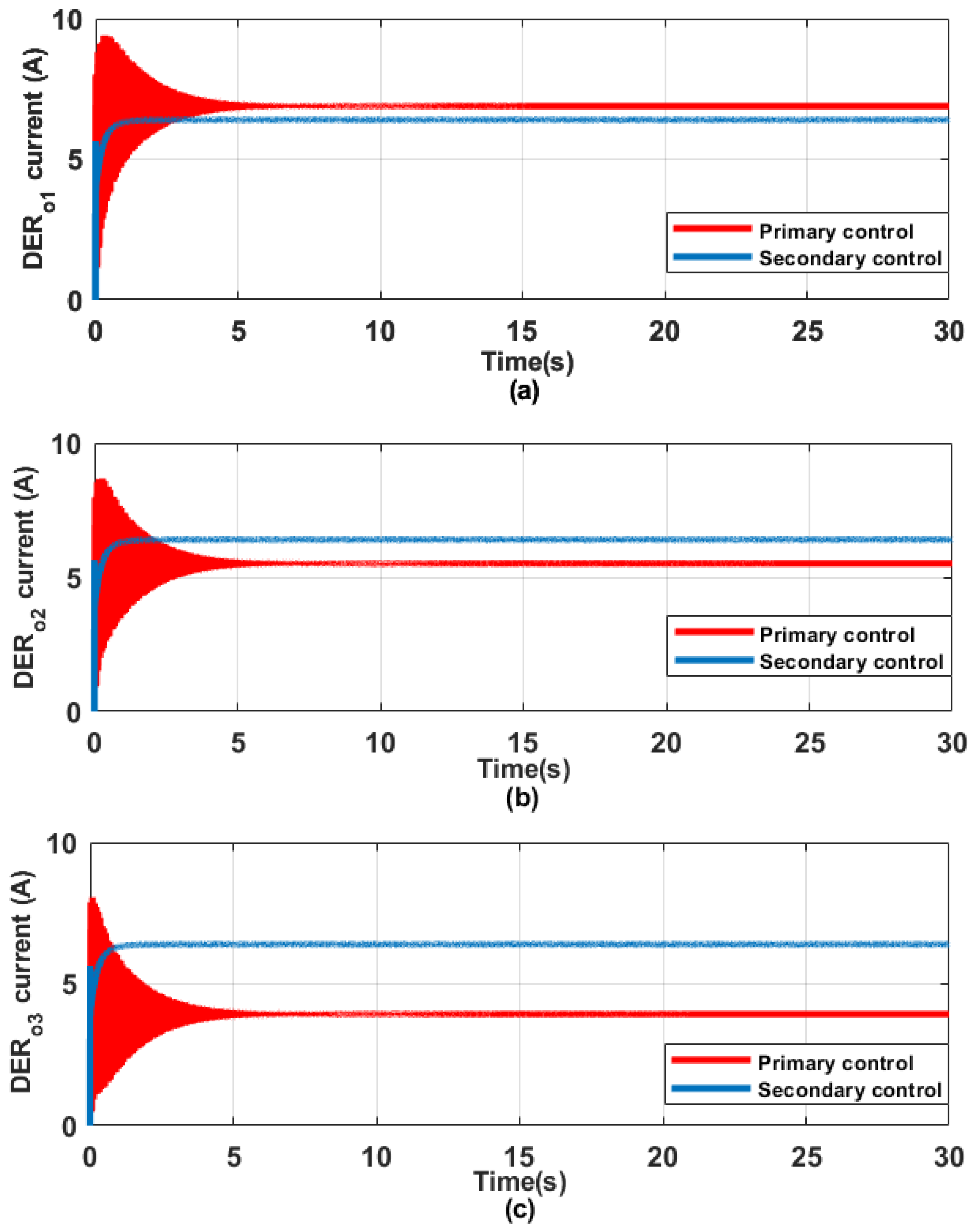
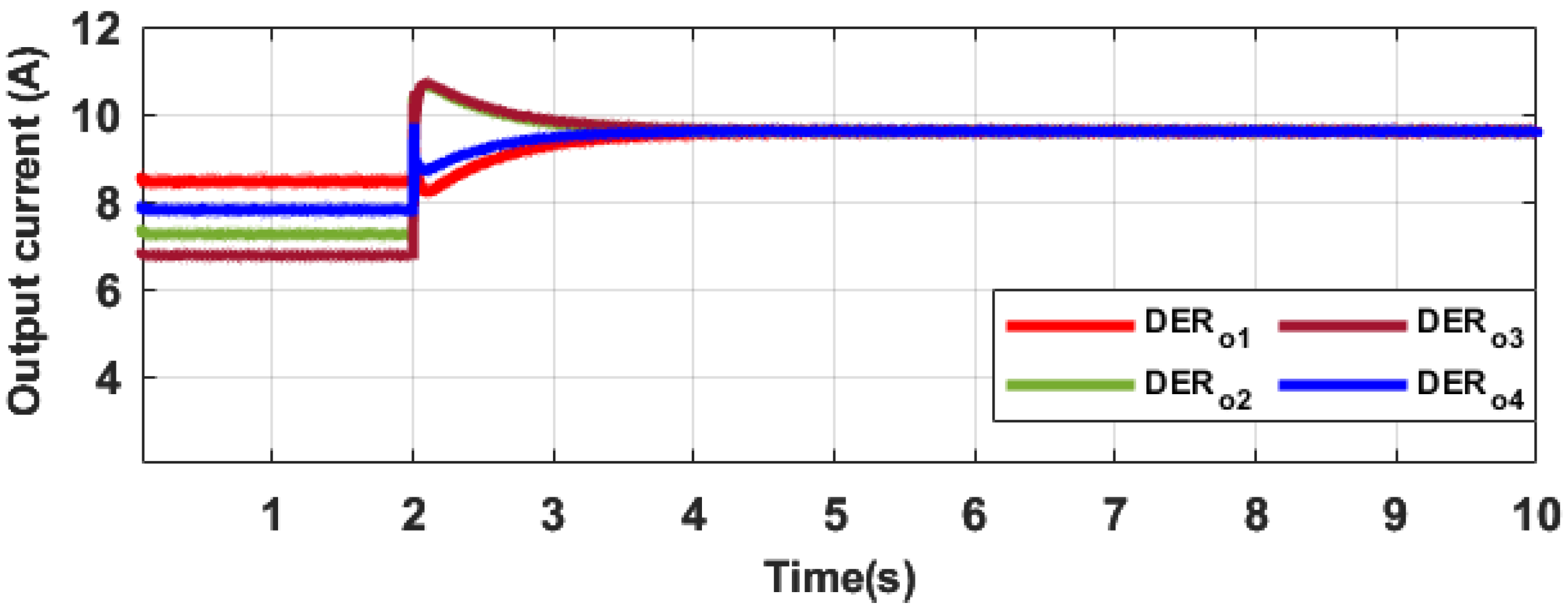
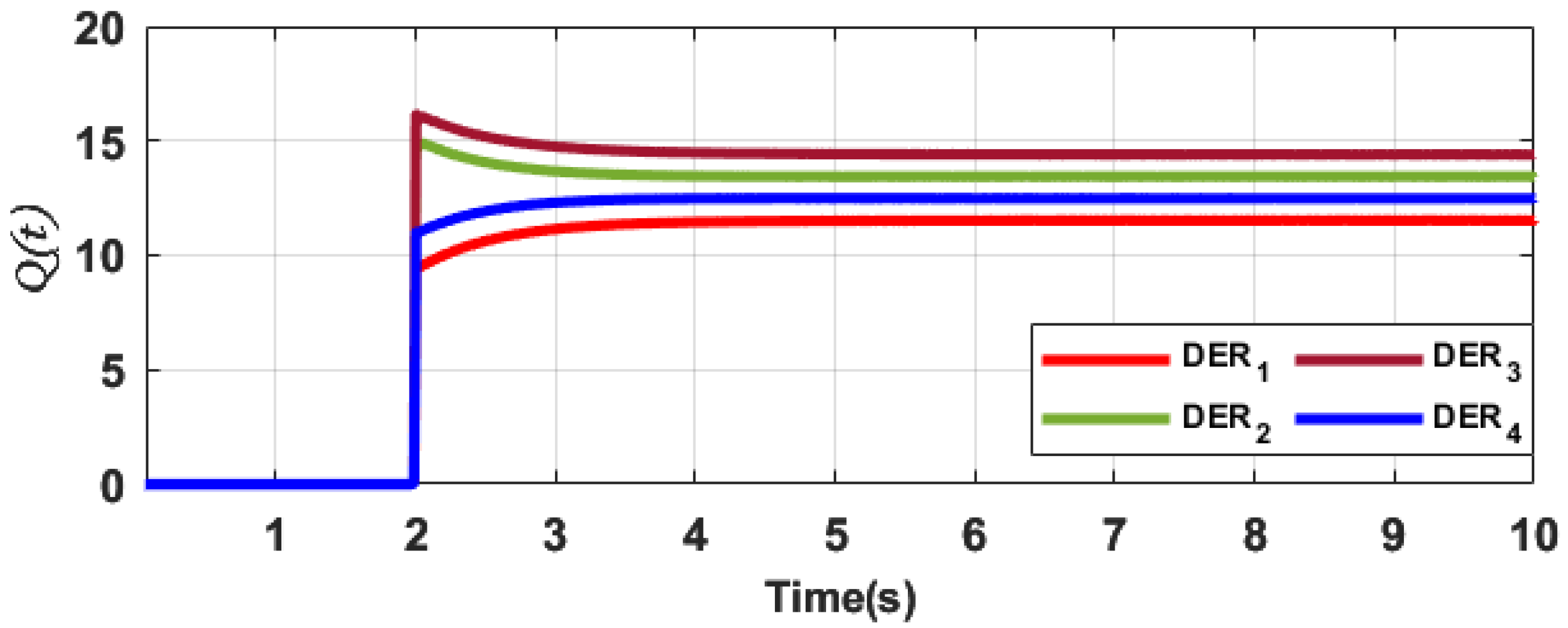
5.2. Realization of Control Objectives
5.3. Real-Time Experimental Simulation Validation
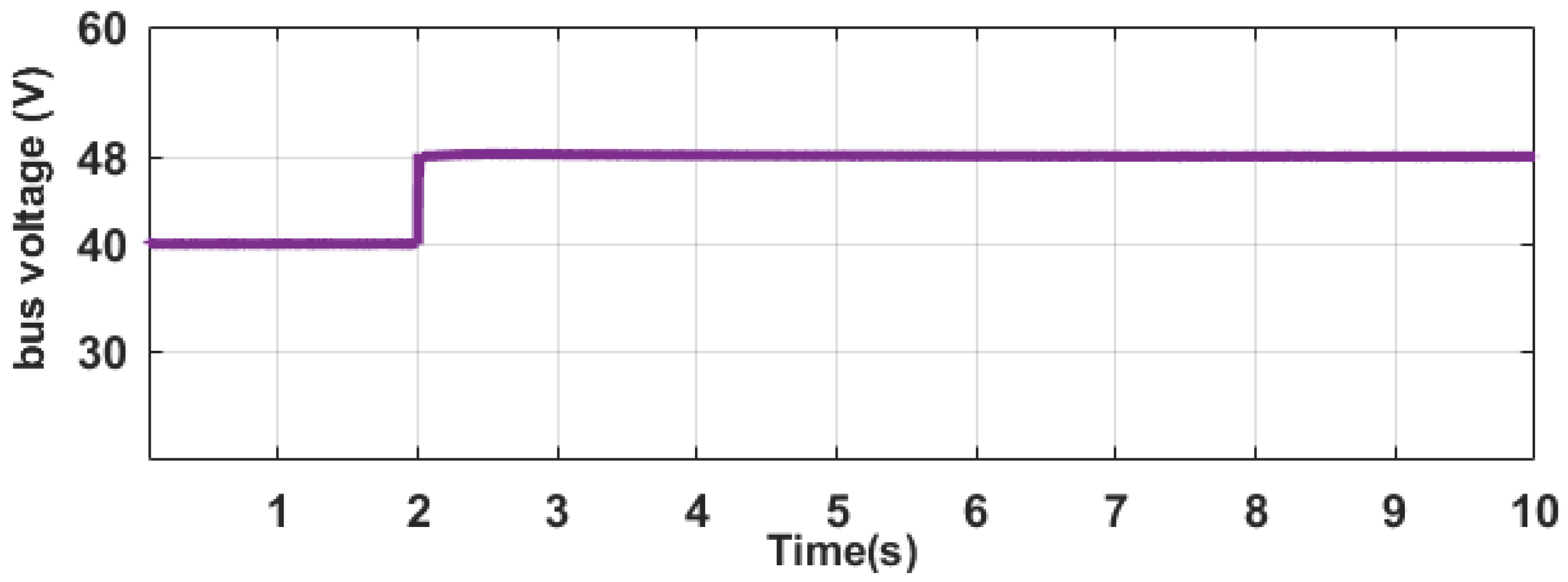
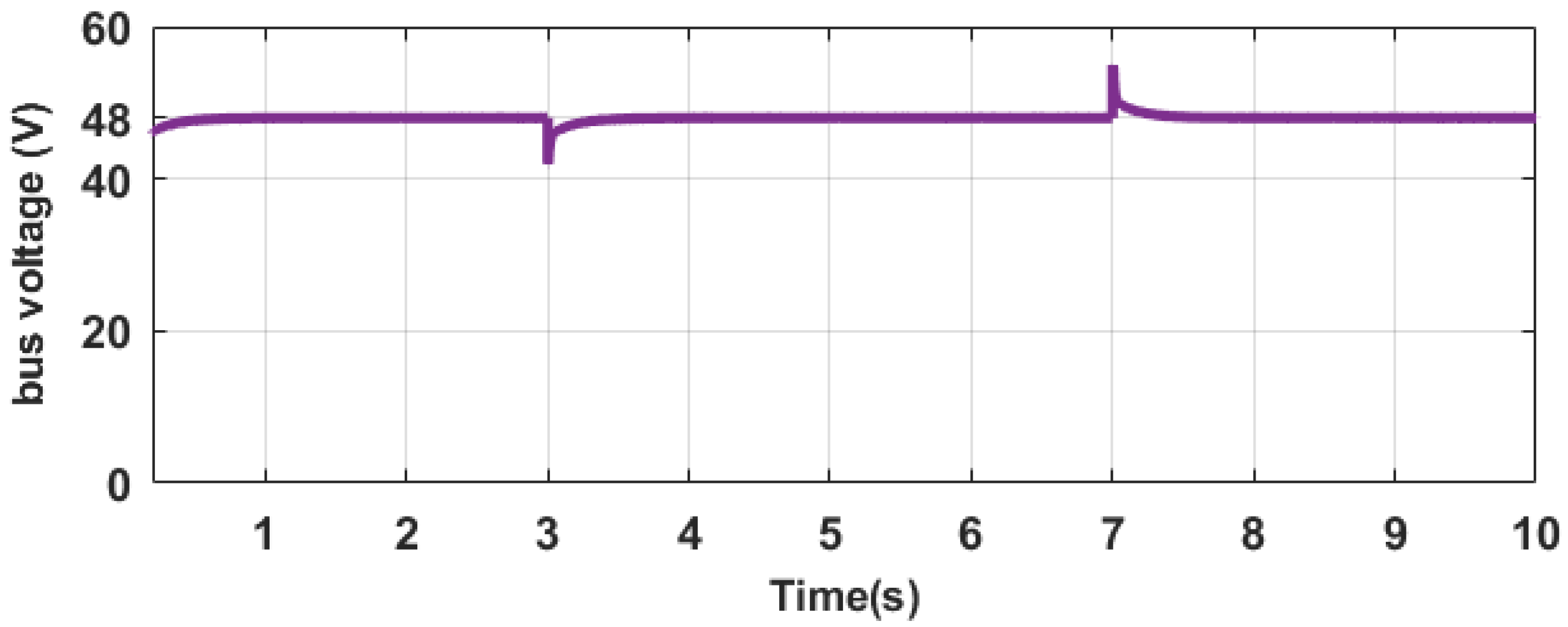
5.3.1. Voltage Restoration and Current Distribution Test
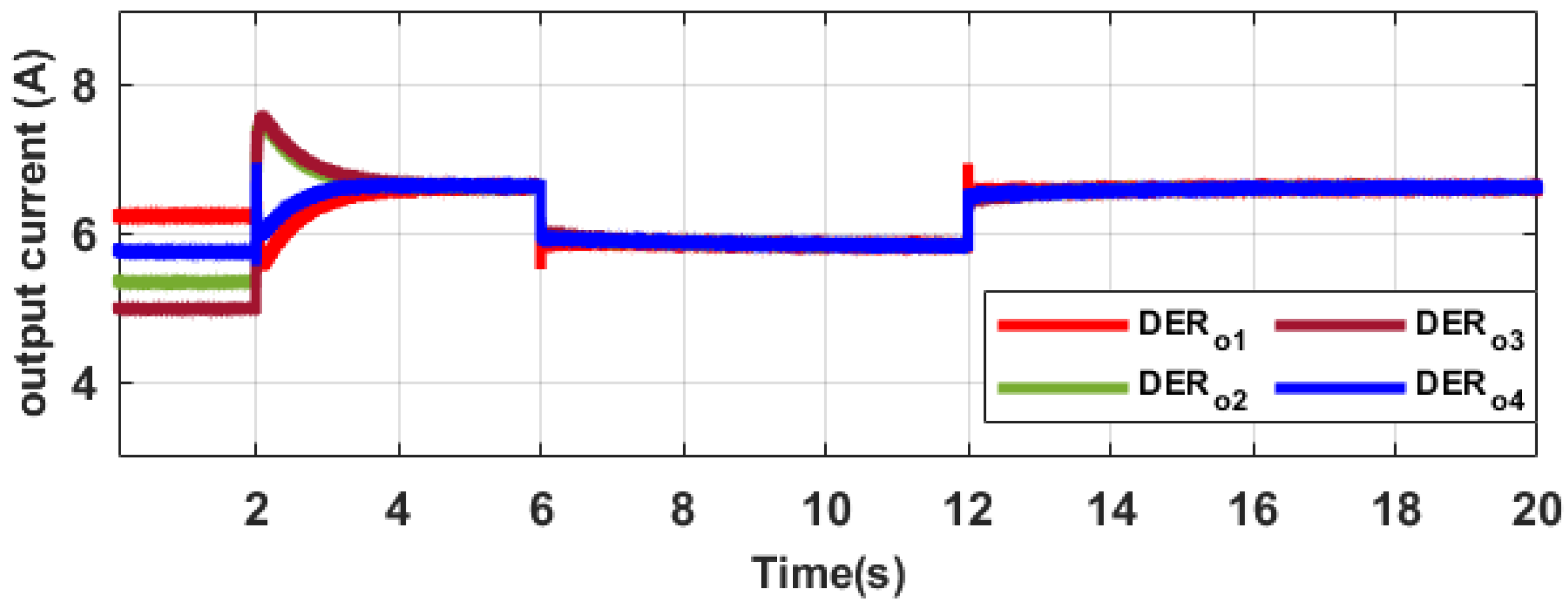
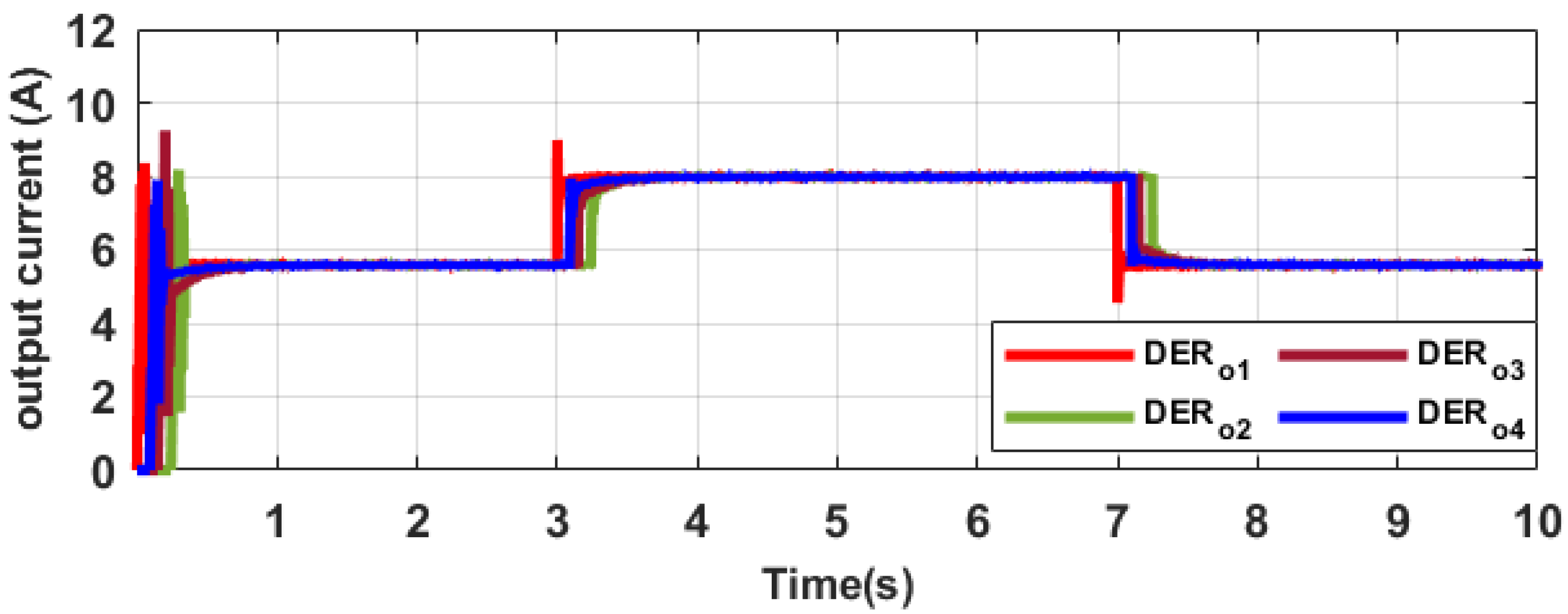
5.3.2. Proposed Secondary Control Performance under Load Variations
5.3.3. Proposed Secondary Control Performance under Communication Time Delays
5.4. Comparison with other Distributed Secondary Control Approach
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RESs | Renewable Energy Sources |
| MGs | Microgrids |
| AC | Alternating Current |
| DERs | Distributed Energy Resources |
| MHO | Meta-Heuristic Optimization |
| PSO | Particle Swarm Optimization |
| FFA | Firefly Alorithim |
| DC | Direct Current |
| FFA–PSO | Firefly–Particle Swarm Optimization |
| SS | State-Space |
| CPL | Constant Power Load |
References
- Cervantes, X.L.G. La Generación Distribuida y las Fuentes Renovables de energía en el Ecuador. Dominio Cienc. 2021, 7, 884–895. [Google Scholar]
- Ullah, Z.; Elkadeem, M.; Kotb, K.M.; Taha, I.B.; Wang, S. Multi-criteria decision-making model for optimal planning of on/off grid hybrid solar, wind, hydro, biomass clean electricity supply. Renew. Energy 2021, 179, 885–910. [Google Scholar] [CrossRef]
- Moya, A.P.; Pazmiño, P.J.; Llanos, J.R.; Ortiz-Villalba, D.; Burgos, C. Distributed Secondary Control for Battery Management in a DC Microgrid. Energies 2022, 15, 8769. [Google Scholar] [CrossRef]
- Pata, U.K. Linking renewable energy, globalization, agriculture, CO2 emissions and ecological footprint in BRIC countries: A sustainability perspective. Renew. Energy 2021, 173, 197–208. [Google Scholar] [CrossRef]
- Chen, C.; Pinar, M.; Stengos, T. Determinants of renewable energy consumption: Importance of democratic institutions. Renew. Energy 2021, 179, 75–83. [Google Scholar] [CrossRef]
- Rodriguez, M.; Espin, V.; Arcos-Aviles, D.; Martinez, W. Energy management system for an isolated microgrid based on Fuzzy logic control and meta-heuristic algorithms. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 462–467. [Google Scholar]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Kumar Verma, B.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar] [CrossRef]
- Gholami, M.; Pisano, A. Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units. Electricity 2022, 3, 33–50. [Google Scholar] [CrossRef]
- Ali, S.; Shengxue, T.; Jianyu, Z.; Ali, A.; Nawaz, A. An implementation of parallel buck converters for common load sharing in DC microgrid. Information 2019, 10, 91. [Google Scholar] [CrossRef]
- Jha, S.; Hussain, I.; Singh, B.; Mishra, S. Optimal operation of PV-DG-battery based microgrid with power quality conditioner. IET Renew. Power Gener. 2019, 13, 418–426. [Google Scholar] [CrossRef]
- Lasabi, O.; Swanson, A.; Jarvis, L.; Aluko, A.; Brown, M. Enhanced Distributed Non-Linear Voltage Regulation and Power Apportion Technique for an Islanded DC Microgrid. Appl. Sci. 2023, 13, 8659. [Google Scholar] [CrossRef]
- Rezaei, O.; Mirzapour, O.; Panahazari, M.; Gholami, H. Hybrid AC/DC provisional microgrid planning model considering converter aging. Electricity 2022, 3, 14. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC microgrid planning, operation, and control: A comprehensive review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Aluko, A.; Buraimoh, E.; Oni, O.E.; Davidson, I.E. Advanced distributed cooperative secondary control of Islanded DC Microgrids. Energies 2022, 15, 3988. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Control strategies of DC microgrids cluster: A comprehensive review. Energies 2021, 14, 7569. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Lee, H.H. A survey on cooperative control strategies for DC microgrids. Neurocomputing 2022, 486, 225–236. [Google Scholar] [CrossRef]
- Li, M.; Zhang, D.; Lu, S.; Tang, X.; Phung, T. Differential evolution-based overcurrent protection for DC microgrids. Energies 2021, 14, 5026. [Google Scholar] [CrossRef]
- Modu, B.; Abdullah, M.P.; Sanusi, M.A.; Hamza, M.F. DC-Based microgrid: Topologies, control schemes, and implementations. Alex. Eng. J. 2023, 70, 61–92. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity 2022, 3, 19. [Google Scholar] [CrossRef]
- Madurai Elavarasan, R.; Ghosh, A.; Mallick, K.T.; Krishnamurthy, A.; Saravanan, M. Investigations on performance enhancement measures of the bidirectional converter in PV–wind interconnected microgrid system. Energies 2019, 12, 2672. [Google Scholar] [CrossRef]
- Yaqub, R. Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement. Electricity 2021, 2, 20. [Google Scholar] [CrossRef]
- Sahoo, S.; Mishra, S.; Fazeli, S.M.; Li, F.; Dragičević, T. A distributed fixed-time secondary controller for DC microgrid clusters. IEEE Trans. Energy Convers. 2019, 34, 1997–2007. [Google Scholar] [CrossRef]
- Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cardenas-Dobson, R.; Martinez-Gomez, M.; Saez, D. Distributed control strategies for microgrids: An overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
- Lasabi, O.; Swanson, A.; Jarvis, L.; Aluko, A. Dynamic Distributed Collaborative Control for Equitable Current Distribution and Voltage Recovery in DC Microgrids. Energies 2023, 16, 6657. [Google Scholar] [CrossRef]
- Wan, Q.; Zheng, S. Distributed cooperative secondary control based on discrete consensus for DC microgrid. Energy Rep. 2022, 8, 8523–8533. [Google Scholar] [CrossRef]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2019, 7, 227–242. [Google Scholar] [CrossRef]
- Guo, F.; Wang, L.; Wen, C.; Zhang, D.; Xu, Q. Distributed voltage restoration and current sharing control in islanded DC microgrid systems without continuous communication. IEEE Trans. Ind. Electron. 2020, 67, 3043–3053. [Google Scholar] [CrossRef]
- Liu, X.K.; Wang, Y.W.; Lin, P.; Wang, P. Distributed supervisory secondary control for a DC microgrid. IEEE Trans. Energy Convers. 2020, 35, 1736–1746. [Google Scholar] [CrossRef]
- Dong, M.; Li, L.; Nie, Y.; Song, D.; Yang, J. Stability analysis of a novel distributed secondary control considering communication delay in DC microgrids. IEEE Trans. Smart Grid 2019, 10, 6690–6700. [Google Scholar] [CrossRef]
- Guo, F.; Huang, Z.; Wang, L.; Wang, Y. Distributed event-triggered voltage restoration and optimal power sharing control for an islanded DC microgrid. Int. J. Electr. Power Energy Syst. 2023, 153, 109308. [Google Scholar] [CrossRef]
- Yuan, Q.F.; Wang, Y.W.; Liu, X.K.; Lei, Y. Distributed fixed-time secondary control for DC microgrid via dynamic average consensus. IEEE Trans. Sustain. Energy 2021, 12, 2008–2018. [Google Scholar] [CrossRef]
- Liu, X.K.; Jiang, H.; Wang, Y.W.; He, H. A distributed iterative learning framework for DC microgrids: Current sharing and voltage regulation. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 119–129. [Google Scholar] [CrossRef]
- Keshta, H.E.; Saied, E.M.; Malik, O.P.; Bendary, F.M.; Ali, A.A. Fuzzy PI controller-based model reference adaptive control for voltage control of two connected microgrids. IET Gener. Transm. Distrib. 2021, 15, 602–618. [Google Scholar] [CrossRef]
- Aydilek, I.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Kaveh, A.; Zakian, P. Improved GWO algorithm for optimal design of truss structures. Eng. Comput. 2018, 34, 685–707. [Google Scholar] [CrossRef]
- Sadeeq, H.T.; Abdulazeez, A.M. Giant trevally optimizer (GTO): A novel metaheuristic algorithm for global optimization and challenging engineering problems. IEEE Access 2022, 10, 121615–121640. [Google Scholar] [CrossRef]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. Elephant clan optimization: A nature-inspired metaheuristic algorithm for the optimal design of structures. Appl. Soft Comput. 2021, 113, 107892. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Zuščák, T. A new human-inspired metaheuristic algorithm for solving optimization problems based on mimicking sewing training. Sci. Rep. 2022, 12, 17387. [Google Scholar] [CrossRef]
- Oyelade, O.N.; Ezugwu, A.E.S.; Mohamed, T.I.; Abualigah, L. Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm. IEEE Access 2022, 10, 16150–16177. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Khan, A.; Hizam, H.; bin Abdul Wahab, N.I.; Lutfi Othman, M. Optimal power flow using hybrid firefly and particle swarm optimization algorithm. PLoS ONE 2020, 15, e0235668. [Google Scholar] [CrossRef] [PubMed]
- Bilal; Pant, M. Parameter Optimization of Water Distribution Network–A Hybrid Metaheuristic Approach. Mater. Manuf. Process. 2020, 35, 737–749. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Mijatovic, N.; Dragičević, T. A robust cooperative distributed secondary control strategy for DC microgrids with fewer communication requirements. IEEE Trans. Power Electron. 2023, 38, 271–282. [Google Scholar] [CrossRef]
- Ghanbari, N.; Bhattacharya, S.; Mobarrez, M. Modeling and stability analysis of a DC microgrid employing distributed control algorithm. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Zhang, N.; Yang, D.; Zhang, H.; Luo, Y. Distributed control strategy of DC microgrid based on consistency theory. Energy Rep. 2022, 8, 739–750. [Google Scholar] [CrossRef]
- Almabrok, A.; Psarakis, M.; Dounis, A. Fast tuning of the PID controller in an HVAC system using the big bang–big crunch algorithm and FPGA technology. Algorithms 2018, 11, 146. [Google Scholar] [CrossRef]
- Chandrasekar, A.; Sengupta, S.; Hingane, S.; Gururaja, C.; Pandit, S. Comparative Analysis of Model Predictive Control (MPC) and Conventional Control in Supervisory Controller of a Retrofit HEV; Report 0148-7191, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]







| Nominal Bus Voltage | 48 V | |
| Voltage Source | 100 V | |
| Switching Frequency | 10 kHz | |
| Filter Inductance and Capacitance | 10 mH, 200 F | |
| Load | 3 , 5 , 5 | |
| Hybrid FFA–PSO Algorithm Parameters | ||
| Maximum no. of Iterations | 300 | |
| Population Size | 50 | |
| Inertia Constants | , | 0.9, 0.5 |
| Maximum Velocity | 0.1() | |
| Minimum Velocity | ||
| Acceleration Coefficients | = | 1.49 |
| Attractiveness at Origin | 2 | |
| Absorption Coefficient | 1 | |
| Randomization Factor | 0.5 | |
| No. of Design Variables | 1 | |
| Primary Controls | ||
| Droop Resistance | 1 | |
| Current Loop | 2.5, 5 | |
| Voltage Loop | 0.248, 2 |
| −158.35 | −278.68 + i347.11 | |
| 8.65 + i105.21 | −278.68 − i347.11 | |
| 8.65 − i105.21 | −15.60 | |
| −10.87 | −9.54 | |
| −5.2 + i75.40 | −11.38 | |
| −5.2 + i75.40 | −1.03 + i5.08 | |
| −3.8 + i56.54 | −1.03 − i5.08 | |
| −3.8 + i56.54 | −367.94 | |
| −3.41 | − 367.94 | |
| −3.41 | −1.03 + i5.08 | |
| — | −1.03 − i5.08 | |
| — | −5.49 | |
| — | −5.49 |
| Voltage Source | 100 V | |
| Switching Frequency | 10 kHz | |
| Nominal Bus Voltage | 48 V | |
| Line Resistance | 0.2 , 0.3 , 0.5 , 0.6 | |
| Filter Capacitance and Inductance | 120 F, 20 mH | |
| Constant Power Load | 200 W | |
| Resistive Load | 3 , 5 , 5 | |
| Primary Controls | ||
| Droop Resistance | 1 | |
| Current Loop | 0.05, 148 | |
| Voltage Loop | 0.248, 36 | |
| Secondary Controls | ||
| Coefficient of Voltage Deviation | 1.25 | |
| Coefficient of Current Deviation | 7.5 |
| Control Objectives | Proposed | ||||
|---|---|---|---|---|---|
| Voltage Regulation | 2 s | 1.3 s | 1.72 s | 3 s | ≤0.2 s |
| Current Sharing | 2.8 s | 1.5 s | 2 s | 3.4 s | ≤1.4 s |
| Robustness | low | high | moderate | low | very high |
| Implementation Complexity | simple | complex | simple | simple | complex |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lasabi, O.; Swanson, A.; Jarvis, L.; Aluko, A.; Goudarzi, A. Coordinated Hybrid Approach Based on Firefly Algorithm and Particle Swarm Optimization for Distributed Secondary Control and Stability Analysis of Direct Current Microgrids. Sustainability 2024, 16, 1204. https://doi.org/10.3390/su16031204
Lasabi O, Swanson A, Jarvis L, Aluko A, Goudarzi A. Coordinated Hybrid Approach Based on Firefly Algorithm and Particle Swarm Optimization for Distributed Secondary Control and Stability Analysis of Direct Current Microgrids. Sustainability. 2024; 16(3):1204. https://doi.org/10.3390/su16031204
Chicago/Turabian StyleLasabi, Olanrewaju, Andrew Swanson, Leigh Jarvis, Anuoluwapo Aluko, and Arman Goudarzi. 2024. "Coordinated Hybrid Approach Based on Firefly Algorithm and Particle Swarm Optimization for Distributed Secondary Control and Stability Analysis of Direct Current Microgrids" Sustainability 16, no. 3: 1204. https://doi.org/10.3390/su16031204
APA StyleLasabi, O., Swanson, A., Jarvis, L., Aluko, A., & Goudarzi, A. (2024). Coordinated Hybrid Approach Based on Firefly Algorithm and Particle Swarm Optimization for Distributed Secondary Control and Stability Analysis of Direct Current Microgrids. Sustainability, 16(3), 1204. https://doi.org/10.3390/su16031204










